Abstract
We propose here optical resonance imaging (ORI), a direct optical analog to magnetic resonance imaging (MRI). The proposed pulse sequence for ORI maps space to time and recovers an image from a heterodyne-detected third-order nonlinear photon echo measurement. As opposed to traditional photon echo measurements, the third pulse in the ORI pulse sequence has significant pulse-front tilt that acts as a temporal gradient. This gradient couples space to time by stimulating the emission of a photon echo signal from different lateral spatial locations of a sample at different times, providing a widefield ultrafast microscopy. We circumvent the diffraction limit of the optics by mapping the lateral spatial coordinate of the sample with the emission time of the signal, which can be measured to high precision using interferometric heterodyne detection. This technique is thus an optical analog of MRI, where magnetic-field gradients are used to localize the spin-echo emission to a point below the diffraction limit of the radio-frequency wave used. We calculate the expected ORI signal using 15 fs pulses and 87° of pulse-front tilt, collected using f/2 optics and find a two-point resolution 275 nm using 800 nm light that satisfies the Rayleigh criterion. We also derive a general equation for resolution in optical resonance imaging that indicates that there is a possibility of superresolution imaging using this technique. The photon echo sequence also enables spectroscopic determination of the input and output energy. The technique thus correlates the input energy with the final position and energy of the exciton.
Keywords: Ultrafast Microscopy, Superresolution Imaging, Spectral Interferometry, Exciton Imaging, Pulse-front Tilt
The diffraction limit theoretically constrains an imaging system’s spatial resolution,1,2 and yet several approaches can resolve structures below the diffraction limit. Near-field techniques require having a small aperture, or scattering material in close proximity (<10 nm) to the sample to measure the electromagnetic fields before they propagate into the radiation zone,3–5 while in the far-field some techniques collect fluorescence from a diffuse array of emitters and localize the source to a sub-diffraction-limited spot.6–8 Other far-field fluorescence techniques require illumination of the widefield image with a structured laser field to generate interference effects in the illumination that effectively illuminate a sub-diffraction limited slice of the sample.9,10 All approaches require milliseconds to seconds of collection time to produce an image. Thus, an apparatus can overcome the diffraction limit with these techniques but cannot simultaneously observe dynamical processes on timescales faster than the acquisition time.11 Faster dynamics, such as those on the femtosecond (fs) to picosecond (ps) timescale, play a critical role in diverse physical and chemical processes ranging from energy transfer in photosynthetic light harvesting12–14 and excitonic diffusion in materials,15–17 to photochemistry18,19 and the molecular dynamics of liquids.20–22 ORI will allow access to these faster dynamics.
Leveraging time to gain spatial information is always necessary to beat the diffraction limit in the optical regime. For example, the first successful approach to far-field, sub-diffraction-limited imaging in the optical region of the spectrum exploited the time domain by stimulating emission prior to fluorescence. STimulated-Emission Depletion (STED) microscopy7,23 makes use of a diffraction-limited excitation beam that is followed in short succession by a toroidal depletion beam. The depletion beam stimulates emission from the outside edge of the diffraction-limited spot, leaving an excitation area that is smaller than that originally illuminated by the excitation beam, thus decreasing the point-spread function and enabling superresolution imaging of diverse systems ranging from cells to nanomaterials.24 Fluorescence-based superresolution techniques such as PALM6 or STORM8 use the spatial information from different emitters collected at different times to produce a superresolution image, whereas near-held techniques, like NSOM, as the name implies, must raster scanning over different positions at different times.
Superresolution at radio frequencies, also known as Magnetic resonance imaging (MRI), has shown that it is possible to decouple an image’s resolution from the wavelength of light by creating spatially-defined magnetic held gradients across a sample.25 The gradients change the Larmor frequency of the precessing nuclear spins (and thus the emitted photon energy) as a function of spatial position.26,27 The diffraction limit does not constrain the differences in photon energy, which can be measured to higher precision than their source could be imaged with optics. As a result, MRI maps a spatial coordinate to energy and uses meter-long light waves to generate images with millimeter-scale resolution, which has transformed the helds of medicine and neuroscience.28
In this work, we propose an optical analog of MRI to achieve widefield, sub-diffraction-limited imaging using ultrashort (femtosecond) laser pulses, which we call optical resonance imaging (ORI). To gain information about dynamics faster than the nanosecond timescale of fluorescence, ORI employs a three-pulse, photon-echo pulse sequence to stimulate emission from the sample. Unlike other photon-echo measurements, the stimulating pulse has significant pulse-front tilt. As such, ORI maps a lateral spatial coordinate of the sample to the emission time of the signal. The ultrashort character of the tilted pulse at the sample ensures that the emission of a photon-echo signal will occur at different times. The ultrafast temporal resolution makes sub-diffraction-limited imaging possible by measuring a difference in arrival time at the detector of different parts of the signal with high precision. In essence, we exploit the same approach as in MRI, but instead of mapping space to energy, we map space to the time of emission. Being Fourier conjugates for electromagnetic fields, both time and energy allow us to escape the diffraction limit in a similar way, while the diffraction limit still determines time-independent, wave-like properties of the EM field such as the focal-spot size and pulse-front tilt that can be generated. We discuss below the conditions necessary for optical resonance imaging, and the possibilities for widefield, superresolution ultrafast imaging.
Results and Discussion
Two key concepts from ultrafast nonlinear spectroscopy enable ORI measurements – the stimulated emission of a photon echo, and interferometric heterodyne detection. A photon echo results from a third-order nonlinear optical process.29,30 Three separate interactions of the sample with an optical electric field (in this case, three laser pulses) generate a polarization, P(3) (τ, T, tR), in the material that emits a signal, , where τ is the time between pulses 1 and 2, T is the time between pulses 2 and 3, and tR is the time after pulse 3 interacts with the sample. Third-order perturbation theory ultimately shows that P(3) (τ, T, tR) is the time-ordered convolution of the material response function, R(3) (τ, T, tR), with the three laser pulses that interact with the sample at different times. In the impulsive limit, where the laser pulse duration is much shorter than the timescale of the dynamics of interest, the laser pulses can be thought of as delta functions, yielding a direct measurement of the response function. The photon-echo response can be isolated experimentally from other contributions to by using a phase-matching geometry of the input beams that selects for the rephasing Liouville space pathways.31,32
Beams with pulse-front tilt (PFT) have a non-separable coupling between space and time that results in the intensity front of the beam having an angle relative to the phase front.33 Fig. 1 shows the calculated intensity profile focused at the sample position of a beam that has PFT, with γ the angle between the pulse-front and the phase front. The electric field of a beam containing PFT can be written as
| (1) |
where Ex is the spatial component in a direction perpendicular to the direction of propagation, Et is the temporal component, and p is the coupling term representing PFT. Thus, the arrival time of the electric field is also a function of the position along the beam. When a laser pulse with PFT is incident on a sample, different parts of the pulse interact with different parts of the sample at different times. This can be thought of as a time-dependent local spot size that sweeps across the diffraction-limited, time-integrated focal spot.34
Figure 1.
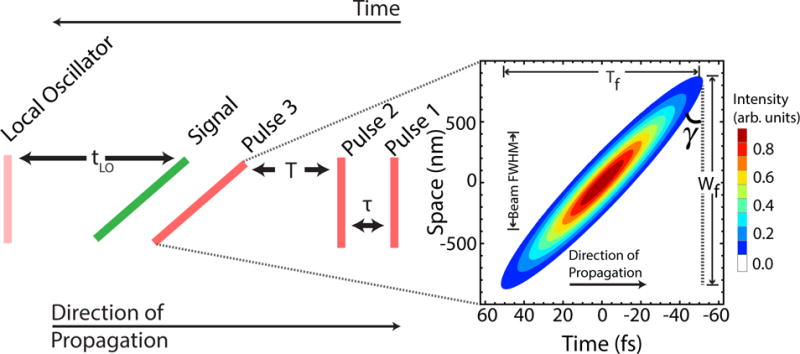
The pulse sequence for ORI. Pulses 1 and 2 are separated by time τ and prepare a population state which evolves for the waiting time T. pulse 3 stimulates emission of a photon echo from the sample. Since pulse 3 has significant pulse-front tilt, different parts of the sample will emit an echo at different times. The signal is emitted some time after pulse 3 and is shown in green. The right portion of the figure shows a plot of the calculated spatial and temporal extent of the third pulse with pulse-front tilt, focused at the sample using f/0.5 optics. The contours are plotted for the pulse intensity. A representative phase front of the pulse is illustrated by the dashed black line, and the angle γ defines the pulse-front tilt, Wf is the focused spot size and Tf is the length swept out by the pulse-front tilt. At the focus, the FWHM of the tilted pulse in the direction of propagation is 15 fs, the same as for the flat pulses (pulses 1 & 2).
The pulse sequence needed for ORI can also be seen in Fig. 1. The pulse order and phasematching condition are identical to a photon-echo pulse sequence used in 2D electronic or infrared spectroscopy.31 The ORI pulse sequence differs from the sequence used for a conventional photon echo in that pulses 1 and 2 have no PFT, while the third pulse that stimulates the coherent emission and generates the photon-echo signal has a large angle of PFT. The PFT of the third pulse ensures that emission from different parts of the sample is stimulated at different times. This approach introduces a coupling between space and time into the third-order response of the system such that R(3) (τ, T − px, tR).35
To make this coupling between space and time possible, one must deliver a pulse with PFT to the sample and have it retain its ultrashort character. One way to generate PFT can be found if we consider Eqn. 1. If we take the fourier transform of both space and time we find
| (2) |
where we have made two uses of the shift theorem of Fourier analysis.36 Clearly then, dω/dk = p, which is closely related to angular dispersion, dθ0/dk = p/k0, where θ0 is defined as the propagation angle.33 The angular dispersion gained by a beam after diffracting off of a grating will generate PFT when that beam is re-imaged. Experimental results in the literature have shown that when the grating generating a tilted pulse is appropriately imaged, the imaged pulse retains its femtosecond character across its entire focal spot.37 Though not relevant to ORI, it should be noted that not all electric fields can be written as in Eqn. 1, so PFT can also be generated from the product of spatial chirp and group velocity dispersion in a beam.33
We calculated the tilted beam profile of pulse 3 at the focus of an image producing optical system by propagating a Gaussian beam through an optical system calculated using the Kostenbauder extension to ray-transfer matrices.38 The result is shown in the right portion of Fig. 1. The Kostenbauder matrices allow us to follow spatio-temporal couplings as a beam propagates through an optical system. Traditional ray-transfer linear algebra involves 2-dimensional vectors (containing position and angle) and 2 × 2 ABCD matrices that represent the operations performed by different optical elements.39,40 Kostenbauder extended this analysis to include frequency and time using 4-dimensional vectors and a 4 × 4 matrix:
| (3) |
where A,B,C,D are defined in the same way as in the 2 × 2 ray transfer matrices. A Gaussian beam can be propagated through an optical system where the optical elements are represented by these matrices and the explicit inclusion of frequency and time enable calculations of beams with spatio-temporal coupling. The pulse plotted in Fig. 1 was calculated by starting with an initial beam radius of 5 mm, and a 15 fs FWHM pulse centered at 800 nm. A lens matrix transformation allows us to calculate the beam spot at the grating position. A grating with 2000 lines/mm and an incident angle of 42° was used to generate angular dispersion in the calculated field. This calculated electric field was propagated through an optical system consisting of two lenses spaced by the sum of their focal lengths, and the result shows that an ultrashort tilted pulse can be delivered to the focus of an optical system. A tilted pulse can only be focused down to the diffraction limit, denoted as Wf in Fig. 1. However, the pulse-front tilt ensures that sub-diffraction-limited parts of the pulse will interact with the sample at different times.34 In essence, we exploit the interference between different colors incident from different angles to generate a transform-limited pulse over a sub-diffraction limited area. More details about this calculation are available in the methods section and supplemental information.
Since the angle of PFT, γ, is defined as the angle of the intensity front of the pulse with respect to the phase fronts, we can calculate γ from the beam profile shown in Fig. 1 via the inverse tangent. We find , where Wf and Tf are labeled in Fig. 1, and correspond to the size of the focused spot and the time it takes the beam to sweep over that spot respectively; c is the speed of light. The successful encoding of space into the time-dependent polarization, P(3)(γ, T − px, tR), in the sample ensures that different parts of the sample will emit a photon echo at different times. We note that the three time intervals upon which P(3) depends result from the different arrival times of three independent ultrafast pulses. Thus, in addition to the spatial information, P(3) also contains all the spectral information that is contained in a measurement such as 2D electronic spectroscopy provided that all time intervals are scanned.
Interferometric heterodyne detection of the signal field, , measures the precise arrival time of the signal compared to a local-oscillator (LO) reference pulse.41,42 As in 2DES, a set of optics, often in a 4f imaging configuration, collect the emitted signal and focus both the signal and LO pulse into a spectrometer. The spectrometer converts the time-domain signals into the frequency domain and the resultant interference pattern between the LO and the signal is measured on a square-law detector. The frequency-domain signal on the detector can be expressed as
| (4) |
| (5) |
| (6) |
where ϕ is the phase difference between and ELO, and we used the shift theorem of Fourier analysis to go from Eq. (4) to Eq. (5).36 We note that if ϕ is nonzero, it can be set to zero through a phasing procedure in post-processing of the data.43 The order of operations, a Fourier transform followed by taking the absolute square, reflects the experimental detection process, and ILO and Isig are the intensity of the LO and the signal pulses, respectively. The Isig contribution is weak enough that it does not contribute to the measured signal, and ILO produces a constant signal that can be removed experimentally in a variety of ways. Lock-in detection can remove this contribution, as can filtering in the conjugate Fourier domain (the time domain) of the signal, tω. In this domain, we can think of ILO as interference between ELO with itself, and this homodyne process appears at time tω = 0. The measured interference between ELO(ω) and is modulated by the difference in arrival time between the LO and the signal, and appears at time tω = tLO. As such, this interference pattern provides a direct measurement of the time between the LO and the signal. In addition, as long as tLO is greater than zero, we can isolate the final term in Eq. (6) that contains the information about the third-order molecular response of the sample.44
In an optical resonance imaging measurement, interferometric heterodyne detection allows us to discriminate between arrival times of signals from different parts of the sample. Repeating the same mathematical analysis above for a signal with PFT we have
| (7) |
| (8) |
where we assume ϕ = 0.
The value ELO(ω) is simply the amplitude at a given frequency and it can be found from the measurement of ILO, since ILO = |ELO (ω)|2. Using this information in combination with the simplification of S(ω) discussed above, we can write the signal that contains our spatial information as
| (9) |
where in the last step we set tLO = 0. In an ORI measurement, tLO represents the difference in arrival time between the LO pulse and the start of the tilted signal pulse as shown in Fig. 1. Since tLO can be thought of as a constant phase, we set it equal to zero.
Generating the final image can be accomplished with a final Fourier transform of Eqn. (9) back to the time domain
| (10) |
| (11) |
| (12) |
where Simage(t)_ corresponds to one side of the time axis generated by the Fourier transform. We can ignore the other side of the axis since it contains identical information because the signal field is a real valued function. Thus, the spatial information encoded into our signal can be extracted from the measured experimental data. We note that since the bandwidth of the transition that generates is not infinite, it will provide a fundamental limit on the resolution of the instrument.
To assess the feasibility of this approach, we simulated the electric field emitted by a finite number of point emitters. We divided our sample into 5 nm blocks. Each block represented a dipole (e.g. a collection of molecules or atoms) that interacted with pulses 1 and 2, placing the system in an excited state from which pulse 3 stimulated emission. The size of the illuminated area was determined by Wf from Fig. 1, as we can set the spot size of beams 1 & 2 to be larger than Wf. The magnitude of a photon echo signal scales as
| (13) |
so if |E1| and |E2| are roughly constant, then the Gaussian width across Wf scaled the magnitude of the stimulated emission generated by pulse 3.
The emitting polarization in the sample was approximated as a dipole source because the size of a single emitting block is much smaller than the wavelength of light. We simulated a dipole field with a carrier-wave wavelength of 800 nm, and a Gaussian temporal envelope that has a FWHM of 15 fs in the paraxial approximation, where a spherical wave is represented by a complex quadratic phase. A 15 fs pulse duration is equivalent to a transition with 60 nm of bandwidth centered at 800 nm. We calculated the electric field in the spatial dimension with PFT, perpendicular to the optical axis as a function of time. To simulate what the signal will look like at the detector, we propagate the emitted dipole field through an f/2 optical imaging system using Fourier optics to simulate focusing the signal into our spectrometer and then perform the operations outlined mathematically above that simulate interferometric heterodyne detection with a 15 fs FWHM LO pulse.
The results of this simulation, shown in Fig. 2, were calculated for a pair of emitters spaced by 275 nm. This separation satisfies the Rayleigh criterion for identifying distinct point sources. The image produced by the ORI simulation is plotted as the red trace in Fig. 2. The black lines plotted in the figure correspond to where the expected peak centers are based on the simulation settings. Fig. 2 also shows the diffraction-limited image generated in these calculations.
Figure 2.
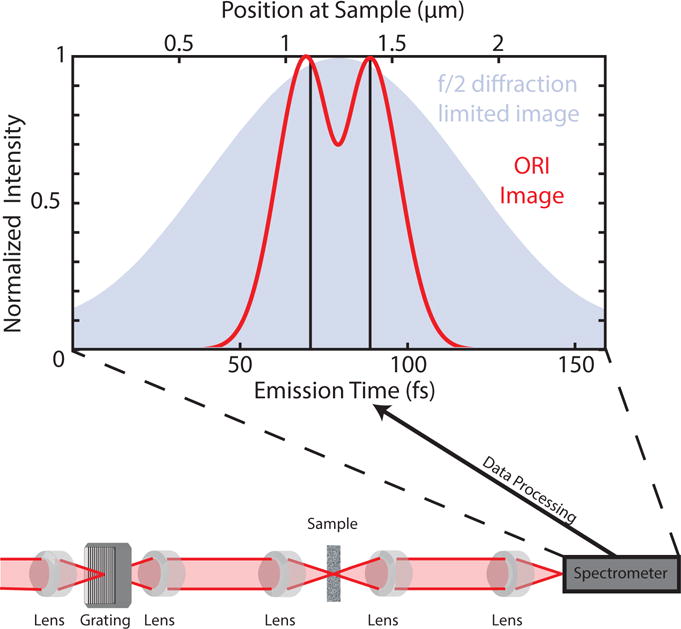
The calculated ORI image and diffraction-limited image. The ORI image is in red, with the dipole source positions identified with black lines. The the difference in the peak centers returns the spacing of the emitters. The diffraction-limited image of a set of individual, incoherent emitters located at the positions of the red lines and imaged with f/2 optics is shown in the filled trace behind. The bottom portion of the figure shows a possible optical apparatus that could generate ORI signals.
The result in Fig. 2 demonstrates that ORI can resolve structures below the diffraction limit of the optics used in the experiment. As clearly seen in Fig. 2 for f/2, diffraction-limited imaging only yields one feature, while ORI can resolve two features using these optics, spaced below the diffraction limit of f/0.5 optics. The limits placed on spatial resolution then become dependent upon the separation in time of the emitted signal from different parts of the sample under study. In any real optical system, the physical optics cannot collect all possible steradians of emitted signal. However, in ORI, if the signals are measurably separated in time, this will determine the resolution and not the numerical aperture of the collection optics. As such, for the simulation of the signal shown in Fig. 2, we can calculate a smaller number of solid angles, and because of the spacing of the emitted spherical waves in time, accurately measure the spacing of the two point emitters below the diffraction limit.
Optical resonance imaging can overcome the diffraction limit of the optics used and offers the potential for superresolution imaging. It is possible to write a general equation that specifies the resolution of an image generated with ORI. Starting with the definition of PFT from Eqn. 1 we have
| (14) |
| (15) |
where c is the speed of light, and Tf and Wf are defined in Fig. 1. To generate an image, the instrument must be able to distinguish between different points emitted by the sample as a function of time. The maximum possible number of independent time points that can be measured across the emitted signal, N, can be written as
| (16) |
where τs is the FWHM of the signal. This is true as long as the pulse duration of the LO pulse is as short or shorter than the temporal duration of the emitted signal. Since different portions of the sample emit at different times, the lateral spatial resolution (lr) of the experiment can then be thought of as the number of independent points measured across the focused spot size
| (17) |
We can then make use of Eqn. 15 to find that
| (18) |
The result in eqaution 18 shows that the resolution in an ORI experiment only depends upon the pulse front tilt applied and the temporal duration of the sample response (put equivalently, the emission bandwidth of the sample). As such the resolution of an ORI image will improve with larger PFT and faster sample response. For the results discussed in this work, using f/0.5 optics to generate angle of γ equal to 87 degrees produces a PFT of 0.0636 fs·nm−1. For a value of τs = 15 fs, we find a resolution of 240 nm, independent of the wavelength of the light.
The value of p in Eqn. 18 is the PFT of the emitted signal. We have derived this result assuming that the PFT of pulse 3 is equal to the PFT of the emitted signal. The above result is quite general, implying that the PFT of the signal is independent of the method in which PFT is delivered to the sample. This presents opportunities to significantly improve the resolution if novel ways can be found to generate significant PFT of the emitted signal.
Conclusion
Excitons generated by the absorption of photons are routinely studied with nonlinear spectroscopy, however they cannot be imaged directly because techniques do not yet exist that have the requisite spatio-temporal resolution. Excitation imaging with ultrafast temporal resolution will offer new insights into the process of energy transfer and provide a tool to design and control how energy moves through materials.
Most experiments that can measure dynamics on femtosecond-to-nanosecond timescales remain diffraction-limited.15,45 Some recent work has demonstrated superresolution pump-probe microscopy; however, it is still limited to raster scanning a beam across the sample to generate an image.46 In comparison, ORI generates a widefield image since different parts of the sample emit at different times and contribute to different parts of the image. Resolution is thus decoupled from wavelength and is determined by the bandwidth of the emitter and pulsefront tilt emitted by the sample.
A single ORI experiment to extract spatial information from the sample can be performed for a fixed time intervals, τ, T, and tR. In this fashion, each acquisition will have temporal resolution on the order of the pulse-front tilt (ps), while a series of images will provide temporal resolution limited by the length of the untilted pulse (15 fs) or the molecular response function, whichever is longer. Changing the waiting time changes the population evolution, analogously to pump-probe spectroscopy (or microscopy). Instead of looking at spectral changes, ORI will image the changes in the sample. An optomechanical delay line can be used to control T out to the nanosecond regime.
Another exciting possibility results from the opportunity spectroscopic resolve the input and output energy. ORI is a third-order nonlinear experiment, therefore, the timing between all three pulses can be experimentally controlled and so a complete measurement of the ORI response function R(3) (τ, T, tR) will also contain spectral information. The ability to vary the time between pulses 1 and 2 is a degree of freedom unavailable in pump-probe microscopy, and Fourier transforming along this coordinate would provide spectral information along the “pump” axis in the same way as two-dimensional electronic spectroscopy. In addition, the heterodyne-detected data in the frequency domain provide the spectral information contained in the signal. Assignment of different spectral features is possible from two-dimensional electronic spectroscopy, and when combined with this extra experimental handle, optical resonance imaging thus correlates the input energy with the final position and energy of the exciton.
Methods
Kostenbauder Simulation of Pulse 3
The Kostenbauder matrix as defined in Eq. (3) can be used to calculate how how a variety of different optical elements affect the propagation of a Gaussian beam. Mirrors and distance propagators are defined in the same way as ABCD matrices with terms E, F, G, H, and I (as defined in Eq. (3)) equal to zero, since mirrors and lenses do not generate spatio-temporal couplings. A diffraction grating is represented as
| (19) |
where ψ and ϕ are the input and output angles defined relative to the grating surface in the same way as in reference.38 The simulated optical system consists of a focusing lens, a grating, and then a pair of lenses to image the grating onto the sample. The electric field of a Gaussian beam can be described in terms of Q-matrices34 such that
| (20) |
The initial Q-matrix, Qin is given by
| (21) |
where
| (22) |
| (23) |
and the off-diagonal terms are zero since the pulse begins with no spatio-temporal coupling. In the above equations, λ0 is the center wavelength, R(z) is the radius of curvature, w2(z) is the beam radius, β is the spatial chirp, and τi is the temporal FWHM of the pulse and we have no spatial chirp in the initial beam.
The Kostenbauder matrix representing the optical system can be found by taking the product of the optical elements
| (24) |
where 1 denotes a lens operator, d a distance propagation operator, and g the grating operator. Given Qin and the matrix K, we can calculate
| (25) |
The value calculated for Qsample can be fed into Eqn. 20 to calculate the electric field at the sample. The data plotted in Fig. 1 are the intensity of the electric field, |E(x, t)|2. The specific choices of values for for the simulation plotted in Fig. 1 can be found in Table 1. These calculations were carried out using Wolfram Mathematica 10.2.
Table 1.
List of Simulation Values
| Kostenbauder | Signal | ||
|---|---|---|---|
|
| |||
| Parameter | Value | Parameter | Value |
| gsp | 500 nma | τs | 15 fs |
| θin | 0.74 radb | Wf,FWHM | 814 nm |
| θout | 1.18 radb | zobs | 210 μm |
| ψ | π/2−0.74 rad | optical aperture (collection) | f/2 |
| ϕ | π/2 + 1.18 rad | spatial stepsize | 5 nm |
| λ0 | 800 nm | temporal stepsize | 10 as |
| w(0) | 5 mm | d | 1 Debye |
| R(0) | 108 mm | ||
| τi | 15 fs | ||
| optical aperture | f/0.5 | ||
| d1 = f of l1 | 125 mmc | ||
| d2 = f of l2 | 100 mmc | ||
| d3 = f of l3 | 25 mmc | ||
spacing between lines on diffraction grating.
θin and θout for diffraction grating defined relative to grating normal.
f in this context denotes the focal length of the lens.
Simulation of Emitted Signal
All calculations of the emitted signal were performed using MAT LABR2015a. The emitted third-order signal, , was modeled as a spherical wave that results from a single dipole emitter. We choose to make the approximation necessary for the use of Fourier optics, where a spherical wave can be represented by a quadratic phase term that approximates the spherical wavefronts as parabolic.47 In addition, since we only have pulse-front tilt in one spatial dimension, x, we choose to calculate the electric field in the x-dimension perpendicular to the direction of propagation, which is defined as z. The signal has a carrier frequency of 375 THz (center wavelength of 800 nm) and a Gaussian temporal envelope with a FWHM of 15 fs. As such, the signal from a given dipole and can be written as
| (26) |
where d is the dipole moment and k is the wavevector, z is the position along the optical axis of the system, and t′ is the time of dipole emission as determined by the pulse-front tilt. The origin of the x-axis is centered about the axis defined by z, and η corresponds to the distance of the dipole emitter from the optical axis. The last term accounts for the Gaussian nature of the spatial illumination of the sample by Pulse 3. Pulse-front tilt leads to emission of different parts of the sample at different times. The emission of the first dipole at a given point in the material starts at a given time, t′ = 0, and we calculate its as a function of x and t for a fixed value of z = zobs. The next dipole to emit is delayed in time from the first by
| (27) |
The time spacing between points in the simulation is 0.01 fs, and the spatial extent of x corresponds to the size of the aperture of f/0.5 optics illuminated by the Gaussian beam plotted in Fig. 1.
To simulate imaging this field into a spectrometer, we model an optical system with f/2 optics, which consists of 2 lenses of focal length f, spaced by 2f. Equation 26 is used to calculate the electric field directly behind the first lens of the imaging system and we calculate the field at the front focal plane of the second lens, where the image forms using Fourier optics in the Fresnel approximation.47 The image forms on the input slit of a spectrometer that will be used to measure the emitted interferogram of with ELO. Taking as the input field of the Fourier optics, Uin, we can write an operator, Ŝ, to model the optical system and calculate Uout, the output field, as
| (28) |
where F and Q are a spatial Fourier transform, and quadratic phase operator as defined by Goodman, respectively,47 and the values in brackets are the input arguments for the operator. All Fourier transforms are calculated numerically using the fast-Fourier transform (FFT) algorithm in Matlab. To simulate the effect of the spectrometer we perform an FFT along the temporal dimension of Uout and then sum down the spatial dimension since the imaging system is diffraction limited, there is no additional spatial information along this axis. Equivalently, we could have used just one line from the calculated array, representing a one-dimensional array of pixels on a detector. An LO signal is calculated using a carrier wavelength of 800 nm and τ = 15 fs FWHM and the FFT of the LO is multiplied by the summed FFT of Uout. Measured electric fields are real valued, so we keep only the real part of the product defined in Eq. (9). Still in the frequency domain, we shift the position of the interferogram so that the peak is centered around zero frequency to remove any high-frequency contributions to the image. Finally we take the inverse FFT and plot the magnitude of the complex signal as the image in Fig. 2.
Supplementary Material
Acknowledgments
The authors thank Kirk Lancaster for reading a draft of the manuscript. This work was supported by the Department of Defense as part of the National Security Science and Engineering Faculty Fellowship (NSSEFF) (N00014-15-1-0048 and N00014-16-1-2513) the Air Force Office of Scientific Research (FA9550-14-1-0367), the Dreyfus foundation, and the Sloan foundation. Additional support was provided by the Chicago MRSEC, which is funded by NSF through grant DMR-1420709. MAA acknowledges support from a Yen Postdoctoral fellowship from the Institute for Biophysical Dynamics at The University of Chicago. PDD acknowledges support from an NIH training grant (T32-EB009412) and the NSF GRFP.
Footnotes
Supporting Information
Supporting Information Available: Discussion of thrid-order response functions and additional figures from simulations are provided. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsphotonics.XXXXXXX.
References
- 1.Abbe E. Beitraege zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung. Archiv fuer mikroskopische Anatomie. 1873;9:413–418. [Google Scholar]
- 2.Rayleigh L. XXXI. Investigations in optics, with special reference to the spectroscope. Philosophical Magazine Series 5. 1879;8:261–274. [Google Scholar]
- 3.Ash EA, Nicholls G. Super-resolution Aperture Scanning Microscope. Nature. 1972;237:510–512. doi: 10.1038/237510a0. [DOI] [PubMed] [Google Scholar]
- 4.Fischer UC, Pohl DW. Observation of Single-Particle Plasmons by Near-Field Optical Microscopy. Phys Rev Lett. 1989;62:458–461. doi: 10.1103/PhysRevLett.62.458. [DOI] [PubMed] [Google Scholar]
- 5.Betzig E, Trautman JK. Near-Field Optics: Microscopy, Spectroscopy, and Surface Modification Beyond the Diffraction Limit. Science. 1992;257:189–195. doi: 10.1126/science.257.5067.189. [DOI] [PubMed] [Google Scholar]
- 6.Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, Davidson MW, Lippincott-Schwartz J, Hess HF. Imaging Intracellular Fluorescent Proteins at Nanometer Resolution. Science. 2006;313:1642–1645. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- 7.Klar TA, Jakobs S, Dyba M, Egner A, Hell SW. Fluorescence microscopy with diffraction resolution barrier broken by stimulated emission. Proc Nat Acad Sci USA. 2000;97:8206–8210. doi: 10.1073/pnas.97.15.8206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rust MJ, Bates M, Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM) Nat Methods. 2006;3:793–796. doi: 10.1038/nmeth929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bailey B, Farkas DL, Taylor DL, Lanni F. Enhancement of axial resolution in fluorescence microscopy by standing-wave excitation. Nature. 1993;366:44–48. doi: 10.1038/366044a0. [DOI] [PubMed] [Google Scholar]
- 10.Gustafsson MGL. Nonlinear structured-illumination microscopy: Wide-field fluorescence imaging with theoretically unlimited resolution. Proc Nat Acad Sci USA. 2005;102:13081–13086. doi: 10.1073/pnas.0406877102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li D, Shao L, Chen BC, Zhang X, Zhang M, Moses B, Milkie DE, Beach JR, Hammer JA, Pasham M, Kirchhausen T, Baird MA, Davidson MW, Xu P, Betzig E. Extended-resolution structured illumination imaging of endocytic and cytoskeletal dynamics. Science. 2015;349 doi: 10.1126/science.aab3500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Blankenship RE. Molecular Mechanisms of Photosynthesis. Blackwell Science; 2002. [Google Scholar]
- 13.Engel GS, Calhoun TR, Read EL, Ahn T-K, Cancal T, Cheng Y, Blankenship RE, Fleming GR. Nature. 2007;446:782–786. doi: 10.1038/nature05678. [DOI] [PubMed] [Google Scholar]
- 14.Collini E, Wong CY, Wilk KE, Curmi PM, Brumer P, Scholes GD. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature. 2010;463:644–647. doi: 10.1038/nature08811. [DOI] [PubMed] [Google Scholar]
- 15.Wan Y, Guo Z, Zhu T, Yan S, Johnson J, Huang L. Cooperative singlet and triplet exciton transport in tetracene crystals visualized by ultrafast microscopy. Nature Chem. 2015;7:785–792. doi: 10.1038/nchem.2348. [DOI] [PubMed] [Google Scholar]
- 16.Heo H, Sung JH, Cha S, Jang B-G, Kim J-Y, Jin G, Lee D, Ahn J-H, Lee M-J, Shim JH, Choi H, Jo M-H. Interlayer orientation-dependent light absorption and emission in monolayer semiconductor stacks. Nature comm. 2015;6:7372. doi: 10.1038/ncomms8372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hong X, Kim J, Shi S-F, Zhang Y, Jin C, Sun Y, Tongay S, Wu J, Zhang Y, Wang F. Ultrafast charge transfer in atomically thin MoS2/WS2 heterostructures. Nature nanotechnol. 2014;9:682–686. doi: 10.1038/nnano.2014.167. [DOI] [PubMed] [Google Scholar]
- 18.Polli D, Altoe P, Weingart O, Spillane KM, Manzoni M, Brida D, Tomasello G, Orlandi G, Kukura P, Mathies RA, Garavelli M, Cerullo G. Conical intersection dynamics of the primary photoisomerization event in vision. Nature. 2010;467:440–443. doi: 10.1038/nature09346. [DOI] [PubMed] [Google Scholar]
- 19.Johnson PJ, Halpin A, Morizumi T, Prokhorenko VI, Ernst OP, Miller RD. Local vibrational coherences drive the primary photochemistry of vision. Nature chemistry. 2015;7:980–986. doi: 10.1038/nchem.2398. [DOI] [PubMed] [Google Scholar]
- 20.Savolainen J, Ahmed S, Hamm P. Two-dimensional Raman-terahertz spectroscopy of water. Proc Nat Acad Sci USA. 2013;110:20402–20407. doi: 10.1073/pnas.1317459110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Allodi MA, Finneran IA, Blake GA. Nonlinear terahertz coherent excitation of vibrational modes of liquids. J Chem Phys. 2015;143:234204. doi: 10.1063/1.4938165. [DOI] [PubMed] [Google Scholar]
- 22.Finneran IA, Welsch R, Allodi MA, Miller TF, Blake GA. Coherent two-dimensional terahertz-terahertz-Raman spectroscopy. Proc Nat Acad Sci USA. 2016;113:6857–6861. doi: 10.1073/pnas.1605631113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hell SW, Wichmann J. Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy. Opt Lett. 1994;19:780–782. doi: 10.1364/ol.19.000780. [DOI] [PubMed] [Google Scholar]
- 24.Müller T, Schumann C, Kraegeloh A. STED Microscopy and its Applications: New Insights into Cellular Processes on the Nanoscale. ChemPhysChem. 2012;13:1986–2000. doi: 10.1002/cphc.201100986. [DOI] [PubMed] [Google Scholar]
- 25.Lauterbur P. Image Formation by Induced Local Interactions: Examples Employing Nuclear Magnetic Resonance. Nature. 1973;242:190–191. [PubMed] [Google Scholar]
- 26.Callaghan P. Principles of Nuclear Magnetic Resonance Microscopy. Oxford University Press; 1994. [Google Scholar]
- 27.Roberts JD. ABCs of FT-NMR. University Science Books; 1991. [Google Scholar]
- 28.Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Glasser MF, Miller KL, Ugurbil K, Yacoub E. Multiplexed Echo Planar Imaging for Sub-Second Whole Brain FMRI and Fast Diffusion Imaging. PLoS ONE. 2010;5:1–11. doi: 10.1371/journal.pone.0015710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cho M, Fleming GR. Photon echo measurements in liquids: Numerical calculations with model systems. J Chem Phys. 1993;98:2848–2859. [Google Scholar]
- 30.Vhringer P, Arnett D, Yang T-S, Scherer N. Time-gated photon echo spectroscopy in liquids. Chem Phys Lett. 1995;237:387–398. [Google Scholar]
- 31.Mukamel S. Principles of Nonlinear Optical Spectroscopy. Oxford University Press; 1995. [Google Scholar]
- 32.Hamm P, Zanni M. Concepts and Methods of 2D Infrared Spectroscopy. Cambridge University Press; 2011. [Google Scholar]
- 33.Akturk S, Gu X, Zeek E, Trebino R. Pulse-front tilt caused by spatial and temporal chirp. Opt Express. 2004;12:4399–4410. doi: 10.1364/opex.12.004399. [DOI] [PubMed] [Google Scholar]
- 34.Akturk S, Gu X, Gabolde P, Trebino R. The general theory of first-order spatio-temporal distortions of Gaussian pulses and beams. Opt Express. 2005;13:8642–8661. doi: 10.1364/opex.13.008642. [DOI] [PubMed] [Google Scholar]
- 35.A more complete discussion of third-order response functions is available in the online supplemental information.
- 36.Kauppinen J, Partanen J. Fourier Transforms in Spectroscopy. Wiley; 2001. [Google Scholar]
- 37.Kreier D, Baum P. Avoiding temporal distortions in tilted pulses. Opt Lett. 2012;37:2373–2375. doi: 10.1364/OL.37.002373. [DOI] [PubMed] [Google Scholar]
- 38.Kostenbauder A. Ray-pulse matrices: a rational treatment for dispersive optical systems. IEEE J Quant Electron. 1990;26:1148–1157. [Google Scholar]
- 39.Gerrard A, Burch JM. Introduction to Matrix Methods in Optics. Dover; 1975. [Google Scholar]
- 40.Born M, Wolf E. Principles of Optics. 7th. Cambridge; 1999. [Google Scholar]
- 41.Albrecht AW, Hybl JD, Gallagher Faeder SM, Jonas DM. Experimental distinction between phase shifts and time delays: Implications for femtosecond spectroscopy and coherent control of chemical reactions. J Chem Phys. 1999;111:10934–10956. [Google Scholar]
- 42.Dorrer C. Influence of the calibration of the detector on spectral interferometry. J Opt Soc Am B. 1999;16:1160–1168. [Google Scholar]
- 43.Singh VP, Fidler AF, Rolczynski BS, Engel GS. Independent phasing of rephasing and non-rephasing 2D electronic spectra. J Chem Phys. 2013;139:084201. doi: 10.1063/1.4818808. [DOI] [PubMed] [Google Scholar]
- 44.Dahlberg PD, Fidler AF, Caram JR, Long PD, Engel GS. Energy Transfer Observed in Five Cells Using Two-Dimensional Electronic Spectroscopy. J Phys Chem Lett. 2013;4:3636–3640. doi: 10.1021/jz401944q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Grumstrup EM, Gabriel MM, Cating EE, Goethem EMV, Papanikolas JM. Pump-probe microscopy: Visualization and spectroscopy of ultrafast dynamics at the nanoscale. Chem Phys. 2015;458:30–40. [Google Scholar]
- 46.Massaro ES, Hill AH, Grumstrup EM. Super-Resolution Structured Pump-Probe Microscopy. ACS Photonics. 2016;3:501–506. [Google Scholar]
- 47.Goodman JW. Introduction to Fourier Optics. 3rd. W. H. Freeman & Co; 2004. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


