Systematic analysis of residual density suggests that a major limitation in well‐refined X‐ray structures of proteins is the omission of ordered solvent

Abstract

In the residual electron density map of a fully refined X‐ray protein model, there should be no peaks arising from modeling errors or missing atoms. Any residual peaks that do occur should be contributed by random residual intensity differences between the model and the data. If the model is incomplete (i.e., some atoms are missing), there will be more positive peaks than negative ones. On the other hand, if the model includes inappropriately located atoms, there will be an excess of negative peaks. In this study, random residual peaks are quantified using the probability density function P(x), which is defined as the probability for a peak having peak height between x and x + dx. It is found that P(x) is single‐exponential and symmetric for both positive and negative peaks. Thus, P(x) can be used to discriminate residual peaks contributed by random noise in complete models from residual peaks being attributable to modeling errors in incomplete models. For a number of representative structures in the PDB it is found that P(x) has far more large (greater than 5 sigma) positive peaks than large negative peaks. This excess of large positive peaks suggests that the main defect in these refined structures is the omission of ordered water molecules.

Introduction

Upon completion of model refinement in X‐ray crystallography, (i) R‐factor gap between model R‐factor and data quality R‐factor should vanish, (ii) residual amplitude differences between the observed F _obs and calculated amplitudes F _calc should approach random noise in the diffraction data, and (iii) residual electron density (ED) map should be featureless over the entire unit cell. For any small‐molecule crystal model, all these goals must be met before such model becomes acceptable. However, these goals are very difficult to achieve for protein crystallography according to recent analysis of the protein models deposited in the PDB.1, 2 Two likely reasons for why it is so are: (i) models being reported are highly incomplete, which is the subject of this study, and (ii) the actual quality of diffraction data is severely overestimated.

For small‐molecule crystal models at Ångstrom or sub‐Ångstrom resolution at the completion of model refinement when there is no R‐factor gap left, fractal dimension has been proposed to quantify the featurelessness of residual ED maps in addition to other quantities such as the range of residual electrons, the absolute number of total residual electrons, and so on.3 These criteria are seldom used in protein crystallography when R‐factor gap remains very large for whatever reasons.1, 2 Thus, it is important to develop some other simple quantification on featurelessness that is independent of R‐factor gap and before R‐factor gap vanishes. Otherwise, featurelessness opens for different interpretations by investigators. In this study, the probability density function of residual peaks as a function of peak height is explored as a quantity for measuring the featurelessness of residual ED map.

Results

Analysis of residual peak distribution for E. coli catalase model reported for 5BV2

E. coli catalase model reported4 for 5BV2 contains ∼30,000 non‐hydrogen atoms determined at 1.53‐Å resolution with model R‐factor of 8.2% and free R‐factor of 13.2% from my laboratory (Table 1). Data in the highest resolution shells collected at corners of square detector are incomplete. The total reflection in the data set is equivalent to the corresponding complete data set at 1.70‐Å resolution, which is about the midpoint between the corners and edges of the detector. This model is one of the most complete protein models in the PDB examined so far (Table 1), and has the smallest R‐factor gap with R _Ratio of 1.22 (see Methods).4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 Evidence will be provided below that its corresponding residual ED map is the closest to true featurelessness with all the residual peaks contributed mainly by random noise present in the intensity data.

Table 1.

R‐Factor Ratios of Selective Protein Entries from the PDB^a

PDB accession	Description	Resolution (Å)	R Ratio	R work (%)	R free (%)	H2O: residue ratiob
5BV2	E. coil C2 catalase	1.53	1.22	8.2	13.2	1.48
5BV2/dry	E. coil C2 catalase	1.53	3.46	18.8	22.9	0.00
3P9Q	E. coli P21 catalase	1.48	2.11	14.3	17.8	1.20
4BFL	E. coli P21 catalase	1.64	3.04	17.4	20.2	0.66
4XOF	Human ubiquitin	1.15	2.69	13.7	17.1	1.45
4PIH	Human ubiquitin	1.50	2.95	16.5	19.0	0.91
4PIJ	Human ubiquitin	1.50	5.36	17.6	19.8	0.53
4WES	Nitrogenase	1.08	1.67	11.0	13.3	1.25
2VB1	Triclinic lysozyme	0.65	3.89	8.5	9.5	1.04
3O4P	Diisopropyl fluorophosphatase	0.85	1.58	10.3	12.1	1.58
4AYP	1,2‐α‐Mannosidase	0.85	2.32	9.6	10.6	1.78
4GHO	Ribonuclease	1.10	2.20	9.8	11.7	1.78
4MJ9	Ru‐10bp‐DNA duplex	0.97	2.96	8.6	9.6	11.6
4F19	Phosphate‐binding protein	0.95	2.41	9.6	11.1	2.17
4F1U	Phosphate‐binding protein	0.98	3.41	8.8	9.6	2.55

^aReferences for these entries are: 5BV2 (⁴), 3P9Q (⁵), 4BFL (⁶), 4XOF (⁷), 4PIH (⁸), 4PIJ (⁸), 4WES (⁹), 2VB1 (¹⁰), 3O4P (¹¹), 4AYP (¹²), 4GHO (¹³), 4MJ9 (¹⁴), 4F19 (¹⁵), and 4F1U (¹⁵). 5BV2/dry is the 5BV2 model after deleting all 4669 ordered water molecules. Either underestimation of experimental errors or the existence of modeling errors can lead to large R _Ratio values.

^bMultiple conformers of ordered water molecules and protein residues are counted independently. Note that 4MJ9 is a nucleic acid model, which has many more ordered water molecules per residue.

Residual F _obs–F _calc ED map for 5BV2 model4 was normalized in the unit of the standard deviation for individual grid points in the entire unit cell. When residual peaks are searched in the map, the relative heights of peaks (x) are sorted in the descending order for the positive peaks, and the ascending order for the negative peaks. The peak ordinary number is proportional to peak density but with a varying window in which the size of window decrease as descending the absolute value of peak height.

The plot of peak number (or density) and its logarithm as a function of peak height shows that the curve for positive peaks and the curve for negative peaks are symmetric, and that the two curves have similar peak numbers at any given contour levels with the exception of above 4.5σ where there are only a few peaks [Fig. 1(A,B)].4 When the two curves are assembled into single curve, it has a large gap in the midpoint where the number of peaks has the highest probability density [Fig. 1(C)]. In the logarithm plot against peak height [Fig. 1(E)], deviations of large peaks are approximately distributed evenly at both sides of a straight line extrapolated from small peaks. In the logarithm plot against peak height squares [Fig. 1(F)], deviations are not evenly distributed on two sides of the line, for example, they are mainly on the up‐right side. This observation suggests that the probability density of peaks appears to follow a single‐exponential, symmetric curve instead of Gaussian function, which would be traditionally expected.

Figure 1.

Analysis of residual peaks from 5BV2 model.4 (a) Conventional peak number as a function of peak height x with separate positive and negative peaks. Complete 5BV2 model is shown in dotted lines, and incomplete 5BV2/dry model is in solid line. (b) Natural logarithm of peak number as a function of x. (c) Conventional peak number but with missing mid‐section. (d) The first derivative of Φ(x) in (c) using overlapping windows, for example, P(x), the probability distribution function. (e) log[P(x)] versus x. (f) log[P(x)] versus x ². In (a, b, e, f), positive peaks are in green or black and negative peaks in red or magenta. In (d) peaks for the complete 5BV2 model are in black and those for the incomplete 5BV2/dry model are in red.

Instead of varying sizes of windows, a common histogram analysis uses a fixed size of peak‐height window of for example Δx = 0.25 is to count the number peaks in each window between x = −5.00 and x+Δx = −4.75, between x = −4.75 and x+Δx =−4.50, between x = −4.50 and x+Δx = −4.25, and so on. When Δx → 0 as dx, the number of peaks becomes the true probability density function P(x) between x and x + dx (after proper normalization when possible). Integration of P(x) results in cumulative probability density Φ(x), for example, after adding all the number in each window to a fixed x value, starting from x = −∞ (see Eq. (2) in Methods). The analysis of this kind for any quantity x can be carried out using either non‐overlapping or overlapping window. For example, x can stand for amplitude or intensity differences.16

When log[Φ(x)] and log[P(x)] are plotted against x for segregated positive and negative peaks, or combined unsigned peaks (Fig. 2), they exhibit a straight line [Fig. 2(A,B)], again suggesting a single exponential distribution function for both Φ(x) and P(x). Of course, only single‐exponential function has exactly the same slope in logarithm plot as the first derivative of another single‐exponential function [Fig. 2(D)]. The physical basis for residual peaks observed here is attributed to random residual intensity differences (see below). However, the mathematical basis behind P(x) observed here remains unknown.

Figure 2.

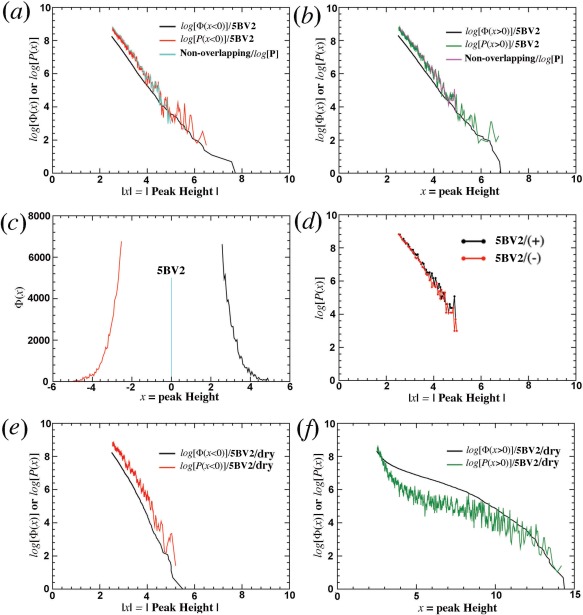
Slopes in Φ(x) and P(x) for 5BV2 model.4 (a,b) 5BV2 model for both positive (+) and negative (−) peak height x. (c,d) 5BV2/dry model. (e,f) 5BV2 model but using non‐overlapping window functions for calculation of P(x). Positive peaks are in green and negative peaks in red.

A systematic analysis of about 300 high‐resolution high‐quality large protein structures retrieved from the PDB using a variety of criteria in the past 5 years shows that most protein models are incomplete, and many of them were described elsewhere.17 A few are selected here for this analysis (Table 1).4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 It is shown that the 5BV2 model4 appears to be the only one whose intensity differences between the model and data are truly limited by random noise present in the diffraction data (see below).

Analysis of residual peaks in an incomplete catalase model

When all 4669 ordered water molecules present in 5BV2 were removed (abbreviated as 5BV2/dry model),4 residual ED map was recalculated for analysis. It is clearly that peak distribution is no longer symmetric: there are ∼3000 more positive peaks than negative peaks at ∼3.5σ contour level (Fig. 1). After this removal, the standard deviation of the residual map increases substantially, and thus the distribution has been rescaled when relative peak heights in unit of the standard deviation are shrunk (Fig. 1). This rescaling slightly increases the slope of log[Φ(x < 0)] and log[P(x < 0)] for negative peaks [Fig. 2(E)]. However, corresponding curves for positive peaks are no longer a straight line with significantly altered shapes of both log[Φ(x > 0)] and log[P(x > 0)] functions [Fig. 2(F)].

Using conventional methods for calculation of residual ED map, the scaling factor k that makes <kF _obs>/<F _calc> = 1 and or <kF _obs–F _calc> = 0 is inadequate when a large fraction of solvent atoms is missing in an incomplete model. In fact, <kF _obs–F _calc> should be greater than 0, a feature that has not been included in the current calculation. This affects the kF _obs(000)‐F _calc(000) term, and the mean <Δρ> density value over the entire unit cell, as well as the heights of all residual peaks. Thus, residual peaks are systematically underestimated: heights for positive peaks should be higher than they are, and heights for negative peaks should be lower than they are. This is why an incomplete model after deleting 4669 water molecules does not result in exactly extra 4669 positive peaks relative to negative peaks in the residual ED map whereas deleting 200 most ordered water molecules in the model has resulted in exactly extra 200 positive peaks. This is also why model refinement is always an iterative process.

Analysis of residual peaks in other protein models

Above analysis was done with a large protein model in which a large number of residual peaks make the analysis robust. When the same analysis is done for small proteins such as ubiquitin, nitrogenase, or lysozyme, it is found that they all have an asymmetric distribution of residual peaks with many more positive peaks than negative peaks (Figs. 3 and 4).7, 8, 9, 10 By this criterion, all of these models should be considered to be incomplete.

Figure 3.

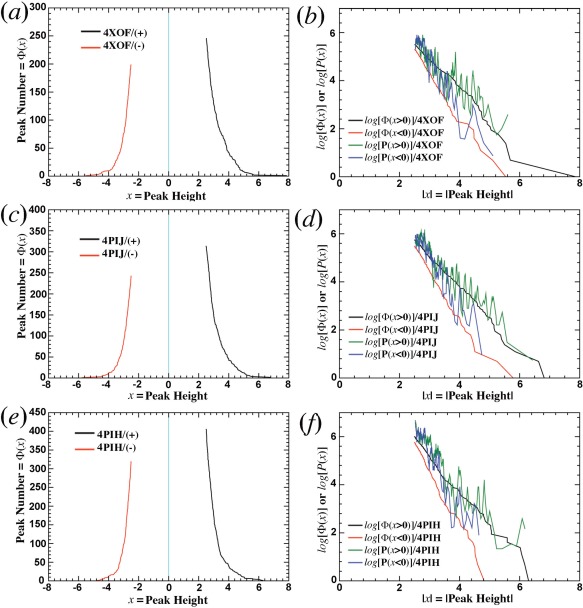
Application of statistical analysis to ubiquitin models.7, 8 (a,b) 4XOF. (c,d) 4PIJ. (e,f) 4PIH. Left side, Φ(x). Right side, logarithms of Φ(x) and P(x).

Figure 4.

Analysis of nitrogenase model (4WES at 1.08‐Å resolution, left, a, c, e) and lysozyme (2VB1 at 0.65‐Å resolution, right, b, d, f) model.9, 10 (a,b) Standard statistics taken from PDB. (c,d) Distribution of positive (green) and negative (red) amplitudes as a function of peak number. (e,f) Distribution of (intensity and amplitude) model (black and blue) and data (red and magenta) R‐factor as a function of reciprocal resolution (1/Å).

Three highest‐resolution models for human ubiquitin models in the PDB are 4XOF at 1.15 Å, and 4PIJ and 4PIH both at 1.50 Å (Table 1).7, 8 Ubiquitin is a small protein of 76‐amino acid residues. In residual ED maps of the three models, there are 30–70 more and larger positive peaks than corresponding negative peaks at 2.5σ cut‐off (Fig. 3), many of which clearly corresponded to missing ordered water molecules. In addition, many other modeling errors also exist, including radiation‐induced structural modifications.18 In each model, the plot of log[P(x > 0)] and log[Φ(x > 0)] for positive peaks differs from the plot of log[P(x < 0)] and log[Φ(x < 0)] for negative peaks. Yet, each of log[P(x > 0)], log[P(x < 0)], log[Φ(x > 0)], and log[Φ(x < 0)] bears a striking similarity across all the three models (Fig. 3), even though they were obtained independently in different space groups.7, 8 This similarity suggests that a common physical basis may exist for why they are incomplete.

Nitrogenase model9 reported for 4WES is at 1.08‐Å resolution and has free R‐factor of 13.3% (Table 1), which is within the top 5% percentile of the smallest working R‐factor/free R‐factor value for all the protein models deposited in the PDB (Fig. 4). Its R‐factor ratio is 1.67 (Table 1). However, when residual ED map is calculated, it is found that the highest positive residual ED peak is 31.3σ, there are 610 more non‐random positive peaks than negative peaks with peak height of above 5σ, there are 1327 more non‐random positive peaks of above 4σ, and so on [Fig. 4(C)]. This model clearly has lots of room for further improvement.

Triclinic lysozyme model10 reported for 2VB1 model is at 0.65‐Å resolution and has free R‐factor of 9.8%. However, the shape of Φ(x > 0) function for positive peaks significantly differs from the shape of Φ(x < 0) function for negative peaks. There are 200 more positive peaks than negative peaks using 2.5σ cut‐off, many of which are very large positive peaks with the highest peak of +14σ [Fig. 4(D) and Fig. S1].

Peak heights for missing H atoms versus non‐random residual peaks

The model of diisopropyl fluorophosphatase11 reported for 3O4P at 0.85‐Å resolution with free R‐factor of 12.1% has been used to demonstrate that sub‐Ångstrom resolution was needed for visualization of H atoms (Table 1). When a residual ED map is calculated using the published model that includes H atoms, the highest non‐random positive peak is 23.6σ, and there are 243 more non‐random positive peaks at the contour level of 4.20σ than negative (282 versus 38) (Fig. 5). In H atom‐deleted models, the highest positive residual peak11 for deleted H atoms was reported to be only at 4.20σ, which ranks at the 283‐th of all the positive peaks in the residual ED map calculated here. After careful model re‐refinement for 3O4P that has already included H atoms, large extra peaks were observed in the residual ED map outside of the Cβ‐H groups of K210 and E104 and outside of the Cγ‐H group of K210 [Fig. 5(C,D)]. These residual peaks clearly correspond to partially added O atoms during data collection.18 Thus, without analysis of this kind, such large positive residual peaks near expected H atoms in H‐deleted models could easily be misinterpreted for the missing H atoms.

Figure 5.

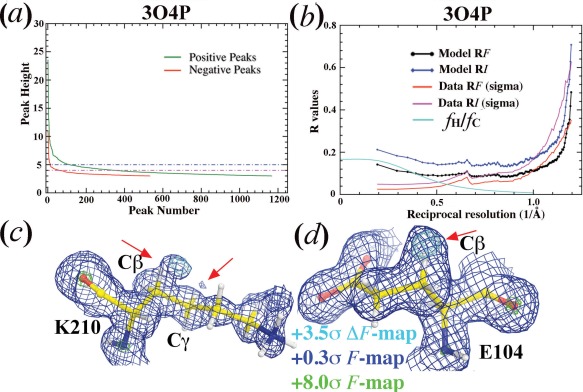
Analysis of diisopropyl fluorophosphatase model at 0.85‐Å resolution (3O4P).11 (a) Residual positive (green) and negative (red) peaks as a function of peak number. (b) Model (black and blue) and data (red and magenta) R‐factor on intensity or amplitude as a function of reciprocal resolution (1/Å). Estimated contribution of H atoms to the total structure factor is shown in cyan curve. (c,d) σ _A‐Weighted F (contoured at 0.3σ, blue, and 8σ, green) and ΔF (contoured +3.5σ) maps for K210 (c) and E104 (d). Arrows indicate likely partial additions of O atoms.

An estimated contribution of H atoms to the amplitudes of a hypothetic protein model is as follows (see Methods): 17% at zero‐scattering angle, 5% at 1.84‐Å resolution, and to only 0.8% at 1.0‐Å resolution, decreasing rapidly with increasing resolution [Fig. 5(B)]. Missing ordered water molecules, which often have relatively large B‐factors, contribute more to diffraction data at low resolution than at high resolution. Thus, there is no doubt that missing ordered water molecules appears a major obstacle to the completeness of model. This is likely to be the main reason why protein crystallographers have a difficult time to see H atoms in ED maps.11 Recent interpretations of cryo‐electron microscopy image reconstruction suggest that ionization states affect both X‐ray and electron structure factors.19, 20 Errors in approximation of neutral X‐ray atomic scattering for ionized atoms can be significant since these errors could not be removed by using either occupancy or B‐factor refinement.

Analysis of residual intensity differences of E. coli catalase models

The observed and calculated amplitudes for the complete and incomplete 5BV2 catalase models4 were scaled for residual analysis under the assumption of <kF _obs>/<F _calc> = 1 with bulk solvent correction applied to the calculated amplitudes. The intensity normalization factors were calculated in 100 resolution shells for 305,824 reflections, and then linearly extrapolated into a specific resolution value for any given Bragg reflection using Wilson plot (see Methods).21

When the normalized intensity differences, z_d, of all Bragg reflections are sorted in the ascending order,22 the ordinary number divided by the total number of reflections in histogram analysis results in the normalized Φ(z_d) function [Fig. 6(A)].23 For the complete 5BV2 model,4 98% of all the reflections have |z_d| < 0.5. However, for the incomplete 5BV2/dry model, only 78% of all the reflections have |z_d| < 0.5, implying that the Φ(z_d) plot is much more sensitive in revealing errors present in both model and data than conventional R‐factors would. This is because the plot treats each reflection the same weight after intensity normalization, which it is equivalent to fractional R‐factors.23, 24, 25, 26 In contrast, conventional R‐factors are heavily weighted on large intensity reflections.

Figure 6.

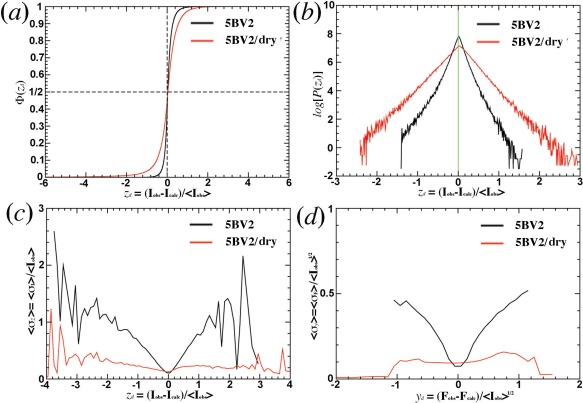
Analysis of intensity and amplitude differences for 5BV2 model.4 (a) Normalized Φ(z_d) as a function of normalized intensity differences, z_d=(I_obs‐I_calc)/<I_obs>. (b) log[P(z_d)] without normalization factor. (c) Measurement errors for normalized intensities grouped together for averaging using an increment of 0.05 in z_d. (d) Measurement errors for normalized amplitudes grouped together for averaging using an increment of 0.05 in y_d, the normalized amplitude, y_d=(F _obs–F _calc)/<I_obs>^1/2.

In the log[P(z_d)] plot,27, 28 the slope corresponds to −1/σ _B, in which σ _B measures the total combined error of modeling errors, incompleteness, and random measurement errors [Fig. 6(B)].23 For the incomplete 5BV2/dry model, modeling errors and the incompleteness are far greater than random measurement errors, the slopes of both log[P(z_d<0)] and log[P(z_d>0)] are almost identical in absolute value. Thus, the σ _B values are independent on z_d and its sign. For the complete 5BV2 model,4 modeling errors and incompleteness are negligible, or much smaller than those in the incomplete 5BV2/dry model so that random measurement errors dominate σ _B. As a consequence, the slope for small z_d reflections is much steeper than large z_d reflections, and more so in the negative side. This suggests that the magnitude of random measurement errors in the data appears correlated strongly with that of intensity differences between the model and data.

If |z_d| is indeed limited by random measurement errors in data, the expected slope in the σ _I versus z_d plot is 2.0, or it is 1/2 in the z_d against σ _I plot (see Methods). When measurement errors of R(sigma) or fractional measurement errors σ_z = <σ _I>/<I> are plotted as a function of z_d, the magnitude of signed z_d value for the complete 5BV2 model4 is proportional to the measurement errors for 98% of all the Bragg reflections that are within |z_d| < 0.5, and the slope of this plot is indeed 1/2 [Fig. 6(C)]. In fact, this feature extends to all the Bragg reflections within |z_d| < 1.5, where fluctuations increase with increasing |z_d| values due to reducing number of reflections in these regions. The same features in slope are also observed in the y_d (normalized amplitude differences, see Methods) versus σ _F (standard derivation of amplitudes) plot [Fig. 6(D)].

When the same analysis is done for the incomplete 5BV2/dry model,4 the slope of the σ _I versus z_d plot is infinite on the z_d > 0 side, which suggests that the terms I _obs‐I _calc represent mainly missing ordered water molecules, but not by random measurement noise present in the data. On the z_d < 0 side of the plot, random measurement noise in some of small‐intensity Bragg reflections appears to contribute part of intensity differences between the model and data [Fig. 6(C,D)].

Discussion

Since its introduction,29 free R‐factor has been useful to prevent over‐fitting during model refinement at medium and low resolution: addition of ordered water molecules to an incomplete atomic model according to positive peaks in residual ED map (aggressive positive residual peak‐filling procedure) should not continue when free R‐factor no longer decreases. However, the applicability of this statistic should be re‐examined in model refinement at Ångstrom and sub‐Ångstrom resolution, such as the triclinic lysozyme model reported for 2VB1 model10 at 0.65‐Å resolution for which over‐fitting should not be an issue.

An analysis of residual ED map for 2VB1 model10 reveals many missing ordered water molecules on the surface of the protein. These water molecules typically have much large B‐factors than protein atoms, which often make no contribution to Bragg reflections at the resolution >1.0 Å. Some of these water molecules make no contribution to Bragg reflections even >2.0 Å. Placement of these water molecules into the model does not affect the overall model free R‐factor as much (which is already quite small, 9.8%) because (i) they would minimally modify the amplitudes of only one‐fourth Bragg reflections <1.0‐Å resolution or modestly modify the amplitudes of mainly 3% Bragg reflection <2.0‐Å resolution in the 2VB1 data set at 0.65‐Å resolution [Fig. 4(F)],10 and (ii) they would affect scaling factor associated with bulk solvent model. In fact, an application of bulk solvent correction may have trapped an atomic model in a local minimum. Replacement of any number of individually ordered water molecules in such atomic model requires readjustments of parameters for bulk solvent model, which may increase free R‐factor transiently before converging to a new minimum.

Concluding Remarks

Evidence is provided that the cumulative probability distribution Φ(x) and the probability density distribution P(x) of residual peaks as a function of peak height x in the residual ED map of any complete model follows a single exponential symmetric function. This results from the fact that the amplitude differences for calculation of residual ED map are largely due to random measurement errors present in intensity data. This analysis as well as the distribution of normalized intensity differences appears much more sensitive to missing scattering atoms such as ordered water molecules than conventional model R‐factors. They can be used in assistance in refinement of protein models.

Methods

R‐factor gap and R‐factor ratio

R‐factor gap² between model R‐factor and data R‐factor can be quantified by their ratio (R _Ratio) on either intensity (I) or amplitude (F) for which the asymptotic value is unity where there is no R‐factor gap. The large the gap, the large the R _Ratio, and the fractional R‐factor gap is R _Ratio–1.

$$R_{\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}}\equiv \left[R_{\mathrm{I},\mathrm{M}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}\right]/\left[R_{\mathrm{I},\mathrm{D}\mathrm{a}\mathrm{t}\mathrm{a}}\right]=\left\{\sum \left|I_{\mathrm{o}\mathrm{b}\mathrm{s}}-I_{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}}\right|/\sum \left|I_{\mathrm{o}\mathrm{b}\mathrm{s}}\right|\right\}/\left\{\sum {\sigma }_I/\sum \left|I_{\mathrm{o}\mathrm{b}\mathrm{s}}\right|\right\}=\sum \left|I_{\mathrm{o}\mathrm{b}\mathrm{s}}-I_{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}}\right|/\sum {\sigma }_I\approx \sum \left|F_{\mathrm{o}\mathrm{b}\mathrm{s}}-F_{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}}\right|/\sum {\sigma }_F\equiv \left[R_{\mathrm{F},\mathrm{M}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}\right]/\left[R_{\mathrm{F},\mathrm{D}\mathrm{a}\mathrm{t}\mathrm{a}}\right],$$ (1)

where R _I,Model is model intensity R‐factor between the model and data, R _I,Data is data intensity R‐factor within the given data set, also known as R(sigma) value, σ denotes standard deviation for observed data, the observed data are indicated with subscript “obs,” and calculated values from models are indicated with the subscript “calc,” the following approximations are made: σ_I ≈ 2Fσ_F, and I = F ², R _F,Model is model amplitude R‐factor, and R _F,Data is data amplitude R‐factor.

Statistical analysis of residual peaks

Diffraction data and protein models were retrieved from the PDB. When F _calc was not available in the retrieved data, they were calculated using Refmac5 by setting refinement cycle of zero using neutral atomic scattering factors.30 With both available F _obs and F _calc, coefficients were generated using σ _A‐weighting function for the calculation of residual maps,31 and peaks were searched and sorted in the descending order of peak amplitudes using the program suite CCP4.32

For negative peaks, the plot of peak number versus the ascending order peak height represents the plot of the cumulative probability density of a modified form as a function of peak height, x, prior to normalization. In this modification, the window‐width variable Δx is not fixed. It can be very large with large x, and becomes smaller with smaller x from infinite to the eventual zero. The histogram distribution with a fixed window‐width dx is the true cumulative probability density, Φ(x). The fixed window‐width dx can be achieved using both non‐overlapping and overlapping of x values. With overlapping, the number of peaks is counted between x‐dx/2 and x + dx/2 for every peak with the amplitude x. With non‐overlapping, the number of peaks is counted between x and x + dx with the pre‐set independent variable x. The first derivative of the cumulative probability density results in the underlying probability density, P(x).

$$P\left(x\right)=d\Phi \left(x\right)/dx;\Phi \left(x\right)={\int }_{-\infty }^{x}P\left(t\right)\mathrm{d}t.$$ (2)

For positive peaks, the cumulative probability density is reversed with the descending order peak amplitude. Whereas large peaks >3.5σ can be individually defined precisely, small peaks <2.5σ may not. For example, in a flat region of residual electron density map with the value ∼1.0σ, it is nearly impossible to define how many peaks are there and where peaks are located. Thus, the total number of peaks in any residual ED map cannot easily be defined, making normalization very difficult.

The root‐mean‐square deviation (RMSD) of residual ED map σ _{Δ ρ} is calculated from individual voxels of the unit cell, which is not the same as RMSD of peak heights σ_x. The relationship between σ_x and σ _{Δ ρ} remains unknown. Without normalization to define the actual normalized probability density P(x = 10) for example, it is difficult to assess whether a 10σ peak in the residual ED map is statistically significant.

Analysis of intensities and intensity differences

When intensity I of each Bragg reflection is treated as independent variable x and sorted in the ascending order, the plot of ordinary number as a function of intensity is the cumulative intensity density of a modified version. Like in analysis of peaks, a proper histogram analysis with a fixed window results in the true cumulative probability function Φ(x). The first derivative of this density results in the probability density P(x) (Eq. (2)). When intensity is rescaled to make σ_x = 1 in individual resolution shells or in the entire data set, P(x) = e^{– x}, which is known as Wilson intensity distribution for non‐centrosymmetric structures of proteins.21

Intensity I of Bragg reflections can be normalized as z variable as follows.22 They are sorted in the ascending order of resolution and grouped in about 100 resolution shells with an approximately same number per shell. For the catalase data set reported for 5BV2, there are a total of 305,824 so that each resolution shell has ∼3058 reflections. With such a large number, analysis is robust. The mean intensity and mean reciprocal resolution squares <s ²> are calculated for each resolution shell, and log[<I>] is plotted against <s ²> (i.e., Wilson plot21). For any given Bragg reflection, its expectation is linearly extrapolated from log[<I>] using the two closest points in the reciprocal resolution squares s ² in the Wilson plot, and intensity can be normalized z = I/<I>.22

Intensity differences can also be normalized in the same way,27 z_d = (I_obs‐I_calc)/<I_obs>, which represent signed individual components of normalized intensity R‐factor or fractional intensity R‐factor. Summation of their absolute values is normalized intensity R‐factors: $\sum \left|z_d\right|=\sum \left[\left|I_{obs}-I_{calc}\right|/〈I_{obs}〉\right]$. If I₁ and I₂ represent two intensity measurements with the same measurement errors for a given Bragg reflection, its mean value is I=(I₁+I₂)/2. Unsigned fractional error of each measurement to its mean intensity is: |I₁–I|/I = |I₂–I|/I = [|I₁–I₂|/2]/I. Thus, if unsigned fraction error represents σ_I, it is half of the difference between the two measurements. Similarly, amplitude differences can also be normalized,27 y_d = (F_obs–F_alc)/<I_obs>^1/2. It has the same property as the normalized intensity differences.

Whereas errors of multiple measurements for given Bragg reflection in a data set indeed follow Gaussian distribution, strictly speaking, measurement errors of the entire data set do not always follow another Gaussian distribution even though it is often so assumed.33 Measurement errors of an entire data set have three components,34, 35, 36 the first one, independent of intensity of individual Bragg reflections (random errors, indeed Gaussian distribution), the second, proportional to the intensity (X‐ray photon exchanges with crystals), the third, proportional to the square root of the intensity (Poisson‐counting limit). To mathematically derive the probability density function of residual peak distribution from measurement errors, one must first define the probability function for measurement errors. Measurement errors currently reported for all the diffraction data do not include X‐ray radiation‐induced intensity modifications due to time‐dependent structural changes,18 which can be very large and is beyond the scope of this study. The magnitudes of these errors are so large that they have often fooled automated space group determination procedure to downshift symmetry.17

Estimation of amplitude contribution of hydrogen atoms in protein models

Because half of protein atoms are hydrogen, it is assumed here in a hypothetical protein model that (i) it consists of the same numbers of H atoms and C atoms in one‐to‐one ratio, (ii) these atoms are randomly distributed in the unit cell, and (iii) they have the same B‐factor. The contribution of H atoms is proportional to H atomic scattering factor (f_H) relative to the total scattering factor (f_Total), which is summed in intensity from both C scattering factor (f_C) and H scattering factor components:21

$$f_H/f_{Total}=f_H/\sqrt{f_C^2+f_H^2 }\approx f_H/f_C .$$ (3)

A Summary of Symbols and Abbreviations

P(x)

Probability distribution function for generic variable x.

Φ(x)

Cumulative probability distribution for generic variable x.

z, z_d

Normalized intensities and normalized intensity differences.

y, y_d

Normalized amplitudes and normalized amplitude differences derived from normalized intensities.

F_obs, I_obs, F_calc, I_calc

Observed or calculated amplitudes or intensities.

R_I,Model, R_I,Data, R_F,Model, R_F,Data

Intensity or amplitude R‐factors for model and for data.

σ, σ_x, σ_I, σ_F

Standard deviation for generic function, for variable x, observed intensity, and amplitude.

σ_A, σ_B

They represent the known and unknown components of structure, respectively, in an error‐free system with [σ _A]²+[σ _B]²=1.

R_Ratio

R‐factor ratio between model and data.

<f(x)>

Expectation of generic function f with random variable x.

<I_obs>

Locally average intensity within ultra thin resolution shells.

f_H, f_C, f_Total

Atomic scattering factor for H, C, and all atoms.

RMSD

Root‐mean‐square deviation.

Conflict of Interest Statement

The author declares no conflict of interest in publishing results of this study.

Supporting information

Supporting Information

Figure S1. Application of statistical analysis on lysozyme 2VB1 model. Left side, Φ(x). Right side, logarithms of Φ(x) and P(x).