Wright–Fisher exact solver (WFES): scalable analysis of population genetic models without simulation or diffusion theory

Abstract

Motivation

The simplifying assumptions that are used widely in theoretical population genetics may not always be appropriate for empirical population genetics. General computational approaches that do not require the assumptions of classical theory are therefore quite desirable. One such general approach is provided by the theory of absorbing Markov chains, which can be used to obtain exact results by directly analyzing population genetic Markov models, such as the classic bi-allelic Wright–Fisher model. Although these approaches are sometimes used, they are usually forgone in favor of simulation methods, due to the perception that they are too computationally burdensome. Here we show that, surprisingly, direct analysis of virtually any Markov chain model in population genetics can be made quite efficient by exploiting transition matrix sparsity and by solving restricted systems of linear equations, allowing a wide variety of exact calculations (within machine precision) to be easily and rapidly made on modern workstation computers.

Results

We introduce Wright–Fisher Exact Solver (WFES), a fast and scalable method for direct analysis of Markov chain models in population genetics. WFES can rapidly solve for both long-term and transient behaviours including fixation and extinction probabilities, expected times to fixation or extinction, sojourn times, expected allele age and variance, and others. Our implementation requires only seconds to minutes of runtime on modern workstations and scales to biological population sizes ranging from humans to model organisms.

Availability and Implementation

The code is available at https://github.com/dekoning-lab/wfes

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Diffusion approximations to the underlying Markov chain models of population genetics have been central to theoretical population genetics since the pioneering work of Kimura (1964). One reason for the success of diffusion approaches has been their ability to enable closed-form solutions to be found under simple models. This ability comes at the cost of typically needing to assume weak mutation and weak selection, which may not always be appropriate. Furthermore, when models aren’t simple enough to allow closed-form solutions to be found, as is the case with most models of practical interest, numerical integration must be used to approximate diffusion solutions. This approach of approximating an approximation is indirect, can be problematic at the extremes of parameter ranges (Zhao et al., 2013), and it still requires a set of standard assumptions like weak selection that lack generality. In these cases, the ability to work directly with the original Markov models is advantageous.

Methods for the direct analysis of Markov chain models, such as the classical Wright–Fisher model, are well known (Ewens, 2004) and are often used in the development of new population genetic theory. However, the utility of direct matrix methods has typically been limited by the computational difficulty of working with very large transition matrices, which are quadratic in size with the effective population size. As a result, it is not uncommon for direct approaches to be applied only to population sizes of 100–200 (e.g., Keightley and Eyre-Walker, 2007).

For direct Markov chain methods, the key computation is typically the determination of the ‘fundamental matrix’ of the absorbing Markov chain (Kemeny and Snell, 1960), which requires a costly matrix inverse computation. We noticed that for most applications this full computation is unnecessary if the number of originating copies of the mutant allele is known. When this is so, only one row of the matrix inverse is needed, which can be obtained by solving a much simpler linear system. Furthermore, because the transition matrices for most Wright–Fisher models are very sparse, sparsity can be exploited to save both computation time and memory. Wright–Fisher Exact Solver (WFES) is our implementation of these and other ideas.

2 Methods

See Supplementary Methods, which are available online.

3 Results

3.1 Implementation

We developed a rapid, parallel sparse linear algebra approach in C for the direct analysis of discrete-time Markov models WFES. This implementation currently performs direct computation of exact solutions (subject to machine precision) for: conditional probabilities of fixation and extinction; expected times to fixation and extinction; sojourn times (the expected number of times each state is visited before absorbing) and the expected age of an allele and its variance (B. De Sanctis and A.P.J. de Koning, submitted for publication). The absorbing states are fixation and extinction, which by definition cannot be left.

3.2 Evaluation

To validate our implementation, we performed a series of comparisons of fixation probabilities to values estimated from forward simulation and diffusion theory under a simple Wright–Fisher model without mutation or dominance (see Supplemental Results). WFES results showed precise correspondence with high-replicate simulation averages (n = 10 000 fixations) over the entire parameter range, while diffusion approximations clearly became biased with strong selection (s > 0.1; Supplementary Fig. S1). The relative error of diffusion approximations is shown in Figure 1, which illustrates the expected bias of standard fixation probability calculations when selection is strong. This expected result is presented as both a validation and as a demonstration of the generality of WFES, which can compute exact solutions for non-classical parameter ranges.

Fig. 1.

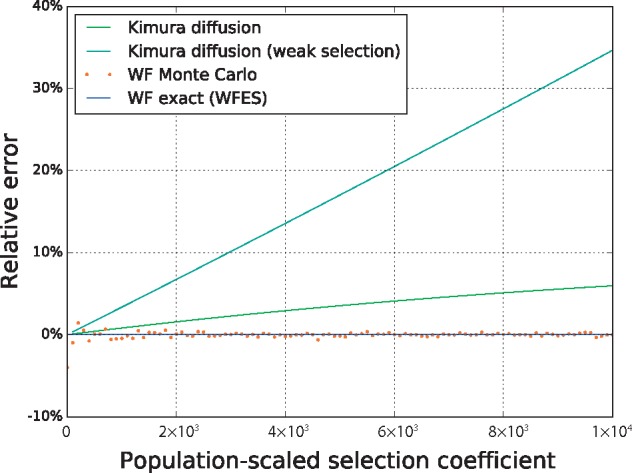
Diffusion theory bias for strongly selected alleles in a population of N_e = 10, 000

3.3 Discussion

WFES has several advantages over simulation, diffusion theory, and other approximate methods. First, it is generally applicable to virtually all Markov chain models in population genetics and can accommodate dominance, two-way mutation, strong selection, and other forces without additional computational cost. Second, it avoids the indeterminacies of numerical integration methods, which arise when computing fundamental quantities with diffusion theory. Third, it is extensible to calculate expectations and variances of various properties of the Wright–Fisher model, such as allele age (B. De Sanctis and A.P.J. de Koning, submitted for publication). Fourth, it permits results for population sizes up to about 30 000 without approximation on typical workstation computers. For larger populations, truncation of the near-zero entries of the transition matrix (Supplementary Table S1) can yield results within desired precision for population sizes beyond 100 000 and still only requires a couple of minutes of wallclock time. While very large population sizes on the order of 1 000 000 are theoretically possible using this approach, they exceed the memory resources of typical computers at this time. For population sizes in the computable range, WFES produces results typically in far less time than running high-replicate simulations. The code is freely available and can be easily modified to implement new calculations.

Funding

This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC DG 03651), a research startup award from the Alberta Children’s Hospital Research Institute, and a Canada Foundation for Innovation award (CFI LOF 31908) to JdK. IK was supported by a doctoral fellowship from Alberta Innovates and BDS was supported in part by an NSERC USRA.

Conflict of Interest: none declared.