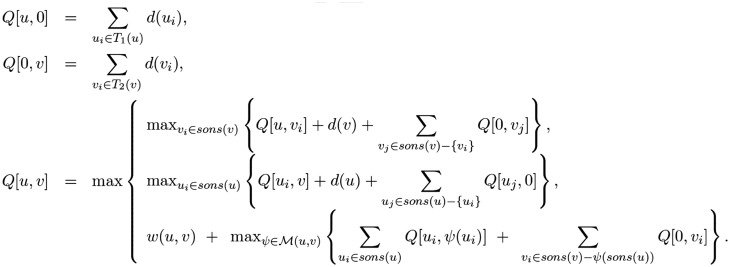Development and application of an algorithm to compute weighted multiple glycan alignments

Abstract

Motivation

A glycan consists of monosaccharides linked by glycosidic bonds, has branches and forms complex molecular structures. Databases have been developed to store large amounts of glycan-binding experiments, including glycan arrays with glycan-binding proteins. However, there are few bioinformatics techniques to analyze large amounts of data for glycans because there are few tools that can handle the complexity of glycan structures. Thus, we have developed the MCAW (Multiple Carbohydrate Alignment with Weights) tool that can align multiple glycan structures, to aid in the understanding of their function as binding recognition molecules.

Results

We have described in detail the first algorithm to perform multiple glycan alignments by modeling glycans as trees. To test our tool, we prepared several data sets, and as a result, we found that the glycan motif could be successfully aligned without any prior knowledge applied to the tool, and the known recognition binding sites of glycans could be aligned at a high rate amongst all our datasets tested. We thus claim that our tool is able to find meaningful glycan recognition and binding patterns using data obtained by glycan-binding experiments. The development and availability of an effective multiple glycan alignment tool opens possibilities for many other glycoinformatics analysis, making this work a big step towards furthering glycomics analysis.

Availability and Implementation

http://www.rings.t.soka.ac.jp

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The aim of our research is to elucidate the glycan recognition patterns of glycan-binding proteins (GBPs). Glycans are molecules that consist of monosaccharides and glycosidic bonds and have branched structures which are more complicated than amino acid sequences. They are synthesized by glycosyltransferases which act on glycans traveling through the endoplasmic reticulum and golgi, and they eventually reach the cell surface, where they contribute to protein binding and function. Glycan binding is known to play significant roles in cell adhesion, virus infection and other biological functions (Varki et al., 2009). GBPs and their recognition are also involved in intracellular signaling. Thus the roles of glycans are important in cellular biology.

One of the main features of glycans in physiological phenomena is their recognition by GBPs. Lectins are a particular type of GBP, which usually recognize and bind to the non-reducing end of glycans. However, it has been suggested that other internal monosaccharides may also involved in recognition (Ohtsubo and Marth, 2006; Varki et al., 2009).

In terms of glycomics research, experimental technologies such as mass spectrometry, glycan arrays, lectin arrays, etc, are conducted to understand glycan structure and their mechanisms. The glycan array was developed for understanding glycan recognition mechanisms (Alvarez and Blixt, 2006; Fukui et al., 2002). This experimental technique can detect binding reactions by detecting fluorescent labels of GBPs that have bound to various glycans attached onto a chip. The glycan-binding affinity of proteins, glycan-binding viruses, antibodies and even cells can be measured. Various databases such as CFG (Consortium of Functional Glycomics) (Raman et al., 2006) and JCGGDB (Maeda et al., 2015) have accumulated such experimental data for glycans. However, informatics techniques for analyzing large data sets for elucidation of glycan function from experimental data is needed. The GlycoPattern web resource was recently developed to aid users in analyzing and mining glycan array data, especially from the CFG (Agravat et al., 2014). However, there are still many methods that could be applied to such data, which are not readily available for glycobiologists to use. For example, there is an algorithmic approach that uses support vector machine technology to classify glycans and detect glycan motifs, but it is not available to glycobiologists as a web tool (Yamanishi et al., 2007). Moreover, GNAT is MATLAB software for simulating glycan structure biosynthesis pathways. To use this software, basic knowledge of programming is necessary, and so glycobiologists can not easily use it (Liu et al., 2013). Many bioinformatics approaches for protein analysis such as BLAST (Altschul et al., 1990) and ClustalW (Thompson et al., 1994) are developed and published on the Web. However, these algorithms cannot be applied directly to glycan structures. Because of the branched nature of glycans, the development of a tool that can analyze complex glycan structures has been difficult.

We have reported the tool of multiple tree alignment, called MCAW (Multiple Carbohydrate Alignment with Weights) for glycan structures previously (Hosoda et al., 2012), but we did not explain details of the scoring and backtracking algorithm. Here, we describe the details for calculating the monosaccharide and bond score as well as the algorithm flow in more detail. Furthermore, we present analysis of multiple alignment of known motifs from customized data sets. In this work, we also demonstrate the effectiveness of MCAW to efficiently align multiple glycans recognized by Galectin-3 to extract biologically meaningful glycan patterns.

2 Background

2.1 Definition of glycan structure

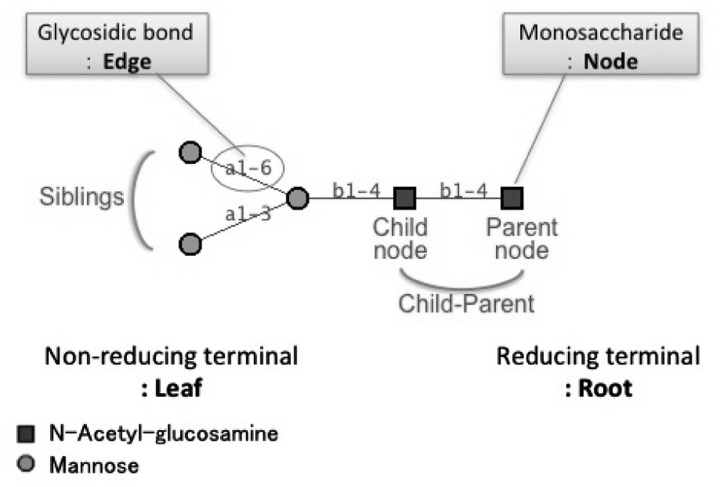
We first describe the vocabulary used in this manuscript for readers to understand our algorithm. Glycans are classified on the basis of subtree patterns in what is called the core section, which include the subtree containing specific monosaccharides and generally containing the root node. Figure 1 is an N-glycan structure which are usually found on an asparagine residue of proteins. These glycans have on average 10–15 monosaccharides in mammalian species. The glycan structure in Figure 1 is represented as an unordered tree that has monosaccharide residues as nodes and glycosidic bonds as edges. The root of the tree is drawn on the right and the leaves are drawn on the left. Adjacent nodes have parent–child relationships, with the node on the root side being the parent. In glycobiology, the root is the reducing end of the glycan, and children are on the non-reducing end. Glycosidic bonds carry three types of information: the anomer (α or β configuration of the child node), the non-reducing side carbon number (usually 1 or 2), and the reducing side carbon number (usually 2, 3, 4 or 6).

Fig. 1.

Description of the core N-glycan structure. Glycan structures are expressed as graphs using symbols that are defined by the CFG. Each monosaccharide is signified as a node and each glycosidic bond is indicated as an edge. The reducing terminal is the root which binds to proteins and lipids, and the non-reducing terminal is the opposite side, known as leaves. Adjacent nodes have parent–child relationships, with the node on the root side being the parent. Children having the same parent are defined as siblings

2.2 PKCF

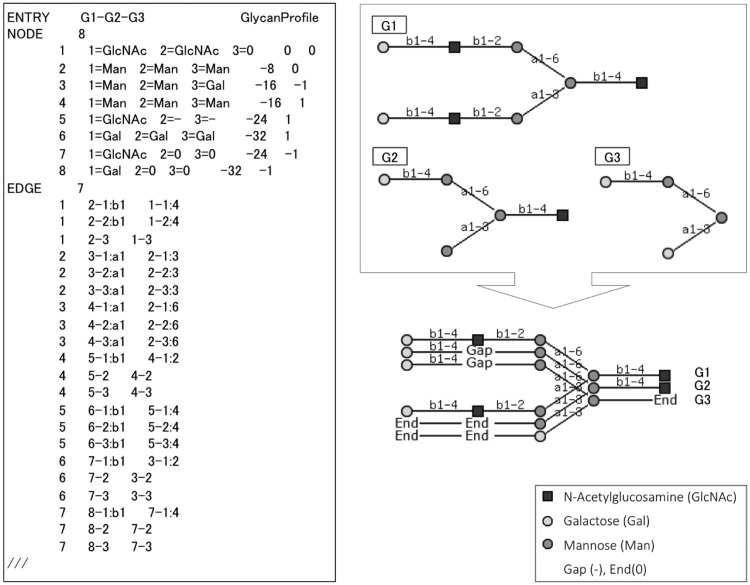
We presented ‘PKCF (ProfileKCF)’ in Hosoda et al. (2012) as the text format for storing glycan profiles, based on the input data which was formatted in KEGG Chemical Function (KCF) format (Aoki-Kinoshita, 2009). Figure 2 illustrates an alignment of three glycans and its corresponding PKCF. The locations where nodes are aligned are called positions. In this example, there are eight positions in this profile (indicated by the number following the NODE line). PKCF includes information indicating the glycans that were aligned, alignment position and the node content of each position, which may include gaps or monosaccharides. This format can also represent a single glycan structure as a profile by simply storing a single glycan, with a single monosaccharide aligned 100% (by itself) at each position. Therefore multiple alignment were possible with PKCF because the format could treat not only a single glycan structure but also multiple aligned glycans as a profile.

Fig. 2.

ProfileKCF format example. The alignment of Glycans G1–G3 (top right) is illustrated below it. The corresponding PKCF is listed on the left

2.3 KCaM

There is pairwise alignment algorithm for glycan structures called KCaM (Aoki et al., 2004), which is a combination of the maximum common subtree and Smith-Waterman local protein alignment algorithms. This algorithm thus incorporated tree edit distance (Bille, 2005) and pairwise protein sequence alignment algorithms (Smith and Waterman, 1981). The global dynamic programming algorithm of KCaM is given in Figure 3.

Fig. 3.

Dynamic programming global alignment algorithm of KCaM for two glycan tree structures T₁ and T₂. u and v refer to a particular node u in one tree and node v in the other, and $Q[u,v]$ computes the alignment score of the subtrees rooted at u and v. sons(x) refer to the children of node x, d(x) refers to the gap penalty of deleting node x, M(u, v) refers to the mapping of sons(u) with sons(v), and w(u, v) refers to the score of matching nodes u and v. Further details are described in the text

In this algorithm, $Q[u,v]$ of two tree structures T₁ and T₂ computes the alignment score of the subtrees rooted at nodes u and v of the two trees being aligned, respectively. sons(x) refer to the children of node x, d(x) refers to the gap penalty of deleting node x, M(u, v) refers to the mapping of sons(u) with sons(v), and w(u, v) refers to the score of matching nodes u and v. w(u, v) is defined below. m, a, n, r are parameters of the match score for monosaccharide, anomer, carbon number on the non-reducing side monosaccharide, and carbon number on the reducing side monosaccharide, respectively. mono(u) is monosaccharide name of node u, anomer(u) is the anomeric configuration (α or β) of the glycosidic linkage between u and p(u), where p(u) is the parent node of node u. nonred is the carbon number on the non-reducing side monosaccharide, and red is the carbon number on the reducing side monosaccharide. δ computes the difference between its two arguments, returning 0 if the same and 1 if different.

$$w(u,v)=\max \left\{\begin{array}{c}0,\hfill \\ m(1-\delta (\text{mono}(u),\text{mono}(v)))\hfill \\ +a(1-\delta (\text{anomer}(p(u),u),\text{anomer}(p(v),v)))\hfill \\ +n(1-\delta (\text{nonred}(p(u),u),\text{nonred}(p(v),v)))\hfill \\ +r(1-\delta (\text{red}(p(u),u),\text{red}(p(v),v)))\hfill \end{array}\right\}$$

3 Materials and methods

Here, we describe the details of the MCAW algorithm, which is based on the progressive alignment algorithm of ClustalW. In this work, we chose a progressive algorithm over an iterative one because the sizes of glycans are small and the resultant error is expected to be minimal.

3.1 MCAW algorithm

In order to avoid too many gaps in the multiple alignment, each glycan is added to the multiple alignment in order of similarity. We also compute weights for each glycan based on the guide tree constructed from the distance matrix which is computed from the similarity scores between all pairs of glycans used as input. The overall MCAW procedure is as follows:

1. Make a distance matrix for all pairs of input glycans by using the global alignment algorithm of KCaM. Since the similarity score computed by KCaM is at most the number of monosaccharides (of the larger glycan) times 100, the distance of two glycans can be computed by subtracting the similarity score from (100 times the number of monosaccharides of the larger glycan being compared). The parameters of m, a, n, r of KCaM are set by default to 70, 10, 10, 10, respectively, totaling 100 for each set of monosaccharide and glycosidic linkage.

2. Create a guide tree of the glycans based on this distance matrix using the Fitch-Margoliash method (Fitch et al., 1967).

3. Calculate the weights of each glycan based on the guide tree; the distance from the root is used as the weight for each glycan. The scores for aligning similar structures will thus be given a small weight so that they have a less significant effect on the alignment, and conversely, the scores for less similar structures will be given a larger weight so that they have a greater influence on the alignment. This is in accordance with the ClustalW algorithm.

4. According to the guide tree, align pairs of glycans (profiles) in order of similarity. Use the MCAW dynamic programming algorithm to align monosaccharides (positions) from the leaves toward the root. The maximum score computed among all pairs of monosaccharides (positions) represents the rootmost monosaccharides (positions) that could best align the glycans (profiles) and thus determines the backtracking point. From this pair, the glycans (profiles) can be aligned. Align the unaligned monosaccharides by inserting Ends where necessary. Repeat with the remaining glycans in the guide tree, in descending order of similarity.

MCAW compares two glycan profiles containing positions that groups monosaccharides and linkages. For simplicity, we can assume that a single glycan is a simple profile of one structure. Based on this, we formulated the dynamic programming algorithm of MCAW to align glycan profiles as follows. This algorithm is based on the local alignment algorithm of KCaM and ClustalW.

$$Q[u,v]=\max \left\{\begin{array}{c}0,\hfill \\ {\max }_{v_i\mathrm{ϵ}sons(v)}\left\{Q[u,v_i]+d(v)\right\},\hfill \\ {\max }_{u_i\mathrm{ϵ}sons(u)}\left\{Q[u_i,v]+d(u)\right\},\hfill \\ \frac{1}{\left|A\right|\left|B\right|}\left\{{\sum }_{n=1}^{\left|A\right|}{\sum }_{m=1}^{\left|B\right|}w(u_n,v_m)a_n{b}_m\right\}+\hfill \\ {\max }_{\psi \mathrm{ϵ}M(u,v)}\left\{{\sum }_{u_i\mathrm{ϵ}sons(u)}Q[u_i,\psi (u_i)]\right\}\hfill \end{array}\right\}$$

Here, u and v refer to a particular position u in one profile and position v in the other, and $Q[u,v]$ computes the alignment score of the subtrees rooted at u and v. sons(x) refer to the children of x, d(x) refers to the gap penalty of deleting node x. $w(u_n,v_m)$ is the same as that used by KCaM and calculates the match score of the monosaccharides, anomers, non-reducing side carbon numbers and reducing side carbon numbers for the monosaccharides at positions u and v of glycans A_n and B_m, respectively. a_n (respectively b_m) signifies the weight of the nth glycan in profile A (respectively mth glycan in profile B). M(u, v) refers to the mapping of sons(u) with sons(v) and $\psi (u_i)$ represents the positions mapped with $sons(u_i)$ (Hosoda et al., 2012).

3.2 Implementation

We implemented steps 1–3 of the MCAW algorithm using Perl, and step 4 was implemented in Java. The Perl program calls the external KCaM program on every pair of input glycans and stores the results of the guide tree as a text file, containing weights calculated for each glycan structure. The Java program reads this file and progressively builds the multiple alignment. The results of the alignment is output in PKCF format. A web form has also been developed to take KCF-formatted glycans as input, compute the PCKF results and display the output graphically on the web.

3.3 Experimental data

First, we prepared a test dataset to confirm MCAW tool performance to align an arbitrary set of glycans containing a predefined motif, the well known sialyl-Lewis X structure composed of the tetrasaccharide of sialic acidα2-3, galactoseβ1-4, N-acetyl-glucosamine and α1-3 fucose (Neu5Ac(a2-3)Gal(b1-4)[Fuc(a1-3)]GlcNAc in IUPAC format). We randomly selected six glycans containing this motif from the RINGS database. Additionally, we prepared three test datasets containing the sialyl Lewis X motif in different locations. This data has been provided in Supplementary Figure S1–S3. First, we randomly selected ten glycans containing more than six saccharides and containing this motif. Second, we modified two of the structures in this first data set so that the terminal sialyl-Lewis X structure has an additional mannose on its sialic acid. This was to test whether MCAW could find motifs that are located internally. Third, we added structures having no sialyl-Lewis X to the first dataset.

We also prepared several analysis datasets to test our MCAW tool using data from the CFG, which are available to the public on the Web. They provide glycan array experiment data as Excel files that have measured the fluorescence intensity of glycan-protein binding affinity. There are experimental data of various lectins, and this database makes it possible to search these data by GBP (analyte) type, including C-type lectins, galectins, viruses etc. We prepared experimental data of galectin-3 which is a lectin that binds to galactose. This lectin is reported to function in eosinophil recruitment and allergic inflammation in airways in vivo (Rao et al., 2007). The CFG provides several glycan array analysis data that has varied the concentration of galectin-3 (2, 5 10 µg). These array experiments were carried out on CFG array version 5 and the primary screen ids of 2, 5 and 10 µg are 6004, 6005 and 6006, respectively. To select the glycans to analyze from these arrays, we selected the high-affinity glycan structures having rank > 75 and a %CV < 20 (Heimburg-Molinaro et al., 2011) from all three datasets. Rank was calculated by taking each average RFUs (relative fluorescence units) value and dividing it by the highest RFU. That is Rank = 100 × (RFUaverage/highest averageRFU) and %CV = (averageRFU/StDev) × 100. For each glycan, we divided its fluorescence intensity value by 10 000, rounded to the nearest unit and used this number as the number of times to duplicate the glycan in the data set. This method of weighting according to RFU is based on the method in (Hosoda et al., 2012), where those glycans with higher affinities were made to be more prevalent than those with lower affinities. This allows us to accurately reflect the binding affinity results from the glycan array experiments. Consequently, the number of glycans that satisfied the criteria rank > 75 and %CV < 20, were as follows: the 2 µg dataset consisted of 12 types of glycans, weighted to total 53 structures; the 5 µg dataset consisted of 19 types of glycans, weighted to total 88 structures; and the 10 µg dataset consisted of 17 types of glycans, weighted to total 88 structures. We provide the actual data and binding affinity RFU values in Supplementary Table S1 Sheet1–3.

4 Result

4.1 Multiple alignment algorithm

To describe the multiple alignment results, we give an example of aligning three glycans G1–G3 in Figure 2. The KCaM similarity scores for each pair of glycans are: for G1–G2 = 56.9, G2–G3 = 67.0 and G1–G3 = 36.3. From this we find that G2–G3 are the most similar. Next, the weights of each glycan were calculated from the guide tree computed by the Fitch-Margoliash method, resulting in weights 376.7, 327.53 and 337.83 for G1, G2 and G3, respectively. Thus the alignment order, the guide tree, has been determined. First, G2–G3 are aligned, followed by the alignment of G1 and the aligned G2–G3 profile. We set the parameters of gap = −10 and (w(u, v)) to m = 60, a = 30, n = 30 and r = 30. As a result, the final alignment score was 545.75, and the final alignment is illustrated on the bottom right of Figure 2.

4.2 Web tool

We have developed MCAW as web tool on RINGS, which can visualize multiple glycan alignments by entering multiple glycan structures. The input glycan structures must be specified in KCF format. RINGS provides tools to convert from a variety of formats into KCF. The glycans can be entered into the text field or specified as a file. The MCAW tool is available from http://www.rings.t.soka.ac.jp. Users can modify the score parameters for comparing structures used in the dynamic programming algorithm, including the scores for matching anomers, monosaccharides, reducing and non-reducing side carbon numbers, and gap penalty by entering values under the advanced weighting options. Default values are preset as follows: gap = −10, matching monosaccharides = 60, matching anomers = 30, matching carbon number on reducing end side and non-reducing end = 30 each. The MCAW tool can then be executed by pressing the Submit button. The alignment result can be viewed as a profile (Fig. 4), and it can also be obtained in PKCF format. The percentage of each node at each position is listed graphically.

Fig. 4.

The glycan profile produced by MCAW as a result of aligning a data set of arbitrary glycans containing the sialyl-Lewis X motif. The result shows that the sialyl-Lewis X structure is aligned 100% in positions 5–8 of the resulting profile

4.3 Data experiment

4.3.1 Sialyl-lewis X motif

We analyzed the dataset of glycans containing the sialyl-Lewis X motif by inputting it into MCAW with the default settings for the advanced weighting options. Figure 4 is the result showing that the motif structure aligned 100% in positions 5 through 8 of the resulting profile. Thus, it was able to successfully align this biological motif without any prior knowledge of the data set. Note that positions 9, 10, 15 and 17 also contain a similar motif, but with varying glycosidic linkages; our tool could visually express such patterns that were unexpected when constructing this data set.

We further analyzed the three customized datasets containing ten glycans having the same motif, but in various positions in the glycans. The results are provided in Supplementary Figure S4. For the dataset of ten glycans containing this motif, we were again able to align it 100%. For the dataset containing terminal sialyl-Lewis X with an additional mannose on the non-reducing terminal, the sialyl-Lewis X motif is aligned internally 100%. Finally, for the dataset containing glycans having no sialyl-Lewis X, the results showed that the motif structure was aligned 90.9% along with Ends. If the Ends were ignored, it would be aligned 100%.

4.3.2 Galectin-3

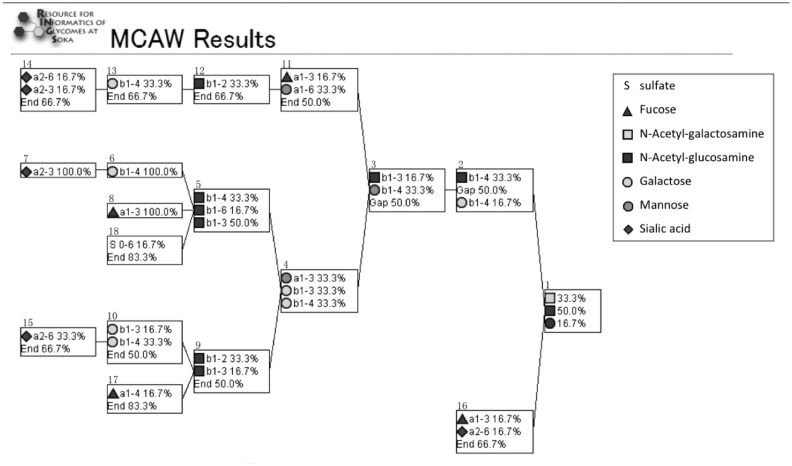
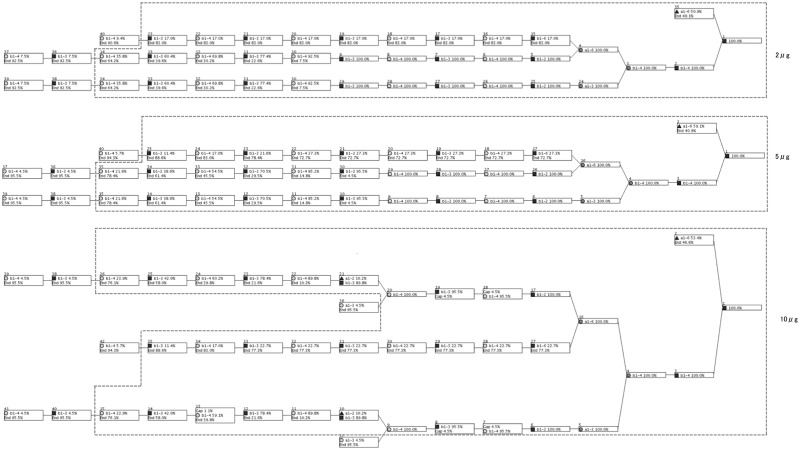
We also analyzed the three galectin-3 datasets of varying concentrations. Figure 5 shows the resulting profiles for 2, 5, 10 µg from top down. We provide a high-resolution version of Figure 5 in Supplementary Figure S5. In these results, the N-glycan core structure and two repeated Galβ1-4GlcNAc (lactosamine) structures are highly aligned in each of the three concentrations. The datasets of lower concentrations (2 and 5 µg) additionally aligned two repeated lactosamine structures 100%, and in the 10 µg result, it was aligned slightly lower because lactosamine was modified by a fucose.

Fig. 5.

Result of analyzing the three datasets of varying concentrations of galectin-3 using MCAW. Our tool shows that the disaccharide Galβ1-4GlcNAc on the N-glycan core is highly aligned. It is known that Galectin-3 interacts with lactosamine structures, and our results reflected this

5 Discussion

5.1 MCAW algorithm

In this work, we provided additional details regarding the MCAW algorithm in terms of the monosaccharide and glycosidic linkage scoring and the backtracking step. Our algorithm is developed for unordered trees so that it can take as input IUPAC and KCF, which do not have strict rules for describing the input glycans. These formats may describe the same glycan but order the children differently (even randomly). In MCAW, these structures can be correctly aligned; however, because it takes the glycosidic linkage information into consideration. Thus it in effect takes into account the order of the children while being flexible to handle unordered trees. In terms of execution time, since we use local alignment dynamic programming, the computation time is $O(T{n}^2)$ where T is the number of trees, and n is the number of monosaccharides in the largest glycan being compared. In other words, this algorithm is loosely bounded by the largest glycans being compared times the total number of glycans. However, because glycan structures are not as large as proteins, the results on average are computed very quickly, and on our local computers they can be obtained in about 2–3 min on average.

5.2 Alignment experiments

The multiple alignment of glycans containing the sialyl-Lewis X structure showed that the motif could be aligned 100%, regardless of the location or presence of the motif across the glycans. In the execution of the MCAW tool using experimental data that measures glycan-protein interaction data from the CFG, polylactosamine was aligned at a high ratio at all the different concentrations of galectin-3, verifying knowledge in the literature (Fukumori et al., 2007). Note here that this same disaccharide motif can also be seen all along towards the non-reducing end, but that they are aligned with Ends.

At the highest concentration of Galectin-3 analyzed on the array, an additional fucose was found to be involved in binding, and in fact, recognition of Fucα1-2Gal by Galectin-3 has been suggested in the literature (Ideo et al., 2002). It is known that Galectin-3 recognizes lactosamine even when carbon 2 or 3 of the galactose is substituted by fucose, sialic acid, GalNAc or sulfate. We searched the structures on the array to see if other glycans containing these modifications were arrayed. The lactosamine structure with sialic acid attached was found on the array in various configurations: one with a maximum of three lactosamines and other structures with terminal sialo-lactosamines on multiple branches. However, all of these structures had low-binding affinity, so we could not see the effect of sialic acid or these other modifications on this array.

The proportion of the nodes aligned on the leaf side is low because the dataset of glycans interacting with galectin-3 contained long and short structures. When omitting the aligned monosaccharides taking up <10% of a position, all concentrations showed the same alignment. Nodes below 10% can be considered as noise, so they can be ignored. Therefore this result shows that the same profile pattern for galectin-3 can be seen across all concentrations. Even if the high-affinity glycans change due to the change in concentration of the GBP, a common glycan pattern was found regardless.

5.3 Comparison with other tools

To compare the results of MCAW with a similar tool, we ran the Glycoviewer tool (Joshi et al., 2010) with the same input that we used for MCAW. This input data and the Glycoviewer results are provided in Supplementary Figure S6. The alignment results for 2 and 5 µg show similar alignment diagrams, but different results were obtained with 10 µg. In particular, it was different in the position of fucose and how branched fucose and galactose were expressed. In Glycoviewer, fucose is expressed on two consecutive galactoses on two antennas of GlcNAc β1-2 Man (small red dots in the center of the yellow circles at four different locations). However, in MCAW, each fucose was found once on the two antennae of GlcNAc β1- 2 Man. This can be explained by the fact that MCAW can calculate and align with gaps, whereas Glycoviewer will align without considering gaps. By arranging the gaps, MCAW can extract profiles without scattering monosaccharides.

5.4 Future work

Our analysis was performed using the default parameters for w(u, v) in the MCAW dynamic programming algorithm, which we set to gap = −10, m = 60, a = 30, n = 30, r = 30. We have found that these parameter values are most suitable for the glycan data we have surveyed so far (data not shown). In the future, we will analyze the effects of modifying these parameters. Moreover, we will perform analysis of other GBPs to obtain more patterns of glycan structure recognition. Future work will focus on finding relationships between these patterns and protein sequence/structure. We will also consider ways to improve the result view similar to Glycoviewer which displays glycan profiles more visually with colors. This could be made an option for the user to select for their results.

As for future prospects of multiple glycan alignment, score matrices of glycans will now be possible to develop, as it greatly depends on multiple glycan alignment (Aoki et al., 2005). Glycan score matrices represent the similarity of monosaccharides bound by a glycosidic bond. By using score matrices for glycan structure comparison, a gradient can be used to compare monosaccharides as opposed to simply matching the same moosaccharides as zero or one. MCAW can also be applied to probabilistic models such as ProfilePSTMM (Aoki-Kinoshita et al., 2006) to determine the state model used for modeling glycan recognition profiles. Therefore, the development and availability of an effective multiple glycan alignment tool opens possibilities for many other glycoinformatics analysis, making this work a big step towards furthering glycomics analysis.