Inefficient crossover maturation underlies elevated aneuploidy in human female meiosis

Summary

Meiosis is the cellular program that underlies gamete formation. For this program, crossovers between homologous chromosomes play an essential mechanical role to ensure regular segregation. We present a detailed study of crossover formation in human male and female meiosis, enabled by modeling analysis. Results suggest that recombination in the two sexes proceeds analogously and efficiently through most stages. However, specifically in female (but not male), ~25% of the intermediates that should mature into crossover products actually fail to do so. Further, this “female-specific crossover maturation inefficiency” is inferred to make major contributions to the high level of chromosome mis-segregation and resultant aneuploidy that uniquely afflicts human female oocytes (e.g. giving Down syndrome). Additionally, crossover levels on different chromosomes in the same nucleus tend to co-vary, an effect attributable to global per-nucleus modulation of chromatin loop size. Maturation inefficiency could potentially reflect an evolutionary advantage of increased aneuploidy for human females.

eTOC blurb

Human female meiosis exhibits inefficient maturation of crossovers. This effect, alone and in synergy with other features, promotes high frequencies of aneuploid eggs.

Introduction

Meiosis is the modified cellular program that underlies sexual reproduction. To achieve the reduction in chromosome complement needed for gamete formation, one round of DNA replication is followed by two rounds of chromosome segregation. Maternal and paternal homologous chromosomes (“homologs”) segregate at Meiosis I (MI); sister chromatids then segregate at Meiosis II (MII).

Regular segregation of homologs at MI is ensured by the presence of physical linkages between homologs (chiasmata). Each chiasma is created by one DNA crossover (CO) in combination with cohesion between sister-chromatid arms. If chiasma(ta) are absent, or poorly placed, MI segregation is defective (Discussion).

The meiotic recombination process is broadly conserved from fungi to human (Figure 1; Hunter, 2015). However, we were interested to further explore this process in human male and female meiosis, for two reasons. First, female and male CO outcomes exhibit certain provocative differences whose explanation is not obvious. Second, human female meiosis uniquely exhibits an extraordinarily high level of MI mis-segregation as compared to human male or other organisms (reviewed in Nagaoka et al., 2012; Franasiak et al., 2014). Roughly 10% of human pregnancies involve trisomic and/or monosomic embryos whose aneuploidy is of maternal origin; and for women nearing the end of their reproductive lifespan, the incidence likely exceeds 50%. Segregation errors in the human male germline are significantly rarer (2–5%). It has long been suspected that female meiotic recombination might be “error prone” (e.g. Nagaoka et al., 2012; Cole et al., 2012). However, it has not been possible to understand whether this is really true and, if so, what type(s) of effect(s) might be involved.

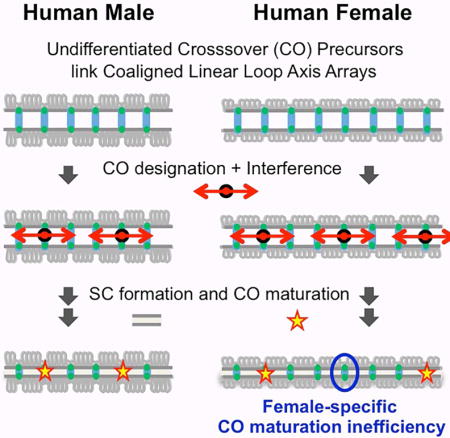
Figure 1. CO formation and patterning via chromosome structure.

Prophase chromosomes comprise co-oriented sister linear loop arrays, along which DSBs occur in tethered loop-axis complexes (top line). DSBs mediate homolog pairing via inter-axis bridge ensembles (green lines), which are presumptively the undifferentiated precursors acted upon by CO-designation and accompanying interference (red arrows). Via this process, CO-designation events are evenly spaced along the chromosomes and their number scales with physical chromosome length (compare male versus female). In contrast to male (left), in female (right) ~25% of CO-designated interactions fail to finally mature into an actual CO (bottom line). See also Figure S1.

To address these issues, we took advantage of extensive cytological data describing the number(s) and position(s) of CO recombination sites, along the pachytene chromosomes of human spermatocytes and primary oocytes (Gruhn et al., 2013; T.H. and P.H. unpublished; Figure 2AB). Analysis of these data reveals that female CO formation is defective, as compared to male CO formation; that this defect plays a major role in aneuploidy by increasing the levels of CO/chiasma configurations that are prone to mis-segregation; and that CO recombination in both sexes is subject to global per-nucleus regulation via modulation of chromatin loop size.

Figure 2. Analysis of male and female COs and SCs.

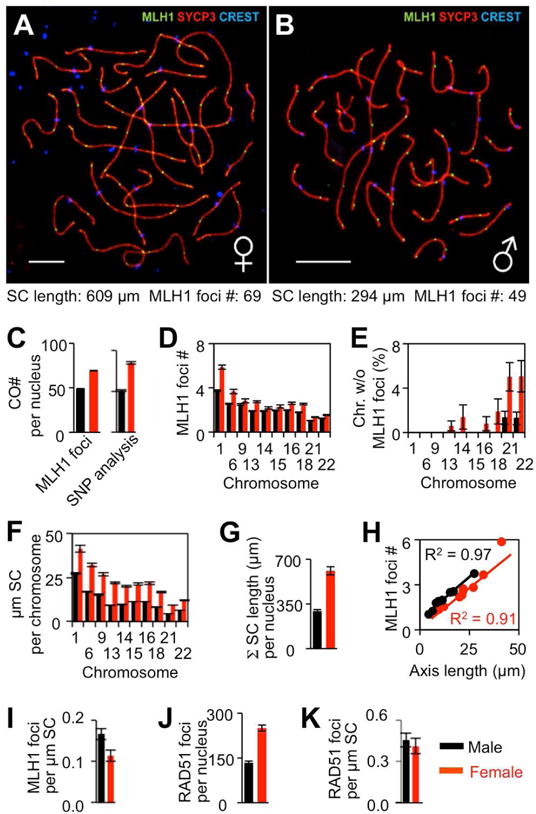
(A,B) Surface spread of pachytene bivalents in human primary oocyte (A) and spermatocyte (B). SC-linked axes are Immunostained by axis marker SYCP3, CO-diagnostic foci by MLH1 and centromeres by CREST. Scale bars, 10 μm. (C–K) Comparisons of chromosome features in males (black) and females (red). Bars = Standard Error (SE) in (C–G, J) and 95% confidence intervals in (I, K). p-values for male/female differences in (C–J) are <0.001, one-tailed, except in (D) p=0.06 for chromosome 9 and p=0.004 for chromosome 15. p=0.35 (K). p-values determined by Mann-Whitney test for (C), (D), (F), (G), (J); Fisher’s Exact test for (E); Pearson correlation test for (H) and from confidence intervals in (I, K). Data sources, sample sizes and further details of statistical analysis are given in STAR Methods. See also Figure S1.

Results

Background

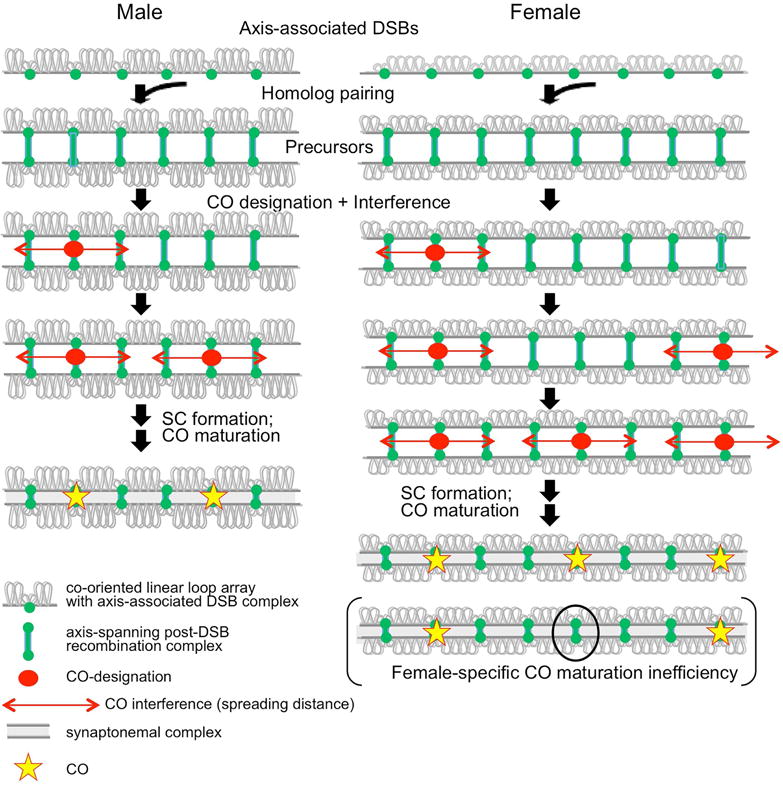
Human meiotic recombination utilizes the “standard” pathway (Figure 1; e.g. reviewed in Zickler and Kleckner, 2015; Zhang et al., 2014c; Hunter, 2015; Gray and Cohen, 2016). (i) Recombination is initiated by a large number of programmed DNA double-strand breaks (DSBs), which occur in recombination complexes that are directly associated with chromosome axes. (ii) DSBs then mediate pairing of homolog axes, giving coalignment at a distance of ~400nm. Total DSB/partner interactions are thus ultimately seen as discrete inter-axis “bridges” (also Figure S1). (iii) A small subset of DSB/partner complexes are specifically designated to become COs via a programmed spatial patterning process (below). Concomitantly, as a downstream outcome, synaptonemal complex (SC) forms, linking homolog axes along their lengths at a distance of 100nm. (iv) CO-designated interactions mature to actual COs via a series of further biochemical steps. Interactions not designated to become COs mature to other fates (not shown). (v) SC then disassembles and chromosomes reorganize. By diplotene, CO sites have further evolved into chiasmata, which link individualized homologs until segregation. Classically, these are “bivalents”, also used to mean “a pair of homologs”, regardless of stage.

Although COs tend to occur at different positions in different meiotic nuclei, they tend to be evenly spaced (Figure 1). This pattern reflects the classical phenomenon of CO interference: occurrence of a CO at one position is accompanied by a reduced probability that another CO will occur nearby. Current considerations favor a “fill-in-the-holes” model (e.g. Zickler and Kleckner 2015; Kleckner et al., 2004; Zhang et al., 2014a; Wang et al., 2015; White et al., 2017; Figure 1). An array of undifferentiated “precursor” interactions (e.g. inter-homolog bridges) is subjected to a CO-designation and interference process. The first precursor designated to become a CO, sets up a surrounding domain of inhibition (interference) that disfavors the occurrence of additional COs nearby. Since subsequent CO designations occur in regions away from established domains of inhibition, they fill in the holes between prior events, ultimately producing an array of evenly spaced CO-designated intermediates which then mature to CO products. As part of this process, every bivalent usually acquires at least one CO designation and thus CO, as required to ensure correct MI chromosome segregation (Jones and Franklin, 2006; Zhang et al., 2014b).

Given this “fill-in-the-holes” scenario, the final array of COs will be a function of several factors (Zhang et al., 2014a; White et al., 2017; STAR Methods): (i) the number and spacing of DSBs; (ii) the probabilities that DSBs will produce active “CO precursor” interactions; (iii) the distribution of sensitivities of those precursor interactions to the CO designation process; (iv) the strength of that CO-designation process; and (v) the way in which interference decays with distance. Importantly, the metric of this spreading CO interference signal is physical distance along the chromosome (i.e. μm) rather than genomic distance (Mb) as previously thought (e.g. Zhang et al., 2014a,b; Figure S1).

A Female-Specific Paradox: More COs than Males, but Some Seem to be Missing

CO positions and patterns in human germ cells can be defined by genetic analysis, molecular analysis of DNA polymorphisms (e.g. SNPs), chiasma analysis, or cytological analysis of foci of MLH1, which likely mediate the final step of CO maturation (e.g. Cheng et al., 2009; Lenzi et al., 2005; Figure 2AB). MLH1 focus analysis is particularly reliable (STAR Methods). Evaluation by all of these methods reveals that level of meiotic COs is ~50% higher in female than in male, both per nucleus and along each individual chromosome (Figure 2CD).

This male/female difference results from events that occur during or prior to DSB formation and is related to the fact that female chromosome axes are longer than male axes, as manifested in SC lengths (Figures 1, 2AB and 2FG; Gruhn et al., 2013; Lynn et al., 2002; Tease and Hulten, 2004; Bojko, 1985). CO number will thus scale directly with chromosome axis length as long as the density of DSBs (and thus CO “precursors”) and the strength of CO interference both remain constant (Kleckner et al., 2003). Both requirements are met for male versus female human meiosis. (i) DSB levels, as defined cytologically by RAD51 foci, are higher in female than male (Lenzi et al., 2005; Gruhn et al., 2013; Figures 2J and S1G). We show here that DSB density (Rad51 foci/μm SC length) is the same in both sexes (Figure 2K). (ii) CO interference is the same/similar in males and females as illustrated by direct comparison of MLH1 focus patterns in the present study and previous work (Figure S1; Hou et al., 2013; also e.g. Figure 3AB). Correspondingly, more COs occur in female versus male in relation to their relative axis lengths (Figure 2CD; below). This effect is ultimately attributable to variations in chromaitn loop size (Discussion)

Figure 3. Simulation analysis of male and female CO patterns.

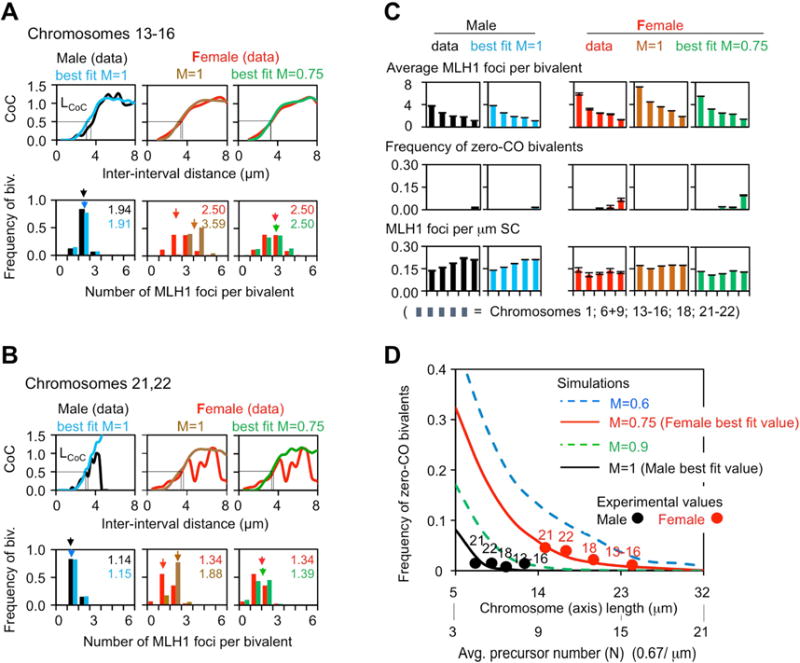
CO patterns from MLH1 focus analysis (male black and female red) were compared with patterns predicted from fill-in-the-holes simulation analyses performed under conditions of interest (text; STAR Methods). (A,B) Descriptions for two groups of similar chromosomes: 13–16 (A) and 21–22 (B). Top: Coefficient of Coincidence (CoC) curves; bottom: frequencies of bivalents with different numbers of COs (and the average). For CoC analysis, each chromosome is divided into a series of intervals. CoC is the ratio of the frequency of “observed” double COs to the frequency of “expected ”double COs, which is defined by the product of the CO frequencies in each of the two component intervals considered individually. A CoC curve plots this ratio, for every pair of intervals, as a function of inter-interval distance. In the presence of CO interference, the frequency of double COs is much lower than expected for closely-spaced intervals, increases to the level expected for independent occurrence (CoC = 1), and then fluctuates around that value due to the tendency for even spacing (STAR Methods and Figure S1). No rigorous statistical test exists to evaluate the difference between two CoC curves. However, a sensitive and reliable quantitative indicator is the inter-interval distance at which CoC = 0.5, “L_CoC” (STAR Methods). Examples of non-matching CoC curves are in Figure S3. (C) The goodness-of-fit of each simulated CO number distribution per bivalent as compared to the experimental data was evaluated by the sum of the squares of the differences (SSD): Chromosome 13–16: female M=1, SSD=0.353; M=0.75, SSD=0.004. Chromosomes 21, 22: female M=1, SSD=0.349; M=0.75, SSD=0.025. (D) Simulation-predicted frequencies of zero-CO bivalents as a function of chromosome length (or, equivalently, number of “precursors”, i.e. DSBs) at different levels of maturation efficiency (“M”) (STAR Methods). Note close matches of experimental (filled circles) and predicted (curves) values. See also Figures 4B, S2–S4. MLH1 data in Table S1.

Higher levels of zero-CO bivalents in female meiosis

Paradoxically, despite the fact that the total number of COs is higher in female than in male, the frequency of zero-CO bivalents is also higher in female than in male, for every measured chromosome (Figure 2E; Cheng et al., 2009; Gruhn et al., 2013). This difference has provided one indication that female recombination might be “error prone” (Nagaoka et al., 2012). It seems as if some COs are “missing” in female as compared to male.

Modestly lower CO densities along the SC in female meiosis

Moreover, although chromosome axis (SC) length and CO number are very tightly correlated for individual chromosomes, in both female and male (Figure 2H), in accord with the relationships described above and previous reports (Lynn et al., 2002; Kleckner et al., 2003; Zhang et al., 2014b) our analysis now also reveals an unexpected modulation of this relationship: the overall density of COs along the axes (i.e. number per μm SC length) is ~33% lower for the total genome complement in female versus male (Figure 2I), by 25–40% for individual chromosomes (Figure 2H). Since recombination initiation and CO interference appear to be the same in both sexes (above), this finding provides a second hint that some COs might be “missing” in female as compared to male.

Identification of Female-Specific CO Maturation Inefficiency

To evaluate how the recombination process could be compromised in female meiosis, we evaluated different possibilities with our previously-described recombination simulation approach, which allows us to quantitatively model CO patterns under various desired conditions (Zhang et al., 2014a,b; White et al., 2017).

Components of the recombination process, as parameterized for such simulations, comprise three functional groups (STAR Methods).

• Category I: Three features affect the final array of active “precursor” interactions (e.g. the “bridges” in Figures 1 and S1). (i) The average number of DSBs (N) as well as their spacing (E) and distribution among different nuclei (B); (ii) the efficiency with which a DSB progresses to an active CO “precursor” (Y); and (iii) the distribution of sensitivities of those precursors to the CO designation process (A; discussion in White et al., 2017).

• Category II: Features of the patterning process per se: (i) the strength of the CO-designation process relative to the sensitivities of precursors to that process (Smax) and (ii) the distance over which the interference signal acts (L), assuming exponential decay as a function of distance away from the designation site.

• Category III: The efficiency of CO maturation, i.e. probability that a CO-designated interaction will ultimately progress to an actual CO (M).

For modeling, a particular set of parameter values is selected and the simulation algorithm is applied (STAR Methods; White et al., 2017). Each simulation gives the predicted positions of COs along different “bivalents” (here, 5000). The resulting total population is then analyzed as desired. By carrying out such simulations with different sets of parameter values, one can identify the set of values that best explains a particular experimental data set. We showed previously that such best-fit simulations can very accurately describe both wild-type and mutant CO data in a wide variety of organisms, can reveal new features of CO patterning, and can be used to explore interplay among parameter values in theoretical situations (Zhang et al., 2014a,b; STAR Methods).

Here we applied such simulation analysis to human CO patterns, as defined by MLH1 foci, in both female and male, for all chromosomes for which data is available (a set comprising ten representative chromosomes of different shape and size; Figure 2D–F; STAR Methods). Data for chromosomes of similar length and CO pattern were grouped to provide larger sample sizes (e.g. 6+9; 13–16 and 21+22; Figures 3A–C, S1, S2, S3 and S5). The average number of DSBs is given by experimental data for RAD51 foci and per-chromosome SC lengths provide a proxy for axis lengths at all stages (Figures 2FG and S1G). Simulation outcomes are insensitive to modest variations in DSB number and thus to any potential imprecision in RAD51 focus identification (Figure S1).

We have evaluated various sets of parameter values for their ability to accurately predict two basic descriptors of CO (MLH1 focus) patterns: (i) interference relationships, which are defined by Coefficient of Coincidence curves and the diagnostic parameter L_CoC (explanations in Figure 3 legend, Figure S1 and STAR Methods); and (ii) the average number and distribution of CO(s) per bivalent, including the frequency of bivalents lacking even one CO (“zero-CO bivalents”).

In male, a best-fit simulation that closely matches experimental data can be achieved under parameter conditions that correspond to a very robust recombination process (Figures 3A–D and S2A,C). As in other organisms (Zhang et al., 2014a,b): (i) DSBs progress efficiently to CO precursors; (ii) the distribution of precursor sensitivities to CO designation is relatively regular; (iii) The strength of CO designation and the CO interference distance fall into reasonable ranges; and (iv) CO-designated interactions develop into mature COs with 100% efficiency (M=1).

For female, we first simulated CO patterns using the best-fit parameter values derived for male meiosis, but with the number of DSBs adjusted to the appropriate higher value. Such simulations do not give satisfactory outcomes when compared to experimental data, essentially because they predict too many COs. Both the number of COs per bivalent and the density of COs along the SC are too high; and the frequency of zero-CO bivalents is too low (Figures 3A–D and S3A). These results are concordant with, and thus further support, the idea that human female recombination gives fewer COs per μm axis length than male recombination due to a significant difference in the recombination process.

To ask specifically how female recombination might differ from male recombination, we systematically explored the consequences of changing each relevant parameter individually, over a suitable range of values. An excellent match between predicted and observed female CO patterns is obtained by a single change in which CO maturation efficiency is reduced from 100% in male to ~75% in female (M=1.0 versus M=0.75, range M=0.7–0.8 for different chromosomes; Figures 3A–D and S2B,C). This “Category III” change appropriately shifts the number and distribution of COs to lower values, including an appropriately increased frequency of zero-CO bivalents (Figures 3A–D and S2B). There is no change in CO interference. This is expected because reduced CO maturation efficiency cannot theoretically (and does not experimentally) alter CO interference and CO relationships as defined by CoC analysis (Zhang et al., 2014a).

Importantly, no satisfactory predicted match to experimental data could be obtained by altering any other feature (Figures S3–S5). Changes in the patterning process per se (Category II) fail to give any acceptable result because any variation that is large enough to significantly reduce CO levels also confers an alteration in CO interference relationships (e.g. Figure S3BC). Changes in any of the three features that reduce the number of active precursors (Category I) all have equivalent inappropriate effects. Plausible matches to experimental data for CO number/distribution can be obtained (Figure S5) but are not appropriate for two reasons. First, obtaining such a match requires severe degradation of the recombination process (Figure S5): a 50–60% reduction in the density of DSBs along the chromosomes which is not compatible with experimental RAD51 focus data (Figure S1G); a 50–60% reduction in the efficiency with which a DSB is converted to a precursor; or a highly skewed distribution of precursor sensitivities to CO designation (A=7 which, thus far, has not been required to explain any other experimental data; Zhang et al., 2014a,b; White et al., 2017). Second, these matches significantly alter CO interference relationships: predicted CoC curves rise too slowly, with a too-high L_CoC, implying a deficit of closely-spaced COs (Figure S5). This is an expected consequence of subtraction of (closely-spaced) precursors (Figure S7; Zhang et al., 2014a).

To further evaluate CO maturation inefficiency (Category III) versus pre-designation effects that alter the number of active precursors (Category II) as possible female-specific features, we examined their predictions for experimentally observed CO positions.

CO maturation inefficiency acts after CO-designation and interference have been imposed. Thus, it directly “subtracts” one or more COs from what would otherwise have been a relatively evenly-spaced array. Since most human chromosomes exhibit only a few COs per bivalent (one to four for shorter to longer chromosomes, e.g. chromosomes 22 to 9 in Figure 2D), subtraction of even one CO can have a relatively dramatic effect. In contrast, any effect that reduces the number of active precursors comes into play prior to CO-designation and interference and, to achieve a suitable reduction in COs, will require subtraction of multiple precursors at multiple different random positions from among a large number of actual/potential precursors. Such subtractions are unlikely to cluster in such a way as to dramatically alter the overall positions of COs that eventually arise.

To further evaluate which effect might pertain, we examined CO distributions along the two shortest chromosomes, 21 and 22 that exhibit the smallest number of DSBs/precursors and the smallest number of COs, and thus should be maximally sensitive to either type of “subtraction effect” (Figure 4 for chromosome 21; analogous results for chromosome 22 in Figure S5).

Figure 4. Female-specific CO maturation inefficiency: effects.

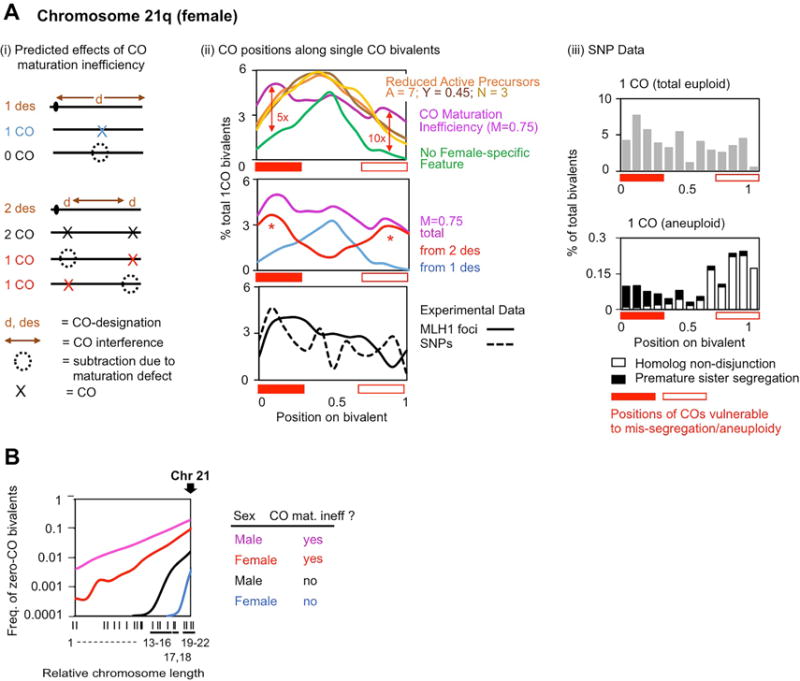
(A) Observed and predicted CO patterns on chromosome 21q. (i) Cartoon of predicted effects of CO maturation inefficiency on 21q bivalents with one (top) or two COs (bottom). (ii top): CO positions on single-CO bivalents as predicted by simulations to occur either: without any type of female-specific feature/deficit (green); with CO maturation inefficiency (purple); or with CO reduction by subtraction of active CO precursors prior to CO designation/interference (three different possibilities, gold, brown and orange; text). CO maturation inefficiency uniquely gives a broad distribution (purple) that matches the experimental distribution (II bottom; panel (iii) top) and results (II, middle) from the combined effects of single-designations with ensuing CO maturation (blue) or two designations, only one of which matures to a CO (red). Red open/closed bars: positions of COs in mis-segregation-prone bivalents (panel iii bottom). Red vertical arrows (top) and red asterisks (middle): contribution of CO maturation inefficiency to such bivalents. (iii) Experimentally-defined positions of COs along single-CO bivalents that have undergone either normal segregation (top) or mis-segregation (bottom) (adapted from Oliver et al., 2014). Mis-segregations are of two different types (filled and open vertical black bars). (B) Predicted frequencies of zero-CO bivalents for males and females, with and without CO maturation inefficiency (derived from Figure 3D). Arrow: position of chromosome 21. See also Figure S5.

Chromosome 21 comprises essentially a single arm (21q). COs on the short arm, 21p, are extremely rare and can be ignored. CO designation patterns are dictated by the effects of CO interference, which extends over ~60% the length of 21q (Figure 4A (i); brown “d”s). As a result: if a first CO-designation occurs near the center of the arm, interference precludes other CO-designations from occurring to either side; and if a first designation occurs near one end of the arm, it will be accompanied by a second designation at the other end of that arm (Figure 4A (i)). In the absence of any “subtraction” effects, these designation patterns would give, respectively, one centrally-localized CO (Figure 4A (i top), (ii top, green)) or two- widely-separated COs (Figure 4A (i bottom)) located near the two ends of the arm, as illustrated by simulation analysis (Figure 4A(ii top, green).

Given this baseline, the predicted consequences of the two different “subtraction” scenarios are dramatically different. CO maturation inefficiency creates a very different array of CO positions because ~25% of single-designation 21q bivalents will now have no COs and ~38% of double-designation bivalents will now have only a single CO which, importantly, will tend to occur at either one end or the other of the arm (Figure 4A (i)). As a result, single-CO 21q bivalents will now exhibit COs not only in the middle of the arm but also toward the ends, yielding a more even distribution along length of the arm than if CO inefficiency were absent (simulated in Figure 4A (ii) top, purple; middle, light blue, red and purple). In contrast, if CO levels are reduced by subtracting active precursor interactions all along the length of the chromosome, COs will exhibit the same tendency for central localization as that observed in the fully robust situation (simulated in Figure 4A (ii) top, brown/tan/gold versus green).

Strikingly, in experimental data, COs along single-CO 21q bivalents are broadly distributed (Figure 4A (ii) bottom; Figure 4A (iii) top). This pattern does not match that expected for a robust recombination process (compare with Figure 4A (ii) top green). It is also not the pattern predicted for inefficient development of active precursor interactions (Figure 4A (ii) top brown/tan/gold). Instead, it is exactly the pattern predicted to result from CO maturation inefficiency (Figure 4A (ii) top, middle purple). Importantly, these conclusions are apparent from simple qualitative consideration of the effects of CO interference (Figure 4A (i)). Simulations simply provide quantitative validation.

Taken together, the above considerations support the conclusion that human female recombination exhibits inefficient CO maturation, with the defect arising after CO-designation and before appearance of MLH1 foci.

CO Maturation Inefficiency Creates High Levels of Aneuploidy-Prone CO Configurations

Studies of human aneuploidy reveal that chromosomes which have undergone mis-segregation exhibit lower numbers and/or altered positions of COs as compared to regularly segregated chromosomes (Nagaoka et al., 2012; Oliver et al. 2012, 2014; Middlebrooks et al., 2014).

Two explanations could be envisioned. (1) Either recombination occurs regularly in female meiosis and bivalents with special mis-segregation-vulnerable CO configurations are relatively rare, but would be strongly selected for mis-segregation by later events, or (2) recombination is aberrant in such a way as to increase the frequencies of mis-segregation-vulnerable configurations and thus high levels of aneuploidy. Diverse considerations favor the latter hypothesis, with female-specific CO maturation inefficiency comprising the female-specific aberrancy.

Three CO patterns are characteristically associated with female aneuploidy. (i) The average number of COs per bivalent is lower. (ii) The frequency of chromosomes that lack even a single CO (“zero-CO bivalents”), and thus are intrinsically prone to mis-segregation, is higher. (iii) Involved bivalents have one or more COs but those COs tend to be distributed in certain particular configurations. By its intrinsic nature (above), female-specific CO maturation inefficiency is qualitatively predicted to increase the frequencies of all three effects. (i). CO subtraction will, by its nature, increase the frequency of bivalents with lower numbers of COs. (ii) Subtraction of CO(s) from a bivalent with one (or a few) CO-designation(s) will increase the frequency of zero-CO bivalents. (iii) Since CO interference normally generates a relatively even array of CO-designations (Figure 1, top), subtraction of CO(s) will necessarily increase the frequency of unique “uneven” configurations (e.g. Figure 1 right, bottom panel), among which would be the specific configurations that predispose a bivalent to mis-segregation.

Chromosome 21 exhibits one of the highest levels of aneuploidy in women of all ages; and trisomy 21 is compatible with viability, giving rise to Down syndrome (Nagaoka et al., 2012; Franasiak et al., 2014). This chromosome provided the first, most paradigmatic example of altered CO patterns in mis-segregating bivalents (Oliver et al., 2012 and 2014). CO patterns on mis-segregated chromosome 21q bivalents differ from those on regularly segregated bivalents in all three canonical respects. (i) The frequency of COs is ~30% lower: 1.23 versus 1.75 (Middlebrooks et al., 2014). (ii) The frequency of zero-CO bivalents is dramatically higher: ~45% versus ~6%. (iii) In bivalents with a single CO, those COs are located either very proximal (towards the centromere) or very distal (towards the telomere) (Figure 4A(iii) bottom, open and closed black boxes and red bars; Figure S5DE), rather than being spread along the length of the chromosome arm as in regularly-segregating bivalents (above; Figures 4A (ii) bottom and 4A(iii) top) (Oliver et al., 2014).

Simulation analysis predicts dramatic increases in the frequency of zero-CO bivalents (Figures 3D, 4B; below) and large increases in the frequencies of the two at-risk single-CO 21q configurations (Figure 4A(ii) top, red arrows comparing green versus purple), showing that these arise almost entirely from two-CO-designation bivalents from which one event has been subtracted (Figure 4Aii middle, compare red and blue). Together these subtraction effects also explain why total CO frequency is lower among mis-segregating bivalents as compared to normal bivalents.

CO maturation inefficiency appears to account also for essentially all of the aneuploidies with Zero-CO bivalents (sometimes called “non-exchange bivalents” or “E0’s”) that comprise 20–30% of trisomies for several chromosomes (e.g. Nagaoka et al., 2012). It is predicted to increase the frequency of zero-CO bivalents by 50- to 100-fold for the shorter chromosomes that are especially prone to mis-segregation (Table 1; Figure 4B, compare red and blue). Interestingly, in the absence of this CO maturation inefficiency, the frequencies of zero-CO bivalents in female would be dramatically lower than those observed in male meiosis (Figure 4B, compare blue and black). This effect occurs because female chromosomes are longer than male chromosomes and thus, absent CO maturation inefficiency, will have a lower probability of failing to acquire at least one CO designation.

Table 1.

CO maturation inefficiency accounts for almost all zero-CO aneuploidies.

	Zero-CO bivalents	Chromosome
13–16		18	21	22
A	Freq. observed (MLH1 foci)+	0.008	0.018	0.07	0.067
B	Freq. predicted with CO inefficiency*	0.016	0.015	0.09	0.07
C	Freq. predicted without CO inefficiency*	0	2×10−4	1.3×10−3	1.4×10−3
D	Increase due to CO inefficiency (A/C; B/C)	>100x	76x	70x	50x
	= reduction if CO inefficiency absent

⁺Data from Figure 2E;

^*Predictions from Figure 3D.

We next analyzed CO distribution in Chromosome 16, which is a small metacentric chromosome. Regularly-segregating bivalents exhibit an average of 3.4 COs per bivalent, which are well-distributed all along the chromosome (Figure S5F–H Hassold et al., 1995). In mis-segregating bivalents, the average number of COs per bivalent is reduced to 2.6 and this reduction is due to a specific deficit of COs in the middle of the chromosome, symmetrically on both sides of the centromere (Figure S5F–H; Hassold et al., 1995). CO maturation inefficiency can generate these configurations by subtracting COs from the central region of the chromosome (Figure S5GH).

Taken together, these observations imply that CO maturation inefficiency is an essential active contributor to the high levels of aneuploidy characteristic of human female gametes.

Nucleus-to-Nucleus Co-variation of CO Levels and of SC Lengths on Different Chromosomes

Aneuploidy for chromosome 21, which is associated with lower-than-normal number of COs (above), tends to occur in nuclei with lower numbers of total COs (Middlebrooks et al., 2014). This observation raised the possibility that, as a general feature of normal meiosis, in any given nucleus, CO levels might vary coordinately on all bivalents. Quantitative analysis shows that this hypothesis is correct, in both female and male meiosis. Within an individual nucleus, the number of COs on one bivalent (or group of bivalents) tends to be correlated with the number of COs on another bivalent (or group of bivalents) (Figure 5C). The same effect also occurs in other organisms (S.W. and L.Z. unpublished).

Figure 5. Variation in the total number of COs per nucleus.

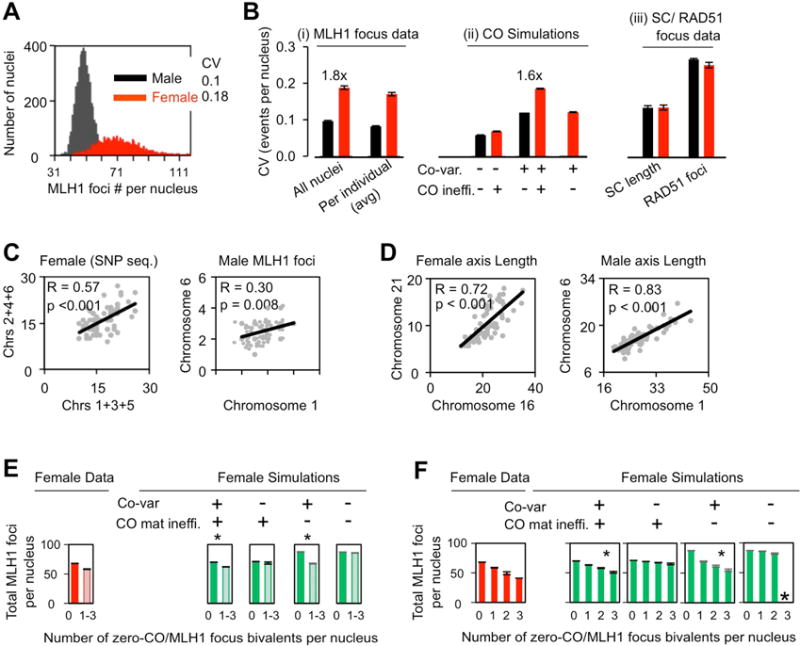
(A,B) Nucleus-to-nucleus variation in total CO levels is greater in female (red) versus male (black) due to global co-variation plus female-specific CO maturation inefficiency as defined by Coefficients of variation (CV). (A; B(i, left)) CVs of MLH1 foci per nucleus as defined for all nuclei taken together. (B(i, right)) Average CVs for each sex: CVs of total COs per nucleus were determined for all nuclei from each of 57 males and, separately, from 62 females. (B (ii)) CVs of total COs per nucleus (all individuals) were predicted by simulations under indicated conditions (text; STAR Methods). (B (iii)) CVs of total SC lengths per nucleus and total number of RAD51 foci per nucleus. (B): Bars = SE. Significances of male/female differences: (B (i left) p<0.001 (likelihood ratio test); (B (i right)) p<0.001 (t-test). (B (iii): For SC length, p=0.377; for RAD51 foci, p=0.61 (likelihood ratio tests). (C, D) (C, D) Co-variation of CO numbers (C), or SC lengths (D), on two different chromosomes (or comparable groups of chromosomes) within individual nuclei (Pearson correlation, one tailed). (E, F). Tendency of zero-CO bivalent(s) to occur in female nuclei with a lower total number of COs (E left); progressive clustering of multiple zero-CO bivalents in a single nucleus is correlated with a progressive decrease in the total number of COs per nucleus (F left). Simulations show that these differences are attributable to global regulation of CO levels whereas CO maturation inefficiency is not significantly involved (E right; F right). The goodness of fit of each simulated data set to experimental data was defined by SSDs: (E) Left to right: SSD=101, 62, 6, 432, 2. (F) Left to right: SSD=244, 124, 12, 439, 17; underlining marks cases with significant match (also see small asterisks). Large asterisk = no cases in 5000 nuclei. (A–F): data sources, sample sizes and further details of statistical analysis in STAR METHODS. See also Figure S6.

We further find that analogous co-variation is seen for axis (SC) lengths on different bivalents (or groups of bivalents) (Figure 5D). This further exemplifies the close correlation of axis length and CO number observed in other situations (above) and implies per-nucleus global modulation of chromatin loop size (Discussion).

Dramatic Nucleus-to-Nucleus Variation of Total CO Number in Female Results from Female-Specific CO Maturation inefficiency Plus Global Per-Nucleus Modulation

An additional unique feature of female CO patterns, as compared to male patterns, is that the total number of COs per nucleus varies dramatically from one nucleus to another, as seen by both MLH1 focus analysis and SNP analysis (Lenzi et al., 2005; Ottolini et al., 2015). Moreover, this effect is seen even among different nuclei from the same mother, and thus is not a consequence of higher genetic variability from one individual to another in female versus male (e.g. Cole et al., 2012; Gruhn et al., 2013; Figure S6A–D). Our MLH1 focus analyses robustly document both effects. On a population basis, the Coefficient of Variation (CV) for CO number per nucleus is 18% (0.18) in female, 1.8-fold that in male (10% or 0.1) (Figures 5A and Bi, left) and a very similar female/male difference is observed when the CVs for oocytes/spermatocytes from the same single mother/father are averaged, implying that the effect pertains for a single individual (Figures 5Bi and S6A–D). Correspondingly, in both sexes, CVs for different individuals are very similar (not shown).

We assessed the basis for higher per-nucleus variability in female using simulation reconstruction analysis. For each autosome, in female and in male, CO positions for 5000 bivalents were generated by the appropriate best-fit simulation. Then, for each sex, the resulting simulated bivalents were sorted into 5000 “nuclei”, for which the CV of total COs per nucleus could be determined (STAR Methods).

If the bivalents of different autosomes are sorted randomly (independently) into different nuclei, the outcome is much less nucleus-to-nucleus variability than is observed, for both sexes (albeit with a slight elevation in female versus male; CVs of 0.07 and 0.06, respectively; Figure 5Bii left). Thus: nucleus-to-nucleus variability in total CO number does not arise simply from the chance occurrence of nuclei whose bivalents happen to have independently acquired lower or higher CO numbers.

In contrast, simulation reconstructions that incorporate per-nucleus co-variation of CO levels on different bivalents (STAR Methods) gives predicted CVs that closely match experimental values in both sexes, and thus with greater variability in female versus male (1.6-fold predicted versus 1.8-fold observed; Figure 5Bi left versus 5Bii middle). Thus, global regulation plays a critical role in increasing nucleus-to-nucleus variability. This is sensible because global regulation will increase the frequencies of nuclei in which all bivalents tend to have very low or very high CO levels, thereby increasing the overall variability in CO levels per nucleus.

Importantly, also, for female meiosis, an appropriate outcome requires CO maturation inefficiency. (i) If female bivalents are generated by simulations that lack this feature (i.e. with a male-specific maturation efficiency of M=1), rather than the best-fit simulations for female (with M=0.75), the CV of total COs per nucleus in female is reduced to essentially the same value seen for male (Figure 5Bii red, right vs middle). (ii) The experimentally observed CVs for events that occur prior to CO maturation inefficiency, i.e. total DSBs (RAD51 foci) and total axis (SC) lengths per nucleus, are the same for male and female (Figures 5Biii and S6E), despite the fact that females have about twice DSBs number and axis length than males (Figures 2FG and S1G). Thus: the dramatically higher nucleus-to-nucleus variability in COs per nucleus in female results from the combined effects of female-specific CO maturation inefficiency plus global per-nucleus modulation of CO levels. The high CV of COs per nucleus in female is seen also by SNP assay (Figure S6C; Ottolini et al., 2015; Hou et al., 2013), thus confirming that female-specific CO maturation inefficiency is a fundamental effect, not a unique feature of MLH1 focus analysis (Figure S9; STAR Methods)].

Intriguingly, aneuploidies tend to occur in nuclei with lower-than-average numbers of COs (above; Middlebrooks et al., 2014; Ottolini et al., 2015) and oocytes with multiple mis-segregated chromosomes tend to occur in nuclei with lower total CO levels (e.g. Middlebrooks et al., 2014). Analogously, by MLH1 focus analysis: (i) nuclei with one or more zero-CO bivalents have lower total CO levels than nuclei lacking any such bivalent(s) (Figure 5E left); and (ii) nuclei with increasing numbers of zero-CO bivalents exhibit decreasing number of total COs per-nucleus (Figure 5F left). Simulations show that these effects result solely from global regulation of total per-nucleus CO levels, with no contribution of CO maturation inefficiency (Figures 5E right, 5F right). This conclusion matches the fact that global regulation is a collective effect whereas CO inefficiency affects each bivalent independently.

Discussion

Analysis of CO recombination patterns in human male and female meiosis reveals that female CO recombination is afflicted by a specific effect, CO maturation inefficiency, which is absent in male. Moreover, this feature creates high levels of specific chromosome configurations known to be vulnerable to mis-segregation and, thereby, is a major contributor to elevated female aneuploidy. The attribution of elevated female aneuploidy to a specific “defect” gives further weight to the notion that the phenomenon could be an evolutionarily favored trait. We further find that the total number of COs per nucleus is globally modulated on a per-nucleus basis, in both sexes, with implications for mis-segregation and aneuploidy. This and other effects implicate nucleus-wide modulation of chromatin loop size as a major general mechanism for regulation of CO frequencies.

Female-Specific CO Maturation Inefficiency: a Major Contributor to Human Female Aneuploidy

Early events of meiotic recombination, up to and including CO-designation, with accompanying CO interference, occur in the same, regular way in male and female meiosis, giving the typical array of evenly-spaced CO designations in both cases (above). However, in the female program (but not in the male program), ensuing maturation of COs is defective. As a result of this feature, ~25% of the recombination interactions that have been designated to be COs never become actual COs (Figures 3 and 4). This maturation inefficiency must arise at CO-specific step(s) that precede appearance of MLH1 foci, which is thought to mediate the final step of CO formation, resolution of double Holliday junctions (dHJs) into CO products (Hunter, 2015). Maturation inefficiency could thus arise during the first CO-specific step, in which the DSB/partner interaction at the leading double-strand break end is extended to give a single-end invasions, or the second major step, in which the lagging double-strand break end is incorporated into the developing recombination complex to give double Holliday junction (Hunter, 2015).

The current study suggests also that the high frequency of at-risk configurations is actively promoted by female-specific CO maturation inefficiency. The frequency of zero-CO bivalents, which mis-segregate due to intrinsic absence of any chiasmata, is predicted to increase by >50-fold for the shorter chromosomes and by orders of magnitude in longer chromosomes (Table 1). Maturation inefficiency also substantially increases the frequencies of non-zero CO configurations that are prone to mis-segregation, as illustrated for chromosomes 21 and 16 (Figures 4A (ii) and S5D–H). By implication, if female-specific CO inefficiency did not exist, the frequency of aneuploidy in human females would be significantly reduced.

CO Maturation Inefficiency Promotes Mis-Segregation by Both Direct and Indirect Effects

Most segregation errors occur, or are initiated, during the MI division (versus MII) (Nagaoka et al., 2012). At MI, homologs are physically connected by the combined effects of one or more COs/chiasmata plus links between sister chromatids along chromosome arms. As physically connected homologs are becoming bi-oriented at metaphase I (Figure 6A left), spindle forces cause tension to arise on homolog centromere/kinetochore complexes. This tension (and/or accompanying stretching effects) is critical for regular MI segregation, for two reasons. (i) It stabilizes kinetochore/microtubule attachments, reinforcing homolog bi-orientation (Tanaka, 2010). (ii) It stabilizes the MI-specific reductional/monopolar kinetochore configuration in which sister units are co-oriented so as to move to same pole. If tension is sub-optimal, sister kinetochores tend to deteriorate into the equational/back-to-back configuration characteristic of mitotic/MII segregation, giving premature segregation of sister chromatids at MI (Watanabe, 2012; Zielinska et al., 2015; Hugerat and Simchen, 1993; Figure 6A middle, right). In fact, premature separation of sister chromatids is a common type of mis-segregation (Nagaoka et al., 2012; Ottolini et al., 2015; Wolstenholm and Angell, 2000).

Figure 6. Contribution of CO maturation inefficiency to human female aneuploidy.

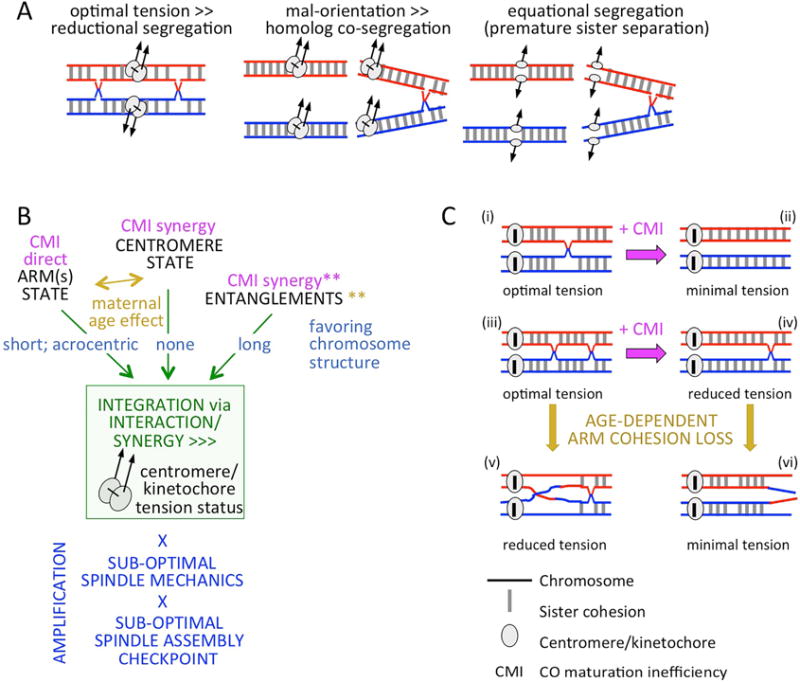
(A left): regular MI segregation. (A middle and right): two types of mis-segregation due to suboptimal level of tension imposed upon homolog kinetochore complexes (as created by absence of a CO/chiasma or presence of distal COs/chiasmata; illustrated for one arm only). (B) The kinetochore complex (rectangle) can serve as a hub for integrating diverse interactive/synergistic inputs (e.g. CO maturation inefficiency (CMI) and loss of sister cohesion (maternal age effect)) into its overall “tension status” as determined by the level of tension that is either exerted upon the complex, or is sensed or transduced by the complex to the segregation process (green arrows). **When persistent, entanglements can synergize with the above effects (text), or they can be resolved by CMI and age-dependent cohesion loss. Centromere/kinetochore tension status can also be amplified by sub-optimal spindle function and/or sub-optimal SAC (bottom, blue). (C) CMI can create the two at-risk configurations shown in panel (A): (i)–(ii) and (iii)–(iv). Age-dependent loss of cohesion can cause loss of chiasma(ta) from CO-containing bivalents (iv-to-vi) or reduced mechanical linkage between chiasma and kinetochore (e.g. iii-to-v). (Illustrated for one chromosome arm only).

Thus the tendency for MI mis-segregation will be favored by any chromosomal feature or configuration that either: (i) reduces the level of tension imposed on the kinetochore complex or (ii) alters the capacity of that complex to sense or transduce such tension (Figure 6B top). Further, since stress (e.g. tension) automatically redistributes throughout any mechanical system, the effects of two or more different sub-optimal features may be integrated within the kinetochore complex, giving interactive/synergistic defects (Figure 6B middle). In addition, human female oocytes are thought to be intrinsically sub-optimal with respect to both spindle function and to the spindle assembly checkpoint (review by Bennabi et al., 2016), which will, further exacerbate all sub-optimal chromosomal features (Nagaoka et al., 2012; Figure 6B bottom).

Given this framework, the “subtraction effect” of crossover maturation inefficiency has three primary consequences, each of which will, per se, compromise the tension arising on kinetochore complexes. (i) It increases the frequency of zero-CO bivalents. (ii) It increases the frequency of non-zero-CO bivalents whose CO(s) are located far from their centromere (Figure 6C (i)–(iv)), thereby reducing mechanical linkage between the chiasma connection and the centromere/kinetochore complex and, as a result, reducing tension (Figure 6A middle, right). (iii) Optimal tension arises when COs are present in both arms (Figure 6A, left). Subtraction will increase the frequency with which two-armed chromosomes have a CO on only one arm.

• -These direct effects of CO maturation inefficiency will also indirectly enhance/synergize with two other tension-compromising effects. (i) Centromere regions may be locally compromised, either because they are intrinsically genetically sub-optimal (Hugerat and Simchen, 1993) and/or because a chiasma is located too nearby, thus creating a zone of cohesion depletion that compromises the reductional kinetochore configuration (e.g. Storlazzi et al, 2008). (ii) Human female chromosomes are dramatically more prone to entanglement of unrelated chromosomes (“interlocks”) during the pairing process than are male chromosomes (Bojko, 1983). An interlock allows tension to arise inappropriately between unrelated chromosomes, while concomitantly disfavoring regular segregation. Moreover, interlockings are favored both by greater chromosome length per se and also by the accompanying larger numbers of CO linkages, which impede interlock resolution (Storlazzi et al, 2010).
• -Human female meiosis is prominently characterized by a dramatic progressive increase in aneuploidy with increasing maternal age. This “maternal age effect” is proposed to result from age-dependent loss of sister-chromatid cohesion (e.g. Wolstenholm and Angell, 2000; Storlazzi et al., 2008; Jessberger, 2012; reviews in Nagaoka et al., 2012; Handyside et al, 2012; Chiang et al., 2012). Thus: (i) loss of cohesion centromere-distal to all COs will eliminate the corresponding chiasma(ta) connections, minimizing tension (Figure 6C iv-to-vi). (ii) Loss of cohesion proximal to a CO can also reduce tension, by reducing mechanical linkage to kinetochore complex (Figure 6C iii-to-v). (iii) Loss of sister cohesion in centromere regions will locally compromise tension status. The first two effects will be exacerbated by the tendency of CO maturation inefficiency to give fewer COs, with a resultant increase in bivalents that have only more distally-placed COs (above) (Figure 6C (iii–iv); e.g. simulated for chromosome 16 in Figure S5D–H) and, via tension redistribution, will indirectly interact/synergize with the third effect. Additionally, all of these effects will interact/synergize with others of the chromosome structure-based effects, as well as with spindle mechanics/checkpoint effects.
• -Finally, as aneuploidy is dramatically more prominent on shorter and/or acrocentric chromosomes (e.g. Nagaoka et al., 2012; Franasiak et al., 2014), all of the subtraction effects of CO maturation inefficiency will be more prominent in such cases.

Taken together, these considerations suggest that, in human female meiosis, CO maturation inefficiency plays a major underlying role in promoting MI mis-segregation, and thus aneuploidy, both directly and via diverse indirect effects. We also note that CO maturation inefficiency provides an easy and robust way to significantly alter CO patterns via a single, mechanistically simple effect.

Is Aneuploidy an Evolutionarily Selected Trait?

Since female-specific CO maturation inefficiency effectively comprises “defect” relative to the normal process as seen in male, it seemingly should, or could, have been eliminated over evolutionary time. While the period of evolution of anatomically modern humans is relatively short, persistence of this feature in female meiosis raises the possibility that it might have an evolutionary advantage. Since the primary consequence of CO maturation inefficiency is elevated female aneuploidy, this high level of aneuploidy, itself, may be the evolutionarily-selected trait. The analogous argument has been made based on inefficiencies of human female MI spindle assembly and spindle checkpoint (Bennabi et al., 2016) and from the prominent maternal age effect in human as compared to mouse (Warburton, 1987; Nagaoka et al., 2012).

What could be the evolutionary advantage of increased aneuploidy? Since aneuploidy usually leads to implantation failure and miscarriage, an elevated level will increase the time between successive pregnancies, thereby preserving maternal resources and increasing the likelihood of long-term survival of live-born progeny (Warburton, 1987). Alternatively, or in addition, aneuploidy will decrease the likelihood of pregnancy when a woman is too old to raise children. In both cases, female aneuploidy could enable evolution of the protracted post-natal development requiring sustained parental/social investment that is likely to have been critical for evolution of the human species.

Global Modulation of Chromatin Loop Size as a Universal Modulator of CO Levels

The analysis above elucidates the basis for overall CO-SC length co-variation in human male versus female meiosis and documents, for both sexes, the existence of CO-SC length co-variation from nucleus-to-nucleus (which we also observe in other organisms; S.W. and L.Z. unpublished). In brief, CO number scales with axis length when DSB density (number per axis length) and CO patterning, including the distance over which CO interference spreads (in μm axis length) are the same. Thus, the observed co-variations imply global modulation of axis length on both a sex-specific and a nucleus-specific basis.

As development of chromosome axes results from the formation of a linear array of loops (Figure 1), axis length is determined by (and is inversely correlated with) chromatin loop size (e.g. Kleckner, 2003, 2006; Gruhn et al., 2013; Novak et al., 2008). Taken together these considerations imply that regulation of chromatin loop size comprises a major, universal mechanism for global regulation of overall CO frequency, with no required alteration in any basic aspect of the recombination process per se.

STAR METHODS

KEY RESOURCES TABLE uploaded as separate file

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to the Lead Contact Nancy Kleckner at kleckner@fas.harvard.edu.

METHOD DETAILS

CO assays

CO positions and patterns in human germ cells can be defined by genetic analysis, molecular analysis of DNA polymorphisms (e.g. SNPs), chiasma analysis, or cytological analysis of recombination complexes along pachytene chromosomes, e.g. foci of MLH1, which likely mediates the final step of CO maturation (e.g. Cheng et al., 2009; Lenzi et al., 2005; Hunter, 2015; Figure 2AB). MLH1 focus analysis is particularly powerful. (i) Large numbers of nuclei can be examined, from each of many individuals, permitting robust intra- and inter-individual quantitative analyses. (ii) Focus positions directly mark the locations of COs along the physical lengths of the chromosome as defined by the synaptonemal complex (SC), a structure that links the structural axes of maternal and paternal homologs. This is important because the entire program of meiotic recombination, from initiation through CO completion, occurs in biochemical complexes that are physically and functionally associated with the chromosome axes, with physical distance along the chromosome in μm axis length as the important metric throughout (e.g. above; Zhang et al., 2014a, 2014b). (iii) MLH1 focus positions report the primary outcome of CO recombination, prior to any potential effects of maternal age, which come into play only after completion of CO formation at the DNA level (Nagaoka et al, 2012). (iv) MLH1 focus analysis very accurately reports CO patterns. For both males and females, the number of COs defined by MLH1 focus analysis is very similar to that defined by SNP analysis (Figures 2C; STAR Methods (below); e.g. Cheng et al., 2009; Lu et al., 2012; Hou et al., 2013; Ottolini et al., 2015). Also, another feature seen specifically in female meiosis (dramatic nucleus-to-nucleus variability in CO number) is detected analogously by both assays (below). (v) The MLH1 focus data used for this study were obtained by parallel analysis of male and female nuclei (Gruhn et al., 2013; Table S1), permitting robust comparison between CO patterns in the two sexes.

Analysis of crossover patterns by CoC (Coefficient of Coincidence) relationships. (Figures 3, S1–S5)

CoC analysis is a classic way to define crossover interference because it directly represents the extent to which COs in two different intervals do or do not occur independently. Properly applied, CoC curves can accurately describe CO patterns (discussion in refs. Zhang et al., 2014a and White et al., 2017).

For the present study, CoC curves were obtained using the “Analyze crossover data” function in the beam-film program as described in refs. Zhang et al., 2014a and White et al., 2017. The starting point is a dataset of bivalents for which the positions of COs have been defined along each bivalent. Such a data set may be provided either by experimental or simulation analysis. For convenience, a bivalent is divided into a number of intervals of equal size. On each bivalent, each CO can be then assigned to a specific interval. The dataset of bivalents is then analyzed as follows. (1) The frequency of bivalents containing a CO in each given interval is defined. (2) Intervals are then considered two at a time, in all pairwise combinations. Each pair of intervals is then examined with respect to the frequency of “observed” double COs, i.e. the frequency of bivalents with COs in both intervals, and the frequency of “expected” double COs on the assumption that COs occur independently in the two intervals. The quotient of observed/expected is the Coefficient of Coincidence (CoC). The frequency of observed double COs is given by the dataset. The frequency of expected double COs is given by the product of the observed frequencies of crossovers in the two intervals considered individually. (3) The CoCs for all pairs of intervals are then plotted, for each pair, as a function of the distances between the two intervals, giving a CoC curve. Consistent with the fact that crossover interference is stronger in short distance from a crossover, the coefficient of coincidence value is very low at short inter-interval distances and increases with increasing inter-interval distance to a value of one (implying independent occurrence in the two intervals). Thereafter, the CoC value fluctuates around or above one, with values higher than one reflecting the tendency for COs to be evenly spaced at certain inter-CO distances. For accurate CoC analysis, a small interval size (and thus a large number of intervals) will give a better description of CoC relationships; however, larger numbers of intervals also require a larger data set to provide a statistically significant number of double COs. Thus the number of intervals (or the interval size) must be carefully considered. As discussed previously, the minimum number of intervals for a proper CoC curve analysis is roughly 5 times the average number of COs on that bivalent. This proportion is sufficient to give an accurate CoC curve and, in contrast to smaller interval numbers, minimizes the probability that a given interval on a given bivalent will acquire more than one CO, which obscures CoC relationships (more discussion in ref. Zhang et al., 2014a). In the present study, each chromosome or chromosome group is divided into 20 intervals (there is no difference for CoC curves when 30 intervals were used) except when otherwise indicated.

Beam-film (BF) simulation analyses. (Figures 3–5, S1–S5)

Detailed descriptions of the beam-film model and the program are in refs. Zhang et al., 2014a; Kleckner et al., 2004 and White et al., 2017. The program, which is written in MATLAB, can be downloaded at https://app.box.com/s/hv91q2nrtq0cp9n8iy9m.

In beam-film simulation analysis, as described in refs. Zhang et al., 2014a and White et al., 2017, there are three types of parameters. (1) The array of precursor interactions. These parameters define the average number of precursors per bivalent (N), the distribution of the number of precursors among each bivalent in different nuclei (B), the distribution of precursors on each bivalent (the extent to which precursors are evenly versus randomly spaced (E)) and a new parameter (Y) which defines the fraction of “active” precursors, i.e. the effective CO precursors (below). (2) The nature of the patterning process per se. These parameters define the strength of the CO-designation process (Smax), the interference distance (the distance over which the inhibitory interference signal spreads outward to both sides of a CO designation) (L) and the distribution of the relative strengths of precursor sensitivities (A). (3) The probability that a crossover designation will mature into to an experimentally detectable crossover (or crossover-correlated marker) (M). Complex biochemical reactions and chromosome structure changes are required for a CO-designated recombinational interaction to mature into a final CO product. A defect(s) in any of these effect(s) could decrease maturation probability. Parameter values for best fit simulations of CO patterns carried out for this study are presented in Figure S2C.

Best-fit simulations

There are two ways to get a best-fit simulation for a given data set (for more details, please see the Protocol S1 (“instruction for BF program”) in Zhang et al., 2014a). For new users, the simulation program can automatically scan a range of parameters to get a best-fit to an experimental data set based on the goodness-of-fit levels calculated by Projected Likelihood Score (PLS) with improvements (Zhang et al., 2014a). However the PLS is not an optimal maximum likelihood method, so when doing so, it outputs the results ordered by PLS and also outputs the results for all parameter combinations scanned. Thus the user can get the actual best fit by further comparing experimental and simulated data sets for CoC curves, the average number of COs per bivalent and the distribution of CO number per bivalents. And this can be further optimized by trial-and-error. To scan a large number of parameter combinations, the automatic method may take a long time.

For experienced users, this can be done manually, step by step as described below. (i) Decide the approximate values of N and L. The precursor level of N could be roughly estimated by total DSB levels (e.g. the number of RAD51 or DMC1 foci), total levels of inter-homolog events (COs+NCOs), numbers of inter-axis bridges (e.g. RPA foci), EM-defined SC-associated recombination nodules, etc. Fortunately, great precision in the value of N is not necessary because of the phenomenon of CO homeostasis, which tends to keep CO levels constant even despite variations in DSBs (discussion in Zhang et al., 2014a). The level of L was set roughly at the inter-interval distance at which CoC=0.5, which is a good indicator of the CO interference distance from our experience. Other parameters could be set according to the distribution of COs along the chromosome. (ii) Smax was set to optimize the fit between experimental and predicted CO number and distribution (especially the fraction of bivalents lacking a single CO, i.e. zero-CO bivalents, sometimes called “E0s”). (iii) The best-fit values for all parameters were obtained by trial-and-error.

Determination of the inter-interval distance at CoC=0.5 (L_CoC)

The best and classical way to describe the crossover interference is to use the CoC curve, and the best way to compare the crossover interference levels between two data sets (either simulated or experimental data sets) is to directly compare the two CoC curves. However, to directly compare two CoC curves is complicated given (1) there is no proper way for the statistical analysis and (2) high quality CoC curves require reasonably large data sets. As discussed previously (Zhang et al., 2014a,b), and from our experience, the crossover interference distance is roughly equal to the inter-interval distance at which CoC=0.5 (for convenience, we call this distance L_CoC). Thus, L_CoC is a good indicator for CO interference distance and allows the interference levels between two data sets to be easily compared. L_CoC can be obtained in either by visual inspection of the CoC curve or fitting a sigmoid function to the first part of the CoC curve, with the first part of the CoC curve defined as being from 0 to the mean distance between adjacent COs, and L_CoC defined by the sigmoid function as the value of x (the inter-interval distance) at y (the CoC) =0.5 (M.A.W. unpublished).

An L_CoC can be obtained directly from one CoC curve by either a manual or an automatic way. (1) Manually we can get the L_CoC as described in below: drawing a line to cross the CoC curve from the axis at CoC=0.5 parallel to the axis of inter-interval distance; and then draw a second line from this cross site to cross the axis of inter-interval distance and parallel to the CoC axis. And the value of the cross site on the inter-interval distance axis is L_CoC. (2) The automatic method which is written as a MATLAB application (M.W., unpublished). Briefly, we firstly get a “smooth” CoC curve by fitting the CoC data points to a sigmoid function and then we can find the inter-interval distance at CoC=0.5 from the function.

Simulations with reduced numbers of “active” precursors

In previous studies we have referred to the number of CO precursors. The number of such precursors can be easily and directly set with the precursor parameters N, B and E, which define, respectively: the average precursor number per bivalent (N), the number distribution among different nuclei (B) and the extent to which precursors tend to be distributed along a bivalent randomly or more evenly (E). In the present study, N is determined based on RAD51 foci and RPA foci (Gruhn et al., 2013; Lenzi et al., 2005; Oliver-Bonet et al., 2005), and B and E are determined based on studies from human and other organisms, and also best-fit simulations on short chromosomes (Oliver-Bonet et al., 2007; more discussion in Zhang et al., 2014a). However, it is not clear whether all Rad51/PRA foci are actually CO precursors. It could be possible (especially in human female meiosis) that a fraction of DSB sites labeled with a RAD51/RPA focus is actually in an “inactive” state such that they never become CO precursors. Here, to exclude the possible effects of “inactive precursors” on CO patterns in female, the number of active precursors was reduced by three different approaches. (1) The number of precursors was directly reduced by using a small value of N. (2) The number of active precursors was reduced by changing the parameter A. This parameter defines the relative sensitivities of different parameters to CO designation and it is possible to select a value of A that dramatically reduces the fraction of precursors that are sensitive enough to ever undergo CO designation under the conditions modeled. (3) Some precursors were randomly removed from the original precursor array (defined by N, E, B and a more typical value of A) to reduce the number of active precursors. This latter effect was achieved using a new parameter, Y, which represents the fraction of CO precursors can actually be used as such. Implementation of this parameter is described in White et al., 2017. All three approaches reduce the number of active precursors and thus exert their effects prior to CO designations. Correspondingly, all three approaches affect CO patterns very similarly. The following effects are observed:

To get a good fit for female meiosis, the number of active precursors must be dramatically reduced, to 40–50% of the level obtained based on the number of RAD51 and RPA foci (Text, Figure 4Aii legends and Figure S5A–C legends). This requirement stems from the existence of CO homeostasis, by which reductions in DSBs (active precursors) have less then commensurate effects on CO levels (Cole et al., 2012; Zhang et al., 2014a,b; Wang et al., 2015). Thus: only a big change of active precursor number can effectively change CO number and, essentially, the active precursor number required for a reasonable match to female data turns out to be the same as or lower than that in male. (ii) Interference relationships are also be altered modestly but significantly: the CoC curves rise more slowly with decreased precursor number, because of the interplay between the CO interference distance and the inter-adjacent precursor distance as discussed in Zhang et al 2014a. (iii) COs on single-CO bivalents will tend to be more centrally located because of the interplay between chromosome length and CO interference distance which are comparable on such chromosomes: when the first CO designation occurred close to the middle, the interference signal would inhibit further CO designation on both sides, however when the first CO designation occurs close to one end, a second CO designation could occur on the other end. Thus, on single CO bivalents, the CO would be located around the middle region (text Figure 4A(i)). As discussed in the text, dramatically reduced active precursors are unlikely to explain the patterns of COs seen in human female meiosis.

Simulation analysis is a powerful tool for studying CO patterns

Simulations were carried out using a set of mathematical expressions originally known as the “beam-film” model. This model was originally developed on the basis of a specific mechanical mechanism for CO patterning. However, in fact, it corresponds to a much more general scenario, the “fill-in-the-holes” model (text Figure 1), which is now broadly accepted in the field. If one accepts the basic logic of this scenario, the simulation model simply parameterizes various steps of the process that must exist for such a process, with the values for some of these parameters constrained by experimental data. Thus, it is essentially a convenient method for analyzing CO patterns according to the fill-in-the-holes logic. The only exception to this statement is that the model assumes that CO interference decays exponentially with distance away from the CO designation site. Other relationships can be imagined. However, it is our experience that changing this to, for example, linear decay (vs exponential decay) really doesn’t change very much. The most recently updated version of the program, with clear explanations of all features, will be published soon as an invited book chapter (titled with “Modeling of meiotic crossover interference as inspired by the beam-film model” in Meiosis for Methods in Molecular Biology (White et al., 2017)).

We note that the simulation model can accurately simulate the crossover number and distribution in multiple organisms (Kleckner et al., 2004; Zhang et al., 2014a, 2014b; White et al., 2017 and this paper). It can provide a framework for understanding the effects of mutations and other genetic variations (Zhang et al., 2014a, 2014b, White et al., 2017 and this paper), e.g. it was used to accurately simulate CO patterns to identify a top2 meiosis-null mutant for decreased CO interference, and inhere, to identify CO maturation inefficiency in human female meiosis. It can be used to explore the interplay among different aspects of the patterning process, and also the effects of different aspects, in theoretical scenarios, thus help to deepen our understanding of potential effects in more details, generate new hypotheses, e.g. it can be used to quantitatively simulate CO homeostasis and reasonably explain the relationships between several aspects of CO control, especially between CO homeostasis, CO interference and obligatory CO (Zhang et al., 2014a, 2014b).

Simulation of per-nucleus co-variation in axis length (= DSBs number) and its effects on the coefficient of variation (CV) of CO number per nucleus and the clustering of E0 bivalents. (Figures 5Bii and 5EF)

Axis length and the precursor array

1. The average axis length per nucleus is ~300 μm in males and ~600 μm in females (Gruhn et al., 2013; Tease and Hulten, 2004). Female meiosis has twice the axis length of male also at earlier stages, as observed from EM 3D reconstruction analysis (Bojko, 1985).

2. The human genome size is ~3000Mb. Assuming that each chromosome has the same ratio of Mb per unit length of axis (μm), in each sex, there would be ~10 Mb per μm in male and ~5 Mb per μm in female.

3. The average number of DSBs (and thus precursor interactions that are subject to CO-designation and interference) per nucleus is ~200 in males and ~400 in females (text; Figure S1G). Assuming that the number of precursors per unit length of axis (μm) is the same on all chromosomes in both males and females, and these precursors occur in about the same number along a given chromosome in different nuclei (discussion in ref. Zhang et al., 2014a), there would be one precursor per 1.5 μm axis length in both males and females.

4. Note: (i) since the BF program normalizes all analyses to chromosome length = 1, the L was defined as appropriate percentages of chromosome length, and total N was scaled with the absolute chromosome length. (ii) These criteria are also used to predict the frequencies of zero-CO bivalents (Figures 3D and 4B).

Simulation of CO formation

CO formation was simulated in male versus female meiosis and, in females, in the presence and absence of CO inefficiency. For this purpose, the same set of best-fit parameters was applied to all chromosomes in both sexes except for maturation efficiency (M). M=1 in males and, also, in the hypothetical case of females without CO inefficiency. In females with CO inefficiency (i.e. normal females), M= ~0.75.

Simulation of axis length variation

To mimic variation in axis length along a given chromosome from one nucleus to another in a relatively simple way, we mixed two simulated populations. The two populations were simulated with same set of parameters except that the axis length in one population was 20% shorter than the actual axis length (thus the precursor number is also 20% less, and consequently this population give less COs) while the other population is 20% longer than the actual axis length (thus the precursor number is also 20% more, and consequently this population give more COs). We then combined these two populations and recalculated the distribution of COs per bivalent and the CoC curve to confirm that this mixed population still fits the actual data.

Sorting bivalents into individual nuclei

We simulated CO formation for each of the 22 autosomes, in both males and females, as described above. Each simulation yielded 5000 different bivalents. We then sorted the bivalents emerging from these simulations into 5000 corresponding individual nuclei, in each of two methods. (1) Different chromosomes were assigned randomly into different nuclei. In this case, in each given nucleus, the states of the different chromosomes are independent and the resulting CV of COs per nucleus is low (although the CV is higher for the female case (M=0.75, without co-variation; Figure 5Bii) than in male (M=1, without co-variation; Figure 5Bii) or in female in the absence of co-variation (M=1; without co-variation; not shown)). (2) To sort different chromosomes into a single nuclei according to axis length, we first performed the simulation of axis length variation with two populations of different axis length as described above. Then, in each of the two simulated populations, we randomly sorted different chromosomes into single nuclei (above). Finally, the two populations of nuclei were summed. By this approach, half of the nuclei have longer axes (and CO numbers) on each of the 22 chromosomes while the other half have shorter axis (and CO numbers) on each of the 22 chromosomes. When these two populations are summed, the resulting whole population accurately mimics observed axis length and CO number variations (text). Note, when the two simulated populations were mixed and assigned randomly into different nuclei as in method (1), the CV of COs per nucleus is as low as that obtained from method (1).

Simulating the contribution of CO maturation inefficiency to at-risk CO configurations. (Figures 4A, S5C–H)

Chromosome 21

On chromosome 21, essentially all crossovers are on the long arm (21q). Crossover patterns on chromosome 21q for euploid and aneuploid gametes are well-defined by SNP analysis (e.g. Oliver et al., 2014). To explore the possible source(s) of the “at-risk” CO configurations that gave rise to aneuploidy, we simulated crossover patterns on chromosome 21q and compared the outcomes with experimentally-defined patterns. As a starting point, we carried out a best-fit simulation for crossover patterns on chromosome 21q. The thus-defined values for all parameters, including the interference distance (4.4 μm which is corresponding to L=0.55 for 21q) and the maturation defect characteristic of CO inefficiency (M=~0.75) are the same as the best-fit simulations for the whole chromosome (Figure S2) with the exception of one parameter which is related to “end-effects”. The value of this parameter, cL, was defined as 1.5, which is higher than the value for the entire chromosome. This change accommodates effects resulting from the fact that one end of 21q is the centromere, rather than a true end.

To explore the contribution of CO maturation inefficiency to crossover patterns, we then took two approaches. First, to determine the patterns that would be observed in the absence of this feature, we compared the outputs of simulations carried out under best-fit parameter values for 21q (M=0.75) with outputs of simulations carried out under the same parameter values except that maturation efficiency was set at 100% (M=1). Second, we explored in detail the consequences of the fact that CO inefficiency acts to “subtract” COs from an original array of CO designation sites (text). For this purpose, we began with the simulation at M=1, where the output effectively gives the arrays of “CO designation sites” along the bivalents. The 75% maturation efficiency was then applied to these arrays to give resultant arrays of “matured” COs, which could then be analyzed in further detail. Together these analyses permit the definition of CO patterns for relevant subsets of CO configurations, e.g.: (1) bivalents with one CO when M=1; (2) bivalents with one CO when M=0.75; (3) bivalents with one CO that arise from bivalents with two CO designations after one eliminated due to CO maturation inefficiency; (4) bivalents with one CO that arise from bivalents with one CO designation when M=0.75. For each of these cases, the CO density distribution along the chromosome was calculated and plotted as a function of position along the chromosome arm (13 intervals with equal size were used).

Chromosome 16

For chromosome 16, the contribution of CO maturation inefficiency to bivalents with at-risk crossover configurations was simulated by the same approach used for chromosome 21.

Description and prediction of aneuploidy levels for chromosome 21q

Plots of experimental data

For Figures 4A and S5D, plots of experimental data were adapted from ref. Oliver et al., 2014. The aneuploid cases comprise a mixture obtained from women in different age groups. The analyzed experimental samples comprised only single-CO bivalents, which were divided into three groups: “normal” euploid gametes, or aneuploid gametes, where the bivalents were categorized as having mis-segregated at either Meiosis I or Meiosis II. For each of the three categories, the experimental data defined the number of COs observed at different positions along the chromosome. For the current presentation (Figures 4A and S8DE) these data were converted to absolute percentages of total bivalents based on two considerations. First: the overall aneuploidy level for chromosome 21 is ~3% (Nagaoka et al., 2012). Second, on chromosome 21, the number of individuals with an apparent MII error is about half the number of individuals with an apparent MI error (e.g. Nagaoka et al., 2012; Middlebrooks et al., 2014).

Estimation of aneuploidies resulting from simulated CO patterns (Figure S5E)

Simulation analysis describes CO configurations in the total meiotic population (Figure 4A). Experimental analysis defines the CO configurations that appear in aneuploid gametes, which arise specifically from at-risk bivalent configurations, with different probabilities for different at-risk configurations. Thus, the array of CO configurations observed in aneuploid gametes reflects both the frequencies of different configurations in the total population and the relative probabilities that those different configurations will then ultimately give rise to aneuploidy. In order to simulate the way by which simulated CO configurations might give rise to aneuploid gametes (Figure S5E), it is necessary to make some assumptions as to the probabilities that different at-risk CO configurations will undergo mis-segregation. We therefore made the assumption that the probability, that a bivalent with a single CO will give rise to mis-segregation and thus aneuploidy, will increase with decreased distance from the CO to one end of the chromosome. This assumption emerged from visual comparison of the CO configurations in euploidies and aneuploidies. Systematic comparison of experimental SNP data (above) with simulated data (above) suggests that the data are well matched if pMI = −0.6*log(1.15)/log(1-d) and pMII = −0.83*log(1.3)/log(1-d). Here, pMI and pMII are the probabilities that a single CO bivalent developed to an MI or MII aneuploidy, respectively; d is the distance from the CO to the end of the chromosome. The optimally simulated MI and MII error levels as calculated from the above functions are graphed in Figure S5E. The good match between observed and predicted data (Figure S5E) validates the underlying assumption that the probability that a bivalent with a single CO will give rise to mis-segregation and aneuploidy will exponentially increase with decreased distance from the CO to one end of the chromosome, thus providing a quantitative relationship for the generally-assumed qualitative relationship that aneuploidy results from a CO being located too close to a chromosome end or too close to a centromere (as in the case of 21q).

CO density is lower in females than males

Much of the presented conclusions derive from analysis of MLH1 foci. Importantly, diverse lines of evidence suggest that MLH1 foci correspond very closely to the sites of interactions that ultimately form COs as detected by genetic analysis or SNP analysis of post-pachytene meiotic cells. Thus, female-specific CO inefficiency is an intrinsic feature of female CO patterns, not an “artifact” of MLH1 focus analysis.

The total level of COs is ~50% higher in females than in males

~70 and ~50 per nucleus in the two sexes, respectively, by analysis of CO-correlated MLH1 foci along spread pachytene chromosomes (Figure 2C left and also Cheng et al., 2009; Lenzi et al., 2005). This difference is observed on all analyzed chromosomes (Figure 2D).

By genetic analysis of COs (including SNP analysis of sperm/oocyte chromosomes and STRP analysis of family), the numbers in the two sexes are ~90 in female and ~55 in male (Figure 2C right and also Lu et al., 2012; Hou et al., 2013; Ottolini et al., 2015). There are many reasons to suspect a priori that genetic analysis may be less accurate than MLH1 focus, which agree with one another (above). But even considering that the genetic data are more accurate, the fundamental conclusion that CO density per μm SC is lower in female (and thus one manifestation of female-specific CO inefficiency) remains valid.

SC length: female ~600μm; male ~300μm (text)

CO density (MLH1): female 70/600=0.117; male 50/300=0.167; thus, female/male=70%; i.e. density in female is ~30% lower than in male.

CO density (Genetic COs): female 90/600=0.15; male 55/300=0.183; thus, female/male=80%; i.e. density in female is ~20% lower than in male. Thus, even in a “worst case scenario”, the estimate of CO density reduction in female based on MLH1 foci would be only slightly overestimated.

As noted in the text: Female-specific CO inefficiency is required to explain the high CV of COs/nucleus in female, which is seen by both MLH1 focus analysis and SNP analysis, and thus is not an “artifact” of MLH1 focus analysis.

The effects of CO inefficiency on chromosome 16

Chromosome 16 is somewhat longer than Chromosome 21, with a centrally-located centromere. Aneuploid gametes sometimes arise from zero-CO bivalents. However, most arise from bivalents that exhibit COs. Furthermore, among such bivalents, there is a specific depletion of events in the central region of the chromosome and a specific increase in events towards the ends of the chromosome (Figure S5F). Female-specific CO inefficiency is, once again, predicted to increase the frequencies of bivalents with such patterns. Aneuploidies exhibit an average of ~2.6 COs per bivalent. Two-CO bivalents may arise from two CO-designations without inefficiency subtraction (Figure S5G, top) or three CO-designations with subtraction of one CO (Figure S5G, bottom), which necessarily will skew the distribution towards one end or the other or both (Figure S5H). Just as for chromosome 21, the effect of such subtraction on the frequency of “at-risk” bivalent configurations is dramatic (Figure S5H).

QUANTIFICATION AND STATISTICAL ANALYSIS

Details of Statistical Analyses

CVs (Figure 5)

The levels of variation within different samples were determined as the ratio of the standard deviation to the mean, that is, the coefficient of variation (CV), which is also known as the relative standard deviation.

p-values for CVs (Figure 5)

The p values for the significant difference between two CVs were evaluated by a likelihood ratio test (Wang et al., 2013).

95% confidence levels

The 95% of confidence intervals (CI) of CVs (coefficients of variation) (Figure 5B) and of the percentages of chromosome without MLH1 foci (Figures 2E and 3C middle) were both estimated by bootstrap resampling with “bootstrp” function in MATLAB 2014b.

Standard Error

Figures 2E, 3C and 5B: the standard error (SE) was estimated from the 95% of CI as SE = ΔCI/3.92.

Figures 2I and 2K: the standard error of two means is calculated as described in Fieller 1940.

Figures 2CD, 2FG, 2J and 5EF: SE calculated with EXCEL.

Pearson correlations (Figures 2H and 5CD)

Pearson correlations and corresponding p values were analyzed in MATLAB with “corr” function

Sum of the squares of differences (SSD) (Figures 3AB and 5EF)

SSD analysis was used to compare the goodness-of-fit of a set of values obtained by simulation analysis, relative to experimental data, e.g. for the distribution of COs per bivalent (Figure 3AB) and the percentages of nuclei zero or some other number(s) of COs (Figure 5EF).

Sample Sizes

Figure 2 (C) MLH1 foci data: male, n=4660; female, n=2038. SNP data: male, n=91; female, n=81; (D, F, H) Chromosome 1 (male, n=139; female, n=83), 6 (male, n=174; female, n=30), 9 (male, n=58; female, n=34), 13 (male, n=139; female, n=109), 14 (male, n=142; female, n=70), 15 (male, n=139; female, n=83), 16 (male, n=204; female, n=63), 18 (male, n=187; female, n=100), 21 (male, n=302; female, n=218), 22 (male, n=313; female, n=161). (E) Chromosome 1 (male, n=185; female, n=83), 6 (male, n=174; female, n=30), 9 (male, n=58; female, n=34), 13 (male, n=139; female, n=171), 14 (male, n=142; female, n=70), 15 (male, n=130; female, n=45), 16 (male, n=247; female, n=120), 18 (male, n=187; female, n=158), 21 (male, n=421; female, n=279), 22 (male, n=428; female, n=217); (G) male, n=13; female, n=7; (I) males, SC length, n=13, MLH1 foci, n=4660; females, SC length, n=7, MLH1 foci, n=2038. (J, K) For male: RAD51 foci, n=44; SC length, n=13; for female: RAD51 foci, n=39; SC length, n=7.

Figure 5. (A, B (i left)): Total nuclei analyzed: Male, n=4660; female, n=2038. (B (i right)). CVs were determined for all nuclei from 57 different males and, separately, from 62 different females. (The average CVs for each sex are presented). (B (iii)) For SC length: male, n=13; female, n=7; for RAD51 foci: ale, n=44; female, n=39. (C) For CO number, female, n=68; male, n=71. (D) For axis length, female, n=85; male, n=71. Note re (C,D): For female SNP data, chromosomes are grouped for greater statistical significance. The same relationship is observed for all comparisons of pairs of single chromosomes (not shown). For male, MLH1 focus data and SC are shown for the same pair of longer chromosomes. The same per-nucleus co-variations of COs and of SC lengths are seen in several other organisms (S.W. and L.Z. unpublished). (E left) n=5412 and 472 for nuclei without and with zero-CO bivalents, respectively. (F left) from left to right, n=5412, 451, 20, 1.

Data Sources and Availability

The data used in this study are provided in Table S1.

Figure 2. Pictures, provided by T. Hassold; MLH1 foci and SC/axis length, from ref. Gruhn et al., 2013; SNP data, from refs. Lu et al., 2012 and Kong et al., 2004 (males); Hou et al., 2013, Kong et al., 2004 and Ottolini et al., 2015 (females).

Figure 3. MLH1 foci, from ref. Gruhn et al., 2013 and provided by T. Hassold.

Figure 4. Panel A, SNP data, adapted from ref. Oliver et al., 2014; MLH1 data, from ref. Gruhn et al., 2013 and provided by T. Hassold.

Figure 5. (A, B) MLH1 foci, RAD51 foci and SC length data, from ref. Gruhn et al., 2013 and provided by T. Hassold; (C) CO data are from refs. Ottolini et al., 2015 and Hou et al., 2013 for females and from refs. Gruhn et al., 2013 and T. Hassold unpublished for males. (D): SC data are from ref. Gruhn et al., 2013. (E, F) All data from T. Hassold.

Table 1. MLH1 foci from ref. Gruhn et al., 2013 and provided by T. Hassold.

Figure S6. 1, 10, 22, 27 (Gruhn et al., 2013); 2, 23 (Lynn et al., 2002); 3, 26 (Pan et al., 2012); 4 (Sun et al., 2008); 5 (Sun et al., 2006); 6 (Codina-Pascual et al., 2006); 7 (Sun et al., 2004); 8 (Hassold et al., 2004); 9 (Oliver-Bonet et al., 2005); 11 (Cheng et al., 2009); 12, 13, 14 (Tease et al., 2002); 15 (Lenzi et al., 2005); 16,19 (Campbell et al., 2015); 17 (Lu et al., 2012); 18, 21 (Coop et al., 2008); 20 (Hou et al., 2013); 24, 25, 28, 29, 30 (Tease et al., 2004).

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
Beam-Film Applications	Zhang et al., 2014a White et al., 2017	https://app.box.com/s/hv91q2nrtq0cp9n8iy9m http://projects.iq.harvard.edu/kleckner_Jab/lab-software
MATLAB	MathWorks	N/A
R code (likelihood ratio test of CVs)	Wang et al., 2013.	http://www.echobelt.org/web/UploadFiles/cvtest.html
Other
Data used in this paper	See “Data Sources” section	N/A

Supplementary Material

Suppl. Table S1. MLH1 focus data analyzed, Related to Figures 2, 3, S1–S3 and Table 1.

This table gives MLH1 focus positions on the 10 representative chromosomes analyzed in both male and female and also the length of each chromosome.

Suppl Fig 1. Figure S1. DSB-mediated recombination occurs in the context of chromosome structural axes with same (similar) interference distance (in μm) between male and female meiosis, related to Figures 1–3.

Recombination occurs in the context of chromosome structural axes. (A) Meiotic prophase chromosomes are organized as loop/axis arrays (Kleckner, 2006). Recombinosome complexes (not shown) form in sequences that occur in chromatin loops but are physically associated with underlying chromosome axes, giving a structure like that in (ii), although it is not known whether both sister loops are present in this structure or not. After a DSB forms (the double red arrow heads) within one loop, one end of the DSB is released and searches for its homolog partner. Once the partner is engaged, the two homolog axes are then brought into spatial juxtaposition by an unknown mechanism, yielding inter-axis bridges comprising DNA and recombination proteins. (B, C) Immunofluorescence analysis of human oocytes/spermatocytes. (B) DSBs can be visualized as RAD51 or H2AX foci at leptotene (Picture is adapted from ref. Lenzi et al., 2005). (C) At late leptotene, homologs are linked by inter-axis bridges, each of which is mediated by early recombination interactions includes RPA (picture is adapted from ref. Oliver-Bonet et al., 2007). CO designation with accompanying CO interference are thought to occur at late leptotene in human meiosis because CO-correlated recombination nodules (seen in EM) are visible during zygotene (discussion in Zhang et al., 2014c).

Same (similar) interference distance (in μm) among different chromosomes and between male and female meiosis. CO interference has classically been defined by Coefficient of Coincidence (CoC) analysis. For this purpose, a chromosome is divided into a desired number of intervals. In the present case, 20 intervals were used, and there is no difference for CoC curves when 30 intervals were used. Each observed CO is assigned to its corresponding interval. Then, for each interval, the frequency of COs per bivalent is defined. For a given pair of intervals, a particular frequency of bivalents will exhibit COs in both intervals; these are “observed” double COs. By comparison, the frequency of “expected” double COs can be defined on the assumption that COs occur independently in the two intervals as given by the product of the frequencies observed in the two intervals considered individually. The CoC for a given pair of intervals is the ratio of “observed”/“expected” double CO frequencies. To construct a CoC curve, CoCs are determined for all possible pairs of intervals and the resulting ratios are plotted as a function of the distances between the two involved intervals (“inter-interval distance”). When an inter-interval distance represented by more than one pair of intervals, the average CoC for all intervals is plotted (see Zhang et al., 2014a and STAR Methods for more details). A CoC curve begins at zero or a low level at short inter-interval distances and rises with increasing inter-interval distance. This pattern reflects/defines the fact that CO interference is stronger over short distances and decays in strength with increasing inter-interval distance until, finally, events in the two intervals are independent of one another and CoC = 1.

Later parts of the curves tend to fluctuate, in part because each inter-interval distance is represented by fewer interval pairs and in part because of intrinsic periodic fluctuations above/below CoC=1 due to the tendency of COs to be evenly spaced: at inter-interval distances corresponding to the average inter-CO distance (or multiples of this distance), there is a higher than average probability of observing a double CO (CoC > 1) (see Zhang et al., 2014a for further discussion).

Panels (D–F) show that CoC relationships are the same or very similar for male and female. (D) Data from SNP and MLH1 focus analysis, with averages for all chromosomes considered together. (E, F) MLH1 focus analysis for indicated individual/grouped chromosomes. Panel (E) compares male and female data for the indicated chromosomes/chromosome groups. Panel (F) compares all chromosomes in male (left) or female (right). Note that chromosome 1 behaves differently from all other chromosomes in both sexes, differently in male vs female.

There is no proper statistical test to evaluate the difference between two CoC curves. Thus, for these comparisons and others throughout this work, a first evaluation is made “by eye”, focusing on the rising part of the curve, which is most sensitive and reliable (see also the legend to Figure 3). Additionally, the inter-interval distance at which the CoC = 0.5 (“L_CoC”; STAR Methods) provides a simple, quantitative comparison (see Zhang et al., 2014a for more discussion).

Importantly, the metric for CO interference is known to be physical length along the chromosome (μm) rather than genomic length (Mb) (text; Zhang et al., 2014a, 2014b). Panels (D) and (E) show that the effective interference distance (e.g. L_CoC) as defined in μm is very similar for human male and female. It can be noted that early studies suggested that CO interference was weaker in female than in male (e.g. Campbell et al., 2015). This conclusion was based on analyses that used Mb as the metric of interference. However, female chromosomes have shorter loops than male chromosomes, and those loops are apparently spaced similarly in both cases (text and Figure 1). Thus, female chromosomes have fewer Mb per μm physical length as compared to male chromosomes. Correspondingly, if CoC curves are constructed using Mb as a metric instead of μm, interference seems weaker in female versus male, rather than the same or similar as is actually the case (above).

DSB/precursor numbers in males and females: per se and relation to the value of simulation parameter “N”. (G) Female meiotic prophase nuclei have approximately twice the number of CO precursors as male nuclei as shown by published results of RAD51 and RPA focus numbers in human male and female meiosis. The most reliable comparison is provided by Gruhn et al., 2013 who analyzed Rad51 foci in male and female nuclei in parallel (reporting 134 and 250, respectively; indicated in bold) but a similar ~2x ratio can be inferred also from other studies. Importantly, also, the number of RPA foci is similar to the number of RAD51 foci, implying that there is no decrease in the number of precursors from the early DSB stage (RAD51) to the bridge stage (RPA) (see Figure S1). With respect to the absolute numbers of precursors, we use values of ~200 and ~400 per nucleus in male and female meiosis, respectively, for all simulations unless otherwise noted. These values are somewhat higher than that reported by Gruhn et al. (2013) because that study slightly underestimated the number of precursors by only counting large round foci and are similar to values from other studies. (H,I) Simulations of CO patterns on chromosomes 13–16 in male and female are used as examples to show that modest differences in precursor number (±20% in these examples) have little effect on best-fit simulation predicted outcomes, implying that this level of imprecision in the number of precursors does not affect the validity of our conclusions. Thus robustness of CO levels is attributable to strong crossover homeostasis, which buffers CO numbers against variations in precursor number (Zhang et al., 2014a). CoC curves were done as in Figure S1 legend (see STAR Methods for more details).

Suppl Fig 2. Figure S2. Best-fit simulations for individual or grouped chromosomes in male and female, related to Figure 3.

CoC curves were constructed as in Figure S1 legend (see STAR Methods for more details). The average number of COs and frequency of bivalents absence of the obligatory CO (E0) are also shown. Parameter values for best-fit simulations are given in panel C. Values for all parameters are the same or very similar for male and female except that M=1 for male and M=~0.75 for female (explanation in text). Includes data also shown in Figure 3. (C) Parameters used for best-fit simulations. *As described in STAR Methods and refs. Zhang et al., 2014a and White et al., 2017, L_BF defines the distance over which CO interference is effective. This distance is similar among all chromosomes and between male and female (~4.5 μm); Smax corresponds to the strength of CO designation; A defines the distribution of the relative strengths of precursor sensitivities to CO designation. The average number of precursors (N) is calculated based on chromosome length assuming ~200 and ~400 precursors in male and female meiosis (and thus 0.67 precursors per μm SC length for both male and female), respectively. B defines the distribution of the number of precursors among different nuclei. E defines the distribution of precursors along chromosomes, i.e. the extent to which precursors tend to be evenly vs randomly spaced. cL/cR defines the conditions of chromosome ends, and in simulations in this study both ends configured so as to give more regular CO numbers near chromosome ends (technically, “over-clamped”). Y defines the fraction of “active” precursors. M defines the CO maturation efficiency. In female, M is ~0.75 which means ~25% CO designations did not develop into detectable crossovers (see text).

Suppl Fig 3. Figure S3. Female data are not well-explained under the assumption of 100% CO maturation efficiency or with changes to patterning parameters Smax and L (Category II; text), related to Figure 3.

Simulations of MLH1 focus data were carried out with the same parameters as for best-fit simulations of the corresponding chromosomes (Figure 3; Figure S2) but with the indicated changes. (A) M=1 (vs M=0.75) gives too many crossovers, shown here for additional cases beyond those in Figure 3. (B) Decreased Smax implies a weaker CO designation process. Such a change can provide a proper number of average crossovers but concomitantly shifts the CoC curve to right, implying a decrease in nearby COs. This effect reflects a decreased capacity for CO-designation to overcome the inhibitory effect of CO interference, which is stronger over shorter distances. (C) Increased L implies an increase in the distance over which CO interference spreads. The effect is analogous to that achieved by decreased Smax. CoC curves were done as in Figure S1 legend (see STAR Methods for more details).

Suppl Fig 4. Figure S4. The effect of single parameter changes on the best-fit results, illustrated with male chromosome 1, related to Figure 3.

(A) Simulations using best-fit parameters in Figure S2C. (B–H) Simulations of MLH1 focus data carried out after changing only one parameter, relative to best-fit parameters, illustrate the robustness of the best-fit simulation parameters. (B) Reduced maturation efficiency (M=0.75) results in too-few COs while not changing CO interference (as documented in more detail for effects on female CO patterns in the text). (C–F) Changes in several other parameters alter both CoC relationships and CO number/distribution. (C, D) Changes in patterning parameters (text Category II) (further discussion in Figure S3). (E) A=7 changes the distribution of precursor sensitivities from a uniform distribution (A=1 in the best-fit simulation) to a distribution in which precursor sensitivities exponentially decreased, thus most precursors are suppressed as inactive states (White et al., 2017). (F) Parameters cL and cR define end effects. A reduction from the best fit values from cL, cR=1.1 to cL, cR=0.5 has the effect of suppressing COs near the chromosome ends over a distance comparable to the distance over which interference spreads (Zhang et al., 2014a; White et al., 2017). (G, H) Parameters B and E define, respectively, the distribution of precursor number among different nuclei (B) and the extent to which precursors tend to be evenly spaced along each individual chromosome (E). Variations in these parameters have little effects on long chromosomes, e.g. chromosome 1 as illustrated here. However, the value of parameter B is critical for crossover patterns on short chromosomes and the value of parameter E similarly has more obvious effects on crossover patterns on short chromosomes (more discussion in ref. Zhang et al., 2014a). Best-fit simulation values were therefore optimized based on analysis of shorter chromosomes and experimental results (discussion in ref. Zhang et al., 2014a). CoC curves were done as in Figure S1 legend (see STAR Methods for more details).

Suppl Fig 5. Figure S5. CO maturation inefficiency contributes to CO distributions in aneuploidies, but the decreased number of active precursors cannot explain female CO patterns, related to Figures 3 and 4.

Simulation analysis of CO patterns involves specification of three types of parameters that describe the array of CO precursors (I), the patterning process per se (II) or the efficiency of CO maturation (III). Female CO patterns are not well fit using the same parameter values that give best-fit simulations of male CO patterns but are well fit if, uniquely, maturation efficiency is reduced from the male value of M=1 to M=0.75 (text, Figure 3, Figure S2). In contrast, female CO patterns cannot be well fit if, uniquely, the values of patterning parameters are altered (Figure S3). Female CO patterns are plausibly fit by changes in Category I parameters that reduce the total number of active CO precursors but, finally, fail to explain the distribution of COs along chromosomes (and, as a result, the high levels of error-prone bivalents that arise in female meiosis (text, Figure 4; below)). Three different Category I changes have essentially equivalent predicted effects, resulting in effective subtraction of multiple precursors randomly along the chromosomes (relative to the array that would have occurred in the absence of these changes): (i) a 50–60% reduction in total DSBs; (ii) a 50–60% reduction in the efficiency with which DSBs “mature” to active CO precursors; and (iii) a change in the distribution of precursor sensitivities to the CO designation process that dramatically reduces the proportion that will be adequately sensitive to undergo CO designation (discussion in Figure 4Aii and White et al., 2016).

Panel (A) illustrates the plausible fit between experimental data (red) and simulation predictions that involve reductions in either maturation efficiency (green; M=0.75) or the number of active precursors (brown, tan, gold) with respect to female CO interference and CO numbers and distributions as illustrated for chromosome 21. All three changes that reduce the number of active precursors have similar effects.

Panel (B) illustrates that, with respect to CoC relationships on three chromosomes/chromosome groups: (top) all three changes that reduce the number of active precursors have similar effects; (middle) simulations with M=0.75 give very close matches to experimental CoC relationships; and (bottom) simulations with reduced precursor levels systematically give CoC curves that rise too slowly as compared to experimental data or simulations with M=0.75. Since this type of effect is characteristic of reduced precursor levels (Zhang et al., 2014a), these data provide strong evidence that female CO patterns cannot be explained by such a reduction.

Panel (C) shows analysis of the CO position distribution along the long arm of chromosome 22, 22q. COs on the short arm, 22p, are rare and can be ignored. A simulation that incorporates CO maturation inefficiency results in a broader distribution of COs along the chromosome arm that matches the experimental distribution. In contrast, simulations that incorporate precursor reductions all give a narrower distribution. Asymmetry in the distribution reflects effects of the centromere located at the left end of the arm. These effects are exactly analogous to those seen for chromosome 21 (text; Figure 4A). The basis for these effects is likely the same in both cases, since the two chromosomes have similar sizes and structures.

Parameter values for simulations are as follows (male-analogous values; Figure S2C). Values of other parameters for the presented cases are: Panels (A, B) chromosome 21: M=0.75; A=7; Y=0.4; N=3. Panel (B) chromosome 13–16: M=0.7; A=7; Y=0.4; N=5. Chromosome 6+9: M=0.72; A=7; Y=0.4; N=7. Panel (C) chromosome 22q: for the best-fit, L=0.5, Smax=3.8, cL=1.8; cR = 0.8, M=0.74; for the reduced number of active precursors A=7; Y=0.5; N=4.

The contribution of CO maturation inefficiency to CO distributions in aneuploidies. (D,E) chromosome 21q; (F–H) chromosome 16. (D) For single-CO cases, the CO densities for the two types of aneuploid gametes (top, bottom) of chromosome 21q (adapted from ref. Oliver et al., 2014). MI errors are homolog non-disjunctions; MII errors probably actually result from premature sister separation at MI (Nagaoka et al., 2012). (E) Distributions of CO positions in aneuploid gametes predicted in the presence (purple) or absence (green) of CO maturation inefficiency as compared to the observed distributions (grey; smoothed versions of data in panel (D)). Simulations assume that the probability of mis-segregation/aneuploidy decreases exponentially with the distance of the CO from the adjacent end of the chromosome arm (STAR Methods).

(F–H) Role of female-specific CO maturation inefficiency for aneuploidy on chromosome 16. (F) Genetic maps constructed from analysis of euploid and aneuploid gametes of chromosome 16 showing loss of COs in the middle region (light blue) versus end-proximal regions (orange) (adapted from ref. Hassold et al., 1995). (G) Female-specific CO maturation inefficiency “subtracts” COs from primary patterning-mediated arrays of CO-designation sites, creating irregular patterns on non-zero-CO bivalents, illustrated for specific relevant cases. (H) Positional distributions of two-CO bivalents of chromosome 16 as defined by simulations. Total arising without (green) or with (purple) inclusion of CO inefficiency. Among two-CO bivalents that arise when CO-inefficiency is included (purple), most (~90%) arise by “subtraction” (3des. > 2CO; red) rather than no subtraction (2des. > 2CO; blue) (G).

Suppl Fig 6. Figure S6. Higher CVs of CO number in females than in males (A–D) but similar CVs of SC/axis length in females and males (E), related to Figure 5.

(A) CVs for total MLH1 foci per nucleus in males (black) and females (red). (B) CVs of CO number per nucleus in spermatocytes (B, left), oocytes (B, right), sperm (C, left) and eggs (C, right) from several data sources and the average CV. (D) CVs of CO number per bivalent in spermatocytes (black) and oocytes (red). The significance of difference between males and females were evaluated by a likelihood ratio test (Wang et al., 2013), all p<0.001. Sample size is the same as Figure 2D. (E) Both male and female have similar CV of SC/axis length. Spermatocyte and oocyte CVs of the number of the CO from pachytene MLH1 foci data; sperm and egg CVs from SNP data. Bar = SE. See STAR Methods for data sources.

SOFTWARE AVAILABILITY.

Human crossover patterning was simulated using custom MATLAB scripts (“The Beam Film Program”). The Beam Film program was used for analysis as described in METHOD DETAILS above. The Beam Film applications (Zhang et al., 2014a; White et al., 2017) can be downloaded at https://app.box.com/s/hv91q2nrtq0cp9n8iy9m or from the website of Kleckner lab at http://projects.iq.harvard.edu/kleckner_lab/lab-software.

Highlights.

Human female meiosis, uniquely, exhibits crossover maturation inefficiency Maturation inefficiency creates crossover configurations prone to mis-segregation Maturation inefficiency is synergistic with other features for increased aneuploidy Global modulation of chromatin loop size underlies crossover level variation