Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2017 Apr 5;2(4):1302–1308. doi: 10.1021/acsomega.7b00053

Hamming Distance as a Concept in DNA Molecular Recognition

Mina Mohammadi-Kambs †,*, Kathrin Hölz ‡, Mark M Somoza ‡, Albrecht Ott †
PMCID: PMC5410656  PMID: 28474009

Abstract

graphic file with name ao-2017-00053h_0010.jpg

DNA microarrays constitute an in vitro example system of a highly crowded molecular recognition environment. Although they are widely applied in many biological applications, some of the basic mechanisms of the hybridization processes of DNA remain poorly understood. On a microarray, cross-hybridization arises from similarities of sequences that may introduce errors during the transmission of information. Experimentally, we determine an appropriate distance, called minimum Hamming distance, in which the sequences of a set differ. By applying an algorithm based on a graph-theoretical method, we find large orthogonal sets of sequences that are sufficiently different not to exhibit any cross-hybridization. To create such a set, we first derive an analytical solution for the number of sequences that include at least four guanines in a row for a given sequence length and eliminate them from the list of candidate sequences. We experimentally confirm the orthogonality of the largest possible set with a size of 23 for the length of 7. We anticipate our work to be a starting point toward the study of signal propagation in highly competitive environments, besides its obvious application in DNA high throughput experiments.

Introduction

Molecular recognition in the crowded environment of DNA microarrays plays an important role in processing information. Recognition often requires the discrimination of one specific molecule among many similar, competing molecules. In 1894, Emil Fischer proposed the lock and key model to describe the recognition of an enzyme and a substrate.1 According to this model, the substrate possesses the perfect size and shape to accommodate the active site of its complement. However, in crowded environments, binding between noncomplementary molecules may occur and result in introduction of errors. For DNA, specific-binding of two single strands, that is the formation of a stable double helix, occurs only if the bases A and T as well as C and G pair along the sequence. DNA microarrays are a widely used platform that, besides many applications in medicine and biology, enables the study of the fundamentals of DNA hybridization.2−10 These microarrays consist of single-stranded DNA oligonucleotides immobilized on a surface (probes). If these probes are exposed to a bulk mixture of fluorescently labeled target sequences, only complementary targets are expected to hybridize. However, hybridization of a probe to a noncomplementary target still occurs, albeit with a lower binding affinity than the corresponding perfectly matching sequence. Therefore, similarities among probes can lead to a significant amount of nonspecific cross-hybridization. On a DNA microarray with complex target mixtures, imperfect recognition introduces noise and makes results difficult to interpret.

The kinetics of hybridization in the presence of competitors and the importance of cross-hybridization for quantitative interpretation of microarray data have been intensely studied,11−13 especially for the purpose of single nucleotide polymorphism detection and the accurate assessment of gene expression levels.14−17 One strategy to avoid cross-hybridization is to construct sets of probes with minimized pairwise competition so that they do not cross-hybridize. Such probes are often referred to as orthogonal. Previous theoretical research18−24 developed different strategies to find sets of orthogonal sequences. The most intuitive approach to decide, which sequences cross-hybridize, is based on the free energy difference between the perfectly matched and mismatched hybridization.25 However, estimating free energies led to poor predictions of hybridization intensities on microarrays.26 In this work, we apply a well-known local search algorithm and implement graph-theoretical methods to find such sets. Following the concept of Hamming distance from coding theory, we consider that two sequences do not cross-hybridize if they differ by at least a certain number of bases. This threshold is called minimum Hamming distance d.27 We determine a suitable d experimentally. One of the fundamental problems in coding theory is finding the maximum size of a code, where a code is a set of codewords with the length L and minimum Hamming distance d.28 In analogy, here, we experimentally and theoretically find maximal sets of independent (i.e., orthogonal) sequences (MIS) with a certain minimum Hamming distance that can coexist on a microarray without exhibiting cross-hybridization.

Results and Discussion

Theoretical Results

For a given strand with L bases, according to all permutations of DNA bases (A,C,T,G), there are 4L distinct sequences. However, some of these sequences exhibit undesired structures that prevent them from binding to their complement. An example is the sequences with runs of at least four guanines that we call 4G sequences. These sequences are capable of forming complex structures such as G-quadruplexes, which restrict hybridization. Moreover, they have abnormal affinities and tend to show increased cross-hybridization and reduced target-specific hybridization, which makes the measurement of gene expression unreliable.29−31 Therefore, in this work, we eliminate 4G sequences and their complement sequences 4C. The number of sequences for a given length L that exhibit at least one run of 4G is given as

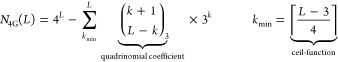graphic file with name ao-2017-00053h_m001.jpg 1

where the sum represents the number of sequences that are not 4G. The quadrinomial coefficient equals the number of permutations of L–k guanines within a sequence length of L (for the derivation of eq 1, see section S1).

To verify eq 1, we numerically calculate N4G(L) by generating 4L sequences for a given L ≤ 7 and discarding the ones that contain 4G sequences. Figure 1 illustrates N4G(L) in comparison to the total number of sequences 4L, for different lengths. As depicted in Figure 1, for L ≤ 7, this fraction stays below 1.5%, whereas for longer lengths, it rises, so that for L ≥ 200, around 50% of all possible sequences contain 4G structures.

Figure 1.

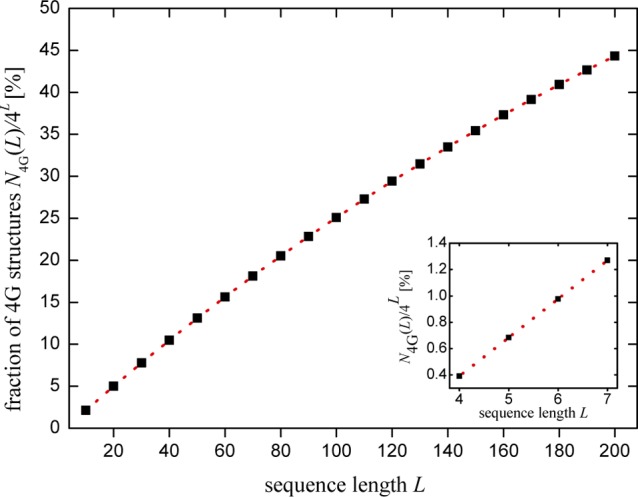
Figure 1

Open in a new tab

Fraction of all possible 4L sequences that contain 4G structures for different oligonucleotide lengths. The inset shows this fraction stays below 1.5% for L ≤ 7. For longer lengths, it rises. Dotted lines are a guide for the eye.

The second category of sequences that will not contribute to recognition are self-complementary sequences. We neglect them as we work with short sequences where self-complementarity only plays a minor role.32−34 For longer lengths, however, this must be considered.

Coding theory is a branch of mathematics that studies codes and their properties for different applications. A code is a set of codewords. The length of a codeword L is the number of letters that create the codeword, where the letters are often taken from an alphabet. In our case, DNA sequences are taken as the codewords, where L is the number of bases (A,C,G,T) that make up the sequence. The number of positions that two codewords of the same length differ is the Hamming distance.27 In case of DNA sequences, we define this distance as the number of bases by which they differ. We assume that for every sequence of a given length there is a minimum Hamming distance d in such a way that there is no cross-hybridization as long as the Hamming distance k is larger (or equal) than d. If two sequences differ by less than d, they may cross-hybridize. For a given sequence, N(d) is the number of sequences from which one can choose a competitor with k ≥ d. N(d), decreases by increasing d (Figure 2). Equation 2, for a given length L, gives the number of sequences PL(k) with the Hamming distance k. Figure 2 depicts N(d) obtained by summing PL(k) over all k ≥ d for L = 7 and a given minimum Hamming distance.

graphic file with name ao-2017-00053h_m002.jpg 2

Figure 2.

Figure 2

Open in a new tab

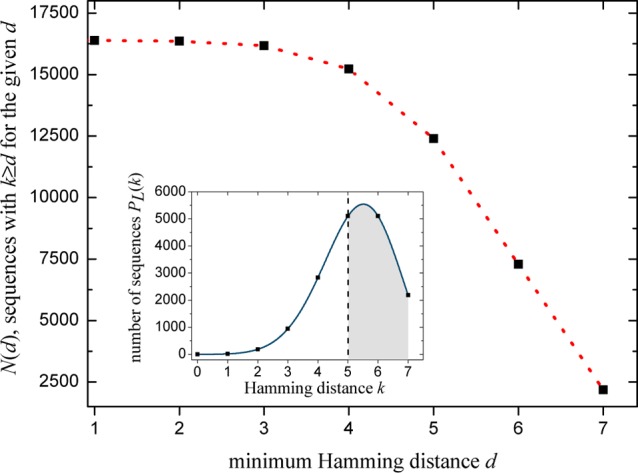
N(d) is the number of sequences with k ≥ d for a given sequence with L = 7. This number decreases for larger d. The inset depicts the number of sequences PL(k) for each Hamming distance k. If d = 5, the shaded region represents the sum over all sequences with k ≥ 5 which do not cross-hybridize with the given sequence. Dotted lines are a guide for the eye.

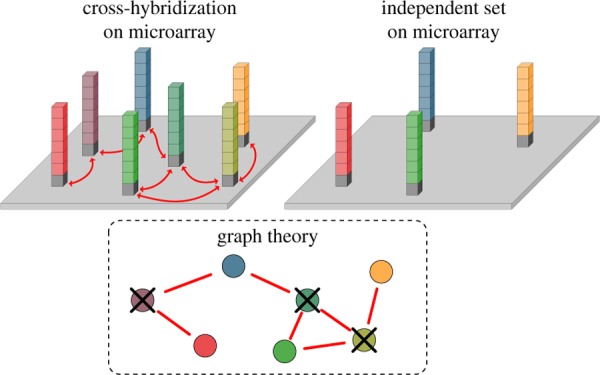
Solving maximum independent set problems is believed to be NP-hard. There is no general exact solution, however, there are approximations.35,36 Finding maximal independent set (MIS) in N(d) is a problem related to graph theory.36,37 A graph consists of vertices represented by red circles in Figure 3a. Two vertices are called adjacent if they are connected by an edge (blue line). We represent the probes by vertices. If two sequences are such that they hybridize to each other, we connect them by an edge (Figure 3b). An independent set is a subset with no adjacent vertices. If adding any sequence to the set corrupts its independency, the set is called MIS. The largest possible size of a maximal set refers to the maximum independent set. Here, MIS corresponds to the largest number of independent oligonucleotides that can be found. For our approach, we create an adjacency matrix for a given L and d, where the number of rows and columns correspond to the number of sequences; thus, it is a 4L × 4L square matrix (Figure 3c). If the Hamming distance between sequences i and j is less than d, they cross-hybridize, that is, they are connected by an edge. In this case, Aij = 1, otherwise Aij = 0. Sequences are not self-adjacent, that is, Aii = 0 ∀ i.

Figure 3.

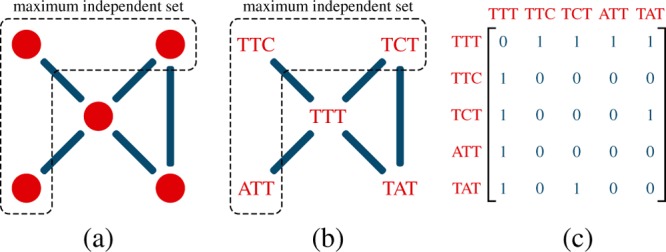
Figure 3

Open in a new tab

Concept of the graph-theoretical approach. (a) Vertices of one graph (red circles) along with the edges (blue lines) between adjacent vertices. The vertices inside of the dashed area form the maximum independent set. (b) Sequences that are connected by blue lines lead to cross-hybridization. ATT, TTC, and TCT are generating the maximum independent set. (c) Adjacency matrix for the corresponding set of sequences.

We apply a constructive local search algorithm38,39 that iteratively adds orthogonal sequences to an existing set until the available sequences are depleted. To identify the orthogonal sequences the algorithm employs the adjacency matrix constructed beforehand. The algorithm is restricted as it does not try all combinations of sequences. Therefore, it does not necessarily find the maximum independent set but proposes many maximal independent sets instead. We consider the largest set among them as an approximate solution to the exact size of the maximum independent set. All obtained set sizes are within the known Singleton and Gilbert–Varshamov28,40 bounds and are summarized in Tables S2 and S3 along with a comparison to literature values. The size of the adjacency matrix increases exponentially with the sequence length. This requires a large memory. Therefore, we are limited to short sequences L ≤ 7.

Figure 4 illustrates the possible sizes of different independent sets for L = 7 and d = 5 before discarding 4G and 4C sequences and afterward. The MIS size M(L, d) in both cases is 23. Removing these sequences for L ≤ 7 does not change the size of MIS in most cases (refer to Table S2). However, for longer lengths, the fraction of 4G rises and we expect that discarding such sequences reduces the size of a MIS (Figure 1). This algorithm creates independent sets, based on the pool of available sequences. Removing all sequences containing 4C and 4G changes this pool. Therefore, we obtain different independent sets (blue columns) compared with the cases where we did not discard these sequences (red columns). A significant trend toward smaller or bigger set sizes by removing 4C and 4G sequences cannot be identified.

Figure 4.

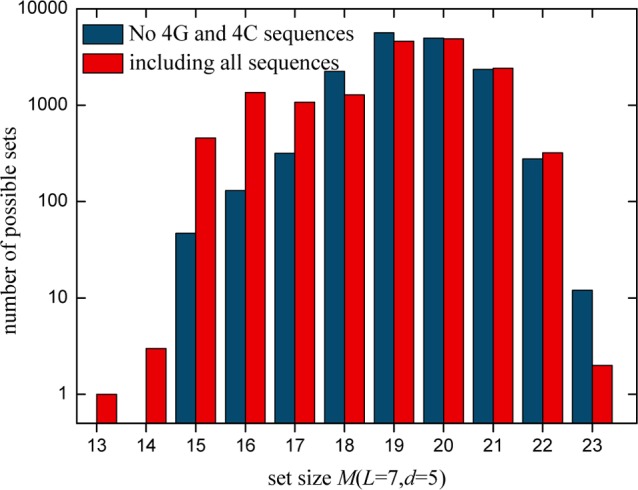
Figure 4

Open in a new tab

Size of all independent sets for L = 7 with d = 5 before (red columns) and after removing 4G and 4C sequences (blue columns). The height of each column gives the number of possible sets for a given M(L, d).

Experimental Results

A suitable minimum Hamming distance d must be determined experimentally. Because the longest sequences studied with our algorithm are 7-mers, we design a microarray consisting of oligonucleotides of length 7 (plus four additional terminal bases, see Material and Methods). We immobilize, complementary to a perfectly matching target (PM), an arbitrary sequence and some of its related mismatched sequences. To study the dependency of hybridization probability on the positions of defects, we locate the mismatches at the ends, in the middle of the sequence, or uniformly distribute them. Hybridizing the PM target on the microarray yields the results shown in Figure 5. Each feature block, as depicted in Figure 5a–d, corresponds to a set of sequences with one to four mismatches MM1–MM4, respectively. They are all surrounded by a frame of PMs. Each sequence appears 8 times within a feature block. To have better statistics, the hybridization intensities from all sequences are averaged, and their standard deviations σ are calculated. Then, all intensities are normalized relative to the average PM intensity on the microarray. The PM and mismatched sequences are all subject to the same constant synthesis error rate (see Material and Methods), which leads to an overall loss of hybridization intensity. For the results presented in the following, the relative intensity is of importance, which is not affected by this loss. Fluorescence intensity variations are due to inhomogeneities of the microarray surface, fluorescent stains in the feature blocks, or illumination gradients during synthesis.9 For all MM ≥ 4, we detect no other intensity than PM hybridization (not shown).

Figure 5.

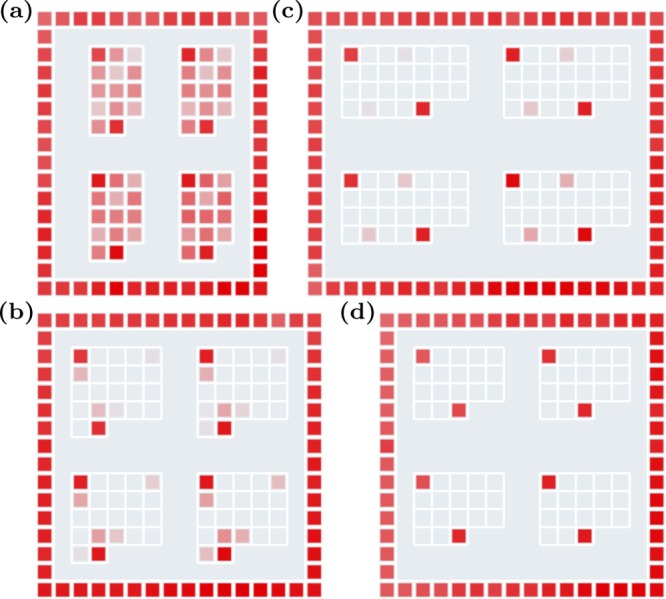
Figure 5

Open in a new tab

Fluorescent intensity from a hybridized PM target on a microarray. Each feature block (a–d) corresponds to a set of sequences with one to four mismatches, respectively. They are surrounded by a frame of PMs. Each sequence appears eight times within a feature block.

Figure 6 presents the normalized fluorescent intensities of hybridization for a sequence with one mismatch as a function of defect positions. The intensity for sequences with single mismatches in the middle is smaller because the defects in the middle of the duplex increase the base pair opening probability and destabilize the duplex. This result agrees well with previously reported work.10,41

Figure 6.

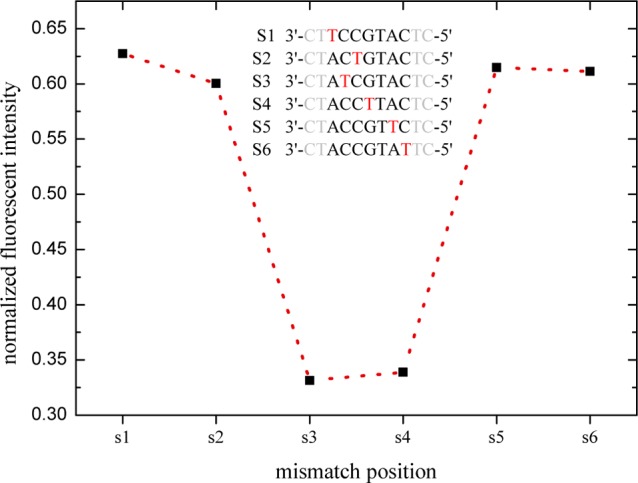
Figure 6

Open in a new tab

Normalized hybridization intensity for the sequences with one mismatch as a function of their mismatch position. The intensity for sequences including a single mismatch in the middle is smaller than for a MM located at the end.

We assume all eight fluorescence intensities of one probe measured at different positions on the microarray to be normally distributed and described by a standard deviation σ. To discriminate the PM binding intensity from all other nonspecific binding, the normal distributions of their hybridization intensities must be well separated. We show in Figure 7, the distributions of the fluorescence intensities of PM and the sequences which exhibit the highest cross-hybridization intensities IMM,max for MM1–MM3. The normal distributions are based on a statistical analysis of the microarrays shown in Figure 5. The peak centers in Figure 7 correspond to the average value of the fluorescence intensities and their widths to the standard deviations (shown in Table 1). In DNA microarrays, the binding affinities can largely vary, depending on the precise sequence and its concentration,41 that is, fluorescence intensities of perfectly matched sequences span a large range. To illustrate that we determine the hybridization free energy of the sample sequence 3′-CTATATATATC-5′ binding to its PM using Nupack software42 and the corresponding expected fluorescence intensity using the Langmuir isotherm.9 As this sequence does not contain any G or C bases within the seven core bases, its fluorescence intensity is amongst the lowest of all possible sequences. In fact, we find that it has just 16.5% of the fluorescence intensity, obtained by the same procedure, for the PM sequence 3′-CTACCGTACTC-5′ used on the microarray shown in Figure 5. Accordingly, it should be expected that some perfectly matched but weakly binding sequences will have lower hybridization intensities than the 27% signal of IMM,max for three mismatches. This clearly shows that a minimum Hamming distance of d = 3 cannot be used for a reliable discrimination between PM and MM hybridization. Therefore, we investigate sets with d ≥ 4 in subsequent experiments. Table 1 shows the sequences and their intensities as well as the corresponding standard deviations for each mismatch.

Figure 7.

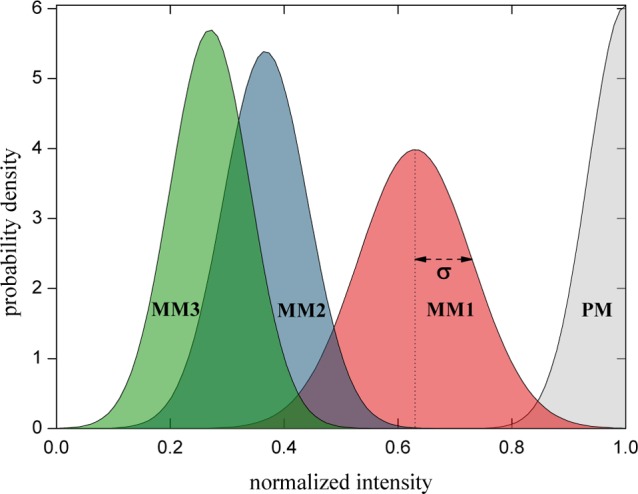
Figure 7

Open in a new tab

Normal distribution of the PM and MM1–MM3 hybridization intensities. Assuming a normal distribution with average intensity (peak centers) and standard deviation σ as given in Table 1. Even the average cross-hybridization intensity of IMM3,max = 27% is too high for accurate discrimination of PM-binding and unwanted cross-hybridization (compare main text).

Table 1. Sequences with Different Numbers of Mismatches, Which Yield the Highest Hybridization Intensities among All Probes within Each Feature Block (Figure 7) along with Their σ.

number of mismatches sequence Imax ± σ
0 3′-CTACCGTACTC-5′ 1 ± 0.066
1 3′-CTTCCGTACTC-5′ 0.63 ± 0.1
2 3′-CTACCGTCTTC-5′ 0.37 ± 0.074
3 3′-CTACCGACTTC-5′ 0.27 ± 0.073
Open in a new tab

To test sets with d ≥ 4, we first design a microarray consisting of 23 sequences (see Table S1) as predicted by our algorithm, corresponding to d = 5 (compare Figure 4). To verify its independence, we record the hybridization intensities of three arbitrarily chosen PM targets of this set simultaneously. Figure 8a shows the measured normalized hybridization intensities Iseq in a barplot after background subtraction. It can be clearly seen that the PM targets, which are present in solution, hybridize to their corresponding complementary probes only (green bars). By using the highest hybridization intensity as a reference, the other hybridized PM sequences reach 24 and 31% of that level. On the other hand, the measured hybridization intensities of all other probes (blue bars) scatter with σ = 0.3% around their average value of zero, which can be attributed to the background fluorescence noise. Negative values correspond to the intensities below the average background level. The intensities of the probes, whose PM targets are not present in a solution, stay well below 2% within a large confident interval (5σ environment). To cross-check that the sets with d ≤ 4 are not independent, we synthesize another microarray including 83 sequences with d = 4. Hybridization of one PM leads to cross-hybridization of 11 other probes that rise above 2%, as can be seen for the red bars in Figure 8b. This underlines that d < 5 is not sufficient to achieve independency.

Figure 8.

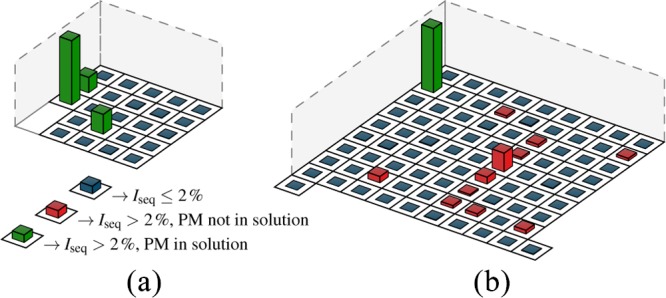
Figure 8

Open in a new tab

Two microarrays consisting of sequences with two different minimum Hamming distance, (a) independent set with d = 5 and (b) set with d = 4. In both cases, the green bars present the probes whose PM targets are present in solution. The blue color corresponds to the hybridization intensities of sequences with Iseq ≤ 2%. Red bars represent the cross-hybridized sequences with Iseq > 2%.

Conclusion

In this work, we experimentally determined a minimum Hamming distance d between DNA oligonucleotides. Sequences with a distance of d can make up an orthogonal set, which means they do not cross-hybridize. By applying a local search algorithm, we found orthogonal sets for different L and d. For the length of 7, we determined a MIS with the size of 23 and experimentally confirmed its orthogonality with an appropriate minimum distance of 5. The small set size of 23 compared with 47 possible sequences arises from the minimum Hamming distance of 5. Technology of optically directed synthesis introduces errors into sequences.43−46 Single-nucleotide polymorphism detection in bulk has been achieved, albeit with higher synthesis fidelity and optimized experimental conditions.47 Moreover, d can be reduced by increasing the temperature to reduce nonspecific bindings, which can improve the discrimination among the sequences of a set.47 For longer sequences lengths, higher temperatures are particularly important to increase the number of complementary bases that enable binding.48 At a given concentration, the discrimination increases near a melting temperature.

In the course of our experiments, we found a minimum Hamming distance of five for a sequence length of 11 (7 core bases and four terminal extra ones) in a good agreement with the discrimination level of d ≈ L/2 that is reported.18,19 Our set size, on the other hand, does not gain from the four additional bases. By extending our algorithm to longer sequences, these extra bases are redundant, and we expect d ≈ L/2 will remain applicable. With the same d, larger lengths lead to larger set sizes than we have determined here.

We also derived an analytical expression to calculate the number of 4G sequences. As we have shown, eliminating these sequences for short lengths does not change the size of MIS in most cases. However, we anticipate an impact for higher sequence lengths, as the fraction of sequences containing 4G structures increases. Although we could show how to avoid cross-hybridization in our synthesis microarray, we cannot easily transfer it to the real world microarray application as developed by Affymetrix. Following the protocol for expression studies, Affymetrix targets are very long compared with their surface bound probes. Such sequence lengths introduce a large variety of conformations. Therefore, in expression studies one should consider additional effects such as the brush effect49 and surface density of probes.7,50

Materials and Methods

DNA Microarray Hybridization Experiment

The light-directed in situ synthesis method and some of the analysis software were described previously.4,41,51 We use in-house synthesized DNA microarrays. Probes on a microarray are tethered to the surface from their 3′-end. To increase the hybridization probability at the given temperature, we extended all sequences by adding four bases, CT at the 3′ and TC at 5′ end. The microarray synthesis used in our work has a stepwise coupling efficiency of ≥99%. Considering the sequence length 7, this leads to an estimation of probes free of any synthesis defects of 93%.52 The remaining 7% have mostly one defect. The targets are prepared in 25 nM concentration in a 5× SSPE buffer solution. Their terminus is labeled by a Cy3 fluorescent dye. Hybridization is performed in equilibrium with the buffer in a chamber designed for that purpose. We use an UPlanApo 10× 0.40 NA objective for observation. Figure 9 shows the image of a hybridized microarray as obtained after 100 s exposure time. The particular probe sequence species are restricted to small areas commonly called features. To determine the amount of bound targets to a probe, we measure the fluorescence intensities (hybridization intensity) by taking images from DNA microarray surfaces with an electron multiplying EM-CCD camera (EM-CCD C9100-02, Hamamatsu). We correct for background fluorescence originating from the unhybridized targets in the buffer by subtraction. Microarray pictures shown in the Experimental Results are computationally reconstructed by using these intensities, for example, Figure 5a is produced from Figure 9. The hybridization temperature is 32 °C.

Figure 9.

Figure 9

Open in a new tab

Image of a hybridized microarray. The bright features correspond to the fluorescent intensities of hybridized targets.

Acknowledgments

We thank Benjamin Kambs (Saarland University) for his support in theoretical calculations. The authors acknowledge financial support by the Deutsche Forschungsgemeinschaft (DFG) with the collaborative research center SFB 1027 and Austrian Science Foundation (FWF P27275).

Glossary

Abbreviation

MIS

maximal independent set

PM

perfectly matching target

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b00053.

  • Derivation of eq 1 that gives the number of sequences with runs of at least 4G, largest orthogonal set of sequences with the size of 23 for L = 7 and d = 5, and comparison of our set sizes with the previous works (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao7b00053_si_001.pdf (444.8KB, pdf)

References

  1. Fischer E. Einfluss der Configuration auf die Wirkung der Enzyme. Ber. Dtsch. Chem. Ges. 1894, 27, 2985–2993. 10.1002/cber.18940270364. [DOI] [Google Scholar]
  2. Naef F.; Lim D. A.; Patil N.; Magnasco M. DNA hybridization to mismatched templates: A chip study. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2002, 65, 040902. 10.1103/physreve.65.040902. [DOI] [PubMed] [Google Scholar]
  3. Held G. A.; Grinstein G.; Tu Y. Modeling of DNA microarray data by using physical properties of hybridization. Proc. Natl. Acad. Sci. U.S.A. 2003, 100, 7575–7580. 10.1073/pnas.0832500100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Naiser T.; Mai T.; Michel W.; Ott A. Versatile maskless microscope projection photolithography system and its application in light-directed fabrication of DNA microarrays. Rev. Sci. Instrum. 2006, 77, 063711. 10.1063/1.2213152. [DOI] [Google Scholar]
  5. Dorris D. R.; Nguyen A.; Gieser L.; Lockner R.; Lublinsky A.; Patterson M.; Touma E.; Sendera T. J.; Elghanian R.; Mazumder A. Oligodeoxyribonucleotide probe accessibility on a three-dimensional DNA microarray surface and the effect of hybridization time on the accuracy of expression ratios. BMC Biotechnol. 2003, 3, 6. 10.1186/1472-6750-3-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Deng Y.; He Z.; Van Nostrand J. D.; Zhou J. Design and analysis of mismatch probes for long oligonucleotide microarrays. BMC Genomics 2008, 9, 491. 10.1186/1471-2164-9-491. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Michel W.; Mai T.; Naiser T.; Ott A. Optical study of DNA surface hybridization reveals DNA surface density as a key parameter for microarray hybridization kinetics. Biophys. J. 2007, 92, 999–1004. 10.1529/biophysj.106.092064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Binder H. Thermodynamics of competitive surface adsorption on DNA microarrays. J. Phys.: Condens. Matter 2006, 18, S491. 10.1088/0953-8984/18/18/s02. [DOI] [Google Scholar]
  9. Naiser T.; Kayser J.; Mai T.; Michel W.; Ott A. Stability of a surface-bound oligonucleotide duplex inferred from molecular dynamics: A study of single nucleotide defects using DNA microarrays. Phys. Rev. Lett. 2009, 102, 218301. 10.1103/physrevlett.102.218301. [DOI] [PubMed] [Google Scholar]
  10. Naiser T.; Kayser J.; Mai T.; Michel W.; Ott A. Position dependent mismatch discrimination on DNA microarrays–experiments and model. BMC Bioinf. 2008, 9, 509. 10.1186/1471-2105-9-509. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Bishop J.; Chagovetz A. M.; Blair S. Kinetics of multiplex hybridization: Mechanisms and implications. Biophys. J. 2008, 94, 1726–1734. 10.1529/biophysj.107.121459. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Bishop J.; Wilson C.; Chagovetz A. M.; Blair S. Competitive displacement of DNA during surface hybridization. Biophys. J. 2007, 92, L10–L12. 10.1529/biophysj.106.097121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Harrison A.; Binder H.; Buhot A.; Burden C. J.; Carlon E.; Gibas C.; Gamble L. J.; Halperin A.; Hooyberghs J.; Kreil D. P. Physico-chemical foundations underpinning microarray and next-generation sequencing experiments. Nucleic Acids Res. 2013, 41, 2779. 10.1093/nar/gks1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Halperin A.; Buhot A.; Zhulina E. B. On the hybridization isotherms of DNA microarrays: The Langmuir model and its extensions. J. Phys.: Condens. Matter 2006, 18, S463. 10.1088/0953-8984/18/18/s01. [DOI] [Google Scholar]
  15. Halperin A.; Buhot A.; Zhulina E. B. Hybridization isotherms of DNA microarrays and the quantification of mutation studies. Clin. Chem. 2004, 50, 2254–2262. 10.1373/clinchem.2004.037226. [DOI] [PubMed] [Google Scholar]
  16. Halperin A.; Buhot A.; Zhulina E. B. Sensitivity, specificity, and the hybridization isotherms of DNA chips. Biophys. J. 2004, 86, 718–730. 10.1016/s0006-3495(04)74150-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Held G. A.; Grinstein G.; Tu Y. Relationship between gene expression and observed intensities in DNA microarrays—A modeling study. Nucleic Acids Res. 2006, 34, e70 10.1093/nar/gkl122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Frutos A. G.; Liu Q.; Thiel A. J.; Sanner A. M. W.; Condon A. E.; Smith L. M.; Corn R. M. Demonstration of a word design strategy for DNA computing on surfaces. Nucleic Acids Res. 1997, 25, 4748–4757. 10.1093/nar/25.23.4748. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Li M.; Lee H. J.; Condon A. E.; Corn R. M. DNA word design strategy for creating sets of non-interacting oligonucleotides for DNA microarrays. Langmuir 2002, 18, 805–812. 10.1021/la0112209. [DOI] [Google Scholar]
  20. Liu W.; Wang S.; Gao L.; Zhang F.; Xu J. DNA sequence design based on template strategy. J. Chem. Inf. Comput. Sci. 2003, 43, 2014–2018. 10.1021/ci025645s. [DOI] [PubMed] [Google Scholar]
  21. Gaborit P.; King O. D. Linear constructions for DNA codes. Theor. Comput. Sci. 2005, 334, 99–113. 10.1016/j.tcs.2004.11.004. [DOI] [Google Scholar]
  22. King O. D. Bounds for DNA codes with constant GC-content. Electron. J. Combin 2003, 10, 33. [Google Scholar]
  23. Montemanni R.; Smith D. H. Construction of constant GC-content DNA codes via a variable neighbourhood search algorithm. J. Math. Model. Algorithm. 2008, 7, 311. 10.1007/s10852-008-9087-8. [DOI] [Google Scholar]
  24. Tulpan D. C.; Hoos H. H.; Condon A. E.. Stochastic local search algorithms for DNA word design. In International Workshop on DNA-Based Computers; Springer, 2002; pp 229–241. [Google Scholar]
  25. Shortreed M. R.; Chang S. B.; Hong D.; Phillips M.; Campion B.; Tulpan D. C.; Andronescu M.; Condon A.; Hoos H. H.; Smith L. M. A thermodynamic approach to designing structure-free combinatorial DNA word sets. Nucleic Acids Res. 2005, 33, 4965–4977. 10.1093/nar/gki812. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Pozhitkov A.; Noble P. A.; Domazet-Lošo T.; Nolte A. W.; Sonnenberg R.; Staehler P.; Beier M.; Tautz D. Tests of rRNA hybridization to microarrays suggest that hybridization characteristics of oligonucleotide probes for species discrimination cannot be predicted. Nucleic Acids Res. 2006, 34, e66 10.1093/nar/gkl133. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Bierbrauer J.Introduction to Coding Theory, 2nd ed.; Taylor & Francis, 2016. [Google Scholar]
  28. El Rouayheb S.; Georghiades C. N.. Graph theoretic methods in coding theory. In Classical, Semi-Classical and Quantum Noise; Springer, 2012; pp 53–62. [Google Scholar]
  29. Lech C. J.; Heddi B.; Phan A. T. Guanine base stacking in G-quadruplex nucleic acids. Nucleic Acids Res. 2013, 41, 2034–2046. 10.1093/nar/gks1110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Wu C.; Zhao H.; Baggerly K.; Carta R.; Zhang L. Short oligonucleotide probes containing G-stacks display abnormal binding affinity on Affymetrix microarrays. Bioinformatics 2007, 23, 2566–2572. 10.1093/bioinformatics/btm271. [DOI] [PubMed] [Google Scholar]
  31. Benabou S.; Ferreira R.; Aviñó A.; González C.; Lyonnais S.; Solà M.; Eritja R.; Jaumot J.; Gargallo R. Solution equilibria of cytosine- and guanine-rich sequences near the promoter region of the n-myc gene that contain stable hairpins within lateral loops. Biochim. Biophys. Acta, Gen. Subj. 2014, 1840, 41–52. 10.1016/j.bbagen.2013.08.028. [DOI] [PubMed] [Google Scholar]
  32. Vet J. A. M.; Marras S. A. E.. Design and optimization of molecular beacon real-time polymerase chain reaction assays. In Oligonucleotide Synthesis; Humana Press Inc., 2005; pp 273–290. [DOI] [PubMed] [Google Scholar]
  33. Bao G.; Suresh S. Cell and molecular mechanics of biological materials. Nat. Mater. 2003, 2, 715–725. 10.1038/nmat1001. [DOI] [PubMed] [Google Scholar]
  34. Wang K.; Tang Z.; Yang C. J.; Kim Y.; Fang X.; Li W.; Wu Y.; Medley C. D.; Cao Z.; Li J.; Colon P.; Lin H.; Tan W. Molecular engineering of DNA: Molecular beacons. Angew. Chem., Int. Ed. 2009, 48, 856–870. 10.1002/anie.200800370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Bomze I. M.; Budinich M.; Pardalos P. M.; Pelillo M.. The maximum clique problem. In Handbook of Combinatorial Optimization; Springer, 1999; pp 1–74. [Google Scholar]
  36. Robson J. M. Algorithms for maximum independent sets. J. Algorithm. 1986, 7, 425–440. 10.1016/0196-6774(86)90032-5. [DOI] [Google Scholar]
  37. Tarjan R. E.; Trojanowski A. E. Finding a maximum independent set. SIAM J. Comput. 1977, 6, 537–546. 10.1137/0206038. [DOI] [Google Scholar]
  38. Hoos H. H.; Stützle T.. Stochastic Local Search: Foundations and Applications; Elsevier, 2004. [Google Scholar]
  39. Varshamov R. Estimate of the number of signals in error correcting codes. Dokl. Akad. Nauk SSSR 1957, 739–741. [Google Scholar]
  40. Barg A.; Guritman S.; Simonis J. Strengthening the Gilbert–Varshamov bound. Lin. Algebra Appl. 2000, 307, 119–129. 10.1016/s0024-3795(99)00271-2. [DOI] [Google Scholar]
  41. Naiser T.Characterization of Oligonucleotide Microarray Hybridization: Microarray Fabrication by Light-Directed in Situ Synthesis–Development of an Automated DNA Microarray Synthesizer, Characterization of Single Base Mismatch Discrimination and the Position-Dependent Influence of Point Defects on Oligonucleotide Duplex Binding Affinities. Ph.D. Thesis, University of Bayreuth, 2008. [Google Scholar]
  42. Dirks R. M.; Bois J. S.; Schaeffer J. M.; Winfree E.; Pierce N. A. Thermodynamic analysis of interacting nucleic acid strands. SIAM Rev. 2007, 49, 65–88. 10.1137/060651100. [DOI] [Google Scholar]
  43. Koren A.; Tirosh I.; Barkai N. Autocorrelation analysis reveals widespread spatial biases in microarray experiments. BMC Genomics 2007, 8, 164. 10.1186/1471-2164-8-164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Tan P. K.; Downey T. J.; Spitznagel E. L. Jr.; Xu P.; Fu D.; Dimitrov D. S.; Lempicki R. A.; Raaka B. M.; Cam M. C. Evaluation of gene expression measurements from commercial microarray platforms. Nucleic Acids Res. 2003, 31, 5676–5684. 10.1093/nar/gkg763. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Miklos G. L. G.; Maleszka R. Microarray reality checks in the context of a complex disease. Nat. Biotechnol. 2004, 22, 615–621. 10.1038/nbt965. [DOI] [PubMed] [Google Scholar]
  46. Ma S.; Saaem I.; Tian J. Error correction in gene synthesis technology. Trends Biotechnol. 2012, 30, 147–154. 10.1016/j.tibtech.2011.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Zhang D. Y.; Chen S. X.; Yin P. Optimizing the specificity of nucleic acid hybridization. Nat. Chem. 2012, 4, 208–214. 10.1038/nchem.1246. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Trapp C.; Schenkelberger M.; Ott A. Stability of double-stranded oligonucleotide DNA with a bulged loop: A microarray study. BMC Biophys. 2011, 4, 20. 10.1186/2046-1682-4-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Halperin A.; Buhot A.; Zhulina E. B. Brush effects on DNA chips: Thermodynamics, kinetics, and design guidelines. Biophys. J. 2005, 89, 796–811. 10.1529/biophysj.105.063479. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Peterson A. W.; Heaton R. J.; Georgiadis R. M. The effect of surface probe density on DNA hybridization. Nucleic Acids Res. 2001, 29, 5163–5168. 10.1093/nar/29.24.5163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Sack M.; Hölz K.; Holik A.-K.; Kretschy N.; Somoza V.; Stengele K.-P.; Somoza M. M. Express photolithographic DNA microarray synthesis with optimized chemistry and high-efficiency photolabile groups. J. Nanobiotechnol. 2016, 14, 14. 10.1186/s12951-016-0166-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Agbavwe C.; Kim C.; Hong D.; Heinrich K.; Wang T.; Somoza M. M. Efficiency, error and yield in light-directed maskless synthesis of DNA microarrays. J. Nanobiotechnol. 2011, 9, 57. 10.1186/1477-3155-9-57. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao7b00053_si_001.pdf (444.8KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES