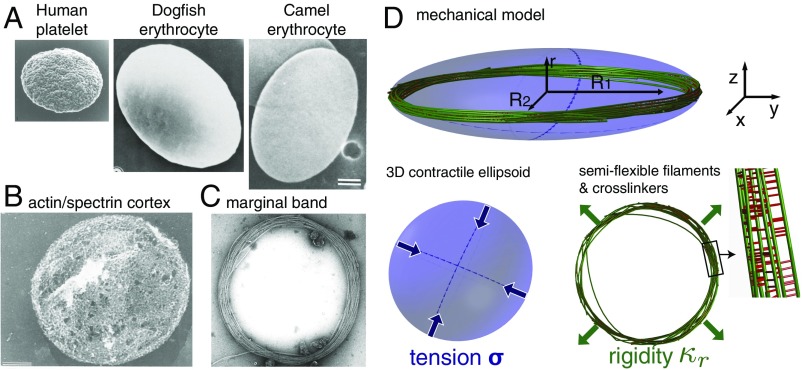
Significance
The discoidal shape of many blood cells is essential to their proper function within the organism. For blood platelets and other cells, this shape is maintained by the marginal band, which is a closed ring of filaments called microtubules. This ring is elastic and pushes on the cell cortex, a tense polymer scaffold associated with the plasma membrane. Dmitrieff et al. examined how the mechanical balance between these two components determine cell size, uncovering a scaling law that is observed in data collected from 25 species. The analysis also indicated that the cell can resist much higher mechanical challenges than the microtubule ring alone, in the same way as a tent with its cloth is stronger than the poles alone.
Keywords: cytoskeleton, scaling, mechanics, blood platelet, theory
Abstract
The fast bloodstream of animals is associated with large shear stresses. To withstand these conditions, blood cells have evolved a special morphology and a specific internal architecture to maintain their integrity over several weeks. For instance, nonmammalian red blood cells, mammalian erythroblasts, and platelets have a peripheral ring of microtubules, called the marginal band, that flattens the overall cell morphology by pushing on the cell cortex. In this work, we model how the shape of these cells stems from the balance between marginal band rigidity and cortical tension. We predict that the diameter of the cell scales with the total microtubule polymer and verify the predicted law across a wide range of species. Our analysis also shows that the combination of the marginal band rigidity and cortical tension increases the ability of the cell to withstand forces without deformation. Finally, we model the marginal band coiling that occurs during the disk-to-sphere transition observed, for instance, at the onset of blood platelet activation. We show that when cortical tension increases faster than cross-linkers can unbind, the marginal band will coil, whereas if the tension increases more slowly, the marginal band may shorten as microtubules slide relative to each other.
The shape of animal cells is determined by the cytoskeleton, including microtubules (MTs), contractile networks of actin filaments, intermediate filaments, and other mechanical elements. The 3D geometry of most cells in a multicellular organism is also largely determined by their adhesion to neighboring cells or to the extracellular matrix (1). This is, however, not the case for blood cells because they circulate freely within the fluid environment of the blood plasma. Red blood cells (RBCs) and thrombocytes in nonmammalian animals (2, 3), as well as platelets and erythroblasts in mammals (4, 5), adopt a simple ellipsoidal shape (Fig. 1A). This shape is determined by two components: a ring of MTs, called the marginal band (MB), and a protein cortex at the cell periphery.
Fig. 1.
(A) Scanning electron micrographs of platelets and erythrocytes shown at the same scale (6–8). (Scale bar, m). (B) The actin/spectrin cortex of platelets; EM from ref. 9, Hartwig and DeSisto, 1991. Journal of Cell Biology, DOI:10.1083/jcb.112.3.407. (Scale bar, m). (C) The MB of platelets is made of multiple MTs bundled by motors and cross-linkers (10); EM reprinted with permission from ref. 6; www.sciencedirect.com/science/book/9780123878373. (D) In our model, the shape of the cell is determined by the balance of two forces. Because of MT stiffness , the MB pushes against the tense cortex, which resists by virtue of its surface tension .
In the case of platelets and nonmammalian RBCs, both components are relatively well characterized (Fig. 1). The cortex is a composite structure made of spectrin, actin, and intermediate filaments (Fig. 1B), and its complex architecture is likely to be dynamic (11–13). It is a thin network under tension (14), that on its own would lead to a spherical morphology (15). This effect is counterbalanced by the MB, a ring made of multiple dynamic MTs, held together by cross-linkers and molecular motors into a closed circular bundle (4, 16) (Fig. 1C). The MB is essential to maintain the flat morphology, and treatment with a MT-destabilizing agent causes platelets to round up (17). Platelets also respond to biochemical signals indicating a damage of the blood vessels, and during this activation, the MB is often seen to buckle (3). This phenomenon is reminiscent of the buckling of a closed elastic ring (18), but an important difference is that the MB is not a continuous structure of constant length.
Indeed, the MB is made of multiple dynamic MTs that are linked by MT-associated proteins. Because these connectors are not static, but instead bind and unbind, MTs could slide relative to one another, allowing the length of the MB to change. It was suggested in particular that molecular motors may drive the elongation of the MB (19), but this possibility remains mechanistically unclear. Moreover, the MB changes as MTs assemble and disassemble. However, in the absence of sliding, elongation or shortening of single MTs would principally affect the thickness of the MB (i.e., the number of MTs in the cross-section) rather than its length. These aspects have received little attention so far, and much remains to be done before we can understand how the original architecture of these cells is adapted to their unusual environment and to the mechanical constraints associated with it (7).
We argue here that, despite the potential complexity of the system, the equilibrium between MB elasticity and cortical tension can be understood in simple mechanical terms. We first predict that the main cell radius should scale with the total length of MT polymer and inversely with the cortical tension, and test the predicted relationship by using data from a wide range of species. We then simulate the shape changes observed during platelet activation (20), discussing that a rapid increase of tension leads to MB coiling, accompanied by a shortening of the ring, whereas a slow increase of tension leads to a shortening of the ring without coiling. Finally, by computing the buckling force of a ring confined within an ellipsoid, we find that the resistance of the cell to external forces is dramatically increased compared with the resistance of the ring alone.
Results
Cell Size Is Controlled by Total MT Polymer and Cortical Tension.
We first apply scaling arguments to explore how cell shape is determined by the mechanical equilibrium between MB elasticity and cortical tension. In their resting state, the cells are flat ellipsoids, and the MB is contained in a plane that is orthogonal to the minor cell axis. Assuming that the cell is discoid for simplicity (), the major radius is also approximately the radius of the MB (Fig. 1D), and thus the MTs bundled together in the MB have a curvature and length of the ring is ∼. Generically, the deformation energy of a such ring can be written , in which is the rigidity of the bundle, often written as (with the young modulus of the material and its moment of inertia) (21). We first consider time scales larger than the dynamics of MT cross-linker binding and unbinding [approximately 10 s (22)], for which we can ignore the mechanical contribution of cross-linkers (10). In this limit, the MTs are mechanically independent, and we can assume , with the number of MTs in a cross-section of the ring and the rigidity of an individual MT (23). We can define , which corresponds to the sum of the MTs’ lengths, and write the total elastic energy as . At time scales larger than a few seconds, the cortex can reorganize, and therefore we do not have to include contributions from its rigidity (24). Its effect can then be modeled by a surface energy associated with a surface tension (Fig. 1D). The surface area of a cell of thickness is , and if the cell is sufficiently flat, we can approximate the energy as . The equilibrium of the system corresponds to , leading finally to:
| [1] |
All other things constant, we thus expect . To verify this relationship, we used data from the literature (2), and for 25 species calculated by multiplying the number of MTs in a cross-section by the length of the marginal band. The scaling is remarkably respected, over more than two orders of magnitude (Fig. 2A). By using Eq. 1, the fit provides an estimate of the cortical tension of , which is low compared with the tension of the actomyosin cortex of blebbing cell (25). However, RBCs have a cortex made of spectrin rather than actomyosin, and a much lower cortical tension is expected. Human RBCs, which are devoid of a marginal band, have a cortical tension of (26), because the spectrin cortex opposes the membrane tension (27). In contrast to this, we predict for human blood platelets, given that m and m (28), and this is close to the tension of blood granulocytes (m) (14).
Fig. 2.
(A) Cell radius as a function of total MT length . Dots represent data from 25 species (2). was estimated from the number of MTs in a cross-section, measured in EM, and the cell radius. (B) Cell radius as a function of in simulations with (gray dots) or 10,000 (black dots) cross-linkers. On both graphs, the dashed line indicates the scaling law .
The scaling observed across 25 species seems to confirm that, at long time scales, the mechanical balance between bending rigidity of the MTs and cortical tension define cell size (Fig. 1D). To verify the validity of this result for a ring made of multiple dynamically cross-linked MTs, we developed a numerical model in Cytosim, a cytoskeleton simulation engine (29). Cytosim solves the Langevin equation (viscosity velocity = forces + Brownian noise), describing the motion of bendable filaments that are discretized into model points. The forces stem from the rigidity of the filaments (tending to minimize bending energy), links between filaments (modeled as Hookean springs between filaments), and confinement within the cell. The Brownian noise is a stochastic force calibrated from temperature. For this work, we extended Cytosim to be able to model a contractile surface under tension that can be deformed by the MTs. The cell shape is restricted to remain ellipsoidal and is described by six parameters: the lengths of three axes , , and and a rotation matrix (i.e., three angles describing the cell orientation in the space). Because RBCs have active mechanisms to maintain their volume (30), we also constrained the three lengths to keep the volume of the ellipsoid constant. To implement confinement, any MT model point located outside the cell is subject to inward-directed force , in which is the shortest vector between the point and the surface and the confining stiffness. Here, for each force applied on a MT, an opposite force is applied to the surface, in agreement with Newton’s third law. The rates of change of the ellipsoid parameters are then given by the net force on each axis, divided by , an effective viscosity parameter (SI Text, section 1.3 and Fig. S1). The value of affects the rate at which the cell shape can change, but not the shape that will eventually be reached. This approach is much simpler than using a tessellated surface to represent the cell, and still general enough to capture the shape of blood platelets (3, 6) and several RBCs (8, 31) (Fig. 1A).
Fig. S1.
Phase diagram of the degree of buckling as a function of the length and the tension. Red means that the filament is buckled and gray that it is flat. The dashed line represents the critical tension calculated in Eq. S16.
To model resting platelets, we simulated marginal bands made of – MTs of fixed length –m (4) with or cross-linkers, confined in a cell of volume with a tension –m. Initially the filaments had random orientations, and we simulated the system for >6 min, which was enough time for them to align at the periphery and balance the cortical tension given the viscosity. This also allowed for multiple rounds of cross-linker binding/unbinding events. We found that the numerical results agree with the scaling law over a very large range of parameter values, as illustrated in Fig. 2B. Interestingly, simulated cells were slightly larger than predicted analytically. This is because MTs of finite length do not exactly follow the cell radius, and their ends are less curved, thus exerting more force on the cell. This means that the value of the tension computed from the biological data (m) is slightly underestimated. More importantly, a simulated cell has the same size at equilibrium with or without cross-linkers (compare black and gray dots on Fig. 2B). This shows that, if they are given time to freely reorganize, cross-linkers do not affect the mechanical equilibrium of the system. To understand the response of the system that occurs at short time scale, it is, however, necessary to consider the cross-linkers.
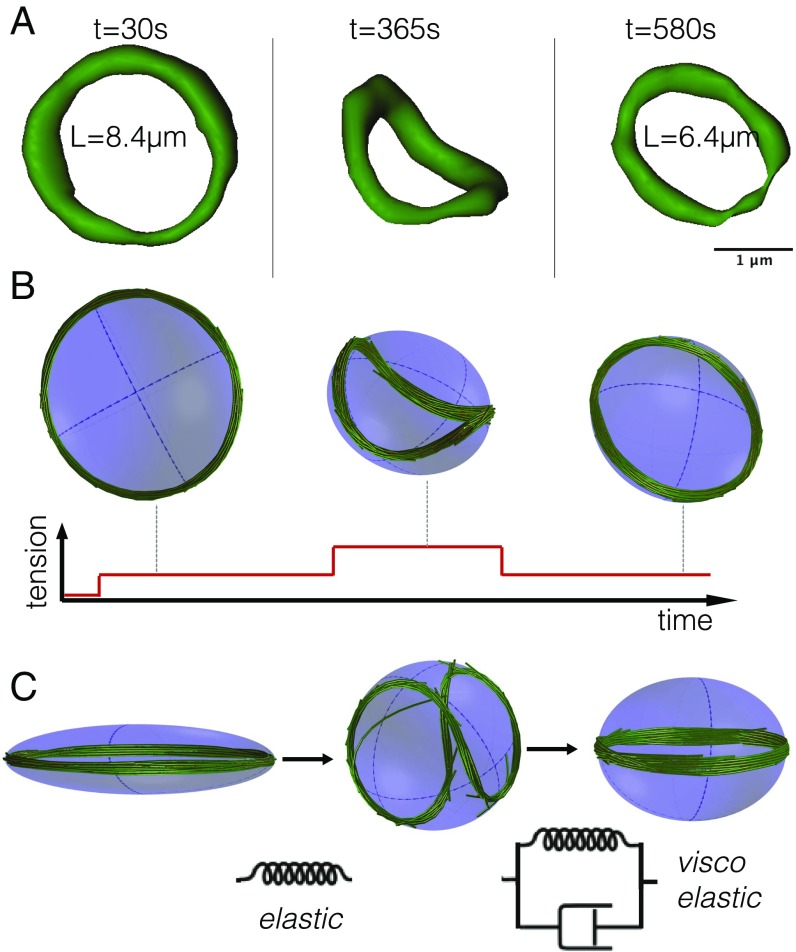
The MB Behaves Like a Viscoelastic System.
During activation, mammalian platelets round up before spreading, and within a few seconds, their MB coils (19). A similar response is seen also in thrombocytes (3). This process can be triggered by several activators, including thrombin and ADP, that bind to G-protein-coupled receptors (32) and activate several downstream events. Among them, RhoA may induce actin contraction (33), possibly through its role in myosin light-chain phosphorylation (34). To observe platelet activation experimentally, we extracted mice platelets and exposed them to ADP, causing an often-reversible activation. By monitoring the MB with SiR-tubulin, a bright docetaxel-based MT dye, we could record the MB coiling live, Fig. 3A (SI Text, section 4). The MB coils according to the baseball-seam curve, which is the shape that an incompressible elastic ring would adopt when constrained into a sphere smaller than its natural radius (35). Thus, at short time scale, the MB seems to behave as an incompressible ring, and we reasoned that this must be because cross-linkers prevent MTs from sliding relative to each other. To analyze this process further, we returned to Cytosim. After an initialization time, in which the MB assembles as a ring of MTs connected by cross-linkers, cortical tension is increased stepwise. The cell as a consequence becomes nearly spherical, and, because we assumed that the volume should be constant, the radius of this sphere was smaller than the largest radius that the cell had at low tension. As a result, the MB adopted a baseball-seam shape (Fig. 3B). Over a longer period, however, the MB regained a flat shape, as MTs rearranged into a new, smaller ring (Fig. 3A). In conclusion, the simulated MB is viscoelastic (Fig. 3B). At short time scales, MTs do not have time to slide, and the MB behaves as an incompressible elastic ring. At long time scales, the MB behaves as if cross-linkers were not present, with an overall elastic energy that is the sum of individual MT energies. Thus, overall, the ring behavior seems to transition from purely elastic at short time scales, to viscoelastic Kelvin–Voigt law at long time scales (Fig. 3C). The transition between the two regimes is determined by the time scale at which cross-linkers permit MTs to slide.
Fig. 3.
(A) MB of a live platelet labeled with SIR-tubulin dye. Fluorescence images were segmented at the specified time after the addition of ADP, a platelet activator, to obtain the MB size . (B) Simulation of a platelet at different times. A limited increase of the tension (m) causes the MB to shorten, whereas a large increase of the tension (m) causes the MB to buckle. (C) In simulations, the MB buckles if cell rounding is fast enough because cross-linkers cannot reorganize. This represents an elastic behavior, but at longer times, the MB rearranges, leading to a viscoelastic response.
The Cell Is Unexpectedly Robust.
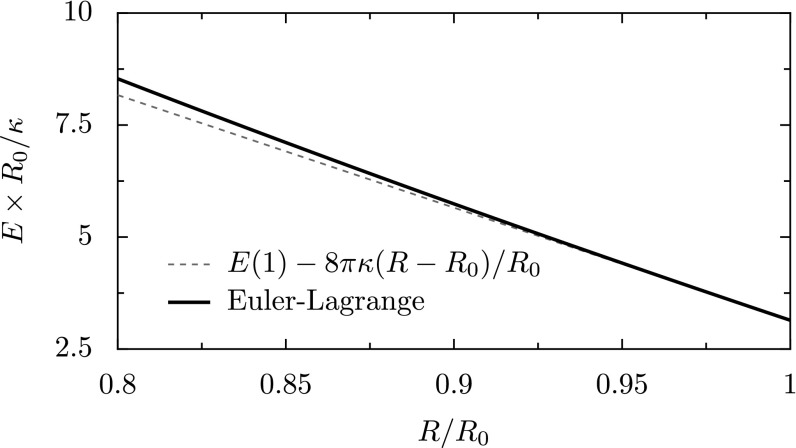
The MB in blood cells is necessary to establish a flat morphology, but also to maintain this morphology in the face of transient mechanical challenges, for example as the cell passes through a narrow capillary (7). We thus investigated how the cortex effectively reinforces the MB, making the cell a stronger object than the MB alone. Specifically, we calculated the resistance of the cell to deformations that would require its marginal band to coil, on a short time scale, during which cross-linkers do not reorganize. We therefore considered the MB as a closed ring of constant length and uniform rigidity . We first examined the mechanics of this ring within a sphere and then extended these results to a nondeformable ellipsoid. The shape of a ring in a sphere was previously calculated numerically (35), and we extended this result by deriving analytically the force required to buckle a confined ring (SI Text, section 1.2.2 and Fig. S2). If is the energy of a buckled MB, the force is:
| [2] |
Fig. S2.
Bending energy of an incompressible elastic ring of length (the MB) in a sphere of radius . The solid line represents the numerical solution to the Euler–Lagrange equations (Eq. S22), while the dashed line represents the small deformation approximation, Eq. S32.
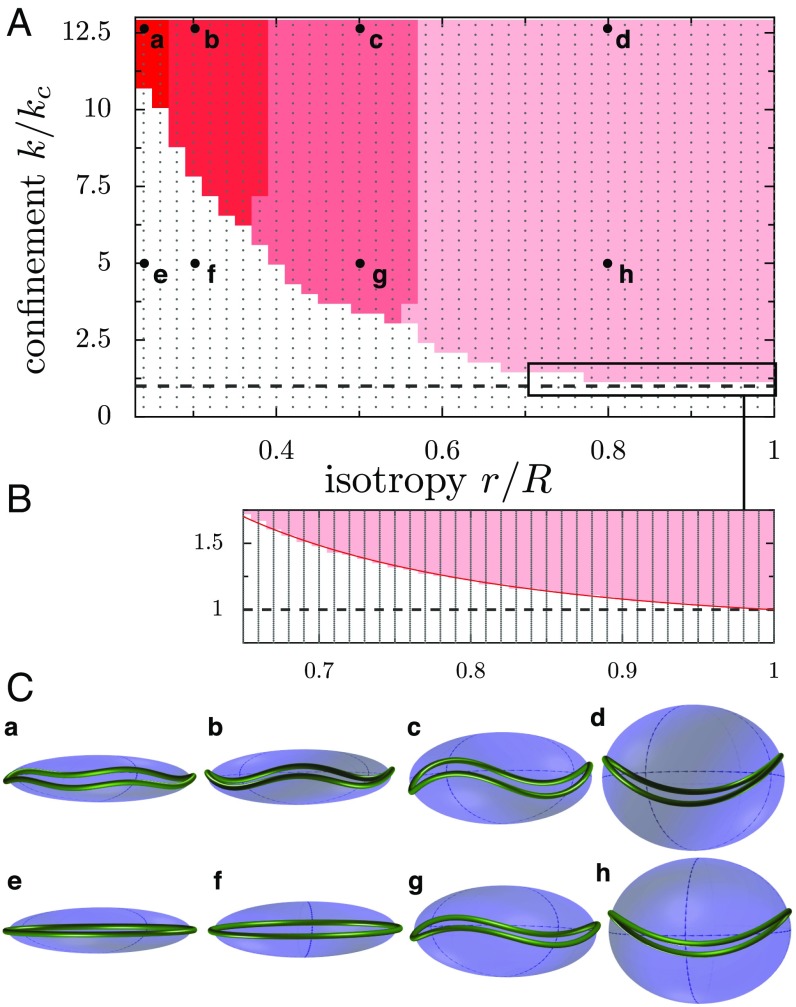
We verified this relation in simulations, with , where , which made the ring slightly oversized compared with its confinement. Given the confining stiffness , the force applied to each model point of the ring is . If is the number of model-points in the rings (i.e., where is the discretization parameter of the ring), the total centripetal force is . Hence, we expected that the ring would buckle if exceeds . Upon systematically varying in the simulation (Methods), we indeed found that the ring coils for (Fig. 4A). We next simulated oblate ellipsoidal cells, with and , and we varied the flatness of the cell by changing . We found that the measured critical confinement is indeed for , but increases strongly with (Fig. 4 A and B). We also found that the mode of deformation increases with the cell flatness (Fig. 4A, shades of red). This is because, as the cell gets flatter, large deformations along the short axis are increasingly penalized, and higher modes of deformation (such as the chair shape; Fig. 4C, c) become more favorable than the baseball-seam curve (Fig. 4C, d), because the magnitude of their out-of-plane deviations is smaller. This increase of the critical buckling force with cell flatness implies that an uncoiled marginal band in a flat cell could be metastable.
Fig. 4.
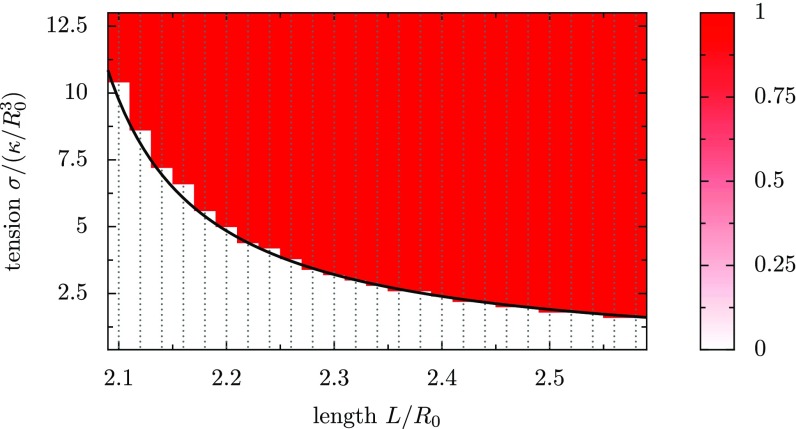
(A) Coiling diagram of an elastic ring confined inside a fixed oblate ellipsoid. The configuration of the ring is indicated by the color (white, uncoiled; colored, coiled), as a function of the isotropy of the confining ellipsoid and the normalized confinement stiffness . The gray dots indicate the simulations performed to calculate the diagram. The dashed line indicates the predicted critical buckling confinement in a spherical cell (i.e., ). The color indicates the main Fourier mode, from 2 (pink) to 5 (darker red). (B) A closeup reveals that the critical confinement is exponential for mode 2: (red line), where is a phenomenological parameter that depends on the excess length , defined from the MB length as . (C) Illustrations of MB shapes from the phase diagram, as indicated by the letters. Flatter cells (C, a and b) are deformed in higher modes than rounder cells (C, c and d). The normal physiology of a resting platelet corresponds to condition (C, e).
Platelets and nonmammalian RBCs have an isotropy ratio (Fig. 4C, e), which makes them >10 times more resilient than a spherical cell with similar characteristics. Direct micropipette aspiration showed that destabilizing MTs or actin lead in both cases to an increased deformability, confirming that actin and MT systems determine the rigidity of the cell together (36).
Coiling Stems from Cortical Tension Overcoming MB Rigidity.
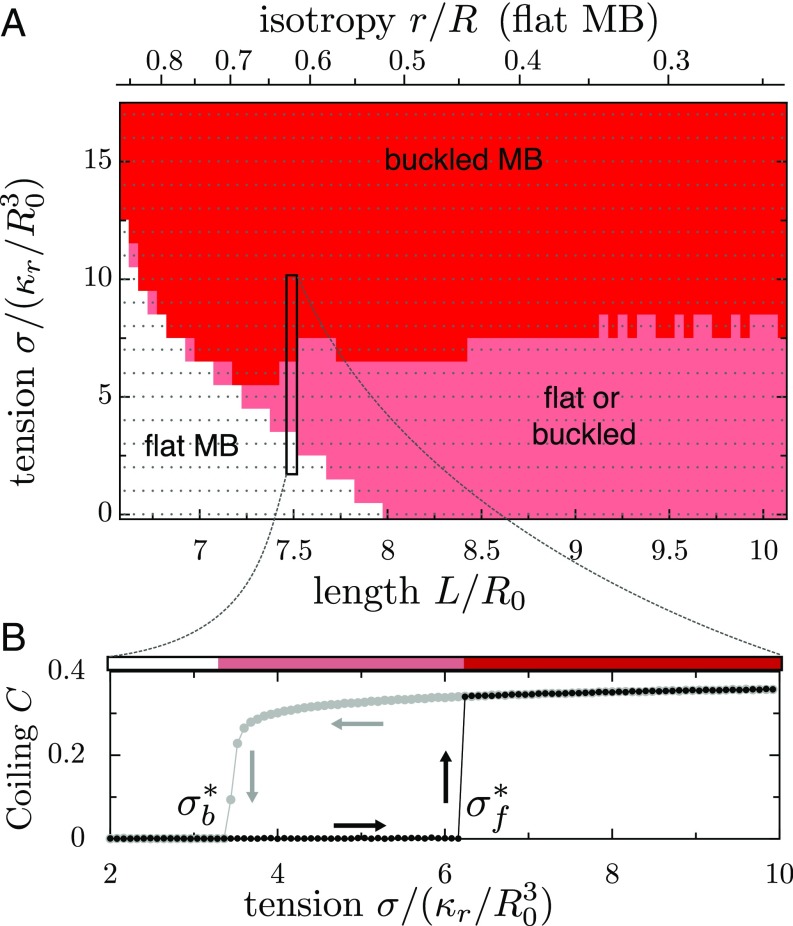
We then considered the case of a ring inside a deformable ellipsoid of constant volume , governed by a surface tension . The length of the ring is set with , such that we expected the ring to remain flat at low tension and to be coiled at high tension, because it does not fit in the sphere of radius . In simulations, starting from a flat ring, we observed as predicted the existence of a critical tension , above which the ring is buckled (Fig. 5A). This shows that increasing (i.e., increasing the ratio of cortical tension over ring rigidity) leads to cell rounding. Thus, either increasing the cortical tension or weakening the ring will lead to coiling. Starting from a buckled ring, decreasing the tension below a critical tension also leads to the cell flattening, as predicted. However, our simulations showed that , and thus for , a cell initially flat remains flat, whereas a cell initially round remains round (Fig. 5). Hysteresis is the hallmark of bistability, and we had predicted this bistability in the previous section by showing that the flat configuration is metastable. This metastability (i.e., the fact that a MB in a flat cell has a higher buckling threshold than in a spherical cell) allows the cell to withstand very large mechanical constraints such as shear stresses. A platelet typically has (i.e., an isotropy ) and is therefore in the region where the flat MB is extremely metastable. In this regime, extending the MB does not cause buckling, but increasing the tension does.
Fig. 5.
(A) The equilibrium configuration of the MB is calculated as a function of renormalized tension and renormalized MB length , in which the volume of the cell is . The gray dots indicate the simulations performed to calculate the diagram. The configuration of the MB is indicated by colors: white, flat; red, buckled; and pink, bistable (i.e., buckled or flat). The topmost scale indicates the shape parameter of the cell (isotropy ), at equilibrium in the case where the MB is flat and has a length equal to the cell perimeter. (B) A cut through the phase diagram, for a MB of length . The degree of coiling (see Methods for definition) is indicated as a function of tension, for a cell that is initially flat (black dots) or buckled (gray dots). In the metastable region, the two trajectories are separated, and the arrows illustrate hysteresis in the system.
Discussion
We have examined how MB elasticity and cortical tension determine the morphology of blood cells. Equilibrium between these forces predicts a scaling law, , in which is the sum of the lengths of the MTs inside the cell, is the bending rigidity of MTs, and is the cortical tension. Remarkably, values of and measured for 25 species conform to this scaling law. We caution that these observations were made for nondiscoidal RBCs (where the two major axes differ), indicating that other factors not considered here must be at work (7). In human RBCs, perturbation of the spectrin meshwork can lead to elliptical RBCs (37), suggesting that the cortex can impose anisotropic tensions, whereas another study suggests that MB-associated actin can sequester the MB into an elliptical shape (38). Cortical anisotropy would be an exciting topic for future studies, but this may not be needed to understand wild-type mammalian platelets.
Using analytical theory and numerical simulations, we analyzed the mechanical response of cells with MB and uncovered a complex viscoelastic behavior characterized by a time scale that is determined by cross-linker reorganization. At long time scales (), the MB behaves elastically, and its elasticity is the sum of all MTs’ rigidity. At short time scales (), the MB behaves as an incompressible elastic ring of fixed length because cross-linkers do not yield. At this time scale, the stiffness of the ring exceeds the sum of the individual MT stiffness, as long as the cross-linkers connect neighboring MT tightly (39). Buckling leads to the baseball-seam curve, which is a configuration of minimum elastic energy. This explains the coiled shape of the MB observed in mouse platelets (Fig. 3A), human platelets (19), and dogfish thrombocytes (3). Thus, an increase of cortical tension over bundle rigidity can cause coiling, if the cell deforms faster than the MB can reorganize. A fast increase of tension is a likely mechanism supported by evidence of several experiments (40–42). In dogfish thrombocytes and platelets, blebs are concomitant with MB coiling, suggesting a strong increase of cortical tension (3). A recent study concluded that MB coiling could be triggered by the extension of the MB, leading to coiling without an increase of cortical tension (19). However, the fact that the MB elongates during activation was inferred there by averaging over populations of fixed platelets, rather than observed at the single cell level.
Finally, calculating the buckling force of a cell containing an elastic ring and a contractile cortex led to a surprising result. We found that the buckling force increased exponentially with the cell flatness, because the cortex reinforces the ring laterally. This makes the MB a particularly efficient system to maintain the structural integrity of blood cells. For transient mechanical constraints, the MB behaves elastically, and the flat shape is metastable, allowing the cell to overcome large forces without deformation. However, as we observed, the viscoelasticity of the MB allows the cell to adapt its shape when constraints are applied over long time scales, exceeding the time necessary for MB remodeling by cross-linker binding and unbinding. It will thus be particularly interesting to compare the time scale at which blood cells experience mechanical stimulations in vivo with the time scale determined by the dynamics of the MT cross-linkers.
Methods
Simulations.
MTs of persistence length are described as bendable filaments of rigidity , in which is the thermal energy. The associated bending energy is , where is the position as a function of the arclength along the filament. The dynamics of such a system was simulated in Cytosim, an Open Source simulation software (29). In Cytosim, a filament is represented by model points distributed regularly defining segments of length . Fibers are confined inside a convex region of space by adding a force to every model point that is outside . The force is , where is the projection of the model point on the edge of , and is a stiffness constant. For this work, we implemented a deformable elliptical surface confining the MTs, parametrized by six parameters. The evolution of these parameters is implemented using an effective viscosity (SI Text, section 1.3). To verify the accuracy of our approach, we first simulated a straight elastic filament, which would buckle when submitted to a force exceeding , as shown by Euler. Cytosim recovered this result numerically. We then calculated the critical tension necessary for the buckling of MTs in a prolate ellipsoid. The simulated critical tension corresponds very precisely to the theoretical prediction (43) (SI Text, section 1.4 and Fig. S1).
To calculate the cell radius as a function of , we used a volume of (close to the volume of a platelet), with a tension to m, consistent with physiological values. We simulate MTs with a rigidity as measured experimentally (23). MTs have lengths in m and are finely represented with a segmentation of . The cross-linkers have a resting length of nm, a stiffness of m, a binding rate of , a binding range of nm, and an unbinding rate of . An example of simulation configuration file is provided in SI Text, section 2. When considering an incompressible elastic ring, we used a cell of volume , where is the radius of the spherical cell. For simplicity, we can renormalize all lengths by and thus all energies by , where is the ring rigidity. We simulate a cell with a tension , and a ring of length . To test the effect of confinement, we place an elastic ring of rigidity in an ellipsoid space of principal radii , in which . The elastic ring has a length , in which . An extensive list of parameters and their values are given in SI Text, section 1.2. To estimate the coiling level of a MB, we first perform a principal component analysis using all of the MTs’ model points. The coordinate system is then rotated to bring the vector in the direction of the smallest eigenvalue. We then define the degree of coiling as the deviation in divided by the deviations in : . Thus, is independent of the size of the cell and only measures the deformation of the MB.
To measure the critical value of a parameter (e.g., tension or confinement) leading to coiling, we computed the derivative of the degree of coiling , with respect to this parameter. Because buckling is analogous to a first-order transition, the critical value can be defined by: . We calculated the Fourier modes of deformation by transforming the -coordinates of the MT model points.
SI Text
1. Simulation of MTs/Cortex Interaction
To understand cell shape maintenance, one needs to model the interaction between the cellular cortex and the MB. The structure of the MB is well known, compared with the organization of the cortex, which is less well characterized. We thus decided to represent the MTs individually, and the cortex effectively as a continuous deformable surface. Treating the interactions between a discretized (e.g., triangulated) surface and discrete filaments can be demanding computationally, because such a surface would have a very large number of degrees of freedom. In contrast, we describe here how the problem remains relatively simple for a continuous shape that is defined by a small set of parameters.
1.1. General Formulation.
1.1.1. Forces and parametrization.
Let be a surface defined by parameters . Let be the set of forces applied on at the points . Assuming forces to be conservative, they are defined as , where is the energy of the system (excluding the surface). One can define “effective forces” associated with each degree of freedom of the surface:
| [S1] |
We can define the infinitesimal change in energy after an infinitesimal set of displacements , and then compute it as a function of the infinitesimal set of parameter changes .
| [S2] |
| [S3] |
| [S4] |
To write Eq. S3, we had to assume that any displacement of the surface (allowed by the constraints) can be described in terms of , i.e., that is surjective. It is interesting here to note that has the dimension of a force if is a length, whereas it has the dimension of a torque (i.e., an energy) if is an angle.
1.1.2. Constraints.
In many cases, constraints can be added by modifying the energy functional following the method of Lagrange. For instance, to maintain the volume constant, we define an energy , where is the volume and is the pressure; here is also a Lagrange multiplier, and we have to calculate its value appropriately to obtain . The pseudoforces associated to pressure are:
| [S5] |
1.2. Deformable Ellipsoid.
In this section, we describe a surface in 3D. We model an ellipsoid centered around the origin, with a fixed volume and a surface tension , which an associated energy , if is the surface area of the ellipsoid. The ellipsoid is described by its principal directions and their length (i.e., the radii of the ellipse) . We will also use the orientation matrix . By construction, is a rotation matrix of determinant 1. In the simulation, this rotation matrix describes the orientation of the ellipse in space and does not apply to filaments within. This matrix is thus more appropriately seen as the inverse rotation that applies to all of the filaments, with respect to the cell envelope that confines them. The orientation in space of the ellipsoid (cell) is not relevant for this study, which is solely concerned with cell shape.
1.2.1. Surface tension.
We can compute the pseudoforces associated to surface tension as:
| [S6] |
The surface area of an ellipsoid is a complex special function that is not a combination of the usual functions. For convenience, we used an analytical approximation of the area:
| [S7] |
for which is an empirical parameter. This formula yields an error usually below a percent.
1.2.2. Point forces.
To add the contribution of the external forces exerted by the MTs on the surface, we need to determine . The position of a point on the surface of the ellipsoid is defined by two angles , as:
| [S8] |
Therefore, we have:
| [S9] |
Because we assumed that the boundaries offer no friction, all forces are normal to the surface. The contribution of a force at a point of the surface is
| [S10] |
We can now compute the torque generated by . In 2D, it would be convenient to describe the ellipse orientation by an angle , and the result is that the “angular force” is the torque . We will assume that this is general and stays true in 3D; thus, we can write directly as a vector:
| [S11] |
1.2.3. Volume conservation.
To implement volume conservation, we need to find a pressure such that , where is a (small) tolerance parameter. We used Newton’s method to find a zero of and reach the desired aim for . This method works very well if is monotonous, which is always the case here.
The volume of the ellipse is , and, therefore, using the Lagrange multiplier to conserve the volume, we can write:
| [S12] |
1.3. Time Evolution.
We can now define the time evolution of the ellipse. We assume a unique viscosity associated to the change of size of the ellipse and a rotational viscosity .
| [S13] |
| [S14] |
in which is the rotation matrix generated from the moment vector . We effectively used .
1.4. Validations.
To validate our numerical method and its implementation, we first simulated a MT bundle confined inside an ellipsoid cell of tension and volume . A classical result of analytical mechanics is that a filament should buckle under a tangential force if this force is larger than a critical force:
| [S15] |
We confined the MT in a deformable ellipsoid, which thus takes the shape of a prolate ellipsoid. Let us call the longer axis of this ellipsoid, and the shorter axis is . The force exerted on the MT is , with defined in Eq. S7. Starting with a MT of length , buckling will occur for a critical tension:
| [S16] |
In simulations, we find that the MT buckles for , as we predicted (Fig. S1).
2. Mechanics of a Confined Elastic Ring
2.1. Formulation.
Let us consider a rod of length lying on a sphere of radius . We can describe this rod by its position , parametrized by its arc length , such that the energy reads:
| [S17] |
Because the rod lies on the unit sphere, and because is the arclength, we have the constraints:
| [S18] |
We can introduce this as constraints in the energy using two Lagrange multipliers and , to define:
| [S19] |
Minimizing this energy yields the Euler–Lagrange equation:
| [S20] |
Because the curve is lying on a sphere, we can use the identity:
| [S21] |
in which is the intrinsic (geodesic) curvature. Eventually, we find:
| [S22] |
where is a negative constant (35). Finally, one needs to find the value of and , such that the curve is closed and of length :
| [S23] |
Numerically, we determined and using a shooting method.
2.2. Case of a Weakly Deformed Ring.
For a weakly deformed ring, Eq. S22 can be simplified to
| [S24] |
Periodicity imposes , when , in which . Because the lowest energy curve has a period , we can conclude that , i.e., for . Although analytically solving the full shape equation is arduous (18), even in this weakly deformed approximation, we can construct a shape equation that satisfies Eq. S24 for small deformation as follows:
| [S25] |
in which is an angle coordinate. For small deformations , one finds:
| [S26] |
| [S27] |
with as expected. From Eq. S25, we can compute the bending energy of the MB:
| [S28] |
For small deformations , we have:
| [S29] |
We can also compute the length of the MB, and the energy:
| [S30] |
| [S31] |
We then find the force exerted by a nearly flat ring on the sphere :
| [S32] |
This result is in agreement with solving the full shape equation (Eq. S22), as illustrated in Fig. S2. is the force exerted by a nearly flat ring on a sphere; by construction, it is also the critical force at which a ring will buckle. Numerically, we can study ring buckling in two cases: when the ring is undergoing an elastic confinement, and when the ring is confined by a deformable ellipsoid.
2.3. Ring Under Elastic Confinement.
Let us consider a ring of length confined in a sphere of radius , such that by an elastic confinement (see ref. 29 for the implementation of confinement). The confinement force is here , in which is the number of points describing the discrete ring. The ring will buckle if ; using Eq. S32, we find that the ring will buckle above a critical confinement:
| [S33] |
in which , where is the segmentation.
2.4. Ring Confined in a Deformable Ellipsoid.
Using our computed value of , we can compute analytically the critical value of the tension that will buckle a ring in a deformable space, assuming that space to be ellipsoid and near-spherical. For this, we take the very same approach as we did for the bundle in a prolate ellipsoid, although now the ellipsoid is oblate, and the buckling force is that of a ring rather than an open bundle.
| [S34] |
3. Simulation Parameters
The parameters used for Figs. 4 and 5 were:
| Parameter | Symbol | Value |
| Ring rigidity | ||
| Time step | ||
| Filament segmentation | m |
For the incompressible elastic ring in a fixed shape ellipsoid (Fig. 4), we built a closed ring by linking the first and lastpoint of the filament with a zero-resting length link of rigidity m. We also add a torque component (29) to ensure that the bending elasticity is uniform in every point of the ring. In these simulations, additional parameters were:
| Parameter | Symbol | Value |
| Cell major radius | m | |
| Cell minor radius (thickness) | to m | |
| MB length | m | |
| Confinement stiffness | to m | |
| Thermal energy | m |
For the simulations of the incompressible elastic ring in a deformable ellipsoid (Fig. 5), we used:
| Parameter | Symbol | Value |
| Cell volume | ||
| MB Length | to m | |
| Cortical tension | to m | |
| Ellipse effective viscosity | ||
| Confinement stiffness | m | |
| Thermal energy | m | |
| Tolerance parameter for cell volume |
4. Experimental Methods
The experiments were performed on platelets extracted from the blood of the common inbred laboratory mouse strain (C57BL/6) and prepared according to standard protocols (44). Blood was collected by cardiac puncture and mixed with L of acid–citrate–dextrose solution to prevent coagulation. Once obtained, the blood was immediately centrifuged for 4 min at 200 × g. The upper phase (platelet-rich Plasma), was carefully removed and centrifuged at 2,000 × g for 2 min. The plasma was discarded, and the platelet pellet was resuspended in Tyrode’s albumin buffer. We labeled MTs with nM SiR tubulin (Spirochrome) and incubated the cells for at least 1 h before imaging. Imaging was performed by using a spinning disk microscopy setup (Perkin-Elmer Ultraview VoX). Live platelets were imaged by using a 63× (1.4-NA) oil objective, which produced images with a lateral pixel size of nm. The 3D stacks were acquired with a spacing of m in the axial dimension. An image stack was acquired every 5 s over 10 min. The image analysis was performed by using Fiji (fiji.sc/Fiji).
Acknowledgments
We thank S. Correia for technical assistance; A. Diz-munoz, R. Prevedel, and N. Minc for critical reading; and European Molecular Biology Laboratory (EMBL) IT support for performance computing. This work was supported by the EMBL and the Center for Modeling in the Biosciences (S.D.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1618041114/-/DCSupplemental.
References
- 1.Lecuit T, Lenne PF. Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat Rev Mol Cell Biol. 2007;8(8):633–644. doi: 10.1038/nrm2222. [DOI] [PubMed] [Google Scholar]
- 2.Goniakowska-Witalinska L, Witalinski W. Evidence for a correlation between the number of marginal band microtubules and the size of vertebrate erthrocytes. J Cell Sci. 1976;22(2):397–401. doi: 10.1242/jcs.22.2.397. [DOI] [PubMed] [Google Scholar]
- 3.Lee KG, Miller T, Anastassov I, Cohen WD. Shape transformation and cytoskeletal reorganization in activated non-mammalian thrombocytes. Cell Biol Int. 2004;28(4):299–310. doi: 10.1016/j.cellbi.2004.01.008. [DOI] [PubMed] [Google Scholar]
- 4.Patel-Hett S, et al. Visualization of microtubule growth in living platelets reveals a dynamic marginal band with multiple microtubules. Blood. 2008;111(9):4605–4616. doi: 10.1182/blood-2007-10-118844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Van Deurs B, Behnke O. The microtubule marginal band of mammalian red blood cells. Z Anat Entwicklungsgesch. 1973;143(1):43–47. doi: 10.1007/BF00519909. [DOI] [PubMed] [Google Scholar]
- 6.White JG. Platelet structure. In: Michelson AD, editor. Platelets. 3rd Ed. Academic; New York: 2013. pp. 117–144. [Google Scholar]
- 7.Joseph-Silverstein J, Cohen WD. The cytoskeletal system of nucleated erythrocytes. III. Marginal band function in mature cells. J Cell Biol. 1984;98(6):2118–2125. doi: 10.1083/jcb.98.6.2118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schroter R, Filali RZ, Brain A, Jeffrey P, Robertshaw D. Influence of dehydration and watering on camel red cell size: A scanning electron microscopic study. Respir Physiol. 1990;81(3):381–390. doi: 10.1016/0034-5687(90)90118-i. [DOI] [PubMed] [Google Scholar]
- 9.Hartwig JH, DeSisto M. The cytoskeleton of the resting human blood platelet: Structure of the membrane skeleton and its attachment to actin filaments. J Cell Biol. 1991;112(3):407–425. doi: 10.1083/jcb.112.3.407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bathe M, Heussinger C, Claessens MM, Bausch AR, Frey E. Cytoskeletal bundle mechanics. Biophys J. 2008;94(8):2955–2964. doi: 10.1529/biophysj.107.119743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Patel-Hett S, et al. The spectrin-based membrane skeleton stabilizes mouse megakaryocyte membrane systems and is essential for proplatelet and platelet formation. Blood. 2011;118(6):1641–1652. doi: 10.1182/blood-2011-01-330688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Thon JN, et al. Microtubule and cortical forces determine platelet size during vascular platelet production. Nat Commun. 2012;3:852. doi: 10.1038/ncomms1838. [DOI] [PubMed] [Google Scholar]
- 13.Cohen WD, Bartelt D, Jaeger R, Langford G, Nemhauser I. The cytoskeletal system of nucleated erythrocytes. I. Composition and function of major elements. J Cell Biol. 1982;93(3):828–828. doi: 10.1083/jcb.93.3.828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Evans E, Yeung A. Apparent viscosity and cortical tension of blood granulocytes determined by micropipet aspiration. Biophys J. 1989;56(1):151–160. doi: 10.1016/S0006-3495(89)82660-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stewart MP, et al. Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding. Nature. 2011;469(7329):226–230. doi: 10.1038/nature09642. [DOI] [PubMed] [Google Scholar]
- 16.Bender M, et al. Microtubule sliding drives proplatelet elongation and is dependent on cytoplasmic dynein. Blood. 2015;125(5):860–868. doi: 10.1182/blood-2014-09-600858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.White JG, Rao G. Microtubule coils versus the surface membrane cytoskeleton in maintenance and restoration of platelet discoid shape. Am J Pathol. 1998;152(2):597–609. [PMC free article] [PubMed] [Google Scholar]
- 18.Ostermeir K, Alim K, Frey E. Buckling of stiff polymer rings in weak spherical confinement. Phys Rev E. 2010;81(6):061802. doi: 10.1103/PhysRevE.81.061802. [DOI] [PubMed] [Google Scholar]
- 19.Diagouraga B, et al. Motor-driven marginal band coiling promotes cell shape change during platelet activation. J Cell Biol. 2014;204(2):177–185. doi: 10.1083/jcb.201306085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kuwahara M, et al. Platelet shape changes and adhesion under high shear flow. Arterioscler Thromb Vasc Biol. 2002;22(2):329–334. doi: 10.1161/hq0202.104122. [DOI] [PubMed] [Google Scholar]
- 21.Landau LD, Lifshitz EM. Course of Theoretical Physics: Theory and Elasticity. Vol 7 Pergamon, Oxford; 1959. [Google Scholar]
- 22.Braun M, et al. Adaptive braking by Ase 1 prevents overlapping microtubules from sliding completely apart. Nat Cell Biol. 2011;13(10):1259–1264. doi: 10.1038/ncb2323. [DOI] [PubMed] [Google Scholar]
- 23.Gittes F, Mickey B, Nettleton J, Howard J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J Cell Biol. 1993;120(4):923–934. doi: 10.1083/jcb.120.4.923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Salbreux G, Charras G, Paluch E. Actin cortex mechanics and cellular morphogenesis. Trends Cell Biol. 2012;22(10):536–545. doi: 10.1016/j.tcb.2012.07.001. [DOI] [PubMed] [Google Scholar]
- 25.Tinevez JY, et al. Role of cortical tension in bleb growth. Proc Natl Acad Sci USA. 2009;106(44):18581–18586. doi: 10.1073/pnas.0903353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Turlier H, et al. Equilibrium physics breakdown reveals the active nature of red blood cell flickering. Nat Phys. 2016;12(5):513–519. [Google Scholar]
- 27.Fournier JB, Lacoste D, Raphaël E. Fluctuation spectrum of fluid membranes coupled to an elastic meshwork: Jump of the effective surface tension at the mesh size. Phys Rev Lett. 2004;92(1):018102. doi: 10.1103/PhysRevLett.92.018102. [DOI] [PubMed] [Google Scholar]
- 28.Kenney DM, Linck R. The cystoskeleton of unstimulated blood platelets: Structure and composition of the isolated marginal microtubular band. J Cell Sci. 1985;78(1):1–22. doi: 10.1242/jcs.78.1.1. [DOI] [PubMed] [Google Scholar]
- 29.Nedelec F, Foethke D. Collective langevin dynamics of flexible cytoskeletal fibers. New J Phys. 2007;9(11):427. [Google Scholar]
- 30.Cala PM. Volume regulation by Amphiuma red blood cells. The membrane potential and its implications regarding the nature of the ion-flux pathways. J Gen Physiol. 1980;76(6):683–708. doi: 10.1085/jgp.76.6.683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cohen WD. The cytoskeletal system of nucleated erythrocytes. Int Rev Cytol. 1991;130:37–84. doi: 10.1016/s0074-7696(08)61501-6. [DOI] [PubMed] [Google Scholar]
- 32.Wettschureck N, Offermanns S. Mammalian g proteins and their cell type specific functions. Physiol Rev. 2005;85(4):1159–1204. doi: 10.1152/physrev.00003.2005. [DOI] [PubMed] [Google Scholar]
- 33.Mills JC, Stone NL, Erhardt J, Pittman RN. Apoptotic membrane blebbing is regulated by myosin light chain phosphorylation. J Cell Biol. 1998;140(3):627–636. doi: 10.1083/jcb.140.3.627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Moers A, et al. G13 is an essential mediator of platelet activation in hemostasis and thrombosis. Nat Med. 2003;9(11):1418–1422. doi: 10.1038/nm943. [DOI] [PubMed] [Google Scholar]
- 35.Guven J, Vázquez-Montejo P. Confinement of semiflexible polymers. Phys Rev E. 2012;85(2):026603. doi: 10.1103/PhysRevE.85.026603. [DOI] [PubMed] [Google Scholar]
- 36.White JG, Burris SM, Tukey D, Smith C, 2nd, Clawson C. Micropipette aspiration of human platelets: Influence of microtubules and actin filaments on deformability. Blood. 1984;64(1):210–214. [PubMed] [Google Scholar]
- 37.Lux S, John K, Ukena TE. Diminished spectrin extraction from ATP-depleted human erythrocytes. Evidence relating spectrin to changes in erythrocyte shape and deformability. J Clin Invest. 1978;61(3):815–827. doi: 10.1172/JCI108996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cohen WD, Sorokina Y, Sanchez I. Elliptical versus circular erythrocyte marginal bands: Isolation, shape conversion, and mechanical properties. Cell Motil Cytoskeleton. 1998;40(3):238–248. doi: 10.1002/(SICI)1097-0169(1998)40:3<238::AID-CM3>3.0.CO;2-9. [DOI] [PubMed] [Google Scholar]
- 39.Ward JJ, Roque H, Antony C, Nédélec F. Mechanical design principles of a mitotic spindle. Elife. 2014;3:e03398. doi: 10.7554/eLife.03398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hartwig JH. Mechanisms of actin rearrangements mediating platelet activation. J Cell Biol. 1992;118(6):1421–1442. doi: 10.1083/jcb.118.6.1421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Carroll RC, Gerrard JM. Phosphorylation of platelet actin-binding protein during platelet activation. Blood. 1982;59(3):466–471. [PubMed] [Google Scholar]
- 42.Li Z, Kim ES, Bearer EL. Arp2/3 complex is required for actin polymerization during platelet shape change. Blood. 2002;99(12):4466–4474. doi: 10.1182/blood.v99.12.4466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lee NK, Johner A, Hong SC. Compressing a rigid filament: Buckling and cyclization. Eur Phys J E. 2007;24(3):229–241. doi: 10.1140/epje/i2007-10230-4. [DOI] [PubMed] [Google Scholar]
- 44.Cazenave JP, et al. 2004:13–28. Preparation of washed platelet suspensions from human and rodent blood. Platelets and Megakaryocytes: Volume 1: Functional Assays, Methods in Molecular Biology, eds Gibbins JM, Mahaut-Smith MP (Humana, New York),pp 13–28. [Google Scholar]