Context-dependent spatially periodic activity in the human entorhinal cortex

Significance

In the mammalian brain, neurons in the hippocampus represent unique places and neurons in the entorhinal cortex, so-called grid cells, provide an internal coordinate system of the environment. Dysfunction in this circuit causes memory problems and disorientation, which are early symptoms of Alzheimer’s disease. Much of what we have learned from this circuit is based on rodent studies. Here, we report that grid cells in the human brain represent space in a more environmentally adaptive manner than in rodents. Human grids show an increased scalability with the environment relative to rodents. The enhanced context dependency of spatial representations is probably a late development of evolution.

Abstract

The spatially periodic activity of grid cells in the entorhinal cortex (EC) of the rodent, primate, and human provides a coordinate system that, together with the hippocampus, informs an individual of its location relative to the environment and encodes the memory of that location. Among the most defining features of grid-cell activity are the 60° rotational symmetry of grids and preservation of grid scale across environments. Grid cells, however, do display a limited degree of adaptation to environments. It remains unclear if this level of environment invariance generalizes to human grid-cell analogs, where the relative contribution of visual input to the multimodal sensory input of the EC is significantly larger than in rodents. Patients diagnosed with nontractable epilepsy who were implanted with entorhinal cortical electrodes performing virtual navigation tasks to memorized locations enabled us to investigate associations between grid-like patterns and environment. Here, we report that the activity of human entorhinal cortical neurons exhibits adaptive scaling in grid period, grid orientation, and rotational symmetry in close association with changes in environment size, shape, and visual cues, suggesting scale invariance of the frequency, rather than the wavelength, of spatially periodic activity. Our results demonstrate that neurons in the human EC represent space with an enhanced flexibility relative to neurons in rodents because they are endowed with adaptive scalability and context dependency.

Neurons in the hippocampus and entorhinal cortex (EC) exhibiting spatially modulated activity are highly relevant in research and medicine because they construct an agent-independent (allocentric) metric of space for localizing and remembering places, often referred to as the cognitive map (1–4). Beyond their scientific relevance, the hippocampus and EC are clinically implicated in Alzheimer’s disease (5, 6), where these structures show the earliest expression of plaques and tangles and concomitant progressive cell death, causing spatial disorientation and spatial memory loss. Coincidentally, the two structures, as part of the mesial temporal lobe, are highly susceptible to epileptic seizure (7). These cells offer a glimpse into how the brain integrates multimodal and movement-dependent sensory inputs and converts them into a coherent environment-referenced neuronal representation. Among the neurons with the greatest spatial specificity are the place cells of the hippocampus (2), head direction cells of the pre- and postsubiculum (8), border cells in the subiculum and EC (9), and grid cells in the medial EC (10). Although a place cell is only activated when the animal traverses through a unique location in its environment (2), grid-cell activity is elicited in multiple locations that the animal visits (11), and these locations span the environment periodically as vertices of a hexagonal grid formation (10). The two neuroanatomical subsystems are thought to complement each other such that individual place cells represent specific spatial locations and grid cells provide an environment-invariant metric upon which to reference the agent’s (animal or human) location (12). Although the adaptive flexibility of spatial tuning of neurons in the rodent hippocampus is evident from remapping their receptive fields when switching between environments (13–17), the association between grid patterns of cells in the EC and the environment is less clear (13, 18–20). Here, we focus on three main features of grid-cell patterns: scale invariance, orientation, and rotational symmetry.

The robust grid scale invariance across differently sized (10) and shaped (20) environments is one of the key characteristics of grid cells in the rodent EC. It has repeatedly been shown that the distance between grid nodes remains constant when the animal is transferred between environments of different size (10) and shape (20). However, past studies have demonstrated that although grid distances are rigid, they are not completely inflexible. Barry et al. (19) showed that manipulations to the width and length of a familiar enclosure resulted in similar transformations of the rodents’ grids: When the familiar environment was elongated, the grid patterns elongated similarly. Also in rats, grids have been shown to display expansion upon introduction to a novel environment and then relax back to the original scale when the environment becomes familiar (18). Combined, these results suggest that grid cells might have a default scale but that the default scale could be influenced by experience in the given environment.

Another key characteristic of grid cells is the alignment of grids with environmental cues. For a given environment, an animal’s grid-cell population shares the same grid orientation, seemingly aligned and “anchored” to a particular landmark. Rotation of a distal visual cue, serving as a landmark, resulted in similar rotations of the rodents’ grids in a feature-poor circular enclosure (10). Meanwhile, if proximal cues, such as the edges and boundaries of noncircular environments, are available, they may also function as anchors to which the grids become aligned (20). Consistent with the reliance on local cues, the orientation of grids in square-shaped environments tends to align with the walls at an angle that minimizes symmetry with respect to boundaries (21). Hence, the orientation of grids seems to rely primarily on local cues, but it can be based on distant cues when local cues are ambiguous or absent.

A third key characteristic of grids in the medial EC is their 60° rotational symmetry (10). Accordingly, grids recorded in circular or symmetrical enclosures tend to exhibit a narrow range of 60 ± 5° rotational symmetry quantified from autocorrelograms (ACs) (18). However, a comprehensive analysis of spatial periodicity evident from cells in the presubiculum and medial EC of rats revealed that only about 35–50% of medial EC cells exhibited canonical 60° rotational symmetry (12% and 28% in the presubiculum and parasubiculum, respectively) (11, 22), whereas a significant fraction of medial EC neurons (43%) displayed spatially periodic activity different from the 60° rotational symmetry (11). Nonhexagonal grid structures were most prevalent in enclosures with polarized geometry (20). The modulation of rotational symmetry was also evident in the two other studies that manipulated the size and geometry of the environment (19, 20). The control of grid rotational symmetry remains a subject of active research in rodents, although it is unexplored in the human brain.

The task of informed spatial navigation is an evolutionary problem posed to all animals. The study of human grid cells is especially interesting because it might reveal specific evolutionary adaptations beyond those adaptive features seen in lower level animals. For one thing, humans’ visual faculties are far more advanced than rodents’ visual faculties. If grid-cell activity depends on the predominant sensory input to the EC, we would expect this fact to be reflected in the nature of grid formation, perhaps with increased variability in grids according to an individual’s visual appraisal of the environment. For instance, the rat’s reliance on active exploration for the formation of place fields in the hippocampus indicates that kinesthetic and proximal cues are more crucial for this process in rats than visual cues are (23, 24). Consistent with this finding, rat exploration in virtual environments, where kinesthetic and proximal cues are absent, compromises the spatial specificity of their place cells (24). The opposite might be true in humans, where the likely predominance of visual input to the EC in the human brain might compensate for the otherwise kinesthetic-deprived sensory experience during virtual navigation. Despite the overall similarity between the anatomies of the rat and human EC, primate data suggest that the human EC receives a larger contribution from higher visual cortical areas (25). In primates, behavior as restricted as eye movements over static visual displays is sufficient to elicit spatially periodic (“grid-like”) patterns of neuronal activity that correlate with saccade direction (26, 27). Interspecies differences in sensory processing make the spatial representations of place cells display marked variability. Chiropterans, for example, distinctly rely on spatioacoustic cues, developing uniquely 3D place fields as opposed to the 2D place fields seen in other animals (28, 29). In humans, then, it is plausible for a visually presented virtual environment to elicit place cell (30) and grid-like activity in the EC (31) without proprioceptive and kinesthetic cues. The predominance of visual cues in spatial navigation makes human subjects less dependent on the hippocampus and EC except when spatial memory is involved. After mesial-temporal lobectomy, patients were still able to perform path integration (32). Studying the grid scale invariance in humans in light of the differences in the sensory input organization of the EC between rodents and primates may elucidate aspects of spatial awareness that remain hidden in rodents and are specific to our species.

Here, we investigated the influence of virtual (i.e., purely visual) surroundings on the spatially periodic activity of neurons in humans by exposing the same set of EC neurons to four different virtual environments in a spatial memory task. Specifically, we addressed how parameters of the spatially periodic activity changed in response to independent variables of environment size, environment length-to-width ratio, and availability of spatial environmental cues. To understand these effects, we analyzed how these independent variables correlated with dependent variables: grid quality (“gridness”), grid scale, grid orientation, and grid rotational symmetry. If the dependent variables (i.e., the parameters of spatially periodic activity) show dependence on environmental features, that would suggest that the increased reliance on visual cues in the human EC allows for quick adaptation (or rescaling) of the neuronal coordinate system to the environment, a behavior that expands models developed based on animal studies. To ascertain the scalability of neuronal representations of space in the human brain, our goal was to quantify the environmental dependency of the spatially periodic activity of EC cells and to test for the consistency of environment-dependent changes of grid-like activity over time and their consistency between subjects. To attain a relatively unbiased estimate of spatially periodic activity, we constructed three main neuronal datasets and two subsets within each dataset, resulting in a total of six datasets. The largest dataset included neurons classified as displaying significant spatially periodic activity based on spatial spectral analysis of the single units. The other two smaller datasets were both classified as “putative grid cells” (PGCs) based on their conformity of gridness scores to the definition used in studies and referred to herein as the Barry–Krupic (BK) method (11, 18). The difference between the second and third datasets was that the third dataset, in addition to being defined based on the BK method, was subjected to a thorough validation against theta modulation and directional tuning. In addition, we constructed two subsets of each of the three main datasets that included cells maintaining significant spatial periodicity or gridness scores in at least three of the four environments. Because we analyzed these datasets separately and the results were highly concordant among them, we posit that the spatially periodic and grid cell-like activity in the human EC is analogous to the grid cells described in rodents but with markedly increased variations.

Results

Two male epilepsy patients, H and K (aged 33 y and 40 y, respectively; SI Appendix, Table S1.2), who previously consented to participate in the experiment and to allow publication of data and MRI images, were implanted with microelectrode arrays in layer 2/3 of their medial EC (Fig. 1A) in preparation for surgical resection of epileptic foci. During their days of clinical recording in the hospital epilepsy monitoring unit, participants H and K were asked to perform a virtual, memory-aided navigation task on a tablet computer in four environments each day and for 7 or 8 consecutive days, respectively. Accordingly, the dataset was organized by day (days 1–8) and environment (environments 1–4). Electrophysiology was recorded from the EC and spike-sorted offline. All four environment trials were recorded in single file with maintained electrode stability, allowing us to monitor how individual cells behaved with progression through each environment (SI Appendix, SI Experimental Procedures). In the following sections, we compare the environmental dependency of neuronal activity (i) within each day across game environments (/environments) (ii) and across games played in the same environment but on different days (/days). Each game’s objective was to locate randomly placed space aliens and return them to their spaceship waiting at remembered locations (SI Appendix, SI Experimental Procedures and Movie S1). We constructed realistic 3D models of four different environments with accurate sizes relative to the average adult eye height and modeled the first-person visual experience of walking in these environments with an average step size and constant walking speed. The environments consisted of a large open space (OS) with a boundless horizon and minimal external cues, a small open-air backyard (BY), a medium-sized area modeled after the Louvre’s courtyard (LV), and a medium-sized covered space modeled after the main hall of the Temple of Luxor in Egypt (LX) (Fig. 2 A and B and SI Appendix, SI Experimental Procedures, Properties of Environments and Fig. S1). These environments were designed to differ in several salient features, including but not limited to size (area), aspect ratio (shape), boundaries, obstacles, and external landmarks (cues) (SI Appendix, Table S1.1).

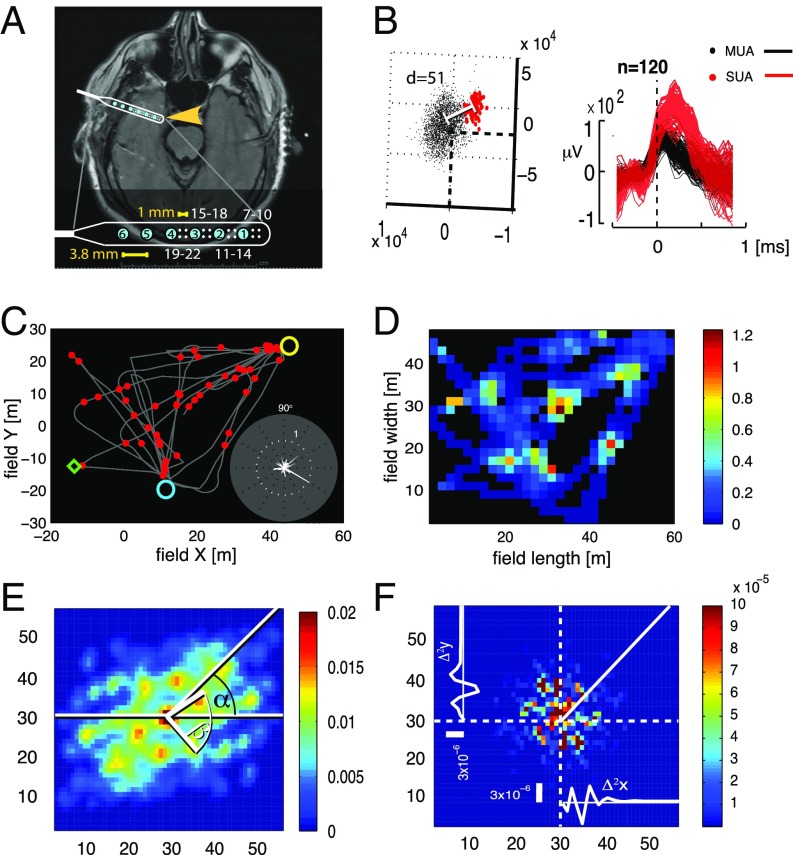
Fig. 1.

Grid-cell expression in the human EC. (A) Position of EC electrode strip (yellow arrow) revealed on an axial MRI section. (Inset) Electrode location in the brain. The electrode design is magnified at the lower part of the image. Blue circles numbered from 1 to 6 are macroelectrode contacts. Dots grouped in square quartets and numbered from 7 to 22 are the microelectrodes. (B) Single-unit clusters (Left) and corresponding spike waveforms (Right). The separation of single-unit activity (SUA; red markers) from multiunit activity (MUA; black markers) is indicated by the Mahalanobis distance (d). (C) Trajectory of the subject’s navigation in an environment overlaid with the SUA (red circles; same neuron as in B). Yellow and blue circles indicate the positions of spaceship targets, and the green diamond indicates an example target location (SI Appendix, SI Experimental Procedures). (Inset) Neuron’s firing rate at different heading directions. (D) Average firing rate map. Color scale (spike * s⁻¹). (E) Spatial AC of SUA computed from D. (F) Two-dimensional autoperiodogram of the AC from E. The X and Y axes represent frequency.

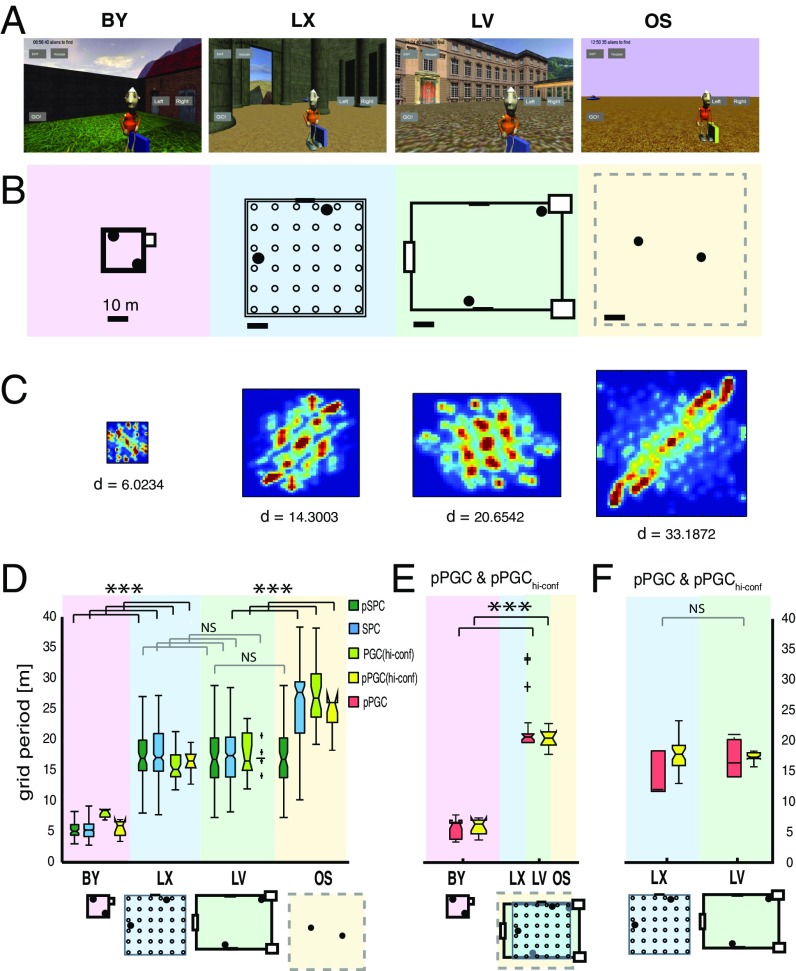
Fig. 2.

Adaptive rescaling of grids in different virtual environments. Screenshots (A), with space alien target objects and scale layouts (B) of the four different environments. Filled circles are space ships. Empty circles in LX are columns. (C) Spatial ACs from the same cell across all four environments capture the spatial periodicity of spikes generated by the same cell across the four environments. (D–F) Boxes represent the distribution of grid periods from four datasets. (D) Environment-associated differences in grid distances derived from four datasets: SPCs (all cells), n_{(trials,cells)} = 824,206 (blue boxes); PGC_hi-confs, n_{(trials,cells)} = 262,65 (light-green boxes), pSPCs and pPGC_hi-confs active in all three confined environments, n_{(trials,cells)} = 276,92 (dark-green boxes) and n_{(trials,cells)} = 260,65 (yellow boxes), respectively. (E) Grid distances produced by pPGCs and pPGC_hi-confs that were active in the BY and at least one of the large environments (LX, LV, and OS) (n = 20) (red and yellow boxes, respectively). (F) Comparing grid distances of pPGCs and pPGC_hi-confs between LX and LV environments (n = 5) when the cells were active in both environments. The horizontal lines in boxes are medians, and boxes contain the 25th through 75th percentiles. Whiskers cover the most extreme data points and + signs are outliers. Grid periods were combined from both subjects during navigation in all four environments. The daily sequence of environments was randomized. ***P < 0.001. NS, not significant.

From these two patients, we recorded single-unit activity over successive days. We isolated 397 single units (neurons) over 7 and 8 consecutive days from patients H and K, respectively (average overall firing rates between 0.02 Hz and 1 Hz). By keeping track of these cells’ activity across four environments, a database of 1,588 single-unit spike trains (trials) was created, with each trial representing a single-unit activity in one environment. Because we sampled a different subset of electrodes each day, we treated single units recorded from different days as independent. Only single units obtained within the same day were treated as being produced by the same cells in different environments (SI Appendix, SI Experimental Procedures). Each of the 1,588 trials associated with a navigation pathway was converted to a firing rate map and AC using the BK method (11, 18). Despite the aperiodic patterns of movement trajectories (Fig. 1C), as much as 52% of total trials (824 trials from 206 neurons) resulted in significant spatially periodic activity patterns based on a 2D spectral analysis (11) after validation of their spectral periodicity scores against ACs of a randomly displaced collection of 2D Gaussian firing rate clusters (SI Appendix, Experimental Procedures and Fig. S3H). We could rule out the possibility that spatial periodicity was a result of spike-sorting artifact (33, 34) by including only single units, which produced nonoverlapping waveform clusters with an average Mahalanobis intercluster distance of >20 (mean_{Mahal_d} = 230; SI Appendix, Figs. S2 and S10–S28). We refer to these 824 trials from 206 neurons as spatially periodic cells (SPCs; SI Appendix, Fig. S35 and Table S2). Among SPCs, 92 (45%) exhibited spatial periodicity in all three environments with architectural landmarks (BY, LX, and LV). We refer to this subclass of cells as persistent spatially periodic cells (pSPCs). Among those pSPCs, 47 displayed 60 ± 10° rotation symmetry. Moreover, to classify grid cell-like activity, we further subjected the 206 SPCs to a quantification of their gridness relative to their own time-shuffled spike ACs strictly following the BK method (11, 18). To meet the definition of grid cells, we constrained this analysis by selecting cells that displayed 60 ± 10° rotation symmetry (10). This analysis resulted in 73 neurons from the two subjects (n^subj-H = 40 and n^subj-K = 33) with significant grid-like quality, 35% of the total 206 spatially periodic neurons. We further refer to this dataset as PGCs because they shared all attributes with grid cells classified in the rodent medial EC. All PGCs were a subset of SPCs. Although none of the PGCs exhibited significant gridness in all four environments (and very few in three environments), 39 of the 73 PGCs (53%) exhibited significant gridness in at least two environments. We refer to these cells as persistent putative grid cells (pPGCs) (SI Appendix, Fig. S3I, Table S2, and Movie S1).

Additionally, to reduce the chance of detecting false-positive results brought about by nonlocal covariates in our sample, such as theta modulation, spiking bursts, or direction tuning, we isolated a subset of PGC activity that was tested against a combination of theta and alpha modulations, bursting firing pattern, and directional tuning (SI Appendix, SI Experimental Procedures). Although directional tuning did not covary with the environments (SI Appendix, Fig. S33 and Tables S9.1–S9.3), to ensure the immunity of grids to direction tuning, we isolated a subset of spatially modulated single units that passed the BK test against direction-tuned and theta-modulated surrogate spike trains.

Single units with significant gridness relative to the temporally and directionally modulated null yielded a population denoted as high-confidence putative grid cells (PGC_hi-confs; n = 262, n^subj-H = 118, n^subj-K = 144). Similar to the pPGC dataset, we separated a subset of PGC neurons, including only those PGC neurons that displayed significant spatial modulation in at least two differently sized environments (BY-LV or BY-LX), and denoted them as persistent high-confidence putative grid cells (pPGC_hi-confs). This set included n = 65 single units active in at least two nonequally sized environments and n = 28 single units active in all three environments with spatial cues (BY, LV, and LX).

The purpose of the pSPC, pPGC, and pPGC_hi-conf datasets was to enable us to compare grid parameters between environments using a repeated measures design. To enhance robustness, all statistical analyses were performed separately on six datasets: SPC, pSPC, PGC, pPGC, PGC_hi-conf, and pPGC_hi-conf. Although all six datasets exhibited significant spatial periodicity of firing patterns, by definition, as quantified based on a spectral method (11), only the PGC and pPGC subsets qualified as “canonical” grid cells defined by traditional methods (10, 11, 18). PGC_hi-conf and pPGC_hi-conf datasets further extended the BK method by applying a more stringent null for computing gridness.

Because the clinical time constraints limited the test times to 5 min per environment, there was a concern that the stability of grid patterns might be compromised. Therefore, the temporal stability and stationarity of periodic patterns and grid patterns were tested by applying a twofold cross-validation and stationarity analysis for all of the cells in the SPC and PGC_hi-conf datasets, and both tests confirmed at the population level the stability and stationarity of grid patterns [Wilcoxon test on twofold cross-validation: for the SPC dataset, P_{(n = 879)} = 4.726e⁻⁴⁹ and for the pSPC dataset, P_{(n = 285)} = 1.4887e⁻¹⁹; SI Appendix, Figs. S5 F and G, S36, and S37 and Table S10].

Dependence of Grid Period on Environment.

Grid period is the distance between adjacent grid nodes as determined based on the spatial AC (SI Appendix, SI Experimental Procedures). Although grid periods were uniform across all electrode positions and neurons, they varied by environment (three-way ANOVA: P^subj-H < 0.001, P^subj-K < 0.001; Fig. 2 and SI Appendix, Tables S3.1 and S3.2). Studies in rodents using environmental manipulations, such as partitioning and transformation (10, 13, 19), suggest that the grid period produced by a particular grid cell is conserved across environments and only changes after transformation of a familiar environment (18, 19). To investigate what specific feature of the environment could best explain the observed variation (Fig. 2C and SI Appendix, Fig. S29), we sought to determine whether any of the varying spatial features of the four environments had a strong correlation with grid periods displayed by individual neurons. To do so, we quantified the grid’s spatial frequency from the 2D spectral density of the AC (Fig. 1F). In contrast to rodent data (10), we observed a significant difference in average grid periods between environments in all of our six datasets (Fig. 2 D and E), including the spatial periods of the complete SPC dataset (Kruskal–Wallis test, P = 2.498e⁻¹³⁴; Fig. 2D and SI Appendix, Table S3.5). The grid scale difference was also significant when we compared the spatial behavior of the same neurons across the four environments within the pSPC dataset [Friedmann test, P_{(n = 73)} = 8.4344e⁻³²; Fig. 2D and SI Appendix, Table S3.8]. The difference in average grid distance in the pSPC dataset was significant when the smallest environment was contrasted against any of the three larger environments or all three combined [Friedman’s test, P_{(n = 115)} = 2.1748e⁻²⁶; Fig. 2D and SI Appendix, Table S3.9], but grid distance was no different between large environments (SI Appendix, Table S3.11). The PGC dataset reflected the same pattern (SI Appendix, Fig. S7). Additionally, we compared the average grid periods of pPGCs between the small and large environments. Because not all PGCs were active in both the small and large environments, we compared a subset of PGCs, including only those PGCs that were active in both. To achieve sufficient statistical power, we selected neurons that were active in both the smallest environment (BY) and in at least one of the two larger environments with well-defined spatial landmarks (LV and LX) and compared their grid periods (n = 19). The average grid period of PGCs determined in the small environment showed a significant expansion when probed in the larger environments [Wilcoxon signed rank test, P_{(n = 19)} = 1.2937e⁻⁰⁴; Fig. 2E and SI Appendix, Table S3.10]. No significant difference in grid periods between the large environments (LV and LX) was found owing to the similarity of their dimensions [Wilcoxon signed rank test, P_{(n = 5)} = 0.3125; Fig. 2F and SI Appendix, Table S3.11]. To verify the validity of grid scale dependence on environment size, we repeated the test in our PGC_hi-conf dataset (SI Appendix, Fig. S8). Both PGC_hi-conf and pPGC_hi-conf datasets accurately reproduced the significant grid rescaling between small and large environments seen in the other four datasets [Kruskal–Wallis test on PGC_hi-conf: P^subj-H_{(n = 113)} = 1.0719e⁻¹⁴, P^subj-K_{(n = 85)} = 3.7179e⁻¹⁵; Friedmann’s test on pPGC_hi-conf: compared across three environments, interpolated, and combined between subjects, P_{(n = 10)} = 5.5560e⁻⁰⁶; compared between the small and any of the larger environments, P_{(n = 10)} = 0.0016; SI Appendix, Tables S3.9.1–S3.9.3]. Conversely, no grid rescaling was observed between the two similarly sized (LX and LV) environments [Wilcoxon signed rank test P_{(n = 32)} = 0.5475; SI Appendix, Table S3.9.4]. Hence, the neurons in our sample tested against spike trains endowed with theta modulation and directional tuning retained a significant environment-dependent rescaling of grid distance, no less than those neurons tested against Poisson spike time shuffling (Fig. 2 D–F).

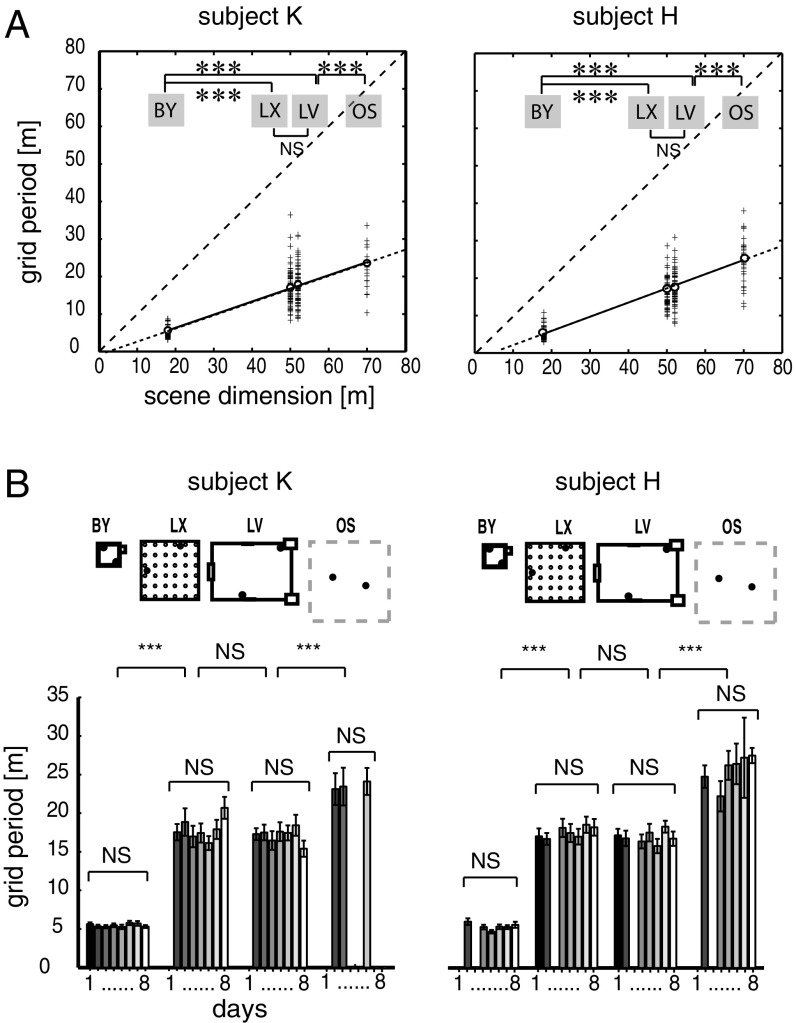
The described grid-scale differences were consistent between the two subjects (Fig. 3A and SI Appendix, Fig. S8 A and B and Table S3.15) and remarkably stable over successive days (Fig. 3B). Grid distances within a specific environment displayed substantially less variation across different days than across environments (Kruskal–Wallis one-way ANOVA, P^subj-H > 0.05 and P^subj-K > 0.05; Friedman’s test, the exact P values are listed in SI Appendix, Tables S3.6 and S3.7, respectively). Because the grid periods did not differ between the two subjects with respect to any of the three datasets (P > 0.05, Wilcoxon rank-sum test), we combined the same type of datasets from the two subjects for statistical evaluation. The effect of the environment was consistent over all three datasets (Kruskal–Wallis test with independent samples on the SPC dataset, P < 0.001, SI Appendix, Table S3.5; Friedman’s test with repeated measures on the same cells’ pSPC dataset, P < 0.001, SI Appendix, Table 3.8; and Wilcoxon signed rank tests on the pPGC dataset, P < 0.001, SI Appendix, Tables S3.10 and S3.11). The grids transformed in a fashion similar to what is found when rodents are presented with a transformed version of a familiar environment (19); the rescaling was proportional to the edge length of the environment because it was smallest in BY, larger in LX and LV, and largest in OS (Fig. 3B and SI Appendix, Figs. S6A and S7C and Table S3.10). LX and LV were not different (SI Appendix, Table S3.11). We reasoned that if grid periods linearly scale with the size of environment (Fig. 3A and SI Appendix, Figs. S5A, S6A, and S7A), then normalizing them to the size of the environment should reduce the grid period differences across environments (SI Appendix, Figs. S6B and S7B). This hypothesis was confirmed because the environment size-normalized average grid period difference either disappeared, as it did in the SPC, pSPC, and PGC datasets [two-way ANOVA, P_{(df = 3,6)} > 0.3, and Kruskal–Wallis test, P_{(df = 3,6)} = 0.0509, compare SI Appendix, Tables S3.1 and 3.2 with SI Appendix, Tables S3.3 and S3.4; PGC dataset: two-way ANOVA, P^subj-K = 0.4547 and P^subj-H = 0.3819, SI Appendix, Table S3.14] or was greatly reduced in the pPGC dataset between small and large environments when comparing the difference between before [Friedman’s test, P_{(BY-LV, LX, OS)} = 1.2937e⁻⁰⁴; SI Appendix, Table S3.10] and after [P_{(BY-LV, LX, OS)} = 0.011; SI Appendix, Figs. S6B and S7B and Table S3.12] normalization. Normalization of grid periods did not affect the similarity of grid distances between large environments [Friedman’s test, P_{(n = 5)} = 0.91; SI Appendix, Table S3.13]. For both subjects, correlations between grid periods and environment sizes in both types of datasets, SPC and pPGC, were high (SPC: Pearson’s r^subj-H = 0.877, P < 0.0001; pPGC: Pearson’s r^subj-K = 0.879, P < 0.0001, Fig. 3A; pPGC combined: Pearson’s r = 0.5139, P < 0.0001, SI Appendix, Figs. S6A and S7A) and displayed an average grid period-to-environment dimension ratio of 0.3954 [f(x)^subj-H = 0.4047x-2.81] and 0.3509 [f(x)^subj-K = 0.3509x-0.6187] and 0.4108 [f(x)^subj-H = 0.4108x-0.241] and 0.4153 [f(x)^subj-K = 0.4153x-4.218) in the SPC (Fig. 3A) and pPGC datasets (SI Appendix, Fig. S7A), respectively.

Fig. 3.

Grid period is environment-dependent and stable over days. (A) Grid periods are shown as a function of the size of the environment. Data were combined over multiple days from navigation trials in the same four environments and are displayed according to environments (BY, LX, LV, and OS) and subjects (patients K and H) (n = 436 and n = 388 segments, respectively). The length of the shorter axes of given environments (X) is plotted against the grid period (Y). The sparse-dashed lines represent identity lines. The fine-dashed lines are extrapolations of slopes. (B) Average grid periods from the two subjects grouped according to the environments (layouts on top) and consecutive days (days 1–8). The variation of grid periods over days was insignificant relative to the variation across environments. Error bars represent SEM. ***P < 0.001. NS, not significant.

The variation in grid period might have also been affected by factors such as covariance with the cells’ gridness, the firing rate difference between environments, and the unequal coverage of environments by exploration. However, no consistent covariations of gridness scores and environments were observed across datasets. Although the general spatial periodicity (gsp score; Materials and Methods and SI Appendix, Experimental Procedures) decreased with increasing environment sizes in the large SPC dataset (P < 0.001, ANOVA with independent measures; SI Appendix, Fig. S30 A and B and Table S4.1), other datasets (pSPC and PGC) did not confirm any environmental dependency of the magnitude of spatial periodicity [pSPC: one-way ANOVA, P_{(n = 26)}^subj-H = 0.4248 and P_{(n = 24)}^subj-K = 0.2575; SI Appendix, Fig. S31 A and B and Table S4.2], not even when gridness scores were determined based on the BK method [P_{(n = 12)}^subj-K = 0.1258 and P_{(n = 16)}^subj-H = 0.1330; SI Appendix, Table S4.3]. The firing rate was also uniform across environments for all datasets (SPC, pSPC, and pPGC; SI Appendix, Tables S5.1–S5.3, respectively) across different environments (SI Appendix, Fig. S30C).

Differences in environment coverage was inherent in the task design because the areas of modeled environments varied between 324 m² and 4,900 m². This variation naturally affected the coverage (SI Appendix, Tables S6.1–S6.3) because the large environments received an average of 60% of the coverage of the smallest. To compensate for the effect of uneven coverage across environments, in a separate analysis, we shortened the navigation trajectories in the BY environment by 50% of their original length (hence, the duration of navigation as well) and recomputed the grid distances of all 1,588 segments (397 neurons). This manipulation reduced the difference in path density across all environments (SI Appendix, Fig. S9A), whereas it left the average gridness scores, $\left(\widehat{g}\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n}gsp$, and environmental grid scale differences unaffected relative to the complete datasets [gridness scores: two-sample t test, $\widehat{g}$^subj-K_halfpath = −0.1000, $\widehat{g}$^subj-K = −0.1454, P_{(n = 59,8)} = 0.2594; $\widehat{g}$^subj-H_halfpath = −0.2064, $\widehat{g}$^subj-H = −0.2817, P_{(n = 58,33)} = 0.2165; grid distances: Kruskal–Wallis test, P^subj-H_{(n = 79)} = 5.8221e⁻¹⁴, P^subj-K_{(n = 164)} = 4.2568e⁻²⁶; SI Appendix, Fig. S9 B–D and Table S6.4]. The average slope and y-intercept of the regression line [f(x) = 0.4130x-3.7295] reproduced the f(x) = 0.3954 regression line observed in datasets, including the complete navigation path. Hence, the increased coverage in the smallest environment did not account for the smaller grid distances consistently observed across all six datasets.

Altogether, the consistency of the environment-specific magnitude of grid rescaling across datasets and between the two subjects, the independence of grid scale from the variations of firing rate and gridness scores, and the invariance of the effect of environmental coverage speaks strongly to the overall environment dependency of grid scaling in the human EC.

Grid Orientation.

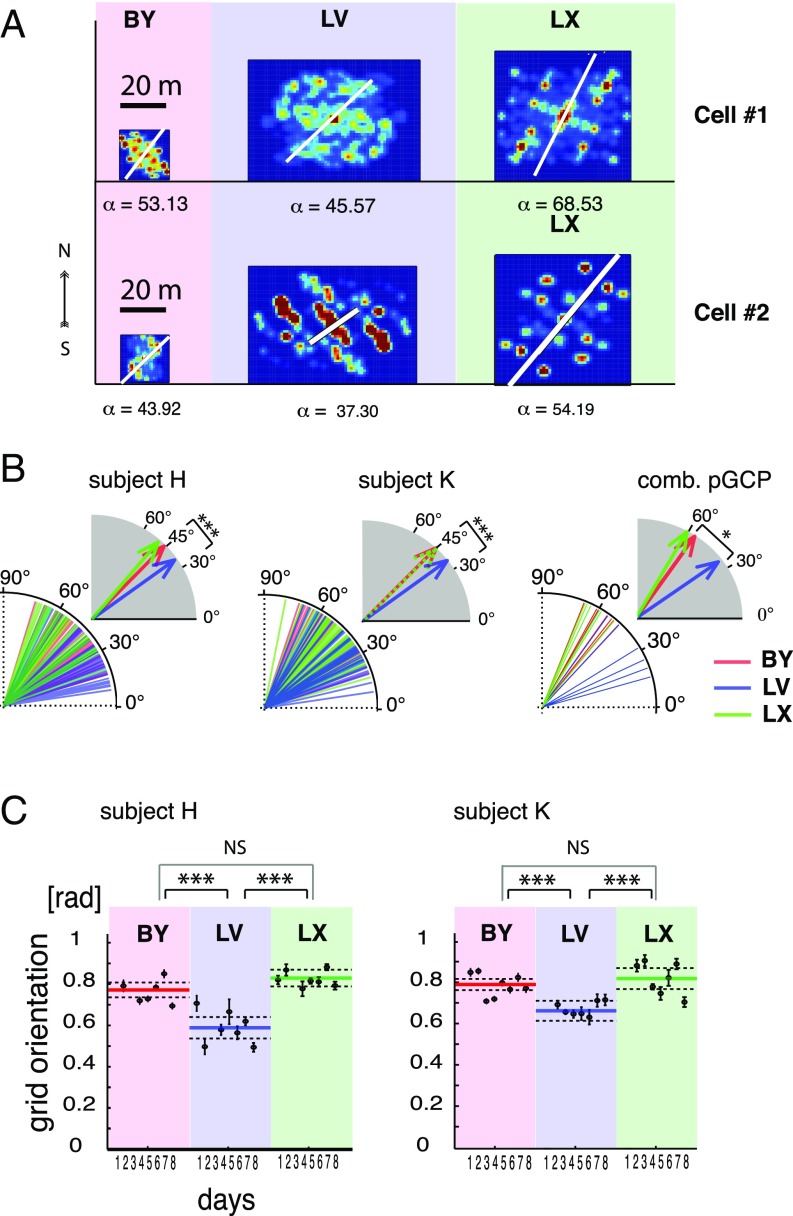
Rodent grids normally orient themselves relative to distant or local landmarks, whichever provides the most consistent spatial cue in repeated visits to an environment. Because grid orientation was a stable feature of grid cells in rodents (10, 21), we sought to determine if this grid orientation was preserved in humans. Aside from OS, all of our environments had two types of spatial landmarks available: initial orientation and architectural cues. Because each navigation session in the same environment always started from the same location and facing the same direction, thus providing unambiguous initial visual orientation cues (SI Appendix, Fig. S1), our subjects could orient themselves in each environment based on the initial orientation cues, except in the OS, where those cues were lacking. The consistency of spatial references at the start of each trial had the theoretical possibility of providing sufficient input to the neurons in the EC to anchor their grid orientation. Therefore, we calculated the principal orientation of ACs for all recorded single units with significant spatial periodicity, including the SPC and PGC datasets. Due to the poor orientation cues available in the OS environment (SI Appendix, Fig. S1) and lower gridness scores (SI Appendix, Fig. S30A), we excluded the OS environment from this analysis. In the remaining three environments with rich visual cues, where grid orientation could be determined more accurately, we found that neurons in all datasets tended to adopt environment-specific orientations (Fig. 4 A and B). Grid orientations in the SPC dataset displayed a predominantly 45° alignment in the two square-shaped environments relative to the main axes defined by the architecture (BY^Subj-H: 45.24°, LX^Subj-H: 46.84°, n = 311; BY^Subj-K: 44.21°, LX^Subj-K: 47.47°; n = 376; SI Appendix, Fig. S32). In contrast, the only rectangular environment (LV) generated grid orientations close to 33° (LV^Subj-H: 38.28°, LV^Subj-K: 33.92°). Neither of these orientations were aligned with 60°, the initial orientation of the avatar (SI Appendix, Fig. S1). Instead, the average grid orientations reflected the 45° direction of corners in both square-shaped environments (BY and LX). If grid orientation aligns with the corners, then we expect a deviation from the 45° angle in the rectangular environment (LV). Consistent with this hypothesis, we observed an average 34.89° grid orientation that closely matches the 33° direction of corners in the LV environment relative to the center and the east–west cardinal axis of the environment (Fig. 4B and SI Appendix, Figs. S1A and S32), which also served as the axis of the ACs. Cells maintained these orientation differences across days of recording [two-way circular ANOVA on the SPC dataset, P_{(df = 2,5)}^subj-H < 0.0001 and P_{(df = 2,6)}^subj-k < 0.0001, Fig. 4C; two-way circular ANOVA in the pSPC dataset, P_{(df = 2,4)}^subj-H < 0.02 and P_{(df = 2,4)}^subj-K < 0.02, SI Appendix, Figs. S12–S28 and Tables S7.1 and S7.2, respectively]. Closer examination of the polar histograms revealed that the distribution of grid orientations in the rectangular environment (LV) was bimodal and divided between 30° and 45° (SI Appendix, Fig. S32).

Fig. 4.

Environment-dependent grid orientation. (A) ACs of two example neurons (cells 1 and 2) with their grid orientations in each environment within the same day of recording. The white line and corresponding α-values (in angular degrees) indicate grid orientation. (B) Population plots of grid orientations from all cells of the SPC dataset color-coded according to environments from the two subjects (Left and Center) and the same for the pPGC dataset (Right). comb., combined. Vectors in gray-shaded quadrants represent angular averages of the corresponding population of grid orientations, according to environments. (C) Grid orientations from the SPC dataset grouped according to environments (large groups) and consecutive recording days (individual filled symbols) from the two subjects (Left and Right, n = 311 and n = 376 segments, respectively). Error bars indicate angular dispersion. Colored lines represent grand averages of grid orientation associated with the three environments. Dashed lines are confidence intervals. Asterisks represent statistical significance of differences (*P < 0.05, ***P < 0.001). [rad], radian.

Furthermore, the grids seemed to adopt very similar grid orientations between the patients [Watson–Williams test, P_{(n = 49)} > 0.05; SI Appendix, Tables S7.3 and S7.6 for the pSPC dataset], a possible indication that both patients used the same landmark in each environment to anchor grids. This finding allowed us to combine both subjects’ data and gain the necessary statistical power for the analysis of grid orientation in the pPGC dataset as well. With the grouped data, the average grid orientations displayed by the same cells (pPGC dataset; SI Appendix, Table S7.5) inside the two square-shaped environments, BY and LX, were 56° and 61°, respectively; neither was significantly different from 60° or from one another (SI Appendix, Table S7.7). Note that a hexagonal grid with a 60° orientation is in perfect alignment with the east–west axis of both environments and reflects the avatar’s initial orientation. However, both of those average grid orientations were significantly different from the 36.22° mean grid orientation displayed by the same cells in the rectangular environment (LV) (circular ANOVA and circular test for mean grid orientation, P < 0.05; SI Appendix, Tables S7.7, S7.8, and S7.13 for pPGC, pSPC, and pPGC_hi-conf datasets, respectively). These grid orientation-related differences between square-shaped and rectangular environments were significant in all datasets (SPC, pSPC, PGC, pPGC, PGC_hi-conf, and pPGC_hi-conf) and stable over days when comparing them by circular ANOVA using independent and repeated samples, respectively (days effect: P_(pSPC) > 0.05; environment effects: P_(SPC) < 0.001, P_(pSPC) < 0.05, and P_(pPGC) < 0.05, SI Appendix, Tables S7.1, S7.2, and S7.4; P_(PGChi-conf) < 0.01, SI Appendix, Tables S7.9 and S7.10; and P_{(pPGChi-conf)} < 0.05, SI Appendix, Tables S7.11–S7.13). The specificity of grid orientation to the aspect ratio of the environment and consistency of adopted grid orientations over days, as well as between the two subjects, strongly suggest that grid orientation is dependent on the geometry of the environment (Fig. 4C). We could rule out that the consistency of grid orientation with environment geometry depended on the neurons’ directional tuning, because we did not observe any difference in directional tuning between neurons active in multiple environments [repeated measures ANOVA on resultant vectors with the factors of /days and /environments, F_(4,2) =1.2264, P_{(n = 74)} = 0.758; SI Appendix, Fig. S32 and Tables S9.1–S9.3]. This result further corroborates the result that grid cells align their orientation to the virtual environment as opposed to the patient’s actual orientation in the hospital or respond uniformly to different environments.

The Rotation Symmetry of Grid Patterns.

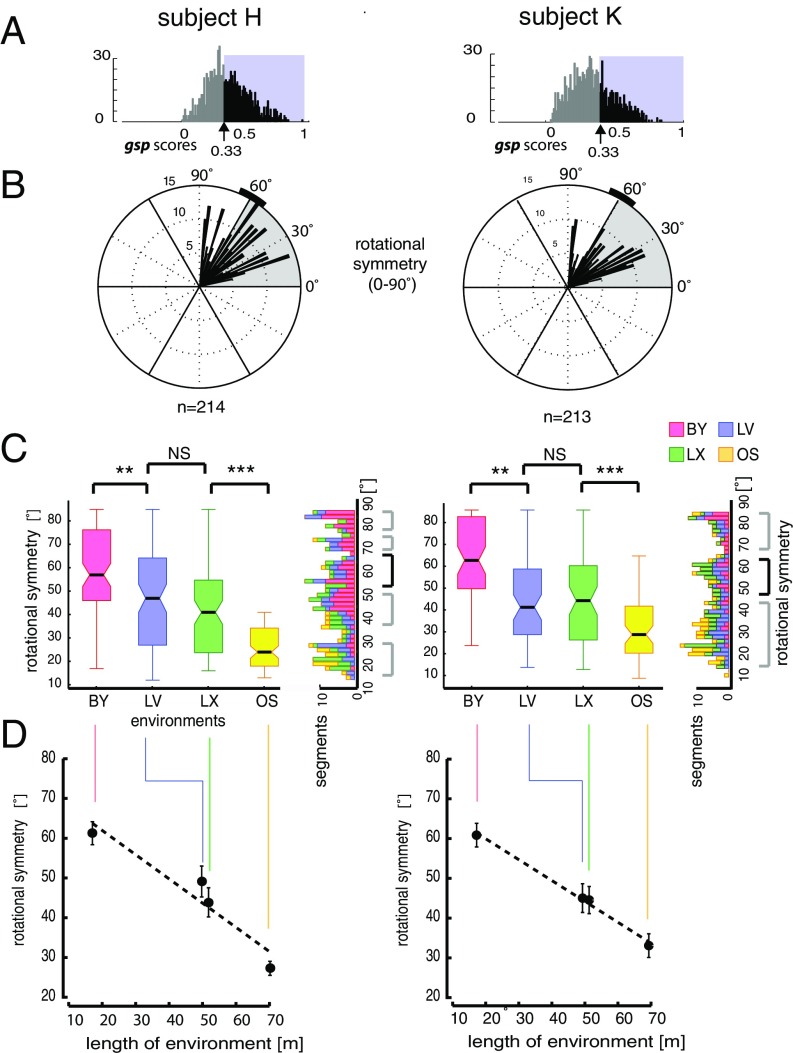
Despite the consistent coordination of the grid orientation with the geometry of the environment, grid angles in the square-shaped environments differed between the two datasets, pSPC and pPGC, with a notable 12.73° (mean β_pSPC = 45.85° and β_pPGC = 58.59°). Because grid geometry (i.e., square, hexagon, pentagon) may affect grid orientation, the variation of rotational symmetry of spatially periodic activity patterns in different environments was investigated next. We focused this analysis on the SPC dataset (Fig. 5A), because the gsp scores [SI Appendix, SI Experimental Procedures, Quantifying “General Spatial Periodicity” (gsp Score) and Fig. S3G] were agnostic to rotational symmetry, thus allowing for quantification of a broader range of 15–90° rotation symmetries, and not only 60° (±10°).

Fig. 5.

Rotational symmetry of spatial periodicity. (A) Distribution of gsp score per subject determined based on the spectral method. We selected neurons with gsp scores >0.33, the 5% confidence interval of the randomized spatial ACs (SI Appendix, SI Experimental Procedures and Fig. S3H). (B) Distributions of angles of rotational symmetry from the two subjects over all environments using a 2° bin size. The n values indicate the number of data segments. (C, Left) Box and whisker plots for grid rotational symmetries observed in each environment color-coded according to environments. (C, Right) Rotated histograms show the composition of rotation symmetries according to the environment. Note that in addition to data segments displaying ∼60° rotational symmetries (black bracket), comparable numbers of data segments exhibited rotational symmetry at other angles (gray brackets). **P < 0.01, ***P < 0.001. (D) Angle of rotational symmetry negatively correlated with environment size. Significant differences in angles of rotational symmetry were found across environments, except between LV and LX, consistent between both subjects (SI Appendix, Tables S8.1–S8.5). Error bars represent angular variance (Subjects H and K, n = 214 and n = 213 segments, respectively).

We were surprised to observe that a substantial fraction of spatially periodic activity deviated from the hexagonal geometry (11). In addition to a number of data segments with predominantly 60° rotational symmetry, characteristic of grid cells in the rodent brain, we observed a significant number of nonhexagonal grid-like patterns (Fig. 5 B and C). We classified these cells as SPCs to discriminate them from the PGCs of our PGC population. Many of the SPCs displayed variants of rectangular or octagonal grid geometry with a 90° or 45° rotational symmetry, respectively (SI Appendix, Figs. S13, S15–S20, S22, S23, and S25–S28), which is undocumented in rodents and primates to date. The fraction of SPCs deviating from the 60° rotational symmetry accounted for 65% of neurons with significant spatially periodic activity (SI Appendix, Fig. S3I). Overall, the population mean of rotational symmetries for the complete dataset did not conform to 60° [circular one-sample test for specified mean direction, subject H: P_{(n = 435)} > 0.05, subject K: P_{(n = 387)} > 0.05], and the distribution was asymmetrical around the median [circular symmetry test, subject H: P_{(n = 435)} = 0.0078, subject K: P_{(n = 387)} = 0.0412].

Next, we investigated whether or not an environmental dependency of the rotational symmetry of the ACs may underlie the heterogeneity of grid geometry displayed by the same or a mixed population of neurons (pSPCs and SPCs) during navigation in different environments (Fig. 5B). We focused the analysis on the rotational symmetry of the ACs computed from the SPC dataset. The comparison of rotational symmetry across environments revealed a predominant 60° angle of rotational symmetry in the BY, our smallest virtual environment. In contrast, a significant decrease in the proportion of hexagonal grids was evident in the other environments, consistent between both subjects [Fig. 5B; one-way circular ANOVA, P_{(n = 213)}^subj-H < 0.001 and P_{(n = 214)}^subj-K < 0.001; SI Appendix, Tables S8.1 and S8.3]. No significant difference between the circular means of rotational symmetry between the two similarly sized larger environments (LV and LX) was found [circular ANOVA, P_(1,132)^subj-H = 0.8875, P_(1,136)^subj-K = 0.1640; SI Appendix, Table S8.2]. However, differences in rotational symmetry between environments of much different sizes were significant in both subjects’ datasets [circular ANOVA, BY and LV: P_(1,102)^subj-H < 0.005 and P_(1,160)^subj-K < 0.005; circular ANOVA, LX and OS: P_(1,106)^subj-H < 0.001 and P_(1,92)^subj-K < 0.001]. In general, the proportion of cells expressing the canonical 60° angle of rotational symmetry negatively correlated with the dimensions of the environment (Pearson’s r^subj-H = −0.4293, P < 0.0001 and Pearson’s r^subj-K = −0.3915, P < 0.0001; Fig. 5D and SI Appendix, Table S8.3). The dependency of grid rotation symmetry on environments was confirmed within the pSPC dataset containing neurons that displayed persistently significant spatial periodicity in all three environments (with well-defined external cues) during the same session (BY, LX, and LV; SI Appendix, Table S8.4). Although the negative correlation was consistent over days and subjects [two-factor circular ANOVA: environment effect, P_{(n = 74)}^subj-H < 0.01 and P_{(n = 71)}^subj-K < 0.001; days effect: P_{(n = 74)}^subj-H = 0.4871 and P_{(n = 71)}^subj-K = 0.1571; SI Appendix, Table S8.5], factors such as the differing complexity of environments, the relative position invariance of external cues in larger environments, or the decreasing reliance on external cues and lack of boundaries in the OS environment, might have also played a role separately or in combination. Other factors, such as the partial coverage of larger environments, could have also contributed to incomplete grid formations. Therefore, we also tested the rotational symmetry of grids under a balanced coverage condition. Even after a 50% reduction of navigation paths in the BY environment, the 60° rotational symmetry of cells prevailed, whereas other rotation symmetries predominated in the larger environments [circular ANOVA: F_(3,75) = 9.034 P_{(n = 78)} < 0.001; F_(3,134) = 23.7839, P_{(n = 140)} < 0.001; SI Appendix, Tables S8.6 and S8.7]. Hence, among other factors, we can rule out that the significant deviation from 60° rotational symmetry in the larger environments was a result of incomplete spatial coverage of these environments.

Discussion

Context-dependent spatial representations in the hippocampus of various species have been widely documented. Neurons in CA1 and CA3 remap their place fields upon changes made in the environment, as demonstrated in rodents (13–17), Chiroptera (35), and primates (36). Because the adaptive remapping of hippocampal place fields is a relatively fast and EC-dependent process (13, 37), it is plausible to assume that neurons in the EC are endowed with some degree of flexibility. Contrary to this hypothesis, initial reports on grid cells based on rodent experiments suggested a universal metric for path integration-type navigation (10, 12). This metric appeared to be scale-invariant with respect to the geometry and size of the environment, despite having been challenged by a number of rodent studies (18–20). One such challenge involved moving the walls of the enclosure, which induced temporary elastic changes of the grid geometry (19). In a more common scenario, mere environment novelty elicited expanded grids (18), while neither novelty nor stretching affected border cell activity (9). Likewise, grid cells in rats exploring polarized asymmetrically shaped (trapezoidal) enclosures develop heterogeneous gridness of activity between different parts of the enclosure in contrast to the homogeneous gridness typical in symmetrical enclosures (e.g., square, rectangle). Nevertheless, grid distances in trapezoid enclosures remained uniform (20). Although the grid scale invariance might be robust across species of the rodent order, comparing it with the human analog might reveal aspects of neuronal representation of space that are specific to the human brain.

We obtained stable recordings of different neurons in the human EC across spatial navigation trials in multiple virtual environments (Fig. 2) over successive days. More than half of the neurons displayed spatially periodic activity (a fraction of those neurons specifically displayed grid-like activity), and they did so consistently and specifically for given environmental features, independent of the order of presentation of the environments and day of recording (SI Appendix, Figs. S2 and S5). Convincingly, these effects of the environment were consistent between the two subjects.

The observed proportion of neurons with spatial tuning is consistent with data from the rat EC (11), but larger than observed in the primate EC during visual tasks (35) and in the human EC during other virtual navigation tasks (31). Because our electrodes were nonmoveable, selective sampling could not bias this ratio. The relatively high ratio of neurons displaying spatially periodic activity has two implications. First, consistent with earlier results (31), neurons in the human EC are able to form neural representations of space in a virtual reality environment induced by a small, handheld display (25.6 cm diagonal and ∼23° horizontal visual field) in the absence of proprioceptive and kinesthetic cues. Second, these neural representations, relying mainly on visual cues, showed adaptive scaling.

The spatial periodicity of neuronal activity was not uniform across all four studied environments. Instead, spatial periodicity systematically decreased with the increasing size of the environments (SI Appendix, Fig. S30 A and B). However, this finding was not confirmed by the gridness of PGCs (SI Appendix, Fig. S31 A and B). Although we could rule out partial coverage as a potentially confounding factor contributing to cells in the OS environment showing less spatial periodicity than in any other environment, other factors, such as the lack of orienting spatial cues or the lack of polarity of the environment (20), might have played a role. We remark that in the absence of orienting distal cues, the grids were less consistently aligned.

Besides gridness, a key factor regarding the effect of the environments on grids is the parameter of grid scale. Although the original report of grid cells in rodents documented scale independence of grids (10), other studies have found an experience-dependent rescaling of grid cells under special conditions, such as in response to distortion of the aspect ratio of a familiar environment (19, 20) and transient rescaling during exposure to a novel environment (18). Similar to the grid transformations brought about by adjusting environments, we observed elastic transformations of grids across environments (Figs. 2 and 3). The EC neurons in both patients investigated over multiple days showed a consistent environment-dependent preservation of grid geometry and orientation over days with small variance, suggesting that each grid type was optimal for the environment it was applied to. We can rule out both effects: the distortion effect, because our subjects were fully aware of the switch between the environments, and the novelty effect, because none of the investigated grid parameters changed over time. However, we cannot rule out the contribution of proprioceptive cues to the scale invariance of grids observed in rodents and the effect of eliminating those cues in the virtual navigation condition.

The second key feature of the observed grids was the preserved orientation of the main grid axis across repeated trials in an environment. These data suggest that, as in rats, human grids utilize cues, such as environment geometry, to anchor grid orientation (20). However, in our virtual navigation task, there were three independent but consistent orienting cues available. The first was the starting orientation of the avatar relative to the walls (SI Appendix, Fig. S1A), the second was the constant presence of architectural cues (except in the OS environment), and the third was the memory of the environment. The starting orientation of the avatar was the same relative to the X–Y axes in all environments (SI Appendix, Fig. S1A), which may have predisposed the grids toward assuming a similar orientation within each environment. In contrast, comparisons between the three enclosed environments showed that average grid orientation in LV differed significantly from average grid orientation in BY and LX (Fig. 4 and SI Appendix, Fig. S32). Although grids of SPCs in square-shaped environments aligned with the angle of a 45° orientation, they tended to align at an angle of 33° in a rectangular environment relative to the same cardinal axes (SI Appendix, Fig. S1A). Because both angles represent the direction toward the corner of the actual environment from the starting position, the difference suggests that the geometry of the environment determines grid orientation rather than the avatar’s starting orientation or architectural cues. The environmental dependency of grid orientation is in agreement with studies on rodents showing that grid orientation is aligned with the boundaries of the enclosure (20, 21); however, in contrast to the findings of rodent EC, which minimizes the symmetry of grid angles relative to the walls (21), human EC grids tend to align with the corners of environments.

The third key grid feature we investigated was the rotational symmetry of grids. Studies in rodent EC have described neurons with firing fields organized in periodic bands (11), in addition to cells with canonical hexagonal grids. We quantified the distribution of grid rotational symmetry for neurons from human EC and observed a wide range of symmetries (Fig. 5 B and C), with a strong negative correlation between the angle of symmetry and environment size (Fig. 5D). With a post hoc analysis of balanced environmental coverage, we were able to rule out that the higher prevalence of hexagonal grids in the smallest environment (BY) was only due to the more complete coverage relative to the larger areas of the other environments. Nevertheless, the incomplete coverage might have compromised the interpretation of these factors. Whether the relatively large proportion of noncanonical symmetry observed in our human grid cells compared with the rodent’s grid cells reflects an adaptation to a predominantly Cartesian organization of our human-made environments, or if it is constrained by other physiological mechanisms, is beyond the scope of this study.

On several occasions, we omitted one trial to double the time spent in another environment, which helped to affirm that none of the rescaling effect was due to the limited sampling time and poor spatial coverage. To compensate for the poor spatial coverage and increase our confidence in the sparse sampling of grid-cell activity, one can combine spikes of neurons from the same electrode (SI Appendix, Fig. S10) and confirm the hexagonal tessellation on the firing rate maps consistent with rodent, primate, and human studies (10, 26, 31, 38).

Contrary to rats, in which grid fields initially expanded in novel environments (18), all three monitored grid features were stable across 7–8 d and showed no systematic variation over time (Fig. 3 and 4 and SI Appendix, Figs. S7C and S8B). Nodes of spatial periodicity (putative grid vertices) were also stable over time within the same environment during the same session, as illustrated by individual examples of spatial mapping of single-unit activity between the first and fourth segments of a 20-min recording session (SI Appendix, Fig. S5 A–E). Moreover, the stability and stationarity of grids in the firing rate maps were confirmed at a population level by cross-validation and stationarity analysis that included both SPC and PGC_hi-conf datasets (SI Appendix, Fig. S5 F and G). Consistent with the stability of grid nodes, the environment-dependent scaling and rescaling in our human datasets were instantaneous. We observed no gradual adaptation within each day (SI Appendix, Fig. S5) or across days of recordings (Fig. 3B and SI Appendix, Tables S3.6 and S3.7). The rapid adaptation to environmental parameters suggests a dynamic reconfiguration of neuronal activity consistent with attractor switching (39–41) or oscillatory interference (42–44) models.

The advantage of a visual system in spatial navigation is multifold. First, endowed with a larger visual information-processing capacity with which to assess an environment, humans are able to form a cognitive map or a “survey representation” of their environment without the need for visiting all parts, and adapt grids based on visual spatial cues accordingly. Second, the dimensions of the environments can be ascertained by a few saccadic eye movements prior to physical exploration. Third, considering the complexity and scalability of human environments, humans might rely on extracting information from optic flow more efficiently than rats do, given that there is theoretically sufficient information available from optic flow for grid formation (45). The predominance of visual input in the human brain allows detection and mapping of spatial cues more quickly and may influence grid parameters to a greater degree than is possible in the rat brain (35–37). It might also allow the human hippocampus and EC to perform more naturally in virtual navigation tasks, where proprioceptive and kinesthetic cues are absent (30, 31, 46, 47).

Nevertheless, our results corroborate evidence that a visually cued, active navigation task in a virtual reality environment provides sufficient input to the human EC to elicit spatially coherent localized activity, similar to the spatially coherent localized activity found before in humans (31) and rodents (10, 38, 48). This discovery is intriguing because it occurs despite the conflict between the patient’s simulated self-motion and natural vestibular and proprioceptive signals, as well as an awareness of the patient’s true location relative to the hospital. As initial evidence of sufficient stimulation, we observed that the baseline activity of EC neurons substantially increased when the patients began playing the game.

Despite the common cellular mechanisms in rodent and human brains, spatial navigation and spatial memory may involve slightly different networks in the human brain. For instance, human subjects are able to perform path integration without the hippocampus and EC (32), except when the navigation involves memory recall of places like in our task. The human EC may also contribute to the formation of declarative/semantic memories or abstract conceptual representations (49) as a part of the mesial temporal lobe that cannot be studied adequately in the rodent brain. With the help of virtual reality (30, 46), our experimental paradigm establishes a common ground to compare neural mechanisms of representing space across different species and to study the evolution of spatial navigation in the mesial temporal lobe in relation to memory and perception of locations and more abstract visual spaces (26). Furthermore, with instructed navigation in virtual reality environments, we will be able to investigate the relationship between memory and anticipation experimentally (50), which is currently unattainable by neuroimaging techniques. We argue that with these experiments, the virtual reality paradigm is not only well-suited for investigating the complex environmental determinants of neuronal representations, including grid formation, but that these complex environmental determinants may also help us to understand the neural representation of spatial, episodic, and semantic memory, which are fundamental aspects of our internal model of reality.

Materials and Methods

Subjects.

One female and three male patients with epilepsy (ages: 33–41 y, average age of 38.5 y; SI Appendix, Table S1.2), who had previously provided informed consent, were implanted with microelectrode arrays in their EC (Fig. 1A) in preparation for surgical resection of epileptic foci. All surgical and experimental procedures were approved by the Seton Institutional Review Board. From two patients (subjects H and K), we could record well-isolated single-unit activity throughout a 7-d period and an 8-d period in the hospital’s epilepsy monitoring unit while they performed a virtual navigation task on a tablet computer.

Tasks.

The subjects’ task was to play a computer game on a tablet they held on their lap. The game’s objective was to locate space aliens and return them to their spaceship parking at memorized locations (SI Appendix, SI Experimental Procedures). Four different virtual environments were modeled: BY, LV, LX, and OS (Fig. 2 A and B and SI Appendix, Fig. S1). These environments differed in several features, including scenery, size, aspect ratio, and presence of obstacles or boundaries (SI Appendix, SI Experimental Procedures, Table S1.1, and Movie S1).

Recordings.

Single-unit activity was obtained from five microelectrodes implanted in layers II and III of the medial EC in the right hemisphere. Microelectrodes were integrated or plug-in components of a macroelectrode strip made by Ad-Tech Medical and PMT. The electrode strip was placed and secured by the neurosurgeon at the surface of the EC such that only the blunt tip of microelectrodes penetrated the pia. The wide-band signal was recorded at a sampling frequency of 24 kHz and bandpass-filtered between 300 and 6,000 Hz. Spike sorting was done off-line on the continuous recording (including all environments) using WaveClus software (51) on MATLAB (MathWorks), and spike trains were segmented according to environments later. Only single units with Mahalanobis distances of >20 separations were included.

Analysis of Grid Parameters.

Firing rate maps, spatial ACs, and autoperiodograms were computed using standard methods (11). We quantified the gridness scores, grid orientation, and grid rotational symmetry (52, 53) by precisely following the method outlined by Barry et al. (18), Sargolini et al. (54), and Krupic et al. (11) (SI Appendix, SI Experimental Procedures and Fig. S3 A–F). Grid distance was determined based on the autoperidogram and manually cross-validated with the ACs. To compute confidence intervals for statistical significance of gridness scores, we applied a standard Poisson bootstrap method and shuffled spike times 1,000 times (SI Appendix, Fig. S3G), as well as theta, alpha, and direction-modulated surrogate spike trains. Validation of spatial periodicity against the by-chance was done using a Monte Carlo method by comparing the spectral modulation depth (gsp scores; SI Appendix, SI Experimental Procedures) of each AC against the distribution of gsp scores of 1,000 randomized ACs generated from mixtures of 2D Gaussians.

If X and Y are the coordinates of the largest peak near the center in the autoperiodogram, the grid distance is defined as the Euclidean distance of the peak from the center: $\lambda =\sqrt{X^2+Y^2}$. After $\lambda$ was computed, it was and manually cross-validated with the ACs.

Grid orientations were computed from the autoperiodograms (SI Appendix, SI Experimental Procedures and Fig. 1F). Given X and Y as the coordinates of the largest peak on the 2D autoperidogram, the principal orientation (β) is defined as $\beta =\text{arctan}\left(\frac{X}{Y}\right).$

The angle of rotational symmetry was defined by the angle (γ) of rotation that maximized the Pearson's correlation between the original and rotated AC [SI Appendix, SI Experimental Procedures, Quantifying“Gridness” (Gridness Score)].

Datasets and Statistical Methods.

Based on the spatial spectral analysis, gridness scores, and persistence of single-unit activity in different environments, we constructed six datasets: SPC, pSPC, PGC, pPGC, PGC_hi-conf, and pPGC_hi-conf (SI Appendix, Table S2). To compare gridness scores and grid periods across environments for the SPC, PGC, and PGC_hi-conf datasets, the general linear model ANOVA and its nonparametric version, the Kruskal–Wallis test (MATLAB), were applied. The main factor was the environment (BY, LV, LX, and OS), and the dependent variables were gridness and grid period. For the pSPC, pPGC, and pPGC_hi-conf datasets, ANOVA with repeated measures or its nonparametric version, the Friedman test, was used. To compare grid orientations and grid symmetry between environments, we applied circular ANOVA (Watson–Williams test) on von Mises distributions (53) or the Wheeler–Watson test as an alternative when von Mises distributions did not qualify (55). We performed Rayleigh tests for testing nonuniformity of circular data and Watson’s goodness-of-fit test for testing conformity with the von Mises distribution (MATLAB Circular Statistics Toolbox) (53) (SI Appendix, SI Experimental Procedures).