A fully Bayesian application of the Copas selection model for publication bias extended to network meta-analysis

Abstract

The Copas parametric model is aimed at exploring the potential impact of publication bias via sensitivity analysis, by making assumptions regarding the probability of publication of individual studies related to the standard error of their effect sizes. Reviewers often have prior assumptions about the extent of selection in the set of studies included in a meta-analysis. However, a Bayesian implementation of the Copas model has not been studied yet. We aim to present a Bayesian selection model for publication bias and to extend it to the case of network meta-analysis where each treatment is compared either to placebo or to a reference treatment creating a star-shaped network. We take advantage of the greater flexibility offered in the Bayesian context to incorporate in the model prior information on the extent and strength of selection. To derive prior distributions, we use both external data and an elicitation process of expert opinion.

1. Introduction

Possibly the greatest threat to the validity of a systematic review is the presence of publication bias which, broadly speaking, is defined as the tendency in journals to publish studies showing significant results [1]. The use of registries for trials, change in editorial policies of the journals (i.e. publication of all high-quality studies regardless their conclusion) and a meticulous search for unpublished studies in a systematic review process are suggested safeguarding strategies against the effects of publication bias [2]. A plethora of statistical methods to detect and adjust for publication bias once the review has been completed are also available. A common characteristic of all strategic and statistical approaches is however that they can be used to minimize the effects of publication bias but not eliminate it.

Available statistical methods range from simple inspection of the funnel plot to carrying out formal tests and fitting statistical model [2–4]. Meta-regression, an extension of meta-analysis where the effect size is written as a linear function on a measure of its precision or variance is often applied to test for funnel plot asymmetry. A statistically significant regression slope indicates funnel plot asymmetry and suggests that there are differences between small and large studies which may or may not be caused by publication biases. Such regression models have also been used to adjust the pooled estimate for publication biases by focusing on the prediction the regression model gives for studies with (infinitely) small standard errors [3]. A non-parametric method that also attempts to adjust results for publication bias, while estimating the number of unpublished studies, is the trim-and fill method [5,6]. The basic idea of the method is the correction of the asymmetry of the funnel plot via the addition of studies and it is based on the assumption that asymmetry is solely attributed to publication bias. Both methods have been proven to give poor results as unexplained heterogeneity increases or the number of studies decreases but generally the regression-based methods outperform the trim-and-fill method [3]. Nevertheless, the trim-and-fill method remains very popular; its popularity is probably due to the fact that, unlike regression methods, it directly relates to the intuitive interpretation of the publication bias as a case of ‘missing studies’.

An alternative approach to the publication bias problem, which addresses directly the issue of missing studies, is offered by selection models. The idea behind this class of models is that the observed sample of studies is considered to be a ‘biased’ sample which has been produced via a specific selection process. Different authors have considered different selection processes in their modelling. Specifically, two different classes of weight functions have been suggested. One class suggests that the likelihood a study is available/published (i.e. selected) is a function of the p-value obtained under the hypothesis that there is not a significant treatment effect [7–9]. Copas and colleagues introduced further sophistication by assuming the selection process (study publication) is a function of both p-value and effect size [10–12]. This work is based on Heckman’s two stage regression model which has been well documented in the area of econometrics [13]. The process of study selection is described by introducing a latent variable which is described as the ‘propensity of publication’ and is correlated with the study effect size. A regression model is assumed to model the propensity as a function of the study variance. Importantly, this model is weakly identified since we do not know the number of unpublished studies and consequently it is not clear how to model the ‘propensity for publication’. What is being adopted in practice is a sensitivity analysis and the probability of a study being published is computed under various possible scenarios. The model, first introduced by Copas [11] has been evaluated in several subsequent papers. It has been shown that the Copas selection model is superior to the trim-and-fill method [14]. However, it has been shown that the Copas selection model may not fully eliminate bias and that regression-based approaches might be preferable as they do not require a sensitivity analysis [15]

Despite the promising performance and the elegance of the selection models, the approach has not received much attention in medical applications. This could be attributed to the fact that parameterization of the model involves quantities that are difficult to interpret clinically (the parameters of the propensity function), the fitting of the model requires specialized software clinicians are not familiar with (although software routines available in S-Plus [16] and R [17], [18] have become available) and the choice of the propensity score values to be used in the sensitivity analysis maybe difficult to make. In this paper we consider a fully Bayesian implementation of this selection model. By including prior beliefs about the probability of publication for a study in the analysis, the estimation of parameters in the Copas selection model becomes tractable; and this is one of the main advantages of the work presented here.

There has been an explosion of interest in network meta-analysis recently due to the ability of the approach to answer clinically relevant questions such as which treatment is superior when more than two options exist. This creates the need to develop publication bias tools that can be used in this extended meta-analytical framework. Perhaps the closest published consideration of this is an attempt to model publication bias in multi-arm trials in indirect comparisons[19].

Since, network meta-analysis is often implemented in a Bayesian framework using the WinBUGS software[20] it is desirable to develop a compatible modelling approach to address publication bias in this environment. The aim of this paper is to provide a Bayesian implementation of the Copas selection model using informative priors and extend the idea in the case of a meta-analysis that involves multiple interventions. We restrict ourselves to a specific but not uncommon network structure where all treatments are compared to a common comparator (often placebo or usual care) and all trials have two arms.

The paper is organized as follows. First, the Copas selection model is revisited from a Bayesian perspective and model variations are presented in Section 2.1. Extensions for multiple treatments where each treatment is compared to the same reference (placebo) creating a star-shaped network, are presented in Section 2.2. Alternative sources to inform prior distributions regarding the selection process are discussed in Section 2.3 (external, empirical evidence and expert opinion). Section 3 presents an application on a network that evaluates the effectiveness of 12 antidepressants compared to placebo and illustrates the various model alternatives [21].

2. Methods

2.1. Bayesian selection model for two treatment pairwise meta-analysis

The selection model assumes that there is a population of studies which have been conducted in the area of interest. Let us assume that there are N published studies (indexed with i) that report an estimated treatment effect denoted by y_i and a standard error denoted by s_i. In the presence of publication bias these studies are a non-random sample of all studies that have been conducted on the topic of interest. In building the selection model Copas and Shi assumed that very large studies have a probability of being published very close to one, reflecting the fact that sponsors and investigators who conduct big studies will make sure that the results will be disseminated and that journals tend to trust large studies for publication [12]. On the other hand, small studies have a small probability of publication. On the top of publication bias, selective reporting of the outcomes within studies might also operate and will result in biased meta-analysis results. As with publication bias, selective reporting is likely to be more severe in smaller rather than in larger studies; large studies are more likely to have a protocol or to be submitted to a high-profile journal in which reviewers ask more persistently for the major outcomes.

If the effect size y_i is correlated with the probability of a study to be published (which is a function of the study size), then bias arises. Therefore, the model assumes that for a given sample size the probability of publication is a monotonic function of the effect size; if negative values of the effect size indicate a significant treatment effect then the probability of a study being published is a decreasing function of the effect size. In summary, the model suggests that the probability of publication is both a function of the treatment effect size y_i and the study precision as reflected by s_i.

2.1.1. Model structure

In a random-effects meta-analysis model it is assumed that each observed effect size y_i is drawn from a normal distribution with mean value θ_i, the mean relative treatment effect in the study, and variance ${\sigma }_i^2$. In conventional meta-analysis it is assumed that the number of participants in each study i is large enough for the sample variance $s_i^2$ to be an accurate estimate of the true within-study variance ${\sigma }_i^2.$

$$y_i~N({\theta }_i,s_i^2)$$ (1)

Across studies the effects θ_i are related via a normal distribution with an overall mean effect size μ and heterogeneity variance τ²

$${\theta }_i~N(\mu ,{\tau }^2)$$ (2)

In the presence of a selection process, we assume there is a latent continuous variable z_i (propensity score) underlying each study so that when z_i > 0 the study i is published and hence y_i is observed. The propensity score depends on the size of the study (as expressed by the standard error s_i) and it is positively correlated with effect size y_i so that studies with larger and more precise effects have more chances to be published.

This can be modelled by assuming that the two random variables y_i and z_i follow a truncated bivariate normal distribution

$$\left(\begin{array}{c}{y}_i\\ z_i\end{array}\right)~N_2\left(\left(\begin{array}{c}{\theta }_i\\ u_i\end{array}\right),\left(\begin{array}{cc}{s}_i^2& \rho s_i\\ \rho s_i& 1\end{array}\right)\right)I_{z_i>0}$$ (3)

where I_A is an indicator function which takes value 1 if expression A is true and 0 otherwise.

The expected mean of z_i is set as u_i = f(s_i) where f(s_i) is a function of the standard error. Copas and Shi define $f(s_i)=\alpha +\frac{\beta }{s_i}$. The parameter α controls the overall proportion of published studies with Φ(α) being the marginal probability of publishing a study with infinite standard error. The parameter β controls the dependence of the probability of publication on the standard error; β is expected to be positive to reflect the fact that the larger the standard error the less the probability the study is published. Section 2.1.2 elaborates further on the interpretation of parameters α and β.

The observed effect sizes and the propensity score are correlated with correlation ρ = corr(y_i,z_i); this reflects the belief that the propensity for publication is associated with the observed effect size. Copas and Shi derived estimates for the expected value and the variance of y_i when by numerically maximizing the likelihood function for given values of α and β. The derived expression for the variance takes into account that the publication process has an impact on the resulting within-study variances. These expressions play a key role in the Copas and Shi methodology[10]. However, we take a different approach by using informative priors for α and β and estimate all parameters using Markov Chain Monte Carlo (MCMC) methods.

Sampling from the joint distribution of y_i and z_i could be accomplished by rejection methods i.e. repeatedly sampling from the bivariate normal distribution and keeping those draws that meet the truncation constraints. Generally, for a multivariate normal random variable, all conditional and marginal distributions are normal. For a truncated bivariate normal distribution only the conditional (but not marginal) distributions are truncated normal [22]. Additionally, in this specific case where truncation refers only to z_i, the marginal distribution of z_i for z_i > 0 is a truncated normal distribution (see Appendix). Consequently, the bivariate normal distribution (3) can be approximated by sampling from the marginal truncated distribution $z_i~N(u_i,1)I_{z_i>0}$ and then sampling from y_i conditional on z_i as y_i | z_i ~ N(E(y_i | z_i), var(y_i | z_i)) where (E(y_i | z_i) = θ_i + ρs_i (z_i−u_i) and $\text{var(}{y}_i|z_i)=s_i^2(1-{\rho }^2)$.

2.1.2. Model interpretation

The probability that a specific study i with standard error s_i is published is equal to

$$P(z_i>0)=\Phi \left(\alpha +\frac{\beta }{s_i}\right)=\Phi (u_i)$$ (4)

This provides us with an interpretation of parameters α and β as those parameters that control the marginal probability that a study with standard error s_i is published. Parameter α controls the overall proportion of studies published and parameter β is a discrimination parameter, discriminating the probabilities of publication between studies with different standard errors. If β = 0 and α is a large number (such as α = 10) then the probability of any study being published is Φ(10) = 1 irrespective of its standard error meaning that that is that there is no publication bias. The larger the value of β, the more intensive the dependence of the selection process on the study sample size. It is expected that β will be positive so that very large studies (with s_i being very small) are most likely to be accepted for publication. This is formally explored in section 2.3.1. Note that variations of the model described above may result from different specifications of the function f (s_i). Setting f (s_i) = α + βs_i we can have a less ‘steep’ association between the standard error and the probability of publication. In this parameterization it is expected that in the presence of publication bias β will be negative. Copas and Shi suggested a likelihood ratio statistic to evaluate if the adjusted model gives a good fit to the funnel plot. The test actually tests the hypothesis H₀ : β = 0 and in the special case of no heterogeneity it is equivalent to Egger’s test [23].

If large positive values of the effect size signify a better treatment effect, then positive values of ρ will result in positive and large values of z_i and then, the meta-analysis of the available studies will be overestimating the true mean μ, which is indicative of publication bias. If ρ = 0 then y_i and z_i are independent and y_i has no effect on the study being published or not, therefore the only selection process will depend on the size of the study alone.

The importance of interpreting the selection models in terms of the estimated number of unpublished studies has been highlighted [5,6]. The inverse of Φ(u_i) gives us the expected number of studies with standard error s_i that have been conducted. By summing up the expected number of studies for each observed standard error we get an estimate of the total number of studies, published and unpublished, conducted on the topic of interest

$$TS={\displaystyle \sum _{i=1}^N\frac{1}{P(z_i>0|s_i)}}$$

The model is fitted in a Bayesian framework using MCMC to obtain posterior distributions for all parameters of interest. This offers the advantage that uncertainty intervals can be obtained for all quantities of interest including the total number of studies TS. The posterior distribution of the correlation coefficient ρ with respect to the null and the change in treatment effect μ can be monitored to infer whether publication bias is present and how much it affects the results. If the posterior distribution for ρ lies away from zero there is a strong indication that the effect size of a study is correlated with its probability of being published.

2.2. Selection model with multiple treatments

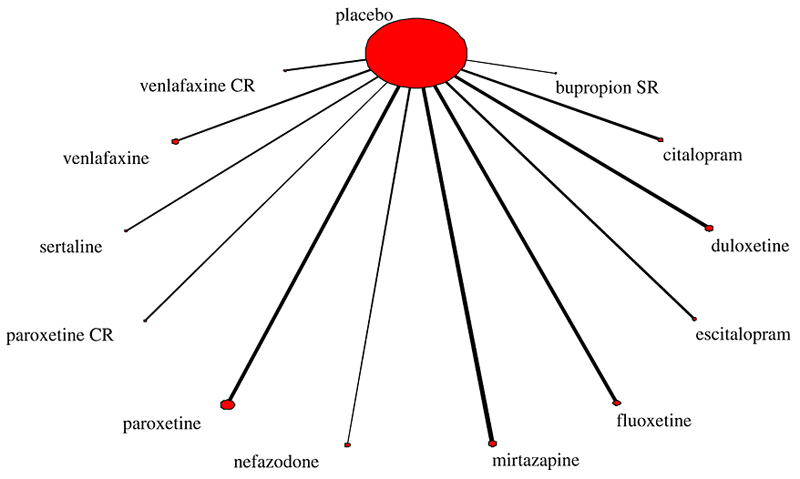
Assume multiple treatments involved in the meta-analysis, each compared to a common comparator creating a star-shaped network of evidence of the form presented in Figure 1 (which is described in Section 3). Let T denote the number of treatments in the analysis. Assume there are n_j studies comparing treatment j to a common comparator with j = 1,…, T and ${\displaystyle {\sum }_{j=1}^T{n}_j=N}$ the total number of studies. Then, the model is a simple multi-treatment adaptation of the model presented above. We assume that the effect size of the i-study involving treatment j is denoted by $y_i^j$ and it follows a normal distribution $y_i^j~N({\theta }_i^j,s_i^j)$ with ${\theta }_i^j~N({\mu }_j,{\tau }_j^2)$. The selection model is $z_i^j~N({\alpha }_j+\frac{{\beta }_j}{s_i},1)I_{z_i^j>0}$ where $y_i^j$ and $z_i^j$ are correlated as before with correlation ρ_j. Considerations need to be made regarding the selection model parameters (α_j, β_j, ρ_j), and the heterogeneity parameters τ_j.

Figure 1.

Star network of evidence for the twelve antidepressants

2.2.1. Selection model parameters for multiple treatments

There are as many pairs of selection model parameters (α_j, β_j) as treatment comparisons in the data set. Three approaches are considered in this paper to model the selection parameters:

• Common selection model: All treatment comparisons are assumed to have the same susceptibility to publication bias (α_j, β_j) = (a, β).

• Group-specific selection model: Treatment comparisons can be categorized in l groups of various degrees publication bias. Then, denoting with c_(j) the group that treatment j belongs to the parameters follow prior distributions $a_j~N\left(A_{c_{(j)}},{\omega }_a^2\right)$ and ${\beta }_j~N\left(B_{c_{(j)}},{\omega }_{\beta }^2\right)$.

• Treatment-specific selection model: Each treatment has different susceptibility to publication bias $a_j~N\left(A_j,{\omega }_a^2\right)$ and ${\beta }_j~N\left(B_j,{\omega }_{\beta }^2\right)$.

Similar assumptions could be made for the correlation parameters ρ_j; here we assume equal parameters ρ_j = ρ ∀ j.

2.2.2. Heterogeneity for multiple treatments

If publication bias is present it would impact on the inferences regarding the overall treatment effects as well as on the heterogeneity. It has been demonstrated using a simple weight function that very strong assumptions are needed to revise heterogeneity estimates in the presence of publication bias and that tests for heterogeneity are also affected [24]. It has also been suggested that it is not realistic to disentangle the effects of heterogeneity and publication bias unless large meta-analyses are considered [25].

Depending on the context, assumptions can be made regarding the heterogeneity across treatment comparisons; it may be assumed that it is different across comparisons or similar (i.e. τ_j = τ). The assumption of equal heterogeneity parameters is difficult to defend but the estimation of different τ_j is problematic when few studies contribute to a comparison. Alternatively we may assume that heterogeneities are exchangeable across the different treatments through a hierarchical random effect model, i.e. drawn from a common distribution

$$\begin{array}{c}{\tau }_j~N(\gamma ,1)I_{{\tau }_j>0}\\ \gamma ~U(0,1)\end{array}$$

This model was described as the unstructured heterogeneity model by Lu and Ades [26]. Our default approach is the equal heterogeneities model, with priors discussed in section 2.3.1.

2.3. Prior specification for model parameters

Since the model is fitted within a Bayesian context, all parameters are treated as random variables and are given prior distributions. Model parameters μ, τ, ρ, α, and β. A non-informative normal distribution is assumed for μ (μ ~ N(0,1000)) and a uniform ρ ~ U(−1, 1) for the correlation which is also assumed to be minimally informative. Other choices were also considered for prior information on the correlation parameter. As part of a sensitivity analysis we employed informative Beta priors (such as ρ ~ Beta(3,3)) and a uniform prior U(1,1) on the Fisher transformation of ρ. Both priors assign less weight on the boundaries and are appropriate when we have prior information regarding the direction of publication bias.

2.3.1. Deriving informative prior distributions for α and β

In order to derive the distribution for the observed effect sizes the values of a and β are required. These parameters connect to the probability of publication of studies with various precisions. In the model presented by Copas and Shi a and β are fixed values rather than parameters and the authors suggested to identify a range of (a,β) parameters which cover all reasonable probabilities[12] and explore the impact of the range of values in a sensitivity analysis. In the Bayesian paradigm, we treat a and β as random variables with statistical distributions and the uncertainty in them is propagated through into the adjusted pooled treatment estimate. To achieve this, one can set a lower and an upper bound to the probability of publication. These two probabilities, denoted as P_low and P_large, can be interpreted as the probabilities of publication for the study with the largest and smallest standard error. Here we often identify P_low and P_large as referring to the study with the smallest and largest sample size (assuming that the variance in the outcome would be comparable across studies). The reason the prior information is included via specification of P_low and P_large is that we believe it is easier to provide prior knowledge on the distribution of the probabilities rather than on the selection parameters themselves which are difficult to interpret. Then (a,β) can calculated from the inequalities

$$P_{low}\le P(z_i>0|s_i)\le P_{large}\forall i$$

The inequalities above hold for the standard errors we observe in the meta-analysis constrained by the assumption that the selection probability cannot decrease as the standard error decreases. This forces the upper bound to refer to the study with the smallest standard error s_min and the lower bound to refer to the study with the largest standard error s_max. So, there is an ‘one to one’ relationship between the pairs of variables (α, β) and (P_low, P_large) and setting up the distributions of the two probabilities, we can derive the distributions of a and β as

$$\begin{array}{l}\alpha +\frac{\beta }{s_{max}}~{\Phi }^{-1}\left(P_{low}\right)\\ \alpha +\frac{\beta }{s_{min}}~{\Phi }^{-1}\left(P_{large}\right)\end{array}$$

In order to obtain prior distributions for P_low ~ U(L₁, L₂) and P_large ~ U(U₁, U₂) external evidence might be available or expert opinion might be collected. Reviewers need to establish plausible values for the intervals (L₁, L₂) and (U₁, U₂) which refer to the probabilities for publication of a study with the largest and the lowest standard error respectively. Here we consider two possible sources of evidence that can be applied.

1. Registries of studies: In the meta-analysis of randomized controlled trials it is possible to get an estimation of the total number of unpublished studies by looking at registries of protocols such as the FDA (US Food and Drug Administration) database, the websites of pharmaceutical companies etc. Then, an estimate of the number of published studies out of the total registered by sample size can provide priors for P_low and P_large. Note that what is required from registries is only the number of studies that have been carried out and their sample size, not their results.

2. Expert opinion: Reviewers may ask experts in the field to provide estimates of the probability for a study of given sample size to be published and identified for inclusion in the review. This approach has the advantage that the completeness and type of the trial search can be taken into account in the formulation of priors. For example if the review has included studies identified by searching sites of pharmaceutical industries, the transparency policy of each company and the usefulness of their websites can and should be taken into account when forming prior beliefs about the completeness of the database at hand.

Any of the model parameters described in section 2.2.1 can be estimated from registry data or expert opinion. Expert opinion might be a more viable option for treatment-specific selection parameters as one would need much detailed external information to be available from registries. In cases where both sources of information are available (registry data and expert opinion), priors can be built using their combination. However, if the two sources disagree and provide different priors combination will be problematic and can lead into unrealistic priors.

2.3.2. Approximately non-informative prior distributions for the heterogeneity parameter

Various non-informative priors have been suggested to model heterogeneity. The half-normal distribution is a popular choice for variance parameters in a hierarchical model. However, for heavy-tailed data, the half-normal distribution may give a poor approximation and other models such as a half-t distribution could be considered. The impact of assuming different priors in the context of meta-analysis has been examined by Lambert et. al. who investigated 13 different priors and revealed that the impact of the prior distribution is significant for meta-analyses with only five studies or when heterogeneity is close to the boundary at zero[27]. Gelman also explored prior specification for variance parameters and concluded that Inverse-Gamma priors, though conditionally conjugate, behave poorly if they are vague (having very small shape and scale values) and when true heterogeneity is low [28]; he suggested using uniform, half-t or half-Cauchy prior. As publication bias can manifest itself as heterogeneity, we will explore the impact of various prior specifications in the results of the selection model, including τ ~ N(0,100)I_τ>0, τ ~ U(0,30), τ² ~ IG(0.1,0.1) and τ² ~ IG(0.01,0.01). Our default model assumes τ ~ N(0,100) I_τ>0.

1. Implementation of the model

The model was fitted in OpenBUGS (an open source version of WinBUGS) using Markov Chain Monte Carlo methods [20]. A particular challenge in using this software environment for the model fitting is that there is no closed-form expression for the inverse of the cumulative distribution of a standard normal distribution. Therefore we programmed a closed form approximation [29]

$${\widehat{\Phi }}^{-1}\left(p\right)=5.531\left\{\begin{array}{cc}{\left(\frac{1-p}{p}\right)}^{0.1193}& -1\end{array}\right\}\text{if}\hspace{0.17em}p\ge \frac{1}{2}.$$

All results pertain to 100 000 sample iterations taken after 10 000 burn-in iterations. The model OpenBUGS code and data are available in http://www.mtm.uoi.gr (under ‘Material from Publications’).

3. Application

3.1. Description of the data

Turner and colleagues compared the published results regarding the randomized controlled trials for 12 antidepressants compared to placebo to the corresponding results from trials submitted to the FDA and found evidence of bias towards results favouring the active intervention (Figure 1)[21]. Briefly, there are 73 studies with results as reported to the FDA (74 originally but two of them were subsequently combined) used for the licensing of antidepressants drugs between 1987 and 2004. The outcome was improvement in depression symptoms and was measured using the standardized mean difference (SMD). The authors found that 50 out of the 73 studies were subsequently published with their reported results sometimes being different to those reported in FDA database. From the 38 FDA studies with statistically significant results only one was not published; whereas from the 36 FDA with non-statistically significant results only three were published and another 11 were published with results conflicting those presented in the FDA report [30]. The dataset has also been used previously in evaluating regression-based methods of adjusting for publication bias [31].

The data set of the 50 published studies is our ‘analysis data set’. To form priors for P_low and P_large we need information regarding the proportion of ‘large’ (for P_large) and ‘small’ (for P_low) published studies out of the total carried out. One source of information is the FDA registry; to form the priors only the number of registered studies and their sample size are required as described in section 2.3.1. The FDA dataset contains more than the minimum information necessary to form priors; the study outcomes as extracted by Turner et al are also available. Therefore, the meta-analysis from the 73 registered studies can be used as a ‘reference standard’ to comment on the performance of the selection model when external data or expert opinion is used to derive priors.

3.2. Selection model for head-to-head meta-analysis: Active antidepressant versus Placebo

We first applied the model considering all antidepressants as a single active treatment whose effectiveness is evaluated against placebo. To estimate P_low and P_large we use only external data, namely the FDA database. We split the studies into four intervals of approximately equal width according to the standard error. Studies with large standard errors are used to estimate the lowest probability of publication, P_low, whereas studies with small standard errors are used to estimate the largest probability of publication, P_large. The fourth group defines the ‘small’ studies group with standard errors larger than 0.29 and is used to estimate P_low whereas the first group defines the ‘large’ studies group with standard errors less than 0.15 and is used to estimate P_large. Then the average P_low and P_large were estimated as the proportion of studies that were included in both published and FDA dataset (0.4 and 0.8 respectively). To account for uncertainty we considered a 5% variability from the average probability values thus P_low ~ U(0.35,0.45) and P_large ~ U(0.75,0.85).

Table 1 shows the posterior mean values for α and β for each selection model, the meta-analysis estimates from the FDA data (‘reference’ standard), the published studies and the two selection models. For selection model 1, the mean effect is closer to the FDA reference effect size. The posterior values of the correlation coefficient ρ suggest that there is a positive and possibly strong correlation between effect sizes and the probability of publication. Note that the trim-and-fill method yields an overall treatment effect 0.35 (0.31, 0.39) and an estimated number of 18 unpublished studies. The estimate μ using meta-regression on the variance is 0.29 (0.23, 0.35). The wide interval for the regression-based method reflects the uncertainty caused by the fact that the extrapolated effect size corresponds to a standard error that is far away from the observed ones.

Table 1.

Estimates (SMD) and 95% Confidence Intervals for treatment effect μ, heterogeneity τ and total number of studies NS for the FDA data, the published data and the two selection models for the published data with priors for selection parameters derived from the FDA data.

	f(si)	ρ	μ	τ	NS
FDA			0.309 (0.271,0.352)	0.052 (0.002,0.122)	73
Published data			0.409 (0.365,0.463)	0.042 (0.002,0.106)	50
Selection model 1	−0.693 + 0.161/si	0.806 (0.521,0.985)	0.348 (0.305,0.393)	0.054 (≅ 0,0.118)	86 (83,92)
Selection model 2	1.483 − 5.342 × si	0.786 (0.440,0.989)	0.365 (0.322,0.409)	0.054 (≅ 0,0.113)	76 (73,81)

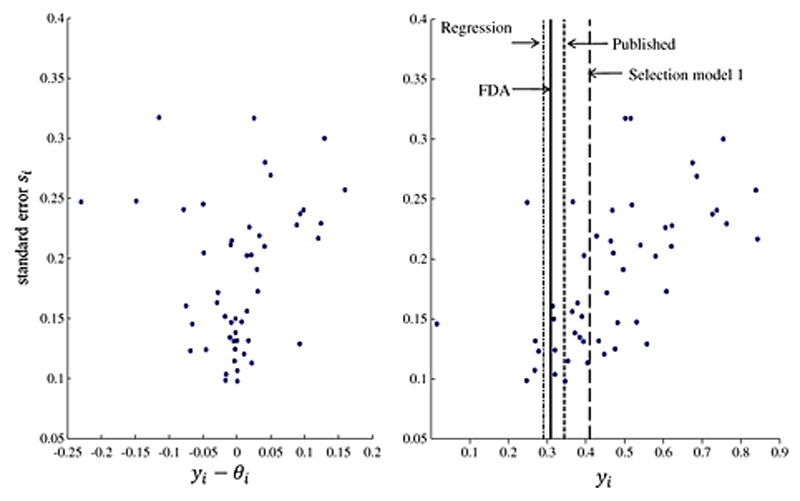
Figure 2 shows the scatter plot of y_i − θ_i (where θ_i is the underlying study-specific effect size adjusted for publication bias) versus the standard error (left panel) for selection model 1. It seems that bias tends to increase with standard error and that most biases are positive suggesting the effect sizes have been overestimated. The second plot (right panel) suggests that smaller studies with larger standard errors tend to yield larger effect sizes and significant results. Vertical lines are used to indicate the overall treatment effects using the FDA dataset, the published set of studies, a regression-based adjustment and the selection model.

Figure 2.

Panel A plots the bias y_i − θ_i versus standard error s_i where θ_i is the underlying study-specific effect size adjusted for publication bias. Panel B plots the (observed) effect size y_i versus the standard error s_i. The solid line is the treatment effect estimated from the 73 studies registered with the FDA, The dashed line on the left is the treatment effect estimate by regressing effect size on its variance weighted by the standard error, the dashed line on the right is the treatment estimate by using Copas selection model with $z_i=\alpha +\frac{\beta }{s_i}+{\delta }_i$ and the dashed-dotted line is the unadjusted estimated treatment effect by the 50 published studies

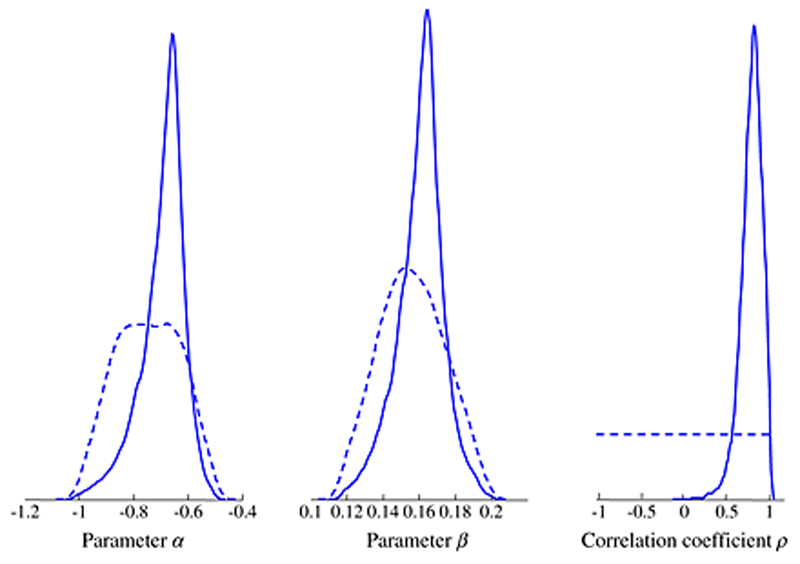
Figure 3 depicts the prior and posterior distributions for parameters α, β and ρ estimated from selection model 1 with P_low ~ U(0.35,0.45) and P_large ~ U(0.75,0.85). Although informative priors are given to α and β, the parameters are partly informed from the data. The flat prior of the correlation parameter ρ is updated considerably. Its posterior distribution lies away from zero implying that the published effect sizes are positively correlated with the propensity for publication. Using a more informative prior like Beta or uniform on the Fisher transformation resulted to the same posterior mean ρ with more narrow credible intervals.

Figure 3.

Prior (dashed lines) and posterior distributions (solid lines) for parameters α, β and ρ under the selection model $f\left(s_i\right)=\alpha +\frac{\beta }{s_i}$ when the 50 published studies are considered

Variations of selection model 1 for different values of P_low and P_large do not seem to impact a lot on the estimated summary effects. When the prior probabilities for publication drop the summary estimates decrease whereas the uncertainty and the number of total studies increase (Appendix Table 1). We further explored the impact of various prior distributions for the heterogeneity parameter in both selection models 1 and 2 (Appendix Table 2). Posterior heterogeneity and total number of studies vary for different model assumptions. The estimated heterogeneity parameter becomes substantially larger when an inverse-gamma prior distribution is assumed. However, there is no autocorrelation between MCMC draws when an inverse-gamma prior is assumed. Also, in line with Gelman’s remark we could not assign very small values for the parameters of the inverse-gamma (i.e. τ² ~ IG(0.001,0.001) that would ensure non-informativeness as this yielded a posterior density we cannot sample from [28].

3.3. Sensitivity analysis for network meta-analysis

One can differentiate between the effectiveness of the interventions (via network meta-analysis) and their susceptibility to publication bias (as outlined in section 2.2.1). In the common selection model the effectiveness parameters are assumed to be treatments-specific (μ_j) but the selection parameters are fixed across treatments (α_j,β_j) = (α,β) with α,β estimated from the FDA data (P_low ~ U(0.35,0.45) and P_large ~ U(0.75,0.85)). For group-specific and treatment specific selection models we employed expert opinion to derive the probability priors for each category and treatment.

In the group-specific selection model we identified l=3 groups of drugs with different degrees of publication bias. A psychiatrist with experience in antidepressant trials and systematic reviews on major depression (AC) categorized the 12 treatments into three groups (c₁, c₂, c₃) according to similarities in the policy of the manufacturing companies and transparency (Table 2). For each of the three groups the expert was then asked to fill in the probabilities of publication estimating percentages for two different scenarios, studies with an overall sample size of 400 or 100 participants. This rating was carried out without considering results from Turner et al. 2008 [21]. The two probabilities refer to, broadly speaking, P_large and P_low and a variation of 0.05 was employed to derive the intervals.

Table 2.

Expert’s categorization, probabilities of publication by sample size for each bias group

Group according to expected publication bias	Antidepressant	Plow	Plarge
		n=100	n=400
Low risk of bias cl	buproprion, escitalopram, paroxetine, paroxetine CR	80%	95%
Medium risk of bias c2	citalopram, fluoxetine, sertraline, venlafaxine and venlafaxine XR	70%	85%
High risk of bias c3	duloxetine, mirtazapine and nefazodone	50%	70%

In the treatment-specific model nine experienced psychiatrists were given the sample sizes (as extracted from our data for each treatment) and were asked to fill in columns 3 and 5 in Table 3 with the corresponding probabilities that a study comparing the specific antidepressant to placebo is published. Table 3 shows the average probabilities for each drug. As only one study for bupropion was available, the sample sizes from the FDA data were used (3 studies).

Table 3.

Expert’s prior probabilities of publication for studies of given sample size by drug and estimated selection parameters

Drug name	n	Plow	n	Plarge
Bupropion	250	83%	350	97%
Citalopram	100	64%	350	94%
Duloxetine	100	48%	300	87%
Escitalopram	250	81%	400	94%
Fluoxetine	40	38%	350	93%
Mirtazapine	80	41%	150	72%
Nefazodone	90	43%	200	73%
Paroxetine	20	49%	350	98%
Paroxetine CR	200	86%	400	98%
Sertraline	90	69%	350	97%
Venlafaxine	90	67%	300	96%
Venlafaxine XR	200	79%	250	93%

Table 4 shows the estimated effect sizes for each treatment estimated from each selection model assuming there is a common heterogeneity parameter across treatments. It is clear that all treatment effects with the exception of fluoxetine are overestimated in the published data compared to those computed from FDA. This is particularly evident for the studies in the ‘high risk of bias’ group. The effectiveness of fluoxetine is reduced beyond the estimate from the FDA data; this can be explained by the fact that all studies involving fluoxetine are published but the expert’s opinion in Tables 2 and 3 considered that studies involving fluoxetine are possibly missing. Similarly, Paroxetine is placed in the ‘low risk of bias’ group (Table 2) but only 10 out of the 16 studies registered with the FDA are published. This results to an adjusted effect for Paroxetine that is less than the estimated from the FDA dataset when a group-specific selection model is assumed (Table 4 column 5).

Table 4.

Estimated effect sizes (SMDs), heterogeneity τ and number of trials NS and correlation ρ for the FDA dataset, the published set of studies and the three selection models. It is assumed that the heterogeneity is the same across treatments. Credible intervals are given in parentheses.

	FDA	Published	Common selection	Group-specific selection	Treatment-specific selection
Bupropion μ	0.18 (0.03,0.35)	0.27 (0.02,0.52)	0.21 (-0.06,0.43)	0.21 (-0.04,0.45)	0.22 (-0.01,0.45)
Citalopram μ	0.24 (0.09,0.39)	0.31 (0.18,0.46)	0.25 (0.10,0.38)	0.25 (0.11,0.37)	0.26 (0.14,0.38)
Duloxetine μ	0.30 (0.19,0.4)	0.40 (0.30,0.51)	0.35 (0.26,0.45)	0.34 (0.24,0.44)	0.36 (0.27,0.45)
Escitalopram μ	0.31 (0.18,0.44)	0.35 (0.22,0.49)	0.33 (0.21,0.44)	0.35 (0.21,0.47)	0.34 (0.22,0.46)
Fluoxetine μ	0.27 (0.11,0.41)	0.27 (0.13,0.40)	0.19 (0.05,0.33)	0.18 (0.05,0.31)	0.20 (0.07,0.33)
Mirtazapine μ	0.35 (0.21,0.35)	0.56 (0.36,0.81)	0.42 (0.27,0.58)	0.44 (0.29,0.61)	0.42 (0.29,0.55)
Nefazodone μ	0.26 (0.12,0.4)	0.46 (0.29,0.68)	0.34 (0.20,0.48)	0.35 (0.19,0.53)	0.34 (0.20,0.47)
Paroxetine μ	0.42 (0.30,0.53)	0.60 (0.46,0.73)	0.43 (0.29,0.56)	0.34 (0.19,0.52)	0.46 (0.35,0.58)
Paroxetine CR μ	0.31 (0.13,0.51)	0.35 (0.19,0.51)	0.32 (0.16,0.45)	0.33 (0.17,0.50)	0.33 (0.18,0.48)
Sertaline μ	0.25 (0.10,0.40)	0.42 (0.25,0.61)	0.37 (0.18,0.52)	0.37 (0.21,0.53)	0.39 (0.23,0.55)
Venlafaxine μ	0.40 (0.26,0.54)	0.49 (0.36,0.63)	0.41 (0.29,0.55)	0.42 (0.29,0.54)	0.44 (0.30,0.55)
Venlafaxine XR μ	0.39 (0.21,0.58)	0.51 (0.31,0.72)	0.44 (0.26,0.61)	0.44 (0.25,0.62)	0.44 (0.28,0.59)
τ	0.061 (0.013,0.12)	0.041 (≅ 0,0.083)	0.042 (0.01,0.102)	0.045 (≅ 0,0.108)	0.036 (≅ 0,0.102)
TS	73	50	92 (85,100)	130 (109,168)	82 (80,86)
ρ			0.78 (0.41,0.96)	0.73 (0.37,0.94)	0.78 (0.41,0.96)

The studies registered with FDA appear to be more heterogeneous than the published studies (τ is 0.061 and 0.041 respectively) although their 95% credible intervals overlap. The group-specific selection model gives a larger number of missing studies. The correlation coefficient ρ suggests similar positive values for all three approaches confirming that the propensity for publication is positively correlated with the effect size. Bupropion does not seem to have a significant effect probably because there is only one published study comparing bupropion to placebo and there is not enough power to detect a significant treatment effect.

Table 5 shows the estimated effect sizes for each treatment for each selection model assuming heterogeneities are exchangeable across treatments through a hierarchical model as described in section 2.2.2. The estimates are similar to those shown in Table 4 but the 95% Credible Intervals are wider as they reflect the fact that heterogeneities are modelled separately for each treatment which also increases the uncertainty in ρ. Consequently, bupropion, fluoxetine, paroxetine CR, sertraline, venlafaxine are no longer associated with statistically significant effects as there are very few studies comparing these antidepressants.. The 95% credible intervals for ρ do not include zero indicating that the effect sizes are positively correlated with the propensity for publication. The overall mean heterogeneity is much larger than the one observed when a common heterogeneity is assumed (Table 4).

Table 5.

Estimated effect sizes (SMDs), average heterogeneity γ , number of trials NS and correlation ρ for the FDA dataset, the published set of studies and the three selection models. It is assumed that the heterogeneity is the same across treatments. The hierarchical model with dependent priors is assumed. Credible intervals are given in parentheses.

	FDA	Published	Common selection	Group-specific selection	Treatment-specific selection
Bupropion SR μ	0.18 (-0.27,0.64)	0.25 (-2.05,2.53)	0.22 (-2.17,2.62)	0.21 (-2.12,2.60)	0.19 (-2.10,2.39)
Citalopram μ	0.23 (-0.01,0.48)	0.32 (0.06,0.61)	0.25 (0.05,0.47)	0.25 (0.05,0.44)	0.27 (0.05,0.47)
Duloxetine μ	0.30 (0.17,0.42)	0.41 (0.25,0.55)	0.35 (0.23,0.48)	0.34 (0.21,0.47)	0.36 (0.23,0.49)
Escitalopram μ	0.31 (0.01,0.60)	0.35 (≈ 0,0.73)	0.33 (0.02,0.63)	0.35 (≈ 0,0.72)	0.35 (≈ 0,0.68)
Fluoxetine μ	0.26 (-0.08,0.60)	0.32 (-0.01,0.70)	0.23 (-0.07,0.58)	0.20 (-0.07,0.49)	0.23 (-0.04,0.55)
Mirtazapine μ	0.35 (0.14,0.57)	0.58 (0.34,0.82)	0.43 (0.22,0.66)	0.44 (0.24,0.65)	0.41 (0.23,0.62)
Nefazodone μ	0.26 (0.05,0.46)	0.45 (0.12,0.78)	0.35 (0.09,0.63)	0.35 (0.10,0.60)	0.35 (0.12,0.59)
Paroxetine μ	0.43 (0.29,0.58)	0.59 (0.42,0.76)	0.43 (0.26,0.64)	0.31 (0.14,0.53)	0.46 (0.31,0.62)
Paroxetine CR μ	0.32 (-0.64,1.28)	0.37 (-0.61,1.38)	0.30 (-0.70,1.23)	0.33 (-0.61,1.31)	0.33 (-0.55,1.21)
Sertaline μ	0.25 (0.04,0.45)	0.42 (-0.56,1.44)	0.36 (-0.64,1.33)	0.37 (-0.50,1.31)	0.39 (-0.50,1.31)
Venlafaxine μ	0.40 (0.18,0.63)	0.51 (0.26,0.78)	0.44 (0.18,0.71)	0.42 (0.19,0.66)	0.44 (0.23,0.69)
Venlafaxine XR μ	0.41 (-0.20,1.02)	0.51 (-0.46,1.50)	0.43 (-0.58,1.32)	0.44 (-0.60,1.44)	0.42 (-0.56,1.35)
TS	73	50	92 (88,95)	130 (109,167)	83 (80,85)
γ	0.121 (≅ 0,0.42)	0.134 (≅ 0,0.46)	0.138 (≅ 0,0.48)	0.137 (≅ 0,0.50)	0.133 (≅ 0,0.46)
ρ			0.80 (0.37,0.99)	0.81 (0.37,0.99)	0.83 (0.37,0.99)

4. Discussion

In this paper we presented a flexible Bayesian implementation of the Copas selection model to account for publication bias in meta-analysis. A selection model addresses publication bias in an intuitive and elegant way as it directly relates probabilities of publication for a study with the study’s effect size and precision. To provide bias adjusted estimates, the Copas selection model requires prior assumptions to be made and therefore should be viewed as a form of sensitivity analysis. However, when fitted within a Bayesian framework as in our approach, the range of values to consider in the sensitivity analysis is summarized in the prior distribution. The model we presented can be applied when there are suspicions that the available dataset is a selected sample, in which case prior assumptions for the probability of publication for ‘small’ and ‘large’ studies need to be made. This information can be taken from registries of trials. The number of registered trials and their sample size, information easily retrieved, suffices to construct priors. Alternatively, expert opinion can be obtained, as described in our methods. Another important advantage of the Bayesian implementation of the model is that it can be easily combined with network meta-analysis models, giving great flexibility to incorporate various assumptions for the susceptibility of bias in different treatment comparisons.

A main challenge in the proposed methodology lies in the evaluation of the alternative selection models. The Deviance Information Criterion (DIC) is often used as a model selection criterion in a Bayesian setting; the more parsimonious model is indicated by lower DIC value. However, DIC values are not directly comparable between models that contain different number of data points or missing data [32]. An alternative could be to use the estimated total number of studies as criterion; the model that approximates at best the number of studies included in a trial registry can be viewed as the most suitable. Such a criterion is very appealing intuitively. However, it is often questionable whether the trial registries are themselves a complete body of studies and whether they can be used as a reference for model selection. In our data there were 23 unpublished studies but there could be studies not registered with the FDA. Moreover, differences between meta-analyses of published and unpublished studies are not solely attributed to publication bias but also to distortion of the study results; in our data 11 studies were published with results contradicting those registered with the FDA.

The total number of estimated studies is expected to be larger than the published number of studies as the former is based on the assumptions made about P_low and P_large. Therefore, even if all studies were observed, the selection model would imply that there would be still unpublished studies but it would not find a relationship between effect size and its standard error. A posterior distribution of ρ that gives little likelihood to zero is an indication of the presence of publication bias. When fitting a selection model to the FDA dataset with the P_low and P_large as in Table 1 we get an estimated number of published and unpublished studies equal to 147 with a 95% CrI (144,153) and ρ=0.474 (−0.059,0.905). The fact that the credible interval for ρ is wide reflects the uncertainty on how effect sizes are correlated with their probability of being published and the fact that zero is included in the credible interval suggests there might not be any correlation between effect sizes and the propensity for publication.

In our application, priors from the FDA and expert’s opinion contradict for some interventions. This could be attributed to several reasons including the small number of studies per treatment, the fact that studies were collected in a wide time-span (from 1987 to 2004) and to the fact that sample size is not the only factor affecting the quality of the study and its probability of getting published. It should also be noted that the elicitation of expert opinion took place after the study by Turner et al was published [21]. As the psychiatrists involved in the prior elicitation were aware of the conclusions of this study their judgment might have been influenced by it. Still, disagreement between the FDA prior distributions and the expert opinion was present for fluoxetine suggesting the formulation of the priors was not purely a translation of the findings of the Turner study.

Recently simple regression models based on a measure of study precision have been proposed to adjust for publication bias by extrapolating to a study of size that is assumed free of publication biases[3]. Such models are simpler than the selection model proposed here, containing only one extra parameter over the standard meta-analysis model but the underlying selection model assumed is not explicit. It would be interesting to compare the performance of the two approaches. Further, there is some evidence that selection in the antidepressants dataset is predominantly driven by p-value (e.g. by inspecting the contour enhanced funnel plots in Moreno et al[33]) hence it would also be interesting to compare the performance of simpler, p-value only based selection models on this dataset.

The selection model adopted here connects the probability of publication for a study to its standard error by assuming a regression model. Similarly, the propensity for publication could be linked to other regressors such as study characteristics that relate to the risk of bias (blinding, allocation concealment etc.) that may influence the summary treatment effect via publication or other routes. Lower quality studies tend to be smaller and it is often assumed that sample size can be viewed as a single proxy to several characteristics which impact via publication mechanism and can explain heterogeneity in the effect sizes. Sensitivity analysis models for publication bias that account for complex selection processes associated with various trial and journal attributes have been previously presented [34,35]. Extensions to Bayesian framework of these models will provide an important additional tool in the evaluation of the robustness of the meta-analysis conclusions.

An important limitation of the presented framework is that it applies to the case of a star-shaped network; extensions of the model are needed for the case of a full network. The direction of the selection process was clear in our database and tends to suppress studies that do not favour the active treatment. This will not be the case in a full network where assumptions about the direction of bias in head-to-head trials need to be built. Moreover, the model should account for different selection processes between head-to-head and multi-arm trials. In the present star network, statistical evaluation of the assumption of consistency was not possible. Detection of inconsistency as the disagreement between direct and indirect estimates is possible only in ‘closed loops’. Application of the selection model in a full network will enable exploration of the association between selection in some or all comparisons in the network and inconsistency.

Finally, the assessment of model fit in a Bayesian framework requires further work. Prior specification is of critical importance and the impact of prior distributions for selection parameters and heterogeneity τ should be investigated. A simulation study and a large scale empirical evaluation might be useful in revealing the properties of the method to identify publication bias when it exists or in its absence. Using realistic scenarios (such as those described in the empirical study by Schwarzer et al [14] and Carpenter et al [18]) and a large range of priors, information on bias and coverage probabilities of intervals shall shed further light on the usefulness and sensitivity of the Bayesian version of the Copas selection model.