The ground truth about metadata and community detection in networks

Troubles with community detection in networks: No ground truth, no free lunch, and the complex coupling of metadata with structure.

Abstract

Across many scientific domains, there is a common need to automatically extract a simplified view or coarse-graining of how a complex system’s components interact. This general task is called community detection in networks and is analogous to searching for clusters in independent vector data. It is common to evaluate the performance of community detection algorithms by their ability to find so-called ground truth communities. This works well in synthetic networks with planted communities because these networks’ links are formed explicitly based on those known communities. However, there are no planted communities in real-world networks. Instead, it is standard practice to treat some observed discrete-valued node attributes, or metadata, as ground truth. We show that metadata are not the same as ground truth and that treating them as such induces severe theoretical and practical problems. We prove that no algorithm can uniquely solve community detection, and we prove a general No Free Lunch theorem for community detection, which implies that there can be no algorithm that is optimal for all possible community detection tasks. However, community detection remains a powerful tool and node metadata still have value, so a careful exploration of their relationship with network structure can yield insights of genuine worth. We illustrate this point by introducing two statistical techniques that can quantify the relationship between metadata and community structure for a broad class of models. We demonstrate these techniques using both synthetic and real-world networks, and for multiple types of metadata and community structures.

INTRODUCTION

Community detection is a fundamental task of network science that seeks to describe the large-scale structure of a network by dividing its nodes into communities (also called blocks or groups), based only on the pattern of links among those nodes. This task is similar to that of clustering vector data, because both seek to identify meaningful groups within some data set.

Community detection has been used productively in many applications, including identifying allegiances or personal interests in social networks (1, 2), biological function in metabolic networks (3, 4), fraud in telecommunications networks (5), and homology in genetic similarity networks (6). Many approaches to community detection exist, spanning not only different algorithms and partitioning strategies but also fundamentally different definitions of what it means to be a “community.” This diversity is a strength, because networks generated by different processes and phenomena should not necessarily be expected to be well described by the same structural principles.

With so many different approaches to community detection available, it is natural to compare them to assess their relative strengths and weaknesses. Typically, this comparison is made by assessing a method’s ability to identify so-called ground truth communities, a single partition of the network’s nodes into groups, which is considered the correct answer. This approach for evaluating community detection methods works well in artificially generated networks, whose links are explicitly placed according to those ground truth communities and a known data-generating process. For this reason, the partition of nodes into ground truth communities in synthetic networks is called a planted partition. However, for real-world networks, both the correct partition and the true data-generating process are typically unknown, which necessarily implies that there can be no ground truth communities for real networks. Without access to the very thing these methods are intended to find, objective evaluation of their performance is difficult.

Instead, it has become standard practice to treat some observed data on the nodes of a network, which we call node metadata (for example, a person’s ethnicity, gender, or affiliation for a social network, or a gene’s functional class for a gene regulatory network), as if they were ground truth communities. Although this widespread practice is convenient, it can lead to incorrect scientific conclusions under relatively common circumstances. Here, we identify these consequences and articulate the epistemological argument against treating metadata as ground truth communities. Next, we provide rigorous mathematical arguments and prove two theorems that render the search for a universally best ground truth recovery algorithm as fundamentally flawed. We then present two novel methods that can be used to productively explore the relationship between observed metadata and community structure, and demonstrate both methods on a variety of synthetic and real-world networks, using multiple community detection frameworks. Through these examples, we illustrate how a careful exploration of the relationship between metadata and community structure can shed light on the role that node attributes play in generating network links in real complex systems.

RESULTS

The trouble with metadata and community detection

The use of node metadata as a proxy for ground truth stems from a reasonable need: Because artificial networks may not be representative of naturally occurring networks, community detection methods must also be confronted with real-world examples to show that they work well in practice. If the detected communities correlate with the metadata, then we may reasonably conclude that the metadata are involved in or depend on the generation of the observed interactions. However, the scientific value of a method is as much defined by the way it fails as by its ability to succeed. Because metadata always have an uncertain relationship with ground truth, failure to find a good division that correlates with our metadata is a highly confounded outcome, arising for any of several reasons: (i) These particular metadata are irrelevant to the structure of the network, (ii) the detected communities and the metadata capture different aspects of the network’s structure, (iii) the network contains no communities as in a simple random graph (7) or a network that is sufficiently sparse that its communities are not detectable (8), or (iv) the community detection algorithm performed poorly.

In the above, we refer to the observed network and metadata and note that noise in either could lead to one of the reasons above. For instance, measurement error of the network structure may make our observations unreliable and, in extreme cases, can obscure the community structure entirely, resulting in case (iii). It is also possible that human errors are introduced when handling the data, exemplified by the widely used American college football network (9) of teams that played each other in one season, whose associated metadata representing each team’s conference assignment were collected during a different season (10). Large errors in the metadata can render them irrelevant to the network [case (i)].

Most work on community detection assumes that failure to find communities that correlate with metadata implies case (iv), algorithm failure, although some critical work has focused on case (iii), difficult or impossible to recover communities. The lack of consideration for cases (i) and (ii) suggests the possibility for selection bias in the published literature in this area [a point recently suggested by Hric et al. (11)]. Recent critiques of the general utility of community detection in networks (11–13) can be viewed as a side effect of confusion about the role of metadata in evaluating algorithm results. For these reasons, using metadata to assess the performance of community detection algorithms can lead to errors of interpretation, false comparisons between methods, and oversights of alternative patterns and explanations, including those that do not correlate with the known metadata.

For example, Zachary’s Karate Club (14) is a small real-world network with compelling metadata frequently used to demonstrate community detection algorithms. The network represents the observed social interactions of 34 members of a karate club. At the time of study, the club fell into a political dispute and split into two factions. These faction labels are the metadata commonly used as ground truth communities in evaluating community detection methods. However, it is worth noting at this point that Zachary’s original network and metadata differ from those commonly used for community detection (9). Links in the original network were by the different types of social interaction that Zachary observed. Zachary also recorded two metadata attributes: the political leaning of each of the members (strong, weak, or neutral support for one of the factions) and the faction they ultimately joined after the split. However, the community detection literature uses only the metadata representing the faction each node joined, often with one of the nodes mislabeled. This node (“Person number 9”) supported the president during the dispute but joined the instructor’s faction because joining the president’s faction would have involved retraining as a novice when he was only 2 weeks away from taking his black belt exam.

The division of the Karate Club nodes into factions is not the only scientifically reasonable way to partition the network. Figure 1 shows the log-likelihood landscape for a large number of two-group partitions (embedded in two dimensions for visualization) of the Karate Club, under the stochastic blockmodel (SBM) for community detection (15, 16). Partitions that are similar to each other are embedded nearby in the horizontal coordinates, meaning that the two broad peaks in the landscape represent two distinct sets of high-likelihood partitions: one centered around the faction division and one that divides the network into leaders and followers. Other common approaches to community detection (9, 17) suggest that the best divisions of this network have more than two communities (10, 18). The multiplicity and diversity of good partitions illustrate the ambiguous status of the faction metadata as a desirable target.

Fig. 1. The stochastic blockmodel log-likelihood surface for bipartitions of the Karate Club network (14).

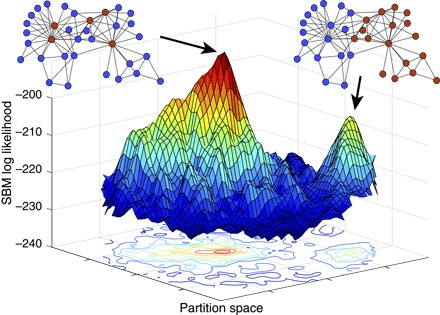
The high-dimensional space of all possible bipartitions of the network has been projected onto the x, y plane (using a method described in Supplementary Text D.4) such that points representing similar partitions are closer together. The surface shows two distinct peaks that represent scientifically reasonable partitions. The lower peak corresponds to the social group partition given by the metadata—often treated as ground truth—whereas the higher peak corresponds to a leader-follower partition.

The Karate Club network is among many examples for which standard community detection methods return communities that either subdivide the metadata partition (19) or do not correlate with the metadata at all (20, 21). More generally, most real-world networks have many good partitions, and there are many plausible ways to sort all partitions to find good ones, sometimes leading to a large number of reasonable results. Moreover, there is no consensus on which method to use on which type of network (21, 22).

In what follows, we explore both the theoretical origins of these problems and the practical means to address the confounding cases described above. To do so, we make use of a generative model perspective of community detection. In this perspective, we describe the relationship between community assignments $\mathcal{C}$ and graphs $\mathcal{G}$ via a joint distribution P($\mathcal{C}$,$\mathcal{G}$) over all possible community assignments and graphs that we may observe. We take this perspective because it provides a precise and interpretable description of the relationship between communities and network structure. Although generative models, like the SBM, describe the relationship between networks and communities directly via a mathematically explicit expression for P($\mathcal{C}$,$\mathcal{G}$), other methods for community detection nevertheless maintain an implicit relationship between network structure and community assignment. Hence, the theorems we present, as well as their implications, are more generally applicable across all methods of community detection.

In the next section, we present rigorous theoretical results with direct implications for cases (i) and (iv), whereas the remaining sections introduce two statistical methods for addressing cases (i) and (ii). These contributions do not address case (iii), when there is no structure to be found, which has been previously explored by other authors, for example, for the SBM (8, 23–27) and modularity (28, 29).

Ground truth and metadata in community detection

Community detection is an inverse problem: Using only the edges of the network as data, we aim to find the grouping or partition of the nodes that relates to how the network came to be. More formally, suppose that some data-generating process g embeds ground truth communities $\mathcal{T}$ in the patterns of links in a network $\mathcal{G}$ = g($\mathcal{T}$). Our goal is to discover those communities based only on the observed links. To do so, we write down a community detection scheme f that uses the network to find communities $\mathcal{C}$ = f($\mathcal{G}$). If we have chosen f well, then the communities $\mathcal{C}$ will be equal to the ground truth $\mathcal{T}$, and we have solved the inverse problem. Thus, the community detection problem for a single network seeks a method f* that minimizes the distance between the identified communities and the ground truth

$$\mathit{f}*=\underset{\mathit{f}}{\text{arg min}}\mathit{d}(\mathcal{T},\mathit{f}(\mathcal{G}))$$ (1)

where d is a measure of distance between partitions.

For a method f to be generally useful, it should be the minimizer for many different graphs, each with its own generative process and ground truth. Often in the community detection literature, several algorithms are tested on a range of networks to identify which performs best overall (12, 30, 31). If a universally optimal community detection method exists, then it must solve Eq. 1 for any type of generative process g and partition $\mathcal{T}$, that is

$$\exists {\mathit{f}}^{*} \mathit{s}.\mathit{t}. {\mathit{f}}^{*}={\displaystyle \underset{\mathit{f}}{\text{arg min}}}\mathit{d}(\mathcal{T},\mathit{f}(\mathrm{g}(\mathcal{T})\left)\right) \forall \{\mathrm{g},\mathcal{T}\}$$ (2)

No such universal f* community detection method can exist because the mapping from generative models g and ground truth partitions $\mathcal{T}$ to graphs $\mathcal{G}$ is not uniquely invertible due to the fact that the map is not a bijection. That is, any particular network $\mathcal{G}$ can be produced by multiple, distinct generative processes, each with its own ground truth, such that $\mathcal{G}={\mathit{g}}_1({\mathcal{T}}_1)={\mathit{g}}_2({\mathcal{T}}_2)$, with $({\mathit{g}}_1,{\mathcal{T}}_1)\ne ({\mathit{g}}_2,{\mathcal{T}}_2)$. Thus, no community detection algorithm method can uniquely solve the problem for all possible networks (Eq. 2), or even a single network (Eq. 1). This reasoning underpins the following theorem, which we state and prove in Supplementary Text C.

Theorem 1: For a fixed network $\mathcal{G}$, the solution to the ground truth community detection problem—given $\mathcal{G}$, find the $\mathcal{T}$ such that $\mathcal{G}$ = g($\mathcal{T}$)—is not unique.

Substituting metadata $\mathcal{M}$ for ground truth $\mathcal{T}$ exacerbates the situation by creating additional problems. In real networks, we do not know the ground truth or the generating process. Instead, it is common to seek a partition that matches some node metadata $\mathcal{M}$. Optimizing a community detection method to discover $\mathcal{M}$ is equivalent to finding f* such that

$${\mathit{f}}^{*}={\displaystyle \underset{\mathit{f}}{\text{arg min}}}\mathit{d}(\mathcal{M},\mathit{f}(\mathcal{G}))$$ (3)

However, this does not necessarily solve the community detection problem of Eq. 1 because we cannot guarantee that the metadata are equivalent to the unobserved ground truth, d($\mathcal{M}$,$\mathcal{T}$) = 0. Consequently, both d($\mathcal{C}$,$\mathcal{T}$) = 0 and d($\mathcal{C}$,$\mathcal{T}$) > 0 are possibilities. Thus, when we evaluate a community detection method by its ability to find a metadata partition, we confound the metadata’s correspondence to the true communities, that is, d($\mathcal{M}$,$\mathcal{T}$) [case (ii) in the previous section], and the community detection method’s ability to find true communities, that is, d($\mathcal{C}$,$\mathcal{T}$) [case (iv)]. In this way, treating metadata as ground truth simultaneously tests the metadata’s relevance and the algorithm’s performance, with no ability to differentiate between the two. For instance, when considering competing partitions of the Karate Club (Fig. 1), the leader-follower partition is the most likely partition under the SBM, yet it correlates poorly with the known metadata. On the other hand, under the degree-corrected SBM, the optimal partition is more highly correlated with the metadata (fig. S1). Based only on the performance of recovering metadata, one would conclude that the degree-corrected model is better. However, if Zachary had not provided the faction information, but instead some metadata that correlated with the degree (for example, the identities of the club’s four officers), then our conclusion might change to the regular SBM being the better model. We would arrive at a different conclusion despite the fact that the network and the underlying process that generated it remain unchanged. A similar case of dependence on a particular choice of metadata is exemplified by divisions of high school social networks using metadata of students’ grade level or race (21). Past evaluations of community detection algorithms that only measure performance by metadata recovery are thus inconclusive. It is only with synthetic data, where the generative process is known, that ground truth is knowable and performance is objectively measurable.

However, even when the generative process is known for a single network or even a set of networks, there is no best community detection method over all networks. This is because, when averaged over all possible community detection problems, every algorithm has provably identical performance, a notion that is captured in a No Free Lunch theorem for community detection, which we rigorously state and prove in Supplementary Text C and paraphrase here.

Theorem 3 (paraphrased): For the community detection problem, with accuracy measured by adjusted mutual information, the uniform average of the accuracy of any method f over all possible community detection problems is a constant that is independent of f.

This No Free Lunch theorem, based on the No Free Lunch theorems for supervised learning (32), implies that no method has an a priori advantage over any other across all possible community detection tasks. (Theorem 3 and its proof apply to clustering and partitioning methods in general, beyond community detection.) That is, for a set of cases that a particular method f_a outperforms f_b, there must exist a set of cases where f_b outperforms f_a—on average, no algorithm performs better than any other. However, this does not render community detection pointless because the theorem also implies that if the tasks of interest correspond to a restricted subset of cases (for example, finding communities in gene regulatory networks or certain kinds of groups in social networks), then there may be a method that outperforms others within the confines of that subset. In short, matching beliefs about the data-generating process g with the assumptions of the algorithm f can lead to better and more accurate results, at the cost of reduced generalizability. (See Supplementary Text C for additional discussion.)

The combined implications of the epistemological arguments in the previous section with Theorems 1 and 3 in this section do not render community detection impossible or useless, by any means. However, they do imply that efforts to find a universally best community detection algorithm are in vain and that metadata should not be used as a benchmark for evaluating or comparing the efficacy of community detection algorithms. These theorems indicate that better community detection results may stem from a better understanding of how to divide the problem space into categories of community detection tasks, eventually identifying classes of algorithms whose strengths are aligned with the requirements of a specific category.

Relating metadata and structure

From a scientific perspective, metadata labels have direct and genuine value in helping to understand complex systems. Metadata describe the nodes, whereas communities describe how nodes interact. Therefore, correspondence between metadata and communities suggests a relationship between how nodes interact and the properties of the nodes themselves. This correspondence has been used productively by researchers to assist in the inference of community structure (21), to learn the relationship between metadata and network topology (33, 34), and to explain dependencies between metadata and network structure (35).

Here, we propose two new methods to explore how metadata relate to the structure of the network when the metadata only correlate weakly with the identified communities. Both methods use the powerful tools of probabilistic models but are not restricted to any particular model of community structure. The first method is a statistical test to assess whether or not the metadata partition and network structure are related [case (i)]. The second method explores the space of network partitions to determine whether the metadata represent the same or different aspects of the network structure as the “optimal” communities inferred by a chosen model [case (ii)].

In principle, any probabilistic generative model (15, 16, 36–39) of communities in networks could be used within these methods. Here, we derive results for the popular SBM (15, 16) and its degree-corrected version (20) (alternative formulations are discussed in Supplementary Texts A and B). The SBM defines communities as sets of nodes that are stochastically equivalent. This means that the probability p_ij of a link between a pair of nodes i and j depends only on their community assignment, that is, ${\mathit{p}}_{\mathit{i}\mathit{j}}={\mathrm{\omega }}_{{\mathrm{\pi }}_{\mathit{i}},{\mathrm{\pi }}_{\mathit{j}}}$, where π_i is the community assignment for node i, and ${\mathrm{\omega }}_{{\mathrm{\pi }}_{\mathit{i}},{\mathrm{\pi }}_{\mathit{j}}}$ is the probability that a link exists between members of groups π_i and π_j. This general definition of community structure is quite flexible and allows for both assortative and disassortative community structure, as well as arbitrary mixtures thereof.

Testing for a relationship between metadata and structure

Our first method, called the blockmodel entropy significance test (BESTest), is a statistical test to determine whether the metadata partition is relevant to the network structure [case (i)], that is, if it provides a good description of the network under a given model. We quantify relevance using the entropy, which is a measure of how many bits of information it takes to record the network given both the network model and its parameters. The lower the entropy under this model, the better the metadata describe the network, whereas a higher entropy implies that the metadata and the patterns of edges in the network are relatively uncorrelated. We derive and discuss the BESTest using five different models in Supplementary Text B. Here, we describe a particularly straightforward version of this test using the SBM.

The BESTest works by first dividing a network’s nodes according to the labels of the metadata and then computing the entropy of the SBM that best describes the partitioned nodes. This entropy is then compared to a distribution of entropies using the same network but random permutations of the metadata labels, resulting in a standard P value. Specifically, we use the SBM with maximum likelihood parameters for the partition induced by the metadata, which is given by ${\displaystyle {\widehat{\mathrm{\omega }}}_{\mathit{r}\mathit{s}}}=\frac{{\mathit{m}}_{\mathit{r}\mathit{s}}}{{\mathit{n}}_{\mathit{r}}{\mathit{n}}_{\mathit{s}}}$, where m_rs is the number of links between group r and group s, and n_r is the number of nodes in group r. Then, we compute the entropy H($\mathcal{G}$;$\mathcal{M}$), which we derive and discuss in detail, along with derivations of entropies for other models, in Supplementary Text B.

The statistical significance of the entropy value H($\mathcal{G}$;$\mathcal{M}$) is obtained by comparing it to the entropy of the same network but randomly permuted metadata. Specifically, we compute a null distribution of these values, derived by calculating the entropies induced by random permutations $\{\tilde{\mathrm{\pi }}\}$ of the observed metadata values $\mathit{H}(\mathcal{G};\tilde{\mathrm{\pi }})$. This choice of null model preserves both the empirical network structure and the relative frequencies of metadata values but removes the correlation between the two. The result is a standard P value, defined as

$$\mathit{P} \text{value} = \text{Pr}[\mathit{H}(\mathcal{G};\tilde{\mathrm{\pi }})\le \mathit{H}(\mathcal{G};\mathcal{M})]$$ (4)

which can be estimated empirically by computing $\mathit{H}(\mathcal{G};\tilde{\mathrm{\pi }})$ for a large number of randomly permuted metadata vectors $\tilde{\mathrm{\pi }}$. Smaller P values indicate that the metadata provide a better description of the network, making it relatively less plausible that a random permutation of the metadata values could describe the network as well as the observed metadata. Note that P values measure statistical significance but not effect strength, meaning that a low P value does not indicate a strong correlation between the metadata and the network structure. Recently, Bianconi et al. (40) proposed a related entropy test for this task, based on a normal approximation to the null distribution under the SBM. The BESTest described here is a generalization of Bianconi et al.’s test that is both more flexible, because it can be used with any number of null models, and more accurate, because the true null distribution is substantially non-normal (fig. S5).

The BESTest is, by construction, sensitive to even low correlations between metadata and network structure. To quantify the sensitivity of this P value, we first apply it to synthetic networks with known community structure (see Supplementary Text B for a complete description of synthetic network generation). For these networks, our ability to detect relevant metadata is determined jointly by the strength of the planted communities and the correlation between metadata and communities. Figure 2 shows that for networks with strong community structure, we can reliably detect relevant metadata even for relatively low levels of correlation with the planted structure. Our method can still identify relevant metadata when the community structure is sufficiently weak that communities are provably undetectable by any community detection algorithm that relies only on the network (8). Statistical significance requires an increasing level of correlation with the underlying structure as community strength decreases; if there is no structure in the network (ϵ = 1), then any metadata partition will be correctly identified as irrelevant. Note that a low P value does not mean that the metadata provide the best description of the network, nor does it imply that we should be able to recover the metadata partition using community detection.

Fig. 2. Expected P value estimates of the blockmodel entropy significance test as the correlation ℓ between metadata and planted communities increases (each metadata label correctly reflects the planted community with probability (1 + ℓ)/2; see Supplementary Text B).

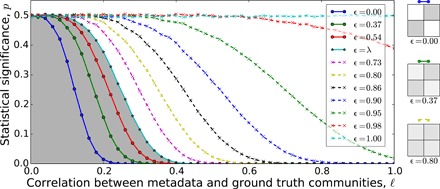
Each curve represents networks with a fixed community strength ϵ = ω_rs/ω_rr. Solid lines indicate strong community structure in the so-called detectable regime (ϵ < λ), whereas dashed lines represent weak undetectable communities (ϵ > λ) (8). Three block density diagrams visually depict ϵ values.

We now apply the BESTest to a social network of interactions within a law firm, and to biological networks representing similarities among genes in the human malaria parasite Plasmodium falciparum (see Supplementary Text D). The first set, the Lazega Lawyers networks, comprises three networks on the same set of nodes and five metadata attributes. The multiple combinations of edge and metadata types that yield highly significant P values (Table 1; see table S3 for results using additional models of community structure) indicate that each set of metadata provides nontrivial information about the structure of multiple networks and vice versa, implying that all metadata sets are relevant to the edge formation process, so none should be individually treated as ground truth.

Table 1. BESTest P values for Lazega Lawyers.

	Metadata attribute
Network	Status	Gender	Office	Practice	Law school
Friendship	<10−6	0.034	<10−6	0.033	0.134
Cowork	<10−3	0.094	<10−6	<10−6	0.922
Advice	<10−6	0.010	<10−6	<10−6	0.205

The second set, the malaria var gene networks, comprises nine networks on the same set of nodes and three sets of metadata. For each network, we find a nonsignificant P value when the metadata denote the parasite genome of origin (Table 2; see table S4 for results using additional models of community structure and additional metadata). In contrast to the Lazega Lawyers network, these genome metadata are statistically irrelevant for explaining the observed patterns of gene recombinations. This finding substantially strengthens the conclusions of Larremore et al. (41), which used a less sensitive test based on label assortativity. However, some metadata for these networks do correlate (see Supplementary Text B).

Table 2. BESTest P values for malaria var genes.

	var gene network number
	1	2	3	4	5	6	7	8	9
Genome	0.566	0.064	0.536	0.588	0.382	0.275	0.020	0.464	0.115

Diagnosing the structural aspects captured by metadata and communities

Our second method provides a direct means to diagnose whether some metadata and a network’s detected communities differ because they reveal different aspects of the network’s structure [case (ii)]. We accomplish this by extending the SBM to probe the local structure around and between the metadata partition and the detected structural communities. This extended model, which we call the neoSBM, performs community detection under a constraint in which each node is assigned one of two states, which we call blue or red, and a parameter q that governs the number of nodes in each state. If a node is blue, then its community is fixed as its metadata label, but if it is red, then its community is free to be chosen by the model. We choose q automatically within the inference step of the model by imposing a likelihood penalty in the form of a Bernoulli prior with parameter θ, which controls for the additional freedom that comes from varying q. The neoSBM’s log likelihood is $\mathcal{L}$_neoSBM = $\mathcal{L}$_SBM + qψ(θ), where ψ(θ) may be interpreted as the cost of freeing a node from its metadata label (see Supplementary Text A for the exact formulation).

By varying the cost of freeing a node, we can use the neoSBM to produce a graphical diagnostic of the interior of the space between the metadata partition and the inferred community partition. In this way, the neoSBM can shed light on how the metadata and inferred community partitions are related, beyond direct comparison of the partitions via standard techniques such as normalized mutual information or the Rand index. As the cost of freeing nodes is reduced, the neoSBM creates a path through the space of partitions from metadata to the optimal community partition and, as it does so, we monitor the improvement of the partition by the increase in SBM log likelihood. A steady increase indicates that the neoSBM is incrementally refining the metadata partition until it matches the globally optimal SBM communities. This behavior implies that the metadata and community partitions represent related aspects of the network structure. On the other hand, if the SBM likelihood remains constant for a substantial range of θ, followed by a sharp increase or jump, then it indicates that the neoSBM has moved from one local optimum to another. Multiple plateaus and jumps indicate that several local optima have been traversed, revealing that the partitions are capturing different aspects of the network’s structure.

To demonstrate the usage of the neoSBM, we examine the path between partitions for a synthetic network with four locally optimal partitions, which correspond to the four distinct peaks in the surface plot (Fig. 3A; see Supplementary Text A for a complete description of synthetic network generation). We take the partition of the lowest of these peaks as metadata and use the neoSBM to generate a path to the globally optimal partition by varying the θ parameter of the neoSBM from 0 to 1. The corresponding changes in the SBM log likelihood and the number of free nodes show three discontinuous jumps (Fig. 3C), one for each time the model encounters a new locally optimal partition.

Fig. 3. The neoSBM on synthetic data.

(A) The stochastic blockmodel likelihood surface shows four distinct peaks corresponding to a sequence of locally optimal partitions. (B) Block density diagrams depict community structure for locally optimal partitions, where darker color indicates higher probability of interaction. (C) The neoSBM, with partition 1 as the metadata partition, interpolates between partition 1 and the globally optimal stochastic blockmodel partition 4. The number of free nodes q and stochastic blockmodel log likelihood as a function of θ show three discontinuous jumps as the neoSBM traverses each of the locally optimal partitions (1 to 4).

Examining the partitions along the neoSBM’s path can provide direct insights into the relationship between metadata and network structure. Figure 3B shows the structure at each of the four traversed optima as block-wise interaction matrices ω. Each partition has a different type of large-scale structure, from core periphery to assortative patterns. In this way, when metadata do not closely match inferred communities, the neoSBM can shed light on whether and how the metadata capture similar or different aspects of network structure.

We now present an application of the neoSBM to the Lazega Lawyers data analyzed in the previous section. When initialized with the law school and office location metadata, the neoSBM produces distinct patterns of relaxation to the global optimum (Fig. 4, A and C), approaching it from opposite sides of the peak in the likelihood surface. Starting at the law school metadata, the model traverses the space of partitions to the global SBM-optimal partition without encountering any local optima. In contrast, the path from the office metadata crosses one local optimum (Fig. 4, A and B), which indicates that the law school metadata are more closely associated with the large-scale organization of the network than are the office metadata. However, both sets of metadata labels are relevant, as we determined in the previous section using the BESTest. Results for other real-world networks are included in Supplementary Text A, including generalizations of the neoSBM to other community detection methods.

Fig. 4. The neoSBM on Lazega Lawyers friendship data (52).

(A) Points of two neoSBM paths using office (red) and law school (blue) metadata partitions are shown on the stochastic blockmodel likelihood surface (grayscale to emphasize paths). (B) Block density diagrams depict community structure for metadata, (1 and 2) intermediate optimal, and (3) globally optimal partitions, where darker color indicates higher probability of interaction. (C) The neoSBM traverses two distinct paths to the global optimum (3), but only the path beginning at the office metadata partition traverses a local optimum (1), indicated by a plateau in free nodes q and log likelihood.

DISCUSSION

Treating node metadata as ground truth communities for real-world networks is commonly justified via an erroneous belief that the purpose of community detection is to recover groups that match metadata labels (11, 13, 31, 42). Consequently, metadata recovery is often used to measure community detection performance (43), and metadata are often referred to as ground truth (21, 44). However, the organization of real networks typically correlates with multiple sets of metadata, both observed and unobserved. Thus, labeling any particular set to be “ground truth” is an arbitrary and generally unjustified decision. Furthermore, when a community detection algorithm fails to identify communities that match known metadata, poor algorithm performance is indistinguishable from three alternative possibilities: (i) The metadata are irrelevant to the network structure, (ii) the metadata and communities capture different aspects of the network structure, or (iii) the network lacks group structure. Here, we have introduced two new statistical tools to directly investigate cases (i) and (ii), whereas (iii) remains well addressed by work from other authors (8, 23–29). We have also articulated multiple mathematical arguments, which conclude that treating metadata as ground truth in community detection induces both theoretical and practical problems. However, we have also shown that metadata remain useful and that a careful exploration of the relationship between node metadata and community structure can yield new insights into the network’s underlying generating process.

By searching only for communities that are highly correlated with metadata, we risk focusing only on positive correlations while overlooking other scientifically relevant organizational patterns. In some cases, disagreements between metadata labels and community detection results may, in fact, point to interesting or unexpected generative processes. For instance, in the Karate Club network, there is one node whose metadata label is not recovered by most algorithms. A close reading of Zachary’s original manuscript reveals that there is a rational explanation for this one-node difference: Although the student had more social ties to the president’s group, he chose to join the instructor’s group so as not to lose his progress toward his black belt (14). In other cases, metadata may provide a narrative that blinds us to additional structure, exemplified by a network of political blogs (1), in which liberal and conservative blogs formed two highly assortative groups. Consequently, recovery of these two groups has been used as a signal that a method produces “good” results (20). However, a deeper analysis suggests that this network is better described by subdividing these two groups, a step that reveals substantial substructure within the dominant patterns of political connectivity (19, 39). These subgroups remained overlooked in part because the metadata labels aligned closely with an attractively simple narrative.

The task of community detection is the network analog of data clustering. Whereas clustering divides a set of vectors into groups with similar attribute patterns, community detection divides a network into groups of nodes with similar connectivity patterns. However, the general problem of clustering is notoriously slippery (45) and cannot be solved universally (46). Essentially, which clustering is optimal depends on its subsequent uses, and our theoretical results here show that similar constraints hold for community detection (47). However, as with clustering, despite the lack of a universal solution, community detection remains a useful and powerful tool in the analysis of complex networks.

There is no universally accepted definition of community structure, nor should there be. Networks represent a wide variety of complex systems, from biological to social to artificial systems, and their large-scale structure may be generated by fundamentally different processes. Good community detection methods like the SBM can be powerful exploratory tools, which can uncover a wide variety of these patterns in real networks. However, as we have shown here, there is no free lunch in community detection. Instead, algorithmic biases that improve performance on one class of networks must reduce performance on others. This is a natural trade-off and suggests that good community detection algorithms come in two flavors: general algorithms that perform fairly well on a wide variety of tasks and inputs, and specialized algorithms that perform very well on a more narrow set of tasks, outperforming any general algorithm, but which perform more poorly when applied outside their preferred domain [an insight foreshadowed in past work (48)]. In some cases, it may be advantageous to use a set of carefully chosen metadata and a narrow set of corresponding networks to train specialized algorithms. Historically, most work on community detection algorithms has focused on developing general approaches. A deeper consideration of how the outputs of community detection algorithms will be subsequently used, for example, in testing scientific hypotheses, predicting missing information, or simply coarse-graining the network, may shed new light on how to design better algorithms for those specific tasks. An important direction of future work is thus to better understand both these trade-offs and the errors that can occur in domain-agnostic applications (49, 50).

A complementary approach is to incorporate the metadata into the inference process itself, which can help guide a method toward producing more useful results. The neoSBM introduced here is one such method. Others include methods that use metadata as a prior for community assignment (21) and identify relevant communities to predict missing network or metadata information (33, 34, 51). However, there is potential to go further than these domain-agnostic methods can take us. Tools that incorporate correct domain-specific knowledge about the systems they represent will provide the best lens for revealing patterns beyond what is already known and ultimately lead to important scientific breakthroughs. By rigorously probing these relationships, we can move past the false notion of metadata as ground truth and instead uncover the particular organizing principles underlying real-world networks and their metadata.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/5/e1602548/DC1

Supplementary Text

table S1. Notation used in Supplementary Text A.

table S2. Notation used in Supplementary Text B.

table S3. Lazega Lawyers: BESTest P values.

table S4. Malaria: BESTest P values for parasite origin metadata.

table S5. Malaria: BESTest P values for CP group metadata.

table S6. Malaria: BESTest P values for UPS metadata.

table S7. Notation used in the Supplementary Text.

table S8. Normalized mutual information for partitions in fig. S6.

table S9. Adjusted mutual information for partitions in fig. S6.

fig. S1. The results of the neoSBM and the degree-corrected neoSBM on the Karate Club network.

fig. S2. Results of the neoSBM on the malaria var gene network at locus one (“malaria 1”) using UPS metadata.

fig. S3. Results of the neoSBM on the malaria var gene network at locus six (“malaria 6”) using UPS metadata.

fig. S4. The block interaction matrix used to generate synthetic networks.

fig. S5. Distributions of permuted partition entropies are negatively skewed.

fig. S6. The five distinct ways to partition three nodes.

References (53–60)