Abstract
The nanometer-sized plate-like morphology of bone mineral is necessary for proper bone mechanics and physiology. However, mechanisms regulating the morphology of these mineral nanocrystals remain unclear. The dominant hypothesis attributes the size and shape regulation to organic-mineral interactions. Here, we present data supporting the hypothesis that physicochemical effects of carbonate integration within the apatite lattice control the morphology, size, and mechanics of bioapatite mineral crystals. Carbonated apatites synthesized in the absence of organic molecules presented plate-like morphologies and nanoscale crystallite dimensions. Experimentally-determined crystallite size, lattice spacing, solubility and atomic order were modified by carbonate concentration. Molecular dynamics (MD) simulations and density functional theory (DFT) calculations predicted changes in surface energy and elastic moduli with carbonate concentration. Combining these results with a scaling law predicted the experimentally observed scaling of size and energetics with carbonate concentration. The experiments and models describe a clear mechanism by which crystal dimensions are controlled by carbonate substitution. Furthermore, the results demonstrate that carbonate substitution is sufficient to drive the formation of bone-like crystallites. This new understanding points to pathways for biomimetic synthesis of novel, nanostructured biomaterials.
Keywords: biomineralization, carbonate, substitution, calcium phosphate, bone
Bone is a composite material composed of the protein type I collagen and plate-like nanocrystals of mineral. The nanometer scale of the mineral crystallites has been shown to be essential to proper bone function and physiology. The nano-size allows the crystallites to be flaw intolerant, thereby optimizing the fracture strength of the bone.[1] In addition, the large surface area of the nano-plates increases the dissolution rate, which allows the body to quickly release necessary ions in response to pathologies such as acidosis.[2–4] Although the nanocrystal size and morphology are essential to bone’s mechanical and physiological functions and must be considered in the creation of bone replacement biomaterials, the mechanism by which these properties are controlled remains unclear.
The mineral phase in bone is often described as hydroxylapatite, a natural geologically occurring OH−-containing calcium apatite. Geological hydroxylapatite forms large hexagonal prisms that derive from its hexagonal lattice structure.[5] However, the mineral in bone resembles nanometer-scale elongated plates or blades while still maintaining an internal hexagonal lattice structure.[6–12] More precisely, the nanocrystals of both bone and biomimetic apatites exhibit a complex substructure composed of (1) an apatitic, often nonstoichiometric core containing ions in apatitic (i.e., lattice) chemical environments and (2) a surface layer containing ions in non-apatitic (i.e., non-lattice) environments and surrounded by water molecules.[13] In order to explain this discrepancy between the morphology of geological (inorganic) and biological apatites, many researchers have suggested that bone’s crystallite size and shape are controlled via templating by or chemical interactions with surrounding proteins and organic moieties. [10–12, 14, 15] It has been theorized that the fibrillar structure of collagen dictates the size of the crystallites via physical confinement within its nanometer-sized gap zones.[12, 16] Others propose that proteins or other organic moieties bind to the mineral surface and control crystal growth.[10, 11, 14, 15, 17] These results seem to suggest that organic interactions are necessary for the formation of plate-like nanocrystals. However, what many of these studies fail to consider is the true composition of bioapatite.
The apatite structure is remarkably accommodating to substitutions. [18] The most common substitutions seen in bone mineral are the coupled substitution of CO32− for PO43− and Na+ for Ca2+, which lead to vacancies on the calcium and hydroxyl sites. [18–20] As a result, bone mineral is more accurately described as a carbonated, calcium- and hydroxyl-depleted apatite. The substitution of carbonate into the apatite structure can occur at one or both of two sites: in exchange for hydroxyl (OH−), defined as A-type, or for phosphate (PO43−), defined as B-type.[21] In mammalian bone, carbonate levels span 2–8 wt%, depending on species and bone location, and are predominantly of B-type substitution. [18, 22–24] Empirical observations have qualitatively shown that carbonate content in the apatite lattice affects crystallite size [25–29], solubility [8, 30, 31], and crystal mechanics [32]. These results suggest that, in addition to possible organic interactions, carbonate concentration plays an essential role in regulating bone mineral morphology. Despite the importance of carbonate substitution on crystal properties, there is no proposed mechanism for this process. We hypothesized that, in the absence of proteins or other organic substances, carbonate substitution, through its control of crystal lattice spacing, atomic order, and solubility, is sufficient to control apatite crystals’ nano-scale size, shape, and mechanics via energetic effects [8, 26, 30, 31]. This work proposes, for the first time, a direct mechanism for substitutional effects on crystallite morphology.
A protein-free solution precipitation technique was used to prepare biomimetic apatites with carbonate concentrations ranging from 1.0–17.8 wt%. The composition, gross morphology, and lattice structure were measured experimentally, providing a comprehensive analysis of biomimetic carbonated apatites. Molecular dynamics (MD) and density functional theory (DFT) calculations, which were validated through comparison to experimental results, evaluated the energetics (i.e., conservation of energy and a trade-off between surface energy and strain energy) of carbonate substitution. This work presents a situation where nanoparticles are not created via templating to enhance the chemical properties but in which the chemistry itself imposes a nanoscopic size. Organic templating is not necessary to form crystallites that exhibit physiological structures; rather, control of carbonate substitution is sufficient to precipitate crystallites with the correct nanometer-scale size and morphology. Experimental and theoretical parameters from these analyses were used in a continuum analysis to derive a proposed mechanism for how carbonate substitution controls crystallite size. Understanding this relationship provides new insight into the formation of biomimetic crystals for tissue engineering.
Methods
Synthesis of Powders
Apatite powders were made according to previously described methods [33–35] and summarized here. All water used in the synthesis was either deionized water further purified by passing through a calcium hydroxylapatite column or doubly deionized Milli-Q (18 MΩ) water in order to minimize the amount of fluoride present. Nitrogen was then bubbled through the water for several hours in order to remove dissolved carbon dioxide. Approximately 250 mL of water was placed in a large beaker and heated to the desired reaction temperature (usually 60°C or 85°C). Mixtures were stirred magnetically. In accordance with the desired degree of carbonate substitution, an appropriate amount of NaHCO3 or Na2CO3 (Acros-Organics, 99.5% or GFS Chemicals, Primary Standard) was dissolved directly in the 250 mL reactor bath, and the pH was elevated to 9.0 ± 0.5 and maintained with 0.1M NaOH (Acros, 97%). To the bath, 25 mL of a 0.15M Ca(NO3)2•4H2O (Sigma-Aldrich, 99%) and 25 mL of a 0.09M NaH2PO4 (Alrich, 98%) solution were added at a rate of 1 drop/2–4 seconds. After addition was complete, the mixture was digested at temperature for 2 hours. After the digestion, heating and stirring were discontinued. The mixture was cooled to room temperature and then filtered in a medium porosity glass filter crucible. The product was washed three times with warm water, air dried in a desiccator overnight, and then dried in a 120°C vacuum pistol or an evacuated vacuum desiccator for a minimum of 24 hours. 20 powders were made with CO32−/PO43− molar ratios ranging from 0.2 to 12 (Table 1).
Table 1.
Values characterizing the composition of the apatite samples. Carbonate values in each sample were determined by CHN-analysis, Raman, and in some cases FTIR. The degree of carbonate substitution in the precipitated apatites was controlled by the CO3/PO4 molar ratio in the precipitation solution. The crystallite dimension of the major axis was determined via visual inspection in the TEM. Stoichiometric formulas were calculated according to [59] based on the compositions acquired by ICP-MS and CHN-analysis.
| Sample | Measured CO3 wt% | CO3/PO4 in soln. | Size (TEM) | Size Std. Dev. | Stoichiometric Formula | ||
|---|---|---|---|---|---|---|---|
| CNH-Analysis | Raman | FTIR | nm | nm | |||
| OHAp | 0 | 0.0 | 71.0 | 52.1 | Ca10Na0(PO4)6(OH)2 | ||
| 1 | 1.625 | 2.5 | 1.2 | 0.0 | 133.6 | 101.3 | |
| 2 | 3.63 | 5.17 | 1.6 | 291.8 | 222.0 | Ca9.4Na0.4(PO4)5.4(CO3)0.6(OH)1.8 | |
| 3 | 4 | 4.1 | 0.2 | 171.2 | 92.2 | ||
| 4 | 4 | 5.17 | 3.3 | 0.3 | 121.0 | 138.0 | |
| 5 | 5.05 | 5.05 | 0.9 | 109.3 | 50.5 | ||
| 6 | 5.1 | 7.39 | 5.3 | 0.2 | 32.0 | 18.7 | |
| 7 | 6.25 | 6.95 | 5.5 | 0.4 | 40.6 | 17.6 | |
| 8 | 6.35 | 6.35 | 1.1 | 62.0 | 39.7 | ||
| 9 | 6.55 | 6.55 | 0.5 | 58.2 | 25.4 | ||
| 10 | 8.2 | 8.79 | 7.8 | 1.3 | 69.5 | 68.5 | |
| 11 | 9.15 | 10.2 | 2.5 | 85.2 | 78.0 | Ca8.6Na0.9(PO4)4.6(CO3)1.4(OH)1.5 | |
| 12 | 11.3 | 12.5 | 5 | 35.2 | 12.7 | Ca8.3Na1.1(PO4)4.3(CO3)1.7(OH)1.4 | |
| 13 | 11.6 | 11.6 | 3.3 | 26.5 | 12.8 | ||
| 14 | 12 | 11.92 | 10.9 | 2.9 | 54.4 | 28.5 | |
| 15 | 12.8 | 12.35 | 12.7 | 4.3 | 68.1 | 28.0 | |
| 16 | 13.3 | 13.3 | 7.0 | 35.5 | 12.5 | ||
| 17 | 13.6 | 13.5 | 4 | 22.1 | 5.7 | Ca8.0Na1.3(PO4)4(CO3)2(OH)1.3 | |
| 18 | 14 | 14 | 4.0 | 105.5 | 47.3 | ||
| 19 | 15.5 | 15.5 | 12.0 | 33.7 | 10.4 | ||
| 20 | 17.8 (22.4) |
(23.7) | 3.0 | 36.0 | 28.4 | Ca7.3Na1.8(PO4)3.3(CO3)2.7(OH)1.1 | |
Carbonate Concentration Determination
CHN analysis
In order to accurately measure the carbonate concentration of the apatite powders Carbon-HydrogenNitrogen (CHN) analysis was performed by Galbraith Labs, Knoxville, TN. Analysis was performed by combusting the samples and measuring the levels of CO2, H2O and N2 (or NOx) by either an infrared cell or a thermal conductivity detector. Levels were reported as weight percents (wt%).
Raman analysis
Raman analysis was also used to determine the carbonate concentration as well as analyze the atomic order. The Raman microprobe apparatus (HoloLab Series 5000 fiber optically coupled Raman Microscope, Kaiser Optical Systems, Inc) has been previously described. [36]. Spectra were acquired using a 532 nm laser focused to a ~1 μm spot size by an 80× objective (N.A. =0.85) at a power of 10 mW on the sample surface. Scattered light was collected in 32 4-sec acquisitions through the objective lens and transferred to a 2048-channel CCD detector. Powders were manually compressed before analysis, and spectra were obtained at six independent locations within each powder.
Spectra for 20 of the powders were analyzed as described previously. [36–39] Briefly, the spectra were background corrected in the region of 700–1200 Δcm−1 and the peaks were deconvolved into their component bands by applying a mixed Gaussian-Lorentzian peak fitting algorithm using the Grams32 software package (Galactic, Salem, NH). The relative carbonate concentration was determined from the ratio of the areas for the band associated with carbonate substituting for phosphate, i.e. 1070 Acm−1, and the v1 P-O stretch band of hydroxylapatite at 960 Δcm−1 (Fig. 1A). Weight percent of carbonate was determined from a calibration curve developed in our laboratory. In addition, full width at half maximum (FWHM) of the 960 Δcm−1 peak was used to evaluate the relative atomic order of 12 of the samples. FWHM is inversely proportional to atomic order with a larger FWHM representing a less atomically ordered structure.
Figure 1.
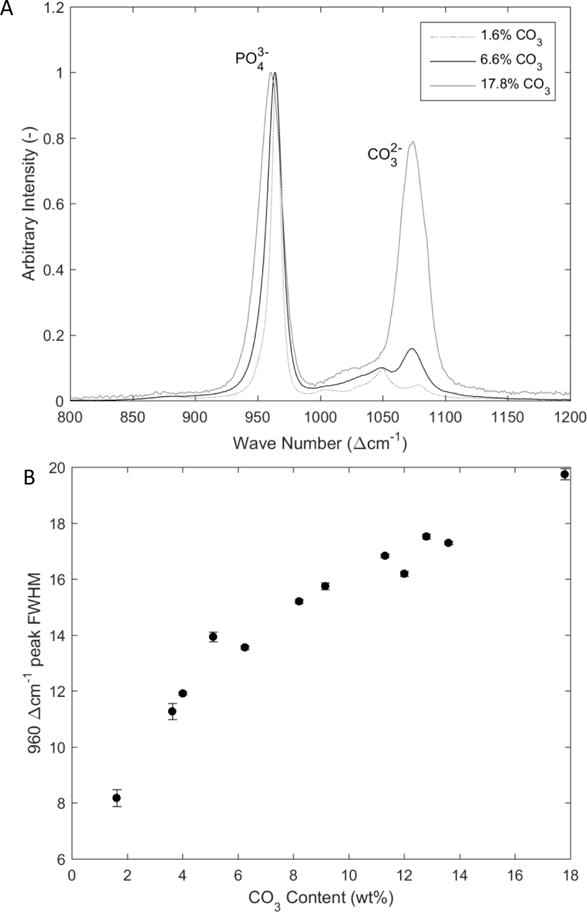
A) Raman Spectra for sample ranging from 1.6–17.8 wt% carbonate. B) Plot of the width of the 960 Δcm−1 Raman peak as a function of wt% carbonate content as determined by CHN analysis. The peak width is inversely proportional to the atomic order component of crystallinity of the sample; Raman-derived atomic order of the samples decreases with increasing carbonate substitution.
FTIR analysis
FTIR analysis was used to determine the carbonate concentration as well as the types of carbonate present in the samples. Transmission Fourier-transform infrared spectroscopy (FITR) analyses were carried out at room temperature on a Thermo Nicolet 5700 spectrometer providing spectral acquisitions in the wavenumber range 400–4000 cm−1. For each acquisition, 128 scans were recorded, with a resolution of 2 cm−1. Of particular interest in this contribution were spectral analyses in the ranges 840–910 cm−1 and 1300–1600 cm−1, where the vibrational modes v2(CO3) and v3(CO3) of carbonate ions in apatite compounds can be observed, respectively (Fig. 2). Prior to the comparison of spectral features (especially in terms of band integrated intensity), all spectra were baseline-corrected and then normalized, taking as reference (fixed to an absorbance of 1) the maximum absorption between 1033 and 1048 cm−1, depending on the samples, arising in the v3(PO4) domain of phosphate ions.
Figure 2.
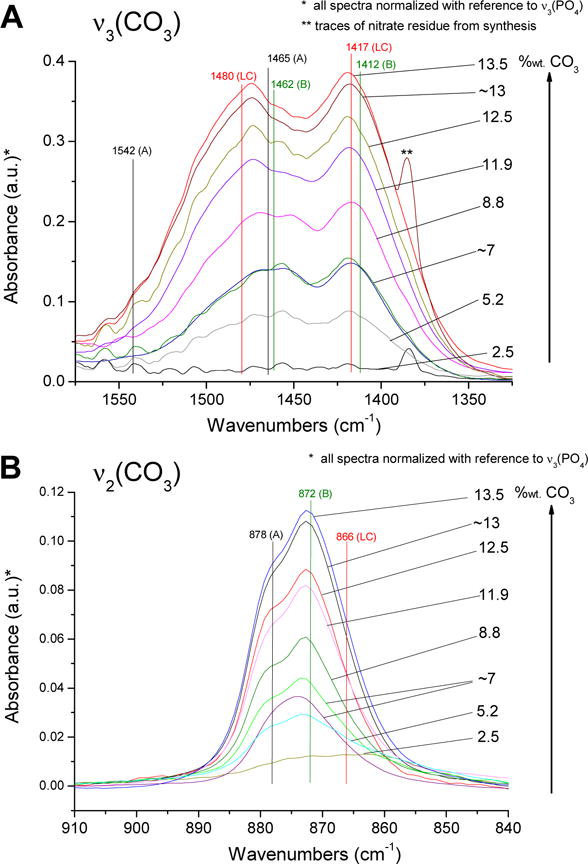
FTIR spectra in the ranges of (A) 1300–1600 cm−1 for the analysis of the carbonate vibration mode v2(CO3), and the range of (B) 840–910 cm−1 for v3(CO3). Peaks at 1462, 1412, and 872 Δcm−1 indicate B-type carbonate substitution for phosphate. Their intensity increases with increased carbonate content. Shoulders and small peaks at 1542, 1465, and 878 Δcm−1 indicate lesser levels of A-type substitution in most samples. In addition all samples exhibit the presence of surface labile carbonate (LC) by peaks at 1480, 1417, and 866 Δcm−1.
The evaluation of carbonate concentrations via FTIR was undertaken by following a recently reported methodology based on the peak area ratio between the v3(CO3) and the v1v3(PO4) contributions[40]. This ratio was indeed previously demonstrated to be directly correlated to the carbonate concentrations of carbonated apatite compounds, whether of biological or synthetic origins, as validated by direct CO2 coulometry titrations.
Solubility determination
An 80-mg sample of each of 6 carbonated apatite powders was added to 50 ml of phosphate buffer (prepared by dissolving 117.1 g NH4H2PO4 in 1 L H2O) and equilibrated for 8 days at room temperature. In each case, excess powder still remained in the beaker. Samples were then centrifuged for 10 min after which the supernatant was removed and filtered through a 22 μm syringe filter. The pH was measured for each solution. The supernatant solutions were further filtered through 0.22 μm filters (PES membranes, Environmental Express), diluted, and acidified to 1% HNO3 before analysis. Concentrations of elements were measured with inductively coupled plasma-mass spectrometry (ICP-MS, Perkin-Elmer). Laboratory blanks (1% HNO3), calibration standards, and internal standards were included for quality control. Blanks were measured before, during, and after apatite samples. Standards for making calibration curves were prepared in a range of 0.05 mg/L to 20 mg/L for major elements (Ca, Mg, Na, and K). Internal standards (20 μg/L In, Li, and Bi) were added online to all samples and standards during ICP-MS analysis. Weighted calibration curves were determined based on external standards and internal standards. The specific detection limit for each element was determined by examination of the blanks and the lowest-concentration calibration standards. Phosphate concentrations were determined by the ascorbic acid method (wavelength at 880 nm for spectrophotometer)[41].
Assuming a simplified formula for carbonated apatite of Ca10−xNa2x/3(PO4)6−x(CO3)x(OH)2−x/3, and considering 100% B-type carbonation and the absence of protonated phosphate ions, x was calculated from the analyzed concentrations of Ca2+, Na+, PO43−, and CO32− using Visual MINTEQ software. Formulas are listed in Table 1.
TEM
Small quantities of each of the 20 carbonated apatite powders were suspended in methanol and sonicated to minimize aggregation. Twenty microliters of each suspension was deposited on holey carbon TEM grids over filter paper. The grids were allowed to dry before imaging. The powders were imaged with a Hitachi H7500 (Hitachi High Technologies) equipped with a 5-megapixel AMT XR50 camera (Advanced Microscopy Techniques, Woburn, MA). All images were obtained at a beam energy of 80kV.
XRD
X-ray diffraction measurements were performed on 6 powder samples on a Bruker d8 Advanced X-ray Diffractometer with a Cu Kα tube source and a LynxEyeXE detector (Bruker, Madison, WI). Scans were performed from 20°–60° with a step size of 0.02° and an acquisition rate of 0.5 sec/step. To avoid issues with preferential orientation, the sample was rotated at rate of 15 rotations per minute. The system voltage and current were set to 40 kV and 40 mA, respectively.
Peak fitting was performed on the x-ray diffraction patterns using Diffract.Suite Topas software. Structural refinement was used to fit the (002) and (300) peaks to obtain crystal size and lattice spacing along the c- and a-axes, respectively (Fig. 3). Rietveld analysis was also performed on the entire diffractogram to obtain values of coherent domain size.
Figure 3.
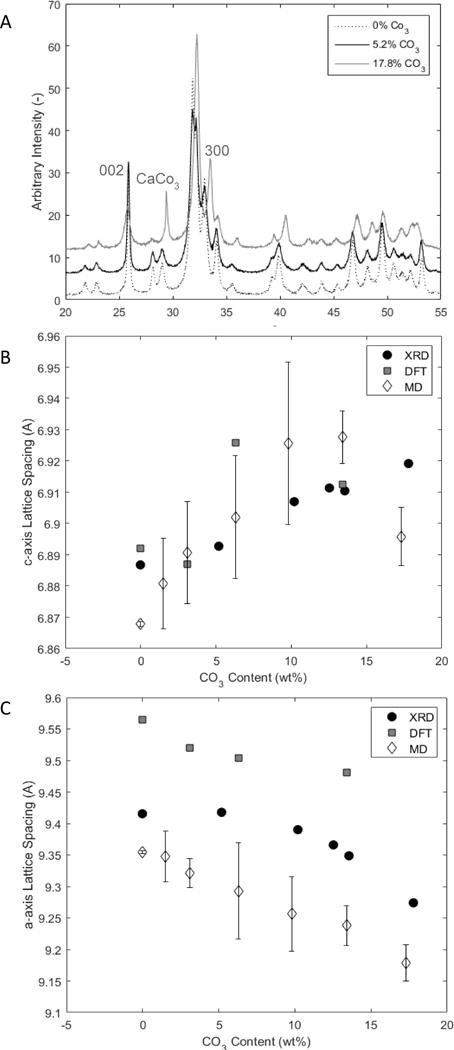
A) XRD pattern for samples containing 0, 5.2, and 17.8 wt% carbonate. The (002) and (300) peaks shift in opposite directions with increased carbonate content. These shifts represent changes in the lattice spacing. B) Lattice spacing along the c-axis as a function of carbonate content measured experimentally from the XRD pattern and theoretically via DFT and MD methods. c-axis lattice spacing increases with the addition of carbonate. C) Lattice spacing along the a-axis as a function of carbonate content measured experimentally from the XRD and theoretically via DFT and MD methods. a-axis lattice spacing decreases with the addition of carbonate.
Modeling
Molecular Simulations
An interatomic force field was used that has been empirically derived specifically for hydroxylapatite based on a variety of experimental parameters, such as the crystal structure and elastic constants, bond dissociation energies, and vibrational data on the phosphate group. [42, 43] In this force field, the non-bonded interactions are modeled by a Buckingham potential, the covalent bond by a Morse potential, and the bond-bending term by a simple harmonic function. This force field shows very good agreement with both density functional theory (DFT) calculations and experiments regarding the crystal structure, the elastic properties, and surface energies. [44–46] This potential has been developed to be compatible with existing carbonate potential and has been used to study the structure of carbonated apatites. [47] In order to reduce the computational cost of the simulations, the electronic polarizability of the oxygen atoms has not been taken into account.
All molecular dynamics simulations were performed using the LAMMPS code. [48] Buckingham and Coulomb interactions were computed with a switch function that ramps the energy and force smoothly to zero between an inner and outer cutoff of 8 Å and 10 Å respectively. The bulk and surface energy models were simulated using periodic boundary conditions and Ewald summation for long-range interactions. The strain was applied by imposing a deformation on the sample. The energies and stresses were recorded after energy minimization.
Atomistic models of apatite crystals
For computational simplification, an 88-atom orthorhombic unit cell was used Instead of the classical 44-atom hexagonal unit cell, to model stoichiometric hydroxylapatite. Hydroxylapatite crystallizes In a hexagonal lattice. However, the modeling of mechanical properties can be simplified by mathematically transforming it into an orthorhombic cell [49] (Fig. 4) (Material Studio 4.4, Accelerys, Inc.). To maintain the periodicity of the lattice In the orthorhombic description, It Is necessary to double the unit cell along the b axis. As a result, the orthorhombic unit cell Is twice as large as the hexagonal unit cell and contains 88 atoms. The Initial lattice parameters were chosen to match reported experimental measurements with the initial values a = 9.424 Å, b = 16.322 Å, c = 6.879 Å, α = β = γ = 90° [50]. The orthorhombic unit cell features characteristics almost Identical to those in the hexagonal unit cell and can include substitution. The model samples were created by replication of the unit cell in three dimensions to form a rectangular prism with initial dimensions 2a × b × 2c. All the surfaces of the samples have been structured in their charge neutral stoichiometric form [51].
Figure 4.
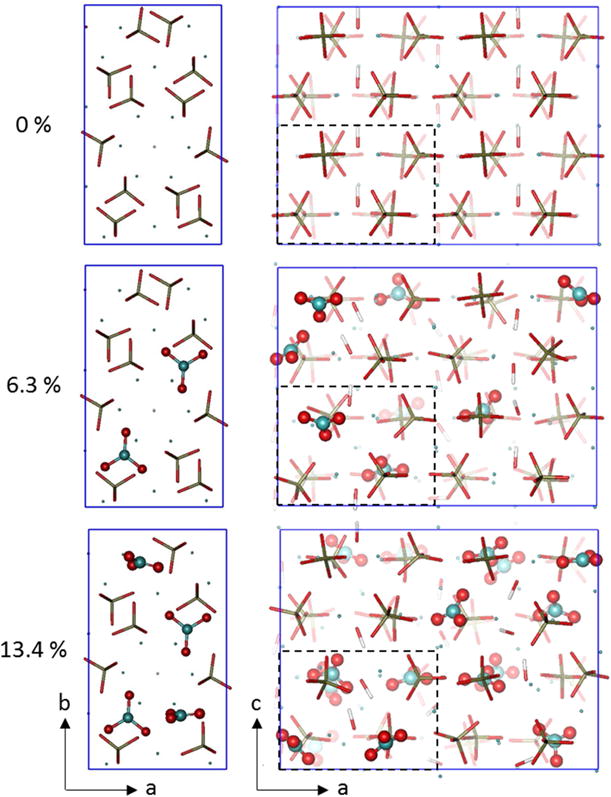
Schematic showing B-type carbonate (shown as wt%) substitution (atoms explicitly shown) for phosphate groups (only bonds shown) in the model. Apatite lattice models shown here are used for the MD and DFT calculations.
In this study, only B-type carbonate substitution, which is the dominant substitution mechanism in bone mineral and in our synthetic carbonated apatites, was investigated. Also, the protonation of some phosphate ions, leading to HPO42− ions instead of PO43−, was not considered in the calculations: the presence of divalent anions was only accounted for here by the presence of carbonate species. In order to introduce substitutions in the models, phosphate ions were randomly selected in the original structure and replaced with carbonate ions (Visual Molecular Dynamics [52]). To make the model computationally more tractable, charge neutrality was simplified by removing one calcium atom for every two carbonate substitutions to compensate for the electron loss occurring during the substitution process [44]. Thus, OH-vacancies were not considered.
The extent of substitution was chosen to span from 0–17wt%, beyond the physiological range of carbonate-substitution measured experimentally in bone apatite. [18, 22, 23] Models were created for 0, 1.5, 3.1, 6.3, 9.8, 13.4, and 17.3 wt% of carbonate substitution. The position and orientation of the carbonate ions were selected randomly to explore the influence of carbonate location on the structure properties. The substitution sites were chosen to be at least 4.5 Å apart. For each amount of substitution modelled, the properties presented here are the average of 5 simulations with different substitution distributions.
Density functional theory calculations
Density functional theory (DFT) was used to compute the lattice constants and elastic constants, of carbonate-substituted apatite and end-member hydroxylapatite. The QUANTUM ESPRESSO package was used for DFT calculations with the exchange and correlation interaction defined by PBE functional and for the electron–core interaction, ultrasoft pseudopotentials were used. [53] The energy cutoff of 60 Ry is used for plane-wave basis sets and 360 Ry for charge density. For bulk calculations a 2×1×2 k-point grid has shown convergence of energy (energy difference between two consecutive steps is smaller than 10−6 Ry), and forces are less than 30 meV/Å (10−3 Ry/Bohr). DFT calculations have been performed for 0wt%, 6wt% and 13wt% carbonate concentration on a single unit cell to determine the lattice and elastic constants. In the DFT models, the positions of the substitutions have been selected based on previous studies to minimize the total energy of the system.[44]
Elastic constants
The elastic constants were computed by fitting Hooke’s law for both stress-strain (Molecular Static) and energy-strain (DFT) relations for infinitesimal deformation. [45, 54] Six different strain modes εαβ, α,β ∈/x, y, z/ were applied with each ranging from −1.0% to 1.0% with a step of 0.2. The ground state energy versus lattice strains were plotted to obtain elastic constants corresponding to each direction x, y and z. The following equation was used for the computation of the elastic constants:
| (1) |
where is the total energy per unit volume in the samples, εij is the strain tensor and Ω is the unit cell volume of the computational model, and Etotal is the ground state unit cell energy. Due to the symmetry of the hexagonal crystals, hydroxylapatite can be considered as a transversely isotropic material and its stiffness matrix can be expressed as:
| (2) |
Surface energies
The surface energy is the excess energy associated with the creation of a free surface for a crystallite with a particular composition. To compute the surface energy, free surfaces were created by adding a 40 Å thick vacuum on each side of the sample in the direction orthogonal to the surface of interest (Fig. 4). The unit cell was duplicated 2 times in the direction orthogonal to the surfaces in order to avoid interactions between the two created surfaces. The dimensions of the sample and vacuum layer were chosen to provide a minimum distance of 10 Å between the free surfaces to avoid interaction between the formed interfaces. After relaxation of the structure, the surface energy is given by:
| (3) |
Where γ is the surface energy, ES is the energy of the sample with free surface, EB the energy of the equivalent bulk crystal, and A the free surface area. This approach was used to determine the (001) plane surface energy (not considering here the presence of a hydrated layer on the crystallites).
Scaling Laws for Crystallite Size
Scaling laws for crystallite size were generated from the first principles simulation data using the Griffith-Irwin framework and Weibull statistics. The probability of fragmentation during crystal growth dominated by extension in a single direction was taken to follow the Weibull distribution [55]:
| (4) |
where F is the probability of fragmentation as a function of the substitution-induced lattice stress (σ) for an apatite crystallite of length L and carbonate concentration C; and Lo(C), σo(C), and m(C) are material parameters that depend upon C. From data for a range of ceramics, it is reasonable to approximate m(C), the Weibull modulus as a function of carbonate concentration, as invariant with respect to C: m(C)=mo. [56] In the carbonated apatite system there is not an external applied load, but rather an internal change in lattice spacing that modifies the atomic organization and crystal energetics. This change in lattice spacing can be defined as a lattice strain, which is simply the change in spacing with carbonate concentration divided by the original spacing at 0 wt% carbonate: ε(C) = (D−Do)/Do. As for substitutional solid solution strengthening within the Hume-Rothery framework, a lattice strain of ε(C) along the length of the crystallite results in both elastic and inelastic effects on the lattice, of which we take the elastic part to be proportional to ε(C): σ = αE(C)∈(C), in which α is a constant of proportionality.
Lo(C) is chosen such that it represents the length expected to contain a single critical flaw when σ=σo(C). This choice is equivalent to arbitrarily choosing a value F= 1−1/e as the probability of fracture that defines the mean crystallite size at a certain value of C. Then,
| (5) |
It was therefore assumed that the distribution of flaw sizes does not vary with C, which follows from the assumption that m is also invariant. The scaling procedure involves identifying the parameters Lo(Co) from the experimental crystallite size data, and applying E(Co) and ε(Co) from the modelling results.
Because the Weibull parameter m can be reasonably approximated as invariant with respect to C, the distribution of critical flaws can also be approximated as such. The scaling arises from Griffith-Irwin arguments by building from the work of Freudenthal, who noted that the density nc(C) of critical flaws (size a>ac(C)) in a specimen arises from the defect density g(a) [57]:
| (6) |
| (7) |
| (8) |
Noting that, at an average fragmentation, nC(C) = 1/(AoLo(C)),
| (9) |
| (10) |
where KIc is the mode I fracture toughness. This relationship is equivalent to noting from equation (4) and the work of Dobbs et al. [58] that the size of the crystallite will be limited by the following equivalences:
| (11) |
Continuing from equation (10) and noting that where γ(C) is the surface energy:
| (12) |
| (13) |
| (14) |
All values in equation (14) can be determined from the modeling and XRD results except for m, the Weibull modulus.
Results
Synthesis of Carbonated Apatite Powders with variable Carbonate Concentrations
Twenty samples of carbonated apatite were synthesized via aqueous chemical precipitation methods.[30] Carbonate levels were controlled by changing relative proportions of carbonate- and phosphate-containing chemicals during the precipitation process. Precipitated powders of carbonated apatite were removed from solution and rinsed before analysis.
Carbonate concentrations in the apatites were measured using Carbon-Hydrogen-Nitrogen (CHN) combustion analysis, Raman spectroscopy, and Fourier Transform Infrared (FTIR) spectroscopy. CHN combustion analysis indicated that the carbonated apatite powders contained between 1.6 and 22.4 wt% carbonate, Table 1. Raman measurements showed similar values in carbonate concentrations. Differences between the Raman and the CHN analyses were more pronounced in samples with low carbonate levels.
X-ray diffraction analysis of sample 20, which appeared to contain 22.4 wt% carbonate, indicated the presence of calcite in the powder sample. Using the carbonate concentrations determined from the CHN analysis and the simplified formula for carbonated apatite as well as the level of calcite determined from Rietveld analysis of the XRD pattern, it was calculated that the carbonated apatite lattice contained 17.8 wt% carbonate.
Types of Carbonate Substitutions in the Carbonated Apatite Powders
FTIR analyses were carried out on 7 of the carbonated apatite samples, with a focus on examining vibrational contributions of carbonate. Two spectral domains were targeted: the range of 840–910 cm−1 for the analysis of the carbonate vibration mode v2(CO3), and the range of 1300–1600 cm−1 for v3(CO3).
The evolution of the v3(CO3) domain for the different samples analyzed showed a general trend of increasing area under the carbonate peaks in this interval, with increasing overall carbonate concentration in apatite (Figure 1A). In carbonated apatite systems, this spectral region is difficult to decompose, as each type of carbonate species (A-type, B-type, or labile surface carbonates denoted LC) roughly gives rise to two main contributions that are overlapping [60]. The general FTIR profiles in this region, however, suggest that more than one type/site of carbonate ion was present in all samples, although in variable amounts. In particular, B-type carbonate appeared to be predominant ; the proportion of A-type carbonate was significantly lower than that of B-type; LC-type (labile non-apatitic surface) carbonate occurred in much lower but non-negligible concentration.
The analysis of the v2(CO3) band (Fig. 2B), with the detection of several shoulders, confirmed the existence of several types of carbonate environments in these samples, as was concluded from the observation of the v3(CO3) domain. However, examination of the v2(CO3) contribution in apatite samples was also complicated by the superimposition of the P-OH vibration band of HPO42− ions, around 870–875 cm−1, as a broad halo at the bottom of the band. B-type carbonate, and to a lesser extent A-type, were clearly identifiable in the spectra, with v2(CO3) bands around 872 and 878 cm−1, respectively. Also, the band relevant to labile surface carbonate species can give rise to a large contribution; its position is difficult to assess exactly but is usually considered close to the value (around 866 cm−1) noted for amorphous carbonate-containing calcium phosphate.[60] As a general trend, the overall area under the peaks in this spectral region increased with the total carbonate concentration of the apatite samples. The reported carbonate values in Table 1 for FTIR are a sum of all of the measured carbonate species.
Determination of Crystallite Size
The size of the crystallites within the carbonated apatite powders was measured manually from transmission electron microscopy (TEM) images of the dispersed powders. In all cases, the crystallites that composed the apatite powders appeared to be flat plates (Fig. 5). Large crystallites looked blade-like, with clearly defined edges and faceting; however, as the crystals became more carbonated and smaller, the crystallite shape became less well defined and facets were harder to identify. The long axis of the plates decreased with increasing carbonate substitution, from 291.8 ± 222 nm to 22.1 ± 5.7 nm for an increase in carbonate concentration of 10 wt% (Table 1). The variability in the crystallites’ long dimension also decreased with increasing carbonate substitution.
Figure 5.

TEM images of three carbonated apatites containing 1.6%, 6.6%, and 17.8 % carbonate by weight. Right hand images are 4× enlargements of indicated areas on the left… As carbonate content increases, the particles tend be smaller and have a greater propensity for aggregation. Scale bars are 500 nm for the left column, 100 nm for the right column.
Strain and Atomic order
XRD was performed on 6 representative samples to obtain information about how lattice parameters of the carbonated apatite crystals were modified with increased carbonate content. XRD patterns indicated that all the samples were solely carbonated apatite, except for the sample containing 22.4 wt% total carbonate, which also exhibited small calcite peaks in XRD patterns and Raman spectra. As explained above, this calcite was accounted for and a true lattice-incorporated carbonate concentration of 17.8 wt% was calculated for this sample. D-spacing values calculated from the peak center for the (002) and (300) peaks indicated a 0.5% increase in lattice spacing along the c-axis (6.887 to 6.919 Å) and a decrease of 1.5% along the a-axis (9.417 to 9.274 Å) as the carbonate value increased from 1 to 17.8 wt% (Fig. 3). With that same increase in carbonate, the coherent domain size, defined as the distance between grain boundaries or significant defects within the crystallites, along the c-axis decreased from 49.8 to 16.3 nm, representing a 67% decrease in domain size. The aspect ratio c:a of the coherent domains also decreased from 3.4 to 0.63 with the same change in carbonate.
The FWHM of the 960 Δcm−1 Raman band, which is inversely proportional to the degree of atomic order or atomic order of the sample, increased with increasing carbonate concentration. The increase was not linear with respect to wt% CO3, but rather exhibited a decrease in slope with increasing carbonate level (Fig. 1).
Modeling of Carbonated Apatite
Molecular statics and molecular dynamics (MD) methods as well as density functional theory (DFT) were used to predict the lattice, elastic and surface energy values of hydroxylapatite and carbonate-substituted apatite. These methods were applied to a geometrically simplified orthorhombic model of apatite, which actually is crystallographically hexagonal (Fig. 4). Since DFT calculations are computationally expensive, DFT was used to validate the MD predictions of elastic and lattice constants for the 0 wt%, 6 wt% and 13 wt% cases. Below, comparisons of both simulation and experimental results are discussed.
Modeled lattice constants and strain
The evolution of the modeled lattice parameters, as a function of carbonate concentration, is presented in Fig. 3B–C. Both DFT and MD results were in good agreement with experimental analyses. Introducing carbonate ions into hydroxylapatite led to a significant decrease in both a and b lattice constants, indicating a decrease in a in the true hexagonal unit cell. The transverse lattice parameters a and b decreased linearly with the amount of substitution, and the lattice strain rose to 1.5% for 13 wt% substitution according to the simulation results (Fig. 3C). In contrast, the lattice parameter along the crystal c-axis increased linearly with carbonate substitution. The lattice strain in the c-direction was more moderate than in the a- and b-directions, reaching 0.5 % for 13 wt% substitution (Fig. 3B). The modeling results showed that the lattice strain along the c-axis was more sensitive than along the a-axis to the location of the substitution sites in the crystal structure.
Elastic moduli
Simulations indicated that carbonate substitution changes the mechanical properties of bone at the nanoscale, i.e., at the crystallite level. The elastic constants of end-member (non-carbonated) hydroxylapatite computed using both DFT and MD (Table 2 and in Fig. 6) were in close agreement with previous simulations [45, 50] and experiments [61]. The simulations predicted a decrease in moduli with increasing carbonate substitution, with significant differences for the constants C33, C13, and C44. These values decreased almost linearly as a function of carbonate concentration. In both the MD and DFT calculations, the transversely isotropic behavior of the crystal was well conserved, as would be expected in the true hexagonal apatite crystal (Table 2).
Figure 6.
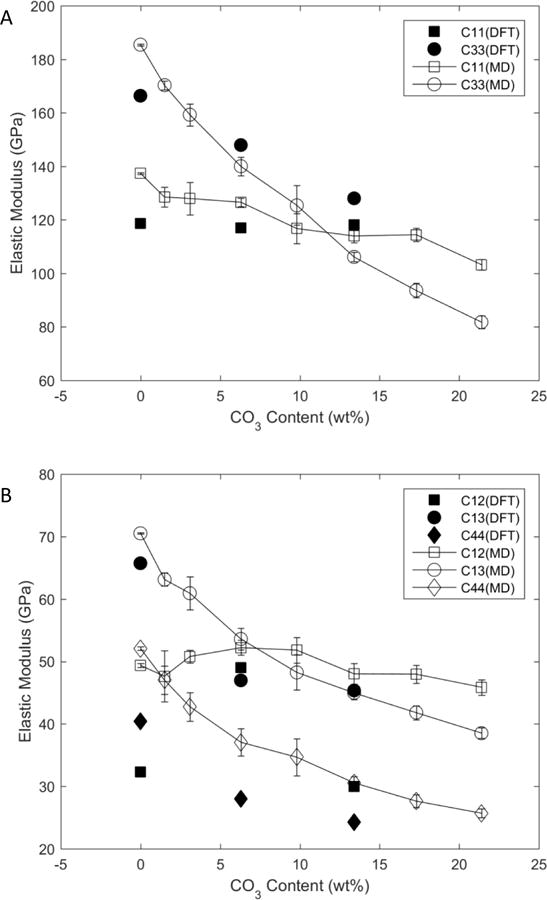
Elastic constants computed with both DFT and Molecular Statics for A) C11 and C33 and B) C12, C13, and C44. The results computed using the two methods show good agreement. Except for C12, all elastic modulus constants decrease significantly with increasing carbonate content in the apatite structure.
Table 2.
Elastic moduli and lattice parameters for pure hydroxylapatite and for 6 and 13.4 wt% carbonated hydroxylapatite computed using both MD and DFT. The elastic constants (Cij), the bulk modulus (B), and the elastic modulus (E) are expressed in GPa; the lattice parameters (a, b, c) are in Å, and the surface energies (γ) are in J/m2. Experimental data from [50, 61, 62].
| 0 wt% CO3 | 6 wt% CO3 | 13.4 wt% CO3 | |||||
|---|---|---|---|---|---|---|---|
| MD | DFT | Experimental | MD | DFT | MD | DFT | |
| Elastic Constants (GPa) | |||||||
| C11 | 137.4±0.3 | 118.58 | 137 | 126.6±1.5 | 117.63 | 114.0±2.5 | 118.21 |
| C22 | 138.2±0.9 | – | – | 124.5±2.6 | – | 117.0±1.5 | – |
| C33 | 185.4±0.3 | 166.38 | 172 | 140.0±3.4 | 148.18 | 106.1 ±1.7 | 128.02 |
| C12 | 49.4±0.3 | 32.27 | 43 | 52.2±1.2 | 49.28 | 48.0±1.7 | 29.95 |
| C13 | 70.5±0.1 | 65.73 | 55 | 53.6±1.7 | 47.39 | 45.0±1.1 | 45.35 |
| C23 | 70.7±0.3 | – | – | 52.8±2.2 | – | 43.6±1.0 | – |
| C44 | 52.1 ±0.1 | 40.4 | – | 37.1 ±1.9 | 28.49 | 30.6±0.9 | 24.26 |
| C55 | 51.4±0.1 | – | – | 37.5±1.8 | – | 30.0±0.9 | – |
| C66 | 44.3±0.1 | – | – | 35.4±1.4 | – | 33.0±0.7 | – |
| Moduli (GPa) | |||||||
| B | 91.7±0.2 | 77.9 | 89 | 78.5±1.4 | 74.3 | 67.5±2.6 | 67 |
| E | 120.9±0.1 | 103.2 | 114 | 96.8±2.1 | 87.7 | 82.8±3.8 | 86.2 |
| Lattice Parameters (A) | |||||||
| a | 9.36±0.00 | 9.56 | 9.42 | 9.29±0.08 | 9.5 | 9.24±0.11 | 9.48 |
| b | 16.19±0.00 | 16.56 | 16.31 | 16.09±0.01 | 16.43 | 15.92±0.11 | 16.33 |
| c | 6.87±0.00 | 6.89 | 6.88 | 6.9±0.04 | 6.93 | 6.93±0.11 | 6.91 |
| Surface Energy (J/m2) | |||||||
| γ001 | 1.04±0.00 | – | – | 0.75±0.04 | – | 0.54±0.03 | – |
Surface energy considerations
The computed surface energy value for the (001) surface using MD is given in Table 2. Introducing CO32− into the crystal lattice led to a decrease in the surface energy for the (001) surface. For example, the computed surface energy value for the (001) surface decreased from γ = 1.04 J/m2 for pure hydroxylapatite to γ = 0.53 J/m2 for a sample containing 13 wt% of substituted carbonate (Table 2). This surface energy evaluation corresponds to an idealized estimate, not considering the presence of a non-apatitic layer on the surface of the nanocrystals. Although this estimate is not fully representative of the nanocrystals’ behavior, it provides insights into how the presence of carbonate ions in the crystalline core may influence the surface energies of a crystallite.
Discussion
The mineral in bone exhibits a nanometer-scale size and plate-like morphology. The nanometer size plays an essential role in bone mechanics allowing the mineral crystallites to be flaw insensitive, thereby increasing bone strength[1]. In addition, the high surface area of the nanocrystals allows for effective dissolution to regulate body pH.[2, 3] Although the importance of the mineral nano-morphology has been established, the mechanisms describing nano-crystal formation, size-control, morphology, and mechanics remain unclear despite extensive study. [22, 25, 26, 30, 63, 64] Here, wide-ranging carbonate concentrations were examined experimentally to establish relationships between carbonate concentration and crystallite size, crystallite shape, and lattice spacing. In addition, MD and DFT modeling approaches successfully interpreted the experimental results. The comprehensive approach of combining experiment with modelling allowed us to define the relationships between carbonate substitution and bioapatite crystal properties in the absence of protein control. Understanding the precipitation of mineral nanocrystals in an in vitro system will help to elucidate physicochemically controlled mineralization mechanisms in bone tissues and provide unique information for tailoring mineral properties in tissue engineering systems.
Successful creation of nano-crystalline bone-mineral analogues was accomplished by aqueous precipitation methods at well below 100 °C. CNH-combustion analysis, Raman spectroscopy, and FTIR spectroscopy showed that the suite of apatite samples under analysis contained carbonate levels from 1.6 to 17.8 wt%, which includes and extends beyond the physiological values of 2–8 wt% CO32− in mammalian bone mineral. [18, 22, 23] Both biological and synthetic precipitation techniques result in some amount of carbonate deposition on the surface of the crystallites, i.e., not integrated into the lattice structure of the nanocrystals, known as labile carbonate.[65] Within the lattice, CO32− can substitute in place of OH− (A-type substitution), PO43− (B-type substitution), or both.[21] FTIR analysis of the samples indicated that the carbonate was indeed in the lattice and predominantly incorporated via B-type substitution (with labile species in a non-negligible amount), as shown in Fig. 2. In all tested samples, there were also peak shoulders indicative of lesser amounts of A-type substitution.
Incorporation of the carbonate into the crystal lattice resulted in specific modifications of the apatite lattice structure. When carbonate substitutes for hydroxyl, the a-axis lattice spacing increases. [66] Conversely, B-type substitution for PO43− causes the a-axis spacing to decrease and the c-axis spacing to increase. [18, 67–69] Lattice spacing values measured via XRD for the carbonated apatite powders showed that, for all of the apatites, the c-axis spacing increased while the a-axis spacing decreased with increasing carbonate concentrations (Fig. 3), indicative of predominant B-type substitution, the substitution type most commonly seen in bone.[24] Analysis of the composition and lattice structure of the apatite crystals confirms that the aqueous precipitation technique presented here created some carbonated calcium apatites similar to those found in bone.
Examination of the TEM images indicated that the apatites exhibited decreased crystallite size with an increase in carbonate (Fig. 5). A carbonate-related decrease in crystallite size has been reported previously in the literature. [8, 25, 27–29, 70] At carbonate concentrations below approximately 10 wt% the maximum crystallite dimension decreased rapidly from values nearing 1 μm to tens of nanometers. Above 10 wt% CO3− the crystallite size plateaued at around 30 nm (Table 1 and Fig. 7). Although there is no distinct shift in lattice spacing at this composition, a drastic change in the OH− resonance upon approach to 8 wt% carbonate substitution has been previously observed via NMR.[29] Coherent domain size, the average distance between grain boundaries (or large defects in a crystalline structure), was measured via examination of the width of the XRD peaks and application of Scherrer’s equation.[71] Coherent domain size was smaller than the TEM -visualized crystallite size. This apparent inconsistency indicates that the visualized crystallites were polycrystalline.[72] The aspect ratio of both the crystallites and the coherent domains within them also decreased according to both the TEM images and XRD patterns, as seen previously [70]. This suggests that the relative growth rates along the dominant axes were in part controlled by the addition of carbonate. Carbonate concentration seems to be a major controller of crystallite size, maintaining the bone-like mineral in a nanometer size range that most benefits the bone mechanics and physiology.
Figure 7.
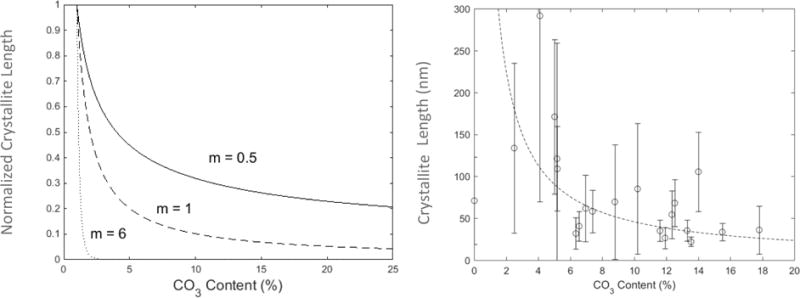
A) Normalized crystallite length vs. carbonate content as calculated from the modified Weibull analysis. Crystallite length exhibits a rapid decrease at low carbonate levels, which plateaus at higher carbonate levels, where the slope and endpoint of the drop are controlled by the Weibull modulus (m). B) Assuming a starting crystallite length at a CO3 concentration of 0wt% of 400 nm, the calculated variation in crystallite sizes as a function of carbonate content matches well with the experimental data when m=1.
The morphology of the apatites was also distinctly affected by carbonate concentration (Fig. 5). The shape of biological and biomimetic apatites has been described as plate-like [7–9], needle-like [9, 26, 27], elongated drop-like [26], rod-like [8, 25], and spheroidal [8, 27]. Variations in the size and shape of crystallites are recognized to be a function of their composition and formation temperature. [8, 9, 25–27, 63] The powders in this study exhibited plate-like morphologies, in which two dimensions appeared much larger than the third, at all carbonate levels. At low levels of carbonate, the crystallites were larger and blade-like, with visibly straight edges. As carbonate levels increased, the edges became less linear and more uneven. It has been suggested that the loss of obvious faceting on the crystallites may be caused by a decrease in atomic order associated with carbonate incorporation.[8] This proposal is supported by our experimental results showing a decrease in both faceting and atomic order (Fig. 1 and 5) with an increase in carbonate concentration. In the range of physiological carbonate concentrations for mammalian bone, [18, 22, 23] the crystallite length (~50–100 nm) and plate like morphology are similar to the mineral sizes and shapes generally seen in bone [72].
Although the mechanisms for mineralization of the collagen matrix in bone are poorly understood, both collagenous and non-collagenous proteins have been intimated as responsible for the plate-like nano-scale morphology of the apatite crystallites.[10–12, 14] Collagen molecules self-assemble into well-organized fibrils that exhibit periodic gap and overlap zones every 67 nm. [73, 74] It has been suggested that collagen residues or acidic non-collagenous proteins promote mineralization in the gap zones by either physically or chemically constraining crystal growth into nanometer scale plates. [10, 75–78] However, our results indicate that there is no need for collagen templating or interference from other organic moieties to produce crystallites that exhibit physiological morphologies and nanometer sizes; instead, controlling carbonate concentrations is sufficient to precipitate such crystallites.
Comparison of the experimental XRD values with the DFT and MD models demonstrated that the models, which assumed 100% B-type substitution, were successful in predicting changes in lattice spacing with increased carbonate concentration (Fig 3B–C). The theoretically derived values, especially in the MD simulations, were overestimates of the experimentally measured changes in lattice spacing. This discrepancy may be a result of mixed A- and B-type substitutions in the powders or the release of lattice strain by additional substitutions, such as the incorporation of Na as a substitute for Ca, which was not accounted for in the models presented here. ICP-MS analyses indicated that there was significant sodium substitution in the structure, which increased with carbonate incorporation, as seen in bone mineral [18–20]. Despite the models’ limitations, their success in predicting the lattice parameters of the carbonated apatites makes them credible for further investigation of the crystal properties.
The models were also used to calculate the mechanical properties and theoretical surface energies of the crystals, which are difficult to obtain experimentally. The model results showed that the elastic modulus of the crystals, i.e., their resistance to elastic deformation, decreased with increasing carbonate substitution. These results are in agreement with previous work that has shown that biological bone apatites, which contain carbonate, have a lower modulus compared to carbonate-poor geological apatites [79, 80]. If bone is considered to be a composite of mineral and collagen, changes to the mineral stiffness and fracture strength due to composition and size effects, as seen here, will have significant consequences for the overall bone mechanics.
The idealized estimated surface energy of the crystals (especially on the (001) face), not considering the presence of a non-apatitic surface layer on the nanocrystals, also decreased significantly as carbonate incorporation increased. A decrease in surface energy will promote the formation of nanocrystals with high surface areas and low volumes. The trends in lattice strain, modulus, and surface/interfacial energy all indicate that the substitution of carbonate into the apatite structure results in important modifications to the crystal energetics.
Beyond simply correlating the changes in crystal energetics and size, a model was developed to elucidate the mechanistic relationship between these two factors. Estimation of crystallite size from first-principles analysis is a well-known challenge due to the number of atoms that must be considered [81]. A scaling law was developed using the Griffith-Irwin framework and Weibull statistics [82] to relate crystal energetics, including surface energy and the elastic parts of the lattice strain, to the experimentally measured crystallite size. As described in the methods section, the Weibull-type scaling law relating the probability F that a growing crystal with carbonate concentration C will fragment before reaching length L or elastic stress σ:
| (4) |
where Lo(C) and σo(C) are normalization parameters, and m is the Weibull modulus, a material parameter that is related to the energetics of surface formation and the distribution of flaws in a material; for a nano-ceramic, a Weibull modulus on the order of 1 is expected. As appropriate for brittle materials that fracture at critical defects, this scaling law predicts an increased probability of failure with increasing crystallite volume, which is associated with an increased probability that the crystallite houses a critical defect. The statistical distribution of defect sizes was held invariant with respect to C; therefore, as described in the methods section, m was also held invariant. This enabled us to test the hypothesis that the change in the crystal energetics due to carbonate substitution controls the crystallite size.
Adapting the Weibull relationship for elastic strain of the crystal lattice due to atomic substitution and applying Griffith-Irwin energetic arguments, the scaling relationship between carbonate content and crystallite size as related to crystal energetics is:
| (14) |
where E is the Young’s modulus, γ is the idealized surface energy on the growing crystal face, and ε is the lattice strain. All values on the right side of this equation can be determined from the modelling and XRD results except for m, the Weibull modulus. For all values of m, crystallite length decreased nonlinearly with carbonate concentration, with a rapid drop off at small carbonate concentrations followed by a plateau (Figure 7A). The smaller the m value the steeper the drop in size towards an asymptote. As expected for a ceramic of this character, m ≈ 1 provided a good fit to the experimentally-determined trends for crystallite size vs. carbonate concentration (Figure 7B); supporting our hypothesis that carbonate content controls the nanometer-scale crystallite size.
A necessary consideration was the possible effect of differences in the saturation state of the solutions from which apatites with increasing carbonate concentration were precipitated. The effect of saturation on the differences in crystallite size was investigated by measuring the solubility of individual samples. The reasoning was that differences in solubility at a fixed temperature could lead to variations in the degree of supersaturation given the constancy of calcium and phosphate in the synthesis solutions. Differences in the degree of supersaturation could in turn cause changes in nucleation rate from sample to sample. Solubility products, Ksp, were measured from the ICP-MS results. Ksp values increased from 6×10−115 to 5×10−103 for apatite containing 3.6 to 17.8 wt% carbonate, respectively (Fig S1). Although this is a large increase in solubility, it is unclear what effects this difference would have on the crystal nucleation and growth rate, since many factors, including the initial crystal shape and kinetic coefficient, are unknown. In addition, it is possible that the increase in solubility with increasing carbonate is not related to the crystallite size, but rather to the change in crystal energetics. It has been shown that the solubility of hydroxylapatite powders is more closely related to the degree of atomic order of the crystallite than to the crystallite size. [83] Furthermore, the presence of a non-apatitic surface layer is expected to modulate solubility behaviors. [60] In the samples examined here, the degree of atomic order of the samples was shown to decrease with increasing carbonate substitution. The carbonate-induced change in lattice structure (XRD) and atomic ordering (Raman), and therefore the crystal energetics, was likely the most important contributor to the change in solubility. [83]
Conclusions
Through aqueous precipitation methods, biomimetic apatite nanocrystals were synthesized with carbonate concentrations from 1 to 17.8 wt%. The carbonate was present predominantly in B-type substitution for phosphate, as found in natural bone mineral. The morphology of the crystallites was plate-like and exhibited decreasing size, aspect ratio, and faceting with increasing carbonate concentration, Fig. 8. These modifications to the morphology appear to be caused by a change in crystal energetics, including surface energies, as seen by the change in atomic order and lattice spacing with carbonate incorporation. In the range of physiological carbonate levels, 2–8 wt% CO3, the crystallites exhibited morphologies similar to those seen in natural bone mineral. Organic (e.g., proteins, citrates) templating was not necessary for the formation of bone-like apatite nanocrystals. Instead, carbonate substitution within the physiological range was sufficient for the production of crystallites with the nano-scale size, shape, and composition under the conditions presented here. MD and DFT models of B-type substituted apatite were able to accurately predict relative changes in the lattice spacing of the crystals as well as in the compliance and theoretical surface energy of the apatites caused by carbonate incorporation. For the first time, a mechanism for how substitution controls morphology was proposed via a modified Weibull analysis. The resulting normalized size vs. carbonate concentration predictions successfully replicated the experimentally measured values. These results strongly suggest carbonation of apatites plays a critical role in controlling crystal energetics and thus the nanometer size of crystallites, which are essential to maintain proper bone mechanics and physiology. With the current focus on tissue engineering and development of biomimetic materials, this study provides a better comprehension of the processes that underlie compositional control of size and shape of crystalline particles. Such understanding can enable the tailoring of crystallite size at the nanometer scale by modification of composition.
Figure 8.
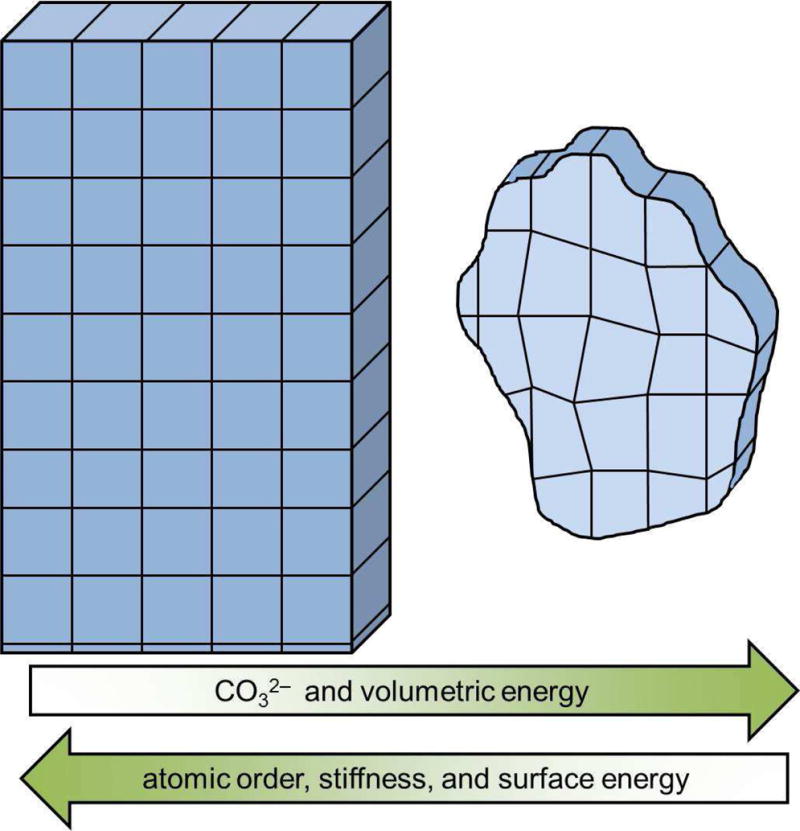
Schematic showing the changes in crystal morphology and energetics as a function of carbonate concentration. At low carbonate concentrations the bioapatite crystals are long faceted blades with lattice spacing close to that of geological hydroxylapatite. However, carbonate incorporation into the lattice changes the lattice parameters and decreases the atomic order, coherent domain size, and surface energy. This results in a decrease in crystal size, faceting, stiffness and aspect ratio.
Supplementary Material
Figure S1: Measured solubility for 5 experimental samples, showing that the solubility increases as the carbonate content increases. This is likely caused by a decrease in the atomic order of the samples.
Acknowledgments
The authors would like to acknowledge Prof. Daniel Giammar at Washington University who performed all of the ICP-MS experiments. This project was funded by the National Institute of Health (NIH) R01 EB016422 and R01 AR057836. Dr. Deymier was funded in part by the National Space Biomedical Research Institute (NSBRI) NSBRI-RFA-13-01 Postdoctoral First Fellow Award. Arun Nair would like to acknowledge support from Department of Mechanical Engineering, University Arkansas. This work was supported in part by the National Science Foundation under the grants ARI#0963249, MRI#0959124 and EPS#0918970, and a grant from Arkansas Science and Technology Authority, managed by Arkansas High Performance Computing Center.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Gao HJ, Ji BH, Jäger IL, Artz E, Fratzl P. Materials become insensitive to flaws at nanoscale: lessons from nature. PNAS. 2003;100(10):5597–5600. doi: 10.1073/pnas.0631609100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bushinsky DA, Lam BC, Nespeca R, Sessler NE, Grynpas MD. Decreased bone carbonate content in response to metabolic, but not respiratory, acidosis. Am J Physiol. 1993;265(4 Pt 2):F530–6. doi: 10.1152/ajprenal.1993.265.4.F530. [DOI] [PubMed] [Google Scholar]
- 3.Hankermeyer CR, Ohashi KL, Delaney DC, Ross J, Constantz BR. Dissolution rates of carbonated hydroxyapatite in hydrochloric acid. Biomaterials. 2002;23(3):743–750. doi: 10.1016/s0142-9612(01)00179-x. [DOI] [PubMed] [Google Scholar]
- 4.Gross KA, Berndt CC. Biomedical Application of Apatites. Reviews in Mineralogy and Geochemistry. 2002;48(1):631–672. [Google Scholar]
- 5.Ropp RC. Encyclopedia of the alkaline earth compounds. Elsevier; Oxford UK: 2013. [Google Scholar]
- 6.Fernandez-Moran J, Engstrom A. Electron microscopy and x-ray diffraction of bone. Biochim Biophys Acta. 1957;23:260–264. doi: 10.1016/0006-3002(57)90327-x. [DOI] [PubMed] [Google Scholar]
- 7.Weiner S, Wagner HD. The material bone: Structure mechanical function relations. Annu Rev Mater Sci. 1998;28:271–298. [Google Scholar]
- 8.Okazaki M, Moriwaki Y, Aoba T, Doi Y, Takahashi J. Solubility behavior of CO3 apatites in relation to crystallinity. Caries Res. 1981;15(6):477–83. doi: 10.1159/000260555. [DOI] [PubMed] [Google Scholar]
- 9.Liao S, Watari F, Xu G, Ngiam M, Ramakrishna S, Chan CK. Morphological effects of variant carbonates in biomimetic hydroxyapatite. Materials Letters. 2007;61(17):3624–3628. [Google Scholar]
- 10.Wang Z, Xu Z, Zhao W, Sahai N. A potential mechanism for amino acid-controlled crystal growth of hydroxyapatite. Journal of Materials Chemistry B. 2015;3(47):9157–9167. doi: 10.1039/c5tb01036e. [DOI] [PubMed] [Google Scholar]
- 11.Gu L-s, Kim YK, Liu Y, Takahashi K, Arun S, Wimmer CE, Osorio R, Ling J-q, Looney SW, Pashley DH, Tay FR. Immobilization of a phosphonated analog of matrix phosphoproteins within cross-linked collagen as a templating mechanism for biomimetic mineralization. Acta Biomater. 2011;7(1):268–277. doi: 10.1016/j.actbio.2010.07.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tomoaia G, Pasca RD. On the Collagen Mineralization. A Review. Clujul Medical. 2015;88(1):15–22. doi: 10.15386/cjmed-359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rey C, Combes C, Drouet C, Cazalbou S, Grossin D, Brouillet F, Sarda S. Surface properties of biomimetic nanocrystalline apatites; applications in biomaterials. Progress in Crystal Growth and Characterization of Materials. 2014;60(3–4):63–73. [Google Scholar]
- 14.Delgado-López JM, Frison R, Cervellino A, Gómez-Morales J, Guagliardi A, Masciocchi N. Crystal Size, Morphology, and Growth Mechanism in Bio-Inspired Apatite Nanocrystals. Advanced Functional Materials. 2014;24(8):1090–1099. [Google Scholar]
- 15.Blumenthal NC, Betts F, Posner AS. Effect of carbonate and biological macromolecules on formation and properties of hydroxyapatite. Calcified Tissue Research. 1975;18(1):81–90. doi: 10.1007/BF02546228. [DOI] [PubMed] [Google Scholar]
- 16.Landis WJ, Hodgens KJ, Arena J, Song MJ, McEwen BF. Structural relations between collagen and mineral in bone as determined by high voltage electron microscopic tomography. Microscopy Research and Technique. 1996;33(2):192–202. doi: 10.1002/(SICI)1097-0029(19960201)33:2<192::AID-JEMT9>3.0.CO;2-V. [DOI] [PubMed] [Google Scholar]
- 17.Chen L, Jacquet R, Lowder E, Landis WJ. Refinement of collagen-mineral interaction: a possible role for osteocalcin in apatite crystal nucleation, growth and development. Bone. 2015;71:7–16. doi: 10.1016/j.bone.2014.09.021. [DOI] [PubMed] [Google Scholar]
- 18.Elliott JC. Calcium Phosphate Biominerals. Reviews in Mineralogy and Geochemistry. 2002;48(1):427–453. [Google Scholar]
- 19.Li Z, Pasteris JD. Tracing the pathway of compositional changes in bone mineral with age: preliminary study of bioapatite aging in hypermineralized dolphin’s bulla. Biochim Biophys Acta. 2014;1840(7):2331–9. doi: 10.1016/j.bbagen.2014.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Barinov SM, Fadeeva IV, Ferro D, Rau JV, Cesaro SN, Komlev VS, Fomin AS. Stabilization of Carbonate Hydroxyapatite by Isomorphic Substitutions of Sodium for Calcium. Russ J Inorg Chem. 2008;53(2):164–168. [Google Scholar]
- 21.McConnell D, Gruner JW. The Problem of the Carbonate-apatites III Carbonate-apatite from Magnet Cove, Arkansas. The American mineralogist. 1940;25(3):157–167. [Google Scholar]
- 22.Gibson IR, Bonfield W. Novel synthesis and characterization of an AB-type carbonate-substituted hydroxyapatite. J Biomed Mater Res. 2002;59(4):697–708. doi: 10.1002/jbm.10044. [DOI] [PubMed] [Google Scholar]
- 23.LeGeros RZ. Calcium phosphates in oral biology and medicine. Monographs in oral science. 1991;15:1–201. [PubMed] [Google Scholar]
- 24.Bigi A, Cojazzi G, Panzavolta S, Ripamonti A, Roveri N, Romanello M, Suarez K Noris, Moro L. Chemical and structural characterization of the mineral phase from cortical and trabecular bone. Journal of inorganic biochemistry. 1997;68(1):45–51. doi: 10.1016/s0162-0134(97)00007-x. [DOI] [PubMed] [Google Scholar]
- 25.Xiao XF, Liu RF, Gao YJ. Hydrothermal preparation of nanocarbonated hydroxyapatite crystallites. Materials Science and Technology. 2008;24(10):1199–1203. [Google Scholar]
- 26.Markovic S, Veselinovic L, Lukic MJ, Karanovic L, Bracko I, Ignjatovic N, Uskokovic D. Synthetical bone-like and biological hydroxyapatites: a comparative study of crystal structure and morphology. Biomedical materials (Bristol, England) 2011;6(4):045005. doi: 10.1088/1748-6041/6/4/045005. [DOI] [PubMed] [Google Scholar]
- 27.Barralet J, Best S, Bonfield W. Carbonate substitution in precipitated hydroxyapatite: An investigation into the effects of reaction temperature and bicarbonate ion concentration. J Biomed Mater Res. 1998;41(1):79–86. doi: 10.1002/(sici)1097-4636(199807)41:1<79::aid-jbm10>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
- 28.Liao J, Yang L, Grashow J, Sacks MS. Molecular orientation of collagen in intact planar connective tissues under biaxial stretch. Acta Biomater. 2005;1:45–54. doi: 10.1016/j.actbio.2004.09.007. [DOI] [PubMed] [Google Scholar]
- 29.Wang Y, Von Euw S, Laurent G, Crevant C, Bonhomme-Coury L, Giraud-Guille MM, Babonneau F, Nassif N, Azais T. Impact of collagen confinement vs. ionic substitutions on the local disorder in bone and biomimetic apatites. Materials Horizons. 2014;1(2):224–231. [Google Scholar]
- 30.Yoder CH, Pasteris JD, Krol KA, Weidner VL, Schaeffer RW. Synthesis, structure, and solubility of carbonated barium chlor- and hydroxylapatites. Polyhedron. 2012;44(1):143–149. [Google Scholar]
- 31.Grøn P, Spinelli M, Trautz O, Brudevold F. The effect of carbonate on the solubility of hydroxylapatite. Arch Oral Biol. 1963;8(3):251–263. doi: 10.1016/0003-9969(63)90016-5. [DOI] [PubMed] [Google Scholar]
- 32.Deymier AC, Almer JD, Stock SR, Haeffner DR, Dunand DC. High Energy X-ray Diffraction Measurement of Load Transfer Between Hydroxyapatite and Collagen in Bovine Dentin. In: Kisailus D, Estroff L, Gupta HS, Landis WJ, Zavattieri PD, editors. Structure-Property Relationships in Biomineralized and Biomimetic Composites. Materials Research Society; Warrendale: 2009. pp. 161–166. [Google Scholar]
- 33.Flora NJ, Hamilton KW, Schaeffer RW, Yoder CH. A Comparative Study of the Synthesis of Calcium, Strontium, Barium, Cadmium, and Lead Apatites in Aqueous Solution. Synthesis and Reactivity in Inorganic and Metal-Organic Chemistry. 2004;34(3):503–521. [Google Scholar]
- 34.Yoder CH, Pasteris JD, Worcester KN, Schermerhorn DV. Structural water in carbonated hydroxylapatite and fluorapatite: confirmation by solid state (2)H NMR. Calcif Tissue Int. 2012;90(1):60–7. doi: 10.1007/s00223-011-9542-9. [DOI] [PubMed] [Google Scholar]
- 35.Yoder C, Pasteris J, Worcester K, Schermerhorn D, Sternlieb M, Goldenberg J, Wilt Z. Dehydration and Rehydration of Carbonated Fluor- and Hydroxylapatite, Minerals. 2012 [Google Scholar]
- 36.Wopenka B, Kent A, Pasteris JD, Yoon Y, Thomopoulos S. The tendon-to-bone transition of the rotator cuff: a preliminary raman spectroscopic study documenting the gradual mineralization across the insertion in rat tissue samples. Applied spectroscopy. 2008;62(12):1285–1294. doi: 10.1366/000370208786822179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Schwartz AG, Lipner JH, Pasteris JD, Genin GM, Thomopoulos S. Muscle loading is necessary for the formation of a functional tendon enthesis. Bone. 2013;55(1):44–51. doi: 10.1016/j.bone.2013.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Schwartz AG, Pasteris JD, Genin GM, Daulton TL, Thomopoulos S. Mineral distributions at the developing tendon enthesis. PLoS One. 2012;7(11):9. doi: 10.1371/journal.pone.0048630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Genin GM, Kent A, Birman V, Wopenka B, Pasteris JD, Marquez PJ, Thomopoulos S. Functional grading of mineral and collagen in the attachment of tendon to bone. Biophys J. 2009;97(4):976–85. doi: 10.1016/j.bpj.2009.05.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Grunenwald A, Keyser C, Sautereau AM, Crubezy E, Ludes B, Drouet C. Revisiting carbonate quantification in apatite (bio)minerals: a validated FTIR methodology. Journal of Archaeological Science. 2014;49:134–141. [Google Scholar]
- 41.Standard Methods for the Examination of Water and Wastewater. American Public Health Association, American Water Works Association, Water Environment Federation; Washington, DC: 1999. [Google Scholar]
- 42.Mkhonto D, de Leeuw NH. A computer modelling study of the effect of water on the surface structure and morphology of fluorapatite: introducing a Ca10(PO4)6F2 potential model. J Mater Chem. 2002;12:2633–2642. [Google Scholar]
- 43.De Leeuw NH. A computer modelling study of the uptake and segregation of fluoride ions at the hydrated hydroxyapatite (0001) surface: introducing a Ca10(PO4)6(OH)2 potential model. Phys Chem Chem Phys. 2004;6:1860. [Google Scholar]
- 44.Astala R, Stott MJ. First Principles Investigation of Mineral Component of Bone: CO3 Substitutions in Hydroxyapatite. Chem Mat. 2005;17(16):4125–4133. [Google Scholar]
- 45.Menendez-Proupin E, Cervantes-Rodriguez S, Osorio-Pulgar R, Franco-Cisterna M, Camacho-Montes H, Fuentes ME. Computer simulation of elastic constants of hydroxyapatite and fluorapatite. J Mech Behav Biomed Mater. 2011;4(7):1011–20. doi: 10.1016/j.jmbbm.2011.03.001. [DOI] [PubMed] [Google Scholar]
- 46.Rabone JAL, de Leeuw NH. Potential routes to carbon inclusion in apatite minerals: a DFT study. Phys Chem Minerals. 2007;34(7):495–506. [Google Scholar]
- 47.Peroos S, Du Z, de Leeuw NH. A computer modelling study of the uptake, structure and distribution of carbonate defects in hydroxy-apatite. Biomaterials. 2006;27(9):2150–61. doi: 10.1016/j.biomaterials.2005.09.025. [DOI] [PubMed] [Google Scholar]
- 48.Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. Journal of Computational Physics. 1995;117(1):1–19. [Google Scholar]
- 49.Ching WY, Rulis P, Misra A. Ab initio elastic properties and tensile strength of crystalline hydroxyapatite. Acta Biomater. 2009;5(8):3067–3075. doi: 10.1016/j.actbio.2009.04.030. [DOI] [PubMed] [Google Scholar]
- 50.Hughes JM, Cameron M, Crowley KD. Structural variations in natural F, OH, and Cl apatites. American Mineralogist. 1989;74(7–8):870–876. [Google Scholar]
- 51.Astala R, Stott M. First-principles study of hydroxyapatite surfaces and water adsorption. Phys Rev B. 2008;78:1–11. [Google Scholar]
- 52.Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. J Mol Graph. 1996;14:33–8. 27–8. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 53.Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Physical review B, Condensed matter. 1990;41(11):7892–7895. doi: 10.1103/physrevb.41.7892. [DOI] [PubMed] [Google Scholar]
- 54.Fast L, Wills JM, Johansson B, Eriksson O. Elastic constants of hexagonal transition metals: Theory. Physical review B, Condensed matter. 1995;51(24):17431–17438. doi: 10.1103/physrevb.51.17431. [DOI] [PubMed] [Google Scholar]
- 55.Weibull W. A statistical distribution function of wide applicability. J Appl Mech. 1951;73:293. [Google Scholar]
- 56.Askeland D, Fulay P, Wright W. The Science and Engineering of Materials Cenage Learning. Independance, KY: 2010. [Google Scholar]
- 57.Freudenthal AM. Statistical approach to brittle fracture, s.n.], S.l. 1968 [Google Scholar]
- 58.Gao X, Ruggieri C, Dodds RH. Calibration of Weibull stress parameters using fracture toughness data. Int J Fract. 92(2):175–200. [Google Scholar]
- 59.Montel G, Bonel G, Heughebaert JC, Trombe JC, Rey C. New concepts in the composition, crystallization and growth of the mineral component of calcified tissues. Journal of Crystal Growth. 1981;53(1):74–99. [Google Scholar]
- 60.Rey C, Combes C, Drouet C, Grossin D. Bioactive Ceramics: Physical Chemistry. In: Ducheyne P, Healy KE, Hutmacher DW, Grainger DW, Kirkpatrick CJ, editors. Comprehensive Biomaterials. Elsevier; 2011. pp. 187–221. [Google Scholar]
- 61.Gilmore RS, Katz JL. Elastic properties of apatites. J Mater Sci. 1982;17(4):1131–1141. [Google Scholar]
- 62.Katz JL, Ukraincik K. On the anisotropic elastic properties of hydroxyapatite. J Biomech. 1971;4(3):221–227. doi: 10.1016/0021-9290(71)90007-8. [DOI] [PubMed] [Google Scholar]
- 63.LeGeros RZ, Trautz OR, Legeros JP, Klein E, Shirra WP. Apatite crystallites: effects of carbonate on morphology. Science. 1967;155(3768):1409–11. doi: 10.1126/science.155.3768.1409. [DOI] [PubMed] [Google Scholar]
- 64.Drouet C. Apatite Formation: Why It May Not Work as Planned, and How to Conclusively Identify Apatite Compounds. BioMed Research International. 2013;2013:12. doi: 10.1155/2013/490946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Rey C, Collins B, Goehl T, Dickson IR, Glimcher MJ. The carbonate environment in bone mineral: a resolution-enhanced Fourier Transform Infrared Spectroscopy Study. Calcif Tissue Int. 1989;45(3):157–64. doi: 10.1007/BF02556059. [DOI] [PubMed] [Google Scholar]
- 66.Suetsugu Y, Takahashi Y, Okamura FP, Tanaka J. Structure Analysis of A-Type Carbonate Apatite by a Single-Crystal X-Ray Diffraction Method. Journal of Solid State Chemistry. 2000;155(2):292–297. [Google Scholar]
- 67.LeGeros RZ, Trautz OR, Klein E, LeGeros JP. Two types of carbonate substitution in the apatite structure. Experientia. 1969;25(1):5–7. doi: 10.1007/BF01903856. [DOI] [PubMed] [Google Scholar]
- 68.Pan Y, Fleet ME. Compositions of the Apatite-Group Minerals: Substitution Mechanisms and Controlling Factors. Reviews in Mineralogy and Geochemistry. 2002;48(1):13–49. [Google Scholar]
- 69.Wopenka B, Pasteris JD. A mineralogical perspective on the apatite in bone. Materials Science and Engineering: C. 2005;25(2):131–143. [Google Scholar]
- 70.Zahedi JAM, Ziaie F, Larijani MM, Borghei SM, Kamaliyanfar A. Synthesis and Characterization of Sodium-carbon Apatite Nano-crystals by Chemical Sedimentation Method. Indian Journal of Science and Technology. 2012;5(3):2464–2467. [Google Scholar]
- 71.Noyan IC, Cohen JB. Residual Stress: Measurement by Diffraction and Interpretation. SpringerVerlag; New York: 1956. [Google Scholar]
- 72.Ziv V, Weiner S. Bone Crystal Sizes: A Comparison of Transmission Electron Microscopic and X-Ray Diffraction Line Width Broadening Techniques. Connect Tissue Res. 1994;30(3):165–175. doi: 10.3109/03008209409061969. [DOI] [PubMed] [Google Scholar]
- 73.Orgel JPRO, Miller A, Irving TC, Fischetti RF, Hammersley AP, Wess TJ. The in situ supermolecular structure of type I collagen. Structure. 2001;9:1061–1069. doi: 10.1016/s0969-2126(01)00669-4. [DOI] [PubMed] [Google Scholar]
- 74.Miller EJ, Gay S, Leon WC. [1] The collagens: An overview and update, Methods in Enzymology. Academic Press; 1987. pp. 3–41. [DOI] [PubMed] [Google Scholar]
- 75.Landis WJ, Song MJ, Leith A, McEwen L, McEwen BF. Mineral and organic matrix interaction in normally calcifying tendon visualized in three dimensions by high-voltage electron microscopic tomography and graphic image reconstruction. J Struct Biol. 1993;110(1):39–54. doi: 10.1006/jsbi.1993.1003. [DOI] [PubMed] [Google Scholar]
- 76.Glimcher MJ. Recent studies of the mineral phase in bone and its possible linkage to the organic matrix by protein-bound phosphate bonds. Philosophical transactions of the Royal Society of London Series B, Biological sciences. 1984;304(1121):479–508. doi: 10.1098/rstb.1984.0041. [DOI] [PubMed] [Google Scholar]
- 77.Nudelman F, Pieterse K, George A, Bomans PHH, Friedrich H, Brylka LJ, Hilbers PAJ, de With G, Sommerdijk NAJM. The role of collagen in bone apatite formation in the presence of hydroxyapatite nucleation inhibitors. Nat Mater. 2010;9(12):1004–1009. doi: 10.1038/nmat2875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.George A, Veis A. Phosphorylated proteins and control over apatite nucleation, crystal growth, and inhibition. Chemical reviews. 2008;108(11):4670–93. doi: 10.1021/cr0782729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Deymier-Black AC, Almer JD, Stock SR, Haeffner DR, Dunand DC. Synchrotron X-ray diffraction study of load partitioning during elastic deformation of bovine dentin. Acta Biomater. 2010;6(6):2172–2180. doi: 10.1016/j.actbio.2009.11.017. [DOI] [PubMed] [Google Scholar]
- 80.Forien JB, Fleck C, Krywka C, Zolotoyabko E, Zaslansky P. In situ compressibility of carbonated hydroxyapatite in tooth dentine measured under hydrostatic pressure by high energy X-ray diffraction. J Mech Behav Biomed Mater. 2015;50:171–9. doi: 10.1016/j.jmbbm.2015.06.005. [DOI] [PubMed] [Google Scholar]
- 81.Mutaftschiev B. The atomistic nature of crystal growth. Springer Science & Business Media; 2013. [Google Scholar]
- 82.Abernethy RB. The New Weibull Handbook. Robert B Abernethy; North Palm Beach, Florida: 2004. [Google Scholar]
- 83.Baig AA, Fox JL, Young RA, Wang Z, Hsu J, Higuchi WI, Chhettry A, Zhuang H, Otsuka M. Relationships among carbonated apatite solubility, crystallite size, and microstrain parameters. Calcif Tissue Int. 1999;64(5):437–49. doi: 10.1007/pl00005826. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1: Measured solubility for 5 experimental samples, showing that the solubility increases as the carbonate content increases. This is likely caused by a decrease in the atomic order of the samples.


