Abstract
Background: Most existing research on the association of parental education with childhood undernutrition focuses on maternal education and often ignores paternal education. We systematically investigate differences in maternal and paternal education and their association with childhood undernutrition.
Methods: One hundred and eighty Demographic and Health Surveys from 62 countries performed between 1990 and 2014 were analysed. We used linear-probability models to predict childhood undernutrition prevalences, measured as stunting, underweight and wasting, for all combinations of maternal and paternal attainment in school. Models were adjusted for demographic and socio-economic covariates for the child, mother and household, country-level fixed effects and clustering. Additional specifications adjust for local area characteristics instead of country fixed effects.
Results: Both higher maternal and paternal education levels are associated with lower childhood undernutrition. In regressions adjusted for child age and sex as well as country-level fixed effects, the association is stronger for maternal education than for paternal education when their combined level of education is held constant. In the fully adjusted models, the observed differences in predicted undernutrition prevalences are strongly attenuated, suggesting a similar importance of maternal and paternal education. These findings are confirmed by the analysis of composite schooling indicators.
Conclusions: We find that paternal education is similarly important for reducing childhood undernutrition as maternal education and should therefore receive increased attention in the literature.
Keywords: child undernutrition; parental education; stunting, wasting; underweight
Key Messages
Both maternal and paternal schooling are negatively associated with child undernutrition.
Models failing to control for important covariates and local area characteristics suggest that the education of the mother is most important but, once these factors are accounted for, differences between maternal and paternal education are strongly attenuated.
The channels through which the education of fathers affects child nutritional status are not yet fully understood and further research is necessary.
Introduction
Much research has shown that maternal education critically affects children’s health and development. Caldwell was one of the first to show links between maternal education and child health, finding lower child mortality among children with better-educated mothers in Nigeria.1 His seminal study inspired many investigations of the effects of parental education on child health and well-being in developing as well as in developed countries.2–5 Specifically related to child nutrition and physical development, evidence showed that higher educational attainment for parents was inversely associated with childhood stunting, underweight and wasting.6 Much of this research has focused primarily on maternal education though, largely ignoring paternal education.7–11
A few studies have compared the influences of mothers’ and fathers’ education on child nutrition and physical development, finding different and often contradictory results. Aslam and Kingdon found that only the mother’s education was a significant predictor of child height and weight.12 Other work finds that both parents’ education levels are equally protective against undernutrition.13 The contrasting findings of these studies show that the relationship between parental education and child nutrition, particularly the relative contributions of maternal and paternal education, is far from clear.
Comparisons of the effects of maternal and paternal education on child health have been marked by key methodological concerns. Using data from 22 countries, Desai and Alva found that associations between maternal education and height for age of children are attenuated in models accounting for paternal education and other characteristics.14 Relatedly, several other studies noted that the effects of maternal education are confounded by social and economic conditions.3–5,15 Another issue is assortative mating—a phenomenon in which women who are more educated tend to choose men with a similar status, which may further complicate comparisons of maternal vs paternal education effects on child health.16,17 Accounting for the correlation between mothers’ and father’s education, Breierova and Duflo found nearly equal effects of mothers’ and fathers’ education on child mortality.16
Glewwe developed a conceptual model to describe pathways through which parental education may affect child health.18 Parental education leads to changes in child health through two interrelated channels. Higher education causes changes in parental values, affecting household income and allocation of resources towards children’s health as well as parents’ health knowledge.18 Second, more years of schooling lead to changes in cognitive skills that also affect parents’ health knowledge, household income, and thus health and nutritional inputs.18
We use the largest available, nationally representative and mutually comparable repeated cross-sectional data sets from low- and middle-income countries to systematically compare the associations of maternal and paternal education with childhood undernutrition.
Methods
Data sources
Data for this study come from the Demographic and Health Surveys (DHS). These surveys are administered by ICF International and are nationally representative cross-sectional surveys in low- and middle-income countries that have been conducted at varying intervals from 1985 and are still ongoing. The DHS are designed to collect nationally representative data of women of reproductive age and their children and households on their health and welfare.
Sampling plan
The DHS used a multi-staged stratified sampling design. Each country was divided into regions, which are political regions such as states or provinces, or geographical areas divided into areas labeled north, south, east and west. Within these sub-national regions, populations were stratified by urban and rural area of residence. Within these stratified areas, a random selection of enumeration areas taken from the most recent population census was drawn. These primary sampling units (PSUs) were selected based on probability proportional to the population size. In the second stage of sampling, all households within the cluster were listed and, on average, 25 houses within a cluster were randomly selected for an interview by equal-probability systematic sampling. Detailed sampling plans are available from survey final reports.
Within each sampled household, the household members were listed and women eligible for a more detailed interview were identified. Typically, this was a woman who was between the ages of 15 and 49 years. In a few surveys, it was limited to ever-married women and, in others, it was women aged 10–49 years. Details of height and weight at the time of interview were also recorded for children born in the last three, four or five years.
Outcome measures
We focus on three child outcomes: stunting, underweight and wasting at the time of interview. We classified children as stunted, wasted and/or underweight based on anthropometric z-scores using the Stata package ‘igrowup_stata’.19 All outcomes are based on measurements by interviewers, with weight and height being recorded with an accuracy of 0.1 kg or 0.1 cm, respectively. Data were available for children under the age of five only. Z-scores for stunting were defined as the difference of a child’s height and the age- and sex-specific median height of the WHO reference population over the standard deviation of their age group within the reference population.20 Underweight and wasting in turn capture whether a child exhibits low weight-for-age or low weight-for-height, respectively.
Variations in measurement methods (i.e. lying or standing) were accounted for in the calculation of z-scores. All outcomes were defined as binary variables denoting whether a child’s z-score (by age and gender) was less than –2. Biologically implausible values are defined by the WHO for stunting as z-scores <–6 or >6; for underweight as <–6 or >5; and for wasting as <–5 or >5. Observations with these biologically implausible values were dropped.
Exposure
To investigate how paternal education affects childhood undernutrition, we used information on complete educational levels and the number of finished school years for both mothers and fathers (or the current partner of the mother). Whereas education systems typically differ across or even within countries, DHS data sets were recoded in a way that allowed comparisons. For educational levels, we define a categorical variable for each parent using the levels ‘no or less than primary education’, ‘primary or incomplete secondary education’ and ‘secondary education and above’ and examine their interaction effect.
The exposure years of schooling is then used to construct a range of composite indicators that aim to investigate whether the identity of the more-educated parent matters. Specifically, we calculate the difference of paternal years of schooling minus maternal years of schooling and the ratio of paternal years of schooling divided by maternal years of schooling. Note that the ratio can only be calculated if years of schooling are non-zero and therefore the sample is restricted to households where mothers and fathers had at least one year of schooling. Lastly, two binary variables are created to capture whether both parents have different years of schooling and whether it is the mother who is the better-educated parent. Descriptive statistics for outcome and exposure variables are shown in Table 1.
Table 1.
Descriptive statistics
| Stunting sample | Underweight sample | Wasting sample | |
|---|---|---|---|
| (n = 952 253) | (n = 981 740) | (n = 941 721) | |
| Mean/% | Mean/% | Mean/% | |
| Undernutrition prevalence | |||
| Stunting (%) | 36.93 | ||
| Underweight (%) | 20.86 | ||
| Wasting (%) | 8.93 | ||
| Maternal education | |||
| Non or incomplete primary (%) | 59.09 | 59.36 | 59.08 |
| Primary or incomplete secondary (%) | 26.59 | 26.44 | 26.58 |
| Secondary or higher (%) | 14.32 | 14.20 | 14.34 |
| Paternal education | |||
| Non or incomplete primary (%) | 49.16 | 49.32 | 49.12 |
| Primary or incomplete secondary (%) | 31.99 | 31.89 | 32.01 |
| Secondary or higher (%) | 18.84 | 18.79 | 18.87 |
| Difference in education levels | |||
| Father < Mother (%) | 16.23 | 16.06 | 16.20 |
| Father = Mother (%) | 49.62 | 49.72 | 49.60 |
| Father > Mother (%) | 34.15 | 34.22 | 34.20 |
| Years of schoolinga | |||
| Maternal school years | 4.67 | 4.64 | 4.67 |
| Paternal school years | 5.90 | 5.88 | 5.90 |
| Difference school years | 1.23 | 1.25 | 1.24 |
| Number of school years differ (%) | 63.92 | 63.63 | 63.87 |
| Mother better educated (%) | 20.10 | 19.87 | 20.05 |
Descriptive statistics are pooled for all surveys and unweighted. n denotes the number of observations in the sample used to calculate a statistic. Weighted versions of this table are provided by Table A3 and A4 in the online appendix (Supplementary data are available at IJE online).
a There are small deviations in sample sizes in specifications based on years of schooling:
Stunting: n = 948 642; Underweight: n = 977 862; Wasting: n = 938 208.
Covariates
Our choice of covariates was motivated by the United Nations Children’s Emergency Fund (UNICEF) conceptual framework of causes of undernutrition (http://www.unicef.org/nutrition/training/2.5/4.html). Covariates include indicator variables for the age and sex of the child, the birth order and whether the child was born in a multiple birth. Child age was classified into four categories: ‘less than one month’ ‘between one and eleven months’ ‘between 12 and 35 months’ and ‘more than 35 months’.
We further adjust for maternal age and relationship status. As before, age was defined as categories: ‘younger than 17 years’, ‘between 17 and 19 years’, ‘20 to 24 years’ ‘between 25 and 29 years’ and ‘more than 29 years’. Relationship status was captured by a dummy indicating whether a woman was in a relationship when the interview took place. For robustness checks, which are available in the online appendix (Supplementary data are available at IJE online), we also constructed a covariate for maternal height.
To adjust for wealth differences, we constructed wealth quintiles using a principal component analysis of a range of household assets such as electricity, radios, televisions, quality of dwelling and type of drinking-water source. Further, we considered whether a household was located in an urban or rural area.
Statistical analysis
To investigate the relative importance of parental education for anthropometric outcomes, we fit a series of linear-probability models (LPMs). Separate models were estimated for stunting, underweight and wasting as dependent variables. Table 2 uses the categorical measures for maternal and paternal educational attainment to predict prevalences of childhood undernutrition for each level of parental education (i.e. main effects). Table 3 additionally includes their interaction as exposure to predict the prevalence of undernutrition for every combination of mothers’ and fathers’ education. We specify three model types. Model 1 is only adjusted for child age, sex and country-level fixed effects. Model 2 further includes the full set of covariates described in the previous section. The last model type (Model 3) also controls for PSU-level fixed effects, which we refer to as local area characteristics. The PSU-level fixed effects are survey specific and capture characteristics of local enumeration areas that are common to all respondents from that area. Such local area characteristics may among others include the local diet, environmental conditions and cultural context. We further suspect that wealth difference may be reflected in a spatial clustering of households and may not be fully captured by the constructed wealth quintiles; therefore, the local area characteristics may provide an additional adjustment for household-level income and wealth. In addition, we clustered standard errors at the PSU level, as respondents residing in the same area may be exposed to common shocks.
Table 2.
Relationship between maternal and paternal education levels with undernutrition in children—main effects (mutually adjusted)
| Model 1 |
Model 2 |
Model 3 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Mother | Father | Mother | Father | Mother | Father | ||||
| Stunting | Non or incomplete primary | Prevalence (%) | 41.96 | 40.61 | 39.95 | 39.00 | 38.77 | 38.55 | |
| (n = 952 253) | 95% CI | (41.77, 42.15) | (40.41, 40.80) | (39.76, 40.13) | (38.81, 39.19) | (38.64, 38.91) | (38.40, 38.70) | ||
| n | 562 691 | 468 144 | 562 691 | 468 144 | 562 691 | 468 144 | |||
| Primary or incomplete secondary | Prevalence (%) | 32.48 | 34.75 | 33.89 | 35.63 | 35.05 | 36.11 | ||
| 95% CI | (32.25, 32.70) | (34.54, 34.95) | (33.67, 34.11) | (35.43, 35.84) | (34.84, 35.26) | (35.94, 36.29) | |||
| n | 253 177 | 304 669 | 253 177 | 304 669 | 253 177 | 304 669 | |||
| Secondary or higher | Prevalence (%) | 24.44 | 31.04 | 30.12 | 33.73 | 32.81 | 34.09 | ||
| 95% CI | (24.12, 24.75) | (30.76, 31.32) | (29.79, 30.45) | (33.45, 34.01) | (32.46, 33.17) | (33.81, 34.38) | |||
| n | 136 385 | 179 440 | 136 385 | 179 440 | 136 385 | 179 440 | |||
| Underweight | Non or incomplete primary | Prevalence (%) | 24.03 | 23.84 | 22.78 | 22.79 | 22.20 | 22.27 | |
| (n = 981 740) | 95% CI | (23.87, 24.19) | (23.67, 24.01) | (22.62, 22.93) | (22.63, 22.95) | (22.09, 22.31) | (22.14, 22.39) | ||
| n | 582 741 | 484 197 | 582 741 | 484 197 | 582 741 | 484 197 | |||
| Primary or incomplete secondary | Prevalence (%) | 16.93 | 18.71 | 17.86 | 19.31 | 18.99 | 19.96 | ||
| 95% CI | (16.75, 17.10) | (18.54, 18.87) | (17.68, 18.04) | (19.14, 19.47) | (18.81, 19.16) | (19.82, 20.11) | |||
| n | 259 558 | 313 121 | 259 558 | 313 121 | 259 558 | 313 121 | |||
| Secondary or higher | Prevalence (%) | 14.95 | 16.69 | 18.44 | 18.43 | 18.74 | 18.70 | ||
| 95% CI | (14.71, 15.19) | (16.47, 16.91) | (18.18, 18.69) | (18.21, 18.65) | (18.48, 19.00) | (18.48, 18.91) | |||
| n | 139 441 | 184 422 | 139 441 | 184 422 | 139 441 | 184 422 | |||
| Wasting | Non or incomplete primary | Prevalence (%) | 9.62 | 9.82 | 9.34 | 9.57 | 9.31 | 9.34 | |
| (n = 941 721) | 95% CI | (9.52, 9.73) | (9.71, 9.94) | (9.24, 9.45) | (9.45, 9.68) | (9.23, 9.38) | (9.24, 9.43) | ||
| n | 556 359 | 462 545 | 556 359 | 462 545 | 556 359 | 462 545 | |||
| Primary or incomplete secondary | Prevalence (%) | 7.95 | 8.20 | 8.19 | 8.35 | 8.45 | 8.66 | ||
| 95% CI | (7.82, 8.07) | (8.08, 8.31) | (8.06, 8.32) | (8.24, 8.47) | (8.33, 8.57) | (8.55, 8.76) | |||
| n | 250 349 | 301 487 | 250 349 | 301 487 | 250 349 | 301 487 | |||
| Secondary or higher | Prevalence (%) | 7.90 | 7.85 | 8.60 | 8.25 | 8.27 | 8.33 | ||
| 95% CI | (7.71, 8.08) | (7.69, 8.01) | (8.40, 8.80) | (8.09, 8.41) | (8.07, 8.47) | (8.16, 8.50) | |||
| n | 135 013 | 177 689 | 135 013 | 177 689 | 135 013 | 177 689 | |||
The table presents unweighted predicted prevalences of undernutrition (all outcomes) with 95% confidence intervals in parentheses below. All models include both maternal and paternal education. Model 1 is only adjusted for child age, sex and country-level fixed effects. Model 2 further controls for child birth order, whether the child was born in a multiple birth, maternal age and partnership status, urban location of household as well as its wealth quintile as measured by household asset ownership. Model 3 is additionally adjusted for local area characteristics (PSU-level fixed effects). All standard errors were clustered on the PSU level.
Table 3.
Relationship between parental education levels and undernutrition in children—interaction effects (Model 3)
| Mother: non or incomplete primary | Mother: primary or incomplete secondary | Mother: secondary or higher | |||
|---|---|---|---|---|---|
| Stunting | Father: non or incomplete primary | Prevalence (%) | 40.37 | 37.05 | 32.72 |
| (n = 952 253) | 95% CI | (40.19, 40.55) | (36.62, 37.49) | (31.59, 33.84) | |
| n | 405 181 | 56 307 | 6656 | ||
| Father: primary or incomplete secondary | Prevalence (%) | 38.11 | 34.21 | 31.41 | |
| 95% CI | (37.83, 38.40) | (33.92, 34.50) | (30.87, 31.95) | ||
| n | 129 600 | 140 678 | 34 391 | ||
| Father: secondary or higher | Prevalence (%) | 35.61 | 31.84 | 30.30 | |
| 95% CI | (34.98, 36.23) | (31.41, 32.28) | (29.90, 30.69) | ||
| n | 27 910 | 56 192 | 95 338 | ||
| Underweight | Father: non or incomplete primary | Prevalence (%) | 23.65 | 20.30 | 18.71 |
| (n = 981 740) | 95% CI | (23.50, 23.81) | (19.95, 20.66) | (17.98, 19.45) | |
| n | 419 823 | 57 541 | 6833 | ||
| Father: primary or incomplete secondary | Prevalence (%) | 21.33 | 18.11 | 17.56 | |
| 95% CI | (21.09, 21.57) | (17.87, 18.35) | (17.19, 17.93) | ||
| n | 133 963 | 144 192 | 34 966 | ||
| Father: secondary or higher | Prevalence (%) | 19.43 | 16.81 | 16.76 | |
| 95% CI | (18.93, 19.92) | (16.48, 17.14) | (16.47, 17.06) | ||
| n | 28 955 | 57 825 | 97 642 | ||
| Wasting | Father: non or incomplete primary | Prevalence (%) | 9.76 | 8.62 | 8.12 |
| (n = 941 721) | 95% CI | (9.65, 9.87) | (8.37, 8.87) | (7.50, 8.74) | |
| n | 400 355 | 55 588 | 6602 | ||
| Father: primary or incomplete secondary | Prevalence (%) | 8.95 | 8.30 | 7.75 | |
| 95% CI | (8.78, 9.12) | (8.13, 8.46) | (7.46, 8.04) | ||
| n | 128 315 | 139 109 | 34 063 | ||
| Father: secondary or higher | Prevalence (%) | 8.49 | 7.75 | 7.80 | |
| 95% CI | (8.11, 8.86) | (7.50, 8.00) | (7.57, 8.02) | ||
| n | 27 689 | 55 652 | 94 348 | ||
The table presents unweighted predicted prevalences of undernutriton with 95% confidence intervals in parentheses below. All models include the depicted parental education levels and their interaction. We adjusted for local area characteristics (PSU-level fixed effects), child age, sex, birth order, whether the child was born in a multiple birth, maternal age and partnership status, urban location of household as well as its wealth quintile as measured by household asset ownership. All standard errors were clustered on the PSU level.
In addition to the main analysis, we report marginal effects of a range of composite schooling indicators in Table 4. There are two rationales for this approach: first, whereas educational levels are useful to summarize educational attainment, the variation in the outcome is substantially higher when school years are used; second, the correlation between maternal and paternal educational attainment is rather high (63.1%) and may not allow a clear separation of effects. Composite indicators, in turn, allow a direct test of whether the identity of the better-educated parent has any separate explanatory power and hence provide a useful supplement to the main analysis. Importantly, all specifications based on composite indicators control for the number of school years attained by the least-educated parent in order to partial out level effects and to focus on within-couple deviations.
Table 4.
Years of schooling and child undernutrition
| Model 1 |
Model 2 |
Model 3 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Stunting | Underweight | Wasting | Stunting | Underweight | Wasting | Stunting | Underweight | Wasting | |
| Maternal years of schooling | –1.50 | –0.90 | –0.20 | –0.92 | –0.58 | –0.14 | –0.56 | –0.42 | –0.13 |
| (–1.53, –1.46) | (–0.93, –0.87) | (–0.22, –0.18) | (–0.95, –0.88) | (–0.61, –0.55) | (–0.16, –0.11) | (–0.60, –0.52) | (–0.45, –0.38) | (–0.15, –0.10) | |
| Paternal years of schooling | –0.72 | –0.60 | –0.19 | –0.40 | –0.40 | –0.14 | –0.36 | –0.31 | –0.09 |
| (–0.75, –0.69) | (–0.63, –0.58) | (–0.20, –0.17) | (–0.43, –0.37) | (–0.43, –0.38) | (–0.16, –0.12) | (–0.39, –0.33) | (–0.34, –0.29) | (–0.11, –0.07) | |
| n | 948 642 | 977 862 | 938 208 | 948 642 | 977 862 | 938 208 | 948 642 | 977 862 | 938 208 |
| Paternal minus maternal school years | –0.03 | –0.13 | –0.07 | 0.01 | –0.09 | –0.05 | –0.07 | –0.08 | –0.02 |
| (–0.06, –0.00) | (–0.16, –0.11) | (–0.08, –0.05) | (–0.01, 0.04) | (–0.12, –0.07) | (–0.07, –0.04) | (–0.10, –0.04) | (–0.11, –0.06) | (–0.04, –0.00) | |
| n | 948 642 | 977 862 | 938 208 | 948 642 | 977 862 | 938 208 | 948 642 | 977 862 | 938 208 |
| Paternal divided by maternal school years | –0.25 | –0.10 | –0.01 | 0.04 | 0.03 | 0.01 | –0.27 | –0.12 | –0.02 |
| (–0.39, –0.12) | (–0.21, –0.00) | (–0.07, 0.06) | (–0.09, 0.17) | (–0.07, 0.13) | (–0.05, 0.08) | (–0.43, –0.12) | (–0.24, –0.00) | (–0.10, 0.06) | |
| n | 541 451 | 553 108 | 534 938 | 541 451 | 553 108 | 534 938 | 541 451 | 553 108 | 534 938 |
| Different number of school years | –3.05 | –4.18 | –1.77 | –1.73 | –3.31 | –1.53 | –1.26 | –1.63 | –0.69 |
| (–3.29, –2.80) | (–4.39, –3.97) | (–1.92, –1.61) | (–1.97, –1.49) | (–3.52, –3.10) | (–1.69, –1.38) | (–1.53, –1.00) | (–1.86, –1.41) | (–0.86, –0.52) | |
| Mother completed more years of schooling than the father | –2.63 | –1.04 | –0.16 | –1.85 | –0.67 | –0.12 | –0.29 | –0.14 | –0.17 |
| (–2.90, –2.36) | (–1.25, –0.83) | (–0.31, –0.01) | (–2.11, –1.58) | (–0.88, –0.47) | (–0.27, 0.03) | (–0.58, 0.00) | (–0.37, 0.10) | (–0.33, 0.00) | |
| n | 948 642 | 977 862 | 938 208 | 948 642 | 977 862 | 938 208 | 948 642 | 977 862 | 938 208 |
The table presents unweighted marginal effects in percentage points on different forms of child undernutrition with 95% confidence intervals in parentheses below. Model 1 is only adjusted for child age, sex and country-level fixed effects. Model 2 further controls for child birth order, whether the child was born in a multiple birth, maternal age and partnership status, urban location of household as well as its wealth quintile as measured by household asset ownership. Model 3 is additionally adjusted for local area characteristics (PSU-level fixed effects). All standard errors were clustered on the PSU level. For each model type, different specifications were estimated, using either maternal and paternal years of schooling or the following composite indicators as exposure: ‘Paternal minus maternal school years’, ‘paternal divided by maternal school years’ or the two binary indicators ‘different number of school years’ and ‘mother completed more years of schooling than the father’. With the execption of the main effects models (i.e. maternal and paternal years of schooling), all specifications control for the number of school years achieved by the least-educated parent.
All presented regression models are unweighted, following recommendations provided by the DHS manual. As a robustness check, we re-estimated all models using sampling weights and present the results in the online appendix.
Ethics
The DHS data collection procedures were approved by the ICF Macro International (Calverton, Maryland) Institutional Review Board as well as by the relevant body in each country, which approves research studies on human subjects. Oral informed consent for the interview/survey was obtained from respondents by interviewers.
Results
Sample description
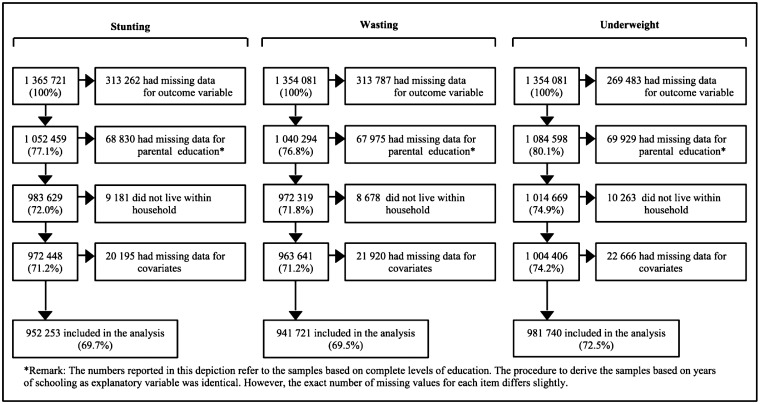
The original sample comprised 190 surveys from 64 countries conducted between 1990 and 2014. The surveys included a total of 1 365 721 observations for children aged between 0 and 59 months. Note that, for the outcomes wasting and underweight, the number of available observations was slightly lower, as one survey conducted in Madagascar only collected information on child height but not weight. We excluded visitors from our analysis, as they were typically not covered by the household questionnaires. Observations were lost due to missing data on outcome variables, parental education or covariates. A small number of observations were also lost because children and parents did not live in the same household. The final sample for the main analysis includes 180 surveys from 62 countries with an overall sample size of 952 253 for stunting, 941 721 for wasting and 981 740 for underweight (Figure 1). A list of all included countries and surveys in the final samples as well as corresponding descriptive statistics are shown in Tables A1 and A2 in the online appendix (available as Supplementary data at IJE online).
Figure 1.
Sample deduction
Note: Out of the missing data for the outcome variables, 63 812 observations in the case of stunting, 38 359 for underweight and 24 158 for wasting were due to biologically implausible values as defined by the WHO.
Overall, 36.9% of children in the sample were stunted, 20.9% were underweight and 8.9% were wasted. Moreover, the majority of children lived in low-education households, with 59.1–59.4% having mothers without complete primary education. Average maternal years of schooling were 4.6–4.7 years and average paternal years of schooling were 5.9 years; 49.6–49.7% of children had mothers and fathers with the same level of education, 16.1–16.2% had better-educated mothers and 34.2 had better-educated fathers. When measured in terms of complete school years, the share of children with a higher-educated mother increased to 19.9–20.1% (Table 1). The online appendix provides population-level estimates for the presented figures using different types of sampling weights derived from the original sampling weights provided in the DHS (Tables A3 and A4, available as Supplementary data at IJE online). In Table A3, sampling weights were rescaled such that they added up to 1 for each country. As a consequence, observations from larger surveys are down-weighted and those from smaller surveys are up-weighted. In contrast, sampling weights in Table A4 add up to the actual population in every country. Doing this is appropriate when the figures should be interpreted as a global individual-level mean.
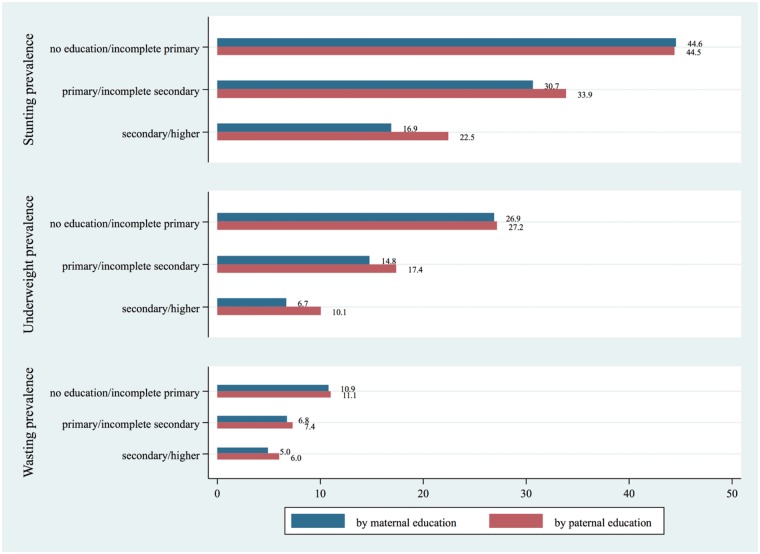
Figure 2 shows stunting, underweight and wasting prevalence for all levels of maternal and paternal education. There is a clear education gradient, with decreasing levels of undernutrition prevalence being associated with increasing levels of education.
Figure 2.
Undernutrition prevalence in percent by parental education level
All depicted numbers are unweighted pooled undernutrition prevalences for the entire sample.
Relationship between parental education and child undernutrition
In Table 2, we present predicted prevalences of childhood stunting, underweight and wasting for all levels of maternal and paternal educational attainment based on the categorical exposure. In all specifications, higher parental education is associated with lower levels of stunting, underweight and wasting. In models only adjusted for child age, sex and country-level fixed effects (Model 1), the predicted prevalence tends to be smaller for higher-educated mothers compared with higher-educated fathers. These differences are strongly attenuated when we adjust for the full set of covariates (Model 2) and even more so when we adjust for local area characteristics instead of country-level fixed effects (Model 3).
In Table 3, we focus on the fully adjusted model with local area characteristics (Model 3) and show predicted prevalences of childhood stunting, underweight and wasting for all combinations of maternal and paternal educational attainment based on regressions including interaction effects between maternal and paternal education. To compare the role of maternal and paternal education, we focus on the opposing off-diagonal elements of each sub-table to hold the overall level of education constant. The predicted prevalence of stunting is 38.1% (95% CI: 37.8%, 38.4%) when the child’s father but not the mother has finished primary education, whereas we find a prevalence of 37.1% (95% CI: 36.6%, 37.5%) in the opposite case. When fathers have finished secondary education and mothers have not completed primary education, the predicted stunting prevalence is 35.6% (95% CI: 35.0%, 36.2%), whereas it is 32.7% (95% CI: 31.6%, 33.8%) in the opposite case. And, finally, when fathers have finished secondary education and mothers have completed primary but not secondary education, the predicted prevalence is 31.8% (95% CI: 31.4%, 32.3%), whereas it is 31.4% (95% CI: 30.9%, 31.9%) in the opposite case. The predicted prevalences are similarly close for underweight and wasting. In Tables B1–B3 (available as Supplementary data at IJE online), we show the same results for Models 1 and 2 as well as for logistic regression models instead of LPMs. It turns out that the differences between maternal and paternal education are much larger in the models that do not adjust for the full set of covariates or local area characteristics. The results are also largely robust to a change in functional form from LPMs to logistic regression models.
In Table 4, we examine the marginal effect of parental years of schooling as well as a range of composite indicators. When maternal and paternal years of schooling are used as exposure variables, we find a slightly stronger association with maternal years of schooling (–1.5 percentage points; 95% CI: –1.5, –1.5) than with paternal years of schooling (–0.7 percentage points; 95% CI: –0.8, –0.7) on stunting in Model 1. Including all covariates and local area characteristics attenuates the associations of both exposures, decreasing their difference to 0.2 percentage points. Similarly to the main analysis, we find a comparable attenuation effect for underweight and no differences between paternal and maternal education in all models when wasting is considered. Appendix Figures B1–B3 (available as Supplementary data at IJE online) show that the assumption of linearity in years of schooling is a reasonable one, as a more flexible functional form yields results close to the linear trends estimated in Table 4.
Table 4 further provides estimates for the association of the composite indicators ‘paternal minus maternal school years’ and ‘paternal divided by maternal school years’ with childhood stunting, underweight and wasting. Both sets of models control for the number of school years that the least-educated parent in a household attained to isolate the effect of within-couple differences. The composite indicators are constructed such that marginal effects larger than zero imply that higher maternal education is associated with lower childhood undernutrition and marginal effects smaller than zero imply that more paternal education is associated with lower childhood undernutrition. In all specifications, the marginal effect of these composite indices is close to zero, suggesting that the identity of the more-educated parent does not explain a substantial part in the variation of child undernutrition.
We investigate the robustness of this finding in a further specification using an indicator stating whether the number of school years differs between both parents and a second indicator capturing whether it is the mother who is more educated. Again, we control for the number of years the less-educated parent attended school. This allows us to measure whether the identity of the better-educated parent bears any separate explanatory power. Whereas, in Model 1, we observe a negative association of having a better-educated mother with stunting (–2.6 percentage points; 95% CI: –2.9, –2.4) and underweight (–1.0 percentage points; 95% CI: –1.3, –0.8), the relationship is close to zero when all covariates and local area characteristics are introduced. Moreover, when wasting is considered, the association is close to zero in all models.
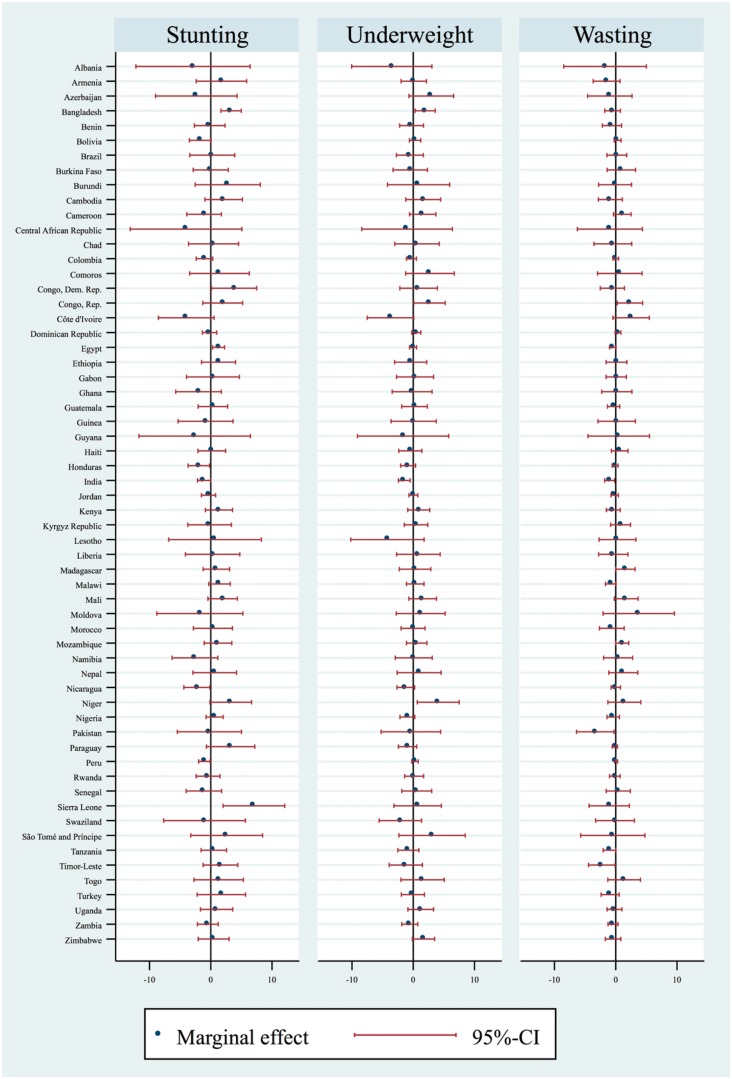
In Figure 3 we show country-level results for the association of the indicator variable of having a better-educated mother with stunting, underweight and wasting. For virtually all countries, the confidence interval includes zero, again indicating that the identity of the better-educated parent does not have any separate explanatory power. The point estimates are sometimes positive and sometimes negative, also indicating that there is no clear pattern that one parent is more important than the other. Appendix Figures B4 and B5 (available as Supplementary data at IJE online) show similar results for differences as well as ratios of years of schooling.
Figure 3.
Marginal effects for binary indicator that the mother completed more years of schooling than the father (country-wise regressions)
This figure depicts point estimates (marginal effects in percentage points) and 95% confidence intervals for the binary exposure that the mother completed more years of schooling than the father from country-wise regressions. The estimated model corresponds to the last specification from Table 4. All regressions include the full set of covariates and local area characteristics (PSU-level fixed effects). Two countries are excluded: no marginal effects could be obtained for the Maldives, as the available number of observations was too low. Similarly, Kazakhstan was excluded due to very long confidence intervals (overlapping with the zero line).
Sensitivity analyses
In the online appendix, we provide a broad range of sensitivity analyses to document that the results are not driven by choices that we made, but appear rather consistent across the board. Tables B4–B7 (available as Supplementary data at IJE online) show alternative results using severe undernutrition as the outcome. The definition of severe stunting, underweight or wasting differs from conventional undernutrition in that all children with a z-score below –3 are classified as malnourished. Moreover, in Tables B8–B23 (available as Supplementary data at IJE online), we investigate whether the findings depend on the period under study. Our finding of similar associations of paternal and maternal education with childhood stunting, underweight and wasting is robust across different periods. In Tables B24–B27 (available as Supplementary data at IJE online), we additionally adjust for maternal height. Despite a reduction in sample size, the results remain almost unaffected when this additional covariate is included. Moreover, we investigate the robustness of our results to the use of sampling weights in Tables B28–B35 (available as Supplementary data at IJE online). We rescale the original DHS sampling weights such that countries are either weighted equally or by population size. Notably, we see a similar attenuation of differences in the association of parental education with childhood undernutrition as in our main analysis when all covariates and local area characteristics are included, regardless of which type of weight is used.
Discussion
We used the largest available, nationally representative and mutually comparable repeated cross-sectional data sets from low- and middle-income countries to systematically investigate the association between maternal and paternal education with childhood undernutrition. We find that both maternal as well as paternal education levels are associated with reduced prevalences of childhood undernutrition. We evaluate a series of regressions to compare the relative importance of maternal education and paternal education.
Whereas, in models adjusted for child age, sex and country-level fixed effects, we found a stronger protective effect of maternal education than of paternal education on stunting and underweight, but not on wasting, these differences were attenuated, once we adjusted for all covariates and local area characteristics. This implies that the stronger association of maternal education with childhood undernutrition in models with minimal adjustment is not observed because maternal education is actually more important for reducing childhood undernutrition than paternal education. It is rather observed because households with higher maternal education seem to systematically differ from households with higher paternal education in their observable characteristics (covariates) or in the environments they live in. Once these differences are accounted for, the association of maternal education with childhood undernutrition becomes very similar to that of paternal education.
Note that we control for relative wealth both directly through the inclusion of wealth quintiles as well as indirectly by adding local area characteristics, as richer households may choose to live in other enumeration areas than poor households. Given our results, it is therefore possible that previous studies failing to sufficiently account for socio-economic status may erroneously attribute effects related to assortative mating (i.e. more-educated women being married to wealthier husbands) directly to maternal education.
The drawback of adding socio-economic controls is that we block a potential channel through which maternal education reduces child undernutrition, as previous studies have posited that increased schooling enables mothers to earn higher incomes, thereby indirectly leading to improved child health.21,22 However, a similar argument can be made for paternal education. Indeed, given the dual role of income as both a cause and a consequence of education, it is difficult to assess the relative importance of income as a mediator for parental education effects. A potential way to address this question could be to collect reliable data on both past and present income or wealth information in upcoming DHS.
Similarly, the DHS do not allow a comparison of mothers’ and fathers’ knowledge about child health. Consequently, we are unable to further investigate at this point how exactly paternal education is related to child nutritional status and how large the relative importance of different pathways is. The incorporation of a module on paternal health knowledge and care indicators in future questionnaires would be highly desirable for this purpose. Another limitation is that, in some cases, we cannot distinguish the biological father of the child from the current partner of the mother.
A potential threat to identification of parental-schooling effects on child undernutrition is omitted variable bias arising from maternal health, as empirical evidence suggests a positive relationship between mothers’ birth size and their children’s birth size.23 To the extent that low birth size is correlated to factors that are detrimental to success in school, stunted mothers could be both more likely to have stunted children and simultaneously exhibit low levels of education. Although we do not have data on mothers’ birth size, we include current maternal height in a robustness check, partially allowing us to control for this source of bias. It would have been desirable to also include paternal body height but this type of information is not collected in most DHS.
Whereas our study supports the previous literature in the sense that maternal education is indeed important for reducing childhood undernutrition, future studies should increase the attention devoted to paternal education to further explore its potential to decrease childhood undernutrition. Our comparison has demonstrated that there are little to no differences in the associations of maternal and paternal education with childhood undernutrition, once omitted variables are accounted for.
Funding
None.
Supplementary Material
Acknowledgements
SV, CB and SVS conceptualized the study, developed the analytical strategy and interpreted the results. SV wrote the first draft of the paper. CB conducted the statistical analysis. CB, AK and SVS contributed to interpretation of the results and writing. KH contributed to the statistical analysis.
Conflict of interest: None declared.
References
- 1. Caldwell JC. Education as a factor in mortality decline: an examination of Nigerian data. Pop Stud 1979;33:395–413. [Google Scholar]
- 2. Behrman JR, Deolalikar AB. Health and nutrition. In Chenery H, Srinivasan TN (eds). Handbook of Development Economics, Vol. 1 Elsevier, 1988, pp. 631–711. [Google Scholar]
- 3. Behrman JR, Wolfe BL. How does mother’s schooling affect family health, nutrition, medical care usage, and household sanitation? J Econometrics 1987;36:185–204. [Google Scholar]
- 4. Strauss J. Households, communities, and preschool children’s nutrition outcomes: evidence from rural Côte d’Ivoire. Econ Dev Cult Change 1990;38:231–61. [Google Scholar]
- 5. Thomas D, Strauss J, Henriques MH. How does mother’s education affect child height? J Hum Resour 1991;26:183–211. [Google Scholar]
- 6. Christiaensen L, Alderman H. Child malnutrition in Ethiopia: can maternal knowledge augment the role of income? Econ Dev Cult Change 2004;52:287–312. [Google Scholar]
- 7. Frongillo EA, De Onis M, Hanson KMP. Socioeconomic and demographic factors are associated with worldwide patterns of stunting and wasting of children. J Nutr 1997;127:2302–9. [DOI] [PubMed] [Google Scholar]
- 8. Headey DD. Developmental drivers of nutritional change: a cross-country analysis. World Dev 2013;42:76–88. [Google Scholar]
- 9. Lakshman R, Zhang J, Zhang J et al. . Higher maternal education is associated with favourable growth of young children in different countries. J Epidemiol Commun H 2013;67:595–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Matijasevich A, Howe LD, Tilling K, Santos IS, Barros AJD, Lawlor DA. Maternal education inequalities in height growth rates in early childhood: 2004 Pelotas birth cohort study. Paediatr Perinat 2012;26:236–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Shroff MR, Griffiths PL, Suchindran C, Nagalla B, Vazir S, Bentley ME. Does maternal autonomy influence feeding practices and infant growth in rural India? Soc Sci Med 2011;73:447–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Aslam M, Kingdon GG. Parental education and child health: understanding the pathways of impact in Pakistan. World Dev 2012;40:2014–32. [Google Scholar]
- 13. Semba RD, De Pee S, Sun K, Sari M, Akhter N, Bloem MW. Effect of parental formal education on risk of child stunting in Indonesia and Bangladesh: a cross-sectional study. Lancet 2008;371:322–8. [DOI] [PubMed] [Google Scholar]
- 14. Desai S, Alva S. Maternal education and child health: Is there a strong causal relationship? Demography 1998;35:71–81. [PubMed] [Google Scholar]
- 15. Handa S. Maternal education and child height. Econ Dev Cult Change 1999;47:421–39. [Google Scholar]
- 16. Breierova L, Duflo E. The Impact of Education on Fertility and Child Mortality: Do Fathers Really Matter Less than Mothers? Working Paper No. 10513. NBER Working Paper Series, 2004. [Google Scholar]
- 17. Lindeboom M, Llena-Nozal A, Van der Klaauw B. Parental education and child health: evidence from a schooling reform. J Health Econ 2009;28:109–31. [DOI] [PubMed] [Google Scholar]
- 18. Glewwe P. Why does mother’s schooling raise child health in developing countries? Evidence from Morocco. J Hum Resour 1999;34:124–59. [Google Scholar]
- 19. WHO. Child growth standards: WHO Anthro (version 3.2.2, January 2011) and macros. 2011. http://www.who.int/childgrowth/software/en/ (29 July 2014, date last accessed).
- 20. WHO. Multicentre Growth Reference Study Group. WHO Child Growth Standards: Length/Height-for-Age, Weight-for-Age, Weight-for-Length and Body Mass Index for Age: Methods and Development. Geneva: World Health Organization, 2006. [Google Scholar]
- 21. Abuya BA, Onsomu EO, Kimani JK, Moore D. Influence of maternal education on child immunization and stunting in Kenya. Matern Child Health J 2011;15:1389–99. [DOI] [PubMed] [Google Scholar]
- 22. Bellessa Frost M, Forste R, Haas DW. Maternal education and child nutrition status in Bolivia: finding the links. Soc Sci Med 2005;60:395–407. [DOI] [PubMed] [Google Scholar]
- 23. Ramakrishnan U, Martorell R, Schroeder DG, Flores R. Role of intergenerational effects on linear growth. J Nutr 1999;129:544S–9S. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.