Goodness of Fit Tests for Linear Mixed Models

Abstract

Linear mixed models (LMMs) are widely used for regression analysis of data that are assumed to be clustered or correlated. Assessing model fit is important for valid inference but to date no confirmatory tests are available to assess the adequacy of the fixed effects part of LMMs against general alternatives. We therefore propose a class of goodness-of-fit tests for the mean structure of LMMs. Our test statistic is a quadratic form of the difference between observed values and the values expected under the estimated model in cells defined by a partition of the covariate space. We show that this test statistic has an asymptotic chi-squared distribution when model parameters are estimated by maximum likelihood or by least squares and method of moments, and study its power under local alternatives both analytically and in simulations. Data on repeated measurements of thyroglobulin from individuals exposed to the accident at the Chernobyl power plant in 1986 are used to illustrate the proposed test.

1. Introduction

The linear mixed model (LMM) (McCulloch and Searle, 2001) extends the linear model by including random effects in addition to the usual fixed effects in the linear predictors. By incorporating random effects LMMs can accommodate clustered or correlated data. Developments in model fitting algorithms and their implementations in statistical packages (e.g. lme in R; PROC Mixed in SAS 9.2; SAS Institute, Cary, NC) have greatly facilitated the applications of LMMs.

Two important steps in modeling are selecting a model and checking its fit. Often model selection is done by comparing nested models, via likelihood ratio or score tests, as part of model building, and approaches are also available for comparing non-nested models (Cox, 1961; Godfrey, 1988). Variables are often selected for inclusion into a model if their p-value obtained from a Wald test meets some significance criterion. AIC, BIC and other model selection principles (Rao and Wu, 1989; Shao, 1997) also focus on selection of covariates. Once a model is selected, its fit should be assessed. For fixed effects models this is done by checking residuals and formal goodness of fit tests, such as score or Wald tests or likelihood ratio tests based on nested models. Khuri, Mathew and Sinha (1998) discussed likelihood ratio testing for fixed effects within LMMs. The literature for assessing the fit of LMMs against general alternatives is limited, and is mostly concerned with specification of the random effect distributions. Likelihood ratio testing for the presence of random effects in LMMs has been discussed by Self and Liang (1987) and Crainiceanu and Ruppert (2004). Jiang (2001) and Ritz (2004) assessed the distributional assumptions for the random effects in LMMs. Claeskens and Hart (2009) proposed tests for normality of the random effects and/or error terms. Lombardía and Sperlich (2008) introduced a test for the hypothesis of a linear fixed effect part in a generalized linear mixed model against the alternative of a semiparametric fixed effect part. Pan and Lin (2005) propose checking the adequacy of 2-level generalized linear mixed models based on the maximum absolute partial sums of residuals over a scalar projection of covariates. Their approach allows for assessing overall model fit as well as the functional form of individual components of the fixed effects part. However, to date there is no general easily computable test for checking the fit of the fixed-effect part of a model against unspecified alternatives, including omitted covariates or interaction terms or misspecifications of the functional form of covariates. Such a test is needed as a model-building tool.

Examination of the residuals of a model is a standard way to judge the quality of model fit. This can be done in many different ways. One useful way is to classify the response into mutually exclusive events defined in terms of the covariates and then assess for each category the deviation of the observed values and the expected values under the model. For survival data, Schoenfeld (1980) presented a class of omnibus chi-squared goodness of fit tests for the proportional hazards regression model, based on the observed minus the expected values of the covariates at each failure time. In this article, we adopt the idea of Schoenfeld (1980) and develop a goodness of fit test for the mean structure of LMMs by comparing the observed and expected values computed from the model within cells of a partition of the covariate space.

The rest of the paper is organized as follows. In Section 2 we present the linear mixed model, introduce the goodness of fit test statistic, and derive its asymptotic properties, including its theoretical power under local alternatives. We first assume that the random effects components and the error term are normally distributed and parameters are estimated by maximum likelihood (Section 2.2). We then relax the assumption of normality and only require finite higher order moments for the random effect and the error term and estimate parameters using least squares and method of moments (Section 2.3). We study the power of the test in simulations in Section 3, present a data example in Section 4 and close with a discussion in Section 5.

2. Goodness of fit test statistic for linear mixed models

2.1. The linear mixed model

We consider the linear mixed model (LMM) with additive random effects,

$$\mathbf{Y}=\mathbf{X}\beta +\sum _{r=1}^R{\mathbf{Z}}_r{\alpha }_r+\epsilon ,$$ (1)

where Y_N×1 is the vector of observations; ${\mathbf{X}}_{N\times p}=({\mathbf{x}}_1^T,\dots ,{\mathbf{x}}_N^T)$ is the design matrix for the fixed effects part of the model, where x_i denotes the p × 1 covariate vector for individual i; β is a p × 1 vector of unknown fixed effects parameters; Z_r is the known N × m_r design matrix for the random effect α_r, an m_r × 1 random vector, for r = 1, …, R. The random effects α₁, …, α_R are i.i.d. and independent of the error term ε. In the next section we assume that the components α_kr of α_r and ε are normally distributed. Within the LMM with a single random effect, we later require no distributional assumptions on the random effect and the error terms, but only the finiteness of their 4 + δ moments for some δ > 0. We let θ = (β, ψ) be the parameters of model (1), where $\psi =({\sigma }_{∊}^2,{\sigma }_1^2,\dots ,{\sigma }_R^2)$ is the vector of all variance components.

An important special case of model (1) is the 2-level LMM, that includes only a single random effect,

$$y_{\mathit{ij}}={\mathrm{x}}_{\mathit{ij}}^T\beta +{\alpha }_i+{∊}_{\mathit{ij}},i=1,\dots ,m,j=1,\dots ,n_i,$$ (2)

where, using a slightly different notation, the 1 × p vector ${\mathbf{x}}_{ij}^T=(1,x_{ij1},\dots ,x_{ij(p-1)})$ denotes covariates for the jth observation within the ith cluster. The first entry in x_ij is set to be 1 to accommodate an intercept term in the model. We let y_i = (y_i1, …, y_ini) denote the vector of observations for the ith cluster. The normally distributed cluster specific random effects ${\alpha }_i~N(0,{\sigma }_{\alpha }^2)$ are assumed to be independent of the error terms ${∊}_{ij}~N(0,{\sigma }_{∊}^2)$. Then under model (2), Y is also normal, Y ~ N(Xβ, V) with a block diagonal covariance matrix V, where each of the m n_i × n_i blocks V_i, i = 1, …, m, has entries ${\sigma }_{\alpha }^2+{\sigma }_{∊}^2$ on the diagonal and entries ${\sigma }_{\alpha }^2$ elsewhere. Throughout this paper, we regard models (1) and (2) as conditional specifications of the distribution of Y given X.

2.2. Test statistic and its asymptotic behavior when parameters are estimated by maximum likelihood

2.2.1. LMM with a single random effect

We first discuss the 2-level LMM in (2) when both the random effect and the error term are normally distributed and derive our test statistic for the setting where the model parameters $\theta =(\beta ,\psi )=(\beta ,{\sigma }_{\alpha }^2,{\sigma }_{∊}^2)$ are estimated by maximum likelihood (MLE). Here X is considered to be fixed.

Under Assumptions 1.1-1.6 stated below in Theorem 1, consistency and asymptotic normality of the MLE $\widehat{\theta }=(\widehat{\beta },\widehat{\psi })$ follow from Miller (1977), i.e. $\sqrt{N}(\widehat{\theta }-\theta )\stackrel{\mathcal{D}}{\to }N(0,{\mathbf{J}}^{-1})$, where J denotes the limiting Fisher information matrix. Wand (2007) showed that under model (2), $\widehat{\beta }$ and $\widehat{\psi }$ are asymptotically uncorrelated and thus

$$\mathbf{J}=\left[\begin{array}{cc}\hfill {\mathbf{J}}_{\beta \beta }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \mathbf{M}\hfill \end{array}\right],$$ (3)

where

$${\mathbf{J}}_{\beta \beta }=\underset{N\to \infty }{\lim }{\mathbf{X}}^T{\mathbf{V}}^{-1}\mathbf{X}∕N.$$ (4)

We assume that J_ββ is positive definite (Assumption 1.5, Theorem 1).

To test the goodness of fit of the mean structure of the LMM (2), we first divide the covariate space into L disjoint regions E₁, …, E_L. These regions are based on categorizations of single covariates or of composites of multiple covariates that may or may not be included in the current model. For example, for a single continuous covariate with support on the interval (a, b), the cells E could be defined by E_l = (c_l, c_l+1], l = 1, …, L − 1 where a = c₁ < c₂ < … < c_L−1 < c_L = b. For a categorical (discrete) variable X that takes the values c_l for l = 1, …, L, the partition can be defined by E_l = {X = c_l}. We compute the observed and expected sums in each region E_l as

$$f_l=\sum _{i=1}^m\sum _{j=1}^{n_i}{I}_{\{{\mathrm{x}}_{\mathit{ij}}\in E_t\}}{y}_{\mathit{ij}},$$ (5)

$$e_l\left(\beta \right)=\sum _{i=1}^m\sum _{j=1}^{n_i}{I}_{\{{\mathrm{x}}_{\mathit{ij}}\in E_t\}}E\left(y_{\mathit{ij}}\right)=\sum _{i=1}^m\sum _{j=1}^{n_i}{I}_{\{{\mathrm{x}}_{\mathit{ij}}\in E_l\}}{\mathrm{x}}_{\mathit{ij}}^T\beta ,$$ (6)

where I denotes the indicator function. When the cell partition is based on covariates not included in the model (2), then we let x_ij denote the vector of all available covariates and ${\mathbf{x}}_{ij}^{\ast }$ the covariates used in the model, and use $e_l\left({\beta }^{\ast }\right)={\sum }_{i=1}^m{\sum }_{j=1}^{n_i}{I}_{\{{\mathbf{x}}_{ij}\in E_l\}}{\left({\mathbf{x}}_{ij}^{\ast }\right)}^T{\beta }^{\ast }$, where β* corresponds to the coefficients of ${\mathbf{x}}_{ij}^{\ast }$. However, for notational simplicity we employ the expressions (5) and (6) throughout.

Letting f = (f₁, …, f_L) and e(β) = (e₁(β), …, e_L(β)), the observed minus the expected vector is

$$\mathbf{f}-\mathbf{e}\left({\beta }_0\right)=\left(\begin{array}{c}\hfill {\sum }_{i=1}^m{\sum }_{j=1}^{n_i}{I}_{\{{\mathrm{x}}_{ij}\in E_1\}}(y_{\mathit{ij}}-{\mathrm{x}}_{\mathit{ij}}^T{\beta }_0)\hfill \\ \hfill ⋮\hfill \\ \hfill {\sum }_{i=1}^m{\sum }_{j=1}^{n_i}{I}_{\{{\mathrm{x}}_{ij}\in E_1\}}(y_{\mathit{ij}}-{\mathrm{x}}_{\mathit{ij}}^T{\beta }_0)\hfill \end{array}\right).$$ (7)

Since the true parameter vector β₀ is unknown, to create a test statistic we must replace it by a consistent asymptotically normal estimator, the MLE $\widehat{\beta }$ as in (7) within Section 2.2 and the generalized least squares estimator (15) in Section 2.3. We further make Assumption 1.7 which, together with Assumptions 1.4 and 1.5, ensures the existence of components of the limiting variance covariance matrix for the test statistic.

Theorem 1. We make the following assumptions:

Assumption 1.1. The true parameter point θ₀ = (β₀, ψ₀) is an interior point of $ϴ=({\mathcal{R}}^p,{\left({\mathcal{R}}^{+}\right)}^{R+1})$.

Assumption 1.2. ${\alpha }_i~N(0,{\sigma }_{\alpha }^2)$ and ${∊}_{ij}~N(0,{\sigma }_{∊}^2)$.

Assumption 1.3. X is fixed and has full rank.

Assumption 1.4. ${\lim }_{K\to \infty }{\lim \sup }_{m\to \infty }\frac{1}{m}{\sum }_{i=1}^m{I}_{\{n_i^2\ge K\}}{n}_i^2=0$.

Assumption 1.5. J_ββ = lim_N→∞ X^TV⁻¹ X/N exists and is positive definite.

Assumption 1.6. The 2 × 2 matrix M with elements defined below exists and is positive definite;

$${\left[M\right]}_{\mathit{st}}=\frac{1}{2}\underset{N\to \infty }{\lim }\mathit{tr}\left(V^{-1}{G}_s{V}^{-1}{G}_t\right)∕N,s,t=0,1,$$

where G₀ = I is the N × N identity matrix and G₁ is the block-diagonal matrix with m blocks and each block is an n_i × n_i matrix of all 1s. After some algebra,

$$\begin{array}{cc}\hfill & {\left[M\right]}_{00}=\underset{N\to \infty }{\lim }\frac{1}{2N}\mathit{tr}\left(V^{-2}\right)=\underset{N\to \infty }{\lim }\frac{1}{2N}\sum _{i=1}^m\left(\frac{n_i-1}{{\sigma }_{∊}^4}+\frac{1}{{({\sigma }_{∊}^2+n_i{\sigma }_{\alpha }^2)}^2}\right),\hfill \\ \hfill & {\left[M\right]}_{01}={\left[M\right]}_{10}=\underset{N\to \infty }{\lim }\frac{1}{2N}\mathit{tr}\left(V^{-2}{1}_N^{\otimes 2}\right)=\underset{N\to \infty }{\lim }\frac{1}{2N}\sum _{i=1}^m\frac{n_i}{{({\sigma }_{∊}^2+n_i{\sigma }_{\alpha }^2)}^2},\hfill \\ \hfill & {\left[M\right]}_{11}=\underset{N\to \infty }{\lim }\frac{1}{2N}\mathit{tr}\left(V^{-1}{G}_1{V}^{-1}{G}_1\right)=\underset{N\to \infty }{\lim }\frac{1}{2N}\sum _{i=1}^m\frac{n_i^2}{{({\sigma }_{∊}^2+n_i{\sigma }_{\alpha }^2)}^2}\hfill \end{array}$$

It is easy to see that matrix M is the average of nonnegative definite matrices. Under Assumption 1.4, M is positive definite if and only if ${\lim \inf }_{m\to \infty }{\sum }_{i=1}^m{n}_i∕m>1$. Thus the main restriction in Assumption 1.6 is the requirement that M exists.

Assumption 1.7. For any cell partition E₁, … E_L of the covariate space, ${\lim }_{N\to \infty }{\sum }_{i=1}^m{\sum }_{j=1}^{n_i}{I}_{\{x_{ij}\in E_l\}}{\mathbf{x}}_{ij}^T∕N$ exists for l = 1, …, L.

For model (2), under Assumptions 1.1-1.7, as N → ∞,

$$\sqrt{N}\left(\begin{array}{c}\hfill \{\mathbf{f}-e({\beta }_0\left)\right\}∕N\hfill \\ \hfill \widehat{\beta }-{\beta }_0\hfill \end{array}\right)\stackrel{\mathcal{D}}{\to }N(0,{\mathit{DVD}}^T),$$

where

$$\mathit{D}={\left(\begin{array}{c}\hfill N^{-1∕2}[I_{\{x_{11}\in E_1\}}\cdots I_{\{x_{{\mathit{mn}}_m}\in E_1\}}]\hfill \\ \hfill ⋮\hfill \\ \hfill N^{-1∕2}[I_{\{x_{11}\in E_L\}}\cdots I_{\{x_{{\mathit{mn}}_m}\in E_L\}}]\hfill \\ \hfill N^{-1∕2}{\mathit{J}}_{\beta \beta }^{-1}{\mathbf{X}}^T{\mathbf{V}}^{-1}\hfill \end{array}\right)}_{(L+p)\times N},$$

and

$${\mathit{DVD}}^T={\left(\begin{array}{cc}\hfill \mathit{H}\hfill & \hfill \Lambda {\mathit{J}}_{\beta \beta }^{-1}\hfill \\ \hfill {\mathit{J}}_{\beta \beta }^{-1}{\Lambda }^T\hfill & \hfill {\mathit{J}}_{\beta \beta }^{-1}\hfill \end{array}\right)}_{(L+p)\times (L+p)}.$$

The off-diagonal and diagonal elements of H, H_lk and H_ll, are

$$H_{\mathit{lk}}={\sigma }_{\alpha }^2\underset{N\to \infty }{\lim }\frac{1}{N}\sum _{i=1}^m\left\{\left(\sum _{j=1}^{n_i}{I}_{\{x_{\mathit{ij}}\in E_l\}}\right)\left(\sum _{j=1}^{n_i}{I}_{\{x_{\mathit{ij}}\in E_k\}}\right)\right\},$$ (8)

$$H_{\mathit{ll}}={\sigma }_{∊}^2\underset{N\to \infty }{\lim }\frac{1}{N}\sum _{i=1}^m\sum _{j=1}^{n_i}{I}_{\{x_{\mathit{ij}}\in E_l\}}+{\sigma }_{\alpha }^2\underset{N\to \infty }{\lim }\frac{1}{N}\sum _{i=1}^m{\left(\sum _{j=1}^{n_i}{I}_{\{x_{\mathit{ij}}\in E_l\}}\right)}^2,$$ (9)

and

$$\Lambda ={\left(\begin{array}{c}\hfill {\Lambda }_1^T\hfill \\ \hfill ⋮\hfill \\ \hfill {\Lambda }_L^T\hfill \end{array}\right)}_{L\times p}=\underset{N\to \infty }{\lim }\frac{1}{N}\left(\begin{array}{c}\hfill {\sum }_{i=1}^m{\sum }_{j=1}^{n_i}{I}_{\{x_{\mathit{ij}}\in E_1\}}{\mathrm{x}}_{\mathit{ij}}^T\hfill \\ \hfill ⋮\hfill \\ \hfill {\sum }_{i=1}^m{\sum }_{j=1}^{n_i}{I}_{\{x_{\mathit{ij}}\in E_L\}}{\mathrm{x}}_{\mathit{ij}}^T\hfill \end{array}\right).$$ (10)

The proof of Theorem 1 is given in Appendix A.

Corollary 1. Consistent estimators for the quantities given in (8), (9), (10) and (4) are

$$\begin{array}{c}\hfill {\widehat{H}}_{\mathit{lk}}={\widehat{\sigma }}_{\alpha }^2\frac{1}{N}\sum _{i=1}^m\left\{\left(\sum _{j=1}^{n_i}{I}_{\{x_{\mathit{ij}}\in E_l\}}\right)\left(\sum _{j=1}^{n_i}{I}_{\{x_{\mathit{ij}}\in E_k\}}\right)\right\}\hfill \\ \hfill {\widehat{H}}_{\mathit{ll}}={\sigma }_{∊}^2\frac{1}{N}\sum _{i=1}^m\sum _{j=1}^{n_i}{I}_{\{x_{\mathit{ij}}\in E_l\}}+{\sigma }_{\alpha }^2\frac{1}{N}\sum _{i=1}^m{\left(\sum _{j=1}^{n_i}{I}_{\{x_{\mathit{ij}}\in E_l\}}\right)}^2,\hfill \\ \hfill {\widehat{\Lambda }}_l^T=\sum _{i=1}^m\sum _{j=1}^{n_i}{I}_{\{x_{\mathit{ij}}\in E_l\}}{\mathrm{x}}_{\mathit{ij}}^T∕N,{\widehat{\mathbf{J}}}_{\beta \beta }=X^T{\widehat{V}}^{-1}\mathit{X}∕N.\hfill \end{array}$$

Corollary 2. For model (2), under Assumptions 1.1-1.7 in Theorem 1, as N → ∞, $\{\mathit{f}-\mathit{e}(\widehat{\beta }\left)\right\}∕\sqrt{N}\stackrel{\mathcal{D}}{\to }N(0,\Sigma )$, where $\Sigma =\mathit{H}-\Lambda {\mathit{J}}_{\beta \beta }^{-1}{\Lambda }^T$ is an L × L matrix that is consistently estimated by $\widehat{\Sigma }=\widehat{\mathbf{H}}-\widehat{\Lambda }{\widehat{\mathbf{J}}}_{\beta \beta }^{-1}{\widehat{\Lambda }}^T$ based on Corollary 1.

The proof of Corollary 2 is given in Appendix B.

Our goodness of fit test statistic is then given by the quadratic form

$$T=\frac{1}{N}{\{\mathbf{f}-\mathbf{e}(\widehat{\beta }\left)\right\}}^T{\widehat{\Sigma }}_{\zeta }^{-}\{\mathbf{f}-\mathbf{e}(\widehat{\beta }\left)\right\},$$ (11)

where ${\widehat{\Sigma }}_{\zeta }^{-}$ denotes the Moore-Penrose generalized-inverse (also called ‘pseudo-inverse’) of a slight modification of the consistent variance estimator $\widehat{\Sigma }$. We define ${\widehat{\Sigma }}_{\zeta }^{-}$ in the following paragraph. Under the null hypothesis that model (2) is the true model, T has an asymptotic central ${\chi }_r^2$ distribution, where with probability converging to 1 as N → ∞, $r=\text{rank}\left({\widehat{\Sigma }}_{\zeta }\right)=\text{rank}\left(\Sigma \right)$. This result applies to the modification ${\widehat{\Sigma }}_{\zeta }$ of any consistent estimator $\widehat{\Sigma }$ of the Σ matrix, such as restricted maximum likelihood (REML) estimators.

The modification ${\widehat{\Sigma }}_{\zeta }$ of variance estimates we describe next applies in several places in this paper. The issue is always to avoid numerical instabilities and asymptotic distributional anomalies due to rank differences between consistent nonnegative-definite variance estimators $\widehat{\Sigma }$ and the true asymptotic variance Σ. Assume in what follows that there exists a known threshold ξ (say, 10⁻⁴) smaller than all non-zero singular values of Σ. Since Σ is nonnegative definite, all singular values are nonnegative. Denoting the spectral decomposition of $\widehat{\Sigma }$ as ${\sum }_{k=1}^q{c}_{kN}{\mathbf{v}}_{kN}{\mathbf{v}}_{kN}^T$, where ${\left\{{\mathbf{v}}_{kN}\right\}}_{k=1}^q$ is an orthonormal basis of eigenvectors of $\widehat{\Sigma }$ and c_kN are the corresponding eigenvalues, the modification ${\widehat{\Sigma }}_{\zeta }$ of $\widehat{\Sigma }$ is defined as ${\widehat{\Sigma }}_{\zeta }={\sum }_{k=1}^N{I}_{[c_{kN}>\zeta ]}{c}_{kN}{\mathbf{v}}_{kN}{\mathbf{v}}_{kN}^T$, and its Moore-Penrose pseudo-inverse is then ${\widehat{\Sigma }}_{\zeta }^{-}={\sum }_{k=1}^q{I}_{[c_{kN}>\zeta ]}{\left(c_{kN}\right)}^{-1}{\mathbf{v}}_{kN}{\mathbf{v}}_{kN}^T$. We prove in Proposition 1, Appendix D, that ${\widehat{\Sigma }}_{\zeta }$ is coordinate-free and unique, that rank $\text{rank}\left({\widehat{\Sigma }}_{\zeta }\right)=r$ with probability converging to 1, and that the asymptotic distribution of T in (11) is ${\chi }_r^2$ and would persist if the Moore-Penrose choice of pseudo-inverse were replaced by any other generalized-inverse of ${\widehat{\Sigma }}_{\zeta }$ as defined in Rao (1973, Sec. 1.b). In addition, the assumption of a fixed known threshold ξ can be replaced by allowing ξ = ξ_N to depend non-randomly on N and converge to 0 sufficiently slowly. (The rate would depend on the specific consistent estimator $\widehat{\Sigma }$.)

2.2.2. LMM with multilevel additive random effects

We now consider the general LMM with multilevel additive random effects given in equation (1) with a fixed covariate matrix X.

Again, the covariate space, comprised of covariates not all of which need be included in the model, is divided into L disjoint regions E₁, …, E_L, and for l = 1, 2, …, L, we define the observed and expected vectors f = (f₁, …, f_L) and e(β) = (e₁(β), …, e_L(β)) as $f_l={\sum }_{k=1}^N{I}_{\{{\mathbf{x}}_k\in E_l\}}{y}_k$, and $e_l\left(\beta \right)={\sum }_{k=1}^N{I}_{\{{\mathbf{x}}_k\in E_l\}}E\left(y_k\right)={\sum }_{k=1}^N{I}_{\{{\mathbf{x}}_k\in E_l\}}{\mathbf{x}}_k^T\beta$. The impact of the choice of L is discussed further in the simulation section (Section 3).

Conditions in Miller (1977) that ensure the consistency and asymptotic normality of the MLE of θ = (β, ψ) are given in the Supplementary Material S1 (assumptions A.1-A.7). We additionally make assumptions A.8-A.9 (Supplementary Material S1) to ensure the existence of large-sample averages involving x_k and I_[xk∈Ej].

Theorem 2. For model (1), under Assumptions A.1-A.9 given in the Supplementary Material S1,

$$T={\{f-e(\widehat{\beta }\left)\right\}}^T{\widehat{\Sigma }}_{\zeta }^{-}\{f-e(\widehat{\beta }\left)\right\}∕N\stackrel{\mathcal{D}}{\to }{\chi }_r^2,$$ (12)

as N → ∞, where $\widehat{\beta }$ is the MLE of β, $\widehat{\Sigma }$ is a consistent estimator of $\Sigma =\mathit{H}-\Lambda {\mathit{J}}_{\beta \beta }^{-1}{\Lambda }^T$, ${\widehat{\Sigma }}_{\zeta }$ is the modification of $\widehat{\Sigma }$ as defined in the last paragraph of Section 2.2.1, ${\widehat{\Sigma }}_{\zeta }^{-}$ denotes the Moore-Penrose pseudoinverse of ${\widehat{\Sigma }}_{\zeta }$, and for r ≡ rank(Σ), $P\left(rank\right({\widehat{\Sigma }}_{\zeta })=r)\to 1$, as N → ∞. Here H = limN→∞ FVF^T, with

$$\mathit{F}=\frac{1}{\sqrt{N}}\left(\begin{array}{c}\hfill I_{\{x_1\in E_1\}}\cdots I_{\{x_N\in E_1\}}\hfill \\ \hfill ⋮\hfill \\ \hfill I_{\{x_1\in E_L\}}\cdots I_{\{x_N\in E_L\}}\hfill \end{array}\right)$$ (13)

and the l-th row of Λ given by

$${\Lambda }_l^T=\underset{N\to \infty }{\lim }\frac{1}{N}\sum _{k=1}^N{I}_{\{x_k\in E_l\}}{\mathrm{x}}_k^T$$ (14)

The proof of Theorem 2 is similar to that of Theorem 1 and is given in Supplementary Material S2.

2.3. Test statistic and its asymptotic properties for two-level LMM with parameters estimated by least squares and method of moments

We consider the LMM (2), but now only require that E(α_i) = E(∊_ij) = 0, $Var\left({\alpha }_i\right)={\sigma }_{\alpha }^2$, $Var\left({∊}_{ij}\right)={\sigma }_{∊}^2$, and that there is a δ > 0, such that $E\left({\alpha }_i^{4+\delta }\right)<\infty$ and $E\left({∊}_{ij}^{4+\delta }\right)<\infty$, instead of assuming normality of α_i and ∊_ij. To compensate for the weaker distributional assumptions, we assume for simplicity in probability limit theorems that the covariate vectors x_ij are random, that {(x_i1, …, x_ini), n_i} are i.i.d. and that $E\left(n_i^2\right)<\infty$ and $\mid \mid E\left({\mathbf{x}}_i^T{\mathbf{x}}_i\right)\mid \mid <\infty$, where x_i denotes the n_i × p matrix of covariates for the ith cluster.

We estimate β by the generalized least squares estimator

$$\tilde{\beta }={\left({\mathbf{X}}^T{\tilde{V}}^{-1}\mathbf{X}\right)}^{-1}\left({\mathbf{X}}^T{\tilde{V}}^{-1}\mathbf{Y}\right)={\left({\mathbf{X}}^T{\tilde{V}}^{-1}\mathbf{X}\right)}^{-1}\left({\mathbf{X}}^T{\tilde{V}}^{-1}\mathbf{Y}\right)+o_p\left(1\right),\text{as}N\to \infty ,$$ (15)

where V depends on the variance components $\psi =({\sigma }_{\alpha }^2,{\sigma }_{∊}^2)$. They are estimated by the method of moments by equating the right-hand sides of

$$E\left\{\sum _{i=1}^m\sum _{j=1}^{n_i}{(y_{\mathit{ij}}-{\stackrel{‒}{y}}_{i.})}^2\right\}=\sum _{i=1}^m\sum _{j=1}^{n_i}{({\mathrm{x}}_{\mathit{ij}}^T\beta -{\stackrel{‒}{\mathrm{x}}}_i^T\beta )}^2+(N-m){\sigma }_{∊}^2$$ (16)

$$E\left\{\sum _{i=1}^m\sum _{j=1}^{n_i}{({\stackrel{‒}{y}}_{i.}-{\stackrel{‒}{y}}_{..})}^2\right\}=\sum _{i=1}^m{n}_i{({\stackrel{‒}{\mathrm{x}}}_{i.}^T\beta -{\stackrel{‒}{\mathrm{x}}}_{..}^T\beta )}^2+\left(N-\frac{1}{N}\sum _{i=1}^m{n}_i^2\right){\sigma }_{\alpha }^2+(m-1){\sigma }_{∊}^2$$ (17)

respectively with their estimates based on the sum of squares within groups (SSW) and the sum of squares between groups (SSB) in the analysis of variance, given by

$$\mathrm{SSW}=\sum _{i=1}^m\sum _{j=1}^{n_i}{(y_{\mathit{ij}}-{\stackrel{‒}{y}}_{i.})}^2\text{and}\mathrm{SSB}=\sum _{i=1}^m\sum _{j=1}^{n_i}{({\stackrel{‒}{y}}_{i.}-{\stackrel{‒}{y}}_{..})}^2=\sum _{i=1}^m{n}_i{\stackrel{‒}{y}}_{i.}^2-N{\stackrel{‒}{y}}_{..}^2.$$

The notation ${\stackrel{‒}{y}}_i$ stands for ${\stackrel{‒}{y}}_{i.}={\sum }_j{y}_{ij}∕n_i$ and ${\stackrel{‒}{y}}_{..}={\sum }_i{\sum }_j{y}_{ij}∕N$, and similar averages apply to the covariates x. Because different clusters are independent, and ${\sum }_{j=1}^{n_i}{(y_{ij}-{\stackrel{‒}{y}}_{i.})}^2,n_i{\stackrel{‒}{y}}_{i.}^2$, and ${\sum }_{j=1}^{n_i}{y}_{ij}$ have finite second moments, SSW/m and SSB/m satisfy the law of large numbers. The estimating equations (15), (16) and (17) can be solved iteratively for $\theta =(\beta ,{\sigma }_{\alpha }^2,{\sigma }_{∊}^2)$ and yield consistent estimates $\tilde{\theta }$ (Richardson and Welsh, 1994; Jiang, 1996).

To obtain the test statistic, we again compute the observed and expected values in each of the L cells of the covariate space as in (5) and (6).

Theorem 3. For the LMM (2), under Assumptions 3.1-3.3 in Appendix D, as N → ∞, $\{\mathit{f}-e(\tilde{\beta }\left)\right\}∕\sqrt{N}\stackrel{\mathcal{D}}{\to }N(0,\Sigma )$, where $\Sigma =\mathit{H}-\Lambda {\mathit{J}}_{\beta \beta }^{-1}{\Lambda }^T$. Thus $T={\{\mathit{f}-e(\tilde{\beta }\left)\right\}}^T{\widehat{\Sigma }}_{\zeta }^{-}\{\mathit{f}-e(\tilde{\beta }\left)\right\}∕N\stackrel{\mathcal{D}}{\to }{\chi }_k^2$, where $\widehat{\Sigma }$ is a consistent estimator of Σ, ${\widehat{\Sigma }}_{\zeta }$ is the modification of $\widehat{\Sigma }$ as defined in the last paragraph of the section 2.2.1, ${\widehat{\Sigma }}_{\zeta }^{-}$ denotes the Moore-Penrose pseudoinverse of ${\widehat{\Sigma }}_{\zeta }$, and $P\left(rank\right({\widehat{\Sigma }}_{\zeta })=rank(\Sigma )=r)\to 1$ N → ∞.

As X is a matrix of random variables in this section, Assumption 3.3 ensures that Assumptions 1.4-1.7 hold, which are needed when X are assumed to be fixed in Section 2.1. The matrices H, Λ and J_ββ are the same as for the two-level LMM (2) when parameters are estimated by maximum likelihood under the assumption of normality of α_i and ∊_ij and are specified in (8), (9), (10) and (4). The proof of the theorem is given in Appendix E.

Remark 1. Theorem 1 and Theorem 3 are still valid when empirical quantiles instead of fixed cut-o s are used to define cell partition, is we assume that the empirical quantiles of coordinates of x_i converge to unique limits or under Assumption 3.3.

2.4. Power of the test

For the multi-level LMM (1), we derive the theoretical power under local, and more specifically under contiguous alternatives for the test in (12) for the situation where some covariates that influence the outcome y are omitted from model (1). This case also covers omitted interactions of covariates or omitted higher order terms and is thus practically relevant.

Let X be the true N × p covariate matrix and X* be a submatrix of X of dimension N × p* used to fit model (1), with p* < p. The null hypothesis is H₀: θ_N = θ₀. We assess the power of T under the alternative

$$H_1:{\theta }_N={\theta }_0+\mathrm{a}∕\sqrt{N},$$ (18)

with θ₀ = (β₀, ψ₀), where several components of β₀ are 0. The vector ${\beta }_0^{\ast }$ corresponding to X*. Here $a∕\sqrt{N}$ is the vector difference between the parameter values under the alternative hypothesis and the parameter values under the null hypothesis.

Based on the derivation for Theorem 2, we have that under H₀, $\{\mathbf{f}-e({\widehat{\beta }}^{\ast }\left)\right\}∕\sqrt{N}\stackrel{\mathcal{D}}{\to }N\left({0,\Sigma }^{\ast }\right)$. By applying Le Cam’s third lemma (see Appendix F for details), we find that under the alternative hypothesis H₁ in (18),

$$\{\mathbf{f}-\mathbf{e}({\widehat{\beta }}^{\ast }\left)\right\}∕\sqrt{N}\stackrel{\mathcal{D}}{\to }N(\tau ,{\Sigma }^{\ast }),$$ (19)

where

$$\tau =\underset{N\to \infty }{\lim }[\Lambda -{\Lambda }^{\ast }{\left\{{\left({\mathbf{X}}^{\ast }\right)}^T{\mathbf{V}}^{-1}{\mathbf{X}}^{\ast }\right\}}^{-1}\{{\left({\mathbf{X}}^{\ast }\right)}^T{\mathbf{V}}^{-1}\mathbf{X}\left\}\right]\mathrm{a},$$ (20)

with Λ given by expression (14). Λ* is computed using X* in place of X in (14).

Thus under H₁, T* has a limiting noncentral χ² distribution

$$T^{\ast }=\frac{1}{N}{\{\mathbf{f}-\mathbf{e}({\widehat{\beta }}^{\ast }\left)\right\}}^T\left({\widehat{\Sigma }}_{\zeta }^{\ast }\right)-\{\mathbf{f}-\mathbf{e}({\widehat{\beta }}^{\ast }\left)\right\}\stackrel{\mathcal{D}}{\to }{\chi }_r^2\left(\lambda \right),$$ (21)

where $r=rank\left({\widehat{\Sigma }}_{\zeta }^{\ast }\right)$ and the non centrality parameter is $\lambda ={\tau }^T{\left({\widehat{\Sigma }}_{\zeta }^{\ast }\right)}^{-}\tau$. For a given type I error level α, the power is thus $P(T^{\ast }>{\chi }_{r,\alpha }^2)$, where ${\chi }_{r,\alpha }^2$ is the 1 − α quantile of the central ${\chi }_r^2$ distribution and P denotes the non central ${\chi }_r^2\left(\lambda \right)$ distribution. In the computation of the power we use the Moore-Penrose inverse of a modification ${\widehat{\Sigma }}_{\zeta }^{\ast }$ as in (11) of a consistent estimator ${\widehat{\Sigma }}^{\ast }$ in (20).

As an illustration, we show the asymptotic power to detect lack of fit for an omitted covariate for the two-level LMM (2). We assume Y ~ N(X^T, V), where X = (1, x₁, x₂, x₃) and V is the block diagonal covariance matrix. The x_ij = (x_ij1, x_ij2, x_ij3), i = 1, …, m; j = 1, …, n_i are i.i.d. and drawn from a multivariate normal distribution

$$\left(\begin{array}{c}\hfill x_1\hfill \\ \hfill x_2\hfill \\ \hfill x_3\hfill \end{array}\right)\sim N\left(\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right],\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill {\rho }_{13}\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill {\rho }_{23}\hfill \\ \hfill {\rho }_{13}\hfill & \hfill {\rho }_{23}\hfill & \hfill 1\hfill \end{array}\right]\right),$$ (22)

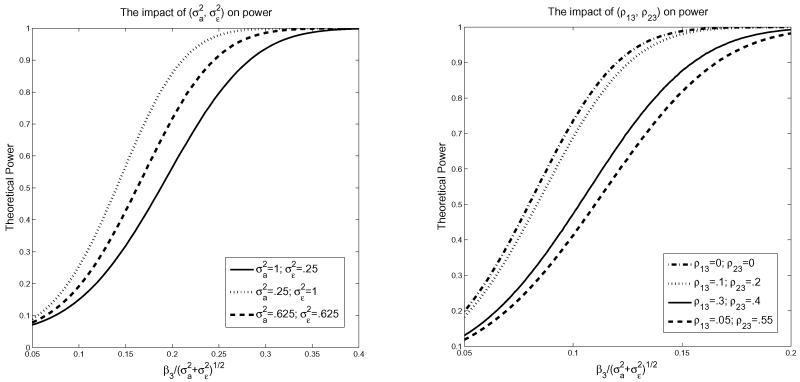
and x_ij and n_i are independent. In fitting the model, we omit x₃ leading to X* = (1, x₁, x₂) and a = (0, 0, 0, β₃) in (20). For this setting, τ in (20) and Σ* in (19) can be computed explicitly as a functions of the moments of X and n_i (section 2.2.3., Tang, 2010). We study the impact of the magnitude of the variance components ${\sigma }_{\alpha }^2$ and ${\sigma }_{∊}^2$ and the correlations ρ₁₃ and ρ₂₃ in (22) between the omitted covariate x₃ and the covariates in the model (x₁ and x₂) on the theoretical power when the cell partition is based on theoretical quantiles of the omitted covariate x₃ with L = 8 cells. For ρ₁₃ = 0.5 and ρ₂₃ = 0.6, Figure 1 (left panel) plots the theoretical power against ${\beta }_3∕{({\sigma }_{\alpha }^2+{\sigma }_{∊}^2)}^{1∕2}$ for three choices of $({\sigma }_{\alpha }^2,{\sigma }_{∊}^2)$ all corresponding to the same overall variance ${\sigma }_{\alpha }^2+{\sigma }_{∊}^2$ and varying β₃ on the x-axis. For any fixed pair of $({\sigma }_{\alpha }^2,{\sigma }_{∊}^2)$, the power of the test, not surprisingly, increases as a function of β₃, the coefficient of the omitted covariate x₃. This can also be seen by taking a first order Taylor expansion of the theoretical power formula around λ = 0, as the power for λ close to zero depends linearly on λ = τ^T(Σ*)⁻¹τ, which is a function of ${\beta }_3^2$. Figure 1 (left panel) shows that for any fixed β₃ the power increases when the random effect ${\sigma }_{\alpha }^2$ decreases compared to the error term ${\sigma }_{∊}^2$. Figure 1 (right panel) plots the power for ${\sigma }_{\alpha }^2=1$, ${\sigma }_{∊}^2=0.25$ for different choices of (ρ₁₃, ρ₂₃). The power increases as ${\rho }_{13}^2+{\rho }_{23}^2$ decreases. For ρ₁₃ = 0 and ρ₂₃ = 0, that is, when x₃ is uncorrelated with x₁ and x₂, the power is not affected by the individual values of ${\sigma }_{\alpha }^2$ and ${\sigma }_{∊}^2$, but only depends on the sum ${\sigma }_{\alpha }^2+{\sigma }_{∊}^2$. The theoretical formulas for power under contiguous-alternatives given here will generally be close to the actual power only for very large sample sizes. However, numerical studies presented in the next section show that these formulas often also agree with empirical power in samples of moderate size (m = 50, N = 150 to N = 200).

Figure 1.

Left: Theoretical power as a function of $({\sigma }_{\alpha }^2,{\sigma }_{∊}^2)$; Right: Power as a function of (ρ₁₃, ρ₂₃).

3. Simulations to assess power and robustness of the test statistic

For a given number of clusters m, we first generated the cluster sizes n_i from a uniform distribution on {2, 3, 4, 5} for i = 1, …, m and then drew $N={\sum }_{i=1}^m{n}_i$ independent covariates x_ij for all simulations presented below. We present scenarios for which we believe out test would be practically most relevant: models with omitted main effects (Scenario I), omitted interaction terms and main effects (Scenarios II and III) and misspecified functional forms of a covariate (Scenario IV). We covered a range of effect sizes to provide a fair assessment of the performance of our test.

3.1. Main effects only (Scenario I)

Here x_ij = (x_1ij, x_2ij, x_3ij) were drawn from the multivariate normal distribution given in (22). Given X = (1, x₁, x₂, x₃), β, σ_α = 1 and σ_∊ = 0.5, we generated Y from a multivariate normal distribution, Y ~ N(X^T β, V).

3.1.1. Size and power of T

To check the size of the test for various choices of cell partition based on X, we let ρ₁₃ = ρ₂₃ = 0 in (22), β = (β₀, β₁, β₂, β₃) = (1, 1, 1, 1), m = 500 and fit model (2) with all covariates X in the model. Table 1 gives the number of cells and the covariates that are the basis of the cell partition in the first column. Cell partitions in the computation of the test statistic T were based on empirical quantiles of the respective components of X. For all cell partitions in Table 1 the empirical sizes were close to the nominal α levels of 0.05 and 0.1.

Table 1.

Empirical size of the test under different cell partitions (Scenario I). m = 500, E(N) = 1750, β₃ = 1, ρ₁₃ = ρ₂₃ = 0, σ_α = 1, σ_ε = .5, K = 2000. L denotes the number of cells for the test statistic.

L	α	Emp. Size	α	Emp. Size
8 (x1)	0.05	0.052	0.1	0.103
3×4 (x1, x2)	0.05	0.053	0.1	0.108
5×4 (x1, x3)	0.05	0.045	0.1	0.094
6×7 (x2, x3)	0.05	0.047	0.1	0.096

To assess the power of the test, we generated data from model (2) that includes all three covariates but then omitted x₃ in fitting the model to the data. We set (ρ₁₃, ρ₂₃) = (0.5, 0.6), β = (β₀, β₁, β₂, β₃) = (1, 1, 1, 0.25). We then generated K = 2000 datasets for a given X. We repeated this data generation process for D = 1000 independently drawn design matrices X. For a given X, we computed the theoretical power of T* in (21) based on the asymptotic χ² distribution with the true values of ${\sigma }_{\alpha }^2$ and ${\sigma }_{∊}^2$. The empirical moments for X were used in the calculation of the non-centrality parameter λ. For a given X and each generated Y, we calculated the estimated theoretical power based on the asymptotic χ² distribution with the variance components estimated based on the given Y and empirical moments of X in (20). We then repeated the calculation of the estimated theoretical power for each of the K = 2000 generated Y and by taking the average, we obtained a mean estimated theoretical power for that given X. For each given design matrix X, we also calculated the empirical power based on K = 1000 iterations on Y. For m = 20 clusters the cell partition was based on the empirical quantiles of the omitted x₃ with L = 8 cells to avoid empty cells, but for m = 50 or 500, we used theoretical quantiles of x₃ as cell boundaries for computational ease.

The mean theoretical power (“Theo.Pow.”), the mean estimated theoretical power (“Theo.Pow.hat”) and the empirical power (“Empi.Pow.n”) agreed very well, even when m is small (Table 2). However, only for m = 500 was there adequate power to detect lack of fit when β₃ = 0.25, which is substantially smaller than the coefficients β₁ = β₂ = 1 of x₁, and x₂, the covariates included in the model. When the effect of the omitted covariate was larger, β₃ = 0.8, the test statistic had approximately 80% power even for m = 50 clusters.

Table 2.

Power and robustness study (Scenario I) with L = 8,K = 2000, D = 1000, (ρ₁₃ ,ρ₂₃) = (.5,.6),σ_α = 1, σ_ε = .5. Standard deviation (std.dev.) relates to variation across the randomly generated 500 covariate matrices X

Power	m = 500, EN = 1750		m = 50, EN = 175		m = 20, EN = 70
β3 = .25	mean	std.dev.	mean	std.dev.	mean	std.dev.
Theo.Pow.	0.800	0.040	0.120	0.023	0.086	0.018
Theo.Pow.hat	0.799	0.039	0.125	0.023	0.090	0.019
Empi.Pow.n	0.799	0.037	0.111	0.022	0.063	0.017
Misspecification of the error term distribution
Empi.Pow.t3	0.798	0.036	0.112	0.023	0.062	0.019
Empi.Pow.t5	0.799	0.036	0.111	0.022	0.063	0.018
Misspecification of the random intercept distribution
Empi.Pow.t3	0.817	0.033	0.132	0.027	0.076	0.021
Empi.Pow.t5	0.799	0.036	0.116	0.023	0.067	0.018

Power	m = 500, EN = 1750		m = 50, EN = 175		m = 20, EN = 70
β3 = .8	mean	std.dev.	mean	std.dev.	mean	std.dev.
Theo.Pow.	1	0	0.847	0.104	0.541	0.189
Theo.Pow.hat	1	0	0.821	0.096	0.512	0.151
Empi.Pow.n	1	0	0.820	0.102	0.444	0.161
Misspecification of the error term distribution
Empi.Pow.t3	1	0	0.821	0.102	0.449	0.164
Empi.Pow.t5	1	0	0.821	0.102	0.444	0.162
Misspecification of the random intercept distribution
Empi.Pow.t3	1	0	0.852	0.074	0.545	0.155
Empi.Pow.t5	1	0	0.824	0.094	0.472	0.159

3.1.2. Robustness of T with respect to error and random effects distributions

In Table 2 we also assessed the impact of misspecification of the error distribution on the power of the test statistic. Using the same setting as in the power calculations given above, we generated ∊ from a t distribution with k = 3 or 5 degrees of freedom (d.f.) instead of from a $N(0,{\sigma }_{∊}^2)$. We rescaled the variance of ∊ so that the noise had the same variance as in the normal case. The power of the test under a t-distribution was virtually the same as with a normal error distribution indicating that our test is robust to symmetric violations of normality. For example, for m = 50 with β₃ = 0.8, the power was 0.83 for the normal error distribution and for t-distributions with 3 and 5 d.f. (Table 2). We also used the same misspecification for the random effects distribution, and observed very similar results (Table 2). We chose the t distribution because it is symmetric but has heavier tails than the normal distribution and it satisfies the conditions given in Section 2.3 on the existence of moments of the random effects and errors.

3.1.3. Impact of choice of the cell partition on power

As is true for Pearson’s chi-squared test, the choice of cell partition strongly impacts the performance of our goodness of fit test. To illustrate the impact of the cell partition on the power of our test we generated y from a model with E(y) = 1 + x₁ + x₂ + 0.15x₃, with σ_α = 1 and σ_∊ = 0.5, but then omitted x₃ in the subsequent model fitting. We studied cell partitions based on only x₁, only x₂, only x₃, both x₁ and x₂, both x₁ and x₃, or both x₂ and x₃, all based on empirical quartiles of the covariates. Table 3 shows that a lack of fit is detectable by our test statistic only when the cell partition involves the omitted covariate x₃, and power decreases as correlations (ρ₁₃, ρ₂₃) between the covariates increase.

Table 3.

Impact of cell partition on empirical power when covariate x₃ with β₃ = .15 is omitted from model fitting (Scenario I) with m = 500, σ_α = 1, σ_ε = 0.5, K = 2000.

Cell Variables	ρ13 = 0, ρ23 = 0		ρ13 = 0.2, ρ23 = 0.3		ρ13 = 0.4, ρ23 = 0.5
	L=12	L=42	L=12	L=42	L=12	L=42
x 1	0.056	0.060	0.046	0.044	0.045	0.044
x 2	0.055	0.046	0.048	0.048	0.051	0.050
x 3	0.985	0.871	0.936	0.748	0.630	0.367
x1, x2	0.054	0.050	0.052	0.046	0.051	0.048
x1, x3	0.968	0.821	0.896	0.732	0.578	0.382
x2, x3	0.962	0.843	0.913	0.752	0.642	0.435

3.2. Normally distributed covariates with an omitted interaction term (Scenario II)

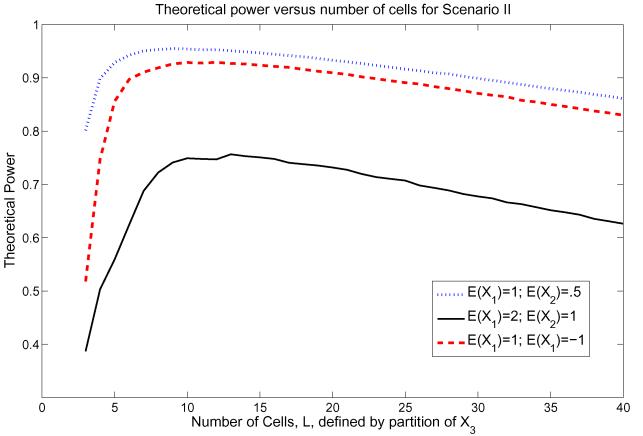
We generated y from a linear model with E(y) = 1 + x₁ + x₂ + β₃x₁x₂, where x₁ and x₂ are independent and $x_i~N({\mu }_i,{\sigma }_i^2)$, i = 1, 2. We first let β₃ = 0.2 and set σ_α = 1, σ_∊ = 0.5. We then fit model (2) without x₃ = x₁x₂. The test had adequate power only when the cell partition is based on empirical quantiles of x₁ and x₂, or on the omitted interaction term x₃ = x₁x₂, but not if the cell partition was based on either x₁ or x₂ alone, for ρ₁₂ = 0 and ρ₁₂ = .3 (Table 1, Web Supplementary Material). Figure 2 shows the power of the test as a function of the number of cells computed based on quantiles of the omitted covariate x₃ for various values of μ_i = E(X_i), i = 1, 2. The power was higher for smaller absolute values of μ₁ and μ₂ and was largest for L = 11 cells for μ₁ = 2 and μ₂ = 1 and L = 7 cells for μ₁ = 1 and μ₂ = 0.5.

Figure 2.

The impact of number of cells for cell partition on theoretical power

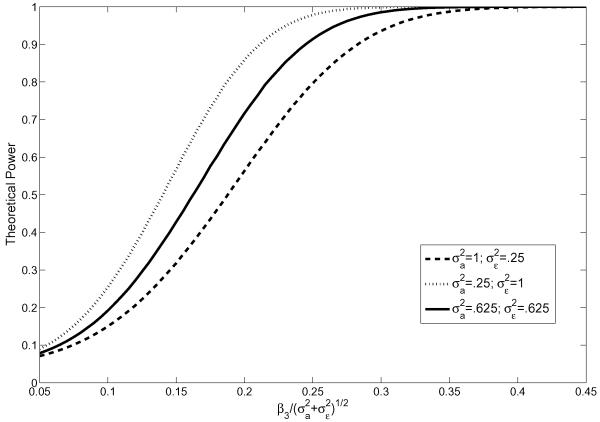
Figure 3 plots the theoretical power against ${\beta }_3∕{({\sigma }_{\alpha }^2+{\sigma }_{∊}^2)}^{1∕2}$ for three choices of $({\sigma }_{\alpha }^2,{\sigma }_{∊}^2)$ corresponding to the same overall variance ${\sigma }_{\alpha }^2+{\sigma }_{∊}^2$ and varying β₃ on the x-axis when the cell partition was based on x₃ with L = 8 cells using fixed cell boundaries. Our conclusions are consistent with those in Section 3.1. For any fixed pair of $({\sigma }_{\alpha }^2,{\sigma }_{∊}^2)$, the power of the test increased as a function of β₃, the coefficient of the omitted covariate x₃. For any fixed β₃, the power increased when the random effect ${\sigma }_{\alpha }^2$ decreases compared to the error term ${\sigma }_{∊}^2$.

Figure 3.

The impact of $({\sigma }_{\alpha }^2,{\sigma }_{∊}^2)$ on theoretical power, ρ₁₂ = 0 (Scenario II)

3.3. Omitted main effect and interaction term (Scenario III)

Here we generated y from a LMM that includes three covariates x₁, x₂ and x₃ through E(y) = 1 + x₁ + x₂ + 0.05x₃ + 0.1x₁x₃, with σ_α = 1 and σ_∊ = 0.5. We then omitted x₃ and any interactions with x₃ from the model fitting and investigate the power of our test in working model M1 with covariates x₁, x₂, and working model M2 with x₁, x₂ and $x_1^2$. The cell partition for M1 and M2 was based on empirical quantiles of x₁ with L = 8 cells. We simulated x₃ ~ N(0, σ²) with σ = 1.5, and let x₁ = e^x₃. The covariate $x_2~{\chi }_1^2$ was generated independently of x₁ and x₃.

Under this setting, with m = 500 clusters, our test had power 1 to detect lack of fit of the working model M1. The Wald test for inclusion of the quadratic term $x_1^2$ in model M2 had power 1. As x₃ is not available, a Wald test cannot be applied for any term related to x₃. We thus would select model M2 (with covariates x₁, x₂, $x_1^2$) and a Wald-type test is not able to further assist in testing model inadequacy. However, our proposed test had power of 0.938 to detect lack of fit of M2, under the cell partition based on x₁, a covariate in M2.

This example, in which the omitted covariate is not available in the dataset but a correlated variable is, shows the usefulness of our test in addition to Wald type tests. However, our test has reasonable power against omitted-covariate alternatives only when the partitions of the covariate space are based on variables that are correlated with the omitted covariates.

3.4. Misspecified functional form of a covariate (Scenario IV)

We generated y from a LMM with $E\left(y\right)=1+x_1+x_2+0.1x_3^2$ with σ_α = 1 and σ_∊ = .5, and studied the power of our test when instead of $x_3^2$ only x₃ is used in the working model. x = (x₁, x₂, x₃) was generated from the multivariate normal distribution given in (22) with (ρ₁₃, ρ₂₃) = (.5, .6). We used empirical quantiles of x₃ to define L = 8 cells for m = 500 or 50 clusters.

When m = 500, our test had approximately 87% power in detecting model inadequacy (Table 4). The Wald test to assess the significance of x₃ however had of only approximately 6% power. Thus based on Wald test, x₃ would not be included in the model and therefore it is unlikely that the higher order term $x_3^2$ would be considered.

Table 4.

Power and robustness study (Scenario IV). L = 8, K = 2000, D = 1000, (ρ₁₃, ρ₂₃) = (.5, .6), β₃ = 0.1, σ_α = 1, σ_ε = .5. Note: The standard deviation (std.dev.) relates to variation across the randomly generated 1000 covariate matrices X. Each number was obtained as the mean over 1000 simulated covariate matrices X and for each generated X, K = 2000 iterations were used to simulate the response vector Y.

	m= 500, EN = 1750		m = 50, EN = 175
	Mean Power	std.dev.	Mean Power	std.dev.
Cell Variable x3	0.873	0.035	0.122	0.028
Wald Test on x3	0.059	0.024	0.065	0.026
Misspecification of the error term distribution
εij simulated from t3
Cell Variable x3	0.873	0.035	0.123	0.030
Wald Test on x3	0.059	0.024	0.065	0.026
εij simulated from t5
Cell Variable x3	0.873	0.035	0.122	0.029
Wald Test on x3	0.060	0.025	0.066	0.030
Misspecification of the random effect distribution
αi simulated from t3
Cell Variable x3	0.878	0.032	0.139	0.033
Wald Test on x3	0.061	0.027	0.067	0.031
αi simulated from t5
Cell Variable x3	0.872	0.035	0.126	0.030
Wald Test on x3	0.061	0.026	0.067	0.031

We also investigated the impact of symmetric misspecification of the error and random effect distribution in this scenario. When the t-distribution was used for the error term (or for the random effect term) results are similar to those for the normally distributed error term (or random effect term) (Table 4). Thus in this scenario, our test was robust to symmetric misspecification of the error or random effect distribution, similar to Scenario I.

3.5. Remarks

The primary purpose of the goodness of fit tests studied in this paper is to assess the quality of the fixed-effect part of the mean response in the presence of a mixed-effect variance structure. Yet it is well known that there is ambiguity in Gaussian linear models as to which terms contribute to the fixed-effect predictors and which terms to the variance. To be specific, we consider the model

$$Y_{\mathit{ij}}={\beta }_0+{{\beta }_1}^T{\mathbf{X}}^{\ast }+\gamma X_3+{\alpha }_i+{∊}_{\mathit{ij}}$$ (23)

where X* = (X₁, X₂), (X*, X₃) are jointly normally distributed with means 0, and $\alpha ~\mathcal{N}(0,{\sigma }_{\alpha }^2)$, and the random error $∊~\mathcal{N}(0,{\sigma }_{∊}^2)$. By grouping the γX₃ term together with the error ∊, we see that model (23) is equivalent to the model

$$Y={\beta }_0+{{\beta }_1}^{\ast T}{\mathbf{X}}^{\ast }+{\alpha }_i+{∊}^{\ast }$$ (24)

where ${\beta }_1^{\ast }$ and ∊* are defined in terms of E(X₃|X*) = M^T X* and $V(X_3\mid {\mathbf{X}}^{\ast })={\sigma }_R^2$ by ∊* = ∊ + γ(X₃−M^TX*), ${\beta }_1^{\ast }={\beta }_1+M\gamma$, and $V\left({∊}^{\ast }\right)={\sigma }_{∊}^2+{\gamma }^2{\sigma }_R^2$. This argument shows that the portion of a normal linear model describing $E(Y\mid \mathcal{D})$ is not uniquely determined, where D denotes the data-vector of covariates, that is $\mathcal{D}=({\mathbf{X}}^{\ast },X_3)$ in (23), and $\mathcal{D}={\mathbf{X}}^{\ast }$ in (24). However, since our goodness of fit tests for adequacy of the mean structure are considered conditional on D, and are specified in terms of covariate-defined cells, these two models (23) and (24) are in fact distinguishable if cells under (23) are taken to depend non-trivially on the omitted covariate X₃.

This argument also highlights the lack of power for the test in the setting of main effects (Scenarios I and III) with an omitted covariate when the cell partition was not based on the omitted covariate or a transformation of it, or for an omitted interaction term, when the cell partition is based on only one of the variables that define the interaction (Scenario II). When cell partitions are based on only on X* no lack of fit in the mean structure can be detected, as it is correctly specified with respect to X*.

4. Data example

On April 26, 1986, an accident at the Chernobyl power plant in Ukraine, close to the border with Belarus, released large amounts of radioactive materials including iodine-131 (I-131) into the atmosphere from the destroyed reactor. Deposition of these materials contaminated the territory. Radioisotopes of iodine, e.g. I-131, are concentrated in the thyroid gland. Belarusians exposed to the accident were enrolled in a cohort study to evaluate the relationship between I-131 doses and thyroid cancer risk (Stezhko et al, 2004). Investigators were also interested in studying iodine deficiency in this population, as it impacts I-131 absorption.

We therefore evaluated the relationship between levels of serum thyroglobulin (TG), a marker of iodine deficiency, and variables that might reflect or impact dietary iodine intake, including age at the time of exam, age at the time of the accident, rural or urban residence, smoking status, urinary iodine levels, serum thyroid-stimulating hormone (TSH) levels, serum anti-thyroglobulin antibody (ATG) levels, thyroid volume, presence of thyroid nodules (yes/no), presence of goiter (yes/no) and presence of any thyroid abnormality (yes/no).

We used data on m = 933 men from four of the five study regions, who had complete covariate information, whose ATG and TSH levels were measured by a luminescence assay, and who had TG ≤ 80 (to exclude those with thyroid disease). Among these men, 404 had a single TG measurement, 484 had two, 42 three and 3 four TG measurements during follow-up, resulting in N = 1510 observations. log(TG) was normally distributed (Anderson-Darling test p-value p=0.09).

We fit various models using Proc GLIMMIX, SAS 9.2. Model 1 included all the variables mentioned above, with the exception of presence of nodules, and an interaction term of ATG levels with presence of any thyroid abnormality that was marginally significant (Wald test p-value p = 0.054) and had a log-likelihood value of −1625.2. The random effect variance estimate was ${\widehat{\sigma }}_{\alpha }^2=0.29$ and the error variance estimate was ${\widehat{\sigma }}_{∊}^2=0.25$. Model 2 had no interaction term, but included presence of nodules and resulted in a log-likelihood of −1621.3. The variance component estimates were similar to model 1, ${\widehat{\sigma }}_{\alpha }^2=0.29$ and ${\widehat{\sigma }}_{∊}^2=0.26$. However, as models 1 and 2 are not nested, we could not compare them using a likelihood ratio test.

To assess the fit of both models, each person in the dataset was assigned to one of the L = 8 cells defined by the quartiles of ATG and the response “yes” or “no” to the question “presence of any thyroid abnormality”. There was no indication of lack of fit for either model, with p = 0.32 and p = 0.40 for models 1 and 2 respectively. We also calculated the test statistic for a second cell partition with L = 4 cells defined by “presence of nodules” (yes/no) and “presence of goiter” (yes/no), with p = 0.19 and p = 0.70 for models 1 and 2 respectively. These results suggested that both models fit the data adequately. Thus omitting the interaction term of the variable “presence of any thyroid abnormality” with ATG levels does not affect the fit to the data.

5. Discussion

Schoenfeld (1980) presented a class of omnibus chi-squared goodness of fit tests for the proportional hazards regression model. We adapted this idea and proposed a class of goodness of fit tests for testing the statistical adequacy of the mean structure of a linear mixed model, with cell partitions based on covariates. We described the asymptotic properties of the test when parameters are estimated and developed its theoretical power under local alternatives. We assessed factors that affect the power, the impact of choice of cell partitions on the test as well as the robustness of the test with respect to error distribution and distribution of random e orts in simulations. When a specific covariate associated with outcome is omitted, such as an interaction term or a covariate correlated with terms already in the model, cell partitions based on the omitted covariate result in adequate power of the test. In our simulations we studied models involving only a few covariates. In such cases, Wald testing and likelihood-based model building tools could undoubtedly be used instead. In practical settings our test would be recommended when there are many potential predictors that should in fact not appear in the model. In such circumstances, many nonlinear terms involving omitted variables would not be Wald-tested. We also found that the estimated theoretical power calculated using Le Cam’s third lemma was reliable at least when the number of clusters m was above 50. However, when m is very small, it may be advisable to rely on the empirical power computed through simulations. Our test was also robust to symmetric violations of the normality assumption of the error distribution as well as the violation of normality of the random effects distribution.

This goodness of fit test can be used to test the statistical adequacy of the fixed effects part of a finally selected LMM. It should not be used if one wants to test if a specific covariate should be included in the model, as standard tests such as the Wald test have better power for that purpose (e.g. Scenario I, Table 2). However, when a covariate is missing from the dataset, our test can detect model inadequacy when the cell partition is based on an existing covariate in the working model, which is correlated with the omitted covariate, while no Wald-type test can be applied (Scenario III). Also, the Wald test did not have power to select a variable that entered the mean model only through a quadratic term (Scenario IV), while our test clearly showed lack of fit of the finally selected model with respect to cells defined by that variable. This is particularly important in the situation when many predictors are available, and testing all possible higher order terms or interactions is not practical. In addition, investigators might not consider the inclusion of a higher order term for a variable that has no main effect. We have shown using simple examples that our proposed test has good power to detect many sorts of model inadequacies, not all of which would be tested exhaustively by other methods.

To implement the test one only needs the final model parameter estimates and their variance covariance matrix, which are standard outputs from any statistical software. As a note of caution, in applying the test one must modify the estimated variance matrix $\widehat{\Sigma }$, projecting its eigenspace corresponding to extremely small eigenvalues to 0, to ensure the correct degrees of freedom for the test statistic.

Pan and Lin (2005) developed methods for checking the adequacy of generalized linear mixed models by comparing the cumulative sums of residuals over covariates or predicted values. Our proposed test has additional flexibility in defining cells based on multiple covariates, the test statistic follows a known distribution and is thus easily computed, and we present a broader class of LMMs.

Our goodness of fit test examines multiple features of the data, corresponding to residuals within each covariate cell and bears some relation to the multiaspect framework by Pesarin and Salmaso (2010), Salmaso and Solari (2005) and Marozzi (2007). Future work could attempt to adapt their permutational approaches for several populations to the goodness of fit test in a single population.

Notably, the cell partition used for our test is based on covariates, not on the response variable as for standard Pearson χ² statistic. In future research we plan to further investigate the choice of covariate-based cells partition on the performance of our proposed test. A related issue is sparse cells. Our asymptotic results were derived letting the sample size go to infinity for a fixed cell partition and thus asymptotically cells are not sparse. However, in a real dataset the issue of sparse cells could arise. Maydeu-Olivares and Joe (2005, 2006) and Cagnone (2012) studied the impact of sparse cells when assessing the goodness of fit of latent variable models. For use with heavily cross-classified and sparse covariate-space cell decompositions the limited-information approach of Maydeu-Olivares and Joe (2005, 2006) could be used in our setting and will be part of future investigations. Other possible extensions include derivation of the distribution of the test statistic for random components with heavy tails, for example, under symmetric α-stable distributional assumption for the errors and random effects. However, these extensions of the mixed model theory presented in our paper are technically difficult and we are not aware of any related results in the literature.

Appendix

Appendix A: Proof of Theorem 1

Let J be the limit of the sample information matrix per observation given in (3). The consistency of the MLE $\widehat{\theta }$ in model (2) follows from Miller (1977). By Taylor series expansion of the score function S(θ) = ▽ log L(θ), where L(θ) denotes the likelihood function,

$$\sqrt{N}(\widehat{\theta }-{\theta }_0)\approx {\left\{-\frac{1}{N}\frac{\partial S\left({\theta }_0\right)}{\partial \theta }\right\}}^{-1}\frac{1}{\sqrt{N}}S\left({\theta }_0\right)\approx {\mathbf{J}}^{-1}\frac{1}{\sqrt{N}}S\left({\theta }_0\right).$$ (25)

As the Fisher information (3) is block diagonal, ${\mathbf{J}}^{-1}=\left[\begin{array}{cc}\hfill {\mathbf{J}}_{\beta \beta }^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathbf{M}}^{-1}\hfill \end{array}\right]$. Under Assumption 1.2 Y − Xβ ~ N(0, V), and the score functions for β, i.e. the first p components of S(θ), are S_β(θ) = X^TV⁻¹(Y − Xβ). By extracting the first p components of (25), with A ≈ B denoting $A-B\stackrel{P}{\to }0$, we have

$$\sqrt{N}(\widehat{\beta }-{\beta }_0)\approx {\mathbf{J}}_{\beta \beta }^{-1}{S}_{\beta }\left({\theta }_0\right)∕\sqrt{N}={\mathbf{J}}_{\beta \beta }^{-1}{\mathbf{X}}^T{\mathbf{V}}^{-1}(\mathbf{Y}-\mathbf{X}{\beta }_0)∕\sqrt{N}.$$

Thus,

$$\begin{array}{cc}\hfill \sqrt{N}\left(\begin{array}{c}\hfill \left\{\right(\mathbf{f}-\mathbf{e}\left({\beta }_0\right)\}∕N\hfill \\ \hfill \widehat{\beta }-{\beta }_0\hfill \end{array}\right)\approx & \left(\begin{array}{c}\hfill N^{-1∕2}[I_{\{x_{11}\in E_1\}}\cdots I_{\{x_{{\mathit{mn}}_m}\in E_1\}}]\hfill \\ \hfill ⋮\hfill \\ \hfill N^{-1∕2}[I_{\{x_{11}\in E_L\}}\cdots I_{\{x_{{\mathit{mn}}_m}\in E_L\}}]\hfill \\ \hfill N^{-1∕2}{\mathit{J}}_{\beta \beta }^{-1}{\mathbf{X}}^T{\mathbf{V}}^{-1}\hfill \end{array}\right)(\mathbf{Y}-\mathbf{X}\beta -0)\hfill \\ \hfill =& {\mathbf{D}}_{(L+p)\times N}(\mathbf{Y}-\mathbf{X}{\beta }_0),\hfill \end{array}$$

which is a linear combination of Gaussian random variables.

Under Assumptions 1.4, 1.5, 1.7, which ensure the existence of components of the covariance matrix of the test statistic, we get as N → ∞,

$$\sqrt{N}\left(\begin{array}{c}\hfill \left\{\right(\mathbf{f}-\mathbf{e}\left({\beta }_0\right)\}∕N\hfill \\ \hfill \widehat{\beta }-{\beta }_0\hfill \end{array}\right)\stackrel{\mathcal{D}}{\to }N(0,{\mathbf{DVD}}^T).$$ (26)

Appendix B: Proof of Corollary 2

Under asymptotic normality of $\sqrt{N}(\widehat{\beta }-{\beta }_0)$,

$$\begin{array}{cc}\hfill & \frac{1}{\sqrt{N}}\{\mathbf{f}-\mathbf{e}(\widehat{\beta }\left)\right\}=\frac{1}{\sqrt{N}}\{\mathbf{f}-\mathbf{e}({\beta }_0\left)\right\}+\frac{1}{\sqrt{N}}\left\{\mathbf{e}\right({\beta }_0)-\mathbf{e}(\widehat{\beta }\left)\right\}\hfill \\ \hfill \approx & \frac{1}{\sqrt{N}}\{\mathbf{f}-\mathbf{e}({\beta }_0\left)\right\}=\frac{1}{\sqrt{N}}\nabla \mathbf{e}\left({\beta }_0\right)\{\widehat{\beta }-{\beta }_0\}\approx \frac{1}{\sqrt{N}}\{\mathbf{f}-\mathbf{e}({\beta }_0\left)\right\}-\Lambda \sqrt{N}\{\widehat{\beta }-{\beta }_0\}\hfill \\ \hfill =& (\mathbf{I}\mid -\Lambda )\sqrt{N}\left(\begin{array}{c}\hfill \{\mathbf{f}-\mathbf{e}({\beta }_0\left)\right\}∕N\hfill \\ \hfill \widehat{\beta }-{\beta }_0\hfill \end{array}\right).\hfill \end{array}$$

Since $N^{-1∕2}\{\mathbf{f}-\mathbf{e}(\widehat{\beta }\left)\right\}$ is a linear combination of components of the left hand side of (26), $N^{-1∕2}\{\mathbf{f}-\mathbf{e}(\widehat{\beta }\left)\right\}\stackrel{\mathcal{D}}{\to }N(0,\Sigma )$, with $\Sigma =\mathbf{H}-{\Lambda J}_{\beta \beta }^{-1}{\Lambda }^T$.

Appendix C: Proposition 1

Proposition 1. Suppose that a sequence Z_N of random q-vectors is asymptotically distributed as $\mathcal{N}(0,{\Sigma }_0)$, where rank(Σ₀) = r ≥ 1 and there exists a known ξ > 0 smaller than the minimum positive eigenvalue of Σ₀, and that $\widehat{\Sigma }$ is a consistent covariance-matrix-valued estimator of Σ₀.

Let the spectral decomposition of $\widehat{\Sigma }$ be given by

$$\widehat{\Sigma }=\sum _{k=1}^q{c}_{\mathit{kN}}{\mathbf{v}}_{\mathit{kN}}{\mathbf{v}}_{\mathit{kN}}^T$$

where c_kN are the eigen values and ${\left\{{\mathbf{v}}_{kN}\right\}}_{k=1}^q$ form an orthonormal eigenbasis determined from $\widehat{\Sigma }$. Define

$${\widehat{\Sigma }}_{\zeta }=\sum _{k=1}^q{c}_{\mathit{kN}}{I}_{[c_{kN}>\zeta ]}{\mathbf{v}}_{\mathit{kN}}{\mathbf{v}}_{\mathit{kN}}^T\text{and}{\widehat{\Sigma }}_{\zeta }^{-}\equiv \sum _{k=1}^q{I}_{[c_{\mathit{kN}}>\zeta ]}(1∕c_{\mathit{kN}}){\mathbf{v}}_{\mathit{kN}}{\mathbf{v}}_{\mathit{kN}}^T$$

and let ${\tilde{\Sigma }}^{-}$ be any other generalized inverse of ${\widehat{\Sigma }}_{\zeta }$, i.e. any matrix such that ${\widehat{\Sigma }}_{\zeta }{\tilde{\Sigma }}^{-}{\widehat{\Sigma }}_{\zeta }={\widehat{\Sigma }}_{\zeta }$. Then

1. $P\left(rank\right({\widehat{\Sigma }}_{\zeta })=rank({\Sigma }_0\left)\right)\to 1$ and ${\widehat{\Sigma }}_{\zeta }\stackrel{P}{\to }{\Sigma }_0$.

2. $Z_N^T{\widehat{\Sigma }}_{\zeta }^{-}{Z}_N\stackrel{\mathcal{D}}{\to }{\chi }_r^2$ and $Z_N^T{\tilde{\Sigma }}^{-}{Z}_N\stackrel{\mathcal{D}}{\to }{\chi }_r^2$ as N → ∞.

Proof of Proposition. Note first that while the eigenvectors v_kN are not necessarily uniquely determined if any eigenvalues have multiplicity greater than 1, the eigenspaces spanned by {v_kN: 1 ≤ k ≤ q, c_kN ≤ s} are uniquely and measurably determined from $\widehat{\Sigma }$ for each real s > 0. Therefore ${\left\{c_{kN}\right\}}_{k=1}^q$ and all of the random variance matrices ${\widehat{\Sigma }}_{\zeta }$, ${\widehat{\Sigma }}_{\zeta }^{-}$ are well-defined, coordinate-free and measurably defined from $\widehat{\Sigma }$.

Without loss of generality, let the eigenvalues c_k,N of $\widehat{\Sigma }$ be indexed in nondecreasing order. Since the k’th smallest eigenvalue is a continuous function on the set of q × q symmetric nonnegative definite matrices (Golub and van Loan 1983, pp. 18-19), it follows from the convergence $\widehat{\Sigma }-{\Sigma }_0\stackrel{P}{\to }0$, that for arbitrarily small ∊ ∈ (0, ξ), the event

$$A_N\left(∊\right)\equiv \left[c_{q-r,N}\le \in ,c_{q-r+1,N}>\zeta ,\underset{x:\Vert x\Vert =1}{\sup }\Vert (\widehat{\Sigma }-{\Sigma }_0)\mathrm{x}\Vert \ge ∊\right]$$

has probability converging to 1 as N → ∞. This implies that on A_N(∊), the range space of ${\widehat{\Sigma }}_{\zeta }$ is exactly the span of the eigenvectors v_kN with k ≥ q − r + 1, and therefore that rank$\left({\widehat{\Sigma }}_{\zeta }\right)=r$ on the event A_N(∊). Moreover, on the event A_N(∊), for all x ∈ R^q with ||x|| = 1,

$$\begin{array}{cc}\hfill \Vert ({\widehat{\Sigma }}_{\zeta }-{\Sigma }_0)\mathrm{x}\Vert \le & \Vert (\widehat{\Sigma }-{\Sigma }_0)\mathrm{x}\Vert +\Vert ({\widehat{\Sigma }}_{\zeta }-\widehat{\Sigma })\mathrm{x}\Vert \hfill \\ \hfill \le & ∊+\Vert \sum _{k=1}^{q-r}{c}_{\mathit{kN}}{\mathbf{v}}_{\mathit{kN}}\left({\mathrm{x}}^T{\mathbf{v}}_{\mathit{kN}}\right)\mid \le ∊+∊\hfill \end{array}$$

since max{|c_kN|: k ≤ q − r} ≤ ∊ and ${\sum }_{k=1}^q{\left({\mathbf{x}}^T{\mathbf{v}}_{kN}\right)}^2={\mid \mid \mathbf{x}\mid \mid }^2=1$. This shows the matrix sup-norm of ${\widehat{\Sigma }}_{\zeta }-{\Sigma }_0$ converges in probability to 0 as N → ∞, completing the proof of (i).

By (i), the asymptotic distribution of Z_N is the same as ${\widehat{\Sigma }}_{\zeta }^{1∕2}W$, where $W~\mathcal{N}(0,{\mathit{I}}_{q\times q})$ is independent of Z_N and the matrix square-root is the symmetric square-root equal to ${\sum }_{k=1}^q{c}_{kN}^{1∕2}{I}_{c_{kN}>\zeta }{\mathbf{v}}_{kN}{\mathbf{v}}_{kN}^T$. Therefore, by the continuous mapping theorem, the asymptotic distribution of $Z_N^T{\widehat{\Sigma }}_{\zeta }^{-}{Z}_N$ is the same as the distribution of $W^T{\left(\widehat{\Sigma }\right)}^{1∕2}{\widehat{\Sigma }}_{\zeta }{\left(\widehat{\Sigma }\right)}^{1∕2}W$, which is ${\chi }_r^2$ since ${\left({\widehat{\Sigma }}_{\zeta }\right)}^{1∕2}{\widehat{\Sigma }}_{\zeta }^{-}{\left({\widehat{\Sigma }}_{\zeta }\right)}^{1∕2}$ is symmetric and idempotent with trace r. The only feature of ${\widehat{\Sigma }}_{\zeta }^{-}$ that has been used in this proof is the generalized-inverse property ${\widehat{\Sigma }}_{\zeta }{\tilde{\Sigma }}^{-}{\widehat{\Sigma }}_{\zeta }={\widehat{\Sigma }}_{\zeta }$ shared by ${\tilde{\Sigma }}^{-}$. This fact about generalized inverses, which completes the proof of assertion (ii), was previously proved in detail by Rao (1973, 1b.5.(viii), 3b.4.(vii) or 3b.5.(iv)).

Appendix D: Assumptions for Theorem 3

For the rest of the Appendices we employ the notation v^⊗2 = vv^T for any vector v.

Assumption 3.1. The true parameter point θ₀ = (β₀, ψ₀) is an interior point of $ϴ=({\mathcal{R}}^p,\left({\mathcal{R}}^{+}\right)R+1)$.

Assumption 3.2. E(α_i) = E(∊_ij) = 0, $Var({\alpha }_i={\sigma }_{\alpha }^2)$, $Var\left({∊}_{ij}\right)={\sigma }_{∊}^2$ and there is a δ > 0, such that $E\left({\alpha }_i^{4+\delta }\right)<\infty$ and $E\left({∊}_{ij}^{4+\delta }\right)<\infty$.

Assumption 3.3. X is a matrix of random variables, (x_i, n_i) are i.i.d. with $\mid \mid E\left({\mathbf{x}}_i^T{\mathbf{x}}_i\right)\mid \mid <\infty$, $E\left({\mathbf{x}}_1^T{\mathbf{x}}_1\right)$ being positive definite, and $E\left(n_i^2\right)<\infty$.

Appendix E: Proof of Theorem 3

The following Lemma is used in proving Theorem 3.

Lemma 1. Let {u_in: n ≥ 1, 1 ≤ i ≤ n} be a triangular array of i.i.d. random variables within each row (i.e., across i) with mean 0 and finite variance ${\sigma }_u^2$, and that these variables are independent of the random array {c_in: n ≥ 1, 1 ≤ i ≤ n which satisfies, as n → ∞, (a) max_1≤i≤n |c_in| → 0 and (b) ${\sum }_{i=1}^n{c}_{in}^2\to \kappa$ in probability, where κ ∈ (0, ∞). Then ${\sum }_{i=1}^n{c}_{in}{u}_{in}\stackrel{\mathcal{D}}{\to }\mathcal{N}(0,\kappa )$ as n → ∞.

Proof of Lemma 1: ${\left\{{\sum }_{i=1}^k{c}_{in}{u}_{in}\right\}}_{k=1}^n$ is a martingale with respect to the filtration ${\mathcal{F}}_{kn}=\sigma \left(\right\{c_{in},.u_{in}:1\le i\le k\left\}\right)$ and the Lemma follows directly from the Martingale Central Limit Theorem (Hall and Heyde, 1980).

Proof of Theorem 3: Let the n_i×p covariate matrix for the i-th cluster be ${\mathbf{x}}_i=({\mathbf{x}}_{i1}^T,\dots ,{\mathbf{x}}_{i{n}_i}^T)$. Then

$$\sqrt{N}(\tilde{\beta }-{\beta }_0)=\sqrt{N}{\left({\mathbf{X}}^T{\tilde{V}}^{-1}\mathbf{X}\right)}^{-1}{\mathbf{X}}^T{\tilde{V}}^{-1}(\mathbf{Y}-\mathbf{X}{\beta }_0)\approx {\left(\frac{{\mathbf{X}}^T{\mathbf{V}}^{-1}\mathbf{X}}{N}\right)}^{-1}\frac{1}{\sqrt{N}}\sum _{i=1}^m{\mathrm{x}}_i^T{\mathbf{V}}_i^{-1}({\mathrm{y}}_i-{\mathrm{x}}_i{\beta }_0).$$

Then

$$\begin{array}{cc}\hfill \{\mathbf{f}-\mathbf{e}(\tilde{\beta }\left)\right\}N=& \{\mathbf{f}-\mathbf{e}({\beta }_0\left)\right\}∕\sqrt{N}+\left\{\mathbf{e}\right({\beta }_0)-\mathbf{e}(\tilde{\beta }\left)\right\}∕\sqrt{N}\hfill \\ \hfill \approx & \{\mathbf{f}-\mathbf{e}({\beta }_0\left)\right\}∕\sqrt{N}-\nabla \mathbf{e}\left({\beta }_0\right)(\tilde{\beta }-{\beta }_0)∕\sqrt{N}\hfill \\ \hfill \approx & \sum _{i=1}^m\frac{1}{\sqrt{N}}\left\{\left(\begin{array}{c}\hfill z_{i1}\hfill \\ \hfill ⋮\hfill \\ \hfill z_{\mathit{iL}}\hfill \end{array}\right)-\frac{\nabla \mathbf{e}\left({\beta }_0\right)}{N}{\left(\frac{{\mathbf{X}}^T{\mathbf{V}}^{-1}\mathbf{X}}{N}\right)}^{-1}{\mathrm{x}}_i^T{\mathbf{V}}_i^{-1}({\mathrm{y}}_i-{\mathrm{x}}_i{\beta }_0)\right\},\hfill \end{array}$$

with $z_{il}={\sum }_{j=1}^{n_i}{I}_{\{x_{ij}\in E_l\}}(y_{ij}-E(y_{ij}\left)\right)={\sum }_{j=1}^n{I}_{\{x_{ij}\in E_l\}}(y_{ij}-{\mathbf{x}}_{ij}{\beta }_0)$, i = 1, …, m, l = 1, …, L. Let $\tilde{\Lambda }=N^{-1}\nabla \mathbf{e}\left({\beta }_0\right)\stackrel{P}{\to }\Lambda$, ${\tilde{\mathbf{J}}}_{\beta \beta }=N^{-1}{\mathbf{X}}^T{\mathbf{V}}^{-1}\mathbf{X}\stackrel{P}{\to }{\mathbf{J}}_{\beta \beta }$. We next show that $(\mathbf{f}-\mathbf{e}(\tilde{\beta }\left)\right)∕\sqrt{N}$ has a limiting Gaussian distribution by using the multivariate Central Limit Theorem. For any constant vector C = (C₁, …, C_L)^T, since the inverse of V_i is ${\mathbf{V}}_i^{-1}={\mathbf{I}}_{n_i}∕{\sigma }_{∊}^2-{\sigma }_{\alpha }^2∕\left({\sigma }_{∊}^2\right({\sigma }_{∊}^2+n_i{\sigma }_{\alpha }^2\left)\right)1^{\otimes 2}$, we have

$$\begin{array}{cc}\hfill & {\mathbf{C}}^T{N}^{-1∕2}\{\mathbf{f}-\mathbf{e}(\tilde{\beta }\left)\right\}\approx \sum _{i=1}^m\frac{1}{\sqrt{N}}\left\{\sum _{l=1}^L{C}_l{z}_{\mathit{il}}-{\mathbf{C}}^T\tilde{\Lambda }{\tilde{J}}_{\beta \beta }^{-1}{\mathrm{x}}_i^T{\mathbf{V}}_i^{-1}({\mathrm{y}}_i-{\mathrm{x}}_i{\beta }_0)\right\}\hfill \\ \hfill =& \sum _{i=1}^m\left[\frac{1}{\sqrt{N}}\sum _{l=1}^{n_i}\left\{\sum _{l=1}^L{C}_l{I}_{\{{\mathrm{x}}_{\mathit{ij}}\in E_l\}}-{\mathbf{C}}^T\tilde{\Lambda }{\tilde{J}}_{\beta \beta }^{-1}\left(\frac{1}{{\sigma }_{∊}^2}{\mathrm{x}}_{\mathit{ij}}-\frac{n_i{\sigma }_{\alpha }^2}{{\sigma }_{∊}^2({\sigma }_{∊}^2+n_i{\sigma }_{\alpha }^2)}{\stackrel{‒}{\mathrm{x}}}_{i.}\right)\right\}\right]{\alpha }_i\hfill \\ \hfill +& \sum _{i=1}^m\sum _{j=1}^{n_i}\frac{1}{\sqrt{N}}\left\{\sum _{l=1}^L{C}_l{I}_{\{{\mathrm{x}}_{\mathit{ij}}\in E_l\}}-{\mathbf{C}}^T\tilde{\Lambda }{\tilde{J}}_{\beta \beta }^{-1}\left(\frac{1}{{\sigma }_{∊}^2}{\mathrm{x}}_{\mathit{ij}}-\frac{n_i{\sigma }_{\alpha }^2}{{\sigma }_{∊}^2({\sigma }_{∊}^2+n_i{\sigma }_{\alpha }^2)}{\stackrel{‒}{\mathrm{x}}}_{i.}\right)\right\}{∊}_{\mathit{ij}}\hfill \\ \hfill =& \sum _{i=1}^m{c}_{i,n_i}{\alpha }_i+\sum _{s=1}^N{w}_s{∊}_s,\hfill \end{array}$$

where the double index (i, j) is placed in one-to-one correspondence with the single index s. Because ${\left\{{\alpha }_i\right\}}_{i=1}^m$ and ${\left\{{∊}_s\right\}}_{s=1}^N$ are i.i.d and satisfy conditions (a) and (b) of Lemma 1, the above sums have limiting normal distributions as m → ∞. Because α_i and ∊_ij are independent ${\sum }_{i=1}^m{c}_{i,n_i}{\alpha }_i$ and ${\sum }_{s=1}^N{w}_s{∊}_s$ are conditionally independent given (x_i, n_i). As the two sums are jointly normal and asymptotically uncorrelated they are asymptotically independent and the limiting distribution of ${\mathbf{C}}^T{N}^{-1∕2}(\mathbf{f}-\mathbf{e}(\tilde{\beta }\left)\right)$ is normal. Moreover, for any constant vector C, its limiting variance is of the form C^TΣC with the same fixed Σ,

$$\begin{array}{cc}\hfill \Sigma =& \underset{N\to \infty }{\lim }\frac{1}{N}\sum _{i=1}^m\mathrm{Var}\left(\begin{array}{c}\hfill \sum _{j=1}^m{I}_{\{x_{\mathit{ij}}\in E_l\}}(y_{\mathit{ij}}-{\mathrm{x}}_{\mathit{ij}}{\beta }_0)\hfill \\ \hfill ⋮\hfill \\ \hfill \sum _{j=1}^{n_i}{I}_{\{x_{\mathit{ij}}\in E_L\}}(y_{\mathit{ij}}-{\mathrm{x}}_{\mathit{ij}}{\beta }_0)\hfill \end{array}\right)-\hfill \\ \hfill & \underset{N\to \infty }{\lim }\left[\frac{\nabla \mathbf{e}\left({\beta }_0\right)}{N}\right]{\left[\frac{{\mathbf{X}}^T{\mathbf{V}}^{-1}\mathbf{X}}{N}\right]}^{-1}{\left[\frac{\nabla \mathbf{e}\left({\beta }_0\right)}{N}\right]}^T=\mathbf{H}-\Lambda {\mathbf{J}}_{\beta \beta }^{-1}{\Lambda }^T.\hfill \end{array}$$

Therefore, $N^{-1∕2}\{\mathbf{f}-\mathbf{e}(\tilde{\beta }\left)\right\}\stackrel{\mathcal{D}}{\to }N(0,\Sigma )$, and $T={\{\mathbf{f}-\mathbf{e}(\tilde{\beta }\left)\right\}}^T{\Sigma }^{-1}(\mathbf{f}-\mathbf{e}(\tilde{\beta }\left)\right)∕N\stackrel{\mathcal{D}}{\to }{\chi }_r^2$, where r = rank(Σ). We replace Σ with ${\widehat{\Sigma }}_{\zeta }$, the reconstructed estimated variance matrix defined as immediately following equation (11) by means of the singular value decomposition applied to any consistent estimator $\widehat{\Sigma }$ of Σ. One such consistent estimator of Σ is to replace all parameters in Σ with least squares and method of moments estimators. Based on Proposition 1 in Appendix C, $\text{rank}\left({\widehat{\Sigma }}_{\zeta }\right)=\text{rank}\left(\Sigma \right)$ for large N. Thus

$$T={\{\mathbf{f}-\mathbf{e}(\tilde{\beta }\left)\right\}}^T{\widehat{\Sigma }}_{\zeta }^{-}\{\mathbf{f}-\mathbf{e}(\tilde{\beta }\left)\right\}∕N\stackrel{\mathcal{D}}{\to }{\chi }_r^2.$$

Appendix F: Derivation of the power of the test

We derive the power of the test for LMM (1) under contiguous alternatives, based on Le Cam’s third lemma (Van der Vaart, 2000).

Lemma 2. (Le Cam’s third lemma) Let P_N and Q_N be two measures on a measurable space, corresponding to a null distribution under investigation, and an alternative hypothesis respectively. Suppose W_N is a real valued statistic for every N. If

$$(W_N,\log \frac{{\mathit{dQ}}_N}{{\mathit{dP}}_N})\stackrel{\mathcal{P}N}{\to }{N}_{L+1}\left(\left[\begin{array}{c}\hfill \mu \hfill \\ \hfill -\sigma ∕2\hfill \end{array}\right],\left[\begin{array}{cc}\hfill \Sigma \hfill & \hfill \tau \hfill \\ \hfill {\tau }^T\hfill & \hfill {\sigma }^2\hfill \end{array}\right]\right),$$ (27)

then $W_N\stackrel{{\mathcal{Q}}_N}{\to }{N}_L(\mu +\tau ,\Sigma )$.

Let H₀ : θ_N = θ₀, and $H_1:{\theta }_N={\theta }_0+a∕\sqrt{N}$, where a is a constant vector and θ_N → θ₀, as n → ∞. By Taylor expansion, under Theorem 5.21 in van der Vaart (2000),

$$\begin{array}{cc}\hfill \log & \frac{{\mathit{dQ}}_N}{{\mathit{dP}}_N}=\log \frac{\text{Likelihood}({\theta }_N;\mathbf{Y},\mathbf{X})}{\text{Likelihood}({\theta }_0;\mathbf{Y},\mathbf{X})}=\log \frac{L\left({\theta }_N\right)}{L\left({\theta }_0\right)}\hfill \\ \hfill & \approx {(\nabla \log (L\left({\theta }_0\right)\left)\right)}^T\frac{\mathrm{a}}{\sqrt{N}}+\frac{1}{2}\frac{{\mathrm{a}}^T}{\sqrt{N}}\left({\nabla }^{\otimes 2}\log \right(L\left({\theta }_0\right)\left)\right)\frac{\mathrm{a}}{\sqrt{N}}\approx {\left(S_N\right({\theta }_0\left)\right)}^T\frac{\mathrm{a}}{\sqrt{N}}-\frac{1}{2}{\mathrm{a}}^T\mathbf{J}\left({\theta }_0\right)\mathrm{a},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill S_N\left({\theta }_0\right)=& \nabla \log \left(L\right({\theta }_0\left)\right)\hfill \\ \hfill =& \left[\begin{array}{c}\hfill {\mathbf{X}}^T{\mathbf{V}}^{-1}(\mathbf{Y}-\mathbf{X}{\beta }_0)\hfill \\ \hfill -\frac{1}{2}\mathit{tr}\left({\mathbf{V}}^{-1}\frac{\partial \mathbf{V}}{\partial {\sigma }_{\alpha }^2}\right)+\frac{1}{2}{(\mathbf{Y}-\mathbf{X}{\beta }_0)}^T{\mathbf{V}}^{-1}\frac{\partial \mathbf{V}}{\partial {\sigma }_{\alpha }^2}{\mathbf{V}}^{-1}(\mathbf{Y}-\mathbf{X}{\beta }_0)\hfill \\ \hfill -\frac{1}{2}\mathit{tr}\left({\mathbf{V}}^{-1}\right)+\frac{1}{2}{(\mathbf{Y}-\mathbf{X}{\beta }_0)}^T{\mathbf{V}}^{-1}{\mathbf{V}}^{-1}(\mathbf{Y}-\mathbf{X}{\beta }_0)\hfill \end{array}\right]\hfill \end{array}$$ (28)

and the limit of the sample Fisher information per observation is

$$\mathbf{J}\left({\theta }_0\right)=\underset{N\to \infty }{\lim }-{\nabla }^{\otimes 2}\log \left(L\right({\theta }_0\left)\right)∕N=\underset{N\to \infty }{\lim }\mathrm{Var}\left({\mathbf{S}}_N\right({\theta }_0)∕\sqrt{N}).$$

Thus

$$\log \frac{{\mathit{dQ}}_N}{{\mathit{dP}}_N}\stackrel{{\mathcal{P}}_N}{\to }N\left(\frac{1}{2}{\mathrm{a}}^T\mathbf{J}\left({\theta }_0\right)\mathrm{a},{\mathrm{a}}^T\mathbf{J}\left({\theta }_0\right)\mathrm{a}\right).$$

For the special case when we fit a reduced model to the data, using ${\mathbf{X}}_{N\times p^{\ast }}^{\ast }$ instead of X_N×p with p* < p, we estimate the coefficient β* corresponding to X*. The sum over the expected values under the model, e(·), in (6) has R^p as its domain. Let e* (·) denote the sum over the expected values under the reduced model, computed using ${\mathbf{X}}_{N\times p^{\ast }}^{\ast }$ instead of X_N×p with domain R^p*. Let $W_N=(\mathbf{f}-{\mathbf{e}}^{\ast }({\widehat{\beta }}^{\ast }\left)\right)∕\sqrt{N}$ be the first vector component of (27). Under the null hypothesis P_N, W_N → N(0, Σ*), based on Corollary 2.

Next, we compute the variance-covariance matrix Σ in (27), which is equivalent to the variance-covariance matrix of ${\mathbf{a}}^T{\mathbf{S}}_N\left({\theta }_0\right)∕\sqrt{N}$ and $(\mathbf{f}-{\mathbf{e}}^{\ast }({\widehat{\beta }}^{\ast }\left)\right)∕\sqrt{N}$.

$$\begin{array}{cc}\hfill & \frac{a}{\sqrt{N}}(\mathbf{f}-{\mathbf{e}}^{\ast }({\widehat{\beta }}^{\ast }\left)\right)\approx \frac{1}{\sqrt{N}}(\mathbf{f}-{\mathbf{e}}^{\ast }({\beta }_0^{\ast }\left)\right)-\frac{1}{\sqrt{N}}\nabla {\mathbf{e}}^{\ast }\left({\beta }_0^{\ast }\right)({\widehat{\beta }}^{\ast }-{\beta }_0^{\ast })\hfill \\ \hfill \approx & \frac{1}{\sqrt{N}}(\mathbf{f}-{\mathbf{e}}^{\ast }({\beta }_0^{\ast }\left)\right)-{\Lambda }^{\ast }\sqrt{N}({\widehat{\beta }}^{\ast }-{\beta }_0^{\ast })\hfill \\ \hfill \approx & \frac{1}{\sqrt{N}}(\mathbf{f}-{\mathbf{e}}^{\ast }({\beta }_0^{\ast }\left)\right)-{\Lambda }^{\ast }{\left({\mathbf{J}}_{\beta \beta }^{\ast }\right)}^{-1}{\left({\mathbf{X}}^{\ast }\right)}^T{\mathbf{V}}^{-1}(\mathbf{Y}-{\mathbf{X}}^{\ast }{\beta }_0^{\ast })∕\sqrt{N}=\frac{1}{\sqrt{N}}(\mathrm{A}-\mathrm{B})(\mathbf{Y}-{\mathbf{X}}^{\ast }{\beta }_0^{\ast }),\hfill \end{array}$$

where ${\mathbf{J}}_{\beta \beta }^{\ast }$ denotes the information matrix corresponding to β*, and

$$\mathbf{A}=\left[\begin{array}{c}\hfill I_{\{x_{11}\in E_1\}}\cdots I_{\{{\mathrm{x}}_{{\mathit{mn}}_n}\in E_1\}}\hfill \\ \hfill ⋮\hfill \\ \hfill I_{\{{\mathrm{x}}_{{\mathit{mn}}_n}\in E_L\}}\cdots I_{\{{\mathrm{x}}_{{\mathit{mn}}_n}\in E_L\}}\hfill \end{array}\right],\mathbf{B}={\Lambda }^{\ast }{\left({\mathbf{J}}_{\beta \beta }^{-1}\right)}^{-1}{\left({\mathbf{X}}^{\ast }\right)}^T{\mathbf{V}}^{-1}.$$

Thus,

$$\begin{array}{cc}\hfill \mathrm{Cov}(\frac{\mathbf{f}-{\mathbf{e}}^{\ast }\left({\widehat{\beta }}^{\ast }\right)}{\sqrt{N}},\log \frac{{\mathit{dQ}}_N}{{\mathit{dP}}_N})=& \mathrm{Cov}(\frac{\mathbf{f}-{\mathbf{e}}^{\ast }\left({\widehat{\beta }}^{\ast }\right)}{\sqrt{N}},\frac{{\mathrm{a}}^T{\mathbf{S}}_N\left({\theta }_0\right)}{\sqrt{N}})\hfill \\ \hfill =& \frac{1}{N}\mathrm{Cov}(\mathbf{f}-{\mathbf{e}}^{\ast }({\widehat{\beta }}^{\ast }),{\mathrm{a}}_1^T{\mathbf{S}}_{\beta }+a_2{\mathbf{S}}_{{\sigma }_{\alpha }^2}+a_3{\mathbf{S}}_{{\sigma }_{∊}^2}).\hfill \end{array}$$ (29)

Under equation (28), since both $tr\left({\mathbf{V}}^{-1}\right(\partial \mathbf{V}∕\partial {\sigma }_{\alpha }^2\left)\right)$ and tr(V⁻¹) are scalars, we have

$$\begin{array}{cc}\hfill & \mathrm{Cov}(\mathbf{f}-{\mathbf{e}}^{\ast }({\widehat{\beta }}^{\ast }),{\mathbf{S}}_{{\sigma }_{\alpha }^2})\hfill \\ \hfill =& \mathrm{Cov}\left((\mathbf{A}-\mathbf{B})(\mathbf{Y}-{\mathbf{X}}^{\ast }{\beta }_0^{\ast }),\frac{1}{2}{(\mathbf{Y}-\mathbf{X}{\beta }_0)}^T{\mathbf{V}}^{-1}\frac{\partial \mathbf{V}}{\partial {\sigma }_{\alpha }^2}{\mathbf{V}}^{-1}(\mathbf{Y}-\mathbf{X}{\beta }_0)\right)\hfill \\ \hfill =& (\mathbf{A}-\mathbf{B})\mathrm{Cov}\left(\mathbf{Y}-{\mathbf{X}}^{\ast }{\beta }_0^{\ast }),\frac{1}{2}{(\mathbf{Y}-\mathbf{X}{\beta }_0)}^T{\mathbf{V}}^{-1}\frac{\partial \mathbf{V}}{\partial {\sigma }_{\alpha }^2}{\mathbf{V}}^{-1}(\mathbf{Y}-{\mathbf{X}}^{\ast }{\beta }_0^{\ast })\right)=0.\hfill \end{array}$$

Similarly, we get $Cov(\mathbf{f}-{\mathbf{e}}^{\ast }({\widehat{\beta }}^{\ast }),{\mathbf{S}}_{{\sigma }_{∊}^2})=0$. Therefore (29) becomes

$$\begin{array}{cc}\hfill & \mathrm{Cov}(\frac{\mathbf{f}-{\mathbf{e}}^{\ast }\left({\widehat{\beta }}^{\ast }\right)}{\sqrt{N}},\log \frac{{\mathit{dQ}}_n}{{\mathit{dP}}_n})=\frac{1}{N}\mathrm{Cov}\left(\mathbf{f}-{\mathbf{e}}^{\ast }\left({\widehat{\beta }}^{\ast }\right),{\mathrm{a}}_1^T{\mathbf{S}}_{\beta }\right)=\frac{1}{N}(\mathbf{A}-\mathbf{B})\mathrm{Var}\left(\mathbf{Y}\right){\mathbf{V}}^{-1}{\mathrm{Xa}}_1\hfill \\ \hfill & =\left\{\Lambda -\frac{1}{N}{\Lambda }^{\ast }{\left({\mathbf{J}}_{\beta \beta }^{\ast }\right)}^{-1}\left[{\left({\mathbf{X}}^{\ast }\right)}^T{\mathbf{V}}^{-1}\mathbf{X}\right]\right\}{\mathrm{a}}_1=\left\{\Lambda -{\Lambda }^{\ast }{\left[{\left({\mathbf{X}}^{\ast }\right)}^T{\mathbf{V}}^{-1}\right({\mathbf{X}}^{\ast }\left)\right]}^{-1}\left[{\left({\mathbf{X}}^{\ast }\right)}^T{\mathbf{V}}^{-1}\mathbf{X}\right]\right\}{\mathrm{a}}_1.\hfill \end{array}$$

Since both $\mathbf{f}-{\mathbf{e}}^{\ast }\left({\widehat{\beta }}^{\ast }\right)$ and ${\mathbf{a}}_1^T{\mathbf{S}}_{\beta }$ can be written as a matrix multiplied by the same normal vector $\mathbf{Y}-\mathbf{X}{\beta }_0=\mathbf{Y}-{\mathbf{X}}^{\ast }{\beta }_0^{\ast }$, we obtain asymptotic joint normality of $\mathbf{f}-{\mathbf{e}}^{\ast }\left({\widehat{\beta }}^{\ast }\right)$ and ${\mathbf{a}}_1^T{\mathbf{S}}_{\beta }$. Because $\mathbf{f}-{\mathbf{e}}^{\ast }\left({\widehat{\beta }}^{\ast }\right)$ is asymptotically uncorrelated with both ${\mathbf{S}}_{{\sigma }_{\alpha }^2}$ and ${\mathbf{S}}_{{\sigma }_{∊}^2}$ as shown in the above, $\mathbf{f}-{\mathbf{e}}^{\ast }\left({\widehat{\beta }}^{\ast }\right)$ and a^TS_N(θ₀) are also asymptotically jointly normal.