Compartmentalized Low-Rank Recovery for High-Resolution Lipid Unsuppressed MRSI

Abstract

Purpose

To introduce a novel algorithm for the recovery of high-resolution magnetic resonance spectroscopic imaging (MRSI) data with minimal lipid leakage artifacts, from dual-density spiral acquisition.

Methods

The reconstruction of MRSI data from dual-density spiral data is formulated as a compartmental low-rank recovery problem. The MRSI dataset is modeled as the sum of metabolite and lipid signals, each of which is support limited to the brain and extracranial regions, respectively, in addition to being orthogonal to each other. The reconstruction problem is formulated as an optimization problem, which is solved using iterative reweighted nuclear norm minimization.

Results

The comparisons of the scheme against dual-resolution reconstruction algorithm on numerical phantom and in vivo datasets demonstrate the ability of the scheme to provide higher spatial resolution and lower lipid leakage artifacts. The experiments demonstrate the ability of the scheme to recover the metabolite maps, from lipid unsuppressed datasets with echo time (TE)=55 ms.

Conclusion

The proposed reconstruction method and data acquisition strategy provide an efficient way to achieve high-resolution metabolite maps without lipid suppression. This algorithm would be beneficial for fast metabolic mapping and extension to multislice acquisitions.

INTRODUCTION

Magnetic resonance spectroscopic imaging (MRSI) enables spatial mapping of multiple tissue metabolites in vivo, many of which are proven to be valuable biomarkers for several diseases (1–3). However, the clinical utility of MRSI is currently restricted by several challenges, resulting from very low metabolite concentrations. Specifically, achievable spatial resolution using Nyquist sampling and conventional recovery schemes is limited by metabolite signal to noise ratio (SNR) and scan time. Broad point spread functions (PSF) result in significant spectral leakage from the extracranial lipid and residual water signals, which have several orders of magnitude higher intensity than metabolites.

Several water and lipid suppression schemes are available in MRSI. Chemical-shift selective saturation methods (4–6), followed by postprocessing methods such as Hankel singular value decomposition (7) can provide reasonable suppression of residual water signal. Popular approaches to attenuate lipid signals include outer volume suppression (OVS) (8–11), inversion recovery (12–14), inner volume excitation (15,16), and use of long echo times (TE) (17,18). None of these methods provide perfect lipid suppression, in addition result in signal loss or reduced brain coverage. Moreover, many of these methods have practical limitations. For example, OVS band placement may be challenging and time-consuming for multislice acquisitions and also limited by allowable radiofrequency (RF) energy deposition limits at higher field strengths. Performance of many of the above methods (e.g., OVS, inner volume excitation) also degrades in presence of field inhomogeneity and chemical shift effects, especially at high field strengths.

Postprocessing methods were introduced for minimizing residual lipids. A popular approach is k-space extrapolation using high-resolution spatial support estimates (19,20). This method provides acceptable spectral quality, when combined with inversion recovery (21). Several authors have proposed dual-density acquisition methods, coupled with dual-resolution reconstruction algorithms, to further improve lipid suppression. The basic idea is to extend k-space coverage to obtain narrower PSF, translating to reduced lipid leakage (18,22–25). Since weak metabolite signals cannot be recovered reliably from small voxels in a short acquisition time, dual-resolution schemes acquire the central k-space regions with more averages. The data are recovered using dual-resolution reconstruction algorithms, which restrict the nominal resolution of the metabolites by the k-space regions collected with more averages, while lipid regions are estimated at a high spatial resolution. Recovery of strong lipid signals at high spatial resolution results in reduced lipid leakage in the brain region. While similar dual-resolution algorithms have been successfully used (26,27), all of them need to be coupled with some form of lipid suppression. In addition, most of these methods are associated with smoothness priors, resulting in low-resolution recovery of metabolite regions. To overcome such limitations, recent works have focused on superresolution MRSI data recovery. An overview of such superresolution methods in MRSI is available in (28,29).

In this work, we combine dual-density spiral MRSI acquisition method with a novel compartmentalized low-rank algorithm to recover metabolic images with higher spatial resolution and minimal lipid leakage artifacts. We model field inhomogeneity compensated dataset as the sum of metabolite and lipid signals, each of which is nonzero within the brain and extracranial regions, respectively. Since each of these signals arise from finite number of anatomical regions with distinct spectral signatures, they can each be efficiently represented as the linear combination of finite number of basis functions. We propose to organize the metabolite and lipid signals as low-rank matrices, and their recovery from noisy measurements can be regularized using nuclear norm penalties. Similar low-rank methods have been recently introduced for signal recovery in many areas, including MRSI (17,30–34) and dynamic imaging (35–39). Unlike dual-density methods that restrict nominal resolution of metabolites to the multiaveraged low-resolution portion of the k-space (18,22–27,40), the proposed scheme recovers metabolites from the entire k-space; low-rank prior makes the recovery scheme well-posed and recovers metabolite maps with improved spatial detail. Metabolite and lipid spectral signatures are drastically different with different chemical shifts and T₂ decay rates. Inspired by the work of Bilgic et al. (40), we propose to decouple the subspaces using an orthogonality penalty, which encourages metabolite and lipid subspaces to remain orthogonal. Denoising of lipid signals offered by the low-rank and orthogonality priors in our framework offers improved lipid suppression, compared to (40) that uses lipid signals estimated from an initial high-resolution reconstruction. We designed a variable density spiral sequence using the numerical algorithm in (41). This sequence enables us to fully acquire a 128 × 128 image matrix in 7.2 min scan time. The sequence acquires the central k-space regions (k-space radius ≤16) with 12-fold oversampling, while outer k-space regions are acquired at Nyquist rate. The spiral sequence is a better alternative to Cartesian dual-density acquisitions that combine data from separate scans (17,23,33,42); since all the data are acquired using a single sequence, no correction methods are needed.

Recently low-rank based method, SPICE was introduced for high-resolution MRSI (17,33,34). SPICE uses a low-resolution data to estimate metabolite and lipid bases based on spectral priors in the first step. MRSI data from high-resolution measurements is recovered using the basis functions in the second step. The proposed method, contrarily uses orthogonality priors and does not rely on accurate prior knowledge of spectral supports of lipid regions to suppress lipids. Our experiments show that the proposed method is applicable to problems where there is considerable field inhomogeneity variations in the lipid region, where use of spectral priors may be difficult. Another benefit of the proposed scheme is that it may be readily applicable to a variety of sampling schemes, compared to (17,33,34) that requires specialized trajectories.

We compare the performance of the proposed scheme to our dual-resolution reconstruction scheme that relies on compartmental smoothness priors (26) and dual-density recovery scheme in (40), followed by denoising using a low-rank approximation. A simulated phantom and in vivo data with and without lipid suppression and TE=55 ms were used to validate the method. Experiments show that the proposed method can provide improved reconstruction than dual-resolution recovery schemes. Specifically, it yields metabolite maps with higher resolution and minimal lipid artifacts, even in absence of lipid suppression.

THEORY

We denote the underlying spatiospectral function in MRSI by x(r, f), where r is the spatial index and f is the spectral index. The measured signal from the j^th coil in k – t space is modeled as,

$${\widehat{s}}_j(\mathbf{k},t)={\int }_{\mathbf{r}\in \mathrm{\Omega }}{\int }_{f}x(\mathbf{r},f)c_j(\mathbf{r})e^{-i2\mathrm{\pi }\mathbf{kr}}{e}^{-i2\mathrm{\pi }(f+\mathrm{\Delta }f(\mathbf{r}))t}d\mathbf{r}\mathit{df}+{\mathrm{\eta }}_j(\mathbf{k},t);j=1,\mathrm{..}\#\text{Ncoils.}$$ [1]

Here, r specifies the spatial location and t denotes time. Δf(r) = γ̄ΔB₀(r) is the field inhomogeneity induced spectral shift at the spatial location r. c_j(r) is the j^th coil sensitivity, and η_j(k, t) is white Gaussian measurement noise. Note that the spatial integral is restricted to Ω, which is a mask that specifies signal support (e.g., head). The entire acquisition scheme can be compactly represented as

$$\mathbf{S}={\mathcal{A}}_{\mathrm{\Omega }}(\mathbf{X})+\mathit{\eta }.$$ [2]

The operator 𝒜_Ω includes coil sensitivity encoding, k-space encoding, and spatially varying chemical shift resulting from field inhomogeneity. S is a matrix, whose entries correspond to the measured k – t space samples. Here, X is the R × N Casorati matrix derived from x(r, f), whose rows correspond to the N point spectra from pixels within Ω:

$$\mathbf{X}=\left[\begin{array}{cccc}x({\mathbf{r}}_1,f_1)& x({\mathbf{r}}_1,f_2)& \cdots & x({\mathbf{r}}_1,f_N)\\ x({\mathbf{r}}_2,f_1)& x({\mathbf{r}}_2,t_2)& \cdots & x({\mathbf{r}}_2,f_N)\\ ⋮& ⋮& \ddots & ⋮\\ x({\mathbf{r}}_R,f_1)& x({\mathbf{r}}_R,t_2)& \cdots & x({\mathbf{r}}_R,f_N)\end{array}\right]$$ [3]

Here, R is number of pixels in Ω.

Compartmental Low-Rank MRSI Signal Model

Several authors have proposed to model signal x(r, f) using low-rank methods (30,32). A challenge with direct application of these methods to lipid unsuppresed data is the strong extracranial lipid signals that are several orders of magnitude stronger than metabolites; low-rank modeling may result in the lower principal components being captured by the lipid signals to account for subtle variations in lipid signal. A high-rank representation will hence be needed to accurately represent the metabolites, which may make the model inefficient.

The lipid and metabolite signals that originate from disjoint spatial supports have finite number of resonant frequencies arising from finite anatomical regions inside the spatial compartments. We assume that brain and lipid regions, denoted by Ω_M and Ω_L respectively, to be known a priori from water reference scans. We denote metabolite and lipid components of x(r, f) as

$$x_M(\mathbf{r},f)=x(\mathbf{r},f)·{\chi }_{{\mathrm{\Omega }}_M}(\mathbf{r})$$ [4]

$$x_L(\mathbf{r},f)=x(\mathbf{r},f)·{\chi }_{{\mathrm{\Omega }}_L}(\mathbf{r})$$ [5]

Here, χ_Ω is the characteristic function of the region Ω:

$${\chi }_{\mathrm{\Omega }}(\mathbf{r})=\{\begin{array}{ccc}1& \text{if}& \mathbf{r}\in \mathrm{\Omega }\\ 0& \text{else.}& \end{array}$$ [6]

Since the regions Ω_M and Ω_L are mutually exclusive, we have

$$x(\mathbf{r},f)=x_M(\mathbf{r},f)+x_L(\mathbf{r},f).$$ [7]

Note that the dynamic range of signals x_M and x_L is individually small, even though the dynamic range of the signal x is very high. We construct matrices X_M and X_L similar to (3) from x_M and x_L by only including pixels from Ω_M and Ω_L, respectively. We assume that X_M and X_L are individually low-rank; the compartmental low-rank model allows these matrices to be represented using distinct basis functions and to independently control their ranks.

We observe that spectra of the metabolite and lipid regions are highly dissimilar, and hence orthogonal (i.e., 〈x_L(r₁, f), x_M(r₂, f)〉 = 0; ∀r₁, r₂). We are inspired by the use of a similar prior in (40) to minimize cross-talk between x_M and x_L. Combining this prior with the decomposition in (7), we obtain

$$\mathbf{X}={\mathbf{X}}_M+{\mathbf{X}}_L;{\mathbf{X}}_L{\mathbf{X}}_M^H=\mathbf{0},$$ [8]

where X^H is the conjugate transpose of the matrix X.

Recovery of the Compartmental Signal Model from k-t Space Data

We pose recovery of the metabolite and lipid components from measured k-space data as the optimization problem:

$$\{{\mathbf{X}}_M,{\mathbf{X}}_L\}=arg\underset{{\mathbf{X}}_L,{\mathbf{X}}_M}{min}\underset{\text{data}\text{consistency}}{\underbrace{{\Vert {\mathcal{A}}_{{\mathrm{\Omega }}_M}({\mathbf{X}}_M)+{\mathcal{A}}_{{\mathrm{\Omega }}_L}({\mathbf{X}}_L)-\mathbf{S}\Vert }^2}}+\underset{\text{low-rank}\text{priors}}{\underbrace{{\lambda }_1{\Vert {\mathbf{X}}_M\Vert }_{\ast }+{\lambda }_2{\Vert {\mathbf{X}}_L\Vert }_{\ast }}}+\underset{\text{orthogonality}\text{prior}}{\underbrace{\beta {\Vert {\mathbf{X}}_M{\mathbf{X}}_L^H\Vert }^2}}.$$ [9]

Here ||X||_* denotes the nuclear norm of X. The first term is the data consistency term, while the second and third terms are the low-rank priors on metabolite and lipid signals, respectively. Note that we do not explicitly use spectral priors of metabolite and lipid regions to discourage cross-talk as in (17,33); the cross-talk is automatically minimized by use of the orthogonality priors. As shown in (40) and our experiments, orthogonality priors will only cause minimal biases in the metabolite signals. We do not use detailed anatomical priors (e.g., masks of gray matter, white matter, and cerebrospinal fluid (CSF) regions) as proposed by several authors (26,28,43–48). The inner-product between metabolite and lipid signals are penalized, weighted by a high regularization parameter β.

We propose to solve the above problem using the iterative reweighted least square minimization algorithm (49,50) for nuclear norm minimization. This approach relies on approximating the nuclear norm penalty at the n^th iteration as the weighted Frobenius norm:

$${\Vert \mathbf{X}\Vert }_{\ast }\approx {\Vert \mathbf{X}\mathbf{Q}\Vert }_{\mathbf{F}}^2,$$ [10]

where the weight matrix at the n^th iteration is chosen as $\mathbf{Q}={\left({\mathbf{X}}_{n-1}^H{\mathbf{X}}_{n-1}\right)}^{-1/4}$; where X_n−1 is the solution of the nuclear norm minimization problem at the (n − 1)^th iteration. The matrix power is evaluated using eigen value decomposition. Specifically, we perform eigen decomposition to obtain $\left({\mathbf{X}}_{n-1}^H{\mathbf{X}}_{n-1}\right)=\mathbf{U}\mathbf{\sum }{\mathbf{U}}^H$ and complete the weight matrix as Q = USU^H, where S = Σ^{− (1/4)}. To avoid division by zero, diagonal entries of S are stabilized as s_i = max(σ_i, ε)^−(1/4), where ε is a stabilization constant. For convergence of the solution, we require ε → 0 as n → ∞. When a target rank K is desired, the stabilization parameter is chosen as ε = γ σ_K, where 0 < γ < 1. Using the iterative reweighted least square minimization scheme to solve (9) amounts to solving the following quadratic criterion at the n^th iteration:

$${\{{\mathbf{X}}_L,{\mathbf{X}}_M\}}_n=arg\underset{{\mathbf{X}}_L,{\mathbf{X}}_M}{min}{\Vert {\mathcal{A}}_{{\mathrm{\Omega }}_M}({\mathbf{X}}_M)+{\mathcal{A}}_{{\mathrm{\Omega }}_L}({\mathbf{X}}_L))-\mathbf{S}\Vert }^2+{\lambda }_1{\Vert {\mathbf{X}}_M{\mathbf{Q}}_M\Vert }_F^2+{\lambda }_2{\Vert {\mathbf{X}}_L{\mathbf{Q}}_L\Vert }_F^2+\underset{\text{orthogonality}\text{penalty}}{\underbrace{\beta {\Vert {\mathbf{X}}_M{\mathbf{Q}}_O\Vert }_F^2}}.$$ [11]

Weight matrices Q_M and Q_L are updated at the n^th iteration using the solutions {X_M,X_L}_n−1 as

$${\mathbf{Q}}_M={\mathbf{U}}_M{\mathbf{\sum }^{\sim }}_M^{(-1/4)}{\mathbf{U}}_M^H,\text{where}{\mathbf{X}}_M^H{\mathbf{X}}_M={\mathbf{U}}_M{\mathbf{\sum }}_M{\mathbf{U}}_M^H$$ [12]

$${\mathbf{Q}}_L={\mathbf{U}}_L{{\mathbf{\sum }^{\sim }}_L}^{(-1/4)}{\mathbf{U}}_L^H,\text{where}{\mathbf{X}}_L^H{\mathbf{X}}_L={\mathbf{U}}_L{\mathbf{\sum }}_L{\mathbf{U}}_L^H.$$ [13]

Diagonal entries of the matrices Σ̃_M and Σ̃_L are stabilized versions of the entries of Σ_M and Σ_L, respectively; i.e., Σ̃(i) = min(Σ(i), ε). Equation [11] may be intuitively interpreted; if the matrices X_M and X_L are low-rank and the singular values decay rapidly, Q_M and Q_L are projection operators onto the noise subspaces of X_M and X_L (corresponding to insignificant singular values), respectively. Thus, the second and third terms enable denoising by minimizing projection of the signals to the null-spaces, estimated from the previous iteration. The projection matrix for orthogonality constraint Q_O in (11) is obtained as

$${\mathbf{Q}}_O={\mathbf{U}}_L{\mathbf{\sum }^{\sim }}_L^{(1/2)}{\mathbf{U}}_L^H,\text{where}{\mathbf{X}}_L^H{\mathbf{X}}_L={\mathbf{U}}_L{\mathbf{\sum }}_L{\mathbf{U}}_L^H$$ [14]

METHODS

Variable Density Spiral Spin-Echo Sequence

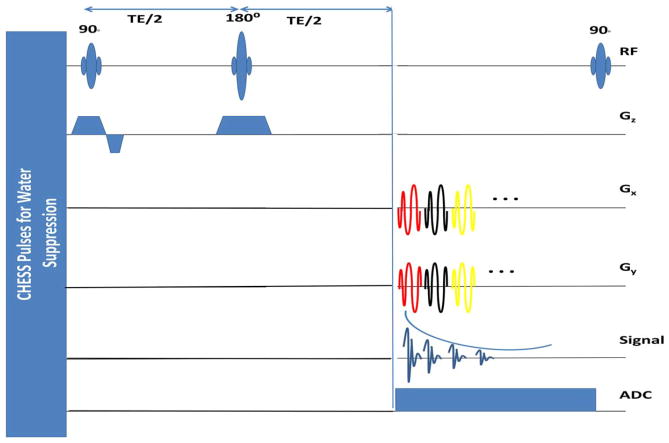
The k-space trajectories are designed using a numerical algorithm (41). The sequence is illustrated in Figure 1. We use a slice selective spin echo sequence with CHESS water suppression. No lipid suppression is used. The parameters are pulse repetition time (TR)/TE=1500/55 ms; total scan time=7.2 mins. A separate water scan, using the same sequence with TR = 500 ms and 2.4 mins of scan time, is used to estimate coil sensitivities, field inhomogeneity map, and spatial supports of lipid and water regions. Coil sensitivities are estimated using the sum of squares method (51). The reduction in lipid leakage due to variable density sampling at high resolution is explained in Figure 2.

FIG. 1.

Pulse sequence diagram for spin echo-based variable density spiral spectroscopic imaging: Water suppression is achieved using CHESS pulses. Slice selective excitation and refocusing RF pulses are applied, followed by repeatedly playing out the spiral gradients, ramp-down gradients, and rewinders. For sake of simplicity, the ramp-down gradients and crushers for each spiral gradient are not shown in the figure. Image matrix size=128 × 128 is acquired with variable density spiral trajectory with 24 interleaves, which samples the lower k-space region of radius less than 16 at the Nyquist rate, and the higher k-space region at $\frac{1}{12}$ times Nyquist rate. Twelve averages are collected by rotating the trajectories by $\frac{2\mathrm{\pi }}{24\times 12}$ degrees at each average. Thus the central k-space regions is averaged 12-fold, while the higher k-space region is Nyquist sampled. The acquisition requires 24 × 12=288 spatial interleaves and thus 288 RF excitations. The spectral bandwidth= 574.7 Hz (4.7 ppm), temporal interleaves=256; which achieves a spectral resolution of 2.2 Hz. The k-space trajectory consists of (a) lower k-space region (35% of sampling time), (b) higher k-space regions, (24% of time, and (c) gradient ramp down and rewinding (41% of time). Field of view=240 mm, maximum gradient amplitude=22.4 mT/m, and a slew rate= 125 T/m/s.

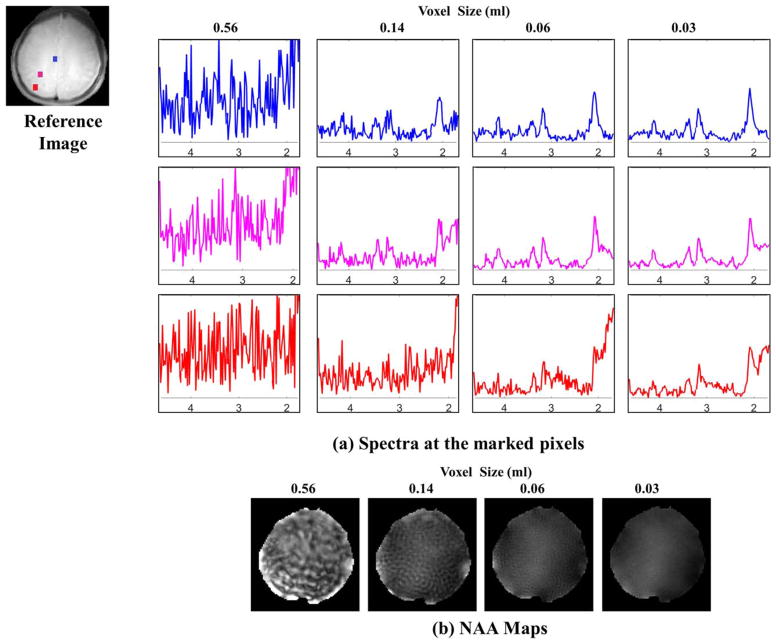
FIG. 2.

Benefit of extended k-space coverage in acquisition without lipid suppression: The top figure (a) shows the spectra at three different locations (blue pixel at the center of the brain, pink pixel between the center and skull, and red pixel near the skull or lipid layer). In the absence of lipid suppression, better line shape and reduction of lipid signal is achieved with increased k-space coverage. The peak integral NAA images in (b) demonstrate the decreased ringing artifacts with increasing k-space coverage.

Digital Phantom for Validation

We developed a numerical MRSI phantom with metabolite and lipid compartments by extending the template and code in (52). This phantom is discretized on a 512 × 512 Cartesian sampling grid as described in Figure 3. Fourier samples of the phantom are numerically evaluated at the k-t space points specified by the above described spiral trajectory. White Gaussian noise was added to the Fourier samples.

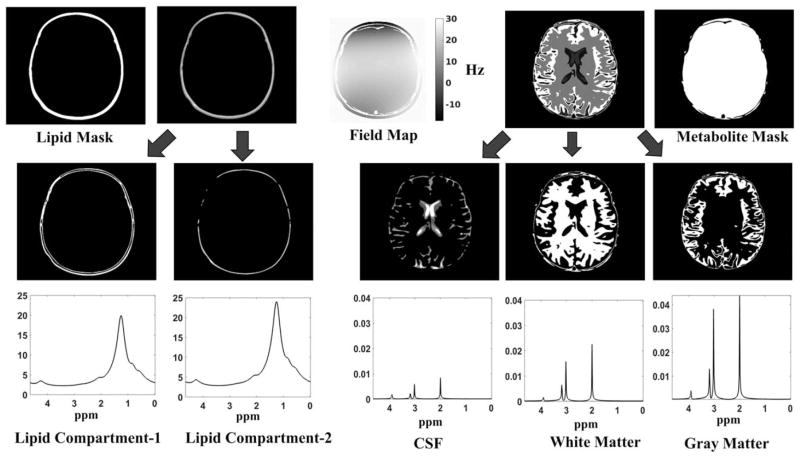
FIG. 3.

Construction of the digital phantom: The phantom is constructed with five different spatial compartmental basis functions (two lipid compartments, CSF, white matter, and gray matter). Each of these compartments has a unique metabolite or lipid spectrum associated with it. The metabolite spectra have peaks corresponding to NAA (at 2.008 ppm), Creatine (at 3.027 and 3.913 ppm) and Choline (3.185 ppm) (53). We choose the concentration of the metabolites in different compartments based on normal brain concentrations reported in literature (54). The lipid peaks are constructed with a six peak model, reported in (60). The lipid peaks are chosen to be 500–1000 times larger in amplitude, in accordance to real data without lipid suppression. We also accounted for the T₂ decay with appropriate parameters, which translates to spectral broadening of the line shapes. A field inhomogeneity map using fourth order polynomial in both the spatial dimensions is also simulated. The spatial masks (support) of lipid and metabolite region are shown on the top left and right, respectively. It is to be noted that uniform spatial masks are used instead of detailed maps with edge weights of white matter, gray matter, and CSF regions.

To study the effect of lipid suppression, we considered two realizations of the digital phantom (a) without any lipid signals (no lipid compartments) and (b) when lipid signals are present. SNR of the k-t space data is 5.26 dB in (a) and 26.7 dB in (b); higher signal energy in presence of lipids translates to higher SNR in (b). We compare the performance of Tikhonov regularized method and the proposed low-rank method for both realizations. Reference reconstruction is obtained by gridding reconstruction of the k-t space data, without lipids and additive noise. All reconstructions are performed on a grid size of 96 × 96 and a field map estimated at the same resolution to correct for field inhomogeneity artifacts.

We also study the sensitivity of the algorithm to inaccurate lipid boundary estimation. Specifically, we used two different lipid masks, obtained by morphologically shrinking and dilating the original mask used for simulation, to reconstruct the MRSI data.

Recovery of MRSI Data Using Other Algorithms for Comparison

We compare the proposed method against the dual-resolution reconstruction scheme, which relies on compartmentalized Tikhonov smoothness regularization (26,27):

$$\{{\mathbf{X}}_M,{\mathbf{X}}_L\}=arg\underset{{\mathbf{X}}_L,{\mathbf{X}}_M}{min}\underset{\text{data}\text{consistency}}{\underbrace{{\Vert {\mathcal{A}}_{{\mathrm{\Omega }}_M}({\mathbf{X}}_M)+{\mathcal{A}}_{{\mathrm{\Omega }}_L}({\mathbf{X}}_L)-\mathbf{S}\Vert }^2}}+\underset{\text{smoothness}\text{priors}}{\underbrace{{\alpha }_1{\Vert {\nabla }_{{\mathrm{\Omega }}_M}{\mathbf{X}}_M\Vert }^2+{\alpha }_2{\Vert {\nabla }_{{\mathrm{\Omega }}_M}{\mathbf{X}}_L\Vert }^2}}.$$

Here, ∇_ΩX denotes spatial gradient of X, restricted to the spatial compartment Ω. This approach is a variational alternative to iterative methods used in (18,22–25). We consider two different settings for choice of α₁ to illustrate tradeoffs in dual-resolution reconstruction. We consider α₁ = 10⁻⁵, which corresponds to minimal blurring of metabolites, referred to as high resolution (HR) Tikhonov recovery. We also consider α₁ = 10⁻³, termed as low-resolution (LR) Tikhonov recovery; this is the choice considered in (26). These settings translate to PSF full width at half maximum (FWHM) of 1 pixel and 2.5 pixels, respectively. In both cases, the parameter α₂ is chosen as 10⁻⁵ to minimize, lipid signal smoothing and lipid contamination of X_M.

We also compare the proposed algorithm against the dual-resolution reconstruction algorithm in (40), which uses orthogonality priors. We used the software provided by the authors for the reconstruction. Metabolite signals were further denoised using low-rank approximation with rank=15 (using truncated singular value decomposition (SVD)) after reconstruction.

In Vivo Experiments

In vivo experiments were performed on a 3T Siemens Trio scanner using a 12 channel receive head-coil under a protocol approved by the Institutional Review Board of the University of Iowa. Single slice proton MRSI data were collected from two healthy volunteers, after receiving informed consent.

Subject 1

An oblique axial slice above the ventricles was acquired with field of view (FOV)=240 × 240 mm² and a slice thickness=10 mm. Whole slice is excited without any lipid suppression.

Subject 2

An oblique axial slice is selected containing the corpus callosum and lateral ventricles and was acquired with a FOV=240 × 240 mm². A lipid suppressed dataset (with eight OVS bands) and another without lipid suppression were acquired.

High resolution B₀ map, lipid, and water images are estimated from the water reference data using (56). Water and lipid images are thresholded to derive lipid region Ω_L and brain region Ω_M, respectively. These masks are used in (9) to define the forward model and to construct matrices X_M and X_L. A gridding recovery is performed, followed by residual water estimation using the Hankel singular value decomposition algorithm (7). The k-space signal corresponding to the residual water signal is subtracted from the measured k-space data before any processing.

We study the benefit in expanding k-space coverage, using variable density spiral k-space trajectory in Figure 2 using data from subject 1. We truncate k-space data to different sizes (radius 32, 64, 96 and 128), corresponding to voxel sizes of 0.56, 0.14, 0.06, and 0.03 mL, respectively. We recover data from these four cases using gridding reconstruction algorithm on an image grid size of 128 × 128. Post recovery, metabolite data within the brain is smoothed with an iterative algorithm after polynomial baseline removal. Smoothing parameters are selected such that the FWHM of the PSF is 2.5 pixels. N-acetyl aspartate (NAA) images are estimated using peak integration.

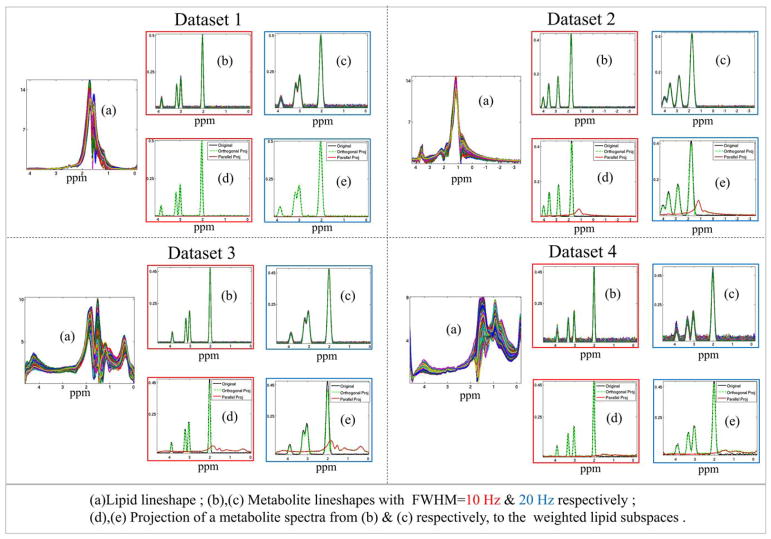
Impact of the orthogonality constraint on the metabolite signals is studied in Figure 4. We obtained lipid spectra from four different datasets. Dataset 1 and 2 were distributed along with the software for (40) and (17). Datasets 3 and 4 correspond to data acquired from subjects 1 and 2, respectively, without any lipid suppression. We modeled 3300 metabolite spectra, as idealized peaks at spectral locations corresponding to NAA, Creatine, & Choline in the real data. We consider simulations with FWHM=10 Hz and 20 Hz. Peak intensities are chosen from a random distribution. Parallel and orthogonal projection of the metabolite spectra to the weighted lipid subspace (given by Eq. [14]) is reported in Figure 4. In Supporting Figure S1, we report the quantitative reductions in metabolite intensities due to orthogonal projection and orthogonal projection energies. We also studied the effect of rank change of the lipid subspace which was found to be practically invariant.

FIG. 4.

Spectral orthogonality of lipid and metabolite line shapes: Orthogonality between lipids and metabolites are demonstrated using four datasets. Dataset 1 and 2 are simulated using real lipid unsuppressed data of (40) and (17), which are distributed with the software. Dataset 3 and 4 are simulated using real data acquired from subject 1 and 2, respectively, without any lipid suppression. For each dataset, lipid line shapes generated from real data are shown in (a). The idealized metabolite spectra consisting of NAA, Creatine, and Choline peaks are simulated with FWHM=10 and 20 Hz (color-coded outline in red and blue, respectively) in (b) and (c), respectively. The metabolites are projected to a rank=20 weighted lipid subspace as given by Equation [14]. The parallel (in red) and orthogonal (in green) projection of a randomly selected metabolite spectra (in black) of the dataset, to the lipid subspace for the two simulations are plotted in (d) and (e), respectively. (For quantitative report of orthogonal projection energy, please refer to Supporting Fig. S1).

Regularization parameters in the proposed algorithm described in (11) are chosen empirically to yield the best results for the experiments on data from subject 2. Effect of changing the regularization parameters is explained in details in the results section. We chose the target rank of 15 for the metabolite signals, and 20 for the lipid signals. The parameter γ in the stabilizing parameter equation, ε = γ σ_K, is chosen as 0.8 for both metabolites and lipids. All reconstructions are performed at a grid size of 96 × 96 and metabolite maps are obtained by peak integration over a 16 Hz bandwidth.

RESULTS

We study the utility of acquiring data using variable density spiral k-space trajectory with extended k-space coverage in Figure 2 using data from subject 1. We show reconstructed spectra from three different pixels within the brain, marked in the reference image. Since no lipid suppression is used, spectra with 32 × 32 spatial coverage is highly distorted at all the three pixels. Noise like variations observed at lower resolutions are essentially systematic artifacts introduced by lipid leakage. At lower resolutions, the spectrum at each pixel is a weighted linear combination of the spectra at all locations (including lipid regions), weighted by sinc PSF. If the magnetic field varies significantly within the lipid regions, the weighted linear combination of shifted lipid spectrum with large amplitudes will appear as noise-like variations. Experiments clearly show benefit of extended k-space coverage. With higher k-space encodes/smaller voxel size, spectrum at the blue pixel in the center of the brain is recovered with minimal distortion. The pink pixel closer to skull exhibits some lipid leakage, while the red pixel close to skull is corrupted by extracranial lipids even with extended k-space coverage. Reduction in leakage-induced ringing artifacts can also be visualized from the NAA map. Extended k-space coverage alone cannot eliminate all spectral leakage artifacts; therefore, we propose to combine it with the compartmentalized low-rank method to further reduce lipid leakage.

Impact of the orthogonality constraint on the metabolite signals is studied in Figure 4. For each of the four datasets, lipid line shapes and metabolite line shapes are shown. Parallel and orthogonal projection of a selected metabolite spectra to the lipid subspace is plotted as well. The tables in Supporting Figure S1 record average (mean) case percentage reduction of metabolite intensities due to orthogonal projection and the orthogonal projection energy. It is observed that the NAA peak attenuation depends on the field inhomogeneity in the lipid regions. These experiments show that loss of metabolite intensities due to the orthogonality assumption is minimal, even for data with poor shimming. These observations are consistent with the findings in (40).

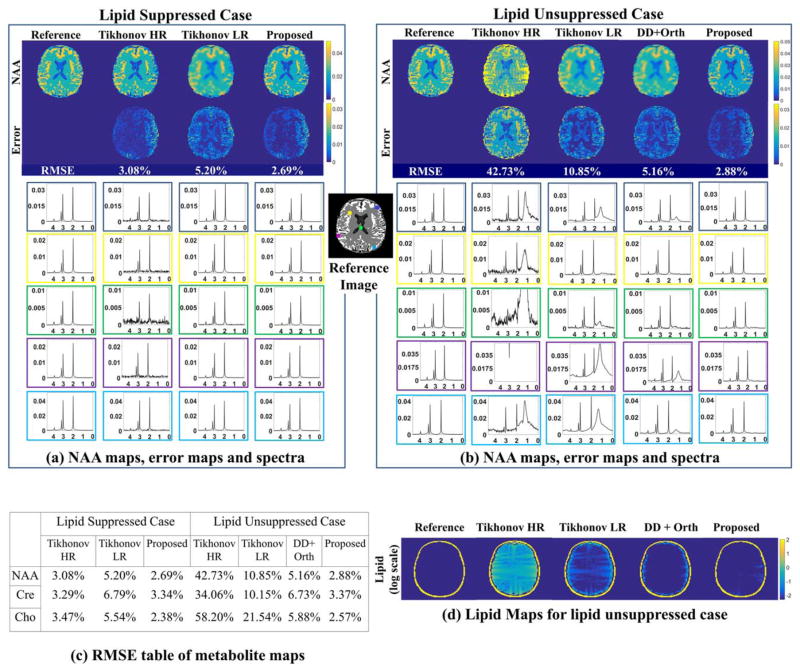
Phantom experiment results are shown in Figure 5. The first column corresponds to simulations without any lipid signal, while the second column is the one with lipid signal. For the lipid-suppressed case, Tikhonov high-resolution (Tikhonov HR), Tikhonov low-resolution (Tikhonov LR), and the proposed algorithm are compared, whereas reconstruction using the scheme described in (40) are added for the lipid unsuppressed case. For comparisons, we recover a reference data from signals without any lipids and noise using gridding, followed by field inhomogeneity compensation. NAA maps, their error maps, and spectra at marked pixels are shown in Figure 5a for lipid-free simulation and in Figure 5b for simulation with lipids. For the lipid free case, we observe that Tikhonov HR method results in relatively noisy maps, while Tikhonov LR method oversmoothes the spatial maps, resulting in systematic edge information loss, seen from the error maps. The proposed method provides maps with reduced noise and minimal blurring. These results can also be appreciated from the spectra corresponding to the pixels marked on the reference image. Root mean square error (RMSE) of NAA maps are calculated to be 3.08% and 5.20% for Tikhonov HR and Tikhonov LR, respectively, while the proposed has the least RMSE of 2.69%. In the lipid unsuppressed phantom experiments (second column), we observe that Tikhonov HR method is noisy and has severe ringing artifacts (seen from maps and spectra in Fig. 5b). Tikhonov LR method on the other hand reduces lipid leakage artifacts, but results in blurred maps. Error maps and spectra show that pixels closer to skull have residual lipid artifacts in the Tikhonov LR method. Dual density with orthogonality method (as in (40)) suppresses lipids efficiently except for pixels close to skull (first and fifth row) but results in blurred maps. By contrast, the proposed method reduces noise and eliminates artifacts without smoothing the data and retains most of the high-resolution details. Tikhonov HR method has a poor RMSE of 42.73%, due to extensive lipid leakage. Tikhonov LR method and (40) have RMSE of 10.85% and 5.16 % for NAA maps, respectively, while the proposed method maintains a RMSE of 2.88%, which is comparable to the lipid suppressed setting. Table (c) reports other metabolite map RMSEs. Thus the reconstruction quality of the proposed method is robust even in presence of lipids. Lipid maps obtained by peak integration over lipid resonances are shown in Figure 5d for the lipid unsuppressed case.

FIG. 5.

Simulated phantom experiments: We consider the recovery of the MRSI phantom in Figure 3 from its noisy k-space measurements on the spiral trajectory. The case without lipid signals (corresponding to perfect lipid suppression) is shown on the left column and the case with lipid signals (no lipid suppression) on the right column. We compare the reconstructions obtained using Tikhonov HR, Tikhonov LR, and the proposed method for the lipid suppressed case whereas the results for dual density with orthogonality (DD+Orth) scheme as proposed in (40) are added for the lipid unsuppressed case. The NAA maps and the corresponding error maps (scaled up) for all the methods under comparison with and without lipids are shown in (a) and (b), respectively. Also the spectra at five representative locations marked in the reference image are shown for all the methods for lipid free and lipid unsuppressed case in (a) and (b), respectively. The lipid maps for the case without lipid suppression are shown in (d). Table (c) shows the RMSEs for the different maps.

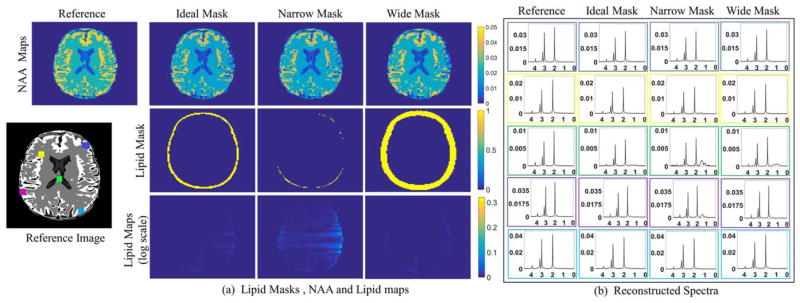
Recovery using different lipid masks, obtained by morphologically dilating or shrinking the original lipid mask is presented in Figure 6. We observe minimal changes in NAA maps, while the spectra show slight increases in lipid leakage when the lipid region is underestimated. These results show that the algorithm is relatively robust to inaccurate mask estimation. Since moderately overestimating the lipid mask provides good reconstructions, we resort to this approach in the remaining experiments.

FIG. 6.

Simulated phantom experiments showing robustness to incorrect lipid mask selection: (a) Reconstructed NAA maps are shown in the first row whereas the corresponding lipid masks and lipid maps are shown in the second and third row, respectively. The NAA maps are of comparable quality. The lipid leakage reduces slightly for an overestimated/wide mask. Only the metabolite region is shown in the lipid maps for better visualization of differences. (b) The spectra at five representative locations shown in the reference image are plotted. The lipid leakage and denoising is comparable even for incorrect mask estimation. However, a wide mask might show improvement in lipid suppression. It is to be noted that the reconstructions with ideal mask (second column) is same as reconstruction with proposed method as in Figure 5b and d. The metabolite mask used in all the simulations is same.

Effect of changing different regularization parameters of the algorithm is studied with the lipid unsuppressed data acquired from subject 2. In Supporting Figure S2, the left box illustrates the effect of changing λ₁, which controls metabolite compartment rank. In these experiments, we set λ₂ = 1e⁻⁸; β = 1000. We observe that increasing λ₁ is associated with spectral denoising, while high values are associated with spatial details loss. We choose λ₁ = 4e⁻⁶, which provide good compromise. The middle box demonstrates the effect of changing λ₂, which controls lipid compartment rank. We set λ₁ = 4e⁻⁶; β = 1000 in these experiments. Over regularizing the lipid compartment (increasing value of λ₂) results in lipid signal attenuation, increased lipid leakage to metabolite signals and noisier metabolite signals. Lipid maps show increased lipid leakage in pixels close to skull. We fix λ₂ to 1e⁻⁶ which offers slight increase in metabolite intensities in comparison to unregularized lipid compartment. In our experiments (right box), we observe the parameter β can be assigned a high value to impose the constraint of lipids being orthogonal to the metabolites; the algorithm’s performance was observed to be relatively insensitive to this parameter, provided it is high enough. Some spatial details are lost when very high β values are chosen, probably due to poor convergence. β is set to 1000 for the remaining experiments.

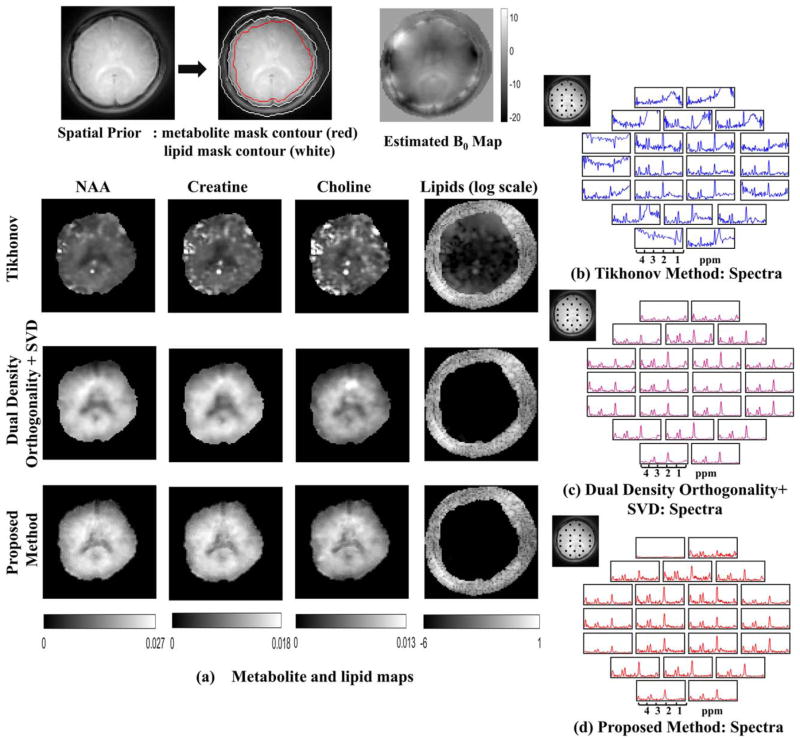
Results for the in vivo experiments with lipid suppression on subject 2 are shown in Figure 7. The proposed method is compared against Tikhonov LR scheme and dual-density scheme in (40), denoised further using low-rank approximation. Lipid region is overestimated based on our findings in Figure 6. From Figure 7a, it is seen that the Tikhonov regularized method has substantial lipid leakage artifacts (maps are scaled by 2.5 times for Tikhonov method). Lipid leakage can also be seen from the spectra. We observe that the dual-density orthogonality method achieves good lipid suppression. However, nominal resolution of the maps is restricted by the extent of central k-space regions. The proposed method is observed to result in negligible lipid leakage artifacts, while the maps are seen to have improved spatial details. This is expected since we estimate metabolite signals from the entire k-space data, which is regularized by low-rank priors. Considering that detailed anatomical priors of gray matter, white matter, and CSF are not used in the recovery, the ability of the algorithm to recover the spatial details is significant. The lipid maps obtained by peak integration of the lipid resonances are shown for all three methods. The Tikhonov method shows heavy lipid leakage in regions close to skull whereas lipid leakage is negligible for the dual-density orthogonality and the proposed method. Spectra at the pixel grid marked in the reference image are shown for the Tikhonov regularized method, dual-density orthogonality method, and the proposed method in Figure 7b–d, respectively. Similar to the phantom simulation results, spectra obtained from Tikhonov method are noisy and have spectral leakage especially in pixels close to skull. By contrast, dual-density orthogonality method and the proposed method denoises the spectra and removes all spectral leakage.

FIG. 7.

In vivo experiments with lipid suppression: The spatial contours for the metabolite and lipid region and the field map are shown in the top row. The metabolite maps and the lipid maps are shown for the Tikhonov method, dual-density orthogonality as in (40) followed by low-rank approximation (using truncated SVD) and proposed method in (a). The metabolite maps obtained from Tikhonov method are scaled up by 2.5 times. The color scale for the metabolite maps in the second and third row are shown below. It is observed that the proposed method has superior spatial details compared to the dual-density orthogonality method. For the dual density method, spatial details are not observed because the metabolite data are constrained to center k-space. The lipid for all the methods is plotted in the same log scale. The Tikhonov method has heavy lipid leakage in the metabolite region whereas the dual-density method and the proposed method has no residual lipid in the metabolite region. Spectra from the locations marked in the reference image are shown in (b) for the Tikhonov method (in blue), (c) dual-density orthogonality followed by truncated SVD (in purple), and in (d) for the proposed method (in red).

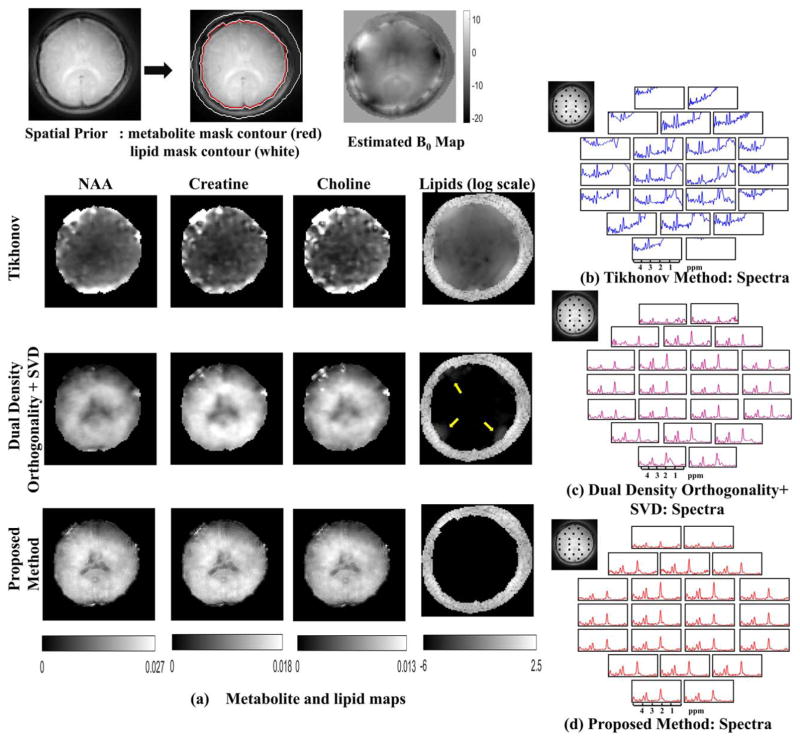
Comparisons of the methods on the lipid unsuppressed dataset from the same subject are shown in Figure 8. Metabolite maps in Figure 8a show quite significant lipid leakage for the Tikhonov regularized method (the images are scaled by 5 times). The dual-density method in this case has some residual lipids close to skull as pointed out by arrows in the lipid maps. The proposed method is seen to recover the data with minimal lipid leakage and with improved spatial details. Spectra at the pixels marked in the reference image are shown in Figure 8b–d for Tikhonov LR, dual-density orthogonality, and proposed method, respectively.

FIG. 8.

In vivo experiments without lipid suppression: The spatial contours for the metabolite and lipid region and the field map are shown in the top row. The metabolite maps and the lipid maps are shown for the Tikhonov method, dual-density orthogonality as in (40) followed by low-rank approximation (using truncated SVD) and proposed method in (a). The metabolite maps obtained from Tikhonov method are scaled up by 5 times. The color scale for the metabolite maps in the second and third row are shown below. It is observed that the proposed method has superior spatial details, whereas the dual-density orthogonality method has some residual lipids at the edges. Spatial details are lost for the dual density method because the metabolite data are limited to center k-space. The lipid for all the methods is plotted in the same log scale. The Tikhonov method has heavy lipid leakage in the metabolite region, whereas the dual-density method has some residual near the edges as shown by the yellow arrows. The proposed method on the other hand has no residual lipid in the metabolite region. Spectra from the locations marked in the reference image are shown in (b) for the Tikhonov method (in blue), (c) dual-density orthogonality followed by truncated SVD (in purple), and in (d) for the proposed method (in red).

DISCUSSION

We introduced a novel compartmentalized low-rank-based algorithm and a spiral dual-density MRSI sequence for high-resolution MRSI reconstruction. The proposed method enables recovery of high-resolution metabolite maps with minimal lipid leakage artifacts from TE=55 ms acquisitions in absence of lipid suppression. This approach may be useful in three dimensional acquisitions, when OVS band placement is difficult.

Low-rank methods have been used in MRSI by several groups for denoising (30) and reconstruction (17,32–34,57). Direct use of global low-rank methods as in (32) may be challenging in our lipid unsuppressed setting. Using a single subspace to represent both lipid and metabolite signal may result in the subspace being dominated by lipid basis functions, especially due to huge dynamic range between lipid and metabolite signals. The proposed single step compartmentalized low-rank algorithm shares conceptual similarities to two step low-rank (SPICE) method (17,33,34). SPICE estimates basis functions from low spatial resolution data, which are separated into metabolite and lipid basis using spatial and spectral prior information in the first step; these basis sets are used for recovery of the signals from high-resolution measurements in the second step. Good recovery is demonstrated using OVS or long TEs to reduce lipid signals. Our preliminary experiments (not shown here) using the software provided by the authors (17) indicate that direct use of these methods in our setting is challenging. Specifically, large field inhomogeneity-induced variations present in the extracranial regions made it difficult to separate the lipid and metabolite basis sets using spectral prior information; the default parameter set for the line shapes did not provide good estimation and lipid suppression. Complexity of the dataset can be appreciated by the huge variability of lipid spectra in the second row (Dataset 3 and 4) of Figure 4, compared to the dataset considered by (17) (Dataset 2). While a more exhaustive optimization of the large parameter set SPICE may provide improved recovery, this is beyond the scope of the present work.

Note that our scheme does not require extensive prior knowledge of lipid line shapes, which is a benefit over (17,33,34), especially with poorly shimmed datasets. The proposed method estimates basis functions from all the available k-space encodes using the orthogonality between the metabolite and lipid signals. This work is inspired by use of orthogonality constraints in (40), where lipid and metabolite signals are shown to have strikingly different spectral signatures (e.g., metabolite are highly localized in frequency, while lipids are very broad due to fast T₂ decay). Distinction between these signals is preserved even in presence of field inhomogeneities. Use of these priors, along with field inhomogeneity compensation, enables metabolite data recovery with minimal leakage, even without lipid suppression.

Low-rank penalty on the lipid signal serves to regularize lipid signal recovery, which in turn can enhance lipid suppression using orthogonality priors. Specifically, noisy lipid signals can result in a large subspace (of large rank); use of this subspace for lipid suppression may result in unwanted metabolite signal attenuation. Denoising enables us to use a larger orthogonality parameter (β), thus effectively suppressing lipids without suppressing metabolites. Impact of the lipid low-rank prior may be more pronounced when the acquisition is more noisy, or undersampled, as proposed in (40).

We observe from Figure 8 that the proposed scheme offers improved lipid suppression than that of the scheme in (40), where an initial high-resolution lipid signal recovery is used in the orthogonality prior. The key difference is that the lipid subspace estimate improves with iterations, due to orthogonality and lipid low-rank priors. Lipid estimate at the first iteration is unregularized and hence is corrupted by noise, and also leakage from metabolites. Use of this subspace can result in unwanted metabolite suppression (due to overlap), especially when used with large β values. As iterations progress, the lipid subspace is decontaminated from metabolite signals (due to orthogonality priors) and denoised (due to low-rank priors). Cleaner lipid subspace improves lipid suppression efficiency, thus reducing metabolite suppression; this allows us to use a larger β values and more effectively suppress lipids without suppressing metabolites.

The dual-density acquisition method is inspired by (18,58). This approach capitalizes the considerably higher lipid signal intensity. Variable density spiral approach is more reliable than dual-density Cartesian scans, which require sophisticated data registration and data mismatch correction to combine data from different acquisitions (17,23,33,34,42). Our future work will include use of only a subset of 288 interleaves, which corresponds to Nyquist sampling of lower k-space regions and subsampling of higher k-space regions. We expect the compartmentalized low-rank method, bolstered with parallel imaging (59,60), to provide good recovery even in this setting. Efficiency may improve by using more spectral interleaves. Specifically, around 40% of acquisition time is now devoted for ramping down the spiral gradients and rewinders. SNR efficiency can be improved by using faster rewinders and also using the k-space data from the rewinders for recovery.

Utility of lipid orthogonality priors in suppressing lipids in short TE data, where higher macromolecule induced baseline signals are present, has not been determined yet. This is also a topic for further research.

CONCLUSION

We introduce a novel compartmentalized low-rank algorithm with orthogonality constraint which enables reconstruction of high-resolution metabolite maps without any lipid suppression method. The proposed method is validated with TE (55 ms) acquisitions. Also an efficient dual-density data acquisition method using variable density spirals has been introduced to achieve high-resolution lipid estimates in a feasible scan time.

Supplementary Material

Supplementary information

Fig. S1. The tables record the average case(mean) percentage attenuation of metabolite intensities due to orthogonal projection and the orthogonal projection energy of the metabolites to the weighted lipid subspace (as shown in Fig. 4) for the four datasets. The orthogonal energy is small which supports our assumption. The effect of changing rank is studied with a rank=5 lipid subspace; the projection energy change due to rank is negligible. The mean orthogonal projection energy of lipid line shapes on a weighted metabolite subspace of rank=15 is reported and is found to be very small.

Fig. S2. Effect of selecting different regularization parameter of the algorithm: The resulting reconstruction with varying regularization parameters is shown. The left block shows the effect of increasing λ₁ for fixed λ₂=1e–6 & β=1000. With increasing low-rank penalty on metabolites, the spectra (at the blue marked pixel in the second metabolite map) become more denoised and decreases in intensity whereas the spatial details are lost. We choose an intermediate value of λ₁=4e–6 so as to achieve a balance between loss of spatial details and denoising spectra. There is no change in lipid maps or spectra (at the blue marked pixel in the first lipid map). In the middle block, effect of increasing λ₂ is shown for fixed λ₁=4e–6 & β=1000. As λ₂ increases lipid signal attenuates as seen from the maps and spectra. This also results in noisier metabolite spectra (at the blue marked pixel in the first metabolite map) and more spectral leakage at the edges. But choosing λ₂ as 1e–6 provides slight increase in metabolite peak heights, which is otherwise attenuated for a unregularized lipid compartment (as seen for λ₂=0 or 1e–8). The last block shows effect of changing β. For any high enough value, orthogonality constraint is imposed without discernible change in reconstruction performance. For very high values of β some spatial details are lost, most likely due to poor convergence.