Regression Models on Riemannian Symmetric Spaces

Summary

The aim of this paper is to develop a general regression framework for the analysis of manifold-valued response in a Riemannian symmetric space (RSS) and its association with multiple covariates of interest, such as age or gender, in Euclidean space. Such RSS-valued data arises frequently in medical imaging, surface modeling, and computer vision, among many others. We develop an intrinsic regression model solely based on an intrinsic conditional moment assumption, avoiding specifying any parametric distribution in RSS. We propose various link functions to map from the Euclidean space of multiple covariates to the RSS of responses. We develop a two-stage procedure to calculate the parameter estimates and determine their asymptotic distributions. We construct the Wald and geodesic test statistics to test hypotheses of unknown parameters. We systematically investigate the geometric invariant property of these estimates and test statistics. Simulation studies and a real data analysis are used to evaluate the finite sample properties of our methods.

1. Introduction

Manifold-valued responses in curved spaces frequently arise in many disciplines including medical imaging, computational biology, and computer vision, among many others. For instance, in medical and molecular imaging, it is interesting to delineate the changes in the shape and anatomy of a molecule. See Figure 1 for four different examples of manifold-valued data. Regression analysis is a fundamental statistical tool for relating a response variable to covariate, such as age. In particular, when both the response and the covariate(s) are in Euclidean space, the classical linear regression model and its variants have been widely used in various fields (McCullagh and A. Nelder, 1989). However, when the response is in a Riemannian symmetric space (RSS) and the covariates are in Euclidean space, developing regression models for this type of data raises both computational and theoretical challenges. The aim of this paper is to develop a general regression framework to address these challenges.

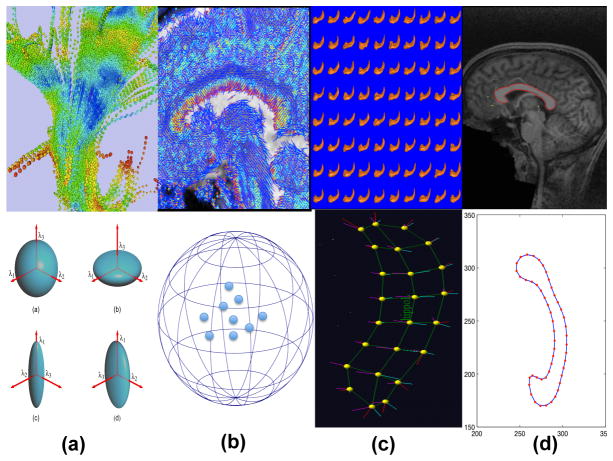
Fig. 1.

Examples of manifold-valued data: (a) diffusion tensors along white matter fiber bundles and their ellipsoid representations; (b) principal direction map of a selected slice for a randomly selected subject and the directional representation of some randomly selected principal directions on S²; (c) median representations and median atoms of a hippocampus from a randomly selected subject; and (d) an extracted contour and landmarks along the contour of the midsagittal section of the corpus callosum (CC) from a randomly selected subject.

Little has been done on the regression analyses of manifold-valued response data. The existing statistical methods for general manifold-valued data are primarily developed to characterize the population ‘mean’ and ‘variation’ across groups (Bhattacharya and Patrangenaru, 2003, 2005; Fletcher et al., 2004; Dryden and Mardia, 1998; Huckemann et al., 2010). In contrast, even for the ‘simplest’ directional data, there is a sparse literature on regression modeling of a single directional response and multiple covariates (Mardia and Jupp, 2000). In addition, these regression models of directional data are primarily based on a specific parametric distribution, such as the von Mises-Fisher distribution (Mardia and Jupp, 2000; Kent, 1982). However, it can be very challenging to assume useful parametric distributions for general manifold-valued data, and thus it is difficult to generalize these regression models of directional data to general manifold-valued data except for some specific manifolds (Shi et al., 2012; Fletcher, 2013; Kim et al., 2014; Shi et al., 2009; Zhu et al., 2009). There is also a great interest in developing nonparametric regression models for manifold-valued response data and multiple covariates (Bhattacharya and Dunson, 2010, 2012; Samir et al., 2012; Su et al., 2012; Muralidharan and Fletcher, 2012; Machado and Leite, 2006; Machado et al., 2010; Yuan et al., 2012).

An intriguing question is whether there is a general regression framework for manifold-valued response in a RSS and covariates in a multidimensional Euclidean space. The aim of this paper is to give an affirmative answer to such a question. The theoretical development is challenging but of great interest for carrying out statistical inferences on regression coefficients. We make five major contributions in this paper as follows: (i) We propose an intrinsic regression model solely based on an intrinsic conditional moment for the response in a RSS, thus avoiding specifying any parametric distributions in a general RSS - the model can handle multiple covariates in Euclidean space. (ii) We develop several ‘efficient’ estimation methods for estimating the regression coefficients in this intrinsic model. (iii) We develop several test statistics for testing linear hypotheses of the regression coefficients. (iv) We develop a general asymptotic framework for the estimates of the regression coefficients and test statistics. (v) We systematically investigate the geometrical properties (e.g., chart invariance) of these parameter estimates and test statistics.

The paper is organized as follows. In Section 2, we review the basic notion and concepts of Riemannian geometry. In Section 3, we propose the intrinsic regression models and propose various link functions for several specific RSS’s. In Section 4, we develop estimation and test procedures for the intrinsic regression models. In Section 5, we carry out a detailed data analysis on the shape of Corpus Callosum (CC) contours obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) study. Finally, we conclude with some discussions in Section 6. Technical conditions, simulation studies, theoretical examples, and proofs are deferred to the Supplementary document. Our code and data are available from http://www.bios.unc.edu/research/bias.

2. Differential Geometry Preliminaries

We briefly review some basic facts about the theory of Riemannian geometry and present more technical details in the Supplementary Report. The reader can refer to (Helgason, 1978; Spivak, 1979; Lang, 1999) for more details.

Let ℳ be a smooth manifold and d_ℳ be its dimension. A tangent vector of ℳ at p ∈ ℳ is defined as the derivative of a smooth curve γ(t) with respect to t evaluated at t = 0, denoted as γ̇(0), where γ(0) = p. The tangent space of ℳ at p is denoted as T_pℳ and is the set of all tangent vectors at p.

A Riemannian manifold (ℳ, m) is a smooth manifold together with a family of inner products, m = {m_p}, on the tangent spaces T_pℳ’s that vary smoothly with p ∈ ℳ, and m is called a Riemannian metric. This metric induces a so-called geodesic distance dist_ℳ on ℳ. The geodesics are, by definition, the locally distance-minimizing paths. If the metric space (ℳ, dist_ℳ) is complete, the exponential map at p is defined on the tangent space T_pℳ by ${\text{Exp}}_{\mathrm{p}}^{\mathcal{M}}(V)=\gamma (1;\mathrm{p},V)$, where t → γ (t; p, V) is the geodesic with γ(0; p, V) = p and γ̇(0; p, V) = V. ${\text{Exp}}_{\mathrm{p}}^{\mathcal{M}}$ is well-defined near 0 and is a diffeomorphism on an open neighborhood 𝒱 of the origin in T_pℳ onto 𝒰 with 𝒱 such that tV ∈ 𝒱 for 0 ≤ t ≤ 1 and V ∈ 𝒱. The inverse map is the logarithmic map at p, denoted by ${\text{Log}}_{\mathrm{p}}^{\mathcal{M}}$. Then, for q ∈ 𝒰, ${\text{dist}}_{\mathcal{M}}(\mathrm{p},\mathrm{q})={\Vert {\text{Log}}_{\mathrm{p}}^{\mathcal{M}}(\mathrm{q})\Vert }_{\mathrm{p}}$. The radius of injectivity of ℳ at p, denoted by ρ^*(ℳ, p), is the largest r > 0 such that ${\text{Exp}}_{\mathrm{p}}^{\mathcal{M}}$ is a diffeomorphism on the open ball B_mp(0, r) ⊂ T_pℳ onto an open set in ℳ near p. Any basis in the tangent space T_pℳ induces an isomorphism from T_pℳ to R^d_ℳ, and then the logarithmic map Log_p provides a local chart near p. If T_pℳ is endowed with an orthonormal basis, such a chart is called a normal chart and the coordinates are called normal coordinates.

A Lie group G is a group together with a smooth manifold structure such that the operations of multiplication and inversion are smooth maps. Many common geometric transformations of Euclidean spaces that form Lie groups include rotations, translations, dilations, and affine transformations on R^d. In general, Lie groups can be used to describe transformations of smooth manifolds.

An RSS is a connected Riemannian manifold ℳ with the property that at each point, the mapping that reverses geodesics through that point is an isometry. Examples of RSS’s include Euclidean spaces, R^k, spheres, S^k, projective spaces, PR^k, and hyperbolic spaces, H^k, each with their standard Riemannian metrics. Symmetric spaces arise naturally from Lie group actions on manifolds, see Helgason (1978). Given a smooth manifold ℳ and a Lie group G, a smooth group action of G on ℳ is a smooth mapping G × ℳ → ℳ, (a, p) ↦ a · p such that e · p = p and (aa′) · p = a · (a′ · p) for all a, a′ ∈ G and all p ∈ ℳ. The group action should be interpreted as a group of transformations of the manifold ℳ, namely, {L_a}_a∈G, L_a(p) = a · p for p ∈ ℳ. The L_a is a smooth transformation on ℳ and its inverse is L_a⁻¹. The orbit of a point p ∈ ℳ is defined as G(p) = {a · p | a ∈ G}. The orbits form a partition of ℳ. If ℳ consists of a single orbit, the group action is transitive or G acts transitively on ℳ, and we call ℳ a homogeneous space. The isotropy subgroup of a point p ∈ ℳ is defined as G_p = {a ∈ G | a · p = p}. When G is a connected group of isometries of the RSS ℳ, ℳ can always be viewed as a homogeneous space, ℳ ≅ G/G_p, and the isotropy subgroup G_p is compact.

From now on, we will assume that the manifold ℳ is an RSS and ℳ = G/G_p with G being a Lie group of isometries acting transitively on ℳ. Geodesics on ℳ are computed through the action of G on ℳ. Due to the transitive action of the group G of isometries on ℳ, it suffices to consider only the geodesic starting at the base point p. Geodesics on ℳ starting from p are the images of the action of a 1-parameter subgroup of G acting on the base point p. That is, for any geodesic γ on ℳ, γ(·) : R → ℳ, starting from p, there exists a 1-parameter subgroup c(·) : R → G such that γ(t) = c(t) · p for all t ∈ R.

3. Intrinsic Regression Model

Let (ℳ, m) be a (C^∞) RSS of dimension d_ℳ and geodesically complete with an inner product m_p and let G be a Lie group of isometries acting smoothly and transitively on ℳ with the identity element e.

3.1. Formulation

Consider n independent observations (y₁, x₁), …, (y_n, x_n), where y_i is the ℳ-valued response variable and x_i = (x_i1, ···, x_idx)^T is a d_x × 1 vector of multiple covariates. Our objective is to introduce an intrinsic regression model for RSS responses and multiple covariates of interest from n subjects.

The specification of the intrinsic regression model involves three key steps including (i) a link function mapping from the space of covariates to ℳ, (ii) the definition of a residual, and (iii) the action of transporting all residuals to a common space. First, we explicitly formalize the link function. From now on, all covariates have been centered to have mean zero. We consider a single-center link function given by

$$\mathit{\mu }(\mathbf{x},\mathrm{q},\mathit{\beta }):R^{d_{\mathbf{x}}}\times \mathcal{M}\times R^{d_{\mathit{\beta }}}\to \mathcal{M},$$ (1)

where μ(x, q, β) is a known link function, q ∈ ℳ can be regarded as the intercept or center, and β = (β₁, …, β_dβ)^T is a d_β ×1 vector of regression coefficients. Moreover, it is assumed that μ(x, q, β) satisfies a single-center property as follows:

$$\mathit{\mu }(\mathbf{0},\mathrm{q},\mathit{\beta })=\mathit{\mu }(\mathbf{x},\mathrm{q},\mathbf{0})=\text{q.}$$ (2)

When the regression coefficient vector β equals 0, the link function is independent of the covariates and thus, it reduces to the single center (or ‘mean’) q ∈ ℳ. When all the covariates are equal to zero, the link function is independent of the regression coefficients and reduces to the center q ∈ ℳ. An example of the single-center link function is the geodesic link function in (Kim et al., 2014; Fletcher, 2013), which is given by

$$\mathit{\mu }(\mathbf{x},\mathrm{q},\mathit{\beta })={\text{Exp}}_{\mathrm{q}}^{\mathcal{M}}(\sum _{k=1}^{d_{\mathbf{x}}}{x}_{ik}{V}_k),$$ (3)

where V_k’s are tangent vectors in T_qℳ and β includes all unknown parameters associated with the tangent vectors.

More generally, we will consider a multicenter link function to account for the presence of multiple discrete covariates and even a general link function defined as μ(x, θ) : R^d_x × Θ → M, where θ is a vector of unknown parameters in a parameter space Θ. For the multicenter link function, θ contains all unknown intercepts, denoted as q(x_D), corresponding to each discrete covariate class and all regression parameters β corresponding to continuous covariates and their potential interactions with the discrete variables. However, the details on these link functions are presented in the Supplementary document, and here, for notational simplicity, we focus on (1) from now on.

Second, we introduce a definition of “residual” to ensure that μ(x_i, q, β) is the proper “conditional mean” of y_i given x_i, which is the key concept of many regression models (McCullagh and A. Nelder, 1989). For instance, in the classical linear regression model, the response can be written as the sum of the regression function and a residual term and the regression function is the conditional mean of the response only when the conditional mean of the residual is equal to zero. Given the points y_i and μ(x_i, q, β) on a RSS ℳ, we need to define the residual as “a difference” between y_i and μ(x_i, q, β). Assume that y_i and μ(x_i, q, β) are “close enough” to each other in the sense that there is an open ball B(0, ρ) ⊂ T_μ(xi,q,β) ℳ such that for all i = 1, …, n,

$$y_i\in {\text{Exp}}_{\mathit{\mu }({\mathbf{x}}_i,\mathrm{q},\mathit{\beta })}(B(0,\rho ))\text{or}{\text{Log}}_{\mathit{\mu }({\mathbf{x}}_i,\mathrm{q},\mathit{\beta })}(y_i)\subset B(0,\rho ).$$ (4)

However, according to a result in Le and Barden (2014), Log_μ(xi,q,β)(y_i) is well defined under some very mild conditions, which require that ∫_ℳ dist_ℳ (p, y_i)²dp(y_i) be finite and achieve a local minimum at μ(x_i, q, β), where p(y_i) is any finite measure of y_i on ℳ. Thus, Log_μ(xi,q,β)(y_i) makes it a good candidate to play the role of a ‘residual’. These residuals, however, lie on different tangent spaces to ℳ, so it is difficult to carry out a multivariate analysis of these residuals.

Third, since ℳ is a RSS, this enables us to “transport” all the residuals, separately, to a common space, say T_pℳ, by exploiting the fact that the parallel transport along the geodesics can be expressed in terms of the action of G on ℳ. Indeed, since ℳ is a symmetric space, the base point p and the point μ(x_i, q, β) can be joined in ℳ by a geodesic, which can be seen as the action of a one-parameter subgroup c(t; x_i, q, β) of G such that c(1; x_i, q, β) · p = μ(x_i, q, β).

We define the rotated residual ℰ (y_i, x_i; q, β) of y_i ∈ ℳ with respect to μ(x_i, q, β) as the parallel transport of the actual residual, Log_μ(xi,q,β)(y_i), along the geodesic from the conditional mean, μ(x_i, q, β), to the base point p. That is,

$$\mathcal{E}(y_i,{\mathbf{x}}_i;\mathrm{q},\mathit{\beta })={\mathcal{E}}_i(\mathrm{q},\mathit{\beta }):={\text{Log}}_{\mathrm{p}}\left(c{(1;{\mathbf{x}}_i,\mathrm{q},\mathit{\beta })}^{-1}·y_i\right)\in T_{\mathrm{p}}M$$ (5)

for i = 1, …, n, where T_pℳ is identified with R^d_ℳ. The intrinsic regression model on ℳ is defined by

$$E[\mathcal{E}(y_i,{\mathbf{x}}_i;{\mathrm{q}}_{\ast },{\mathit{\beta }}_{\ast })\mid {\mathbf{x}}_i]=0,$$ (6)

where (q_*, β_*) denotes the true value of (q, β) and the expectation is taken with respect to the conditional distribution of y_i given x_i. Model (6) is equivalent to E[Log_{μ(xi, q*, β*)} (y_i)|x_i] = 0 for i = 1, …, n, since the tangent map of the action of c(1;x_i,q_*,β_*)⁻¹ on ℳ is an isomorphism of linear spaces (invariant under the metric m) between the fibers of the tangent bundle T ℳ. This model does not assume any parametric distribution for y_i given x_i, and thus it allows for a large class of distributions. The model is essentially semi-parametric, since the joint distribution of (y, x) is not restricted except by the zero conditional moment requirement in (6).

3.2. A Theoretical Example: The Unit Sphere S^k

We investigate the intrinsic regression model for S^k-valued responses and include several other examples in the supplementary document. We review some basic facts about the geometric structure of ℳ = S^k = {x ∈ R^k+1 : ||x||₂ = 1} (Shi et al., 2012; Mardia and Jupp, 2000; Healy and Kim, 1996; Huckemann et al., 2010). For q ∈ S^k, T_qS^k is given by T_qS^k = {v ∈ R^k+1 : v^⊤q = 0}. The canonical Riemannian metric on S^k is that induced by the canonical inner product on R^k+1. Under this metric, the geodesic distance between any two points q and q′ is equal to ψ_q,q′ = arccos(q^Tq′) If the points are not antipodal (i.e. q′ ≠ −q), then there is a unique geodesic path that joins them. Therefore, the radius of injectivity is ρ(S^k) = π. For v ∈ T_qS^k, the Riemannian Exponential map is given by Exp_q(v) = cos(||v||)q + sin(||v||)v/||v||. (Here, sin(0)/0 = 1.) If q and q′ are not antipodal, the Riemannian Logarithmic map is given by Log_q(q′) = arccos(q^T q′)v/||v||, where v = q′ − (q^T q′)q ≠ 0.

The special orthogonal group G = SO(k + 1) is a group of isometries on S^k and acts transitively and simply on S^k via the left matrix multiplication. Specifically, the rotation matrix R_q,q′, which rotates q to q′ ∈ S^k, is given by

$$R_{\mathrm{q},{\mathrm{q}}^{\prime }}={\mathbf{I}}_{k+1}+sin({\psi }_{\mathrm{q},{\mathrm{q}}^{\prime }})\{{\mathrm{q}}^{\prime }{\stackrel{\sim }{\mathrm{q}}}^T-\stackrel{\sim }{\mathrm{q}}{{\mathrm{q}}^{\prime }}^T\}+\{cos({\psi }_{\mathrm{q},{\mathrm{q}}^{\prime }})-1\}\{{{\mathrm{q}}^{\prime }{\mathrm{q}}^{\prime }}^T+{\stackrel{\sim }{\mathrm{q}}\stackrel{\sim }{\mathrm{q}}}^T\},$$

where $\stackrel{\sim }{\mathrm{q}}=\{\mathrm{q}-({\mathrm{q}}^T{\mathrm{q}}^{\prime }){\mathrm{q}}^{\prime }\}/\sqrt{1-{({\mathrm{q}}^T{\mathrm{q}}^{\prime })}^2}$. Thus, q′ = R_q,q′q and R_q,q′v ∈ T_q′S^k, for any v ∈ T_qS^k. Moreover, (−π, π) ∋ t ↦ c_q′,q(t) · q′ is the unique geodesic curve in S^k joining q′ with q, where c_q′,q(t) takes the form

$$c_{{\mathrm{q}}^{\prime },\mathrm{q}}(t)={\mathbf{I}}_{k+1}+sin(t)\{{\stackrel{\sim }{\mathrm{q}}{\mathrm{q}}^{\prime }}^T-{{\mathrm{q}}^{\prime }\stackrel{\sim }{\mathrm{q}}}^T\}+\{cos(t)-1\}\{{{\mathrm{q}}^{\prime }{\mathrm{q}}^{\prime }}^T+{\stackrel{\sim }{\mathrm{q}}\stackrel{\sim }{\mathrm{q}}}^T\}.$$

Suppose that we observe {(y_i, x_i) : i = 1, …, n}, where y_i ∈ S^k for all i. We introduce the three key components of our intrinsic regression model for S^k–valued responses. First, we consider several examples of the general link function μ(x_i, θ). Specifically, without loss of generality, we fix the “north pole” p = (0, …, 0, 1)^T ∈ R^k+1 as a base point. Let e_j be the (k +1)×1 vector with a 1 at the j-th component and a 0 otherwise for j = 1, …, k. Let q ∈ S^k be the ‘center’, and we consider two link functions as follows:

$$\begin{array}{l}\mathit{\mu }({\mathbf{x}}_i,\mathrm{q},\mathit{\beta })={\text{Exp}}_{\mathrm{q}}(\sum _{j=1}^{k}f{({\mathbf{x}}_i,\mathit{\beta })}_j{c}_{\mathrm{p},\mathrm{q}}(arccos({\mathrm{p}}^T\mathrm{q})){\mathbf{e}}_j),\\ \mathit{\mu }({\mathbf{x}}_i,\mathrm{q},\mathit{\beta })=c_{-\mathrm{p},\mathrm{q}}(arccos(-{\mathrm{p}}^T\mathrm{q}))(T_{st,-\mathrm{p}}^{-1}({(f{({\mathbf{x}}_i,\mathit{\beta })}^T,-1)}^T)),\end{array}$$ (7)

where T_st,-p is the stereographic projection mapping from S^k \ {p} onto the d-dimensional hyperplane R^k×{−1} and f(x, β) is a function mapping from R^d_x×R^d_β to R^k with f(0, ·) = f(·, 0) = 0. A simple example of f(·, ·) is f(x_i, β) = Bx_i, where B is a k × d_x matrix of regression coefficients and β includes all components of B.

Second, we define residuals for our intrinsic regression model. The residual in (4) requires that y_i is not antipodal to μ(x_i, θ). In this case, the residual for the i-th subject is given by Log_μ(xi,θ)(y_i) = arccos(μ(x_i, θ)^T y_i)v_i/||v_i||, where v_i = y_i − (μ(x_i, θ)^T y_i)μ(x_i, θ). However, when y_i = −μ(x_i, θ) holds, there is an infinite number of geodesics connecting μ(x_i, θ) and y_i. In this case, Log_{μ(xi, θ)}(y_i) is not uniquely defined, whereas their geodesic distance is unique. However, according to the results in Le and Barden (2014), Log_μ(xi,q,β)(y_i) is well defined almost surely.

Third, we transport all the residuals, separately, to a common space, say T_pS^k. The rotated residual is given by

$$\mathcal{E}(y_i,{\mathbf{x}}_i;\mathit{\theta })={\text{Log}}_{\mathrm{p}}(c_{\mathrm{p},\mathit{\mu }({\mathbf{x}}_i,\mathit{\theta })}(-arccos({\mathrm{p}}^T\mathit{\mu }({\mathbf{x}}_i,\mathit{\theta })))·y_i).$$ (8)

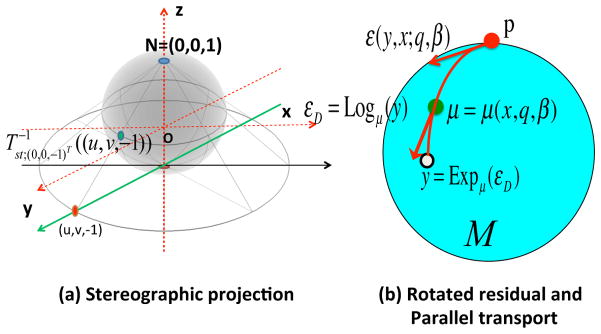
Our intrinsic regression model is defined by the zero conditional mean assumption in (6) on the above rotated residuals (8). A graphic illustration of the stereographic link functions in (7), rotated residual, and parallel transport is given in Figure 2.

Fig. 2.

Graphical illustration of (a) stereographic projection and (b) rotated residual and parallel transport. In panel (a), N and O denote the north pole (0, 0, 1) and the origin (0, 0, 0), respectively. In panel (b), y, μ = μ(x, q, β), ε_D = Log_μ(y), ℰ(y, x; q, β), and p, respectively, represent an observation, the conditional mean, the residual, the rotated residual, and the base point.

Alternatively, we may consider some parametric spherical regression models for spherical responses. As an illustration, we consider the von Mises-Fisher (vMF) regression model. Specifically, it is assumed that y_i|x_i ~ vMF(μ(x_i, θ), κ) or, equivalently, R_{μ(xi, θ),p}y_i|x_i ~ vMF(p, κ), for i = 1, …, n, where κ is a positive concentration parameter and is assumed to be known for simplicity. Calculating the maximum likelihood estimate of θ is equivalent to solving a score equation given by ${\sum }_{i=1}^n{y}_i^T{\partial }_{\mathit{\theta }}\mathit{\mu }({\mathbf{x}}_i,\mathit{\theta })=\mathbf{0}$, where ∂_θ = ∂/∂θ. Since ||μ(x_i, θ)|| = 1 and {∂_θμ(x_i, θ)}^T μ(x_i, θ) = 0 for all subcomponents of θ, we have

$$y_i^T{\partial }_{\mathit{\theta }}\mathit{\mu }({\mathbf{x}}_i,\mathit{\theta })=\sqrt{2}\frac{\sqrt{1-{(\mathit{\mu }{({\mathbf{x}}_i,\mathit{\theta })}^T{y}_i)}^2}}{arccos(\mathit{\mu }{({\mathbf{x}}_i,\mathit{\theta })}^T{y}_i)}{\{R_{\mathit{\mu }({\mathbf{x}}_i,\mathit{\theta }),\mathrm{p}}{\partial }_{\mathit{\theta }}\mathit{\mu }({\mathbf{x}}_i,\mathit{\theta })\}}^T\mathcal{E}(y_i,{\mathbf{x}}_i;\mathit{\theta }),$$ (9)

which is a linear combination of the rotated residual.

4. Estimation and Test Procedures

4.1. Generalized Method of Moment Estimators

We consider the generalized method of moment estimator (GMM estimator) to estimate the unknown parameters in model (6) (Hansen, 1982; Newey, 1993; Korsholm, 1999). We may view the T_pℳ-valued function ℰ as a function with values in R^d_ℳ. Let h(x; q, β) be a s × d_ℳ matrix of functions of (x, q, β) with s ≥ d_ℳ + d_β and W_n be a random sequence of positive definite s × s weight matrices. It follows from (6) that

$$E\{h({\mathbf{x}}_i;{\mathrm{q}}_{\ast },{\mathit{\beta }}_{\ast })E[\mathcal{E}(y_i,{\mathbf{x}}_i;{\mathrm{q}}_{\ast },{\mathit{\beta }}_{\ast })\mid {\mathbf{x}}_i]\}=0.$$ (10)

We define 𝒬_n(q, β) = [ℙ_n(h(x; q, β)ℰ(y, x; q, β))]^T W_n [ℙ_n(h(x; q, β)ℰ(y, x; q, β))], where ${\mathbb{P}}_{n}f(y,\mathbf{x})=n^{-1}{\sum }_{i=1}^n(y_i,{\mathbf{x}}_i)$ for a real-vector valued function f (y, x). The GMM estimator (q̂_G, β̂_G), or simply (q̂, β̂), of (q, β) associated with (h(·, ·, ·), W_n) is defined as

$$({\widehat{\mathrm{q}}}_{\mathrm{G}},{\widehat{\mathit{\beta }}}_{\mathrm{G}})=\underset{(\mathrm{q},\mathit{\beta })\in M\times R^{d_{\mathit{\beta }}}}{\text{argmin}}{\mathcal{Q}}_n(\mathrm{q},\mathit{\beta }).$$ (11)

Under some conditions detailed below, we can show the first order asymptotic properties of (q̂_G, β̂_G) including consistency and asymptotic normality of GMM-estimators. We introduce some notation. Let ||·|| denote the Euclidean norm of a vector or a matrix; ${\partial }^{l}f(\mathbf{t},\mathit{\beta })/\{\partial {(\mathbf{t},\mathit{\beta })}^l\}={\partial }_{(\mathbf{t},\mathit{\beta })}^{l}f(\mathbf{t},\mathit{\beta })$ for l = 1, … ; a^⊗2 = aa^T any matrix or vector a; V = Var[h(x; q_*, β_*)ℰ(y, x; q_*, β_*)]; I_d is the identity matrix; $\stackrel{d}{\to }$ and $\stackrel{p}{\to }$, respectively, denote convergence in distribution and in probability. We obtain the following results, whose detailed proofs can be found in the supplementary document.

Theorem 4.1

Assume that (y_i, x_i), i = 1,…, n, are iid random variables in ℳ × R^d_x. Let (q_*, β_*) be the exact value of the parameters satisfying (6). Let {W_n}_n be a random sequence of s × s symmetric positive semi-definite matrices with s ≥ d_ℳ + d_β.

1. Under assumptions (C1)–(C5) in the Supplementary document, (q̂_G, β̂_G) in (11) is consistent in probability as n → ∞.

2. Under assumptions (C1)–(C4) and (C6)–(C10) in the Supplementary document, for any local chart (U, ϕ) on ℳ near q_* as n → ∞, we have

   $$\sqrt{n}[{(\varphi {({\widehat{\mathrm{q}}}_G)}^T,{\widehat{\mathit{\beta }}}_G^T)}^T-{(\varphi {({\mathrm{q}}_{\ast })}^T,{\mathit{\beta }}_{\ast }^T)}^T]\stackrel{d}{\to }{N}_{d_{\mathcal{M}}+d_{\mathit{\beta }}}(\mathbf{0},{\mathrm{\sum }}_{\varphi }),$$ (12)
   where ${\mathrm{\sum }}_{\varphi }={(G_{\varphi }^{T}W{G}_{\varphi })}^{-1}{G}_{\varphi }^T{\mathit{WVWG}}_{\varphi }{(G_{\varphi }^{T}W{G}_{\varphi })}^{-1}$, in which G_ϕ is defined in (C9). Moreover, for any other chart (U, ϕ′) near q_*, we have

   $${\mathrm{\sum }}_{{\varphi }^{\prime }}=\mathit{diag}(J{({\varphi }^{\prime }\circ {\varphi }^{-1})}_{\varphi ({\mathrm{q}}_{\ast })},I_{d_{\mathit{\beta }}}){\mathrm{\sum }}_{\varphi }\mathit{diag}{(J{({\varphi }^{\prime }\circ {\varphi }^{-1})}_{\varphi ({\mathrm{q}}_{\ast })},I_{d_{\mathit{\beta }}})}^T,$$ (13)

   where J(·)_t denotes the Jacobian matrix evaluated at t.

Theorem 4.1 establishes the first-order asymptotic properties of (q̂_G, β̂_G) for the intrinsic regression model (6). Theorem 4.1 (a) establishes the consistency of (q̂_G, β̂_G). The consistency result does not depend on the local chart. Theorem 4.1 (b) establishes the asymptotic normality of (ϕ(q̂_G), β̂_G) for a specific chart (U, ϕ) and the relationship between the asymptotic covariances Σ_ϕ′ and Σ_ϕ for two different charts. It follows from the lower-right d_β × d_β submatrix of Σ_ϕ′ that the asymptotic covariance matrix of β̂ does not depend on the chart. However, the asymptotic normality of q̂_G does depend on a specific chart. A consistent estimator of the asymptotic covariance matrix Σ_ϕ is given by ${({\widehat{G}}_{\varphi }^T{W}_n{\widehat{G}}_{\varphi })}^{-1}{\widehat{G}}_{\varphi }^T{W}_n\widehat{V}{W}_n{\widehat{G}}_{\varphi }{({\widehat{G}}_{\varphi }^T{W}_n{\widehat{G}}_{\varphi })}^{-1}$ with ${\widehat{G}}_{\varphi }=n^{-1}{\sum }_{i=1}^n[h({\mathbf{x}}_i;\widehat{\mathrm{q}},\widehat{\mathit{\beta }})\frac{\partial }{\partial (\mathbf{t},\mathit{\beta })}\mathcal{E}(y_i,{\mathbf{x}}_i;{\varphi }^{-1}(\mathbf{t}),\widehat{\mathit{\beta }}){\mid }_{\mathbf{t}=\varphi (\widehat{\mathrm{q}})}]$ and

$$\widehat{V}=n^{-1}\sum _{i=1}^n{[h({\mathbf{x}}_i;\widehat{\mathrm{q}},\widehat{\mathit{\beta }})\mathcal{E}(y_i,{\mathbf{x}}_i;\widehat{\mathrm{q}},\widehat{\mathit{\beta }})]}^{\otimes 2}.$$

This estimator is also compatible with the manifold structure of ℳ.

We consider the relationship between the GMM estimator and the intrinsic least squares estimator (ILSE) of (q, β), denoted by (q̂_I, β̂_I). The (q̂_I, β̂_I) minimizes the total residual sum of squares 𝒢_I,n(q, β) as follows:

$$({\widehat{\mathrm{q}}}_I,{\widehat{\mathit{\beta }}}_I)=\underset{(\mathrm{q},\mathit{\beta })\in M\times R^{d_{\mathit{\beta }}}}{\text{argmin}}{\mathcal{G}}_{I,n}(\mathrm{q},\mathit{\beta })=\underset{(\mathrm{q},\mathit{\beta })\in M\times R^{d_{\mathit{\beta }}}}{\text{argmin}}\sum _{i=1}^n{\text{dist}}_{\mathcal{M}}{(y_i,\mathit{\mu }({\mathbf{x}}_i,\mathrm{q},\mathit{\beta }))}^2.$$ (14)

According to (2), the ILSE is closely related to the intrinsic mean q̂_IM of y₁,⋯, y_n ∈ ℳ, which is defined as

$${\widehat{\mathrm{q}}}_{IM}=\underset{\mathrm{q}\in M}{\text{argmin}}\sum _{i=1}^n{\text{dist}}_{\mathcal{M}}{(y_i,\mathrm{q})}^2=\underset{\mathrm{q}\in M}{\text{argmin}}\sum _{i=1}^n{\text{dist}}_{\mathcal{M}}{(y_i,\mathit{\mu }(\mathbf{0},\mathrm{q},\mathit{\beta }))}^2.$$

Recall that μ(0, q, β) is independent of β.

The (q̂_I, β̂_I) can be regarded as a special case of the GMM estimator when we set W_n = I_dℳ+d_β and h’s rows h_j(x, q, β) = (L_{c(1;x, q,β)⁻¹.*}(∂_tj μ(x, ϕ⁻¹(t), β)|_t=ϕ(q)))^T for j = 1,…, d_ℳ, and h_dℳ+j (x, q, β) = (L_{c(1;x,q,β)⁻¹.*}(∂_βj μ(x, q, β)))^T for j = 1,…, d_β, where (U, ϕ) is a chart on ℳ and each row of h(x, q, β) is in R^1×d_ℳ via the identification T_pℳ ≅ R^d_ℳ corresponding to (U, ϕ). It follows from Theorem 4.1 that under model (6), (q̂_I, β̂_I) enjoys the first-order asymptotic properties as well.

4.2. Efficient GMM Estimator

We investigate the most efficient estimator in the class of GMM estimators. For a fixed h(·; ·, ·), the optimal choice of W is W^opt = V⁻¹, and the use of W_n = W^opt leads to the most efficient estimator in the class of all GMM estimators obtained using the same h(·) function (Hansen, 1982). Its asymptotic covariance is given by (G_ϕV⁻¹G_ϕ)⁻¹. An interesting question is what the optimal choice of h^opt(·) is.

We first introduce some notation. For a chart (U, ϕ) on ℳ near q_*, let

$$\begin{array}{lll}\hfill D_{\varphi }(\mathbf{x})& =\hfill & E{[{\partial }_{(\mathbf{t},\mathit{\beta })}\mathcal{E}(y,\mathbf{x};{\varphi }^{-1}(\mathbf{t}),{\mathit{\beta }}_{\ast }){\mid }_{\mathbf{t}=\varphi ({\mathrm{q}}_{\ast })}\mid \mathbf{x}]}^T,h_{\varphi }^{\ast }(\mathbf{x})=D_{\varphi }(\mathbf{x})\mathrm{\Omega }{(\mathbf{x})}^{-1},\hfill \\ \hfill W_{\varphi }^{\ast }& =\hfill & E{[D_{\varphi }(\mathbf{x})\mathrm{\Omega }{(\mathbf{x})}^{-1}{D}_{\varphi }{(\mathbf{x})}^T]}^{-1},\mathrm{\Omega }(\mathbf{x})=\text{Var}(\mathcal{E}(y,\mathbf{x};{\mathrm{q}}_{\ast },{\mathit{\beta }}_{\ast })\mid \mathbf{x}).\hfill \end{array}$$

Let (q̂^*, β̂^*) be the GMM estimator of (q, β) based on $h_{\varphi }^{\ast }(\mathbf{x})$ and $W_{\varphi }^{\ast }$. Generally, we obtain an optimal result of h^opt(·), which generalizes an existing result for Euclidean-valued responses and covariates (Newey, 1993), as follows.

Theorem 4.2

Suppose that (C2)–(C8) and (C10)–(C12) in the Supplementary document hold for $h_{\varphi }^{\ast }(\mathbf{x})$ and $W_{\varphi }^{\ast }$. We have the following results:

1. (q̂^*, β̂^*) is asymptotically normally distributed with mean 0 and covariance $W_{\varphi }^{\ast }$;

2. (q̂^*, β̂^*) is optimal among all GMM estimators for model (6);

3. (q̂^*, β̂^*) is independent of the chart.

Theorem 4.2 characterizes the optimality of $h_{\varphi }^{\ast }(\mathbf{x})$ and $W_{\varphi }^{\ast }$ among regular GMM estimators for model (6). Geometrically, (q̂^*, β̂^*) is independent of the chart. Specifically, for any other chart (U, ϕ′) near q_*, we have

$$\begin{array}{lll}\hfill D_{{\varphi }^{\prime }}(\mathbf{x})& =\hfill & \text{diag}{({[J{({\varphi }^{\prime }\circ {\varphi }^{-1})}_{\varphi ({\mathrm{q}}_{\ast })}]}^{-1},I_{d_{\mathit{\beta }}})}^T{D}_{\varphi }(\mathbf{x}),\hfill \\ \hfill h_{{\varphi }^{\prime }}^{\ast }(\mathbf{x})& =\hfill & \text{diag}{({[J{({\varphi }^{\prime }\circ {\varphi }^{-1})}_{\varphi ({\mathrm{q}}_{\ast })}]}^{-1},I_{d_{\mathit{\beta }}})}^T{h}_{\varphi }^{\ast }(\mathbf{x}),\hfill \\ \hfill W_{{\varphi }^{\prime }}^{\ast }& =\hfill & \text{diag}(J{({\varphi }^{\prime }\circ {\varphi }^{-1})}_{\varphi ({\mathrm{q}}_{\ast })},I_{d_{\mathit{\beta }}})W_{\varphi }^{\ast }\text{diag}{(J{({\varphi }^{\prime }\circ {\varphi }^{-1})}_{\varphi ({\mathrm{q}}_{\ast })},I_{d_{\beta }})}^T.\hfill \end{array}$$

Thus, the quadratic form in (11) associated with $h_{{\varphi }^{\prime }}^{\ast }(\mathbf{x})$ and $W_{{\varphi }^{\prime }}^{\ast }$ is the same as that which is associated with $h_{\varphi }^{\ast }(\mathbf{x})$ and $W_{\varphi }^{\ast }$. It indicates that the GMM estimator (q̂^*, β̂^*)_ϕ based on $h_{\varphi }^{\ast }(\mathbf{x})$ and $W_{\varphi }^{\ast }$ is independent of the chart (U, ϕ).

The next challenging issue is the estimation of D_ϕ (x) and Ω(x). We may proceed in two steps. The first step is to calculate a $\sqrt{n}$-consistent estimator (q̂_I, β̂_I) of (q, β), such as the ILSE. The second step is to plug (q̂_I, β̂_I) into the functions ℰ_i(q̂_I, β̂_I) and ∂_(t,β)ℰ(y_i, x_i; ϕ⁻¹(t), β̂_I)|_t=ϕ(q̂I) for all i and then use them to construct the nonparametric estimates of D_ϕ(x) and Ω(x) (Newey, 1993). Specifically, let K(·) be a d_x-dimensional kernel function of the l₀-th order satisfying ∫K(u₁,…, u_dx)du₁ … du_dx = 1, $\int u_s^{l}K(u_1,\dots ,u_{d_{\mathbf{x}}})d{u}_1\dots d{u}_{d_{\mathbf{x}}}=0$ for any s = 1,…, d_x and 1 ≤ l < l₀, and $\int u_s^{l_0}K(u_1,\dots ,u_{d_{\mathbf{x}}})d{u}_1\dots d{u}_{d_{\mathbf{x}}}\ne 0$. Let K_τ (u) = τ⁻¹K(u/τ), where τ > 0 is a bandwidth. Then, a nonparametric estimator of D_ϕ(x) can be written by

$${\widehat{D}}_{\varphi }{(\mathbf{x})}^T=\sum _{i=1}^n{\omega }_i(\mathbf{x};\tau ){\partial }_{(\mathbf{t},\mathit{\beta })}\mathcal{E}(y_i,{\mathbf{x}}_i;{\varphi }^{-1}(\mathbf{t}),{\widehat{\mathit{\beta }}}_I){\mid }_{\mathbf{t}=\varphi ({\widehat{\mathrm{q}}}_t)},$$ (15)

where ${\omega }_i(\mathbf{x};\tau )=K_{\tau }(\mathbf{x}-{\mathbf{x}}_i)/\{{\sum }_{k=1}^n{K}_{\tau }(\mathbf{x}-{\mathbf{x}}_k)\}$. Although we may construct a nonparametric estimator of Ω(x) similar to (15), we have found that even for moderate d_x, such an estimator is numerically unstable. Instead, we approximate Ω(x_i) = Var(ℰ(y, x; q_*, β_*)|x = x_i) by its mean V_E* = Var(ℰ(y, x; q_*, β_*)). In this case, $h_{\varphi }^{\ast }(\mathbf{x})$ and $W_{\varphi }^{\ast }$, respectively, reduce to

$$h_{E,\varphi }^{\ast }(\mathbf{x})=D_{\varphi }(\mathbf{x})V_{E\ast }^{-1}\text{and}{W}_{E,\varphi }^{\ast }={\{E[D_{\varphi }(\mathbf{x})V_{E\ast }^{-1}\mathrm{\Omega }(\mathbf{x})V_{E\ast }^{-1}{D}_{\varphi }{(\mathbf{x})}^T]\}}^{-1}.$$ (16)

For any local chart (U, ϕ) with q̂_I ∈ U, we construct the estimators of $h_{E,\varphi }^{\ast }$ and $W_{E,\varphi }^{\ast }$ as follows. Let V̂(q, β) =ℙ_nℰ(y, x; q, β)^⊗2, we have

$${\widehat{h}}_{E,\varphi }({\mathbf{x}}_i)={\widehat{D}}_{\varphi }({\mathbf{x}}_i)\widehat{V}{({\widehat{\mathrm{q}}}_I,{\widehat{\mathit{\beta }}}_I)}^{-1},{\widehat{W}}_{E,\varphi }={\left\{{\mathbb{P}}_n{[{\widehat{h}}_{E,\varphi }(\mathbf{x})\mathcal{E}(y,\mathbf{x};{\widehat{\mathrm{q}}}_I,{\widehat{\mathit{\beta }}}_I)]}^{\otimes 2}\right\}}^{-1}.$$ (17)

Then, we substitute ĥ_{E, ϕ} and Ŵ_{E, ϕ} into (11) and then calculate the GMM estimator of (q, β), denoted by (q̂_E, β̂_E). Similar to (q̂^*, β̂^*), it can be shown that (q̂_E, β̂_E) is independent of the chart (U, ϕ) on ℳ near q_* with q̂_I ∈ U. For sufficiently large n, dist_ℳ(q̂_I, q_*) can be made sufficiently small and any maximal normal chart on ℳ centered at q̂_I contains the true value q_* with probability approaching one.

We calculate a one-step linearized estimator of (q, β), denoted by (q̃_E, β̃_E), to approximate (q̂_E, β̂_E). Computationally, the linearized estimator does not require iteration, whereas, theoretically, it shares the first asymptotic properties with (q̂_E, β̂_E) as shown below. Specifically, in the chart (U, ϕ) near q̂_I, we have

$${({\stackrel{\sim }{\mathbf{t}}}_{E,\varphi }^T,{\stackrel{\sim }{\mathit{\beta }}}_{E,\varphi }^T)}^T-{(\varphi {({\widehat{\mathrm{q}}}_I)}^T,{\widehat{\mathit{\beta }}}_I^T)}^T={\left\{-{\mathbb{P}}_n[{\widehat{h}}_{E,\varphi }(\mathbf{x}){\partial }_{(\mathbf{t},\mathit{\beta })}\mathcal{E}(y,\mathbf{x};{\varphi }^{-1}(t),{\widehat{\mathit{\beta }}}_I){\mid }_{\mathbf{t}=\varphi ({\widehat{\mathrm{q}}}_I)}]\right\}}^{-1}{\mathbb{P}}_n\left[{\widehat{h}}_{E,\varphi }(\mathbf{x}){\mathcal{E}}_i(y,\mathbf{x};{\widehat{\mathrm{q}}}_I,{\widehat{\mathit{\beta }}}_I)\right].$$ (18)

Furthermore, if (U′, ϕ ′) is another chart on ℳ near q̂_I, then we have

$${({\stackrel{\sim }{\mathbf{t}}}_{E,{\varphi }^{\prime }}^T,{\stackrel{\sim }{\mathit{\beta }}}_{E,{\varphi }^{\prime }}^T)}^T-{({\varphi }^{\prime }{({\widehat{\mathrm{q}}}_I)}^T,{\widehat{\mathit{\beta }}}_I^T)}^T=\left(\begin{array}{cc}{J}_{\varphi ({\widehat{\mathrm{q}}}_I)}({\varphi }^{\prime }\circ {\varphi }^{-1})& 0\\ 0& I_{d_{\mathit{\beta }}}\end{array}\right)[{({\stackrel{\sim }{\mathbf{t}}}_{E,\varphi }^T,{\stackrel{\sim }{\mathit{\beta }}}_{E,\varphi }^T)}^T-{(\varphi {({\widehat{\mathrm{q}}}_I)}^T,{\widehat{\mathit{\beta }}}_I^T)}^T].$$

Thus, β̃_E,ϕ is independent of the chart ϕ and {t̃_{E, ϕ} − ϕ(q̂_I) | ϕ is a chart on M} defines a unique tangent vector to ℳ at q̂_I. Moreover, if ϕ and ϕ′ are maximal normal charts centered at q̂_I, then γ_ϕ (τ) = ϕ⁻¹(τt̃_E,ϕ) and γ_ϕ′(τ) = ϕ′⁻¹(τt̃_{E, ϕ′}) are two geodesic curves on ℳ starting from the same point q̂_I with the same initial velocity vector, and thus these two geodesics coincide. Therefore, ϕ⁻¹(t̃_E,ϕ) is independent of the normal chart ϕ centered at q̂_I. Finally, we can establish the first order asymptotic properties of (q̃_E, β̃_E) as follows.

Theorem 4.3

Assume that (C2)–(C11) and (C13)–(C18) are valid. As n → ∞, we have the following results:

$$\sqrt{n}[{(\varphi {({\stackrel{\sim }{\mathrm{q}}}_E)}^T,{\stackrel{\sim }{\mathit{\beta }}}_E^T)}^T-{(\varphi {({\mathrm{q}}_{\ast })}^T,{\mathit{\beta }}_{\ast }^T)}^T]\stackrel{d}{\to }{N}_{d_{\mathcal{M}}+d_{\mathit{\beta }}}(\mathbf{0},{\mathrm{\sum }}_{E,\varphi }),$$ (19)

where ${\mathrm{\sum }}_{E,\varphi }={(G_{\varphi ,h_{E,\varphi }^{\ast }}{W}_{E,\varphi }^{\ast }{G}_{\varphi ,h_{E,\varphi }^{\ast }})}^{-1}$. In addition, Σ_{E, ϕ} is invariant under the change of coordinates in ℳ and the asymptotic distribution of β̃_E does not depend on the chart (U, ϕ). Also, if we set

$$\begin{array}{l}{\widehat{\mathrm{\sum }}}_{E,\varphi }=n^{-1}{\left\{{\mathbb{P}}_n[{\widehat{D}}_{\varphi }(\mathrm{x})\widehat{V}{({\widehat{\mathrm{q}}}_I,{\widehat{\mathit{\beta }}}_I)}^{-1}{\widehat{D}}_{\varphi }{(\mathrm{x})}^T]\right\}}^{-1}\\ \times \left\{{\mathbb{P}}_n[{\widehat{D}}_{\varphi }(\mathrm{x})\widehat{V}{({\widehat{\mathrm{q}}}_I,{\widehat{\mathit{\beta }}}_I)}^{-1}\mathcal{E}{(y,\mathbf{x},{\stackrel{\sim }{\mathrm{q}}}_I,{\stackrel{\sim }{\mathit{\beta }}}_I)}^{\otimes 2}\widehat{V}{({\widehat{\mathrm{q}}}_I,{\widehat{\mathit{\beta }}}_I)}^{-1}{\widehat{D}}_{\varphi }{(\mathrm{x})}^T]\right\}\\ \times {\left\{{\mathbb{P}}_n[{\widehat{D}}_{\varphi }(\mathrm{x})\widehat{V}{({\widehat{\mathrm{q}}}_I,{\widehat{\mathit{\beta }}}_I)}^{-1}{\widehat{D}}_{\varphi }{(\mathrm{x})}^T]\right\}}^{-1},\end{array}$$ (20)

then nΣ̂_E,ϕ is a consistent estimator of Σ_E,ϕ, i.e. $n{\widehat{\mathrm{\sum }}}_{E,\varphi }\stackrel{p}{\to }{\mathrm{\sum }}_{E,\varphi }$. This estimator is also compatible with the manifold structure of ℳ.

Theorem 4.3 establishes the first-order asymptotic properties of (q̃_E, β̃_E). If Ω(x) = Ω for a constant matrix Ω, then it follows from Theorems 4.2 and 4.3 that (q̃_E, β̃_E) is optimal. If Ω(x) does not vary dramatically as a function of x, then (q̃_E, β̃_E) is nearly optimal. If Ω(x) varies dramatically as a function of x, one can replace V̂(q̂_I, β̂_I) in (17) by Ω̂(x_i) to obtain ĥ_E,ϕ (x) = D̂_ϕ(x)Ω̂(x)⁻¹ and Ŵ_E,ϕ = {ℙ_n[ĥ_E,ϕ (x)ℰ(y, x; q̂_I, β̂_I)]^⊗2}⁻¹, where Ω̂(x_i) is a consistent estimator of Ω(x_i) for all i, then the optimality of (q̃_E, β̃_E) still holds. We have the following theorem.

Theorem 4.4

Assume that (C2)–(C17) and (C19) are valid. Then, as n → ∞, we have

$$\sqrt{n}[{(\varphi {({\stackrel{\sim }{\mathrm{q}}}_E)}^T,{\stackrel{\sim }{\mathit{\beta }}}_E^T)}^T-{(\varphi {({\mathrm{q}}_{\ast })}^T,{\mathit{\beta }}_{\ast }^T)}^T]\stackrel{d}{\to }{N}_{d_{\mathcal{M}}+d_{\mathit{\beta }}}(\mathbf{0},{\mathrm{\sum }}_{\varphi }^{\ast }),$$ (21)

in which ${\mathrm{\sum }}_{\varphi }^{\ast }$ is given in Theorem 4.2. If we set Σ̂_E,ϕ = n⁻¹{ℙ_n[D̂_ϕ (x)Ω̂(x)⁻¹D̂_ϕ(x)^T]}⁻¹, then nΣ̂_E,ϕ is a consistent estimator of ${\mathrm{\sum }}_{\varphi }^{\ast }$.

4.3. Computational Algorithm

Computationally, an annealing evolutionary stochastic approximation Monte Carlo (SAMC) algorithm (Liang et al., 2010) is developed to compute (q̂_I, β̂_I) and (q̂_E, β̂_E). See the supplementary document for details. Although some gradient-based optimization methods, such as the quasi-Newton method, have been used to optimize 𝒬_n(q, β) (Kim et al., 2014; Fletcher, 2013), we have found that these methods strongly depend on the starting value of (q, β). Specifically, when ℰ(y, x; q, β) takes a relatively complicated form, 𝒬_n(q, β) is generally not convex and can easily converge to local minima. Moreover, we have found that it can be statistically misleading to carry out statistical inference, such as the estimated standard errors of (q̂_E, β̂_E), at those local minima. The annealing evolutionary SAMC algorithm converges fast and distinguishes from many gradient-based algorithms, since it possesses a nice feature in that the moves are self-adjustable and thus not likely to get trapped by local energy minima. The annealing evolutionary SAMC algorithm (Liang et al., 2010) represents a further improvement of stochastic approximation Monte Carlo for optimization problems by incorporating some features of simulated annealing and the genetic algorithm into its search process.

4.4. Hypotheses Testing

Many scientific questions involve the comparison of the ℳ-valued data across groups and subjects and the detection of the change in the ℳ-valued data over time. Such questions usually can be formulated as testing the hypotheses of q and β. We consider two types of hypotheses as follows:

$$H_0^{(1)}:{\mathrm{C}}_0\mathit{\beta }={\mathbf{b}}_0\text{vs.}{H}_1^{(1)}:{\mathrm{C}}_0\mathit{\beta }\ne {\mathbf{b}}_0,$$ (22)

$$H_0^{(2)}:\mathrm{q}={\mathrm{q}}_0\text{vs.}{H}_1^{(2)}:\mathrm{q}\ne {\mathrm{q}}_0,$$ (23)

where C₀ is an r × d_β matrix of full row rank and q₀ and b₀ are specified in ℳ and R^r, respectively. Further extensions of these hypotheses are definitely interesting and possible. For instance, for the multicenter link function, we may be interested in testing whether all intercepts are independent of the discrete covariate class.

We develop several test statistics for testing the hypotheses given in (22) and (23). First, we consider the Wald test statistic for testing $H_0^{(1)}$ against $H_1^{(1)}$ in (22), which is given by

$$W_{n,\varphi }^{(1)}={({\mathrm{C}}_0{\stackrel{\sim }{\mathit{\beta }}}_E-{\mathbf{b}}_0)}^T{\left[{\mathrm{C}}_0{\widehat{\mathrm{\sum }}}_{E,\varphi ;22}{\mathrm{C}}_0^T\right]}^{-1}({\mathrm{C}}_0{\stackrel{\sim }{\mathit{\beta }}}_E-{\mathbf{b}}_0),$$

where Σ̂_E,ϕ is given in Theorem 4.3 or Theorem 4.4, and Σ̂_E,ϕ;22 is its lower-right d_β × d_β submatrix. Since β̃_E and its asymptotic covariance matrix are independent of the chart on ℳ, the test statistic $W_{n,\varphi }^{(1)}$ is independent of the chart.

Second, we consider the Wald test statistic for testing the hypotheses given in (23) when there is a local chart (U, ϕ) on ℳ containing both q̂_E and q₀. Specifically, the Wald test statistic for testing (23) is defined by

$$W_{n,\varphi }^{(2)}={(\varphi ({\stackrel{\sim }{\mathrm{q}}}_E)-\varphi ({\mathrm{q}}_0))}^T{\left[(I_{d_{\mathcal{M}}}\mathbf{0}){\widehat{\mathrm{\sum }}}_{E,\varphi }{(I_{d_{\mathcal{M}}}\mathbf{0})}^T\right]}^{-1}(\varphi ({\stackrel{\sim }{\mathrm{q}}}_E)-\varphi ({\mathrm{q}}_0)).$$

Third, we develop an intrinsic Wald test statistic, that is independent of the chart, for testing the hypotheses given in (23). We consider the asymptotic covariance estimator Σ̂_E,ϕ based on q̃_E and its upper-left d_ℳ × d_ℳ submatrix Σ̂_E,ϕ;11. Since both are compatible with the manifold structure of ℳ, Σ̂_E,ϕ;11 defines a unique non-degenerate linear map Σ̂_E;11(·) from the tangent space T_q̃Eℳ of ℳ at q̃_E onto itself, which is independent of the chart (U, ϕ). In a maximal normal chart centered at q̃_E, then in any such normal chart, the Wald test statistic for testing (23) is given by

$$W_{\mathcal{M},n}^{(2)}={\mathrm{m}}_{{\stackrel{\sim }{\mathrm{q}}}_E}({({\mathrm{\sum }}_{E:11})}^{-1}({\text{Log}}_{{\stackrel{\sim }{\mathrm{q}}}_E}{\mathrm{q}}_0),{\text{Log}}_{{\stackrel{\sim }{\mathrm{q}}}_E}{\mathrm{q}}_0).$$

We obtain the asymptotic null distributions of $W_{n,\varphi }^{(1)},W_{n,\varphi }^{(2)}$, and $W_{\mathcal{M},n}^{(2)}$ as follows.

Theorem 4.5

Let (U, ϕ) be a local chart on ℳ so that q̃_E, q_* ∈ U. Assume that all conditions in Theorem 4.3 hold. Under the corresponding null hypothesis, we have the following results:

1. $W_{n,\varphi }^{(1)}$ and $W_{n,\varphi }^{(2)}$ are asymptotically distributed as ${\chi }_r^2$ and ${\chi }_{d_{\mathcal{M}}}^2$, respectively;

2. $W_{n,\varphi }^{(1)}$ is independent of the chart (U, ϕ);

3. $W_{n,{\varphi }^{\prime }}^{(2)}=W_{n,\varphi }^{(2)}+o_p(1)$, for any other local chart (U, ϕ′) with q̃_E and q₀ in U;

4. $W_{n,\varphi }^{(2)}=W_{\mathcal{M},n}^{(2)}$, for any normal chart (U, ϕ) centered at q̃_E.

Theorem 4.5 has several important implications. Theorem 4.5 (i) characterizes the asymptotic null distributions of $W_{n,\varphi }^{(1)}$ and $W_{n,\varphi }^{(2)}$. Theorem 4.5 (ii) shows that $W_{n,\varphi }^{(1)}$ does not depend the choice of the chart (U, ϕ) on ℳ. Theorem 4.5 (iii) shows that $W_{n,{\varphi }^{\prime }}^{(2)}$ and $W_{n,\varphi }^2$ are asymptotically equivalent for any two local charts. Theorem 4.5 (iv) shows that $W_{n,{\varphi }^{\prime }}^{(2)}$ can be used to construct an intrinsic test statistic.

We consider a local alternative framework for (22) and (23) as follows:

$$H_0^{(1)}:{\mathrm{C}}_0\mathit{\beta }={\mathbf{b}}_0\text{vs.}{H}_{1,n}^{(1)}:{\mathrm{C}}_0\mathit{\beta }={\mathbf{b}}_0+\delta /\sqrt{n}+o(1/\sqrt{n}),$$ (24)

$$H_0^{(2)}:\mathrm{q}={\mathrm{q}}_0\text{vs.}{H}_{1,n}^{(2)}:\mathrm{q}={\text{Exp}}_{{\mathrm{q}}_0}(\mathbf{v}/\sqrt{n}+o(1/\sqrt{n})),$$ (25)

where δ and v are specified (and fixed) in R^r and T_q0ℳ, respectively, and we establish the asymptotic distributions of $W_{n,\varphi }^{(1)},W_{n,\varphi }^{(2)}$ and $W_{\mathcal{M},n}^{(2)}$ under these local alternatives.

Theorem 4.6

Let (U, ϕ) be a local chart on ℳ so that q̃_E, q_* ∈ U. Assume that all conditions in Theorem 4.3 hold. Under the local alternatives (24) and (25), we have the following results:

1. Under $H_{1,n}^{(1)},W_{n,\varphi }^{(1)}$ is asymptotically distributed as noncentral ${\chi }_r^2$ with noncentrality parameter ${\delta }^T{\left[{\mathrm{C}}_0{\widehat{\mathrm{\sum }}}_{E,\varphi ;22}{\mathrm{C}}_0^T\right]}^{-1}\delta$.

2. Under $H_{1,n}^{(2)},W_{n,\varphi }^{(2)}$ is asymptotically distributed as noncentral ${\chi }_{d_{\mathcal{M}}}^2$, with noncentrality parameter J(ϕ ∘ Exp_q0)₀(v)^T [Σ̂_E,ϕ;11]⁻¹ J(ϕ ∘ Exp_q0)₀(v). The noncentrality parameter does not depend on the choice of the coordinate system at q₀. Here, J(f)_a denotes the Jacobian matrix of map f at a.

3. Under $H_{1,n}^{(2)},W_{n,\varphi }^{(2)}$ is asymptotically distributed as noncentral ${\chi }_{d_{\mathcal{M}}}^2$, with noncentrality parameter m_q̃E((Σ̂_E;11)⁻¹(J(Log_q̃E)_q0(v)), (J(Log_q̃E)_q0(v))). The noncentrality parameter does not depend on the choice of the coordinate systems at q̃_E and q₀, respectively.

We consider another scenario that there are no local charts on ℳ containing both q̃_E and q₀. In this case, we restate the hypotheses $H_0^{(2)}$ and $H_1^{(2)}$ as follows:

$$H_0^{(2)}:{\text{dist}}_{\mathcal{M}}(\mathrm{q},{\mathrm{q}}_0)=0\text{vs.}{H}_1^{(2)}:{\text{dist}}_{\mathcal{M}}(\mathrm{q},{\mathrm{q}}_0)\ne 0.$$ (26)

We propose a geodesic test statistic given by

$$W_{\mathit{dist}}={\text{dist}}_{\mathcal{M}}{({\stackrel{\sim }{\mathrm{q}}}_E,{\mathrm{q}}_0)}^2,$$ (27)

which is independent of the chart (U, ϕ). Theoretically, we can establish the asymptotic distribution of W_dist under both the null and alternative hypotheses as follows.

Theorem 4.7

Assume that all conditions in Theorem 4.5 hold.

1. Under $H_0^{(2)}$, nW_dist is asymptotically weighted chi-square χ²(λ₁, …, λ_dℳ) distributed, where the weights λ₁, …, λ_dℳ are the eigenvalues of the matrix Σ_E,Logq0,11, which is the upper-left d_ℳ × d_ℳ submatrix of the asymptotic covariance matrix Σ_E,Logq0 of q̃_E in a normal chart centered at q₀. Moreover, the weights are independent, up to a permutation, of the choice of the normal chart centered at q_*.

2. Under the alternative hypothesis, W_dist is asymptotically normal distributed and we have

   $$\sqrt{n}(W_{\mathit{dist}}-{\mathit{dist}}_{\mathcal{M}}{({\mathrm{q}}_{\ast },{\mathrm{q}}_0)}^2)\stackrel{d}{\to }{N}_{d_{\mathcal{M}}}(\mathbf{0},D_{\mathit{dist}}^T{\mathrm{\sum }}_{E,{\text{Log}}_{{\mathrm{q}}_{\ast }},11}{D}_{\mathit{dist}}),$$
   where D_dist is the column vector representation of grad_q*(dist(·, q₀)²) with respect to the orthonormal basis of T_q*ℳ associated with the normal chart used to represent the asymptotic covariance of q̃_E as the matrix Σ_E,Logq*. In particular, when q₀ is close to q_*, then

   $$\sqrt{n}(W_{\mathit{dist}}-{\mathit{dist}}_{\mathcal{M}}{({\mathrm{q}}_{\ast },{\mathrm{q}}_0)}^2)\stackrel{d}{\to }{N}_{d_{\mathcal{M}}}(\mathbf{0},4{[{\text{Log}}_{{\mathrm{q}}_{\ast }}{\mathrm{q}}_0]}^T{\mathrm{\sum }}_{E,{\text{Log}}_{{\mathrm{q}}_{\ast }},11}[{\text{Log}}_{{\mathrm{q}}_{\ast }}{\mathrm{q}}_0]).$$

Theorem 4.7 establishes the asymptotic distribution of W_dist when q̃_E and q₀ do not belong to the same chart of ℳ. In practice, the covariance matrix Σ_E,Logq*,11 is not available, since Σ_E,Logq* is not known; it also depends on the unknown true value β_*, so we may use the estimate Σ̂_E,Logq* as defined in Theorems 4.3 and 4.4. Therefore, under the null hypothesis, the asymptotic distribution of W_dist can be approximated by the weighted chi-square distribution χ²(λ̂₁, …, λ̂_dℳ), in which the weights λ̂₁, …, λ̂_dℳ are the eigenvalues of the covariance matrix (Σ̂_E,Logq0)₁₁/n.

Finally, we develop a score test statistic for testing $H_0^{(2)}$ against $H_1^{(2)}$. An advantage of using the score test statistic is that it avoids the calculation of an estimator under the alternative hypothesis $H_1^{(2)}$. For notational simplicity, we only consider the ILSE estimator of (q, β), denoted by (q₀, β̃_I), under the null hypothesis $H_0^{(2)}$. For any chart (U, ϕ) on ℳ with q₀ ∈ U, we define

$$\begin{array}{l}{F}_{\varphi i}={(F_{\varphi i,1}^{\top },F_{\varphi i,2}^{\top })}^{\top }={\partial }_{(\mathbf{t},\mathit{\beta })}{\text{dist}}_{\mathcal{M}}{(f({\mathbf{x}}_i,{\varphi }^{-1}(\mathbf{t}),\mathit{\beta }),y_i)}^2{\mid }_{\mathbf{t}=\varphi ({\mathrm{q}}_0),{\stackrel{\sim }{\mathit{\beta }}}_I},\\ {\mathrm{U}}_{\varphi }=\left(\begin{array}{cc}{\mathrm{U}}_{\mathbf{tt}}& {\mathrm{U}}_{\mathbf{t}\mathit{\beta }}\\ {\mathrm{U}}_{\mathit{\beta }\mathbf{t}}& {\mathrm{U}}_{\mathit{\beta }\beta }\end{array}\right)=\sum _{i=1}^n{\partial }_{(\mathbf{t},\mathit{\beta })}^2{\text{dist}}_{\mathcal{M}}{(f({\mathbf{x}}_i,{\varphi }^{-1}(\mathbf{t}),\mathit{\beta }),y_i)}^2{\mid }_{\mathbf{t}=\varphi ({\mathrm{q}}_0),{\stackrel{\sim }{\mathit{\beta }}}_I},\end{array}$$

where the subcomponents F_ϕi,1 and F_ϕi,2 correspond to t and β, respectively. It can be shown that the score test W_SC,ϕ reduces to

$$W_{SC,\varphi }={(\sum _{i=1}^n{F}_{\varphi i,1})}^{\top }{\mathrm{\sum }^{\sim }}_{\varphi ,\mathrm{q}}^{-1}(\sum _{i=1}^n{F}_{\varphi i,1}),$$ (28)

where ${\mathrm{\sum }^{\sim }}_{\varphi ,\mathrm{q}}=(I_{d_{\mathcal{M}}},-{\mathrm{U}}_{\mathbf{t}\mathit{\beta }}{\mathrm{U}}_{\mathit{\beta \beta }}^{-1})[{\sum }_{i=1}^n{(F_{\varphi i}-\overline{F_{\varphi }})}^{\otimes 2}]{(I_{d_{\mathcal{M}}},-{\mathrm{U}}_{\mathbf{t}\mathit{\beta }}{\mathrm{U}}_{\mathit{\beta \beta }}^{-1})}^{\top }$, in which $\overline{F_{\varphi }}=n^{-1}{\sum }_{i=1}^n{F}_{\varphi i}$. Theoretically, we can establish the asymptotic distribution of W_SC,ϕ under the null hypothesis.

Theorem 4.8

Assume that all conditions in Theorem 4.5 hold. We have the following results:

1. For any suitable local chart (U, ϕ), the score test statistic W_SC,ϕ is asymptotically distributed as ${\chi }_{d_{\mathcal{M}}}^2$ under the null hypothesis $H_0^{(2)}$.

2. Under $H_0^{(2)}$, for any other local chart (U, ϕ′) with q₀ ∈ U, we have

   $$W_{SC,{\varphi }^{\prime }}=W_{SC,\varphi }.$$

5. Real Data Example

5.1. ADNI Corpus Callosum Shape Data

Alzheimer disease (AD) is a disorder of cognitive and behavioral impairment that markedly interferes with social and occupational functioning. It is an irreversible, progressive brain disease that slowly destroys memory and thinking skills, and eventually even the ability to carry out the simplest tasks. AD affects almost 50% of those over the age of 85 and is the sixth leading cause of death in the United States.

The corpus callosum (CC), as the largest white matter structure in the brain, connects the left and right cerebral hemispheres and facilitates homotopic and heterotopic interhemispheric communication. It has been a structure of high interest in many neuroimaging studies of neuro-developmental pathology. Individual differences in CC and their possible implications regarding interhemispheric connectivity have been investigated over the last several decades (Paul et al., 2007).

We consider the CC contour data obtained from the ADNI study. For each subject in ADNI dataset, the segmentation of the T1-weighted MRI and the calculation of the intracranial volume were done in the FreeSurfer package^‡ (Dale et al., 1999), while the midsagittal CC area was calculated in the CCseg package, which is measured by using subdivisions in Witelson (1989) motivated by neuro-histological studies. Finally, each T1-weighted MRI image and tissue segmentation were used as the input files of CCSeg package to extract the planar CC shape data.

5.2. Intrinsic Regression Models

We are interested in characterizing the change of the CC contour shape as a function of three covariates including gender, age, and AD diagnosis. We focused on n = 409 subjects with 223 healthy controls (HCs) and 186 AD patients at baseline of the ADNI1 database. We observed a CC planar contour Y_i with 32 landmarks and three clinical variables including gender x_i,1 (0-female, 1-male), age x_i,2, and diagnosis x_i,3 (0-control, 1-AD) for i = 1, …, 409. The demographic info is presented in Table 1.

Table 1.

Demographic information for the processed ADNI CC shape dataset including disease status, age, and gender.

Disease status	No.	Range of age in years (mean)	Gender (female/male)
Healthy Control	223	62–90 (76.25)	107/116
AD	186	55–92 (75.42)	88/98

We treat the CC planar contour Y_i as a RSS-valued response in the Kendall’s planar shape space ${\mathrm{\sum }}_2^{32}$. The geometric structure of ${\mathrm{\sum }}_2^k$ for k > 2 is included in the supplementary document. Each Y_i is specified as a 32 × 2 real matrix, whose rows represent the planar coordinates of 32 landmarks on y_i. Moreover, Y_i = (Y_i,1 Y_i,2) can be represented as a complex vector z_i = Y_i,1 +jY_i,2 in C³², where $j=\sqrt{-1}$ and C is the standard complex space. After removing the translations and normalizing to the unit 2-norm, each contour Y_i can be view as an element $z_i\in {\mathcal{D}}^{32}=\{z={(z^1,\dots ,z^{32})}^T\in C^{32}\mid {\sum }_{m=1}^{32}{z}^m=0\text{and}{\Vert z\Vert }_2=1\}$. Then, after removing the 2-dimensional rotations, we obtain an element y_i = [z_i] in Kendall’s planar shape space, ${\mathrm{\sum }}_2^{32}={\mathcal{D}}^{32}/S^1$, which has dimension 30 and is identified with the complex projective space CP³⁰.

In order to use our intrinsic regression model, we determined the base point p and an orthonormal basis {Z₁, …, Z₃₀} for $T_{\mathrm{p}}{\mathrm{\sum }}_2^{32}$ as follows. We initially set p₀ = [z₀] with $z_0={(1,-1,0,\cdots ,0)}^T/\sqrt{2}$ and an orthonormal basis {Z̃₁, …, Z̃₃₀} in $T_{{\mathrm{p}}_0}{\mathrm{\sum }}_2^{32}$, where ${\stackrel{\sim }{Z}}_l={(1,\cdots ,1,-(l+1),0,\cdots ,0)}^T/\sqrt{(l+1)(l+2)}$. Then, we projected all y_i’s onto $T_{{\mathrm{p}}_0}{\mathrm{\sum }}_2^{32}$ and calculated Log_p0(y_i) for all i. Finally, we set the base point p as ${\text{Exp}}_{{\mathrm{p}}_0}(n^{-1}{\sum }_{i=1}^n{\text{Log}}_{{\mathrm{p}}_0}(y_i))$ and then used the parallel transport to rotate the initial basis {Z̃₁, …, Z̃₃₀} to obtain a new orthonormal basis {Z₁, …, Z₃₀} at p.

We consider an intrinsic regression model with $y_i\in {\mathrm{\sum }}_2^{32}$ as a response vector and a vector of four covariates including gender, age, diagnosis, and the interaction age*diagnosis, that is, x_i = (x_i,1, x_i,2, x_i,3, x_i,4)^T with x_i,4 = x_i,2x_i,3. We used a single-center link function with model parameters $(\mathrm{q},\mathit{\beta })\in {\mathrm{\sum }}_2^{32}\times R^{240}$ as follow. The intercept q is specified by $\mathrm{q}={\varphi }_{\mathrm{p}}^{-1}(\mathbf{t})={\text{Exp}}_{\mathrm{p}}\left({\sum }_{\ell =1}^{30}(t_{2\ell -1}+j{t}_{2\ell })Z_{\ell }\right)$, where t = (t₁, …, t₆₀)^T ∈ R⁶⁰. The regression coefficient vector β includes four 60 × 1 subvectors including β^(g), β^(a), β^(d), and β^(ad), which correspond to x_i1, x_i2, x_i3, and x_i4, respectively. Therefore, there are 300 unknown parameters in (t^T, β^T)^T. We define a 30 × 4 complex matrix as B = B_o+jB_e, with $B_o=\left(\begin{array}{cccc}{\mathit{\beta }}_o^{(g)}& {\mathit{\beta }}_o^{(a)}& {\mathit{\beta }}_0^{(d)}& {\mathit{\beta }}_o^{(ad)}\end{array}\right),B_e=\left(\begin{array}{cccc}{\mathit{\beta }}_e^{(g)}& {\mathit{\beta }}_e^{(a)}& {\mathit{\beta }}_e^{(d)}& {\mathit{\beta }}_e^{(ad)}\end{array}\right)\in R^{30\times 4}$, where ${\mathit{\beta }}_o^{(·)}$ and ${\mathit{\beta }}_e^{(·)}$ are the subvectors of β^(·) formed by the odd-indexed and even-indexed components, respectively, and a link function by $\mathit{\mu }({\mathbf{x}}_i,\mathrm{q},\mathit{\beta })={\text{Exp}}_{\mathrm{q}}([U_{\mathrm{p},\mathrm{q}}{Z}_1,\dots ,U_{\mathrm{p},\mathrm{q}}{Z}_{30}]B{\mathbf{x}}_i)\in {\mathrm{\sum }}_2^{32}$, where $U_{{\mathrm{q}}_1,{\mathrm{q}}_2}\mathbf{v}=U_{z_{{\mathrm{q}}_1},z_{{\mathrm{q}}_2}^{\ast }}\mathbf{v}$, with q₁ = [z_q1], q₂ = [z_q2], $z_{{\mathrm{q}}_2}^{\ast }=e^{j{\theta }^{\ast }}{z}_{{\mathrm{q}}_2}$ the optimal rotational alignment of z_q2 to z_q1, given by ${\overline{z}}_{{\mathrm{q}}_2}^T{z}_{{\mathrm{q}}_1}=e^{j{\theta }^{\ast }}\mid {\overline{z}}_{{\mathrm{q}}_2}^T{z}_{{\mathrm{q}}_1}\mid$, and U_z1,z2v for any v ∈ C^k takes the form of

$$\mathbf{v}-({\overline{z_1}}^T\mathbf{v})z_1-({\overline{{\stackrel{\sim }{z}}_2}}^T\mathbf{v})\stackrel{\sim }{z_2}+\{({\overline{z_1}}^T{z}_2)({\overline{z_1}}^T\mathbf{v})-\sqrt{1-{\mid {\overline{z_1}}^T{z}_2\mid }^2}({\overline{{\stackrel{\sim }{z}}_2}}^T\mathbf{v})\}{z}_1+\{\sqrt{1-{\mid {\overline{z_1}}^T{z}_2\mid }^2}({\overline{z_1}}^T\mathbf{v})+\overline{({\overline{z_1}}^T{z}_2)}({\overline{\stackrel{\sim }{z_2}}}^T\mathbf{v})\}\stackrel{\sim }{z_2},$$

in which $\stackrel{\sim }{z_2}=\{z_2-({\overline{z_1}}^T{z}_2)z_1\}/\sqrt{1-{\mid {\overline{z_1}}^T{z}_2\mid }^2}$, for z₁, z₂ ∈ 𝒟³². Finally, our intrinsic model is defined by $E\left[{\text{Log}}_{\mathrm{p}}\left({\overline{U}}_{\mathrm{p},\mathit{\mu }({\mathbf{x}}_i,\mathrm{q},\mathit{\beta })}^T{y}_i\right)\mid {\mathbf{x}}_i\right]=\mathbf{0}$, for i = 1, …, 409.

5.3. Results

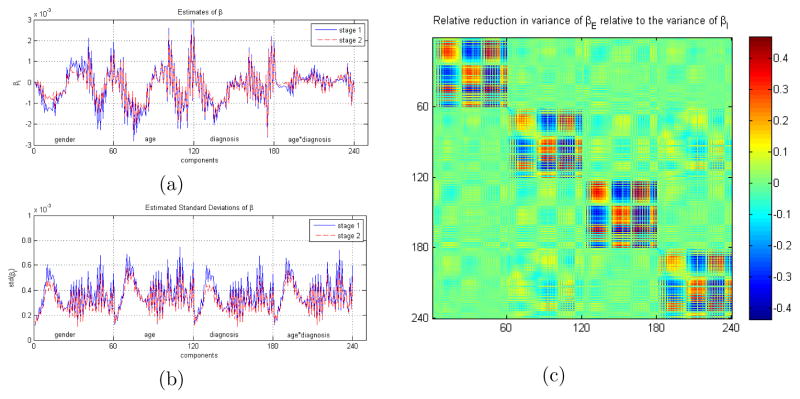
We first calculated $({\widehat{\mathrm{q}}}_I,{\widehat{\mathit{\beta }}}_I)=({\varphi }_{\mathrm{p}}^{-1}({\widehat{\mathbf{t}}}_I),{\widehat{\mathit{\beta }}}_I)$ in (14) and $({\stackrel{\sim }{\mathrm{q}}}_E,{\stackrel{\sim }{\mathit{\beta }}}_E)=({\varphi }_{\mathrm{p}}^{-1}({\stackrel{\sim }{\mathbf{t}}}_E),{\stackrel{\sim }{\mathit{\beta }}}_E)$ in (18). The intercept estimates q̂_I and q̂_E are very close to each other with ${\text{dist}}_{{\mathrm{\sum }}_2^{32}}({\widehat{\mathrm{q}}}_I,{\widehat{\mathrm{q}}}_E)<0.0005$. Second, we compared the efficiency gain in the estimates of β. The estimates β̂_I and β̂_E of regression coefficients and their standard deviations are displayed in Figure 3(a) & (b). The efficiency gain in Stage II is measured by the relative reduction in the variances of β̂_E relative to those of β̂_I, which is shown in Figure 3(c). There is an average variance relative reduction of about 16.77% across all parameters in β. There is an average variance relative reduction of about 12.25% for parameters in β^(ad), whereas there is an average relative reduction of 19.98% for parameters in β^(g).

Fig. 3.

Regression coefficient estimates (a) and their standard deviations (b) from Stages I and II; and (c) the relative reduction in the variances of β̂_E relative to those of β̂_I. There is an average of 16.77% relative decrease in variances all parameters in β, corresponding to 12.25% for β^(ad) and 19.98% for β^(g).

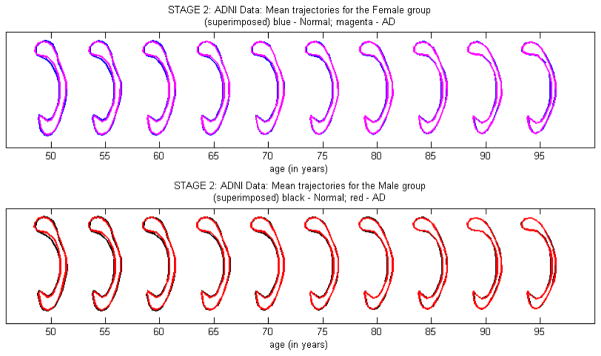
Third, we assessed whether there is an age×diagnosis interaction effect on the shape of the CC contour or not. We tested H₀ : β^(ad) = 0₆₀ versus H₁ : β^(ad) ≠ 0₆₀. The Wald test statistic equals $W_{n,\varphi }^{(1)}=98.20$ with its p-value around 0.001. Thus, the data contains enough evidence to reject H₀, indicating that there is a strong age dependent diagnosis effect on the shape of the CC contours. The mean age-dependent CC trajectories for HCs and ADs within each gender group are shown in Figure 4. It can be observed that there is a difference in shape along the inner side of the posterior splenium and isthmus subregions in both male and female groups. The splenium seems to be less rounded and the isthmus is thinner in subjects with AD than in HCs.

Fig. 4.

Age-trajectories of the intrinsic mean shapes by diagnosis within each gender group.

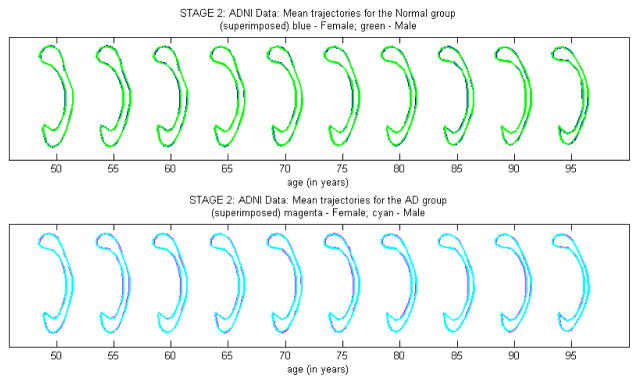
Fourth, we assessed whether there is a gender effect on the shape of the CC contour or not. We tested H₀ : β^(g) = 0₆₀ versus H₁ : β^(g) ≠ 0₆₀. The Wald test statistic is $W_{n,\varphi }^{(1)}=73.34$ with its p-value 0.116. Thus, it is not significant at the 0.05 level of significance. It may indicate that there is no gender effect on the shape of the CC contours. The mean age-dependent CC trajectories for the female and male groups within each diagnosis group are shown in Figure 5. We observed similar shapes of CC contours in males and females.

Fig. 5.

Age-trajectories of the intrinsic mean shapes by gender within each diagnosis group.

6. Discussion

We have developed a general statistical framework for intrinsic regression models of responses valued in a Riemannian symmetric space in general, and Lie groups in particular, and their association with a set of covariates in a Euclidean space. The intrinsic regression models are based on the generalized method of moment estimator and therefore the models avoid any parametric assumptions regarding the distribution of the manifold-valued responses. We also proposed a large class of link functions to map Euclidean covariates to the manifold of responses. Essentially, the covariates are first mapped to the tangent bundle to the Riemmanian manifold, and from there further mapped, via the manifold exponential map, to the manifold itself. We have adapted an annealing evolutionary stochastic algorithm to search for the ILSE, (q̂_I, β̂_I), of (q, β), in the Stage I of the estimation process, and a one-step procedure to search for the efficient estimator (q̃_E, β̃_E) in Stage II. Our simulation study and real data analysis demonstrate that the relative efficiency of the Stage II estimator improves as the sample size increases.