Summary
The aim of this paper is to develop a general regression framework for the analysis of manifold-valued response in a Riemannian symmetric space (RSS) and its association with multiple covariates of interest, such as age or gender, in Euclidean space. Such RSS-valued data arises frequently in medical imaging, surface modeling, and computer vision, among many others. We develop an intrinsic regression model solely based on an intrinsic conditional moment assumption, avoiding specifying any parametric distribution in RSS. We propose various link functions to map from the Euclidean space of multiple covariates to the RSS of responses. We develop a two-stage procedure to calculate the parameter estimates and determine their asymptotic distributions. We construct the Wald and geodesic test statistics to test hypotheses of unknown parameters. We systematically investigate the geometric invariant property of these estimates and test statistics. Simulation studies and a real data analysis are used to evaluate the finite sample properties of our methods.
Keywords: Generalized method of moment, Group action, Geodesic, Lie group, Link function, Regression, RS space
1. Introduction
Manifold-valued responses in curved spaces frequently arise in many disciplines including medical imaging, computational biology, and computer vision, among many others. For instance, in medical and molecular imaging, it is interesting to delineate the changes in the shape and anatomy of a molecule. See Figure 1 for four different examples of manifold-valued data. Regression analysis is a fundamental statistical tool for relating a response variable to covariate, such as age. In particular, when both the response and the covariate(s) are in Euclidean space, the classical linear regression model and its variants have been widely used in various fields (McCullagh and A. Nelder, 1989). However, when the response is in a Riemannian symmetric space (RSS) and the covariates are in Euclidean space, developing regression models for this type of data raises both computational and theoretical challenges. The aim of this paper is to develop a general regression framework to address these challenges.
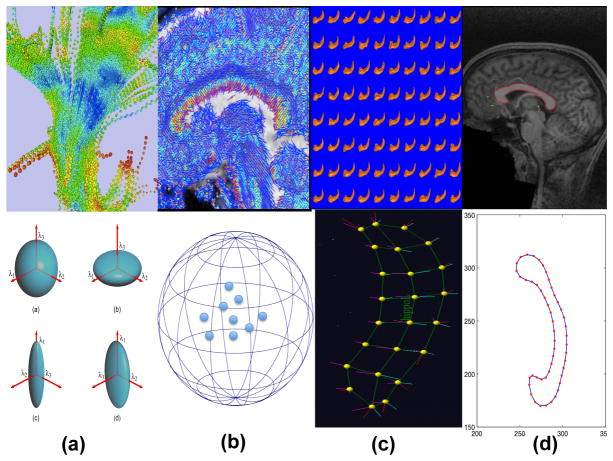
Fig. 1.
Examples of manifold-valued data: (a) diffusion tensors along white matter fiber bundles and their ellipsoid representations; (b) principal direction map of a selected slice for a randomly selected subject and the directional representation of some randomly selected principal directions on S2; (c) median representations and median atoms of a hippocampus from a randomly selected subject; and (d) an extracted contour and landmarks along the contour of the midsagittal section of the corpus callosum (CC) from a randomly selected subject.
Little has been done on the regression analyses of manifold-valued response data. The existing statistical methods for general manifold-valued data are primarily developed to characterize the population ‘mean’ and ‘variation’ across groups (Bhattacharya and Patrangenaru, 2003, 2005; Fletcher et al., 2004; Dryden and Mardia, 1998; Huckemann et al., 2010). In contrast, even for the ‘simplest’ directional data, there is a sparse literature on regression modeling of a single directional response and multiple covariates (Mardia and Jupp, 2000). In addition, these regression models of directional data are primarily based on a specific parametric distribution, such as the von Mises-Fisher distribution (Mardia and Jupp, 2000; Kent, 1982). However, it can be very challenging to assume useful parametric distributions for general manifold-valued data, and thus it is difficult to generalize these regression models of directional data to general manifold-valued data except for some specific manifolds (Shi et al., 2012; Fletcher, 2013; Kim et al., 2014; Shi et al., 2009; Zhu et al., 2009). There is also a great interest in developing nonparametric regression models for manifold-valued response data and multiple covariates (Bhattacharya and Dunson, 2010, 2012; Samir et al., 2012; Su et al., 2012; Muralidharan and Fletcher, 2012; Machado and Leite, 2006; Machado et al., 2010; Yuan et al., 2012).
An intriguing question is whether there is a general regression framework for manifold-valued response in a RSS and covariates in a multidimensional Euclidean space. The aim of this paper is to give an affirmative answer to such a question. The theoretical development is challenging but of great interest for carrying out statistical inferences on regression coefficients. We make five major contributions in this paper as follows: (i) We propose an intrinsic regression model solely based on an intrinsic conditional moment for the response in a RSS, thus avoiding specifying any parametric distributions in a general RSS - the model can handle multiple covariates in Euclidean space. (ii) We develop several ‘efficient’ estimation methods for estimating the regression coefficients in this intrinsic model. (iii) We develop several test statistics for testing linear hypotheses of the regression coefficients. (iv) We develop a general asymptotic framework for the estimates of the regression coefficients and test statistics. (v) We systematically investigate the geometrical properties (e.g., chart invariance) of these parameter estimates and test statistics.
The paper is organized as follows. In Section 2, we review the basic notion and concepts of Riemannian geometry. In Section 3, we propose the intrinsic regression models and propose various link functions for several specific RSS’s. In Section 4, we develop estimation and test procedures for the intrinsic regression models. In Section 5, we carry out a detailed data analysis on the shape of Corpus Callosum (CC) contours obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) study. Finally, we conclude with some discussions in Section 6. Technical conditions, simulation studies, theoretical examples, and proofs are deferred to the Supplementary document. Our code and data are available from http://www.bios.unc.edu/research/bias.
2. Differential Geometry Preliminaries
We briefly review some basic facts about the theory of Riemannian geometry and present more technical details in the Supplementary Report. The reader can refer to (Helgason, 1978; Spivak, 1979; Lang, 1999) for more details.
Let ℳ be a smooth manifold and dℳ be its dimension. A tangent vector of ℳ at p ∈ ℳ is defined as the derivative of a smooth curve γ(t) with respect to t evaluated at t = 0, denoted as γ̇(0), where γ(0) = p. The tangent space of ℳ at p is denoted as Tpℳ and is the set of all tangent vectors at p.
A Riemannian manifold (ℳ, m) is a smooth manifold together with a family of inner products, m = {mp}, on the tangent spaces Tpℳ’s that vary smoothly with p ∈ ℳ, and m is called a Riemannian metric. This metric induces a so-called geodesic distance distℳ on ℳ. The geodesics are, by definition, the locally distance-minimizing paths. If the metric space (ℳ, distℳ) is complete, the exponential map at p is defined on the tangent space Tpℳ by , where t → γ (t; p, V) is the geodesic with γ(0; p, V) = p and γ̇(0; p, V) = V. is well-defined near 0 and is a diffeomorphism on an open neighborhood 𝒱 of the origin in Tpℳ onto 𝒰 with 𝒱 such that tV ∈ 𝒱 for 0 ≤ t ≤ 1 and V ∈ 𝒱. The inverse map is the logarithmic map at p, denoted by . Then, for q ∈ 𝒰, . The radius of injectivity of ℳ at p, denoted by ρ*(ℳ, p), is the largest r > 0 such that is a diffeomorphism on the open ball Bmp(0, r) ⊂ Tpℳ onto an open set in ℳ near p. Any basis in the tangent space Tpℳ induces an isomorphism from Tpℳ to Rdℳ, and then the logarithmic map Logp provides a local chart near p. If Tpℳ is endowed with an orthonormal basis, such a chart is called a normal chart and the coordinates are called normal coordinates.
A Lie group G is a group together with a smooth manifold structure such that the operations of multiplication and inversion are smooth maps. Many common geometric transformations of Euclidean spaces that form Lie groups include rotations, translations, dilations, and affine transformations on Rd. In general, Lie groups can be used to describe transformations of smooth manifolds.
An RSS is a connected Riemannian manifold ℳ with the property that at each point, the mapping that reverses geodesics through that point is an isometry. Examples of RSS’s include Euclidean spaces, Rk, spheres, Sk, projective spaces, PRk, and hyperbolic spaces, Hk, each with their standard Riemannian metrics. Symmetric spaces arise naturally from Lie group actions on manifolds, see Helgason (1978). Given a smooth manifold ℳ and a Lie group G, a smooth group action of G on ℳ is a smooth mapping G × ℳ → ℳ, (a, p) ↦ a · p such that e · p = p and (aa′) · p = a · (a′ · p) for all a, a′ ∈ G and all p ∈ ℳ. The group action should be interpreted as a group of transformations of the manifold ℳ, namely, {La}a∈G, La(p) = a · p for p ∈ ℳ. The La is a smooth transformation on ℳ and its inverse is La−1. The orbit of a point p ∈ ℳ is defined as G(p) = {a · p | a ∈ G}. The orbits form a partition of ℳ. If ℳ consists of a single orbit, the group action is transitive or G acts transitively on ℳ, and we call ℳ a homogeneous space. The isotropy subgroup of a point p ∈ ℳ is defined as Gp = {a ∈ G | a · p = p}. When G is a connected group of isometries of the RSS ℳ, ℳ can always be viewed as a homogeneous space, ℳ ≅ G/Gp, and the isotropy subgroup Gp is compact.
From now on, we will assume that the manifold ℳ is an RSS and ℳ = G/Gp with G being a Lie group of isometries acting transitively on ℳ. Geodesics on ℳ are computed through the action of G on ℳ. Due to the transitive action of the group G of isometries on ℳ, it suffices to consider only the geodesic starting at the base point p. Geodesics on ℳ starting from p are the images of the action of a 1-parameter subgroup of G acting on the base point p. That is, for any geodesic γ on ℳ, γ(·) : R → ℳ, starting from p, there exists a 1-parameter subgroup c(·) : R → G such that γ(t) = c(t) · p for all t ∈ R.
3. Intrinsic Regression Model
Let (ℳ, m) be a (C∞) RSS of dimension dℳ and geodesically complete with an inner product mp and let G be a Lie group of isometries acting smoothly and transitively on ℳ with the identity element e.
3.1. Formulation
Consider n independent observations (y1, x1), …, (yn, xn), where yi is the ℳ-valued response variable and xi = (xi1, ···, xidx)T is a dx × 1 vector of multiple covariates. Our objective is to introduce an intrinsic regression model for RSS responses and multiple covariates of interest from n subjects.
The specification of the intrinsic regression model involves three key steps including (i) a link function mapping from the space of covariates to ℳ, (ii) the definition of a residual, and (iii) the action of transporting all residuals to a common space. First, we explicitly formalize the link function. From now on, all covariates have been centered to have mean zero. We consider a single-center link function given by
| (1) |
where μ(x, q, β) is a known link function, q ∈ ℳ can be regarded as the intercept or center, and β = (β1, …, βdβ)T is a dβ ×1 vector of regression coefficients. Moreover, it is assumed that μ(x, q, β) satisfies a single-center property as follows:
| (2) |
When the regression coefficient vector β equals 0, the link function is independent of the covariates and thus, it reduces to the single center (or ‘mean’) q ∈ ℳ. When all the covariates are equal to zero, the link function is independent of the regression coefficients and reduces to the center q ∈ ℳ. An example of the single-center link function is the geodesic link function in (Kim et al., 2014; Fletcher, 2013), which is given by
| (3) |
where Vk’s are tangent vectors in Tqℳ and β includes all unknown parameters associated with the tangent vectors.
More generally, we will consider a multicenter link function to account for the presence of multiple discrete covariates and even a general link function defined as μ(x, θ) : Rdx × Θ → M, where θ is a vector of unknown parameters in a parameter space Θ. For the multicenter link function, θ contains all unknown intercepts, denoted as q(xD), corresponding to each discrete covariate class and all regression parameters β corresponding to continuous covariates and their potential interactions with the discrete variables. However, the details on these link functions are presented in the Supplementary document, and here, for notational simplicity, we focus on (1) from now on.
Second, we introduce a definition of “residual” to ensure that μ(xi, q, β) is the proper “conditional mean” of yi given xi, which is the key concept of many regression models (McCullagh and A. Nelder, 1989). For instance, in the classical linear regression model, the response can be written as the sum of the regression function and a residual term and the regression function is the conditional mean of the response only when the conditional mean of the residual is equal to zero. Given the points yi and μ(xi, q, β) on a RSS ℳ, we need to define the residual as “a difference” between yi and μ(xi, q, β). Assume that yi and μ(xi, q, β) are “close enough” to each other in the sense that there is an open ball B(0, ρ) ⊂ Tμ(xi,q,β) ℳ such that for all i = 1, …, n,
| (4) |
However, according to a result in Le and Barden (2014), Logμ(xi,q,β)(yi) is well defined under some very mild conditions, which require that ∫ℳ distℳ (p, yi)2dp(yi) be finite and achieve a local minimum at μ(xi, q, β), where p(yi) is any finite measure of yi on ℳ. Thus, Logμ(xi,q,β)(yi) makes it a good candidate to play the role of a ‘residual’. These residuals, however, lie on different tangent spaces to ℳ, so it is difficult to carry out a multivariate analysis of these residuals.
Third, since ℳ is a RSS, this enables us to “transport” all the residuals, separately, to a common space, say Tpℳ, by exploiting the fact that the parallel transport along the geodesics can be expressed in terms of the action of G on ℳ. Indeed, since ℳ is a symmetric space, the base point p and the point μ(xi, q, β) can be joined in ℳ by a geodesic, which can be seen as the action of a one-parameter subgroup c(t; xi, q, β) of G such that c(1; xi, q, β) · p = μ(xi, q, β).
We define the rotated residual ℰ (yi, xi; q, β) of yi ∈ ℳ with respect to μ(xi, q, β) as the parallel transport of the actual residual, Logμ(xi,q,β)(yi), along the geodesic from the conditional mean, μ(xi, q, β), to the base point p. That is,
| (5) |
for i = 1, …, n, where Tpℳ is identified with Rdℳ. The intrinsic regression model on ℳ is defined by
| (6) |
where (q*, β*) denotes the true value of (q, β) and the expectation is taken with respect to the conditional distribution of yi given xi. Model (6) is equivalent to E[Logμ(xi, q*, β*) (yi)|xi] = 0 for i = 1, …, n, since the tangent map of the action of c(1;xi,q*,β*)−1 on ℳ is an isomorphism of linear spaces (invariant under the metric m) between the fibers of the tangent bundle T ℳ. This model does not assume any parametric distribution for yi given xi, and thus it allows for a large class of distributions. The model is essentially semi-parametric, since the joint distribution of (y, x) is not restricted except by the zero conditional moment requirement in (6).
3.2. A Theoretical Example: The Unit Sphere Sk
We investigate the intrinsic regression model for Sk-valued responses and include several other examples in the supplementary document. We review some basic facts about the geometric structure of ℳ = Sk = {x ∈ Rk+1 : ||x||2 = 1} (Shi et al., 2012; Mardia and Jupp, 2000; Healy and Kim, 1996; Huckemann et al., 2010). For q ∈ Sk, TqSk is given by TqSk = {v ∈ Rk+1 : v⊤q = 0}. The canonical Riemannian metric on Sk is that induced by the canonical inner product on Rk+1. Under this metric, the geodesic distance between any two points q and q′ is equal to ψq,q′ = arccos(qTq′) If the points are not antipodal (i.e. q′ ≠ −q), then there is a unique geodesic path that joins them. Therefore, the radius of injectivity is ρ(Sk) = π. For v ∈ TqSk, the Riemannian Exponential map is given by Expq(v) = cos(||v||)q + sin(||v||)v/||v||. (Here, sin(0)/0 = 1.) If q and q′ are not antipodal, the Riemannian Logarithmic map is given by Logq(q′) = arccos(qT q′)v/||v||, where v = q′ − (qT q′)q ≠ 0.
The special orthogonal group G = SO(k + 1) is a group of isometries on Sk and acts transitively and simply on Sk via the left matrix multiplication. Specifically, the rotation matrix Rq,q′, which rotates q to q′ ∈ Sk, is given by
where . Thus, q′ = Rq,q′q and Rq,q′v ∈ Tq′Sk, for any v ∈ TqSk. Moreover, (−π, π) ∋ t ↦ cq′,q(t) · q′ is the unique geodesic curve in Sk joining q′ with q, where cq′,q(t) takes the form
Suppose that we observe {(yi, xi) : i = 1, …, n}, where yi ∈ Sk for all i. We introduce the three key components of our intrinsic regression model for Sk–valued responses. First, we consider several examples of the general link function μ(xi, θ). Specifically, without loss of generality, we fix the “north pole” p = (0, …, 0, 1)T ∈ Rk+1 as a base point. Let ej be the (k +1)×1 vector with a 1 at the j-th component and a 0 otherwise for j = 1, …, k. Let q ∈ Sk be the ‘center’, and we consider two link functions as follows:
| (7) |
where Tst,-p is the stereographic projection mapping from Sk \ {p} onto the d-dimensional hyperplane Rk×{−1} and f(x, β) is a function mapping from Rdx×Rdβ to Rk with f(0, ·) = f(·, 0) = 0. A simple example of f(·, ·) is f(xi, β) = Bxi, where B is a k × dx matrix of regression coefficients and β includes all components of B.
Second, we define residuals for our intrinsic regression model. The residual in (4) requires that yi is not antipodal to μ(xi, θ). In this case, the residual for the i-th subject is given by Logμ(xi,θ)(yi) = arccos(μ(xi, θ)T yi)vi/||vi||, where vi = yi − (μ(xi, θ)T yi)μ(xi, θ). However, when yi = −μ(xi, θ) holds, there is an infinite number of geodesics connecting μ(xi, θ) and yi. In this case, Logμ(xi, θ)(yi) is not uniquely defined, whereas their geodesic distance is unique. However, according to the results in Le and Barden (2014), Logμ(xi,q,β)(yi) is well defined almost surely.
Third, we transport all the residuals, separately, to a common space, say TpSk. The rotated residual is given by
| (8) |
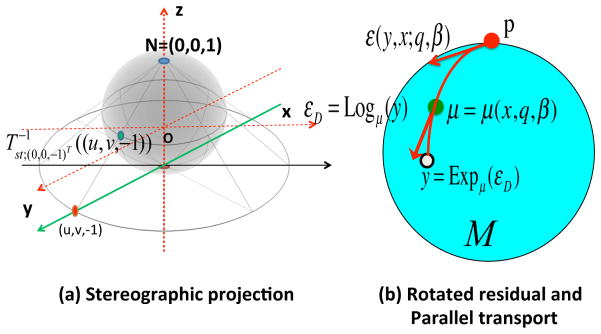
Our intrinsic regression model is defined by the zero conditional mean assumption in (6) on the above rotated residuals (8). A graphic illustration of the stereographic link functions in (7), rotated residual, and parallel transport is given in Figure 2.
Fig. 2.
Graphical illustration of (a) stereographic projection and (b) rotated residual and parallel transport. In panel (a), N and O denote the north pole (0, 0, 1) and the origin (0, 0, 0), respectively. In panel (b), y, μ = μ(x, q, β), εD = Logμ(y), ℰ(y, x; q, β), and p, respectively, represent an observation, the conditional mean, the residual, the rotated residual, and the base point.
Alternatively, we may consider some parametric spherical regression models for spherical responses. As an illustration, we consider the von Mises-Fisher (vMF) regression model. Specifically, it is assumed that yi|xi ~ vMF(μ(xi, θ), κ) or, equivalently, Rμ(xi, θ),pyi|xi ~ vMF(p, κ), for i = 1, …, n, where κ is a positive concentration parameter and is assumed to be known for simplicity. Calculating the maximum likelihood estimate of θ is equivalent to solving a score equation given by , where ∂θ = ∂/∂θ. Since ||μ(xi, θ)|| = 1 and {∂θμ(xi, θ)}T μ(xi, θ) = 0 for all subcomponents of θ, we have
| (9) |
which is a linear combination of the rotated residual.
4. Estimation and Test Procedures
4.1. Generalized Method of Moment Estimators
We consider the generalized method of moment estimator (GMM estimator) to estimate the unknown parameters in model (6) (Hansen, 1982; Newey, 1993; Korsholm, 1999). We may view the Tpℳ-valued function ℰ as a function with values in Rdℳ. Let h(x; q, β) be a s × dℳ matrix of functions of (x, q, β) with s ≥ dℳ + dβ and Wn be a random sequence of positive definite s × s weight matrices. It follows from (6) that
| (10) |
We define 𝒬n(q, β) = [ℙn(h(x; q, β)ℰ(y, x; q, β))]T Wn [ℙn(h(x; q, β)ℰ(y, x; q, β))], where for a real-vector valued function f (y, x). The GMM estimator (q̂G, β̂G), or simply (q̂, β̂), of (q, β) associated with (h(·, ·, ·), Wn) is defined as
| (11) |
Under some conditions detailed below, we can show the first order asymptotic properties of (q̂G, β̂G) including consistency and asymptotic normality of GMM-estimators. We introduce some notation. Let ||·|| denote the Euclidean norm of a vector or a matrix; for l = 1, … ; a⊗2 = aaT any matrix or vector a; V = Var[h(x; q*, β*)ℰ(y, x; q*, β*)]; Id is the identity matrix; and , respectively, denote convergence in distribution and in probability. We obtain the following results, whose detailed proofs can be found in the supplementary document.
Theorem 4.1
Assume that (yi, xi), i = 1,…, n, are iid random variables in ℳ × Rdx. Let (q*, β*) be the exact value of the parameters satisfying (6). Let {Wn}n be a random sequence of s × s symmetric positive semi-definite matrices with s ≥ dℳ + dβ.
Under assumptions (C1)–(C5) in the Supplementary document, (q̂G, β̂G) in (11) is consistent in probability as n → ∞.
-
Under assumptions (C1)–(C4) and (C6)–(C10) in the Supplementary document, for any local chart (U, ϕ) on ℳ near q* as n → ∞, we have
(12) where , in which Gϕ is defined in (C9). Moreover, for any other chart (U, ϕ′) near q*, we have(13) where J(·)t denotes the Jacobian matrix evaluated at t.
Theorem 4.1 establishes the first-order asymptotic properties of (q̂G, β̂G) for the intrinsic regression model (6). Theorem 4.1 (a) establishes the consistency of (q̂G, β̂G). The consistency result does not depend on the local chart. Theorem 4.1 (b) establishes the asymptotic normality of (ϕ(q̂G), β̂G) for a specific chart (U, ϕ) and the relationship between the asymptotic covariances Σϕ′ and Σϕ for two different charts. It follows from the lower-right dβ × dβ submatrix of Σϕ′ that the asymptotic covariance matrix of β̂ does not depend on the chart. However, the asymptotic normality of q̂G does depend on a specific chart. A consistent estimator of the asymptotic covariance matrix Σϕ is given by with and
This estimator is also compatible with the manifold structure of ℳ.
We consider the relationship between the GMM estimator and the intrinsic least squares estimator (ILSE) of (q, β), denoted by (q̂I, β̂I). The (q̂I, β̂I) minimizes the total residual sum of squares 𝒢I,n(q, β) as follows:
| (14) |
According to (2), the ILSE is closely related to the intrinsic mean q̂IM of y1,⋯, yn ∈ ℳ, which is defined as
Recall that μ(0, q, β) is independent of β.
The (q̂I, β̂I) can be regarded as a special case of the GMM estimator when we set Wn = Idℳ+dβ and h’s rows hj(x, q, β) = (Lc(1;x, q,β)−1.*(∂tj μ(x, ϕ−1(t), β)|t=ϕ(q)))T for j = 1,…, dℳ, and hdℳ+j (x, q, β) = (Lc(1;x,q,β)−1.*(∂βj μ(x, q, β)))T for j = 1,…, dβ, where (U, ϕ) is a chart on ℳ and each row of h(x, q, β) is in R1×dℳ via the identification Tpℳ ≅ Rdℳ corresponding to (U, ϕ). It follows from Theorem 4.1 that under model (6), (q̂I, β̂I) enjoys the first-order asymptotic properties as well.
4.2. Efficient GMM Estimator
We investigate the most efficient estimator in the class of GMM estimators. For a fixed h(·; ·, ·), the optimal choice of W is Wopt = V−1, and the use of Wn = Wopt leads to the most efficient estimator in the class of all GMM estimators obtained using the same h(·) function (Hansen, 1982). Its asymptotic covariance is given by (GϕV−1Gϕ)−1. An interesting question is what the optimal choice of hopt(·) is.
We first introduce some notation. For a chart (U, ϕ) on ℳ near q*, let
Let (q̂*, β̂*) be the GMM estimator of (q, β) based on and . Generally, we obtain an optimal result of hopt(·), which generalizes an existing result for Euclidean-valued responses and covariates (Newey, 1993), as follows.
Theorem 4.2
Suppose that (C2)–(C8) and (C10)–(C12) in the Supplementary document hold for and . We have the following results:
(q̂*, β̂*) is asymptotically normally distributed with mean 0 and covariance ;
(q̂*, β̂*) is optimal among all GMM estimators for model (6);
(q̂*, β̂*) is independent of the chart.
Theorem 4.2 characterizes the optimality of and among regular GMM estimators for model (6). Geometrically, (q̂*, β̂*) is independent of the chart. Specifically, for any other chart (U, ϕ′) near q*, we have
Thus, the quadratic form in (11) associated with and is the same as that which is associated with and . It indicates that the GMM estimator (q̂*, β̂*)ϕ based on and is independent of the chart (U, ϕ).
The next challenging issue is the estimation of Dϕ (x) and Ω(x). We may proceed in two steps. The first step is to calculate a -consistent estimator (q̂I, β̂I) of (q, β), such as the ILSE. The second step is to plug (q̂I, β̂I) into the functions ℰi(q̂I, β̂I) and ∂(t,β)ℰ(yi, xi; ϕ−1(t), β̂I)|t=ϕ(q̂I) for all i and then use them to construct the nonparametric estimates of Dϕ(x) and Ω(x) (Newey, 1993). Specifically, let K(·) be a dx-dimensional kernel function of the l0-th order satisfying ∫K(u1,…, udx)du1 … dudx = 1, for any s = 1,…, dx and 1 ≤ l < l0, and . Let Kτ (u) = τ−1K(u/τ), where τ > 0 is a bandwidth. Then, a nonparametric estimator of Dϕ(x) can be written by
| (15) |
where . Although we may construct a nonparametric estimator of Ω(x) similar to (15), we have found that even for moderate dx, such an estimator is numerically unstable. Instead, we approximate Ω(xi) = Var(ℰ(y, x; q*, β*)|x = xi) by its mean VE* = Var(ℰ(y, x; q*, β*)). In this case, and , respectively, reduce to
| (16) |
For any local chart (U, ϕ) with q̂I ∈ U, we construct the estimators of and as follows. Let V̂(q, β) =ℙnℰ(y, x; q, β)⊗2, we have
| (17) |
Then, we substitute ĥE, ϕ and ŴE, ϕ into (11) and then calculate the GMM estimator of (q, β), denoted by (q̂E, β̂E). Similar to (q̂*, β̂*), it can be shown that (q̂E, β̂E) is independent of the chart (U, ϕ) on ℳ near q* with q̂I ∈ U. For sufficiently large n, distℳ(q̂I, q*) can be made sufficiently small and any maximal normal chart on ℳ centered at q̂I contains the true value q* with probability approaching one.
We calculate a one-step linearized estimator of (q, β), denoted by (q̃E, β̃E), to approximate (q̂E, β̂E). Computationally, the linearized estimator does not require iteration, whereas, theoretically, it shares the first asymptotic properties with (q̂E, β̂E) as shown below. Specifically, in the chart (U, ϕ) near q̂I, we have
| (18) |
Furthermore, if (U′, ϕ ′) is another chart on ℳ near q̂I, then we have
Thus, β̃E,ϕ is independent of the chart ϕ and {t̃E, ϕ − ϕ(q̂I) | ϕ is a chart on M} defines a unique tangent vector to ℳ at q̂I. Moreover, if ϕ and ϕ′ are maximal normal charts centered at q̂I, then γϕ (τ) = ϕ−1(τt̃E,ϕ) and γϕ′(τ) = ϕ′−1(τt̃E, ϕ′) are two geodesic curves on ℳ starting from the same point q̂I with the same initial velocity vector, and thus these two geodesics coincide. Therefore, ϕ−1(t̃E,ϕ) is independent of the normal chart ϕ centered at q̂I. Finally, we can establish the first order asymptotic properties of (q̃E, β̃E) as follows.
Theorem 4.3
Assume that (C2)–(C11) and (C13)–(C18) are valid. As n → ∞, we have the following results:
| (19) |
where . In addition, ΣE, ϕ is invariant under the change of coordinates in ℳ and the asymptotic distribution of β̃E does not depend on the chart (U, ϕ). Also, if we set
| (20) |
then nΣ̂E,ϕ is a consistent estimator of ΣE,ϕ, i.e. . This estimator is also compatible with the manifold structure of ℳ.
Theorem 4.3 establishes the first-order asymptotic properties of (q̃E, β̃E). If Ω(x) = Ω for a constant matrix Ω, then it follows from Theorems 4.2 and 4.3 that (q̃E, β̃E) is optimal. If Ω(x) does not vary dramatically as a function of x, then (q̃E, β̃E) is nearly optimal. If Ω(x) varies dramatically as a function of x, one can replace V̂(q̂I, β̂I) in (17) by Ω̂(xi) to obtain ĥE,ϕ (x) = D̂ϕ(x)Ω̂(x)−1 and ŴE,ϕ = {ℙn[ĥE,ϕ (x)ℰ(y, x; q̂I, β̂I)]⊗2}−1, where Ω̂(xi) is a consistent estimator of Ω(xi) for all i, then the optimality of (q̃E, β̃E) still holds. We have the following theorem.
Theorem 4.4
Assume that (C2)–(C17) and (C19) are valid. Then, as n → ∞, we have
| (21) |
in which is given in Theorem 4.2. If we set Σ̂E,ϕ = n−1{ℙn[D̂ϕ (x)Ω̂(x)−1D̂ϕ(x)T]}−1, then nΣ̂E,ϕ is a consistent estimator of .
4.3. Computational Algorithm
Computationally, an annealing evolutionary stochastic approximation Monte Carlo (SAMC) algorithm (Liang et al., 2010) is developed to compute (q̂I, β̂I) and (q̂E, β̂E). See the supplementary document for details. Although some gradient-based optimization methods, such as the quasi-Newton method, have been used to optimize 𝒬n(q, β) (Kim et al., 2014; Fletcher, 2013), we have found that these methods strongly depend on the starting value of (q, β). Specifically, when ℰ(y, x; q, β) takes a relatively complicated form, 𝒬n(q, β) is generally not convex and can easily converge to local minima. Moreover, we have found that it can be statistically misleading to carry out statistical inference, such as the estimated standard errors of (q̂E, β̂E), at those local minima. The annealing evolutionary SAMC algorithm converges fast and distinguishes from many gradient-based algorithms, since it possesses a nice feature in that the moves are self-adjustable and thus not likely to get trapped by local energy minima. The annealing evolutionary SAMC algorithm (Liang et al., 2010) represents a further improvement of stochastic approximation Monte Carlo for optimization problems by incorporating some features of simulated annealing and the genetic algorithm into its search process.
4.4. Hypotheses Testing
Many scientific questions involve the comparison of the ℳ-valued data across groups and subjects and the detection of the change in the ℳ-valued data over time. Such questions usually can be formulated as testing the hypotheses of q and β. We consider two types of hypotheses as follows:
| (22) |
| (23) |
where C0 is an r × dβ matrix of full row rank and q0 and b0 are specified in ℳ and Rr, respectively. Further extensions of these hypotheses are definitely interesting and possible. For instance, for the multicenter link function, we may be interested in testing whether all intercepts are independent of the discrete covariate class.
We develop several test statistics for testing the hypotheses given in (22) and (23). First, we consider the Wald test statistic for testing against in (22), which is given by
where Σ̂E,ϕ is given in Theorem 4.3 or Theorem 4.4, and Σ̂E,ϕ;22 is its lower-right dβ × dβ submatrix. Since β̃E and its asymptotic covariance matrix are independent of the chart on ℳ, the test statistic is independent of the chart.
Second, we consider the Wald test statistic for testing the hypotheses given in (23) when there is a local chart (U, ϕ) on ℳ containing both q̂E and q0. Specifically, the Wald test statistic for testing (23) is defined by
Third, we develop an intrinsic Wald test statistic, that is independent of the chart, for testing the hypotheses given in (23). We consider the asymptotic covariance estimator Σ̂E,ϕ based on q̃E and its upper-left dℳ × dℳ submatrix Σ̂E,ϕ;11. Since both are compatible with the manifold structure of ℳ, Σ̂E,ϕ;11 defines a unique non-degenerate linear map Σ̂E;11(·) from the tangent space Tq̃Eℳ of ℳ at q̃E onto itself, which is independent of the chart (U, ϕ). In a maximal normal chart centered at q̃E, then in any such normal chart, the Wald test statistic for testing (23) is given by
We obtain the asymptotic null distributions of , and as follows.
Theorem 4.5
Let (U, ϕ) be a local chart on ℳ so that q̃E, q* ∈ U. Assume that all conditions in Theorem 4.3 hold. Under the corresponding null hypothesis, we have the following results:
and are asymptotically distributed as and , respectively;
is independent of the chart (U, ϕ);
, for any other local chart (U, ϕ′) with q̃E and q0 in U;
, for any normal chart (U, ϕ) centered at q̃E.
Theorem 4.5 has several important implications. Theorem 4.5 (i) characterizes the asymptotic null distributions of and . Theorem 4.5 (ii) shows that does not depend the choice of the chart (U, ϕ) on ℳ. Theorem 4.5 (iii) shows that and are asymptotically equivalent for any two local charts. Theorem 4.5 (iv) shows that can be used to construct an intrinsic test statistic.
We consider a local alternative framework for (22) and (23) as follows:
| (24) |
| (25) |
where δ and v are specified (and fixed) in Rr and Tq0ℳ, respectively, and we establish the asymptotic distributions of and under these local alternatives.
Theorem 4.6
Let (U, ϕ) be a local chart on ℳ so that q̃E, q* ∈ U. Assume that all conditions in Theorem 4.3 hold. Under the local alternatives (24) and (25), we have the following results:
Under is asymptotically distributed as noncentral with noncentrality parameter .
Under is asymptotically distributed as noncentral , with noncentrality parameter J(ϕ ∘ Expq0)0(v)T [Σ̂E,ϕ;11]−1 J(ϕ ∘ Expq0)0(v). The noncentrality parameter does not depend on the choice of the coordinate system at q0. Here, J(f)a denotes the Jacobian matrix of map f at a.
Under is asymptotically distributed as noncentral , with noncentrality parameter mq̃E((Σ̂E;11)−1(J(Logq̃E)q0(v)), (J(Logq̃E)q0(v))). The noncentrality parameter does not depend on the choice of the coordinate systems at q̃E and q0, respectively.
We consider another scenario that there are no local charts on ℳ containing both q̃E and q0. In this case, we restate the hypotheses and as follows:
| (26) |
We propose a geodesic test statistic given by
| (27) |
which is independent of the chart (U, ϕ). Theoretically, we can establish the asymptotic distribution of Wdist under both the null and alternative hypotheses as follows.
Theorem 4.7
Assume that all conditions in Theorem 4.5 hold.
Under , nWdist is asymptotically weighted chi-square χ2(λ1, …, λdℳ) distributed, where the weights λ1, …, λdℳ are the eigenvalues of the matrix ΣE,Logq0,11, which is the upper-left dℳ × dℳ submatrix of the asymptotic covariance matrix ΣE,Logq0 of q̃E in a normal chart centered at q0. Moreover, the weights are independent, up to a permutation, of the choice of the normal chart centered at q*.
-
Under the alternative hypothesis, Wdist is asymptotically normal distributed and we havewhere Ddist is the column vector representation of gradq*(dist(·, q0)2) with respect to the orthonormal basis of Tq*ℳ associated with the normal chart used to represent the asymptotic covariance of q̃E as the matrix ΣE,Logq*. In particular, when q0 is close to q*, then
Theorem 4.7 establishes the asymptotic distribution of Wdist when q̃E and q0 do not belong to the same chart of ℳ. In practice, the covariance matrix ΣE,Logq*,11 is not available, since ΣE,Logq* is not known; it also depends on the unknown true value β*, so we may use the estimate Σ̂E,Logq* as defined in Theorems 4.3 and 4.4. Therefore, under the null hypothesis, the asymptotic distribution of Wdist can be approximated by the weighted chi-square distribution χ2(λ̂1, …, λ̂dℳ), in which the weights λ̂1, …, λ̂dℳ are the eigenvalues of the covariance matrix (Σ̂E,Logq0)11/n.
Finally, we develop a score test statistic for testing against . An advantage of using the score test statistic is that it avoids the calculation of an estimator under the alternative hypothesis . For notational simplicity, we only consider the ILSE estimator of (q, β), denoted by (q0, β̃I), under the null hypothesis . For any chart (U, ϕ) on ℳ with q0 ∈ U, we define
where the subcomponents Fϕi,1 and Fϕi,2 correspond to t and β, respectively. It can be shown that the score test WSC,ϕ reduces to
| (28) |
where , in which . Theoretically, we can establish the asymptotic distribution of WSC,ϕ under the null hypothesis.
Theorem 4.8
Assume that all conditions in Theorem 4.5 hold. We have the following results:
For any suitable local chart (U, ϕ), the score test statistic WSC,ϕ is asymptotically distributed as under the null hypothesis .
- Under , for any other local chart (U, ϕ′) with q0 ∈ U, we have
5. Real Data Example
5.1. ADNI Corpus Callosum Shape Data
Alzheimer disease (AD) is a disorder of cognitive and behavioral impairment that markedly interferes with social and occupational functioning. It is an irreversible, progressive brain disease that slowly destroys memory and thinking skills, and eventually even the ability to carry out the simplest tasks. AD affects almost 50% of those over the age of 85 and is the sixth leading cause of death in the United States.
The corpus callosum (CC), as the largest white matter structure in the brain, connects the left and right cerebral hemispheres and facilitates homotopic and heterotopic interhemispheric communication. It has been a structure of high interest in many neuroimaging studies of neuro-developmental pathology. Individual differences in CC and their possible implications regarding interhemispheric connectivity have been investigated over the last several decades (Paul et al., 2007).
We consider the CC contour data obtained from the ADNI study. For each subject in ADNI dataset, the segmentation of the T1-weighted MRI and the calculation of the intracranial volume were done in the FreeSurfer package‡ (Dale et al., 1999), while the midsagittal CC area was calculated in the CCseg package, which is measured by using subdivisions in Witelson (1989) motivated by neuro-histological studies. Finally, each T1-weighted MRI image and tissue segmentation were used as the input files of CCSeg package to extract the planar CC shape data.
5.2. Intrinsic Regression Models
We are interested in characterizing the change of the CC contour shape as a function of three covariates including gender, age, and AD diagnosis. We focused on n = 409 subjects with 223 healthy controls (HCs) and 186 AD patients at baseline of the ADNI1 database. We observed a CC planar contour Yi with 32 landmarks and three clinical variables including gender xi,1 (0-female, 1-male), age xi,2, and diagnosis xi,3 (0-control, 1-AD) for i = 1, …, 409. The demographic info is presented in Table 1.
Table 1.
Demographic information for the processed ADNI CC shape dataset including disease status, age, and gender.
| Disease status | No. | Range of age in years (mean) | Gender (female/male) |
|---|---|---|---|
| Healthy Control | 223 | 62–90 (76.25) | 107/116 |
| AD | 186 | 55–92 (75.42) | 88/98 |
We treat the CC planar contour Yi as a RSS-valued response in the Kendall’s planar shape space . The geometric structure of for k > 2 is included in the supplementary document. Each Yi is specified as a 32 × 2 real matrix, whose rows represent the planar coordinates of 32 landmarks on yi. Moreover, Yi = (Yi,1 Yi,2) can be represented as a complex vector zi = Yi,1 +jYi,2 in C32, where and C is the standard complex space. After removing the translations and normalizing to the unit 2-norm, each contour Yi can be view as an element . Then, after removing the 2-dimensional rotations, we obtain an element yi = [zi] in Kendall’s planar shape space, , which has dimension 30 and is identified with the complex projective space CP30.
In order to use our intrinsic regression model, we determined the base point p and an orthonormal basis {Z1, …, Z30} for as follows. We initially set p0 = [z0] with and an orthonormal basis {Z̃1, …, Z̃30} in , where . Then, we projected all yi’s onto and calculated Logp0(yi) for all i. Finally, we set the base point p as and then used the parallel transport to rotate the initial basis {Z̃1, …, Z̃30} to obtain a new orthonormal basis {Z1, …, Z30} at p.
We consider an intrinsic regression model with as a response vector and a vector of four covariates including gender, age, diagnosis, and the interaction age*diagnosis, that is, xi = (xi,1, xi,2, xi,3, xi,4)T with xi,4 = xi,2xi,3. We used a single-center link function with model parameters as follow. The intercept q is specified by , where t = (t1, …, t60)T ∈ R60. The regression coefficient vector β includes four 60 × 1 subvectors including β(g), β(a), β(d), and β(ad), which correspond to xi1, xi2, xi3, and xi4, respectively. Therefore, there are 300 unknown parameters in (tT, βT)T. We define a 30 × 4 complex matrix as B = Bo+jBe, with , where and are the subvectors of β(·) formed by the odd-indexed and even-indexed components, respectively, and a link function by , where , with q1 = [zq1], q2 = [zq2], the optimal rotational alignment of zq2 to zq1, given by , and Uz1,z2v for any v ∈ Ck takes the form of
in which , for z1, z2 ∈ 𝒟32. Finally, our intrinsic model is defined by , for i = 1, …, 409.
5.3. Results
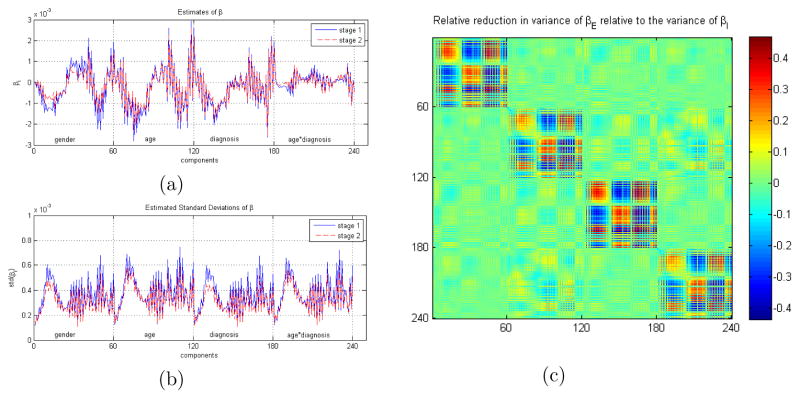
We first calculated in (14) and in (18). The intercept estimates q̂I and q̂E are very close to each other with . Second, we compared the efficiency gain in the estimates of β. The estimates β̂I and β̂E of regression coefficients and their standard deviations are displayed in Figure 3(a) & (b). The efficiency gain in Stage II is measured by the relative reduction in the variances of β̂E relative to those of β̂I, which is shown in Figure 3(c). There is an average variance relative reduction of about 16.77% across all parameters in β. There is an average variance relative reduction of about 12.25% for parameters in β(ad), whereas there is an average relative reduction of 19.98% for parameters in β(g).
Fig. 3.
Regression coefficient estimates (a) and their standard deviations (b) from Stages I and II; and (c) the relative reduction in the variances of β̂E relative to those of β̂I. There is an average of 16.77% relative decrease in variances all parameters in β, corresponding to 12.25% for β(ad) and 19.98% for β(g).
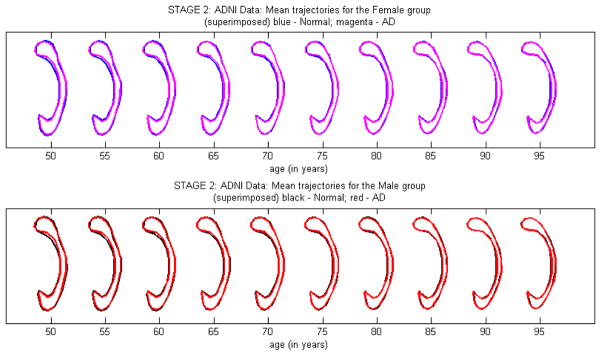
Third, we assessed whether there is an age×diagnosis interaction effect on the shape of the CC contour or not. We tested H0 : β(ad) = 060 versus H1 : β(ad) ≠ 060. The Wald test statistic equals with its p-value around 0.001. Thus, the data contains enough evidence to reject H0, indicating that there is a strong age dependent diagnosis effect on the shape of the CC contours. The mean age-dependent CC trajectories for HCs and ADs within each gender group are shown in Figure 4. It can be observed that there is a difference in shape along the inner side of the posterior splenium and isthmus subregions in both male and female groups. The splenium seems to be less rounded and the isthmus is thinner in subjects with AD than in HCs.
Fig. 4.
Age-trajectories of the intrinsic mean shapes by diagnosis within each gender group.
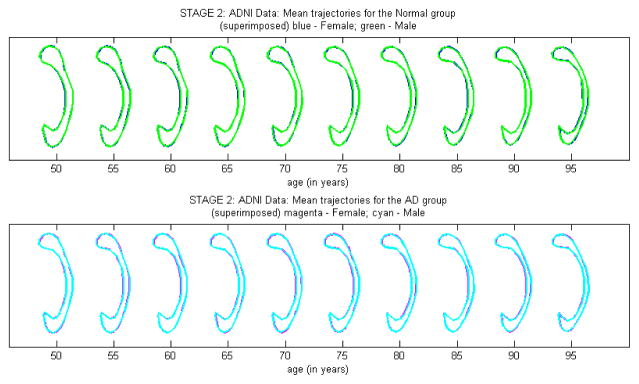
Fourth, we assessed whether there is a gender effect on the shape of the CC contour or not. We tested H0 : β(g) = 060 versus H1 : β(g) ≠ 060. The Wald test statistic is with its p-value 0.116. Thus, it is not significant at the 0.05 level of significance. It may indicate that there is no gender effect on the shape of the CC contours. The mean age-dependent CC trajectories for the female and male groups within each diagnosis group are shown in Figure 5. We observed similar shapes of CC contours in males and females.
Fig. 5.
Age-trajectories of the intrinsic mean shapes by gender within each diagnosis group.
6. Discussion
We have developed a general statistical framework for intrinsic regression models of responses valued in a Riemannian symmetric space in general, and Lie groups in particular, and their association with a set of covariates in a Euclidean space. The intrinsic regression models are based on the generalized method of moment estimator and therefore the models avoid any parametric assumptions regarding the distribution of the manifold-valued responses. We also proposed a large class of link functions to map Euclidean covariates to the manifold of responses. Essentially, the covariates are first mapped to the tangent bundle to the Riemmanian manifold, and from there further mapped, via the manifold exponential map, to the manifold itself. We have adapted an annealing evolutionary stochastic algorithm to search for the ILSE, (q̂I, β̂I), of (q, β), in the Stage I of the estimation process, and a one-step procedure to search for the efficient estimator (q̃E, β̃E) in Stage II. Our simulation study and real data analysis demonstrate that the relative efficiency of the Stage II estimator improves as the sample size increases.
Supplementary Material
Acknowledgments
We thank the Editor, an Associate Editor, two referees, and Professor Huiling Le for valuable suggestions, which helped to improve our presentation greatly. We also thank Dr. Chao Huang and Mr. Yuai Hua for processing the ADNI CC shape data set. This work was supported in part by National Science Foundation grants and National Institute of Health grants.
Footnotes
Data used in preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database. As such, the investigators within the ADNI contributed to the design and implementation of ADNI and/or provided data but did not participate in analysis or writing of this paper. A complete listing of ADNI investigators can be found at: http://adni.loni.usc.edu/wp-content/uploads/how_to_apply/ADNI_Acknowledgement_List.pdf.
References
- Bhattacharya A, Dunson D. Nonparametric Bayes classification and hypothesis testing on manifolds. Journal of Multivariate Analysis. 2012;111:1–19. doi: 10.1016/j.jmva.2012.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhattacharya A, Dunson DB. Nonparametric Bayesian density estimation on manifolds with applications to planar shapes. Biometrika. 2010;97(4):851–865. doi: 10.1093/biomet/asq044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhattacharya R, Patrangenaru V. Large sample theory of intrinsic and extrinsic sample means on manifolds. I. Ann Statist. 2003;31(1):1–29. [Google Scholar]
- Bhattacharya R, Patrangenaru V. Large sample theory of intrinsic and extrinsic sample means on manifolds. II. Ann Statist. 2005;33(3):1225–1259. [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis: I. segmentation and surface reconstruction. Neuroimage. 1999;9(2):179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Dryden IL, Mardia KV. Statistical Shape Analysis. Chichester: John Wiley & Sons Ltd; 1998. [Google Scholar]
- Fletcher PT. Geodesic regression and the theory of least squares on Riemannian manifolds. International Journal of Computer Vision. 2013;105(2):171–185. [Google Scholar]
- Fletcher PT, Lu C, Pizer S, Joshi S. Principal geodesic analysis for the study of nonlinear statistics of shape. Medical Imaging, IEEE Transactions on. 2004;23(8):995–1005. doi: 10.1109/TMI.2004.831793. [DOI] [PubMed] [Google Scholar]
- Hansen LP. Large sample properties of generalized method of moments estimators. Econometrica. 1982;50:1029–1054. [Google Scholar]
- Healy DMJ, Kim PT. An empirical Bayes approach to directional data and efficient computation on the sphere. Ann Statist. 1996;24(1):232–254. [Google Scholar]
- Helgason S. Differential Geometry, Lie Groups, and Symmetric Spaces, Volume 80 of Pure and Applied Mathematics. New York, NY: Academic Press Inc; 1978. [Google Scholar]
- Huckemann S, Hotz T, Munk A. Intrinsic manova for Riemannian manifolds with an application to Kendall’s space of planar shapes. IEEE Trans Patt Anal Mach Intell. 2010;32:593–603. doi: 10.1109/TPAMI.2009.117. [DOI] [PubMed] [Google Scholar]
- Kent JT. The Fisher-Bingham distribution on the sphere. J Roy Statist Soc Ser B. 1982;44(1):71–80. [Google Scholar]
- Kim HJ, Adluru N, Collions MD, Chung MK, Bendlin BB, Johnson SC, Davidson RJ, Singh V. Multivariate general linear models (mglm) on Riemannian manifolds with applications to statistical analysis of diffusion weighted images. IEEE Annual Conference on Computer Vision and Pattern Recognition; 2014. pp. 2705–2712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korsholm L. The GMM estimator versus the semiparametric efficient score estimator under conditional moment restrictions. University of Aarhus, Department of Economics, Building 350; 1999. Working paper series. [Google Scholar]
- Lang S. Fundamentals of Differential Geometry, Volume 191 of Graduate Texts in Mathematics. New York: Springer-Verlag; 1999. [Google Scholar]
- Le H, Barden D. On the measure of the cut locus of a Fréchet mean. Bull Lond Math Soc. 2014;46:698–708. [Google Scholar]
- Liang F, Liu C, Carroll RJ. Advanced Markov Chain Monte Carlo: Learning from Past Samples. New York: Wiley; 2010. [Google Scholar]
- Machado L, Leite FS. Fitting smooth paths on Riemannian manifolds. Int J Appl Math Stat. 2006;4:25–53. [Google Scholar]
- Machado L, Silva Leite F, Krakowski K. Higher-order smoothing splines versus least squares problems on Riemannian manifolds. J Dyn Control Syst. 2010;16(1):121–148. [Google Scholar]
- Mardia KV, Jupp PE. Directional Statistics. Chichester: John Wiley & Sons Ltd; 2000. [Google Scholar]
- McCullagh P, Nelder JA. Generalized Linear Models. 2. London: Chapman and Hall; 1989. [Google Scholar]
- Muralidharan P, Fletcher P. Sasaki metrics for analysis of longitudinal data on manifolds. Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on; 2012. pp. 1027–1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newey WK. Econometrics, Volume 11 of Handbook of Statist. Amsterdam: North-Holland; 1993. Efficient estimation of models with conditional moment restrictions; pp. 419–454. [Google Scholar]
- Paul LK, Brown WS, Adolphs R, Tyszka JM, Richards LJ, Mukherjee P, Sherr EH. Agenesis of the corpus callosum: genetic, developmental and functional aspects of connectivity. Nature Reviews Neuroscience. 2007;8:287–299. doi: 10.1038/nrn2107. [DOI] [PubMed] [Google Scholar]
- Samir C, Absil PA, Srivastava A, Klassen E. A gradient-descent method for curve fitting on Riemannian manifolds. Foundations of Computational Mathematics. 2012;12(1):49–73. [Google Scholar]
- Shi X, Styner M, LJ, Ibrahim JG, Lin W, Zhu H. Intrinsic regression models for manifold-value data. International Conference on Medical Imaging Computing and Computer Assisted Intervention (MICCAI); 2009. pp. 192–199. [PMC free article] [PubMed] [Google Scholar]
- Shi X, Zhu H, Ibrahim JG, Liang F, Liberman J, Styner M. Intrinsic regression models for median representation of subcortical structures. Journal of American Statistical Association. 2012;107:12–23. doi: 10.1080/01621459.2011.643710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spivak M. A Comprehensive Introduction to Differential Geometry. 2. I. Wilmington, Del: Publish or Perish Inc; 1979. [Google Scholar]
- Su J, Dryden I, Klassen E, Le H, Srivastava A. Fitting smoothing splines to time-indexed, noisy points on nonlinear manifolds. Image and Vision Computing. 2012;30(6–7):428–442. [Google Scholar]
- Witelson SF. Hand and sex differences in isthmus and genu of the human corpus callosum: a postmortem morphological study. Brain. 1989;112:799–835. doi: 10.1093/brain/112.3.799. [DOI] [PubMed] [Google Scholar]
- Yuan Y, Zhu H, Lin W, Marron JS. Local polynomial regression for symmetric positive definite matrices. Journal of Royal Statistical Society B. 2012;74:697–719. doi: 10.1111/j.1467-9868.2011.01022.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu H, Chen Y, Ibrahim JG, Li Y, Hall C, Lin W. Intrinsic regression models for positive-definite matrices with applications to diffusion tensor imaging. J Amer Statist Assoc. 2009;104(487):1203–1212. doi: 10.1198/jasa.2009.tm08096. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.