Universal Scaling of Robust Thermal Hot Spot and Ionic Current Enhancement by Focused Ohmic Heating in a Conic Nanopore

Abstract

A stable nanoscale thermal hot spot, with temperature approaching 100 °C, is shown to be sustained by localized Ohmic heating of a focused electric field at the tip of a slender conic nanopore. The self-similar (length-independent) conic geometry allows us to match the singular heat source at the tip to the singular radial heat loss from the slender cone to obtain a self-similar steady temperature profile along the cone and the resulting ionic current conductance enhancement due to viscosity reduction. The universal scaling, which depends only on a single dimensionless parameter Z, collapses the measured conductance data and computed temperature profiles in ion-track conic nanopores and conic nanopipettes. The collapsed numerical data reveal universal values for the hot-spot location and temperature in an aqueous electrolyte.

Ohmic heating in a nanopore has recently been put forth as a means to rapidly establish stable thermal hot spots, with superheated temperatures [1,2]. Such hot spots can be indirectly detected by a stable increase in the ionic current due to the decreased viscosity of the heated water [3]. We extend this concept to slender conic nanopores, where the focused electric field can reduce the longitudinal dimension of the hot spot to nanoscales at the tips of macroscopic (cm-long) pores. Moreover, the self-similar conic geometry allows us to develop a universal size-independent theory for the conductance enhancement and the hot-spot temperature, location, and dimension. With the smaller longitudinal dimensions and universal scaling of these conic nanopore hot spots, nanoscale phenomena such as single-molecule thermophoresis [4], single-biomolecule binding kinetics and thermodynamics, and single-bubble nucleation [5,6] can be studied in a precisely controlled nanoscale location with distinct ion current signatures.

Because of field focusing, the electric field E blows up towards the tip in a conic nanopore as (R⁻²), where R is the local cross-section radius of the cone [see Fig. 1(b)]; hence, the Ohmic heating rate per unit volume, which scales as (E²), blows up as (R⁻⁴). The external temperature profile for a perfect cylinder, however, blows up as ln r in the radial direction and would be responsible for an R-independent heat loss rate per unit length along the cylinder. This seems to suggest that a steady temperature profile with a balance between heat generation and heat loss cannot be established. However, as shown in our analysis, proper accounting of the far-field external longitudinal flux that eliminates the singular ln r dependence for an infinitely long cylinder [7] is able to produce the desirable (R⁻²) scaling for heat loss per unit length. Consequently, the stable steady-state temperature profile that results from a balance between two nearly singular fluxes at the tip of a cone is very mathematically similar to the balance of singular azimuthal capillary forces and electrical Maxwell or Coulombic forces for dc [8] and ac [9] to establish robust interfacial cones. All share the conic geometry responsible for singular electric fields and singular forces or fluxes, and all produce self-similar universal scaling results that are independent of the actual length of the cone. However, unlike the interfacial cones, this thermal analysis involves matched asymptotics instead of local analysis, though the outer length scale does not enter explicitly but only through the angle of the cone due to geometric self-similarity. We use the theory, which depends on only a single dimensionless parameter Z, to obtain scaling laws for our computed steady-state temperature profile within the conic nanopore and our conductance enhancement data from experiments. The collapsed experimental and numerical data then offer very precise estimates of the hot-spot features.

FIG. 1.

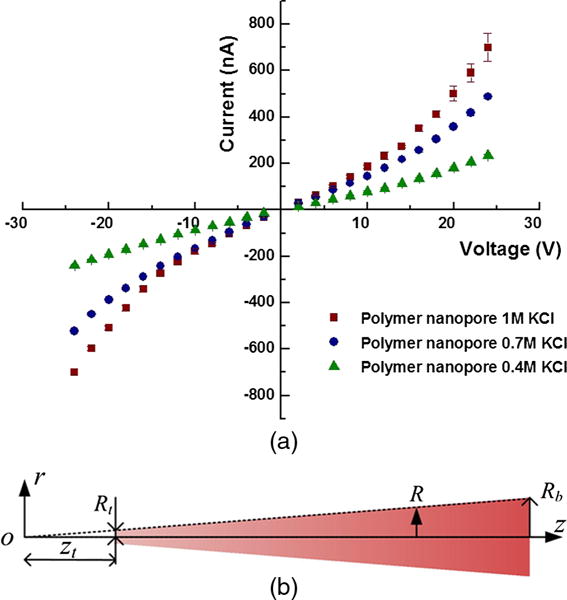
(a) Current voltage characteristic curves for the polymer nanopore. The rectification ratio for all data points is below 1.05. (b) Schematic of temperature profile in the z direction inside a cone with different but self-similar temperature profiles in the r direction at two positions on the cone surface.

Our experiments were done with three kinds of conic nanopores: single polyethylene terephthalate (PET) polymer pores from ion-track irradiation and asymmetric etching [10], silica nanopipettes with a submicron tip radius, and patch pipettes with a 1–3 μm tip radius (for cellular patch-clamp experiments) from laser-assisted pulling. SEM and conductance measurement at room temperature shows a typical tip radius R_t of 5 nm for the polymer conic pores, 100 nm for the silica nanopipettes, and 500 nm for patch pipettes. The inner half angle is 2.6°± 0.15° for our polymer conic pores, 2.5°± 0.3° for our nanopipettes and 4.5°± 0.8° for our patch pipettes. We reduce the surface charge of the silica pipettes with functionalization by N-(3-Triethoxysilylpropyl)gluconamide and validated their low surface charge with ion-current rectification measurements [11]. Fabrication procedures and characterization details are in the Supplemental Material [10,12–14].

Figure 1(a) shows our measured current-voltage characteristic curve of a polymer conic nanopore filled with KCl solutions of different concentrations. A roughly quadratic increase in current is observed with respect to voltage for both biases, and the rectification ratios for all data points of opposite biases are below 1.05. Because surface charge causes higher rectification as the voltage increases [11], the conductance enhancement at higher voltages for both biases must be due to temperature increase inside the pore caused by Ohmic heating. Note that, at the same voltage, conductance enhancement is more significant for electrolytes with higher ionic strength, indicating a higher temperature increase inside the pore. The conductance enhancement is more readily observed if it is normalized by conductance at low voltage when the Ohmic heating effect is negligible. The normalized conductance versus voltage for the polymer nanopore, nanopipette, and patch pipette are plotted in Fig. 2(a).

FIG. 2.

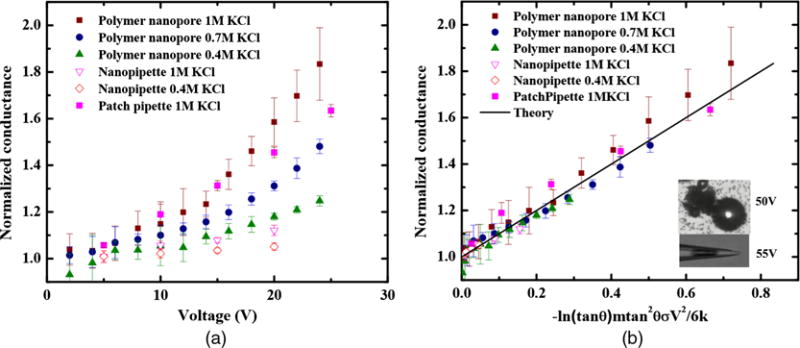
(a) Measured conductance of a single conic nanopore ion-track PET membrane, charge-free nanopipette, and patch pipette, normalized by the zero-voltage conductance of each experiment, as a function of voltage. A quadratic increase with respect to voltage is observed, in violation of Ohmic law with constant conductance. (b) Membrane, nanopipette, and patch pipette data collapsed by the scaling theory into a linear correlation with respect to a normalization factor that contains cone angle θ (2.6°, 2.5° and 4.5° degrees for polymer nanopore, nanopipettes, and patch pipette, respectively), k = 0.15 and 0.6 W m⁻¹ K⁻¹ for the PET membrane pore and the silica pipettes, coefficient of temperature-dependent electrical conductivity m, thermal conductivity outside the cone k, conductivity σ at indicated ionic strength at room temperature, and voltage V. Insets show cavitation in both the nanopore membrane and patch pipette at the corresponding voltages. Cavitating bubbles are first observed within the patch pipette at some distance from the tip, as shown in the second inset, but will eventually grow sufficiently to exit the pipette, as is observed at the membrane surface.

For a slender cone with a half-cone angle of θ, we assume, and check a posteriori, that heat generation in each cone element is balanced by transverse heat loss through side walls. Longitudinal heat flux through the tip will be shown to be smaller than the transverse loss through the side walls by a factor of tan θ ≪ 1, which is small for a slender cone. Based on Gauss’s law, the electric field inside the cone is equal to Vz_t/z², where z_t is the distance from the extrapolated cone apex O to nanopore tip [see Fig. 1(b)] and V is the applied voltage [11]. The heat-generation rate per unit volume is given by σE², where σ is the conductivity of electrolyte and E is the local electric field. The electrolyte is at high ionic strength such that the Debye length is much shorter than the nanopore radius. Consequently, the conductivity is uniform within the nanopore. As such, the temperature gradient in the polar direction on the cone surface can be obtained by relating the heat generation per unit length to the heat loss per unit length, $\left(\partial T/\partial r\right){|}_{r=z\epsilon }-\left[\left(\tan \theta \sigma V^2{z}_t^2\right)/2k\right]\left(1/z^3\right)$, where ε = tan θ is a measure of the slenderness and k is the thermal conductivity outside the cone. The thermal conductivity k for the polymer nanopore is for PET k = 0.15 W m⁻¹ K⁻¹, for water k =0.6 W m⁻¹ K⁻¹, and for silica k = 1.3 W m⁻¹ K⁻¹ [15]. For simplicity, all T represent local temperature difference with respect to the room temperature. We have also neglected electro-osmotic flow or any convection effects on intrapore heat transfer. We have silanized our silica nanopores to reduce electroosmotic flow, but residue surface charge could still exist on the surface. Some reports [16] have shown electro-osmotic velocity in silica conic nanopores as high as 0.3 m=s because of field focusing. However, even with such a high velocity, we estimate our thermal Peclet number for water, UR/α, to be as low as 0.1 near the tip; hence, convective contribution to heat transfer within the conic nanopore is negligible.

Outside the cone, but still within an inner region close to the cone, we study the Laplace equation with the stretched variable ρ = r/εz_t so that the polar coordinate on the cone surface is fixed to be $\overline{z}$, where $\overline{z}=z/z_t$. Using z_t, the longitudinal distance of the tip from the cone apex, as the longitudinal length scale yields a stretched Laplace equation for thermal flux $(1/\rho )(\partial /\partial \rho )\times [\rho (\partial T/\partial \rho )]+{\epsilon }^2[({\partial }^{2}T)/(\partial {\overline{z}}^2)]=0$. The leading-order solution without longitudinal heat flux through the solution is then

$$T(\rho ,\overline{z})~T(\overline{z})+Q(\overline{z})\left(\ln \frac{\rho }{\overline{z}}\right),\rho >\overline{z},$$ (1)

where $T(\overline{z})$ is the unknown temperature on the cone surface. The ln ρ portion arises from the straight cylinder limit (ε → 0). The flux on the cone surface is determined by this term, and balancing with the previously determined Ohmic heat-generation rate at every longitudinal position z allows us to determine the coefficient $Q(\overline{z}).\epsilon z_t(\partial T/\partial r){|}_{r=z\epsilon }=(\partial T/\partial \rho ){|}_{\rho =\overline{z}}=\left[Q(\overline{z})/\overline{z}\right]$. Thus, the line source strength with dimension of temperature is $Q(\overline{z})=-T_{\mathrm{Ohm}}/{\overline{z}}^2$, where T_Ohm = tan²θσV²/2k is the characteristic temperature rise from Ohmic heating at the tip. It corresponds to a virtual sphere at the tip with higher heat loss than the true slender cone. The temperature rise T_Ohm is, hence, an underestimate of the true tip temperature that needs to be corrected with a slender-body-matched asymptotic theory.

Away from the cone, the far-field temperature can be described by the integral formulation with a convolution integral with the Green’s function (single-charge fundamental solution) of the Laplace equation. In the original coordinates, this integral solution that satisfies the far-field condition T(r² + z² → ∞) = 0 is

$$T(r,z)=-{\displaystyle {\int }_{z_t}^{\infty }\frac{q(s)ds}{4\pi \sqrt{r^2+{(z-s)}^2}}}.$$

In the limit of vanishing r, where the cone surface is, this integral has a simple pole at s = z and we can, hence, approximate it by choosing a smaller interval of integration about the pole, r ≪ δ ≪ z_t, such that

$${\displaystyle {\int }_{z_t}^{\infty }\frac{q(s)ds}{4\pi \sqrt{r^2+{(z-s)}^2}}~{\displaystyle {\int }_{z-\delta }^{z+\delta }\frac{q(s)ds}{4\pi \sqrt{r^2+{(z-s)}^2}}}}={\displaystyle {\int }_{-\delta /r}^{\delta /r}\frac{q(z+rt)dt}{4\pi \sqrt{1+t^2}}}$$

after a change of variable s = z+rt. Expanding about r = 0 and respecting the relative scaling between z and r, we obtain

$$T(r,z)~-\frac{q(z)}{2\pi }{\displaystyle {\int }_0^{\delta /r}\frac{dt}{\sqrt{1+t^2}}~-\frac{q(z)}{2\pi }\ln (2\delta /r).}$$ (2)

The finite temperature of the integral solution of a finite cone approaches an asymptote at r = 0 that has the singular limits (at both vanishing r and infinite r) of an infinite cylinder, and z is of the order specified by δ. This limiting asymptote is of the form in Eq. (1) and, hence, allows matching between the two solutions. One can use the intermediate coordinate of Hinch [7] to match Eqs. (1) and (2) and relate q(z)/2π to $Q(\overline{z})$ in the intermediate region at the surface of the tip where r = εz ~ εz_t. It is, however, quite obvious by inspection that $T(\overline{z})\sim Q(\overline{z})$ ln ε and

$$T(\overline{z})~\frac{T_H}{{\overline{z}}^2}=-\ln (\tan \theta )\frac{T_{\mathrm{Ohm}}}{{\overline{z}}^2}.$$ (3)

Through matching, the slender-body heat loss to the bulk has introduced a − ln ε = − ln(tan θ) correction to the original characteristic temperature rise T_Ohm, to obtain a new temperature rise T_H with proper respect to the nearly cylindrical geometry and the ln r fundamental solution.

Although there exists a finite normal gradient at the cone surface (∂T/∂r)|_r=εz, the gradient resides in a thin boundary layer of thickness εR and the temperature is uniform to leading order within most of the local cross section of radius R. The temperature drop across this thin boundary layer is hence small (of order R) compared to the bulk temperature, and one can use the value on the cone surface from Eq. (3) to approximate the temperature within the conic pore.

The conductivity has a temperature dependence of σ = [mT(z) + 1]σ₀, where the conductivity expansion coefficient for aqueous electrolyte is m = 0.02K⁻¹ =1/T_m [17] for water and σ₀ has a linear concentration dependence. The normalized conductance of the cone can be derived from the integration of the equation $\kappa /{\kappa }_0={\displaystyle {\int }_1^{\infty }(1/{\sigma }_0){\overline{z}}^{2}d\overline{z}/{\displaystyle {\int }_1^{\infty }(1/\sigma {\overline{z}}^2)d\overline{z}}}$. When T_H=T_m is small, such that the conductivity does not increase significantly, the expression can be simplified as

$$\frac{\kappa }{{\kappa }_0}=1+\frac{T_H}{3T_m}=1+Z,$$ (4)

where Z = − ln(tan θ)mtan²θσV²/6k. Figure 2(a) shows experimental data of normalized conductance for the polymer nanopore, nanopipette, and patch pipette, showing varying degrees of enhancement when measured at the same voltage. Figure 2(b) shows data to collapse with Eq. (4).

One of the most important results from the slender-body theory is that it provides a way to estimate the temperature inside the cone from normalized conductance even with an unknown cone angle and thermal conductivity. Based on Eqs. (3) and (4), the temperature rise normalized by $T_m/{(\overline{z})}^2$ for any longitudinal z coordinate has a universal linear scaling relationship with respect to the normalized conductance, with a universal slope of 3. The matched asymptotic analysis breaks down at some neighborhoods of the conic tip, where a significant heat loss in the longitudinal direction that is not captured in the current slender-body theory dominates. The temperature, hence, does not increase monotonically towards the tip $\overline{z}=1$, as predicted by Eq. (3), but exhibits a maximum at some distance from the tip. Nonetheless, due to the self-similarity of the conic geometry and the universal validity of the focused Ohmic heating scaling, we expect the hot-spot location to be universal, and the normalized hot-spot temperature to exhibit the same universal scaling of 3 with respect to the normalized conductance.

We have numerically solved the steady-state inhomogeneous heat equation with an Ohmic heating source for polymer nanopore and nanopipette geometry of different cone angles using COMSOL MULTIPHYSICS v3.5a. The temperature dependence of the electrical conductivity of the electrolyte and all physical parameters used in the simulation are the same as those used in the collapse in Fig. 2(b). The simulated data are also collapsed by Eq. (4). The normalized conductances are plotted against the maximum temperature rise normalized by $T_m/{(\overline{z})}^2$ for various conic geometries in Fig. 3. The universal slope is found to be equal to 3 when $\overline{z}=1.2$, which agrees well with the actual position of the maximum temperature increase from the simulation results. This empirically established universality then allows us to predict the hot-spot temperature from Eq. (3) with $\overline{z}=1.2$.

FIG. 3.

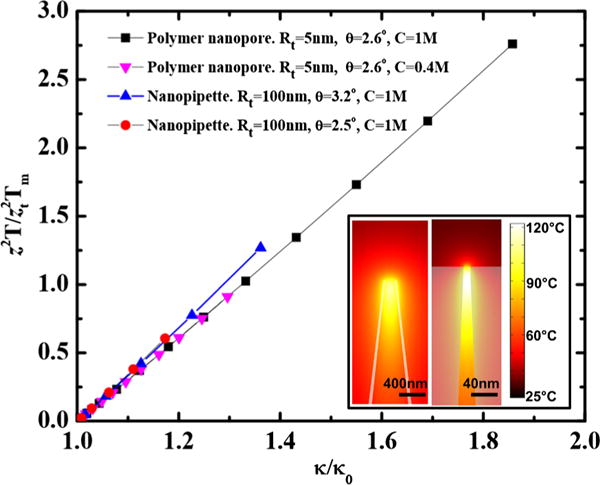
Collapse of simulation result of highest temperature vs normalized conductance for the nanopipette and nanopore with voltages ranging from 2V to 25V. R_t indicates tip radius, which varies by a factor of 20 from polymer nanopores to nanopipettes. C indicates molarity of KCl. Contour plots of the temperature near the tip of the nanopipette and polymer nanopore at 24V are shown in the inset. Room temperature is 25 °C.

That the hot-spot length is of order z_t, the longitudinal distance of the tip from the cone apex, also allows us to validate our negligence of the longitudinal heat flux through the tip. Using the point-source solution of the Laplace equation, the radial heat flux density from the tip scales as k(R_t/r²), where r is the spherical radial coordinate from the tip and R_t is the tip radius. As such, the total longitudinal thermal diffusive flux into the solution scales as πkR_t/2. Using the line source solution in Eq. (2), the transverse heat flux through the wall scales as k(1/r), where r here is the cylindrical radial coordinate transverse to the cone, and the total transverse flux out of the wall scales as 2πkz_t, using the confirmed longitudinal length scale of the hot spot from Fig. 4. Because R_t/z_t = tan θ = ε ≪ 1 for a slender cone, the longitudinal flux into the solution is negligible compared to the radial flux through the side wall.

FIG. 4.

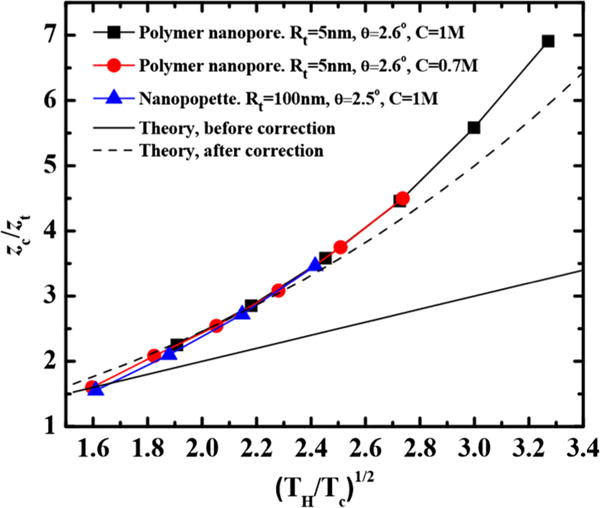
Simulation results of the cutoff position for different voltages and cone geometry using a cutoff temperature rise of 15 °C. The theory that does not account for varying conductivity inside the cone is only valid at low voltages when conductivity variation throughout the cone is small. Once conductivity variation is considered, the theory is valid at both high and low temperatures.

After defining an arbitrary cutoff temperature rise T_c =15 °C to estimate the dimension of the hot spot, we find in Fig. 4 that the theory estimates the lower temperatures well at low T_H, but breaks down at high voltages or large T_H. This error is due to the omission of the nonlinear conductivity variation in the Ohmic heating of our theory. A next-order correction (in the conductivity increase Z) can be made with E = [Vz_t(1 + Z)]/z² [1 + T(z)/T_m], where (1 + Z) accounts for the overall conductivity increase and $[1+T(\overline{z})/T_m]$ balances the current along the cone with varying local electrical conductivity. Using the same asymptotic matching, the expression for the temperature becomes: $T(z)=T_m[\sqrt{4{(1+Z)}^2{T}_H/T_m+{\overline{z}}^2}/2\overline{z}-1/2]$, which represents a higher-order correction to Eq. (3). The position ${\overline{z}}_c$ of the cutoff temperature T_c where $T(\overline{z})=T_c$ is then ${\overline{z}}_c=(1+Z)/\sqrt{(1+T_c/T_m)T_c/T_H}$. This higher-correction collapses the large voltage simulation results in Fig. 4 and offers an estimate of the hot-spot dimension. Using the same cutoff temperature rise of 15 °C, at low Z (T_H/T_m < 1), the thermal hot-spot dimension is quantitatively less than z_t, or less than 100 nm for the membrane nanopore and 2 μm for the nanopipette.