Abstract
The control of spins and spin to charge conversion in organics requires understanding the molecular spin-orbit coupling (SOC), and a means to tune its strength. However, quantifying SOC strengths indirectly through spin relaxation effects has proven difficult due to competing relaxation mechanisms. Here we present a systematic study of the g-tensor shift in molecular semiconductors and link it directly to the SOC strength in a series of high-mobility molecular semiconductors with strong potential for future devices. The results demonstrate a rich variability of the molecular g-shifts with the effective SOC, depending on subtle aspects of molecular composition and structure. We correlate the above g-shifts to spin-lattice relaxation times over four orders of magnitude, from 200 to 0.15 μs, for isolated molecules in solution and relate our findings for isolated molecules in solution to the spin relaxation mechanisms that are likely to be relevant in solid state systems.
Organic semiconductors with long spin lifetime hold promise for future spintronics devices that can process and store information. Here, Schott et al. perform a systematic study of the strength of spin-orbit coupling and its effect on spin lifetime over 32 promising molecules with high charge mobility.
Organic semiconductors and conductors are enabling flexible, large-area optoelectronic devices, such as organic light-emitting diodes, transistors and solar cells. Due to their exceptionally long spin lifetimes, these carbon-based materials could also have an impact on spintronics, where carrier spins play a key role in transmitting, processing and storing information1. The recently observed inverse spin hall effect in organics2,3, the conversion of a spin current to a transverse charge current, potentially enables fully organic spintronics devices.
Spin-orbit coupling (SOC), a relativistic effect which couples the charge's angular momentum to its spin, plays a dual role in such devices: it drives the spin to charge conversion and also provides a pathway for spin relaxation. Despite its fundamental importance for device applications, quantifying SOC strengths in organics based on investigating spin relaxation has proven difficult due to the competing and hard to distinguish contribution from hyperfine interactions (HFI)4, the coupling of the charge's spin to nuclear spins. In fact, both SOC and HFI have been used separately to explain the magnetoresistance5 and spin diffusion length6 in spin valves of the same organic material.
The comparison of spin diffusion lengths λS on the other hand has indeed revealed significant variations between different organic semiconductors5,7,8 but separating effects of the charge carrier mobility and density9 from the spin's coupling to its environment remains challenging. In addition, organic spin valve measurements can be affected by tunnelling magneto resistance through pin hole defects10, which complicates an accurate determintion of λS.
A more direct probe of SOC is the voltage generated by spin to charge conversion (inverse spin hall effect voltage). However, such measurements often only provide the product of λS and the spin Hall angle3 and are prone to artefacts11. A systematic quantitative study of SOC strengths has therefore been hindered by the difficulty in isolating the effect of SOC on spin lifetimes, diffusion lengths or inverse spin hall voltages.
In this work we show that the g-factor (the isotropic part of a spin's coupling to an external magnetic field) of an unpaired spin from a charged molecule can be used as a measure of the effective SOC, over a wide range of SOC strengths. By effective SOC, we mean the overlap between the orbital- and spin angular momentum distributions, which respectively depend on the molecular composition and geometry, and the spin density in the charged molecule. Shifts of the g-factor from its free electron value (Δg) arise from SOC and orbital Zeeman terms in the Hamiltonian and are easily accessible by electron spin resonance (ESR). This provides a method to quickly and unambiguously determine the effective SOC over a wide range of light molecules without relying on indirect measurements. Our results demonstrate a remarkably rich variability—and therefore, potential for purposeful tuning—of molecular g-factors with subtle aspects of the molecular structure and composition.
In the second part of this communication, we correlate the above g-shifts to spin-lattice relaxation times determined by power saturation ESR measurements and demonstrate a change in spin lifetimes over four orders of magnitude, from 200 to 0.15 μs, with increasing Δg. This suggests that the change in g-factor can be indeed attributed to an increase in SOC and a corresponding reduction of the spin lattice relaxation time T1.
While our simulations and measurements were all performed on isolated molecules, we argue that the gained information will be valuable to understand bulk systems, which in these systems are strongly influenced by the single molecule properties.
Results
Materials overview
We compare a set of 32 fused-ring molecular semiconductors with systematically varying geometries and atomic substitutions, most of which are based on central thiophene or selenophene moieties that are commonly found in high-mobility organic semiconductors. Many of the chosen molecules such as 2,7-dioctyl[1]benzothieno[3,2–b][1]benzothiophene (C8-BTBT), 2,9-didecyl-dinaphtho[2,3-b:2′,3′-f]thieno[3,2–b]thiophene (C10-DNTT) or rubrene are widely studied and perform exceptionally well in organic thin film transistors with hole mobilities of 5–10 cm2 V−1 s−1 and signs of coherent charge transport such as a metallic Hall effect12 and a band-like temperature dependence of the mobility13. Since high charge carrier mobilites are expected to improve spin diffusion lengths1 and the spin Hall angle is predicted to increase with reduced energetic disorder14, such systems are natural candidates for spintronics applications. Hence, the chosen series of molecules offers a unique opportunity to systematically study the strength of SOC and its effect on spin lifetimes.
All ESR measurements were performed on radical cations in solution. To quantitatively understand these measurements we have performed density functional theory (DFT) calculations on positively charged molecules in the gas phase. This enables us to calculate spin density distributions with an accuracy that is not achievable for bulk systems and to experimentally resolve the HFI splitting of resonance lines. The latter acts as a probe of the spin density at nuclear coordinates throughout the molecule and provides an experimental method to validate the spin density calculations.
Experimental g-shifts in organic molecules
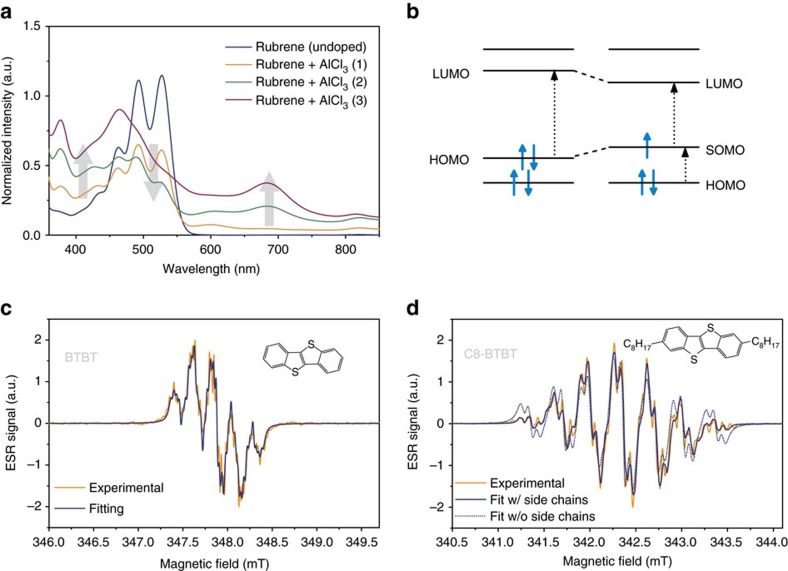
To achieve controllable experimental conditions with spin densities that can be reasonably compared to DFT calculations, we performed all ESR experiments on highly dilute solutions of radical cations in dichloromethane confined in capillary tubes at the cavity centre. The neutral molecules were oxidized in solution by adding aluminium chloride (AlCl3) and the successful p-type doping was confirmed by optical spectroscopy (Fig. 1a,b)15. All ESR spectra were recorded on a Bruker E500 X-band spectraometer and as lock-in measurements with an external magnetic field modulation at 100 kHz. They therefore show the derivatives of the microwave absorption spectra. All experimental details are given in the Methods section.
Figure 1. ESR and optical spectra of doped molecules.
(a) Optical absorption spectra of a 0.5 × 10−3 mol l−1 solution of rubrene in dichloromethane with increasing amounts of AlCl3 (traces 1–3). We observe the expected bleaching of the transition between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) together with the emergence of charge induced transitions in the sub band gap regime from the HOMO to the singly occupied molecular orbital (SOMO). The grey arrows emphasize the increase of charge induced absorption and the decrease of the neutral molecule absorption peaks with higher doping levels. (b) A schematic of energy levels with possible optical transitions for a neutral and positively charged molecule. The shifts of the HOMO and LUMO energy levels reflects the reorganization of the molecular geometry to accommodate the charge. (c,d) Derivative ESR spectra of BTBT and C8-BTBT with best fits including (solid line) or excluding (dashed line) HFI from the first two hydrogens on the side chains.
ESR measures the resonant absorption of microwaves between Zeeman split energy levels in an external magnetic field B. The rapid motion of molecules in a solution causes an averaging over the anisotropic terms in the spin Hamiltonian so that the resulting resonances arise from
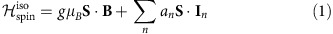 |
where the isotropic HFI couplings an for the nuclear spin In are proportional to the spin density at the nth nucleus. As a result, we observe symmetric spectra where the isotropic g-factor g=ℏω/μBB0 is directly given by the microwave frequency ω and the resonance centre B0 (2πℏ, Planck's constant). The isotropic HFI additionally causes a splitting of resonance lines proportional to an.
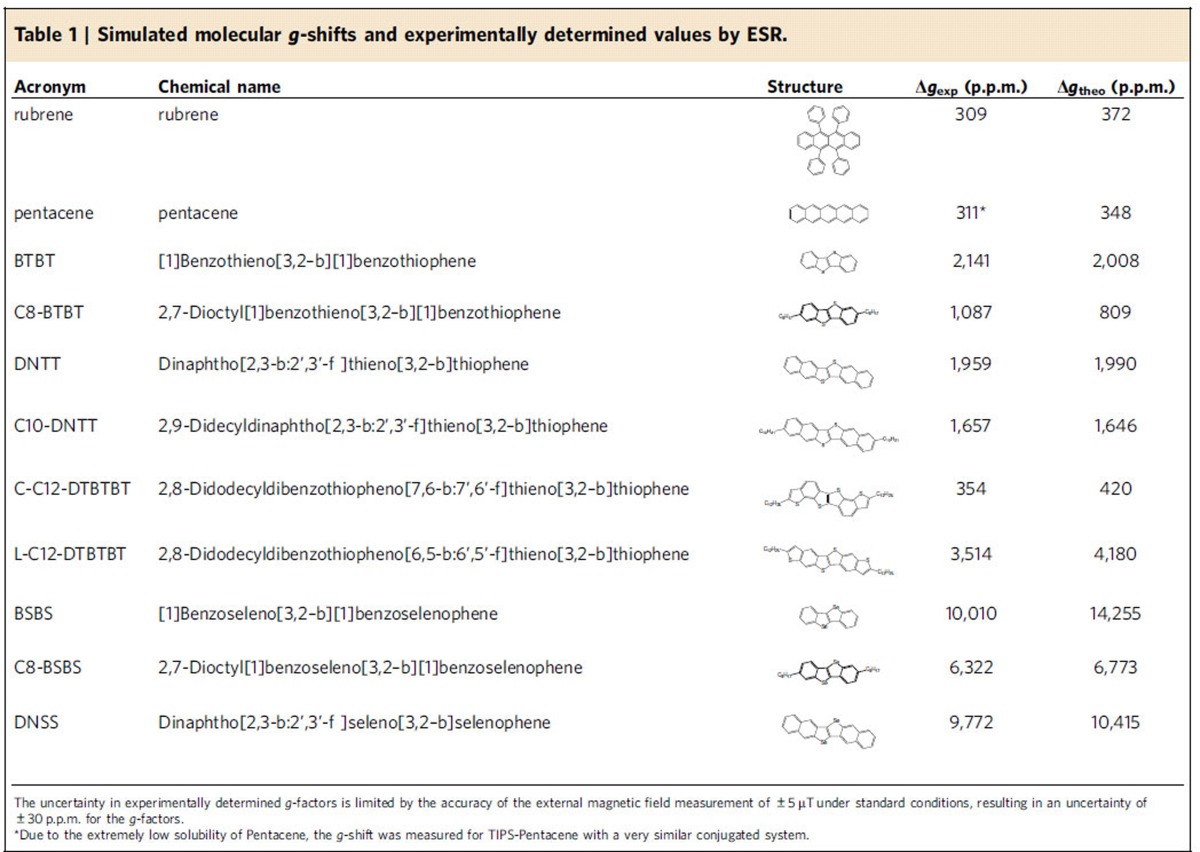
The experimentally investigated molecular structures and their measured and calculated isotropic g-shifts gexp and gtheo are summarized in Table 1; the corresponding ESR spectra are shown in Supplementary Fig. 1. The series begins with the pure hydrocarbons rubrene and pentacene that are expected to show very weak SOC. The remaining set of molecules is based on the BTBT structure, which incorporates heavier sulfur atoms in two central thiophene units. For maximum consistency and rigour, theoretical calculations were performed on a set of systematic variations of this structure, including extending it with a single set of phenyl rings to form dinaphtho[2,3-b:2′,3′-f]thieno[3,2–b]thiophene (DNTT), or two sets to form dinanthra[2,3-b:2′,3′-f]thieno[3,2–b]thiophene (DATT), adding a set of outer thiophene rings (dibenzothiopheno-thieno-thiophene, DTBTBT) in a curved (C-DTBTBT) or linear (L-DTBTBT) geometry and substituting the sulfur in all of these with selenium (BSBS, DNSS, DSBSBS and so on) for a total of 10 distinct geometries. Each of these structures was additionally examined with insulating alkyl chains attached to the outer phenyl or thiophene units (C8-BSBS, C10-DNTT and so on) and with the same side chains shifted one position closer to the closest central sulfur atom (labelled C8s-BTBT and so on, see Fig. 2a for the labelling of side chain positions), in total adding up to 32 distinct molecules. Supplementary Table 1 provides a complete list of all molecular names, structures and the corresponding acronyms.
Table 1. Simulated molecular g-shifts and experimentally determined values by ESR.
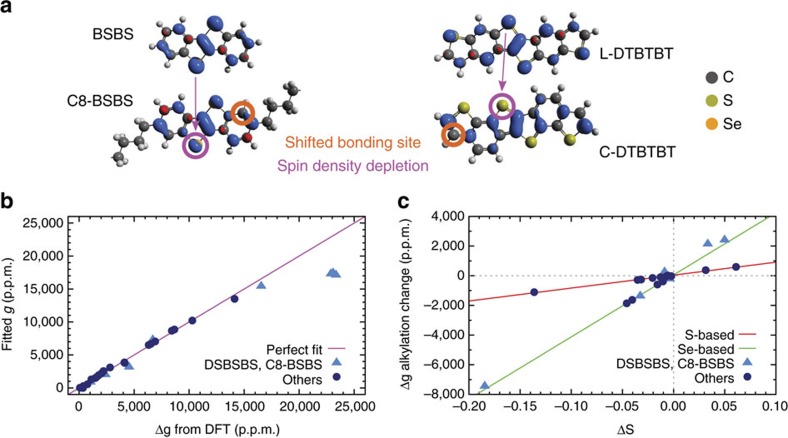
Figure 2. Relationship between g-shift and atomic spin densities.
(a) Spin isodensity contours of cationic (left) BSBS and C8-BSBS, and (right) L-DTBTBT and C-DTBTBT radicals. The C8-BSBS molecule shown has alkyl chains at the outer bonding site. Spin maxima and minima are shown in blue and red, respectively. The shifted bonding site at the phenyl rings has been labelled, and the observed spin depletion at heavy atoms highlighted. Note that only part of the alkyl chains in C8-BSBS are shown. (b) Correlation plot of ΔgOZ/SOC-terms calculated using DFT versus fitted on the form of equation 3. The outliers identified in the text are shown as light blue triangles, with the other numbers represented by dark blue circles. The magenta line y=x represents a perfect fit. For brevity ΔgOZ/SOC has here been relabelled Δg. (c) Plot of changes in ΔgOZ/SOC terms as a function of change of effective heavy atom spin upon alkylation of molecules (see text). Red and green lines represent linear fits to the sulfur- and selenium-based molecules, respectively.
From those 32 molecules, our experimental data is limited to the 11 molecules shown in Table 1 that were physically available. While those molecules have alkyl chain lengths between C8 and C12, all calculations were performed with C8 chains as explained in the Supplementary Note 1.
Some of the g-factor changes follow expected trends. As expected for holes in the highest occupied molecular orbital (HOMO) level with a strong coupling to lower lying σ-orbitals, all g-factors show positive shifts relative to the free electron value ge≈2.002319. The light-element molecules pentacene and rubrene show g-factors close to ge and we see an increase of the g-shift by almost one order of magnitude for BTBT or DNTT with the inclusion of heavier sulfur atoms. Consistently, the next significant jump to ∼104 p.p.m. takes place for BSBS and DNSS when replacing sulfur by selenium, reflecting the stronger SOC of selenium. On the other hand, there is only a minuscule decrease in Δg, on the order of 100 p.p.m., with the addition of phenyl rings on either side of the molecule (BTBT→DNTT or BSBS→DNSS).
Other changes are more surprising. The addition of (insulating) alkyl chains to a molecule does not introduce or remove any atoms with strong SOC from the π-conjugated system, nor should it significantly alter the electronic structure of the latter16. Nevertheless, the g-shift is reduced by half with the introduction of side chains for BTBT→C8-BTBT and by about one quarter for DNTT→C10-DNTT.
To understand the origin of this reduction in Δg, we can exploit the isotropic HFI from the hydrogen nuclei as local probes of the spin density throughout the molecule. We determine the HFI coupling constants from the derivative ESR spectra by diagonalizing the spin Hamiltonian from equation 1 and convoluting the obtained resonance positions with a Lorentzian line to account for the finite line widths. The resulting resonance spectrum is then fitted to the experimental ESR spectrum, as shown in Fig. 1c.
When fitting the spectra of molecules with attached side chains, we had to include the HFI from the first two hydrogens on each side chain in order to reproduce the spectral shape (Fig. 1d for C8-BTBT and Supplementary Fig. 1). The number of hydrogens included in the fit provides clear experimental evidence for a spin density that leaks out onto the side chains and an accompanying change of the spin density distribution on the molecule.
Another striking experimental observation is the large difference in g-shifts between C-C12-DTBTBT and L-C12-DTBTBT. Both molecules are composed of exactly the same atoms and their only difference lies in the position of the outer thiophene units, either introducing a curve (C-C12-DTBTBT) or providing a more linear geometry (L-C12-DTBTBT). Even though both molecules contain four sulfur atoms, the g-shift changes from ∼4,000 to ∼400 p.p.m., when switching from the linear to the curved isomer. This arises from the difference in spin density distributions between the two molecules, as revealed by the changing HFI splitting in the ESR spectra (Supplementary Fig. 1), and is fully consistent with the molecular modelling discussed below.
The changes of the spin density distribution with alkylation, observed indirectly via the HFI, or the introduction of a curvature in the molecule suggest a strong dependance of the g-shift not only on the atomic composition of the molecules but also their geometries and the resulting spin densities. However, we cannot distinguish HFI couplings from different hydrogens experimentally unless they have different numbers of equivalent nuclei17 and common sulfur or selenium isotopes have zero nuclear spins. DFT modelling on the other hand can provide an accurate, spatially resolved picture of the spin wave functions in the molecule.
DFT modelling of g-shifts and spin densities
To explain the experimental results above, and investigate the importance of the spin density distribution for Δg, we performed state-of-the-art DFT calculations of molecular g-tensors and spin densities. We have chosen an all-electron, hybrid exchange-correlation functional DFT level of theory, which also accounts for scalar relativistic and spin-orbit coupling effects. All computational details can be found in the Methods section and in Supplementary Note 1.
As evident from Table 1, the accuracy of the theoretically predicted Δg is generally excellent, validating the quality of our methodology. The only significant discrepancy is found for BSBS as discussed in Supplementary Note 2 (Supplementary Fig. 3). In each of these calculations, the spin density in the cationic radical was calculated, plotted and visualized, as shown in Fig. 2a.
In the left of this figure, the qualitative effect of alkylation at the outer bonding site is shown using BSBS as an example. The effect is identical for the sulfur-based analogues, and similar but weaker in DNTT, DNSS, DATT and DASS. We attribute the reduced magnitude of the effect to the weaker charge confinement in these molecules.
In essence, the significant spin maximum (blue contour) at the outer bonding site causes the spin density to leak onto the alkyl chain, resulting in a net spin density depletion at the heavy atoms, visible in Fig. 2a as a diminished contour at the heavy atom site. Moving the alkyl chain to the shifted bonding site, which in the base molecule shows a spin density minimum (red contour) has a negligible or weakly opposite effect on the heavy atom spin density.
In the right of Fig. 2a, the effect of the geometry on the DTBTBT spin density is similarly shown, with the heavy atoms all but entirely depleted in the curved species. The same is observed in DSBSBS.
Comparing this visual analysis to the corresponding trends in g-shifts in Table 1 confirms the experimentally established picture of the spin density weight at heavy atoms, that is, the overlap of orbital and spin angular momentum distributions, as the key quantity for understanding g-shifts in this class of molecules. To verify this qualitative analysis, we proceed to build a quantitative model of the dependence of Δg on the spin density. In the formulation of Neese18, the molecular Δg can be written as
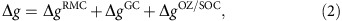 |
where ΔgRMC is a relativistic mass correction, ΔgGC is a diamagnetic gauge correction, and ΔgOZ/SOC is a cross-term between the orbital Zeeman and spin-orbit coupling operators corresponding to the mixed derivative of the molecular total energy with respect to the electron magnetic moment and external magnetic field18. The first of these terms, like other relativistic effects, is generally negligibly small in light organic molecules. The second term is in the current set of molecules also comparably small and of opposite sign, nearly cancelling the first term. g-shifts in this set are therefore virtually identical to the third term, ΔgOZ/SOC.
To establish a quantitative model that relates the g-shift to the spin density distribution, we use an Ansatz with a linear dependence of ΔgOZ/SOC on the local spin density at each atom:
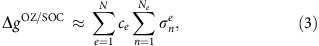 |
Here, 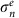 is the effective spin at atom n of element e, Ne is the number of atoms of that element in the molecule, N is the number of different elements and ce is a proportionality constant of element e. The effective atomic spin
is the effective spin at atom n of element e, Ne is the number of atoms of that element in the molecule, N is the number of different elements and ce is a proportionality constant of element e. The effective atomic spin 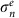 is here treated in units of electronic spin (that is, on the scale of
is here treated in units of electronic spin (that is, on the scale of 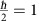 ), and therefore as dimensionless. The proportionality constants represent the net effect of the orbital angular momentum operators in ΔgOZ/SOC. This model then describes g-shifts as dependent on the overlap of orbital and spin angular momentum distributions, or equivalently, an effective spin-orbit coupling. We prove its validity by studying the correlation between g-shifts calculated from DFT, and shifts fitted to the same on the form of equation 3.
), and therefore as dimensionless. The proportionality constants represent the net effect of the orbital angular momentum operators in ΔgOZ/SOC. This model then describes g-shifts as dependent on the overlap of orbital and spin angular momentum distributions, or equivalently, an effective spin-orbit coupling. We prove its validity by studying the correlation between g-shifts calculated from DFT, and shifts fitted to the same on the form of equation 3.
The results of this fit are shown in a correlation plot in Fig. 2 and the fit coefficients ce are given in Supplementary Table 2. Using the coefficient of determination, or ‘R2-value' as a quality measure of the fit, we note that a straight fit of atomic spins to calculated ΔgOZ/SOC values of the full 32 molecule set yields a fairly low R2 of 0.960. For a strictly linear statistical hypothesis, this is unconvincing. However, the statistic is straightforwardly divided into (a) eight outliers consisting of all the Se-substituted DTBTBT molecules (that is, {C-,L-}{C8-,C8s-}DSBSBS), and the alkyl-functionalized, Se-substituted BTBT molecules ({C8-,C8s-}BSBS), and (b) the 24 molecules in the rest of the set. The outliers and the rest are shown in Fig. 2b as light blue triangles and darker blue circles, respectively. Excluding the outliers from the fit yields a very high R2 of 0.996, showing that the model works well for the pure hydrocarbons, all the sulfur-based molecules, the non-functionalized BSBS molecule, and all variations of the DNSS and DASS molecules.
The reason why the Ansatz of equation 3 works better for sulfur than selenium is the non-local terms scaling with the smaller orbital angular momentum in the former. Furthermore, the dual heavy-atom structure in the DSBSBS molecules significantly complicates their electronic structure, with much larger non-local terms compared to the other, simpler molecules. The alkyl-functionalized BSBS molecules are also included in the outliers because the positive charge is much more strongly confined in BSBS than in the larger DNSS and DASS. As will be elaborated below, the spin density of BSBS is consequentially more strongly perturbed when chains are added, leading to stronger non-local interactions and violating the premises of the linear model.
With the range of applicability of this model thus established, we continue by applying it to studying the effect of alkyl-chain functionalization. In Fig. 2c, the difference in ΔgOZ/SOC upon alkylation has been plotted, as a function of the corresponding difference ΔS in effective spin at the heavy atoms of the molecule. For clarity, the sets of outliers and the rest in Fig. 2b have been coloured the same way.
Two things stand out in Fig. 2c. First, the relationship between the change in the spin density on the sulfur-atoms and the change in g-shift on alkylation is linear. This fact explains the, in parts, dramatic alkylation effects on g-shifts. Such large shifts occur when the alkyl chain bonds to a site where the spin density is large in the non-functionalized molecule. The spin density will then spread partly into the chain and will be reduced on the heavy atom, hence allowing for tuning of the effective spin-orbit coupling by targeted alkylation.
Second, the outliers of Fig. 2b are now a much better fit in Fig. 2c. This is due to some non-local terms cancelling when differences are taken between alkylated and non-alkylated g-shifts. Of the outliers, C8-BSBS and C8 s-BSBS respectively exhibit the strongest decrease and increase of spin at the heavy atoms, and are found in Fig. 2c at either extreme of the Se-based statistic. As explained above, this strong alkylation effect is attributed to the confinement of the electron hole in the small BSBS molecule leading to a large shift of the spin density distribution. This point is additionally reinforced by the Se-based molecules not among the outliers: For C8-DNSS and C8 s-DNSS, the electrons are less confined to begin with and the effect of attaching an alkyl chain is therefore less pronounced.
Relationship between g-shift and spin lifetimes
In the previous section, we have argued that the g-shift can be correlated to an effective SOC over a wide range of g-factors. This series of molecules therefore presents a unique opportunity to systematically study the effect of SOC on spin lifetimes. We show in the following that the spin lattice relaxation time T1 indeed scales with Δg over four orders of magnitude and interpret this in the framework of the Bloch-Wagness-Redfield theory of spin relaxation.
The majority of reported experimental architectures in (organic) spintronics employ an external magnetic field B to either generate or control and manipulate spins inside the target material. The employed fields of 10–400 mT (refs 19, 20) are on the same order or smaller than in ESR measurements. In the presence of an external field one must distinguish between longitudinal and transverse spin relaxation. The first manifests itself macroscopically as the decay of the sample magnetization parallel to B and requires transitions between the Zeeman split spin-up and spin-down states. This implies an exchange of energy with the spin's environment (the ‘lattice') and is characterized by the spin lattice relaxation time T1. The decay of the transverse magnetization is characterized by the coherence time T2. It results from spin dephasing and can occur in an energetically neutral process. A long T2 enables the coherent manipulation of spins while a large T1 is crucial to maintain a spin polarization along a preferred axis.
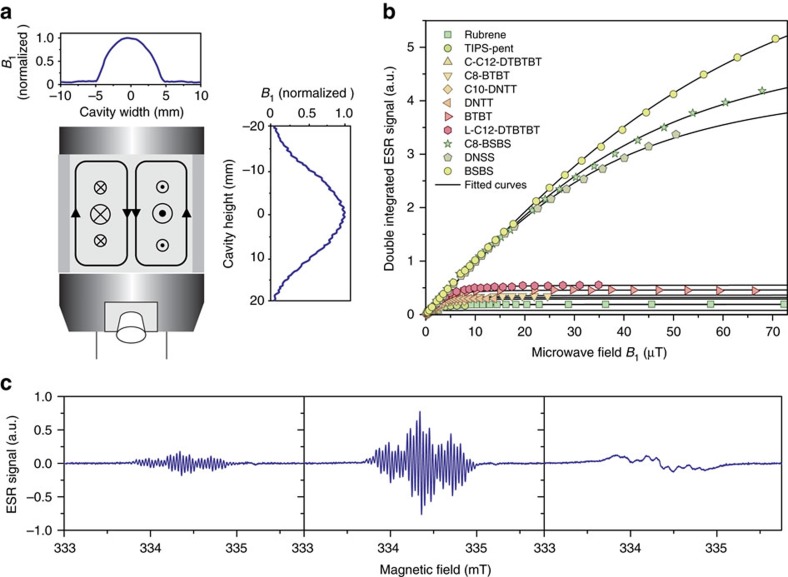
We determine T1 and T2 from the power saturation behaviour of the ESR resonances (Fig. 3) and the unsaturated line width, respectively, as described in Supplementary Note 3. This requires both a sufficiently large microwave field B1 and an exact knowledge of the latter over the sample volume. We therefore minimize the variation of B1 by confining the sample to a capillary tube at the cavity centre and account for the lateral field distribution across the sample, as shown in Fig. 3 and Supplementary Fig. 3.
Figure 3. Power-saturation measurement of spin lifetimes.
(a) Schematic of the Bruker ER 4122SHQE cavity with microwave magnetic and electric fields in-plane and out-of-plane, respectively. Plot insets show the magnetic field strength across the cavity. We account for the vertical distribution of B1 and minimize horizontal variations by confining our samples to a diameter of 1 mm. (b) Power saturation of the integrated ESR absorption spectra for the series of molecules with fitted curves to extract T1 and T2. (c) Evolution of derivative ESR spectrum with increasing microwave powers for the example of L-C12-DTBTBT.
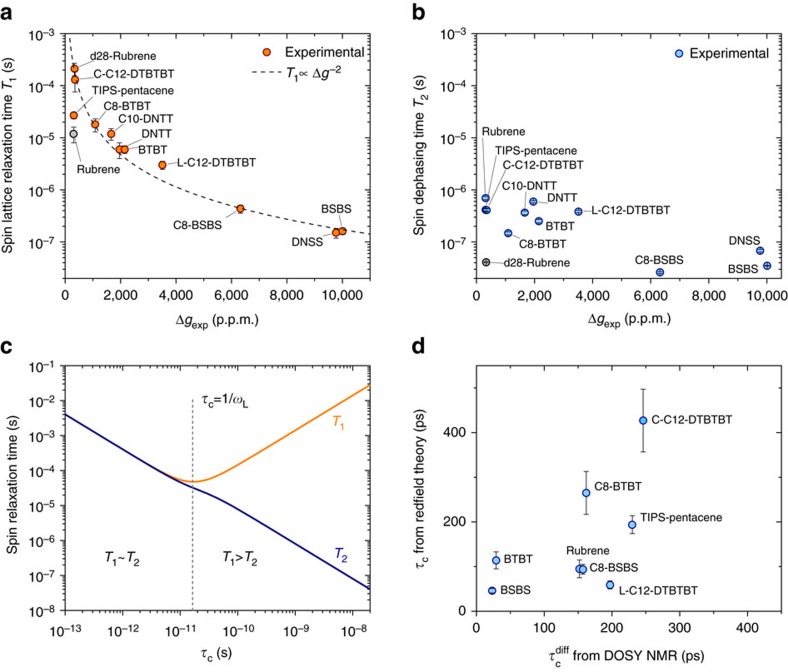
The resulting values for T1 reveal a strong correlation between spin lattice relaxation times and g-shifts: we observe a change in T1 over four orders of magnitude, from 212 μs for molecules with small g-shifts (for example, C-C12-DTBTBT) down to 0.15 μs (BSBS, DNSS) for the largest g-shifts (Fig. 4a). This demonstrates the impact of tuning the g-factor beyond changing the coupling of a spin to the external magnetic field. By increasing the spin density at selenium or sulfur atoms, we increase the effective SOC for the spin and as result the transition rate between spin-up and spin-down levels increases as well.
Figure 4. Dependance of spin relaxation times on the effective SOC.
(a) Spin lattice relaxation time versus Δg for all measured molecules. Error bars represent 95% confidence intervals. Dashed line shows the expected proportionality T1∝(Δg)−2 for relaxation via SOC fields. (b) Spin coherence time versus Δg for all measured molecules. Error bars show the 95% confidence intervals. (c) Dependence of T1 and T2 on the correlation time τC of field fluctuations from the Redfield theory. Model values of ωL/2π=9.4 GHz and 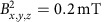 were used for the plot. (d) Correlation times τC as estimated from the Redfield theory and plotted against rotational correlation times obtained from DOSY NMR diffusion constants (when available). Error bars from 95% confidence intervals of T1 and T2 and error propagation.
were used for the plot. (d) Correlation times τC as estimated from the Redfield theory and plotted against rotational correlation times obtained from DOSY NMR diffusion constants (when available). Error bars from 95% confidence intervals of T1 and T2 and error propagation.
The spin coherence times, T2, are systematically smaller than T1 and show a less pronounced dependence on Δg and a larger scatter of values. This can be understood when considering the underlying mechanism that contribute to T2. A spin couples to its environment via magnetic fields and the exchange of energy required for spin lattice relaxation implies that the transitions between Zeeman levels are induced by fluctuating fields. Those typically are internal HFI and SOC fields which fluctuate with lattice vibrations, the tumbling motion of molecules in a solution or (in the rest frame of the spin) due to the spatial motion of the charge carrier in a solid state system. In the framework of the Bloch–Wagness–Redfield theory21,22, those fields are treated classically by adding a time dependent perturbation 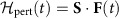 to the spin Hamiltonian and examining the spectral densities kx,y,z(ω) of the fluctuating fields Fx,y,z(t). The spin lattice relaxation time then depends on the spectral density at the Larmor frequency ωL=γeB while the spin coherence time includes an additional contribution from k(0)22:
to the spin Hamiltonian and examining the spectral densities kx,y,z(ω) of the fluctuating fields Fx,y,z(t). The spin lattice relaxation time then depends on the spectral density at the Larmor frequency ωL=γeB while the spin coherence time includes an additional contribution from k(0)22:
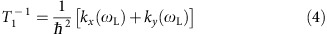 |
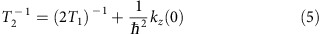 |
Equations 4 and 5 imply that T2≲T1, which is consistent with our measured values. We also see that T2 is susceptible to static local variations such as small inhomogeneities in the external magnetic field. This effectively creates an upper bound for T2 or equivalently a lower bound for the line width (∼3 × 10−3 mT) and introduces larger fluctuations between measurements, for example, due to differences in the sample position, that do not affect T1.
If we consider relaxation caused by SOC fields only, the fluctuations can be written as F(t)=μBΔg(t)·B. This incorporates a time dependance from lattice vibrations or molecular tumbling. Assuming that the amplitude of the SOC fluctuations approximately scales with Δg itself, one expects that the spectral densities follow the proportionality kq(ω)∝(Δg)2 and the relaxation time to follow T1∝(Δg)−2.
Figure 4a shows that T1 indeed follows this proportionality with a remarkable accuracy. We conclude that spin lattice relaxation is therefore dominated by the effective SOC at magnetic fields of ∼350 mT.
Note that fluctuating HFI fields create perturbations of the form Fn(t)=An(t)·In, where An(t) is the coupling tensor for the nuclear spin In. This expression does not depend on the external field and the HFI therefore become less effective at flipping the spin when the Zeeman splitting increases at higher fields. In contrast, spin lattice relaxation by fluctuating SOC fields will remain equally effective at all external field strengths. Measurements on organic spin valves for instance are typically performed at different magnetic fields between 5 and 500 mT, depending on the switching field of the ferromagnetic electrodes. The effect of HFI fields on spin relaxation will therefore be suppressed to different degrees which complicates a systematic comparison of spin diffusion lengths.
Only two outliers, TIPS-pentance and rubrene, stand out for their small T1 relative to the g-shift. Both have a large number of hydrogens attached to the conjugated system and we speculate that the HFI provides an additional relaxation pathway. Naturally, this would be most pronounced for rubrene, where 28 protons contribute to the HFI. In a control experiment, we repeated the measurement on fully deuterated d28-rubrene, which strongly suppresses hyperfine interactions8,23. Together with a reduction of the HFI couplings by a factor of 2–3, we observe an increase of T1 by more than an order of magnitude which brings it in line with the other molecules.
The large deviation from the T1∝(Δg)−2 dependency can therefore be traced back to hyperfine interactions. We can quantify their contribution by summing over SOC and HFI relaxation rates 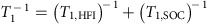 which yields pure HFI relaxation times of ∼13 μs for h28-rubrene and ∼30 μs for TIPS-pentacene. Such an estimate is only meaningful when the deviation from T1∝(Δg)−2 is larger than the measurement uncertainty, that is, when the contribution of T1,HFI to T1 is not negligible. We therefore cannot systematically extract HFI contributions for most of the molecules in this study but instead can identify a domain of weak SOC with Δg≲500 p.p.m., where, in the presence of a sufficient number of nuclear spins, hyperfine fields will significantly contribute to spin lattice relaxation.
which yields pure HFI relaxation times of ∼13 μs for h28-rubrene and ∼30 μs for TIPS-pentacene. Such an estimate is only meaningful when the deviation from T1∝(Δg)−2 is larger than the measurement uncertainty, that is, when the contribution of T1,HFI to T1 is not negligible. We therefore cannot systematically extract HFI contributions for most of the molecules in this study but instead can identify a domain of weak SOC with Δg≲500 p.p.m., where, in the presence of a sufficient number of nuclear spins, hyperfine fields will significantly contribute to spin lattice relaxation.
When excluding the outliers and assuming that both T1 and T2 are dominated by a single relaxation process, SOC in our case, one can find a simple expression for the spectral density 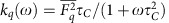 , where τC is the correlation time of field fluctuations and
, where τC is the correlation time of field fluctuations and 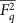 is the mean square of the fluctuating field22. Figure 4c shows the dependence of both relaxation times on τC in this model and demonstrates that spin lattice relaxation becomes most effective when the frequency τC−1 matches the energy difference between the Zeeman split levels.
is the mean square of the fluctuating field22. Figure 4c shows the dependence of both relaxation times on τC in this model and demonstrates that spin lattice relaxation becomes most effective when the frequency τC−1 matches the energy difference between the Zeeman split levels.
In a rough approximation, we can take 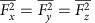 and estimate the correlation time τC from the ratio
and estimate the correlation time τC from the ratio 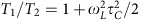 . The resulting values are on the order of
. The resulting values are on the order of 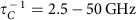 (Fig. 4c). For comparison, simulations of intramolecular vibrational modes of DNTT predict frequencies of 6–50 THz for stretching modes along the molecule's symmetry axes, distortions of the phenyl rings and vibrations of the C-H bonds, in ascending order24. They exceed the Zeeman splitting by orders of magnitude and are therefore less effective at flipping the spin.
(Fig. 4c). For comparison, simulations of intramolecular vibrational modes of DNTT predict frequencies of 6–50 THz for stretching modes along the molecule's symmetry axes, distortions of the phenyl rings and vibrations of the C-H bonds, in ascending order24. They exceed the Zeeman splitting by orders of magnitude and are therefore less effective at flipping the spin.
Alternatively, we consider SOC fields that are static in the molecule's rest frame but fluctuate relative to the external field (and thus the spin quantization axis) with the tumbling motion of molecules in a solution. From diffusion-ordered nuclear magnetic resonance spectroscopy (DOSY NMR) measurements at a concentration of 0.2 mg ml−1, we can calculate the Stokes radius and resulting rotational correlation times for the molecules (Supplementary Note 4). The solubility of DNTT and DNSS in dichloromethane was too small to record DOSY NMR spectra but the rotational correlation times 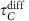 for the remaining molecules are shown in Fig. 4c together with τC values estimated from the spin lifetime ratios. Even though the values of τC are only rough estimates, derived under the previously discussed assumptions, we observe an approximate agreement with
for the remaining molecules are shown in Fig. 4c together with τC values estimated from the spin lifetime ratios. Even though the values of τC are only rough estimates, derived under the previously discussed assumptions, we observe an approximate agreement with 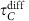 . It is therefore likely that the observed relaxation times are indeed a result of SOC fields which fluctuate due to the molecular rotations in solution.
. It is therefore likely that the observed relaxation times are indeed a result of SOC fields which fluctuate due to the molecular rotations in solution.
Discussion
Isolated molecules, both in the gas phase and in solution, are significantly easier to model and to understand than solid thin films. They also provide us with the unique opportunity to resolve the hyperfine structure of ESR signals and to verify the spin densities from relativistic DFT modelling by comparing experimental and theoretical HFI couplings. Altogether with accurate measurements and predictions of the g-factor, we demonstrate the subtle dependence of SOC strengths on the molecular geometry: the inclusion of heavier atoms in the molecular structure increases SOC but the effect of such substitutions can be almost completely suppressed by the molecular geometry and the resulting spin density distribution. As a result, molecules such as C-C12-DTBTBT with four sulfur atoms exhibit SOC strengths close to pure hydrocarbons. We demonstrate an empirical linear relationship between the g-shift and the atomic spin densities, where the proportionality constants depend only on the type of element and its local SOC, regardless of its molecular environment. This enables the targeted molecular design of materials with excellent charge transport properties and suppressed or enhanced spin-orbit coupling for either spin transport or spin to charge conversion applications.
The mechanism of spin relaxation in solution, which is most likely dominated by molecular tumbling, cannot be directly transferred to solid systems. Nevertheless, we expect to see some parallels. First ESR measurements on field induced charges in thin films reveal relaxation times that come close to the solution values and agree with pulsed ESR data from thin films at room temperature25,26. In the solid state, the fluctuations of SOC fields will not be provided by molecular rotations but by intermolecular phonon modes which lie at smaller frequencies than their intramolecular counterparts or by the hopping motion of spins in the organic semiconductor. When a charge carrier hops between sites with differently oriented molecules, it will experience the change in g-tensor orientation as a fluctuating field in its rest frame. Hopping times are estimated to be in the range of 100–1,000 ps (ref. 27) close to the rotational correlation times in solution and some lower frequency intermolecular modes can reach time scales >10 ps (refs 28, 29). In the solid state, the spin densities are likely to spread over multiple molecules but we expect Δg to still be measure of the effective SOC. Since the fluctuation amplitudes will still scale with the latter, knowing the relaxation times in solution should provide a good estimate for both the coherence and spin lattice relaxation times in thin films.
Methods
ESR experiments
All ESR spectra were recorded on a Bruker E500 X-band spectrometer with a Bruker ER 4122SHQE cavity at frequencies of 9.4–9.7 GHz and with a concentration of cations below 0.5 × 10−3 mol l−1 to prevent interactions between spins on different molecules. The spectra were recorded at low-microwave powers of 0.006–0.06 mW to prevent power saturation and the concurrent line width broadening (Fig. 3c). The external magnetic field was modulated at 100 kHz and the spectra were recorded in lock-in measurements. As a consequence, passage effects can distort the signal shape if the spin packets cannot relax between modulation cycles. This was avoided by choosing a sufficiently small modulation amplitude Bm or frequency ωm so that ωmBm<<1/(γeT1T2) and the spin system remains continually in thermal equilibrium30.
The solutions of molecules in dichloromethane were prepared in a nitrogen glove box and sealed in sample tubes before the measurement. To minimize the perturbation of the microwave field inside the cavity, the solution was confined to a capillary tube with an inner diameter of 1 mm at the cavity centre where the magnetic field is largest (Fig. 3a). This allows us to perform the measurements at high-quality factors of Q≈8,000–10,000 (the ratio between the power stored and the power dissipated per microwave cycle).
The molecules were doped by adding AlCl3, an oxidative Lewis acid, and most solutions remained stable for >12 h (confirmed by both ESR and optical spectroscopy). Acquiring a full series of spectra with varying microwave powers took at most 1.5 h. After 24 h we could observe a noticeable reduction in the number of cations but no spectral changes that would indicate a reaction of AlCl3 with the molecules. The only exception to this are C8-BTBT and C8-BSBS, which exhibit the emergence of a secondary spectrum with a smaller g-factor but partially overlapping with the organic radical signal. The new species are likely to be chlorinated versions of the molecules. We therefore conducted all C8-BTBT and C8-BSBS measurements immediately after adding AlCl3 and before any spectral changes took place.
The fitting of all spectra was performed with the genetic algorithm of the EasySpin Toolbox17 in MATLAB with a population of 40 spectra and 20,000 generations. Each fitting step was performed by diagonalizing the above Hamiltonian for a set of hyperfine couplings an and determining allowed microwave transitions between the resulting energy levels. The resonance positions were then convoluted with a Lorentzian line to account for the finite spin dephasing time with ΔB1/2 as an additional fitting parameter.
DFT modelling
All density-functional theory calculations were performed using the NWChem31 (version 6.5) and ORCA32 (version 3.0.3) quantum chemistry software packages using an all-electron DFT method, with nuclear relativistic effects described by the zeroth-order regular approximation (ZORA33) using the standard point-charge approximation for the atomic nuclei. g-tensors were calculated using the method18 developed by Neese et al.34 and related techniques as implemented in the ORCA software package. Atom spin populations were calculated using the Voronoi deformation density method35, as implemented in the ‘bader' program developed by Henkelman et al.36, version 0.95a.
The fit of equation 3 is performed as follows: for each molecule, the atomic spin populations are summed up per element. Then, the proportionality constants per element ce of equation 3 are fitted using all other molecules in the fit statistic. The molecule fitted for is thus never part of the fit statistic. Finally, the fitted value of ΔgOZ/SOC is calculated as the scalar product between the arrays of per element atomic spin population sums and the corresponding fitted proportionality constants ce. As a negative ce lacks physical meaning in this model, a non-negative multivariate linear regression method (subroutine ‘scipy.optimize.nnls'), as implemented in the Scientific Python software package, version 0.16.1, was used. As an approximate statistical test, we for each fit calculate the R2-value according to
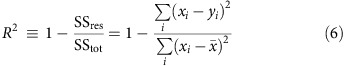 |
where SSres, SStot, xi and yi are the residual sum of squares, the total sum of squares, and the calculated and fitted ΔgOZ/SOC value, respectively.
Calculation of spin lifetimes
For sufficiently large microwave powers, spin relaxation will be too slow to maintain a population difference between the Zeeman split energy levels. The absorbed microwave power, integrated over the whole spectrum, will saturate. The integrated area of the ESR absorption spectrum, or the double integral over the derivative spectrum, follows37,38
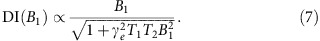 |
Fitting the power saturation curves of Fig. 3b therefore allows us to determine the product of spin lifetimes T1T2.
Before the onset of power saturation and line width broadening, the coherence time is given by T2=(γeΔB1/2)−1, where ΔB1/2 is the half width at half maximum of the individual Lorentzian resonance lines that make up the spectrum37. We determine ΔB1/2 by the least-squares fitting of the hyperfine structure and dividing the product of spin lifetimes by T2 then gives the spin lattice relaxation time T1.
Data availability
The data that support the findings of this study are available at the University of Cambridge data repository at https://doi.org/10.17863/CAM.8126.
Additional information
How to cite this article: Schott, S. et al. Tuning the effective spin-orbit coupling in molecular semiconductors. Nat. Commun. 8, 15200 doi: 10.1038/ncomms15200 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Material
Supplementary Figures, Supplementary Tables, Supplementary Notes and Supplementary References
Acknowledgments
S.S. thanks the Winton Programme for the Physics of Sustainability, the Engineering and Physical Sciences Research Council (EPSRC), C. Daniel Frisbie for supplying d28-rubrene and Shin-ichi Kuroda for useful discussions. Funding from the Alexander von Humboldt Foundation, ERC Synergy Grant SC2 (No. 610115), and the Transregional Collaborative Research Center (SFB/TRR) 173 SPIN+X is acknowledged.
Footnotes
The authors declare no competing financial interests.
Author contributions S.S. carried out the ESR experiments and analyses, E.R.M. performed the simulations and analyses. C.B.N. performed the DOSY NMR measurements. H.-Y.C., K.T. and I.M. provided materials. H.S. and J.S. supervised the project. All authors discussed the results. S.S. and E.R.M. wrote the manuscript with input from all authors.
References
- Szulczewski G., Sanvito S. & Coey M. A spin of their own. Nat. Mater. 8, 693–695 (2009). [DOI] [PubMed] [Google Scholar]
- Ando K., Watanabe S., Mooser S., Saitoh E. & Sirringhaus H. Solution-processed organic spin–charge converter. Nat. Mater. 12, 622–627 (2013). [DOI] [PubMed] [Google Scholar]
- Sun D. et al. Inverse spin Hall effect from pulsed spin current in organic semiconductors with tunable spin–orbit coupling. Nat. Mater. 15, 863–869 (2016). [DOI] [PubMed] [Google Scholar]
- Bobbert P. A., Wagemans W., Van Oost F. W. A., Koopmans B. & Wohlgenannt M. Theory for spin diffusion in disordered organic semiconductors. Phys. Rev. Lett. 102, 156604 (2009). [DOI] [PubMed] [Google Scholar]
- Xiong Z. H., Wu D., Valy Vardeny Z. & Shi J. Giant magnetoresistance in organic spin-valves. Nature 427, 821–824 (2004). [DOI] [PubMed] [Google Scholar]
- Drew A. J. et al. Direct measurement of the electronic spin diffusion length in a fully functional organic spin valve by low-energy muon spin rotation. Nat. Mater. 8, 109–114 (2008). [DOI] [PubMed] [Google Scholar]
- Zhang X. et al. Observation of a large spin-dependent transport length in organic spin valves at room temperature. Nat. Commun. 4, 1392 (2013). [DOI] [PubMed] [Google Scholar]
- Nguyen T. D. et al. Isotope effect in spin response of π-conjugated polymer films and devices. Nat. Mater. 9, 345–352 (2010). [DOI] [PubMed] [Google Scholar]
- Yu Z. G. Suppression of the Hanle Effect In Organic Spintronic Devices. Phys. Rev. Lett. 111, 016601 (2013). [DOI] [PubMed] [Google Scholar]
- Göckeritz R. et al. Nanosized perpendicular organic spin-valves. App. Phys. Lett. 106, 102403 (2015). [Google Scholar]
- Wid O. et al. Investigation of the unidirectional spin heat conveyer effect in a 200 nm thin Yttrium Iron Garnet film. Sci. Rep. 6, 28233 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Podzorov V., Menard E., Rogers J. A. & Gershenson M. E. Hall effect in the accumulation layers on the surface of organic semiconductors. Phys. Rev. Lett. 95, 226601 (2005). [DOI] [PubMed] [Google Scholar]
- Minder N. A. et al. Tailoring the molecular structure to suppress extrinsic disorder in organic transistors. Adv. Mater. 26, 1254–1260 (2013). [DOI] [PubMed] [Google Scholar]
- Yu Z. G. Spin Hall Effect in Disordered Organic Solids. Phys. Rev. Lett. 115, 026601 (2015). [DOI] [PubMed] [Google Scholar]
- Sakanoue T. & Sirringhaus H. Band-like temperature dependence of mobility in a solution-processed organic semiconductor. Nat. Mater. 9, 736–740 (2010). [DOI] [PubMed] [Google Scholar]
- Izawa T., Miyazaki E. & Takimiya K. Solution-Processible Organic Semiconductors Based on Selenophene-Containing Heteroarenes, 2,7-Dialkyl[1]benzoselenopheno[3,2- b][1]benzoselenophenes (C n-BSBSs): Syntheses, Properties, Molecular Arrangements, and Field-Effect Transistor Characteristics. Chem. Mater. 21, 903–912 (2009). [Google Scholar]
- Stoll S. & Schweiger A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Res. 178, 42–55 (2006). [DOI] [PubMed] [Google Scholar]
- Neese F. Prediction of electron paramagnetic resonance g values using coupled perturbed Hartree–Fock and Kohn–Sham theory. J. Chem. Phys. 115, 11080–11096 (2001). [Google Scholar]
- Jiang S. W. et al. Exchange-dominated pure spin current transport in Alq3 molecules. Phys. Rev. Lett. 115, 086601 (2015). [DOI] [PubMed] [Google Scholar]
- Watanabe S. et al. Polaron spin current transport in organic semiconductors. Nat. Phys. 10, 308–313 (2014). [Google Scholar]
- Redfield A. G. On the theory of relaxation processes. IBM J. Res. Dev. 1, 19–31 (1957). [Google Scholar]
- Slichter C. P. Principles of Magnetic Resonance Springer Science & Business Media (2013). [Google Scholar]
- Xie W. et al. High-mobility transistors based on single crystals of isotopically substituted Rubrene- d28. J. Phys. Chem. C 117, 11522–11529 (2013). [Google Scholar]
- Fujita T., Atahan-Evrenk S., Sawaya N. P. D. & Aspuru-Guzik A. Coherent dynamics of mixed frenkel and charge-transfer excitons in Dinaphtho[2,3- b:23-f]thieno[3,2- b]-thiophene thin films: the importance of hole delocalization. J. Phys. Chem. Lett. 7, 1374–1380 (2016). [DOI] [PubMed] [Google Scholar]
- van Schooten K. J., Baird D. L., Limes M. E., Lupton J. M. & Boehme C. Probing long-range carrier-pair spin–spin interactions in a conjugated polymer by detuning of electrically detected spin beating. Nat. Commun. 6, 6688 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker W. J., Keevers T. L., Lupton J. M., McCamey D. R. & Boehme C. Slow hopping and spin dephasing of Coulombically bound polaron pairs in an organic semiconductor at room temperature. Phys. Rev. Lett. 108, 267601 (2012). [DOI] [PubMed] [Google Scholar]
- Olivier Y., Lemaur V., Brédas J. L. & Cornil J. Charge hopping in organic semiconductors: influence of molecular parameters on macroscopic mobilities in model one-dimensional stacks. J. Phys. Chem. A 110, 6356–6364 (2006). [DOI] [PubMed] [Google Scholar]
- Motta C. & Sanvito S. Charge transport properties of durene crystals from first-principles. J. Chem. Theory Comput. 10, 4624–4632 (2014). [DOI] [PubMed] [Google Scholar]
- Cheung D. L. & Troisi A. Modelling charge transport in organic semiconductors: from quantum dynamics to soft matter. Phys. Chem. Chem. Phys. 10, 5941 (2008). [DOI] [PubMed] [Google Scholar]
- Lund A., Sagstuen E., Sanderud A. & Maruani J. Relaxation-time determination from continuous-microwave saturation of EPR Spectra. Radiat. Res. 172, 753–760 (2009). [DOI] [PubMed] [Google Scholar]
- Valiev M. et al. NWChem: a comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 181, 1477–1489 (2010). [Google Scholar]
- Neese F. The ORCA program system. WIREs Comput. Mol. Sci. 2, 73–78 (2012). [Google Scholar]
- van Lenthe E., Baerends E. J. & Snijders J. G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 99, 4597–4610 (1993). [Google Scholar]
- Neese F. Efficient and accurate approximations to the molecular spin-orbit coupling operator and their use in molecular g-tensor calculations. J. Chem. Phys. 122, 034107 (2005). [DOI] [PubMed] [Google Scholar]
- Fonseca Guerra C., Handgraaf J.-W., Baerends E. J. & Bickelhaupt F. M. Voronoi deformation density (VDD) charges: assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD methods for charge analysis. J. Comput. Chem. 25, 189–210 (2004). [DOI] [PubMed] [Google Scholar]
- Tang W., Sanville E. & Henkelman G. A grid-based Bader analysis algorithm without lattice bias. J. Phys.: Condens. Matter 21, 084204 (2009). [DOI] [PubMed] [Google Scholar]
- Abragam A. The Principles of Nuclear Magnetism Oxford University Press (1961). [Google Scholar]
- Matsui H., Mishchenko A. S. & Hasegawa T. Distribution of localized states from fine analysis of electron spin resonance spectra in organic transistors. Phys. Rev. Lett. 104, 056602 (2010). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figures, Supplementary Tables, Supplementary Notes and Supplementary References
Data Availability Statement
The data that support the findings of this study are available at the University of Cambridge data repository at https://doi.org/10.17863/CAM.8126.