A speed limit for conformational change of an allosteric membrane protein

Abstract

Neuromuscular acetylcholine receptors are synaptic ion channels that open and close with rate constants of ≈48,000 s^-1 and ≈1,700 s^-1, respectively (in adult mouse, at 24°C, -100 mV membrane potential). Perturbations of many different sites in the protein can change these rate constants, with those in the extracellular domain mainly affecting channel-opening and many of those in the membrane and intracellular domains mainly affecting channel-closing. We used single-channel recordings to measure the total open time per activation (τ_b) elicited by a low concentration of the natural transmitter, acetylcholine. τ_b increased in constructs with mutations that increased the gating equilibrium constant by either increasing the opening or decreasing the closing rate constant. However, τ_b did not approach the same asymptote in fast-opening and slow-closing constructs. The maximum value for the slow closers was about twice that for the fast openers. One interpretation of this difference is that there is an upper limit to the channel-opening rate constant, which we estimate to be ≈0.86 μs^-1. One possibility is that this limit is the rate of conformational change in the absence of an overall activation barrier and thus reflects the kinetic prefactor for the acetylcholine receptor opening isomerization.

At cholinergic synapses, transmitter molecules trigger acetylcholine (ACh) receptor channels (AChRs) to switch from a stable conformation in which ion permeation is forbidden (“closed”) to one in which cations can permeate rapidly (“open”). This reversible change in structure, known as gating, involves the organized movements of many of the >2,300 residues within the five subunits that comprise this allosteric membrane protein (1–3). The driving energy for the reaction is a change in binding energy for the ligand; thus, gating must, at least, entail movements of residues at the two transmitter binding sites and in the ion conduction pathway.

When activated by the natural transmitter ACh, mouse neuromuscular AChRs open rapidly (≈48,000 s^-1) and close relatively slowly (≈1,700 s^-1) (at 24°C, -100-mV membrane potential) (4). In single-molecule patch-clamp recordings with a time resolution of ≈25 μs, the closed ⇄ open isomerization appears to be a two-state reaction with no directly detectable intermediate states. However, these states can be probed indirectly by using rate-equilibrium free energy (REFER) analyses (5–7). For a series of point mutations, the slope (Φ) of a log–log plot of the opening rate constant vs. the equilibrium constant is an index of the extent of progress of the perturbed site at the transition state of the reaction. In fully liganded AChRs, there is, to a first approximation, a longitudinal gradient in Φ-values, with residues near the transmitter binding sites being open-like (Φ ≈ 1) and some of those in the transmembrane region being closed-like (Φ ≈ 0) at the transition state (8, 9). These results have been interpreted as indicating that gating occurs as a reversible solitary conformational “wave” that links structural changes in the affinity of the binding sites with structural changes that determine ionic conductance. Recent experiments suggest that this wave is coarse-grained, with gating occurring as the sequential, coupled movements of a few rigid-body domains (“blocks”), each composed of residues on the order of dozens (10, 11).

Here, we estimate a maximum rate constant for passing through the short-lived, intermediate states that populate the diliganded AChR gating transition-state ensemble.

Materials and Methods

Expression. cDNA clones of α, β, δ, and ε subunits of mouse AChR in pRBG4 were transiently expressed in human embryonic kidney cells (HEK 293) by transfection with calcium phosphate. A total of 3.5 μg of DNA per 35-mm culture dish was used with a subunit ratio of 2:1:1:1 (α/β/δ/ε). The medium was changed after 24 h, and electrophysiological recording began another 24 h later. All mutations (side-chain substitutions) were made by using the QuikChange (Stratagene) site-directed mutagenesis kit and were confirmed by dideoxy sequencing.

By selecting appropriate combinations of agonist and mutation, we could engineer the gating reaction to study AChRs having a wide range of opening or closing rate constants. The fast-opening constructs had mutations at position D97 [in loop 5, near the transmitter binding site (12)] in both α-subunits. Where noted, a second fast-opening mutation, αS269I, in the extracellular linker (13), was also present. The slow-closing constructs had side-chain substitutions at position L265 or S268 in the membrane domain of the δ-subunit (9).

Electrophysiology and Kinetic Analyses. Single-channel currents were recorded in cell-attached patches (approximately -100-mV membrane potential at 23°C) and sampled at 100 kHz after low-pass filtering at 20 kHz. The acquisition and analyses of the currents were done by using qub software (www.qub.buffalo.edu). Idealization of the currents was done by using the segmental k-means (SKM) algorithm (14) without additional low-pass filtering. Model-based kinetic analyses of the idealized, noise-free intervals were done by using a maximum interval likelihood method (15) with an imposed dead time of 25 μs.

Single-channel currents were elicited by 1 μM ACh. Usually, the open interval duration distributions were fitted by three exponential components. The time constant of the slowest component (τ_b) corresponds to diliganded AChRs. Our goal was to interpret τ_b by using an equation derived from a kinetic model (Scheme 1 and Eq. 3).

In the fast-opening constructs activated by ACh, our time resolution was less than the lifetime of state A₂C (see Scheme 1) and we were therefore unable to measure the opening and closing rate constants directly. Instead, we measured these rate constants (and their ratio, the diliganded gating equilibrium constant, Θ) for each construct using a weak agonist, choline, and then extrapolated these values to what we would expect with ACh as the agonist. The core assumption in this extrapolation was that two kinds of perturbation (ligands and mutations) make energetically independent contributions

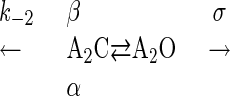Scheme 1.

to Θ. In WT AChRs, Θ_ACh = 28 and Θ_choline = 0.05 (16), and we assumed that this ≈560-fold ratio pertained to all mutant AChRs as well.

Given this estimate of Θ_ACh, we calculated the expected opening and closing rate constants (β and α, respectively) using the following relationships.

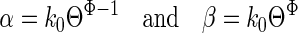[1]

Φ is a fraction between 0 and 1 that describes the extent to which the change in energy of the transition state of the gating reaction, after a perturbation, resembles that of the open state. k₀ is the rate constant when the equilibrium constant is 1. For perturbations in the vicinity of the transmitter binding sites (TBSs), including the site of the fast-opening mutations (residue αD97), k₀ ≈ 2,000 s^-1 and Φ = 0.93 (8, 12). For example, using these values we can calculate (Eq. 1) that the gating rate constants for WT AChRs activated by ACh (Θ= 28) are β = 44,349 s^-1and α = 1,583 s^-1. These are close to the values that have been measured directly (≈48,000 s^-1 and ≈1,700 s^-1). Similarly, for WT AChRs activated by choline (Θ = 0.05), we calculate β = 123 s^-1 and α = 2,446 s^-1, which are again close to the directly measured values, ≈120 s^-1 and ≈2,100 s^-1 (16). That is, in WT AChRs, a switch from choline to ACh induces an ≈560-fold increase in Θ by increasing β by ≈361-fold and decreasing α by ≈1.55-fold.

To arrive at the values in Table 1 we directly measured β and α from single-channel currents elicited by choline and estimated a gating equilibrium constant, Θ_choline (the ratio β/α) for all mutant constructs. We then calculated Θ_ACh using the assumption that ligands and mutations make energetically independent contributions to diliganded gating: Θ_ACh = 560 × Θ_choline. Finally, we used Eq. 1 with Φ = 0.93 and k₀ = 2,000 s^-1 to calculate the rate constants β_ACh and α_ACh. (Below, we consider the possibility that the Φ-value of the TBS and αD97 was not equal to 0.93 for all of the fast-opening mutants.) To estimate the asymptotic limits for the slow-closing and fast-opening series, the experimental τ_b values were fitted by Eq. 3 with β_ACh and α_ACh as the two independent parameters and σ and k_-2 as the two dependent parameters. Fig. 2 shows a plot of the observed value of τ_b vs. the corresponding value of 1/k^* calculated by using the fitted value of k_-2.

Table 1. Gating rate constants for AChR mutants.

Construct	Predicted opening rate constant, β2	Predicted closing rate constant, α2
	Slow-closing
δS268G	43,772	1,897
δS268C	78,566	363
δS268T	93,580	369
δS268V	107,468	131
δS268N	138,751	107
δL265′T	44,349	88
δL265′T+αD97C	191,457	91
δL265′T+αD97E	884,093	86
δL265′T+αD97Q	2.163E6	85
δL265′T+αD97A	4.972E6	72
	Fast-opening
αD97N	96,630	1,617
αD97C	191,457	1,476
αD97M	301,068	1,532
αD97Y	503,342	1,354
αD97H	663,430	1,317
αD97E	883,372	1,410
αD97F	990,819	1,244
αD97Q	2,165E6	1,370
αD97R	3.948E6	1,123
αD97A	4.972E6	1,168

All values are s^-1 and pertain to diliganded AChRs activated by ACh. The predicted opening and closing rate constants are calculated from the corresponding values measured for choline and using Eq 1 (see Materials and Methods). The calculated opening and closing rate constants for WT AChRs activated by ACh are 44,349 s^-1 and 1,583 s^-1, respectively, and are similar to the experimentally determined values of ≈48,000 s^-1 and ≈1,700 s^-1, respectively. The double-mutant constructs in the slow-closing series also open rapidly, but it is mainly their slow α-values that cause k^* to approach zero and, hence, drive τ_b towards σ^-1 (Eq. 3).

Fig. 2.

Slow-closing and fast-opening mutants generate different burst-duration (τ_b) asymptotes. The x-axis values were calculated from the estimated gating rate constants, α_ACh and β_ACh, and the rate constant for ACh dissociation from closed AChRs, k_-2 (Eq. 3b). Each symbol is the mean of more than three patches. The asymptote of the slow-closing mutant series (○) is ≈2-fold greater than that of the fast-opening series (•), even though a simple kinetic model (Scheme 1 and Eq. 3) predicts that they should be the same. The specific mutations for each series (left to right) are given in sequence Table 1. The marked symbols are double mutations (Table 1). One possible explanation for the difference in the asymptote is that in the fast-opening series the opening rate constant reaches an upper boundary of ≈0.86 μs^-1.

To estimate the consequences of channel opening speed limit on the decay of the synaptic current, we modified Eq. 2.

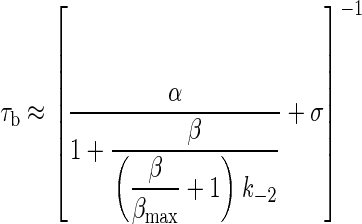[2]

For WT adult mouse neuromuscular AChRs activated by ACh (-100 mV membrane potential, at 24°C), the approximate parameters (in s^-1) are α = 1,700, β = 48,000, k_-2 = 50,000, σ = 70, and β_max = 860,000.

Results and Discussion

Kinetic Model. Scheme 1 encapsulates the kinetic behavior of diliganded closed and open AChRs (A₂C and A₂O).

β and α are the opening and closing rate constants and k_-2 is the agonist dissociation rate constant from closed AChRs. σ is the sum of the rate constants for agonist dissociation (followed by rapid closure) and desensitization from open AChRs.

Under our experimental conditions, sojourns in A₂C are exceedingly brief, and openings that appear to be single events (Fig. 1) are, in fact, “bursts” of individual openings separated by gaps that are too short to be reliably detected or to contribute significantly to the burst duration. In this case (and as shown in ref. 17), the mean duration of a burst (the total open time per activation), τ_b, is as follows.

[3a]

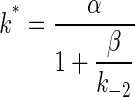[3b]

Fig. 1.

Single-channel currents and burst-duration histograms for selected fast-opening and slow-closing AChR mutants. Currents were activated using 1 μM ACh. The durations are the time constants of the slowest burst-duration component (τ_b). (A) When the effect of the mutation is modest (see Table 1) there is little difference between fast-opening and slow-closing mutants. (B) When the effect of the mutation is large, the τ_b values for the fast-opening mutants are smaller than those for the slow-closing mutants. One possible reason for this difference is that AChRs can close arbitrarily slowly but cannot open arbitrarily fast.

τ_b also describes approximately the time course of the synaptic current decay. For WT neuromuscular AChRs activated by ACh (α ≈ 1,700 s^-1 and β/k_-2 ≈ 1), k^* (≈850 s^-1) is much greater than σ (≈70 s^-1; see below). Thus, at the neuromuscular synapse, bursts terminate mainly by agonist dissociation from A₂C, and τ_b ≈ 1/k^* ≈ 1.2 ms (13, 18).

Estimating the Speed Limit. Scheme 1 implies that perturbations that specifically slow the closing rate constant α and those that specifically increase the opening rate constant β should have the same qualitative effect, namely to increase the probability that bursts terminate from A₂O. Eq. 3 predicts that mutations that decrease α and those that increase β should both shrink k^* and increase the burst lifetime τ_b. Quantitatively, Eq. 3 predicts at the extremes (as α → 0or β → ∞) that both kinds of mutation should result in the same τ_b asymptote, σ^-1.

Fig. 1 shows exemplar single-channel currents and burst-duration histograms from slow-closing and fast-opening AChR constructs. The results are summarized in Table 1 and Fig. 2. The specific side-chain substitutions for both classes of perturbation have previously been shown to alter only the gating rate constants and to have little or no effect on agonist dissociation (to either closed or open AChRs) or desensitization (12, 17).

The fast-opening AChRs had mutations of α-subunit residue D97, which is in loop 5 of the extracellular domain (19). With choline as the agonist, mutations of this position increase β but have only a small effect on α (Φ_αD97 = 0.93). These constructs reduce k^* and increase τ_b mainly by increasing the denominator of Eq. 3b. The slow-closing AChRs had mutations at one of two positions in the δ-subunit (S268 and L265), both of which are in the membrane domain. These mutations significantly reduce α but have little or no effect on β (Φ_δ268 = 0.3 and Φ_δ265 = 0.0). These constructs reduce k^* and increase τ_b mainly by decreasing the numerator of Eq. 3b. Although some of these slow-closing AChRs open more rapidly than those of the WT, we chose to classify them as such because it is their slow α-values that are mainly responsible for reducing the magnitude of k^* and thus driving τ_b toward σ^-1. Eq. 3 predicts that, at the extremes, both kinds of mutation should have the same quantitative effect on τ_b.

To estimate these asymptotic limits for fast-opening and slow-closing mutants, the relationship between the observed values of τ_b and the calculated values of k^* were fitted by Eq. 3 with σ and k_-2 as free parameters. Fig. 2 shows that the fitted values for the slow-closing series were σ = 70.4 ± 5s^-1 and k_-2 = 56,405 ± 22,265 s^-1. In these mutants, α is small and k^* is negligible; hence, we take this value of σ to be equal to the sum of the rate constants for open-channel dissociation and desensitization (17).

Eq. 3 predicts that the asymptote (σ-value) for the fast-opening series should be the same as for the slow-closing series. However, the fitted asymptote for the fast openers was 140 ± 8 s^-1, about twice the expected value. The fitted value of k_-2 for the fast-opening mutant series was 84,561 ± 17,895 s^-1. We do not consider this value to be significantly different from that for the slow-closing series or for WT AChRs estimated by using a variety of methods (≈50,000 s^-1; ref. 17 and references therein).

We consider three possible explanations for this marked difference in maximum burst duration between fast-opening (i.e., as β → ∞) and slow-closing (i.e., as α → 0) AChRs. (i) The αD97 (fast-opening) mutations changed the dissociation and/or desensitization rate constants and, hence, the σ-value. (ii) The αD97 mutations altered the gating reaction energy landscape in such a way as to expose new exit paths from A₂O. (iii) The αD97 mutations were not changing the gating equilibrium constant to the extent that we calculated using the assumption of energetically independent contributions of ligand (choline to ACh) and mutation.

The experimental evidence suggests that none of the mutations altered agonist dissociation or desensitization rate constants. The closed-channel agonist dissociation rate constant has been measured directly for several fast-opening (12) and slow-closing (17) receptors, and this value is essentially unchanged from that of the WT (≈50,000 s^-1). Moreover, when the fast-opening mutations are expressed in a construct with a slow-closing background mutation (indicated by an asterisk in Fig. 2), the asymptote is the same as for the slow-closing constructs alone, indicating that σ was unchanged. These results suggest that none of the fast-opening mutations significantly altered the rate constants for desensitization or agonist dissociation (from either open or closed AChRs), and we seek alternative explanations for the ≈2-fold difference in the asymptotes between slow-closing and fast-opening mutants.

If the αD97 mutations altered the gating reaction energy landscape in such a way as to expose new exit paths from A₂O, then Scheme 1 and Eq. 3 would no longer hold. Consequently, the smaller asymptote in the fast-opening series could result from the addition of this hypothetical (and unspecified) mechanism for terminating a burst. However, when these same αD97 mutations coexist with a background mutation in the transmembrane segment that greatly reduces the channel-closing rate constant (δL265T), the asymptote is unchanged. The unchanging asymptote indicates that this novel route(s) for burst termination, if present, would not be a consequence of the specific mutation but rather might reflect only an energetic consequence of the perturbation. We have no information about such a speculative mechanism and we will not consider it further.

If there are no new exit paths from A₂O (i.e., Scheme 1 and Eq. 3 are valid for all mutants) and if neither k_-2 nor σ is altered by the mutations, then the ≈2-fold difference in asymptotes for the two mutant series must arise from differences in the values of the gating rate constants, β and α. The smaller asymptote for the fast-opening mutants indicates that that k^* is reaching a finite, lower limit in the αD97 mutants. This boundary is equal to the difference between the limits of the fast-opening and slow-closing mutants, 70 ± 6 s^-1.

According to Eq. 3b, k^* will reach a minimum value if α reaches a minimum, if β reaches a maximum, or both. We have no reason to suspect that a rate constant should have a minimum value. Accordingly, we focus our attention on the possibility that the 70 s^-1 limit for k^* is caused by β reaching a ceiling. That is, we hypothesize that the membrane domain mutations can make channel-closing arbitrarily slow but that the extracellular domain mutations cannot make channel-opening arbitrarily fast. Consequently, we propose (Fig. 2) that the fast-opening series deviates from the slow-closing series because the actual β-values and, hence, the calculated (1/k^*) values that are plotted on the x axis are overestimated by using our simple assumptions (see Materials and Methods).

From the limit k^* = 70 s^-1 we can estimate a maximum gating equilibrium constant, Θ_max, and a maximum opening rate constant, β_max. From Eq. 3b, when β >> k_-2, the limiting value of k^* is simply the ratio of the dissociation rate constant k_-2 and Θ_max (which is equal to β_max/α). With k^* = 70 s^-1 and k_-2 = 50,000 s^-1, we calculate Θ_max = 714. If we now make the additional approximation that the closing rate constant does not change throughout the fast-opening mutant series (i.e., Φ ≈ 1 for the αD97 constructs), then we calculate (Eq. 1) that the maximum channel-opening rate constant, β_max, is 1.17 μs^-1. Energy profiles for gating that are consistent with the idea of equilibrium and rate constants having maximum values have been explored (45).

We can refine these estimates by combining Eqs. 1 and 3.

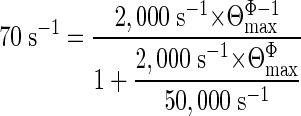[4]

If we assume that Φ = 0.93 for all αD97 mutant constructs (see below for an extended discussion on this point), then we estimate from Eq. 4 that Θ_max = 675, which is the ratio of gating rate constants β_max = 855,623 s^-1 and α = 1,267 s^-1. That is, if we attribute the difference in τ_b-asymptotes for the slow-closing and fast-opening mutants to reflect an upper-limit of the channel-opening rate constant and assume Φ = 0.93 for all constructs, then we estimate a “speed limit” for AChR channel-opening of ≈0.86 μs^-1.

To test this hypothesis, we carried out the following experiment (Fig. 3). If there is a speed limit to channel-opening, then adding a background mutation, that by itself increases the opening rate constant, to a construct that is already operating at the speed limit should have no effect. We tested this prediction by measuring τ_b in AChRs having the mutation αS269I, which is in the extracellular linker and which by itself is predicted to increase the ACh-induced opening rate ≈25-fold and to slow the closing rate constant ≈4-fold (8). Burst durations were measured in constructs having only this mutation as well as in double-substitution constructs that carried a second mutation (αD97A) that alone increased the opening rate constant 130-fold (Table 1). The τ_b-values with [8.8 ± 1.4 ms (mean ± SD), six patches] and without (8.3 ± 1.2 ms, four patches) the additional background mutation were similar. This result is consistent with the hypothesis that AChRs with αD97 mutations cannot open arbitrarily fast. Note that the τ_b-values in AChRs having the mutation in the extracellular linker are somewhat larger than the limiting value of the αD97 series alone because the linker mutation modestly slows α in addition to increasing β.

Fig. 3.

Additional mutations do not increase the speed of channel opening. (Upper) Single-channel currents and burst-duration histograms for αS269I, a mutant that by itself opens with a rate that is near the speed limit. (Lower) αS269I on a background of αD97A, which by itself open at a rate that is near the speed limit. The τ_b values in both the single- and double-mutant constructs were similar, as expected given an upper-limit to the channel opening rate constant.

Φ Values. In this section we consider the implications of our conjecture that Φ_TBS is equal to 0.93 for all of the AChR constructs. The Hammond postulate is that the energy of the transition state tends to resemble that of the less-stable end-state (20). Accordingly, as the energies of the transition state and A₂C converge progressively throughout the fast-opening mutant series, the intersection point between the two parabolic wells of the end states will shift toward A₂C and the Φ value for the reaction (i.e., averaged over all reaction coordinates) will diminish. Consequently, throughout the fast-opening mutant series, the closing rate constant α might shrink more than is expected from our assumption of a constant Φ value of 0.93. Because the opening rate constant is too fast to be measured directly, we have no way of specifically probing the Φ value of the TBS/αD97 domain for the mutant constructs.

To address the possibility that Φ was not 0.93 throughout, we used Eq. 4 to calculate Θ_max and then Eq. 1 to calculate a channel-opening speed limit (β_max) for different values of Φ. Reasonable values of these parameters pertain for Φ values between 0.5 (Θ_max = 289 and β_max = 34,000 s^-1) and 1.0 (Θ_max = 689 and β_max = 1,378,000 s^-1). Any combination of Θ_max and β_max values between these extremes is consistent with our experimental observations. Our results allow us to conclude only that the minimum AChR channel-opening time is >0.72 μs.

We next considered the possibility that Φ was not constant throughout the αD97 mutant series. In our experiments, a Hammond effect might progressively reduce the Φ value as the αD97 mutations progressively increase the gating equilibrium constant. Although we do not know whether, or the precise manner by which, Φ might change, we wanted to examine how a sliding Φ value in the fast-opening mutant series would bias our β_max estimate.

Because we know of no combination of point mutation and agonist that specifically increases the channel-opening rate constant beyond that of αD97/ACh, we were forced to estimate the asymptotic limit of τ_b by fitting by the appropriate analytical function for a constant Φ, which is a rectangular hyperbola (17). A gradual decrease in Φ in the αD97 mutant series (from 1 toward zero) would obviate the use of this exact function. Thus, we wanted to test the possibility that our use of the “wrong” fitting function led us to underestimate the true, asymptotic limit of the burst duration.

The function relating Φ to the overall gating equilibrium constant is unknown. Therefore, we could not derive an exact expression for fitting the τ_b vs. 1/k^* relationship. As a first approximation, we assumed that the relationship between Φ and the natural logarithm of the equilibrium constant (ΔG₀) is linear (δΦ/δΔG₀ is constant), so that Φ would progressively decrease from 0.9 to 0.2 during the course of the αD97 mutant series. The results of using this assumption indicate that the τ_b vs. 1/k^* relationship is indeed altered by this progressive reduction in Φ but in a manner that is inconsistent with the observed difference between the fast-opening and slow-closing series (data not shown). As Φ shrinks, the effect of the change in equilibrium constant is increasingly manifest as a reduction in α, which in turn increases the observed τ_b values more steeply than otherwise. In contrast, our results show a less-steep increase in the observed τ_b values in the fast-opening mutants (Fig. 2). We conclude that a Hammond effect would not impact our estimate of the τ_b asymptote.

Brief Gaps. In both WT and mutants AChRs a short-lived (<30 μs) nonconducting state was apparent (Fig. 1). These events are too long-lived to reflect sojourns in A₂C and are too frequent to reflect first-order channel-block by the agonist. These events, which have been reported previously in AChRs (21), may represent sojourns in nonconducting diliganded states that are distal to A₂O (22) or, perhaps, that populate the A₂C ⇄ A₂O transition-state ensemble (A.A., unpublished work). Because these brief gaps were key determinants of our τ_b measurements, we imposed a dead time of 200 μs to test whether the speed-limit estimate was sensitive to their detection. This change in procedure had a significant effect on the asymptote estimates (70.2 to 15.7 s^-1 for the slow-closing series, and 140 to 59 s^-1 for the fast-opening series) but only a small effect on the β_max estimate (1.4–2.2 μs^-1, assuming a Φ of 1.0). Thus, our estimate of the maximum opening rate constant is not highly sensitive to the detection of these short-lived events.

Interpreting the Speed Limit. Two-state reactions are often rationalized using absolute rate theories, which codify a rate constant (λ) as the product of an exponential term (which contains E^‡, the threshold activation energy) and a preexponential term (A^*).

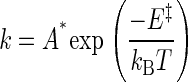[5]

k_B is Boltzmann's constant and T is the absolute temperature. The prefactor, A^*, is not precisely defined for a chemical reaction as complex as protein conformational change, but it incorporates a term for reaching the transition state once the activation energy has been achieved and a term for actually crossing through the transition state once it has been reached. In Kramers' theory (23, 24), the reaction is assumed to proceed in one dimension along a double-well potential energy profile, in which case A^* is a function of the curvature of the reaction-well and barrier top plus a continuum frictional coefficient. These parameters have not been estimated from first principles or from experimental observations for AChR gating. Nonetheless, a rate constant will reach an upper limit (speed limit) if E^‡ reaches a minimum value, which may be zero, in which case the limit, by definition, reflects only A^*. Note that in Eq. 5, A^* is an empirical factor that may be different from the theoretical form of the Kramers prefactor (25). We start with this standard formalism to consider several (nonexclusive) mechanisms by which the experimental value of the apparent AChR channel-opening rate constant could reach an upper boundary.

There are several mechanisms by which β could reach a maximum: (i) the binding site and residue perturbations may not have been energetically independent; (ii) there could be a residual energy barrier(s) along the reaction pathway; or (iii) E^‡ is zero (i.e., the reaction energy profile has no barrier) and, hence, β_max reflects A^*.

The speed-limit estimation was predicated on the assumption that perturbations of residue αD97 (a side-chain substitution) and the transmitter binding sites (a change in the agonist) were independent. For example, we assumed that a 152-fold (5.0 k_BT) increase in the reaction equilibrium constant caused by a D-to-A substitution at α97 and a 560-fold (6.3 k_BT) increase caused by a choline-to-ACh substitution at the transmitter binding sites together result in a 85,120-fold (11.3 k_BT) increase in the gating equilibrium constant, Θ. E^‡ might appear to reach some non-zero, lower limit if this assumption of energetically independent contributions of perturbations is not valid. Where it has been measured directly, many AChR perturbations do behave independently with respect to changing Θ (26). Moreover, the two kinds of perturbation that we used influence the diliganded gating equilibrium constants by different mechanisms. αD97 mutations increase Θ by increasing the unliganded gating equilibrium constant, whereas the choline-to-ACh perturbation increases Θ by increasing the closed/open equilibrium dissociation constant ratio. However, we have no way of testing experimentally whether these two perturbations were indeed independent. In addition, it is possible that these sites behave independently with small perturbations (which elicit rate constants that are in a measurable range) but fail to do so with large excursions in energy.

The second possible explanation for the apparent channel-opening speed limit is that the perturbations at α97 and the transmitter binding sites indeed lower E^‡ in an independent (i.e., energetically additive) manner but that a residual energy barrier(s) along the reaction pathway that was previously too small to contribute significantly to the reaction equilibrium/rate constants now becomes rate-limiting. This mechanism would constitute a change in the transition state, as has been suggested to occur in unliganded AChR gating (27). Although we cannot exclude this possibility, our experiments indicate that the net equilibrium constant for the residual reaction(s) is ≈675 and that this equilibrium constant does not seem to be affected by the mutations and agonists that we have examined.

The third possibility is that at the channel-opening speed limit E^‡ ≈ 0 and that the AChR gating reaction has essentially no activation barrier. In this case, the maximum rate constant is equal to the prefactor, A^*. In these experiments when Θ = 1, which we will call the intrinsic gating condition, the opening and closing rate constants are each ≈2,000 s^-1. Accordingly, we calculate (Eq. 5, with A^* = 0.86 × 10⁶ s^-1) that the intrinsic activation energy for diliganded AChR gating is ≈6.1 k_BT. This estimate is in the range of that estimated using a completely different method (A. Mitra, R. Tascione, A.A., and S. Licht, unpublished work). We have no way of distinguishing between these alternatives.

Natural Selection. Is there a physiological consequence to the gating speed limit that makes it subject to natural selection? Using rate constants that pertain to the mouse neuromuscular synapse (see Materials and Methods), we calculate that synaptic decay time constants (τ_b) are essentially the same with (0.87 ms) and without (0.89 ms) the incorporation of a speed limit. However, for a naturally occurring human AChR mutation that causes a slow-channel congenital myasthenic syndrome [αS269I (12)], we calculate decay time constants of 8.4 ms and 10.2 ms, with and without a speed limit. The experimental τ_b for this construct was 8.3 ms. The existence of a speed limit suggests that in AChRs having a WT dissociation rate constant, the ratio β/k_-2 cannot exceed ≈17 (Eq. 3). Under extreme conditions, the imposition of a channel-opening speed limit can serve as a protective mechanism that shortens the synaptic current decay time constant.

Other Proteins. There have been estimates of speed limits for protein folding (in a microsecond time scale) and intrachain contact formation in unfolded polypeptide chains (in a nanosecond time scale) (28–38). However, there is little known about speed limits for conformational change in native proteins. Eaton et al. (39) estimated that the time required for communication between subunits in hemoglobin during the R-to-T allosteric transition is ≈1 μs. With regard to ion channels, a fast component of the Shaker gating current has a time constant of ≈5 μs and has been interpreted as arising from the diffusion of charges in a potential well (40–42). In gramicidin, the open-channel noise spectrum has an ≈1-μs component that has been attributed to structural fluctuations of pore residues (43). Our estimate for the speed limit for AChR gating, which we deduced indirectly using a simple kinetic model and low-bandwidth recordings, is similar to these direct measurements of the fastest rates for native protein conformational change.

It is remarkable that the AChR, a large, multimeric membrane protein, can undergo a global isomerization in ≈1.2 μs given that slow side-chain motions in native structures (44) would be expected to slow substantially the dynamics of conformational change. In a companion study (45), the observation that residues are organized into discrete, rigid-body gating domains (“blocks”) and the channel-opening speed limit are discussed in terms transition-state energy profiles that are consistent with the Brownian motion of individual blocks.