On contribution of known atomic partial charges of protein backbone in electrostatic potential density maps

Abstract

Partial charges of atoms in a molecule and electrostatic potential (ESP) density for that molecule are known to bear a strong correlation. In order to generate a set of point‐field force field parameters for molecular dynamics, Kollman and coworkers have extracted atomic partial charges for each of all 20 amino acids using restrained partial charge‐fitting procedures from theoretical ESP density obtained from condensed‐state quantum mechanics. The magnitude of atomic partial charges for neutral peptide backbone they have obtained is similar to that of partial atomic charges for ionized carboxylate side chain atoms. In this study, the effect of these known atomic partial charges on ESP is examined using computer simulations and compared with the experimental ESP density recently obtained for proteins using electron microscopy. It is found that the observed ESP density maps are most consistent with the simulations that include atomic partial charges of protein backbone. Therefore, atomic partial charges are integral part of atomic properties in protein molecules and should be included in model refinement.

Introduction

Examination of electrostatic potential (ESP) maps recently obtained for macromolecules from cryo‐electron microscopy (EM) shows that experimental ESP density is very sensitive to partial and full charges of atoms, particularly those of negative charges.1, 2, 3 For exactly the same reason, atomic partial charges for each of 20 amino acids have been derived using restrained partial‐charge fitting procedures into well‐behaved theoretical ESP density, which has been obtained using condensed‐phase quantum mechanical calculations for 20 capped dipeptide models by Kollman and coworkers.4 These atomic partial charges provide the basis for AMBER (Assisted Model Building with Energy Refinement) point‐charge force field parameters for structural biology.5

This study examines how partial charges affect the appearance of ESP features for protein backbone relative to what are expected using neutral atomic models, and how well established atomic partial charges fit experimental EM data. Because partial charges of protein backbone atoms are dependent on backbone torsion angles, two most common torsion angles, namely α‐helix and β‐strand regions, are selected here for computer simulations as was done so previously using quantum mechanical calculations.4, 6 The experimental ESP density recently published for corresponding α‐helix and β‐strand regions inside protein cores are selected for comparison. This examination is also extended to include the chiral volume of backbone Cα‐atom and its chirality features.

Results

Simulations of electrostatic potentials with partially charged protein backbone

Appearance in the ESP density for protein backbone ψ _Total(r) due to partial charges is simulated by separating the component ψ _o(r) of neutral atom from the component ψ _Δ(r) of its partial charge: ψ _Total(r) = ψ _o(r) + ψ _Δ(r) (see Methods section). Partial charges are taken from average values from studies by Kollman and coworkers [Fig. 1(A)].4, 6 Residues selected for simulation are from β‐galactosidase (bGAL) model (PDB accession code: 5A1A).7

Figure 1.

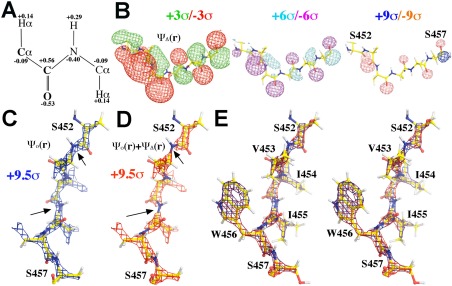
Simulated ESP density for protein backbone. A: Charge assignment for protein backbone atoms. B: ESP density generated by partial charges alone, ψ _Δ(r), at three contour levels, +3σ (green)/–3σ (blue), +6σ (cyan)/–6σ (magenta), and +9σ (blue)/–9σ (salmon). C: ESP density generated map by neutral atoms alone, ψ _o(r), contoured at +9.5σ (blue), rotated by 90° relative to (B) along the viewing axis. D: Total ESP density map by both neutral atoms and backbone partial charges, ψ _o(r) + ψ _Δ(r), contoured at +9.5σ (red). Arrows indicate where visible effects are observed due to partial charges. E: Stereodiagram of (C) and (D) but with all side chain atoms included. See Supporting Information Figure S1 for additional views of the simulations.

Strong interactions between atomic partial charges in different peptide units are evident in simulated ESP density function [Fig. 1(B)]. Even though carbonyl O atom in each peptide unit is given the same value of −0.53e, resulting negative ESP density ψ _Δ(r) for each O atom varies greatly along the polypeptide chain [Fig. 1(B)]. This is because an unshielded charge added to a neutral atom can generate a long‐range electric field that extends far beyond the van der Waals radius (plus positional uncertainty) of the atom. The strength of electric field is inversely proportional to distance. Although the partial charge assigned for the N atom in each peptide unit is −0.40e, the effect of this charge at low resolution is not so visible, partly due to cancellation by the effect of a positive charge of +0.56e assigned to the C atom nearby in the simulated ψ _Δ(r) map. Nonetheless, at ∼+6σ contour level, the presence of the positive charge on C atom is clearly visible in all peptide units in the combined ψ _Total(r) map in simulation [Fig. 1(D)].

In neutral model, variations along the linear chain of the Cα—C—N—Cα peptide are relatively small viewed at the highest contour level of +9.5σ [Fig. 1(C)]. Having −0.40e assigned to N atoms and +0.56e to C atoms in simulation dramatically changes the appearance of the summed ESP density: N atoms have a reduced total ESP value, and C atoms have an increased one [Fig. 1(D), Supporting Information S1]. This results in visible gaps at all the N atoms along the polypeptide chain at the highest contour levels. Because this polypeptide taken from bGAL from residues S452 to S457 contains no charged side chain,7, 8 the changed appearance of ESP density is largely contributed by partial charges in backbone atoms [Fig. 1(E)]. In all the remaining simulations done in this study, charges in ionized side chains were not included so that the altered ESP density for backbone is purely due to partial charges of backbone atoms, that is, dipole moments of peptide backbone.

On the appearance of protein peptide bonds in experimental ESP maps

An ESP density map was recently reported for bGAL (EMDB‐2984/PDB‐5A1A) at 2.2 Å resolution,7 and corresponding X‐ray structure was determined at 1.60 Å resolution (4TTG).8 Least superposition of 4TTG coordinates onto 5A1A shows that the X‐ray derived 4TTG coordinates fit the experimental ESP map far superior to the EM‐derived 5A1A coordinates for the majority of residues.2 Thus, that X‐ray atomic model was chosen for simulations in this analysis after H atoms were added.

An examination of the EMBD‐2984 ESP map7 shows that the highest ESP density features are invariably on the carbonyl C atoms of backbones in the most ordered part of the structure, including both α‐helix and β‐strand regions, for example, visible at ∼+7σ contour level (Fig. 2, Supporting Information S2). The gaps on the all the N atoms along the Cα—C—N—Cα peptide chains are clearly visible at ∼+5σ (Fig. 2, Supporting Information S2). There is very little ESP density for carbonyl O atoms (Fig. 2, Supporting Information S2). These experimental features are consistent with the theoretical ESP density simulated with backbone atomic partial charges included. These features are not unique to bGAL alone, and they are present in all other high‐resolution EM maps examined so far, including an EM map for glutamine dehydrogenase being reported at 1.8 Å resolution.9

Figure 2.

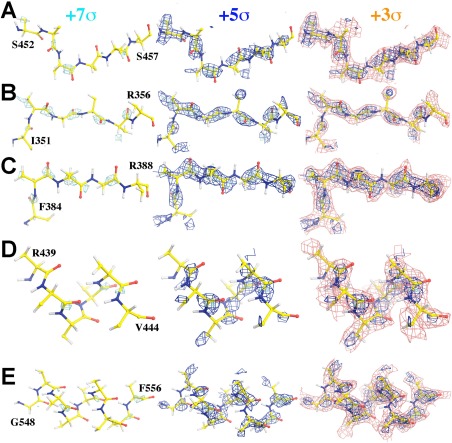
Carbonyl C atom has the highest experimental ESP density in bGAL protein backbones.7 Only β atoms of side chains are kept in this figure along with the backbone atoms. Five stretches of polypeptide backbones are displayed, three in β‐strand (A–C) and two in α‐helix (D,E) superimposed onto the experimental ESP map contoured at +7σ (cyan), +5σ (blue), and/or +3σ (salmon). Stereodiagrams of the last panel for all five stretches of peptide backbones can be found in Supporting Information Figure S2.

An average view of experimental ESP maps for protein backbone structure

An examination of the EMBD‐2984 map7 for backbone Cα chiral centers in bGAL shows that the experimental ESP features for the Cα atom and three non‐H atoms connected to Cα appear to be nearly coplanar, which are distinctively different from the corresponding experimental electron density (ED) map from X‐ray data (Fig. 3, Supporting Information S3).8 They also differ from simulated ESP density using neutral atoms at similar resolution (Fig. 1), suggesting that some atomic partial charges at the Cα centers have altered its ESP appearance.

Figure 3.

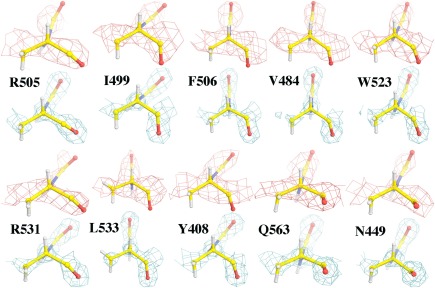
The experimental ESP map7 contoured at +4.0σ (salmon) superimposed onto selected Cα chiral centers, and compared with corresponding electron‐density map8 at 1.6 Å resolution contoured at +3.0σ (cyan). See Supporting Information Figure S3 for additional views of chiral Cα centers.

The appearance of experimental ESP density for peptide units and Cα centers seen individually can be averaged to generate an average view (Fig. 4). This was done by selecting 20 sets of 4‐atom (Cα—CO—N) or 5‐atom (Cα—CO—N—Cα) peptide unit, or 20 sets of 5‐atom Cα unit (CO—Cα—Cβ/N) as single rigid body for least square alignment, followed by averaging their corresponding density. Selection was manually carried out based on visual inspection to be considered the best‐defined regions of the BGal structure in the experimental ESP map. Additionally, the experimental ESP values were also directly evaluated on each atom in rigid units and then averaged for each atom (assuming that coordinate errors were relatively small). Average ESP densities with standard deviations for the Cα—CO—N—Cα rigid peptide unit are 73 ± 19, 100 ± 18, 53 ± 19, 71 ± 20, and 73 ± 12, respectively, with the descending ESP order of C > Cα > N > O (Fig. 4). For the Cα centers of the N—Cα(Cβ)—C rigid unit, they are 64 ± 16, 73 ± 19, 54 ± 26, and 100 ± 18, respectively, with the descending ESP order of C > Cα > N > Cβ (Fig. 4). This suggests that partial charges indeed play an important role in the variations observed in the experimental ESP density.

Figure 4.

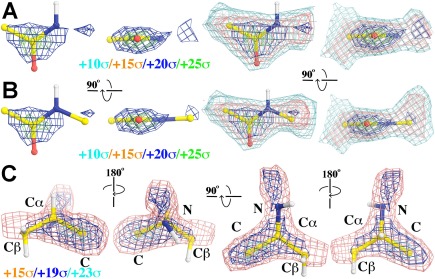
Averaged experimental ESP density maps. A: Using four non‐H atoms of 20 four‐atom peptide units in averaging, contoured at +10σ (cyan), +15σ (salmon), +20σ (blue), and +25σ (green). B: Using 20 five‐atom peptide units in averaging. C: Averaged experimental ESP map for 20 five‐atom chiral Cα centers in four different views contoured at +15σ (salmon), +19σ (blue), and +23σ (cyan).

For comparison, ED values for the same sets of the peptide and Cα center rigid units were also evaluated using X‐ray diffraction data8 reported for 4TTG. The atomic model was re‐refined with R‐factor of 9.6% and free R‐factor of 14.9% from the originally reported values of 16.0% and 18.8% at 1.60 Å resolution. Phases from re‐refined model were used for ED valuations. This data set has Wilson B‐factor of 18.7 Ų at 1.60 Å nominal resolution. To reduce the nominal resolution to match that of experimental ESP maps at ∼2.2 Å resolution, the observed amplitudes were blurred by Wilson B‐factor ΔB = +14.0 Ų. Averaged densities with standard deviations for the Cα—CO—N—Cα rigid peptide unit are 100 ± 75, 100 ± 85, 159 ± 90, 116 ± 74, and 95 ± 68, respectively, with the descending order of O > N > C = Cα. For Cα centers of the N—Cα(Cβ)—C rigid unit, they are 159 ± 90, 100 ± 75, 115 ± 59, and 100 ± 85, respectively, with the descending order of N > Cβ > C = Cα.

Discussion

Large partial charges in protein backbone atoms

Computer simulations here for theoretical ESP density from charged atomic models using electron scattering factors, convoluted with atomic positional uncertainties as measured by atomic B‐factors to a given nominal resolution, have unambiguously shown that atomic partial charges in protein backbone peptides can significantly modify the appearance of ESP density simulated using neutral atomic models (Fig. 1). This is qualitatively consistent with the appearance of experimental ESP density published previously and analyzed here for protein backbone (Fig. 2), as well as with results of all theoretical calculations previously done (with stationary atoms at infinite resolution).10, 11

The reason that backbone atoms have large partial charges is attributable to the high polarizability of the conjugated π‐system of peptide unit. Actual partial charges for backbone atoms in each peptide unit are likely to vary, which is evident in the simulated ESP density due to interactions with unshielded partial charges in other peptide units [Fig. 1(B)], and with any other charges nearby such as charged side chains and/or ions if they exist. For example, a protonated Lys side chain generates an extra electric field centered at Nζ atom that can directly exert on its Cα—Hα bond and the conjugated π‐system of backbone. The strength of this field at the typical distance of ∼4.9–6.4 Å between Nζ and Cα atoms for all of its known rotamers remains about 20% the strength at 1 Å distance.

Recently, it is found that an omission of partial charges of −0.5e on each of two O atoms of carboxylate side chains in atomic models could dramatically affect the accuracy of the models derived for carboxylate sides and other residues nearby from ESP maps.1, 2 Given the fact that any unshielded atomic charge inside protein interior results in long‐range ESP effects, the corresponding electron scattering factor at zero‐scattering angle is infinite. The electron scattering factor of an atom with negative partial charge starts with negative infinite at zero‐scattering angle, and it increases to positive values as increasing resolution, to a maximum before it decreases to the asymptotic value of zero at infinite resolution. Partial charges exist for all protein backbone C, O, N, and Cα atoms as well as for all ionized side chain atoms. Thus, all known atomic partial charges should be included into consideration during interpretation of any experimental ESP map.

The effect of partial charges of protein backbone atoms on the experimental ESP density could be much more significant than that of full charges in ionized atoms of charged side chains. This is because charged side chains are typically on the surface of folded protein structures and partially neutralized by counter‐ions, whereas partial charges of protein backbone atoms are distributed throughout the entire structures of folded proteins, many of which are in interior regions inaccessible to polarizable solvent molecules and with very low dielectric constants. It has been recently demonstrated that extensive counter‐ions are indeed present on many protein surfaces that were not previously detected using conventional X‐ray crystallography,12 which could further complicate the interpretation of ESP density around ionized side chains. In an unfolded state, peptide dipole moment and ionized groups have very short ESP interacting ranges due to polarization effects of solvent molecules. In the folded state, interactions between peptide dipole moments and ionized groups can have very long range terms, and have already been demonstrated to play a dominant effect in protein stability.13 In fact, dipole moments for majority of peptide units in native folds of proteins appear to be aligned with the local electric field generated by the rest of molecule and to have a preferred orientation.14, 15 Thus, ESP interactions may provide some specificity that hydrophobic interactions lack in folded proteins.

Unknown ESP effects on protein Cα centers

The observation made here about the appearance of Cα centers in the EM maps is less well understood (Fig. 3), in part because there is no consensus about partial charges on Cα atoms, which vary in both numbers and signs.11 For example, partial charge for Cα atom was given +0.20 in CHARMM (Chemistry at Harvard Macromolecular Mechanics) parameter set,16 which was also used in X‐PLOR/CNS (X‐ray and NMR system),17 but differs from ones taken from AMBER point‐charge force field parameters used in this study.5 The three most negative partial charges assigned to Cα atom in the AMBER force field are Thr (–0.271e), Arg (–0.131e), and Gly (–0.129e) residues.5 It has been shown that formation of a hydrogen bond (HB) can introduce large chemical‐bonding effects on resulting ESP density.18 The effect of this kind has not yet been included in the dipeptide calculations done by Kollman and coworkers.4, 5, 6

It has been proposed that the Cα—Hα bond may also have a large polarizability, and can be polarized to donate its Hα atom as an HB donor when stereochemistry permits such as in Gly residues.19, 20, 21, 22 In this case, Cα has a negative partial charge and Hα has a positive value. Unfortunately, stereochemistry of most non‐Gly residues would preclude an HB acceptor to approach Hα atoms because HB acceptor typically has a large van der Waals radius. Nonetheless, the presence of charges nearby could polarize the Cα—Hα bond in some ways. For this reason, Hα atoms of Lys and Arg residues in dipeptide models exhibit higher acidity than those of Asp and Glu residues even though their intra‐residue geometry is not ideal for the bond polarization of this kind.4, 5, 6 It is possible that the contribution of Hα atom in total ESP density may appear minimized due to the lack of spatial resolution for directly observing the positions of H atoms in EM maps. Given the fact that the precise reason for the ESP density features observed for Cα centers remains unknown, the best approach in modeling is to use idealized Cα chiral volumes to rigid‐body fit into the EM maps.

Chemical‐bonding interactions and valence electrons

Henderson and coworkers have noted that chemical‐bonding interactions between atoms within a molecule make electron scattering factors deviate from theoretical values from neutral atoms.18, 23 Part of these bonding interactions is characterized here as atomic partial charges, contributed mainly by valence electrons. Since valence electrons are typically located at outer orbitals of atoms, they mainly modify scattering factors of both X‐ray and EM data for stationary atoms at < 2.0 Å resolution. With increasing atomic positional uncertainties, the affected resolution decreases further. They have very little or no effects on data of higher resolution > 1.0 Å.

Large partial charge variations observed here in large number of protein atoms in the folded structures suggests the accuracy of protein X‐ray atomic structures may be improved when all the electron‐density distribution of valence electrons are properly taken into account. Currently, protein crystallographers only use neutral atomic scattering factors, which introduce for example errors of ∼13% in X‐ray scattering factor between O and O^– at zero‐scattering angle (and ∼20% between Mg and Mg²⁺ and so on). Given the atomic number is 6, 7, and 8 for C, N, and O atoms of protein atoms, respectively, which represents the total scattering electron of the neutral atom by X‐ray at zero scattering‐angle, the estimated change of X‐ray scattering factor is 8%, 7%, and 6% when an extra partial charge of ∼0.5e is assigned to each of these atoms. This implies that there may be a large room for further improvement for all the protein crystal structures in the PDB, which is critically needed.

Methods

Average partial charges are taken from studies by Kollman and coworkers for simulations of ESP density described here.4, 6 On average from all 20 amino acids, the mean partial charges for backbone carbonyl O and C atoms are −0.53 ± 0.05 and +0.56 ± 0.10 atomic units, respectively, and it is −0.40 ± 0.10 for amide N atom [Fig. 1(A)]. It is −0.04 ± 0.08 for Cα atom of all the 20 amino acids, but decreases to −0.09 ± 0.07 when the seven amino acids having positive partial charges for Cα atom are excluded. Among the top 10 most acidic Hα atoms bonded to Cα atoms, the mean partial charge is 0.14 ± 0.02, which has a very small standard deviation. When all the 20 amino acids are included in average, its mean value is 0.10 ± 0.05. The mean partial charge for H of the amide N—H bond is 0.29 ± 0.05 for 19 amino acids, which is about twice and three times that of partial charges of Hα in the Cα—Hα bond.

It is assumed as an approximation here that addition of a partial charge to a neutral atom or subtraction from it does not alter core ED distribution of the neutral atom. Thus, partial charge can be added to neutral atom using the Mott equation [Eq. (8)].24

$$\begin{array}{l}{f}^{(e)}(s)=\frac{m_0{e}^2}{8\pi {\epsilon }_0{h}^2}\frac{\left[\left(Z+\Delta Z\right)-f^{(X)}(s)\right]}{s^2}\\ =\left\{\frac{m_0{e}^2}{8\pi {\epsilon }_0{h}^2}\frac{\left[Z-f^{(X)}(s)\right]}{s^2}\right\}+\left\{\frac{m_0{e}^2}{8\pi {\epsilon }_0{h}^2}\frac{\left[\Delta Z\right]}{s^2}\right\}\\ =f_0^{(e)}(s)+f_{\Delta }^{(e)}(s)\end{array}$$ (1)

where f ^{( e )} is electron scattering factor for a charged atom, Z is its atomic number, ΔZ is partial charge, f ^{( X )} is X‐ray scattering factor for the corresponding neutral atom, m ₀ is the stationary mass of the electron, e is the charge of the electron, h is the Planck constant, the electron scattering factor is divided into two parts, the neutral atom $f_0^{(e)}(s)$ and partial charge $f_{\Delta }^{(e)}(s)$ (also see Ref. 25 for additional discussion).

The structure factors for molecular ESP density are summation of independent atomic functions, and simulations for molecular ESP maps were carried as described elsewhere convoluted with atomic positional uncertainties that are characterized by Wilson B‐factors for given nominal resolution.1, 2 However, simulated molecular ESP density maps for charges and neutral atoms were kept apart before being combined in this study.

$${\psi }_{\text{Total}}\left(r\right) ={\psi }_{\mathrm{o}}\left(r\right) +{\psi }_{\Delta }\left(r\right)$$ (2)

X‐ray coordinates taken from 4TTG after refitting into bGAL EM maps at 2.2 Å resolution (EMDB‐2984)7, 8 were used for simulation. Uniform B‐factor of 32 Ų was assigned for all atoms, which corresponds an average resolution of 2.2 Å for X‐ray structures in the PDB. Simulations were further extended to 1.5 Å resolution without additional B‐factor sharpening so that terms added between 2.2 Å and 1.5 Å resolution are relatively small (Fig. 1). In addition, part of simulations were carried out using uniform B = 16 Ų, that is, sharpened with ΔB = −16 Ų relative to average B‐factor for X‐ray structures at 2.2 Å resolution [Supporting Information Fig. S1(B)]. Selected experimental EP maps were rotated and translated to align onto a reference frame for density averaging using the RAVE and CCP4 packages.26, 27 Both ED and ESP maps were visualized using the graphics program Coot.28 Figures were made using the program Pymol.29

Conflict of interest

The author declares no conflict of interest in publishing results of this study.

Supporting information

Supporting Information Figure 1.