Mathematical model of chronic pancreatitis

Significance

Chronic pancreatitis is a progressive inflammatory disease that inflicts hundreds of thousands of people annually in the United State alone, and it has no effective treatment. In the present paper we develop a mathematical model of the progression of the disease and use the model to evaluate the effect of two potential drugs, anti-TNF-$\alpha$ and anti-IL-6. The model is represented by a system of partial differential equations with carefully estimated parameters. The simulation of the model shows that both drugs can reduce significantly the progressive fibrosis of the pancreas. The model has the potential to generate an interesting clinically testable hypothesis.

Abstract

Chronic pancreatitis (CP) is a progressive inflammatory disease of the pancreas, leading to its fibrotic destruction. There are currently no drugs that can stop or slow the progression of the disease. The etiology of the disease is multifactorial, whereas recurrent attacks of acute pancreatitis are thought to precede the development of CP. A better understanding of the pathology of CP is needed to facilitate improved diagnosis and treatment strategies for this disease. The present paper develops a mathematical model of CP based on a dynamic network that includes macrophages, pancreatic stellate cells, and prominent cytokines that are present at high levels in the CP microenvironment. The model is represented by a system of partial differential equations. The model is used to explore in silico potential drugs that could slow the progression of the disease, for example infliximab (anti-TNF-$\alpha$) and tocilizumab or siltuximab (anti-IL-6/IL-6R).

Chronic pancreatitis (CP) is a continuous or recurrent inflammatory disease of the pancreas characterized by progressive and irreversible morphological changes (scarring). Extensive fibrosis and inflammation often lead to exocrine and endocrine insufficiency (1). Symptoms include persistent abdominal pain, steatorrhea, nausea, and vomiting (2, 3). In the United States, CP results in 56,000 hospitalizations each year and 122,000 outpatient visits. The disease usually begins in adulthood and is more common among men. No curative treatment for CP exists. Medical treatment of this condition includes pain control with analgesic agents and replacement of pancreatic enzymes (1–5).

The etiology of CP is complex and multifactorial (2, 5). Recurrent attacks of acute pancreatitis (AP) are thought to precede the development of CP. Factors that may increase risk of recurrent AP or CP include alcohol abuse, gallstones, genetic mutations, autoimmunity, hypercalcemia, the use of certain prescription medications, steroids, trauma, and others. Still, a large number of cases of CP are considered idiopathic. A better understanding of the pathology of CP is needed to facilitate improved diagnosis and treatment strategies for this disease (6–8).

One cell type known to contribute to CP pathology is the pancreatic stellate cell (PSC). PSCs are myofibroblast-like cells that reside in the periacinar regions of the pancreas in a quiescent state (4, 9). Quiescent PSCs contribute to maintenance of proper tissue architecture by regulating the synthesis of extracellular matrix (ECM) (10). Upon stimulation, these PSCs become activated, migrate to injured locations, promote inflammation, and secrete ECM proteins. During CP, PSCs remain persistently activated and are hypothesized to play a pivotal role in the development of CP by facilitating sustained inflammation and fibrosis in the organ (11–13).

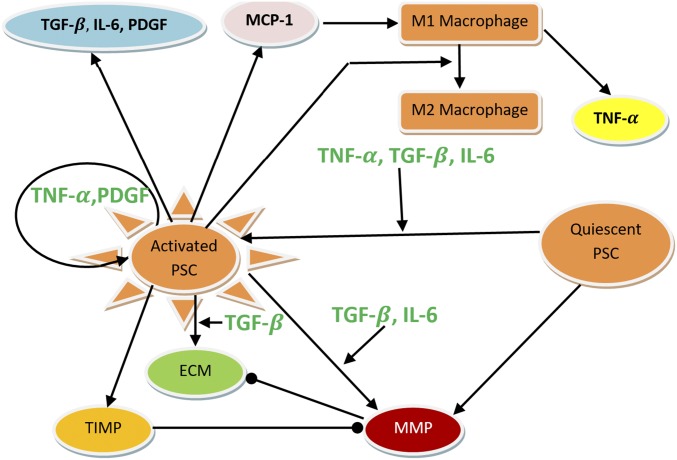
These pathological processes are orchestrated by PSCs, in conjunction with parenchymal and immune cells, via the secretion of soluble signaling factors, including cytokines and chemokines. Interactions between these mediators and the cells of the pancreatic microenvironment are complex and dynamic. During pancreatic inflammation, endothelial cells secrete monocyte chemoattractant protein (MCP-1) (14–19), triggering recruitment of monocytes from the blood into the inflamed area (20, 21). Upon entering the pancreas, monocytes differentiate into macrophages, which secrete tumor necrosis factor alpha (TNF-$\alpha$) (22, 23) and interleukin 6 (IL-6) (24, 25). TNF-$\alpha$ and IL-6 from macrophages, along with other soluble factors, are then capable of causing PSC activation. Once active, PSCs and other inflammatory subsets of fibroblasts secrete proinflammatory cytokines, including platelet-derived growth factor (PDGF), transforming growth factor beta (TGF-$\beta$) and IL-6 (9, 10, 24–27) as well as MCP-1 (14–19). Furthermore, a recent study (28) shows that IL-4 and IL-13 secreted by PSCs preferentially change classically activated macrophages M1 to alternatively activated macrophages M2, which secrete IL-10, TGF-$\beta$, and PDGF. The resultant mixture of cytokines and chemokines in the inflamed pancreas is quite dynamic and characterized by other interactions between these factors. For example, PSC activation may be enhanced by autocrine and paracrine of TGF-$\beta$ (in addition to IL-6 and TNF-$\alpha$) (9, 10, 27). TNF-$\alpha$ and PDGF increase proliferation of active PSCs (APSCs) (9, 10, 12, 29–33), whereas TGF-$\beta$ and IL-6 decrease the proliferation of APSCs (9, 10). Conversely, the production of matrix metalloproteinases (MMPs) (34) and tissue inhibitors of metalloproteinase (TIMP) was enhanced by these same cytokines (34). Taken together, the activation of PSCs is enhanced by TGF-$\beta$, PDGF, and TNF-$\alpha$ (10).

The above processes are summarized in Fig. 1. We did not include in Fig. 1 IL-1 and IL-10, both of which are produced by macrophages. IL-1 and IL-10 are known to affect both the activation and proliferation of PSCs (10), similar to IL-6. For simplicity, however, we do not account for them explicitly and use IL-6 to implicitly represent their activity by adjusting parameter values associated with IL-6.

Fig. 1.

Interaction of cells and cytokines in CP. Arrows represent activation or secretion, and circular heads represent inhibition. Circular arrow (about the activated PSC) means increased proliferation, and circular head means decreased proliferation.

Due to the complexity of these interactions, as well as the synergistic and pleotropic effects of such signaling molecules, it is necessary to better understand—in a quantitative manner—the way each signaling node may affect PSC activation, inflammation, and fibrosis to contribute to CP pathology. Mathematical modeling of these interactions would identify the most relevant targets for future therapies, including neutralizing antibodies against specific cytokines. Such therapies have not been tested in the context of CP.

In the present report, we have developed a mathematical model of cytokine interactions that influence PSCs in the setting of CP. Simulations of the model show significant increases in TNF-$\alpha$, TGF-$\beta$, IL-6, and PDGF in the pancreatic tissue of patients. These predictions were in agreement with clinical data. The model was then used to explore the impact of treatment with anti-IL-6 and anti- TNF-$\alpha$ drugs on this physiological system.

Mathematical Model

The mathematical model for CP includes quiescent PSCs and APSCs. Based on the interactive network in Fig. 1, we include in the model the following densities of cells and concentrations of cytokines:

All terms are in units of grams, centimeters, and days.

Equations for Quiescent PSC (${\text{𝑷}}_{\mathit{\text{0}}}$) and Activated PSC (P).

The evolution of the densities of quiescent and activated PSCs is modeled by the equations

$$\frac{\partial P}{\partial t}-D_P\mathrm{\Delta }P=\underset{migration}{\underbrace{-\nabla ({\chi }_{G}P\nabla G)}}\underset{proliferation}{\underbrace{+({\lambda }_P\frac{T_{\alpha }}{K_{T_{\alpha }}+T_{\alpha }}+{\lambda }_{PG}\frac{G}{K_G+G})P}}\underset{activation}{\underbrace{+({\lambda }_{P{T}_{\alpha }}\frac{T_{\alpha }}{K_{T_{\alpha }}+T_{\alpha }}+{\lambda }_{P{T}_{\beta }}\frac{T_{\beta }}{K_{T_{\beta }}+T_{\beta }}+{\lambda }_{P{I}_6}\frac{I_6}{K_{I_6}+I_6})P_0}}\underset{death}{\underbrace{-d_{P}P}},$$ [1]

$$\frac{\partial P_0}{\partial t}-D_{P_0}\mathrm{\Delta }{P}_0=\underset{source}{\underbrace{A_{P_0}}}\underset{activationofP}{\underbrace{-({\lambda }_{P{T}_{\alpha }}\frac{T_{\alpha }}{K_{T_{\alpha }}+T_{\alpha }}+{\lambda }_{P{T}_{\beta }}\frac{T_{\beta }}{K_{T_{\beta }}+T_{\beta }}+{\lambda }_{P{I}_6}\frac{I_6}{K_{I_6}+I_6})P_0}}\underset{death}{\underbrace{-d_{P_0}{P}_0}},$$ [2]

where $K_{T_{\alpha }}$, $K_G$, $K_{T_{\beta }}$, and $K_{I_6}$ are the half-saturation values of TNF-$\alpha$, PDGF, TGF-$\beta$, and IL-6, respectively. The first term on the right-hand side of Eq. 1 is the migration of PSCs by chemotaxis induced by PDGF (31). The proliferation of APSCs is enhanced by TNF-$\alpha$ (9, 10, 35) and PDGF (12, 29–33). As reported in ref. 10, IL-6, at the very large concentration of ${10}^{-8}$ g/mL, inhibited the proliferation of PSCs, but because the concentration of IL-6 in tissue is of the much smaller order of ${10}^{-10}$ g/ml, we do not include such inhibition. The PSCs are activated by TNF-$\alpha$, TGF-$\beta$, and IL-6 (9, 10, 27).

Equations for MCP-1 (C).

The MCP-1 equation is given by

$$\frac{\partial C}{\partial t}-D_C\mathrm{\Delta }C=\underset{production}{\underbrace{{\lambda }_{CE}{I}_D+{\lambda }_{CP}P}}\underset{degradation}{\underbrace{-d_{C{M}_1}\frac{C}{K_C+C}{M}_1-d_{C}C}},$$ [3]

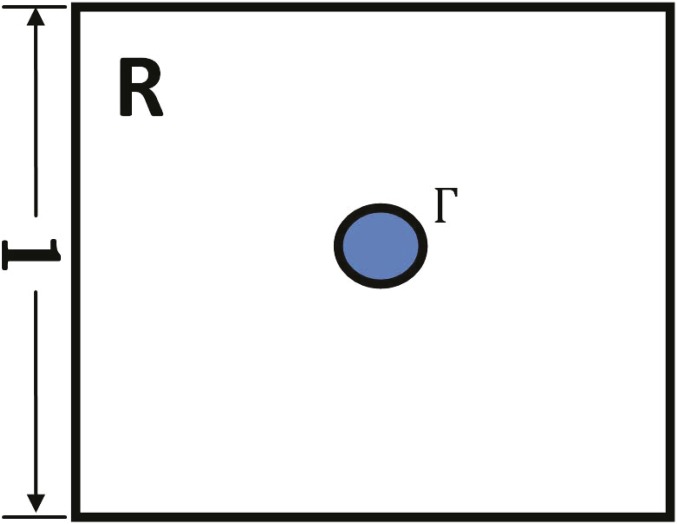
where $I_D$ is the characteristic function of the injured area $D$ in the pancreas, which gives rise to the initial inflammation (Fig. 2). The second term on the right-hand side accounts for the production of MCP-1 by activated PSCs (14–19). MCP-1 is a chemoattractant to M1 macrophages and is therefore internalized by macrophages (the third term) (36, 37).

Fig. 2.

Domain $\mathrm{\Omega }$ with an injured (initially inflamed) area $D$.

Equations for Macrophages (${\text{𝑴}}_{\text{𝟏}}$ and ${\text{𝑴}}_{\text{𝟐}}$).

As reported in ref. 28, in chronic pancreatitis IL-4 ($I_4$) and IL-13 ($I_{13}$) produced by active PSCs preferentially change M1 to M2 macrophages. The velocity of change can be modeled by $(c_1\frac{I_4}{K_{I_4}+I_4}+c_2\frac{I_{13}}{K_{I_{13}}+I_{13}})M_1$, where

$$\frac{d{I}_4}{dt}={\lambda }_{4}P-d_4{I}_4,\hspace{1em}\frac{d{I}_{13}}{dt}={\lambda }_{13}P-d_{13}{I}_{13}.$$

Because the cytokine dynamic is much faster than cell dynamics, we use the steady-state approximation to conclude that IL-4 and IL-13 concentrations are proportional to $P$. Hence the velocity of change from M1 to M2 is modeled by $\beta (P)M_1$, where $\beta (P)=\beta \frac{P}{K_P+P}$.

The evolution of macrophages outside blood vessels is modeled by

$$\frac{\partial M_1}{\partial t}-D_{M_1}\mathrm{\Delta }{M}_1=\underset{chemotaxis}{\underbrace{-\nabla (M_1{\chi }_C\nabla C)}}-\beta (P)M_1-d_{M_1}{M}_1.$$

Here the first term on the right-hand side accounts for recruitment of M1 macrophages by MCP-1 (20), and ${\chi }_C$ is the chemotactic parameter, and the second term is the transition from M1 to M2 macrophages.

Because macrophages are the monocytes that migrated from the blood vessels into the tissue, we assume that $M_1$ satisfies the following boundary condition at the blood vessel’s membrane,

$$\frac{\partial M_1}{\partial 𝐧}+{\alpha }_{\epsilon }(C)(M_1-M_0)=0\hspace{0.17em}\text{on}\hspace{0.17em}\partial {\mathrm{\Omega }}_{\epsilon },$$

where $M_0$ is monocyte density in the blood, and ${\alpha }_{ϵ}(C)$ depends on the MCP-1 concentration, $C$. We assume that the blood vessels (in a cross-section) are distributed according to Fig. 3, and they occupy 5% of the total area.

Fig. 3.

Cross-section of parallel blood vessels. (A) From above. (B) From the side.

Assuming that all of the small circles in Fig. 3 are arranged approximately in a periodic manner and that their diameter $\epsilon$ is small, we can use the homogenization theory (38) to write down the “effective” equation for $M_1$ over the entire tissue,

$$\frac{19}{20}\frac{\partial M_1}{\partial t}-0.8D_{M_1}\mathrm{\Delta }{M}_1=\alpha (C)(M_0-M_1)-\frac{19}{20}(\nabla (M_1{\chi }_C\nabla C)+d_{M_1}{M}_1),$$ [4]

where $\alpha (C)=\alpha \frac{C}{K_C+C}$ ($K_C$ is the saturation level of MCP-1).

Indeed the coefficient $\frac{19}{20}$ arises from the 5% assumption above, and the coefficient $0.8$ arises from the effective diffusion coefficient where ${\nabla }^2$ is replaced by $\sum a_{ij}\frac{{\partial }^2}{\partial x_i\partial x_j}$. The coefficient $a_{ij}$ is computed by

$$a_{ij}={\int }_R\left({\delta }_{ij}+\frac{\partial {\chi }_j}{\partial x_i}\right)dy,$$

where ${\chi }_i$ satisfies the equation

$$\mathrm{\Delta }{\chi }_i=0\hspace{0.17em}\text{in}\hspace{0.17em}R,\frac{\partial {\chi }_i}{\partial n}+n_i=0\hspace{0.17em}\text{on the boundary of}\hspace{0.17em}\mathrm{\Gamma },$$

and ${\chi }_i$ is periodic, with period 1, in the horizontal and vertical directions; here $R$ is a unit square from which a circle located at the center is removed; the area of the circle is 0.5 and its boundary is denoted by $\mathrm{\Gamma }$. (Fig. 4) Computing $a_{ij}$ by finite-element discretization, we find that $a_{11}=a_{22}=\mathrm{\hspace{0.17em}0.8}$ and $a_{12}=a_{21}=\mathrm{\hspace{0.17em}0}$.

Fig. 4.

Homogenization domain.

M2 macrophages satisfy the equation

$$\frac{\partial M_2}{\partial t}-D_{M_2}\mathrm{\Delta }{M}_2=\beta (P)M_1-d_{M_2}{M}_2.$$ [5]

Equation for ECM ($𝝆$).

ECM is produced by both quiescent and activated PSCs (10). The production by $P$ is enhanced by TGF-$\beta$ (12); it is also enhanced by TNF-$\alpha$ and PDGF and is inhibited by IL-6 (10, 12). However, TNF-$\alpha$, PDGF, and IL-6 affect very little the production of ECM in comparison with TGF-$\beta$, and we therefore neglect them in modeling the ECM equation. Finally the ECM is degraded by MMP and remodeled at rate ${\lambda }_{\rho }$, which, for simplicity, is assumed to be a constant. Hence the equation of the density of ECM is given by

$$\frac{\partial \rho }{\partial t}=\underset{production}{\underbrace{{\lambda }_{\rho P}(P_0+P)(1-\frac{\rho }{{\rho }_0})+{\lambda }_{\rho T_{\beta }}\frac{T_{\beta }}{K_{T_{\beta }}+T_{\beta }}P}}\underset{degradation}{\underbrace{-d_{\rho Q}Q\rho -d_{\rho }\rho }}.$$ [6]

Alterations in ECM structure during CP result in enhanced fibrosis and glandular stiffness that may affect PSC activation and cytokine activity within the pancreatic milieu. In one study, Asaumi et al. (39) demonstrate that activation of PSCs is enhanced by externally applied pressure. Several papers have demonstrated the ability of ECM stiffness to promote the activation of hepatic stellate cells, liver fibroblasts that closely resemble PSCs (40, 41). ECM-associated forces have also been shown to alter the activation of latent TGF-$\beta$, which is secreted from active PSCs and promotes the differentiation of myofibroblasts (42, 43). Thus, it is important to note that the effects of ECM structure and pressure are not represented in these models.

Equations for TGF-$𝜷$ (${\text{𝑻}}_{𝜷}$), TNF-$𝜶$ (${\text{𝑻}}_{𝜶}$), IL-6 (${\text{𝑰}}_{\text{𝟔}}$), and PDGF (G).

The equations for TGF-$\beta$, TNF-$\alpha$, IL-6, and PDGF are

$$\frac{\partial T_{\beta }}{\partial t}-D_{T_{\beta }}\mathrm{\Delta }{T}_{\beta }={\lambda }_{T_{\beta }P}P+{\lambda }_{T_{\beta }{M}_2}{M}_2-d_{T_{\beta }}{T}_{\beta },$$ [7]

$$\frac{\partial T_{\alpha }}{\partial t}-D_{T_{\alpha }}\mathrm{\Delta }{T}_{\alpha }={\lambda }_{T_{\alpha }}{M}_1-d_{T_{\alpha }}{T}_{\alpha },$$ [8]

$$\frac{\partial I_6}{\partial t}-D_{I_6}\mathrm{\Delta }{I}_6=({\lambda }_{I_6}+{\lambda }_{I_6{T}_{\beta }}\frac{T_{\beta }}{K_{T_{\beta }}+T_{\beta }})P-d_{I_6}{I}_6,$$ [9]

$$\frac{\partial G}{\partial t}-D_G\mathrm{\Delta }G={\lambda }_{GP}P+{\lambda }_{G{M}_2}{M}_2-d_{G}G.$$ [10]

For simplicity, we assumed that the cytokines are produced (by PSCs or macrophages) at a constant rate, and they undergo a natural decay with constant rates (9, 10, 24, 25, 27). However, in the production of IL-6, we also included enhancement of IL-6 production by TGF-$\beta$ (24).

Equations for MMP (Q) and TIMP (${\text{𝑸}}_{\text{𝒓}}$).

We have the following sets of reaction diffusion equations for MMP and TIMP ($Q$ and $Q_r$):

$$\frac{\partial Q}{\partial t}-D_Q\mathrm{\Delta }Q={\lambda }_{Q{P}_0}{P}_0\underset{depletion}{\underbrace{-d_{Q{Q}_r}{Q}_{r}Q}}\underset{degradation}{\underbrace{-d_{Q}Q}}+\underset{production}{\underbrace{({\lambda }_{QP}+{\lambda }_{Q{T}_{\beta }}\frac{T_{\beta }}{K_{T_{\beta }}+T_{\beta }}}}+\underset{production}{\underbrace{{\lambda }_{Q{I}_6}\frac{I_6}{K_{I_6}+I_6})P}}$$ [11]

$$\frac{\partial Q_r}{\partial t}-D_{Q_r}\mathrm{\Delta }{Q}_r=\underset{production}{\underbrace{{\lambda }_{Q_r{P}_0}{P}_0+{\lambda }_{Q_{r}P}P}}\underset{depletion}{\underbrace{-d_{Q_{r}Q}Q{Q}_r}}\underset{degradation}{\underbrace{-d_{Q_r}{Q}_r}}.$$ [12]

$Q$ and $Q_r$ are produced by PSCs. The production of MMP by APSCs is enhanced by TGF-$\beta$ and IL-6 (34). In Eq. 11, MMP is depleted by binding with TIMP (second to last term); this entails also depletion of TIMP by MMP in Eq. 12.

Equation for Scar (S).

Fibrotic diseases are characterized by excessive scarring due to excessive production and deposition of ECM and disruption of normal healthy protein cross-linking. MMP disrupts collagen cross-linking and increases scarring in cases of excessive collagen concentrations (44, 45). We accordingly represent the state of the scar by the equation

$$S={\lambda }_S(\rho -{\rho }^{*})(1+{\lambda }_{SQ}\frac{Q}{K_Q+Q}).$$ [13]

Boundary Conditions.

We simulate the model in a square domain $\mathrm{\Omega }$ with an injured area $D$ (Fig. 2). We take $\mathrm{\Omega }=\{(x,y)|0\le x\le 1,\mathrm{\hspace{0.25em}0}\le y\le 1\}$ and $D=\{(x,y)|0.45\le x\le 0.55,\mathrm{\hspace{0.25em}0.45}\le y\le 0.55\}$. We assume periodic boundary conditions for all variables.

Initial Conditions.

We assume that initially $P(0)=P_0$, ${Q|}_{t=0}=Q^{\ast }$, ${Q_r|}_{t=0}=Q_r^{\ast }$, and ${\rho |}_{t=0}={\rho }^{\ast }$, where $Q^{\ast }$, $Q_r^{\ast }$, and ${\rho }^{\ast }$ are determined by steady states of Eqs. 6, 11, and 12. All other variables are initially equal to zero.

Results

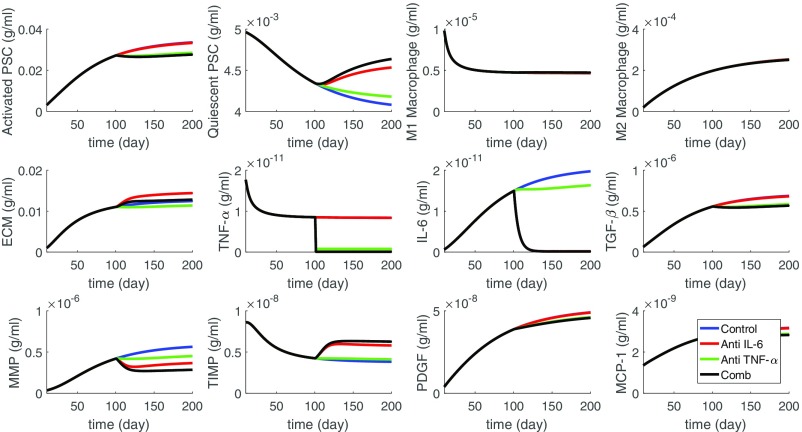
From Fig. 5 (the blue profiles) we see that almost all of the PSCs became activated. As a result, the concentrations of cytokines IL-6, TGF-$\beta$, PDGF, and MCP-1 have significantly increased, by a factor of 5–15 compared with their concentration in healthy normal pancreatic tissue given by the values of $K_{I_6}$, $K_{T_{\beta }}$, $K_G$, and $K_C$ in SI Appendix, Table S2. Also, with the increase in migration of macrophages, the concentration of TNF-$\alpha$ in tissue increased by a factor of 5 compared with $K_{T_{\alpha }}$. The increase in IL-6, TGF-$\beta$, TNF-$\alpha$, and PDGF in tissue of CP patients is documented in refs. 46–49 whereas the increase of MCP-1 in serum of CP patients is reported in ref. 47.

Fig. 5.

Simulation of the average densities of cells and concentrations of cytokines for the first 200 d since the start of the diseases (blue). Anti-IL-6 reduces the production rate of IL-6 by 90% (red) and anti-TNF-$\alpha$ reduces the production rate of TNF-$\alpha$ by 90% (green). All of the parameters are from SI Appendix, Tables S1 and S2.

We also see that more than 90% of the PSCs became activated, and the average ECM concentration increased 70-fold, from ${\rho }^{\ast }=\mathrm{\hspace{0.17em}3.22}\times {10}^{-4}$ g/mL to $2.2\times {10}^{-2}$ g/mL. The disruption of proteins cross-linking in the ECM may be indirectly inferred from the significant increase in MMP and decrease in TIMP.

CP is a chronic inflammatory disease characterized by progressive fibrotic destruction of the pancreas. The current treatment options of CP are limited to supportive and palliative care, and there is an urgent demand to develop drugs that can stop or, at least, slow the progress of the disease (50). As mentioned in ref. 50, several animal studies have been conducted, but they have not been translated into the clinical setting.

We use our model to explore, in silico, the efficacy of two potential drugs proposed in ref. 50: anti-TNF-$\alpha$ (infliximab, golimruab) and anti-IL-6 (tocilizumab).

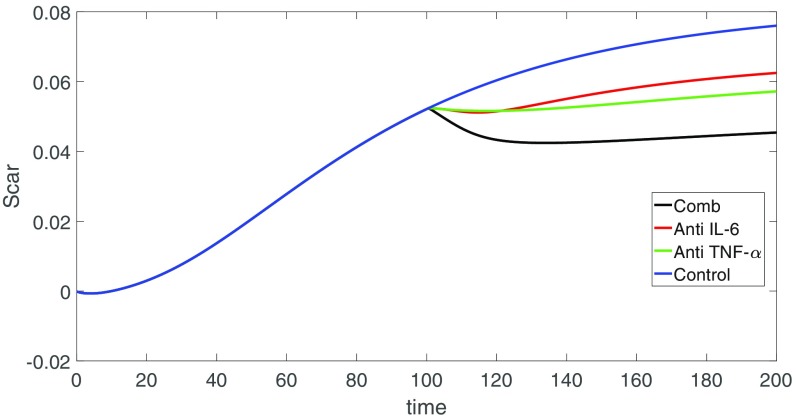
We implemented the treatment by anti-IL-6 and by anti-TNF-$\alpha$ by reducing the production coefficients of IL-6 and TNF-$\alpha$ by a factor of 10. Figs. 5 and 6 show the results of the drugs. The control curves are in the color blue. Some of these profiles are changed only very little by the drugs. When the changes are significant, the profiles corresponding to anti-IL-6 appear in the color red, and the profiles corresponding to anti-TNF-$\alpha$ appear in the color green. We see that anti-TNF-$\alpha$ was more effective than anti-IL-6 in reducing TGF-$\beta$ and PDGF and this results in decreases in ECM. Although anti-IL-6 increases the ECM, it also decreases MMP and thus perhaps does better than anti-TNF-$\alpha$ in preserving the architecture of the tissue. When we used the combination of anti-TNF-$\alpha$ and anti-IL-6, both at the same level as in Fig. 5, we found (not shown here) that there was only slight improvement in the reduction of MMP.

Fig. 6.

Scar concentration for different drugs vs. control. All of the parameters are from SI Appendix, Tables S1 and S2.

Discussion

CP is a progressive inflammatory disease of the pancreas, leading to its fibrotic destruction. There is currently no drug that can stop or slow the progression of the disease. Therefore, animal models are needed for advancing our understanding of the pathophysiological processes associated with CP (51). Animal models with pigs, dogs, opossums, rats, and other animals are reported in refs. 4 and 51–53. But the models, so far, have their limitations and have not reproduced the aspects of histopathology, endocrine/exocrine insufficiency, and pain that characterize human CP (51). In the present paper we developed a mathematical model of the disease. The model is based on a dynamical network of immune cells and cytokines that affect the pancreatic tissue. Simulations of the model indicated that TNF-$\alpha$, TGF-$\beta$, IL-6, and PDGF are likely to increase in the pancreatic microenvironment during chronic pancreatitis. These results are consistent with those observed from prior clinical data (46–49). The model can be used to explore, in silico, the efficacy of treatments that target some of the overexpressed cytokines. We conducted treatments by anti-IL-6 and anti-TNF-$\alpha$ drugs. Assuming that each of these drugs reduces the production of the cytokines by the same percentage, it appears that anti-TNF-$\alpha$ is more effective.

For simplicity we did not include in our model T cells and associated cytokines such as IL-2, IL-10, and IL-12 and IFN-$\gamma$. When clinical data become available, the model could then be further extended, and some of the parameters better adjusted to fit the data, to make the model predictions more reliable. In addition, we have not included in the analysis soluble factors from parenchymal cells or other infiltrating immune cells, such as neutrophils. Furthermore, we have not included in the analysis subclassification of individual fibroblast populations (IL-6 high vs. IL-6 low) that have been identified in the setting of pancreatic cancer (26). Certainly the biologic complexity within the pancreatic microenvironment is appreciated and could be modeled more rigorously as information becomes available on the abundance of other relevant cell populations and soluble factors. Due to the complexity of CP and the lack of standardized data available in serum factor analysis, several shortcomings exist in the data on which we based our analyses. First, data gathered from the literature to use in developing this model may have inherent inconsistencies in the experimental methods and patient inclusion criteria used, and some data defining cytokine circuits may have been derived in part from early studies of stellate cell biology conducted from rat sources. In addition, serum analysis we performed has inherently high levels of variability within disease groups for any given analyte. This may be due to natural human variability or differences in disease severity or staging or may be based on etiology. The spectrum of disease from AP to recurrent AP to CP and the various associated etiologies may significantly impact the cytokine profile of each individual patient. Thus, each stage or etiology could have one or several specific cytokine signaling circuits that predominate. In the future, it may be necessary to analyze these differences in circulating levels of soluble factors for the various subtypes of CP to further refine this model.