Superconductivity and non-Fermi liquid behavior near a nematic quantum critical point

Significance

It has been conjectured that many properties of highly correlated materials, including high-temperature superconductivity, may arise from proximity to a metallic quantum critical point. However, the nature of quantum critical phenomena in metals is incompletely understood. Using numerically exact quantum Monte Carlo methods, we simulated a model that can be tuned through a metallic quantum critical point and observed behaviors that are strikingly reminiscent of experiments. Among these phenomena are high-temperature superconductivity, non-Fermi liquid behavior of the electron Green function, and “bad metal” behavior of the electrical conductivity.

Abstract

Using determinantal quantum Monte Carlo, we compute the properties of a lattice model with spin $\frac{1}{2}$ itinerant electrons tuned through a quantum phase transition to an Ising nematic phase. The nematic fluctuations induce superconductivity with a broad dome in the superconducting $T_c$ enclosing the nematic quantum critical point. For temperatures above $T_c$, we see strikingly non-Fermi liquid behavior, including a “nodal–antinodal dichotomy” reminiscent of that seen in several transition metal oxides. In addition, the critical fluctuations have a strong effect on the low-frequency optical conductivity, resulting in behavior consistent with “bad metal” phenomenology.

Upon approach to a quantum critical point (QCP), the correlation length, $\xi$, associated with order parameter fluctuations diverges; consequently microscopic aspects of the physics are averaged out and certain properties of the system are universal. Asymptotically close to criticality, exact theoretical predictions concerning the scaling behavior of some measurable quantities are possible. However, in solids, it is rarely possible to convincingly access asymptopia; there are few experimentally documented cases in which a thermodynamic susceptibility grows as a function of decreasing temperature, $T$, in proportion to a single power law $\chi \sim T^{-x}$ over significantly more than one decade of magnitude. This is particularly true of metallic QCPs, where the metallic critical point may be preempted by the occurrence of a superconducting dome, a fluctuation-driven first-order transition, or some other catastrophe.

However, there is a looser sense in which a QCP can serve as an organizing principle for understanding properties of solids over a range of parameters: In the “neighborhood” of a QCP, where $\chi$ is large (in natural units) and $\xi$ is more than a few lattice constants, it is reasonable to conjecture that quantum critical fluctuations play a significant role in determining the properties of the material and that, at least on a qualitative level, those properties may be robust (i.e., not strongly dependent on microscopic details), even if they are not universal.

With this in mind, we carried out extensive numerical “experiments” on a simple 2D lattice model of itinerant electrons coupled to an Ising-like “nematic” order parameter field, Eq. 1. By varying a parameter in the Hamiltonian, $h$, the system can be tuned through a quantum or thermal transition from a disordered (symmetric) phase to a nematic phase that spontaneously breaks the lattice symmetry from $C_4$ to $C_2$. Related models of nematic quantum criticality have been studied extensively (1–27), using various analytic methods, and can also be studied with minus-sign–free determinantal quantum Monte Carlo (DQMC) (28–30). Recent Monte Carlo studies have examined the scaling structure of nematic and related QCPs (31, 32) as well as the role of fluctuations in promoting superconductivity (33, 34). Moreover, the model is particularly topical, as there is good evidence that a nematic QCP underlies the superconducting dome in many (possibly all) of the Fe-based superconductors (35–41) and possibly even the cuprate high-temperature superconductors (42–44).

In a previous study (31) of this model, we focused on the critical scaling at the putative metallic QCP with a moderate dimensionless coupling between the itinerant electrons and the nematic fluctuations $\alpha =1/2$. We found that, although superconducting fluctuations are enhanced when the tuning parameter $h$ is close to the quantum critical value, $h_c$, the superconducting $T_c$ (if any) is below the accessible range of temperatures. We documented a possible mild breakdown of Fermi liquid behavior and identified a broad range of small $T$ and $|h-h_c|$ in which some correlation functions are well approximated by simple scaling functions. However, other correlations with the same symmetries do not exhibit the same scaling behavior. This implies that the regime we accessed is far enough from criticality that corrections to scaling are significant or that the scaling behavior we see does not reflect the properties of a metallic QCP at all.

In the present paper, we have focused on the properties of the model in the critical neighborhood and have taken larger values of $\alpha =1-1.5$ so that all of the energy scales are enhanced, making them easier to document in numerical experiments. Our principal findings are as follows:

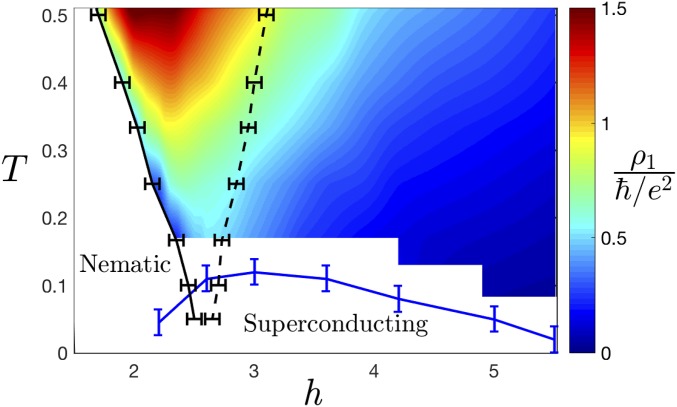
• i)As shown in Fig. 1, there is a broad superconducting dome with its $T_c$ maximum roughly coincident with the value $h=h_c$ at which the nematic transition temperature, $T_{nem}\to 0$. The maximum $T_c$ is found to be about $0.03E_F$, where $E_F$ is the Fermi energy.
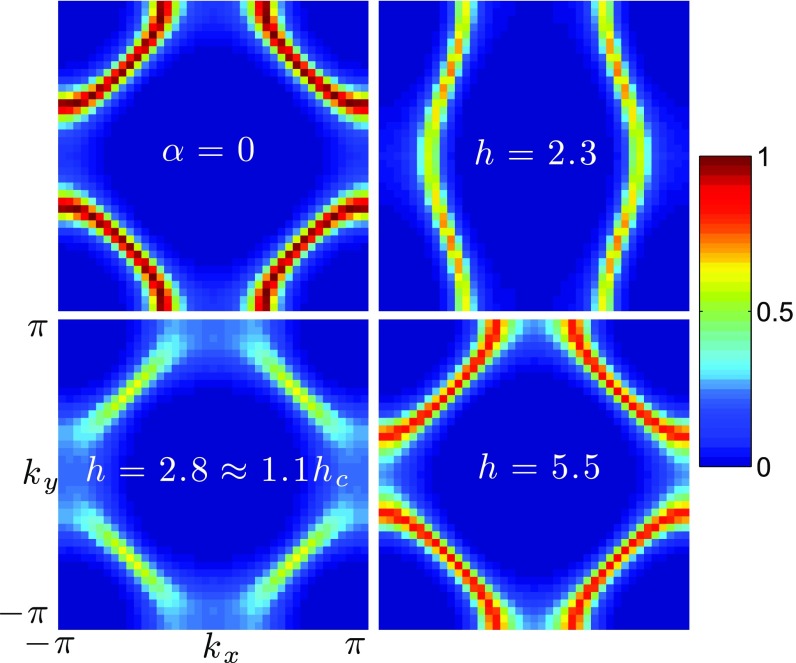
• ii)Fig. 2 shows the electron spectral function, $A(\overrightarrow{k},\omega )$, integrated over a range of energies of order $T$ about the Fermi energy, as defined in Eq. 2. The nematic fluctuations are exceedingly effective in destroying quasiparticles and indeed produce a striking nodal–antinodal dichotomy in which some remnant of the Fermi surface is still visible along the zone diagonal. This is associated with the existence of “cold spots” (2, 45) on the Fermi surface that are required by symmetry.

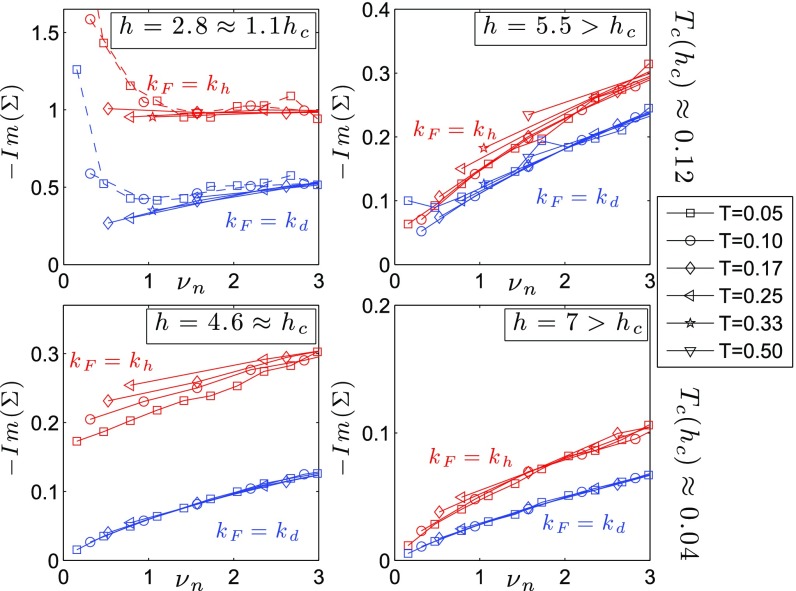
  Away from the cold spots, the imaginary part of the (Matsubara) self-energy, shown in Fig. 3, is dramatically unlike that of a Fermi liquid throughout the quantum critical regime.

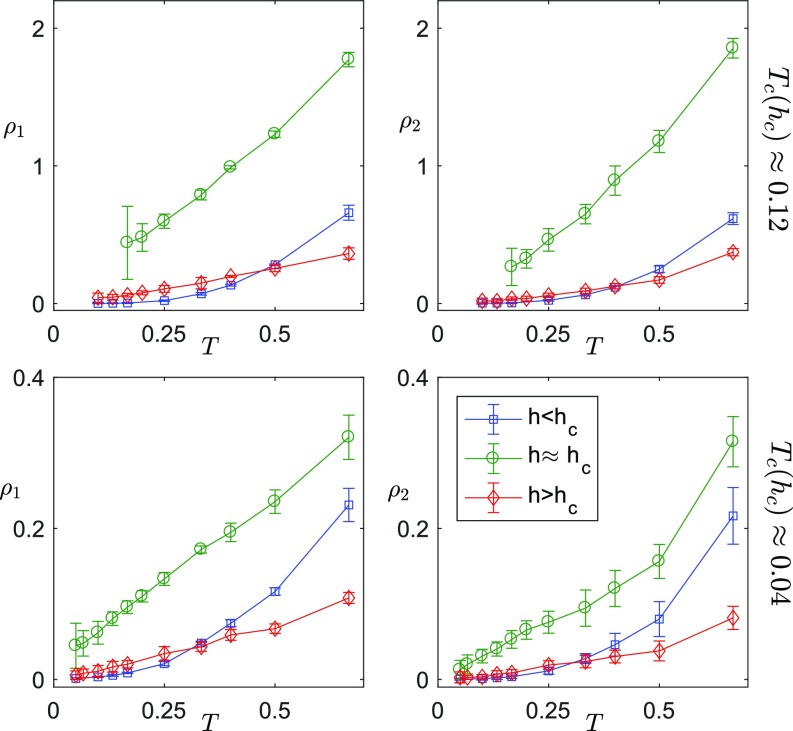
• iii)Transport properties are also strongly affected in the quantum critical regime above $T_c$. Because analytic continuation of imaginary time data to real time is numerically ill posed, we carried out two different procedures to obtain proxies for the resistivity. These proxies, plotted in Fig. 5, track the DC resistivity under certain assumptions described below. The first proxy, ${\rho }_1$, is derived from a simple two-component fit to the DQMC data (Fig. 4) whereas the second, ${\rho }_2$, defined in Eq. 7, is extracted directly from the long (imaginary) time behavior of the current–current correlation function. The results obtained by the two methods are qualitatively similar. At $h=h_c$ both proxies are roughly linearly increasing functions of $T$. For the larger value of the coupling constant, the proxies exceed the quantum of resistance, ${\rho }_q=\mathrm{\hslash }/e^2$, at high temperatures (but still much below $E_F$). Outside the quantum critical fan, the proxies are substantially smaller than ${\rho }_q$ for all $T$ (Fig. 1).

Fig. 1.

Phase diagram as a function of the transverse field $h$ and temperature $T$, both measured in units of the fermion hopping $t$. The solid and dashed black lines indicate, respectively, the boundary of the nematic phase ($T_{nem}$) and a crossover ($T_{nem}^{\ast }$, defined shortly before Eq. 2) marking the edge of the quantum critical fan. The superconducting $T_c$ is indicated by the blue solid line. The color scale shows a proxy for the DC resistivity in units of $\mathrm{\hslash }/e^2$, defined from the fit in Eq. 4. Here, $\alpha =1.5$, $V=0.5t$, $\mu =t$. Error bars reflect finite-size errors, as described in SI Appendix.

Fig. 2.

The low-frequency fermionic spectral weight $\mathcal{G}(\overrightarrow{k})$ (Eq. 2) at temperature $T=0.17$, shown for the noninteracting band structure ($\alpha =0$) and for $\alpha =1.5$ for several values of $h$. For $h=2.3$, a small $C_4$ symmetry-breaking field has been applied in the simulation. Data are for a $20\times 20$ system with various combinations of periodic and antiperiodic boundary conditions. Other parameters are $V=0.5$ and $\mu =1.0$.

Fig. 3.

The imaginary part of the fermion self-energy for two values of parameters $\alpha =1.5,V=0.5,\mu =1.0$ (Top row) and $\alpha =1.0,V=1.0,\mu =0.5$ (Bottom row), for various temperatures and with the nominal Fermi momenta ${\overrightarrow{k}}_d$ and ${\overrightarrow{k}}_h$ along the $(0,0)-(\pi ,\pi )$ and $(0,\pi )-(\pi ,\pi )$ directions, respectively. Data are shown for a $20\times 20$ system both near $h_c$ (Left column) and far in the symmetric phase (Right column). (Top Left) Data points below $T_c$ are connected by dashed lines.

Fig. 5.

The temperature dependence of the resistivity proxies (in units of $\mathrm{\hslash }/e^2$) for parameters $\alpha =1.5,V=0.5,\mu =1$ (Top row, for $h=2.0<h_c$, $h=2.6\approx h_c$, and $h=5.5>h_c$) and $\alpha =1.0,V=1.0,\mu =0.5$ (Bottom row, for $h=4.0<h_c$, $h=4.6\approx h_c$, and $h=7.0>h_c$). For $h<h_c$, a small symmetry-breaking field has been applied, and the smaller component of the resistivity proxy is shown. Values shown are for the largest system size simulated ($L=16$ or $18$ depending on temperature), with error bars estimated as described in SI Appendix, section S-I, C.

Fig. 4.

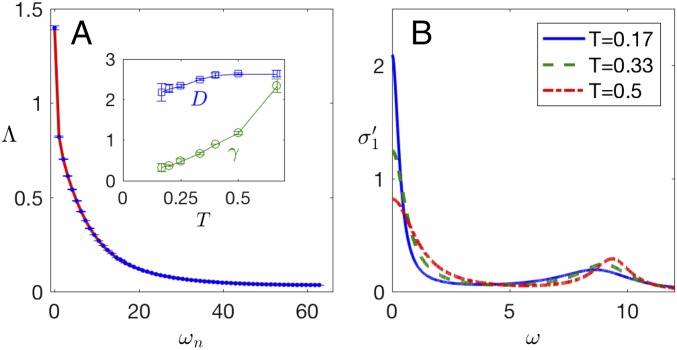
(A) The current−current correlator for a $16\times 16$ system with $h=2.6\approx h_c,T=0.17$, for $\alpha =1.5,V=0.5,\mu =1$. Error bars are comparable to the symbol size. The solid red line is a least-squares fit to two components of the form of Eq. 4. (B) The corresponding real part of the optical conductivity for parameters in A, as well as two higher temperatures, showing how the Drude-like peak sharpens on cooling. The temperature dependence of the half-width at half-maximum $\mathrm{\Gamma }$ of the Drude-like peak, as well as its weight $D$, is shown in A, Inset, with error bars estimated as described in SI Appendix, section S-I, C.

The Model

Our model is defined on a 2D square lattice, where every site has a single Wannier orbital. Each link has a pseudospin-$1/2$ degree of freedom that couples to the fermion bond density. The system is described by the Hamiltonian

$$\begin{array}{l}H=H_f+H_b+H_{\mathrm{int}},\hfill \\ H_f=-t\sum _{⟨i,j⟩,\sigma }{c}_{i\sigma }^{†}{c}_{j\sigma }-\mu \sum _{i,\sigma }{c}_{i\sigma }^{†}{c}_{i\sigma },\hfill \\ H_b=V\sum _{⟨⟨i,j⟩;⟨k,l⟩⟩}{\tau }_{i,j}^z{\tau }_{k,l}^z-h\sum _{⟨i,j⟩}{\tau }_{i,j}^x,\hfill \\ H_{\mathrm{int}}=\alpha t\sum _{⟨i,j⟩,\sigma }{\tau }_{i,j}^z{c}_{i\sigma }^{†}{c}_{j\sigma },\hfill \end{array}$$ [1]

where $c_{j\sigma }^{†}$ creates a fermion on site $j$ with spin $\sigma =\uparrow ,\downarrow$, $⟨i,j⟩$ denotes a pair of nearest-neighbor sites, $t$ and $\mu$ are the hopping strength and chemical potential, respectively, ${\tau }_{i,j}^a$ ($a=x,y,z$) denotes pseudospin-1/2 operators that live on the bond connecting the neighboring sites $i$ and $j$, $V>0$ is the Ising interaction between nearest-neighbor pseudospins (here, $⟨⟨i,j⟩;⟨k,l⟩⟩$ denotes a pair of nearest-neighbor bonds), $h$ is the strength of a transverse field that acts on the pseudospins, and $\alpha$ is the dimensionless coupling strength between the pseudospin and the fermion bond density. In the ordered phase where $V$ dominates, ${\tau }_{i,j}^z$ adopts a staggered configuration, taking different values on horizontal and vertical bonds, thereby generating nematic order.

DQMC Results

A typical phase diagram is shown in Fig. 1, for $\alpha =1.5,V=0.5t,\mu =t$. In addition to the nematic and symmetric phases, there is a “dome” of superconductivity with maximum critical temperature near $h_c$, as anticipated (3, 11, 15, 46). The pair wave function in the superconducting state has spin singlet s-wave symmetry in the symmetric phase and mixed s- and d-wave symmetry in the nematic phase. A value of $\alpha >1$ is problematic microscopically, since the effective hopping matrix element along one direction changes sign deep in the ordered phase. However, we view Eq. 1 as an effective model designed to give a nematic QCP and so do not restrict the value of $\alpha$. Hereafter, we use units in which $t=\mathrm{\hslash }=e^2=1$.

The boundary of the nematic phase $T_{nem}$ and the crossover temperature $T_{nem}^{\star }$ are both derived from an analysis of the thermodynamic nematic susceptibility $\chi (h,T)\equiv \frac{1}{L^2}{\sum }_{i,j}{\int }_0^{\beta }d\tau ⟨N_i(\tau )N_j(0)⟩$, where the nematic order parameter is defined as $N_i={\sum }_j{\eta }_{ij}{\tau }_{ij}^z$, where $\eta$ is a d-wave form factor: ${\eta }_{ij}=1/4$ for ${𝐫}_{ij}=\pm \widehat{𝐱}$, ${\eta }_{ij}=-1/4$ for ${𝐫}_{ij}=\pm \widehat{𝐲}$, and ${\eta }_{ij}=0$ otherwise. $T_{nem}$ is determined using finite-size scaling appropriate to a 2D classical Ising transition, whereas $T_{nem}^{\star }(h)$ is defined implicitly according to $\chi (h,T_{nem}^{*})=\frac{1}{2}\chi (h_c,T_{nem}^{\star })$. The superconducting critical temperature $T_c$ is determined by analysis of the superfluid stiffness (47, 48) and can also be estimated by other methods, yielding similar results. (Further details of the finite-size scaling analysis, the resistivity proxies, the form of the self-energy in the superconducting state, and additional data can be found in SI Appendix.)

The presence of superconductivity limits the region in which any scaling behavior of nematic fluctuations can be identified. That said, for temperatures well above $T_c$, the thermodynamic nematic susceptibility near $h_c$ is similar in structure to that reported in ref. 31. Nematic fluctuations at nonzero frequency have somewhat different structure than those previously reported and have a reduced dependence on momentum.

Turning to single-particle properties, we examine (49)

$$\mathcal{G}(\overrightarrow{k})\equiv 2\stackrel{\sim }{G}(\overrightarrow{k},\tau =\frac{\beta }{2})=\int d\omega \frac{A(\overrightarrow{k},\omega )}{\cosh \left[\beta \omega /2\right]},$$ [2]

where $\stackrel{\sim }{G}$ is the imaginary time fermion Green function and $A$ is the real frequency spectral function. Roughly, $\mathcal{G}$ measures spectral weight within an energy range of order $T$ of the Fermi level, so that a sharp peak in the momentum dependence of $\mathcal{G}$ indicates an underlying Fermi surface. In a Fermi liquid, $\mathcal{G}(\overrightarrow{k})$ is peaked at the Fermi surface with a peak amplitude that approaches the quasiparticle residue $Z_{\overrightarrow{k}}$ as $T\to 0$.

Fig. 2 shows color plots of $\mathcal{G}$ at fixed temperature $T=0.17$ for the noninteracting case ($\alpha =0$) and for $\alpha =1.5$ at a variety of values of $h$. For $h=5.5$, deep in the symmetric phase, there is a clear Fermi surface similar to that of the noninteracting problem. For $h=2.3$, in the ordered phase, there is also a clear Fermi surface consisting of open sheets, reflecting a substantial nematic distortion. For $h=2.8$, near $h_c$, a Fermi surface appears well defined near the cold spots along the zone diagonal, but is increasingly ill defined away from these high-symmetry points. The higher degree of coherence along the zone diagonal is expected by symmetry: Long-wavelength nematic fluctuations cannot couple to fermions with momentum along the zone diagonal.

A complementary probe of single fermion properties is the self-energy, extracted from the Green function $G(\overrightarrow{k},{\nu }_n)$ and the noninteracting Green function $G_0(\overrightarrow{k},{\nu }_n)$ according to $\mathrm{\Sigma }(\overrightarrow{k},{\nu }_n)\equiv G_0^{-1}(\overrightarrow{k},{\nu }_n)-G^{-1}(\overrightarrow{k},{\nu }_n)$. (Henceforth, ${\nu }_n=2\pi T(n+1/2)$ and ${\omega }_n=2\pi Tn$ designate the fermionic and bosonic Matsubara frequencies.) In a Fermi liquid at asymptotically low temperature, $-\mathrm{Im}[\mathrm{\Sigma }({\overrightarrow{k}}_F,{\nu }_n)]={\gamma }_{\overrightarrow{k}}+(1/Z_{\overrightarrow{k}}-1){\nu }_n+\mathcal{O}({\nu }_n^2)$ for ${\nu }_n>0$, where ${\gamma }_{\overrightarrow{k}}(T)\ll T$ is the inelastic scattering rate. More generally, ${\gamma }_{\overrightarrow{k}}$ is obtained by extrapolating $-\mathrm{Im}[\mathrm{\Sigma }]$ to zero frequency. In Fig. 3 we plot $-\mathrm{Im}[\mathrm{\Sigma }(\overrightarrow{k},{\nu }_n)]$ vs. ${\nu }_n$, both close to $h_c$ and deep in the disordered phase. We show data for a variety of temperatures for $\overrightarrow{k}$ at the nominal Fermi momenta ${\overrightarrow{k}}_d$ and ${\overrightarrow{k}}_h$ along the $(\mathrm{0,0})-(\pi ,\pi )$ and $(0,\pi )-(\pi ,\pi )$ directions, respectively.

In the disordered phase, the frequency and temperature dependences of $\mathrm{Im}[\mathrm{\Sigma }]$ at both ${\overrightarrow{k}}_d$ and ${\overrightarrow{k}}_h$ are consistent with Fermi liquid theory—the extrapolated ${\nu }_n\to 0$ intercept (${\gamma }_{\overrightarrow{k}}$) is well below $T$ and the slope is finite (corresponding to $1>Z_{\overrightarrow{k}}>0$) and hardly $T$ dependent. Even for $h\approx h_c$, Fermi liquid theory is loosely consistent with the data at ${\overrightarrow{k}}_d$, but not remotely so at ${\overrightarrow{k}}_h$ where ${\gamma }_{{\overrightarrow{k}}_h}$ exceeds $T$, and appears not to vanish in the $T\to 0$ limit. In the quantum critical regime and above $T_c$, quasiparticles far from the cold spots are not even marginally well defined. (The upturn of $\mathrm{Im}[\mathrm{\Sigma }]$ at low frequency, visible especially for $\alpha =1.5$, is associated with the onset of a superconducting gap.)

The intervention of superconductivity complicates any analysis of the putative low-temperature Fermi liquid properties as $h\to h_c$. However, to obtain a rough sense of trends, one can estimate the dispersion of the quasiparticle-like features as a function of $h$ and $T$ at different parts of the Fermi surface (see SI Appendix, section S-II for details). We see a tendency for the dispersion to become substantially flatter as $h\to h_c$ (i.e., a large increase in the “effective mass”), although any such renormalization is much weaker or nonexistent at the cold spots on the Fermi surface. The electronic spectral function $A(\overrightarrow{k},\omega )$, calculated from $G(\overrightarrow{k},{\nu }_n)$ using the maximum-entropy method, is consistent with such behavior (SI Appendix, section S-III). Near the cold spots $A(\overrightarrow{k},\omega )$ has a well-defined dispersive peak, whereas in the hot regions at $h\approx h_c$ there are only broad features without a clear dispersion. Below the superconducting $T_c$, $A(\overrightarrow{k},\omega )$ clearly displays a superconducting gap in both the cold spots and the hot regions (with a larger gap in the hot regions).

The breakdown of Fermi liquid theory seen in the fermion Green function suggests that transport properties may also be strongly altered near the QCP. One quantity of great interest is the DC conductivity, but the DC limit of transport is particularly difficult to access using analytic continuation of imaginary time data. The analysis we carry out below yields information about the optical conductivity at frequencies of order the temperature, but any statements about the DC conductivity rest on additional, nontrivial assumptions.

We measured the imaginary time-ordered current–current correlator ${\stackrel{\sim }{\mathrm{\Lambda }}}_{ii}(\tau )\equiv ⟨\mathcal{T}{J}_i(\tau )J_i(0)⟩$, where $J_i$ is the uniform current operator in direction $i=x$ or $y$. (We henceforth leave the directional indexes implicit.) $\mathrm{\Lambda }({\omega }_n)$, the Fourier transform of $\stackrel{\sim }{\mathrm{\Lambda }}(\tau )$, is shown in Fig. 4A for $\alpha =1.5,V=0.5,\mu =1,h\approx h_c$ and $T=0.17\approx 1.5T_c$. In a nonsuperconducting state, $\mathrm{\Lambda }({\omega }_n)$ is related to the real part of the optical conductivity $\sigma \prime (\omega )$ by

$$\mathrm{\Lambda }({\omega }_n)=\int \frac{d\omega }{\pi }\frac{{\omega }^2\sigma \prime (\omega )}{{\omega }^2+{\omega }_n^2}.$$ [3]

A clear feature, present throughout the nonsuperconducting portions of the phase diagram, is a substantial jump in $\mathrm{\Lambda }({\omega }_n)$ between the zeroth and the first Matsubara frequency. This is evidence of a Drude-like component of $\sigma \prime (\omega )$ peaked at low frequencies, with a width less than or comparable to $T$. The slow decrease of $\mathrm{\Lambda }({\omega }_n)$ for $n>1$ is indicative of an additional broad feature with optical weight spread over a range of frequencies large compared with $T$.

We performed a simple analytic continuation of our data via a least-squares fit. The fitting function is a sum of two terms (Eq. 4 must be modified to account for the discretization of imaginary time, as discussed in SI Appendix, section S-I, B):

$${\mathrm{\Lambda }}_{\text{fit}}({\omega }_n)=\sum _{j=1}^2\frac{A_j}{{\omega }_n^2+{\gamma }_j|{\omega }_n|+{\mathrm{\Omega }}_j^2}.$$ [4]

${\mathrm{\Lambda }}_{\text{fit}}$ can then be analytically continued to give

$$\sigma \prime (\omega )=\sum _{j=1}^2\frac{A_j{\gamma }_j}{{({\mathrm{\Omega }}_j^2-{\omega }^2)}^2+{\gamma }_j^2{\omega }^2}.$$ [5]

As illustrated in Fig. 4A, the fit agrees with the data within a few percent. The corresponding optical conductivity is shown in Fig. 4B for a variety of temperatures above $T_c$; it consists of a Drude-like component with its maximum at $\omega =0$ (i.e., ${\gamma }_1>\sqrt{2}{\mathrm{\Omega }}_1$) that broadens with increasing temperature and a broad, largely temperature-independent background with a maximum at $\omega =\sqrt{{|{\mathrm{\Omega }}_2|}^2-{|{\gamma }_2|}^2/2}>0$. The zero-frequency limit of this fitted conductivity yields a proxy ${\rho }_1$ for the DC resistivity.

Although physically plausible and in agreement with our data, the fitting analysis is not unique—analytic continuation of numerical data is a famously ill-conditioned problem (50). As one check on our results, we performed the analytic continuation using standard maximum-entropy methods; the results, as shown in SI Appendix, section S-I, E, are very similar to those obtained above. On the other hand, as also shown in SI Appendix, section S-I, D, the quality of the fit is similar if we mandate a third component with width far less than the temperature, which would of course drastically alter the DC conductivity. Such a narrow peak may arise if there is an emergent nearly conserved momentum (23, 51).

Analysis of the current–current correlator in the time domain yields additional information. The value and the derivatives of $\stackrel{\sim }{\mathrm{\Lambda }}(\tau )$ near $\tau =\beta /2$ contain information about the moments of the low-frequency part of the optical conductivity:

$${[{\partial }_{\tau }^{2m}\stackrel{\sim }{\mathrm{\Lambda }}]}_{\tau =\beta /2}=\int \frac{d\omega }{2\pi }\frac{{\omega }^{2m+1}\sigma \prime (\omega )}{\sinh \left(\frac{\beta \omega }{2}\right)}.$$ [6]

The first two such moments obtained from our QMC simulations are shown in SI Appendix, section S-I, A. (Interestingly, these moments can also be straightforwardly computed from empirical data, enabling direct comparison with experiment.)

The two lowest-order moments can be combined into a quantity with units of resistivity according to

$${\rho }_2\equiv [{\partial }_{\tau }^2\stackrel{\sim }{\mathrm{\Lambda }}/(2\pi {\stackrel{\sim }{\mathrm{\Lambda }}}^2){|}_{\tau =\beta /2}.$$ [7]

This quantity tracks the DC resistivity at low temperatures whenever the low-frequency ($\omega \lesssim T$) conductivity can be described by a single Drude-like component that has either Lorentzian shape or a width of order $T$. This is a parsimonious (although not unassailable) assumption and consistent with our data. With caveats in place, we now describe the behavior of the two resistivity proxies ${\rho }_{\mathrm{1,2}}$ defined above.

${\rho }_1(h,T)$ is represented in the coloring of the symmetric metallic region of the phase diagram in Fig. 1. It exhibits a nonmonotonic dependence on $h$, with a maximum near $h_c$. The temperature dependence of ${\rho }_1$ and ${\rho }_2$ is shown in Fig. 5 in the ordered and disordered phases as well as at $h_c$, for both $\alpha =1.5,V=0.5,\mu =1.0$ and $\alpha =1.0,V=1.0,\mu =0.5$. ${\rho }_1$ and ${\rho }_2$ are qualitatively similar over a wide range of temperatures. Both are significantly higher at $h\approx h_c$ than deep in the ordered and disordered phases. In the ordered phase, the data are roughly consistent with the $T^2$ temperature dependence expected of a Fermi liquid. In the disordered phase, the temperature dependence in the range of $T>T_c$ can be fitted to a linear function of $T$ with small slope and a slightly negative extrapolated value at $T\to 0$. (Recalling that small resistivities correspond to a sharp Drude-like feature in the resistivity—precisely the sort of feature that is most difficult to capture reliably from imaginary time data—we have not attempted a serious analysis of the apparently non-Fermi liquid character of this last observation.)

At $h\approx h_c$, the behavior depends somewhat on parameters. For $\alpha =1.0,V=1.0,\mu =0.5$, there is an apparent $T\text{-}linear$ behavior over about a decade of temperature. For $\alpha =1.5,V=0.5,\mu =1.0$, the high $T_c$ leaves an insufficient dynamical range to establish a clear power-law temperature dependence, but both ${\rho }_1$ and ${\rho }_2$ exceed the Ioffe–Regel limit of $\mathrm{\hslash }/e^2$ at a temperature of approximately $3T_c$. Subject always to the uncertainties in analytic continuation, the behavior of our model near $h_c$ is strikingly reminiscent of the bad metal phenomenology seen in many correlated materials (52–54).

We performed additional simulations at lower fermionic densities, with results summarized in SI Appendix, section S-IV. Much of the phenomenology appears to be robust: Close to $h_c$, the imaginary part of the fermionic self-energy at ${\overrightarrow{k}}_h$ approaches a constant and the resistivity is of order of the quantum of resistance. However, the temperature dependence of the resistivity is not linear. Also, for certain values of the couplings, we find evidence that the nematic transition becomes weakly first order at low temperatures.

Discussion

We studied the vicinity of a nematic QCP in a simple lattice model of a metal. The QCP is masked by a dome-shaped superconducting phase. The normal-state quantum critical regime does not exhibit clear scaling behavior; however, it displays strong anomalies that we associate with the approach to the QCP. In particular, the fermion self-energy is strikingly non-Fermi liquid-like over much of the Fermi surface. The optical conductivity at frequencies $\lesssim T$ is also strongly affected by the critical fluctuations. Assuming a simple form of $\sigma (\omega )$, we find that the DC resistivity is anomalously large (exceeding the Ioffe–Regel limit for $\alpha >1$) and nearly linear in temperature.

Although our model does not accurately describe the microscopics of any specific material and ignores physical effects that may be important (55–58), it is plausible that the qualitative behavior proximate to the QCP is relatively insensitive to microscopic details. Our results bear striking similarities to the behavior seen in certain high-temperature superconductors: In several iron-based superconductors, the resistivity is anomalously large and $T$ linear near the putative nematic QCP (36, 59), and the fermionic spectral properties of our model in the critical regime are reminiscent of the nodal–antinodal dichotomy reported in the “strange metal” regime of certain cuprates (60, 61).