Toward a direct and scalable identification of reduced models for categorical processes

Significance

We derive a computational framework that allows highly scalable identification of reduced Bayesian and Markov relation models, their uncertainty quantification, and inclusion of a priori physical information. It does not rely on the prior knowledge or a necessity of estimation of the full matrix of system’s relations in any step. Application to a molecular dynamics (MD) example showed that this methodology opens possibilities for a robust construction of reduced Markov state models directly from the MD data—providing ways of bridging the gap toward longer simulation times and larger systems in computational MD.

Abstract

The applicability of many computational approaches is dwelling on the identification of reduced models defined on a small set of collective variables (colvars). A methodology for scalable probability-preserving identification of reduced models and colvars directly from the data is derived—not relying on the availability of the full relation matrices at any stage of the resulting algorithm, allowing for a robust quantification of reduced model uncertainty and allowing us to impose a priori available physical information. We show two applications of the methodology: (i) to obtain a reduced dynamical model for a polypeptide dynamics in water and (ii) to identify diagnostic rules from a standard breast cancer dataset. For the first example, we show that the obtained reduced dynamical model can reproduce the full statistics of spatial molecular configurations—opening possibilities for a robust dimension and model reduction in molecular dynamics. For the breast cancer data, this methodology identifies a very simple diagnostics rule—free of any tuning parameters and exhibiting the same performance quality as the state of the art machine-learning applications with multiple tuning parameters reported for this problem.

Model reduction and identification of a most appropriate (small) set of collective variables are essential prerequisites for many computational methods and modeling techniques in a number of applied disciplines ranging from biophysics and bioinformatics to computational medicine and image processing. A variety of methods for the identification of collective variables can be roughly subdivided into two major groups: (i) methods that are based on some user-defined agglomeration of the original degrees of freedom into collective variables (e.g., based on the physical intuition) (1) and (ii) methods that produce/derive these agglomerations of original system’s variables based on a reduced approximation of some system-specific relation matrices. These matrices can be defined, for example, as covariance or kernel covariance matrices (2, 3), partial autocorrelation matrices of autoregressive processes (4), Gaussian distance kernel matrices (5, 6), Laplacian matrices [as in the case of spectral clustering methods for graphs (7, 8)], adjacency matrices [in community identification methods for networks (9)], or Markov transition matrices [as in spectral reduction methods for Markov processes (10, 11)]. In most of these reduction methods, the relation matrices are assumed a priori available—and this assumption is true, for example, in social sciences, network science, and many areas of biology. However, in many particular applications (e.g., in biophysics and many medical applications; examples 1 and 2 below), one first needs to estimate these matrices from available data. For systems with a large number of dimensions (for continuous data) or categories (for categorical data) and short available statistics, these matrix estimates will be subject to uncertainty and may lead to biasedness of the derived colvars. Some other reduction approaches that allow for computing the reduced representation from the data directly [e.g., the Probabilistic Latent Semantic Analysis (PLSA; used in mathematical linguistics and information retrieval for analysis and reduction of texts and documents)] (12–14) impose strong assumptions on the data and exhibit issues related to the computational cost scaling (Fig. 1 and SI Appendix, section S5 have detailed discussion), making them practically not applicable to nonsparse data in such areas as, for example, the model and data reduction in biophysics and bioinformatics. Another problem arises when trying to identify the colvars for dynamical systems while simultaneously trying to preserve some essential conservation properties (e.g., conservation of energy or probability) in the reduced representation. For example, deploying spectral methods based on Euclidean eigenvector projections [such as principal component analysis (PCA) and spectral clustering methods] to reduction of probability measures would not guarantee that the components of the projected/reduced representation will also add up to one and all be bigger than or equal to zero (i.e., the resulting reduced models may not be probability preserving).

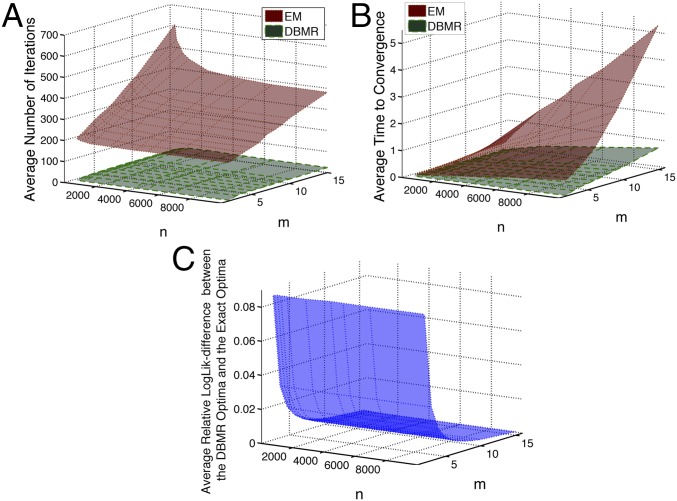
Fig. 1.

Numerical comparison of the PLSA Expectation Maximization reduction (13, 14) and the DBRM reduction algorithms: (A) for the average number of iterations required until reaching the same convergence tolerance, (B) for the average central processing unit time until algorithms reach the same convergence tolerance, and (C) for the average relative log-likelihood difference between the optima achieved with the DBRM and the optima obtained with the exact iterative maximization of Eq. 3. For every combination of problem dimensions $n$ and $m$, averaging was performed over the ensemble of 1,000 randomly generated datasets that were subject to reduction with $K=\mathrm{\hspace{0.17em}2}$ for both of the algorithms. Convergence tolerance was measured in terms of the same normalized log-likelihood measure $1/mn\widehat{L}$. Average relative log-likelihood difference was computed as $𝔼[|{\widehat{L}}_{exac{t}^{*}}-{\widehat{L}}_{DBR{M}^{*}}|/|{\widehat{L}}_{exac{t}^{*}}|]$, where $\widehat{L}$ is defined in Eq. 3. MATLAB code generating this comparison is available at https://github.com/SusanneGerber. The code implementing PLSA Expectation Maximization methods (13, 14) is openly available at the MathWorks webpage (https://ch.mathworks.com/matlabcentral/fileexchange/56302-probabilistic-latent-sematic-analysis–tempered-em-and-em-). EM, Expectation Maximization.

In this paper, we present an algorithmic framework that is scalable for realistic dynamical systems and is designed for the inference and analytically computable uncertainty quantification of reduced probability-preserving Bayesian relation models directly from the data.

Methodology

Below, we will give a brief description of the methodology—detailed derivation can be found in SI Appendix, section S1. Our aim is to come out with a reduction method intending to preserve causality relations—measured in terms of the matrix of conditional probabilities between two categorical processes $Y$ and $X$. Process $Y$ will serve as a reference process, meaning that it will not change when process $X$ is reduced. The terms “categorical process” and “categorical variables” mean that—in every particular case $s$ (e.g., at any given time $s$ or for any given instance $s$ in the dataset)—$Y(s)$ is taking one and only one of the possible values from $m$ categories $\{y(1),y(2),\mathrm{\dots },y(m)\}$ and $X(s)$ is taking values from one and only one of the $n$ categories $\{x(1),x(2),\mathrm{\dots },x(n)\}$. For example, in biomolecular dynamics simulations of polypeptides with $N$ amino acid residues, every peptide residue $i$ at any time $s$ can be assigned to one and only one of three Ramachandran states dependent on its current combination of torsion angle values ${\varphi }_i(s)$ and ${\psi }_i(s)$ (SI Appendix, Fig. S1). Also, every global configuration/conformation X of the entire polypeptide molecule at any time can then be assigned to one of the $n\le {\mathrm{\hspace{0.17em}3}}^N$ categories $\{x(1),x(2),\mathrm{\dots },x(n)\}$—where every particular $x(k)$ is defined by a vector of Ramachandran state combinations [e.g., $x(k)$ is a category when junction 1 is being in state $1$, junction 2 is being in state $2$, and so on]. Efficient approaches based on the Markov state modeling (MSM) framework have been recently introduced, allowing for automated transformation of continuous-valued processes [e.g., molecular dynamics (MD) coordinates time series] into categorical time series (15, 16). Because the system cannot be in two different categories simultaneously, these categories are disjointed, and a relation between the probability for $Y(s)$ to attain a category $y(i)$ in its instance/realization $s$ and the probabilities for $X(s)$ can be formulated exactly via the conditional probabilities and the law of the total probability (17). Defining the column vectors of probabilities ${\mathrm{\Pi }}_Y(s)=\{\mathbb{P}[Y(s)=y(1)],\mathrm{\dots },\mathbb{P}[Y(s)=y(m)]\}$, ${\mathrm{\Pi }}_X(s)=\{\mathbb{P}[X(s)=x(1),\mathrm{\dots },$ and $\mathbb{P}[X(s)=x(n)]\}$, we can write the exact relation between the variables $X$ and $Y$ in a matrix vector form:

$${\mathrm{\Pi }}_Y(s)=\mathrm{\Lambda }{\mathrm{\Pi }}_X(s),$$ [1]

where matrix elements ${\{\mathrm{\Lambda }\}}_{ij}=\mathbb{P}[Y(s)=y(i)|X(s)=x(j)]$ are conditional probabilities. If known, they can be used as indicators for existence of causality relations between the variables $Y$ and $X$ in the randomized studies: if ${\{\mathrm{\Lambda }\}}_{ij}=\mathbb{P}[Y(s)=y(i)]$ for all $j$ and $s$, the processes are then independent—meaning that information about the variable $X$ provides no additional advantage in computing the probability of the outcomes of $Y$. If ${\{\mathrm{\Lambda }\}}_{ij}\ne \mathbb{P}[Y(s)=y(i)]$ for some $j$, consequently, there exists some relation between $X$ and $Y$ (18). To be able to interpret these conditional probabilities as a measure of the true causality relations in practical studies when ${\{\mathrm{\Lambda }\}}_{ij}$ are estimated from the available observations of $X$ and $Y$, one needs to guarantee that the data are appropriately randomized.

In a particular case, where $m=n$, with $s$ being the time index and $X(s)\approx Y(s-\tau )$ (where $\tau$ is a time step), the above formulation (Eq. 1) is equivalent to a so-called master equation of a Markov process [and thereby, is a particular time-discrete case of the well-known time-continuous Fokker–Planck equation (17)]. The $n\times n$ matrix $\mathrm{\Lambda }$ in this case will be a transpose of the Markov transition operator (19). If matrix $\mathrm{\Lambda }$ is known, it provides full information about the relations between processes $Y$ and $X$—and can be used to predict $Y$ if $X$ is available.

In many applications, the relation matrix $\mathrm{\Lambda }$ is not known and needs to be first estimated from the available observational data $\{X(1),X(2),\mathrm{\dots },X(S)\}$ and $\{Y(1),Y(2),\mathrm{\dots },Y(S)\}$ [e.g., by means of the maximum log-likelihood approach that allows us to provide the analytical estimates of the most likely parameter values ${\mathrm{\Lambda }}^{*}$ and their uncertainties (lemma 1 in SI Appendix)]. However, in realistic applications (e.g., in the MD example below), the number of categories $n$ can grow exponentially with the physical dimension of the problem (“curse of dimension”)—leading to the exponential growth of overall uncertainty for the ${\mathrm{\Lambda }}^{*}$ estimates when the available statistics size $S$ and a number $m$ of $Y$-categories are fixed (lemma 2 in SI Appendix). This problem also means that the uncertainty of all additional physical observables obtained from ${\mathrm{\Lambda }}^{*}$ (e.g., the uncertainty of eigenvalues, eigenvectors, metastable sets, etc.) will be growing with the growing $n$, making practical deployment of Eq. 1 problematic for realistic systems with a “large” $n$ and “small” $S$. Therefore, if we want to reduce the dimensionality $n$—for example, through identification of a small number $K$ of collective categorical variables that agglomerate the original $n$ categories of process $X$ into K groups/boxes—then this methodology should not rely on a direct estimation of the full Bayesian causality matrix $\mathrm{\Lambda }$ in these situations.

To circumvent this problem, one can try to identify a latent reduced categorical process $\{\widehat{X}(1),\widehat{X}(2),\mathrm{\dots },\widehat{X}(S)\}$ (being a reduced representation of the full categorical process $X$) that is defined on a reduced statistically disjoint complete set of (the yet unknown) categories $\{\widehat{x}(1),\widehat{x}(2),\mathrm{\dots },\widehat{x}(K)\}$ with $K<n$. Deploying a law of a total probability, we can establish the Bayesian relations between $\widehat{X}$ and $X$ on one side (by means of the conditional probabilities ${\widehat{\mathrm{\Gamma }}}_{kj}=\mathbb{P}[\widehat{X}(s)=\widehat{x}(k)|X(s)=x(j)]$) and between $\widehat{X}$ and $Y$ on the other side (by means of the conditional probabilities ${\widehat{\lambda }}_{ik}=\mathbb{P}[Y(s)=y(i)|\widehat{X}(s)=\widehat{x}(k)]$). Then, it is straightforward to validate (a detailed derivation is in SI Appendix, section S2) that an optimal probability-preserving reduced approximation of the full relation model (Eq. 1) for $K$ colvars takes a form

$${\widehat{\mathrm{\Pi }}}_Y(s)=\widehat{\lambda }\widehat{\mathrm{\Gamma }}{\mathrm{\Pi }}_X(s),$$ [2]

where ${\{{\widehat{\mathrm{\Pi }}}_Y(s)\}}_i=\mathbb{P}[Y(s)=y(i)]$ and $i=\mathrm{\hspace{0.17em}1},\mathrm{\dots },m$. For every particular combination of $k$ and $j$, ${\widehat{\mathrm{\Gamma }}}_{k,j}$ defines a probability for the colvar to be in a reduced collective categorical variable $k$ when the observed original process $X$ is in a category $x(j)$, and therefore, it can be understood as a discrete analog of the continuous projection and reduction operators deployed in methods like PCA; $\widehat{\lambda }$ is a reduced version of the matrix $\mathrm{\Lambda }$ from the full relation model (Eq. 1). Please note that, being basically a reformulation of the exact law of the total probability, reduced model (Eq. 2) is exact in the Bayesian sense, and no additional approximations have been involved.

A similar approach to latent variable dependency modeling is used in the PLSA (13, 14) (that is, used in mathematical linguistics and information retrieval for identification of latent dependency structures in texts and documents). Deploying the definition of a conditional probability, PLSA allows one to parameterize a joint probability distribution $\mathbb{P}[X\hspace{0.17em}\text{and}\hspace{0.17em}Y]$ with the help of the latent process $\widehat{X}$ as $\mathbb{P}[X(s)=x(j)\hspace{0.17em}\text{and}\hspace{0.17em}Y(s)=y(i)]=\mathbb{P}[X(s)=x(j)]{\sum }_{k=1}^K{\widehat{\lambda }}_{ik}{\widehat{\mathrm{\Gamma }}}_{kj}$. To estimate the parameters, one deploys an Expectation Maximization algorithm having the computational iteration complexity of $\mathcal{O}\left(K\cdot \min \{mn,S\}\right)$ and requiring $\mathcal{O}\left((K+1)\cdot \min \{mn,S\}\right)$ memory in a general nonsparse situation (i.e., when the underlying matrix $\mathrm{\Lambda }$ is not assumed to be sparse a priori). However, as shown in SI Appendix, section S5, this problem requires imposing additional strong independence and stationarity assumptions on the latent variable $\widehat{X}$. Moreover, as shown in Fig. 1A, the total average number of Expectation Maximization iterations for this problem grows rapidly with problem dimensions $m$ and $n$—resulting in the overall algorithm complexity that grows polynomially in $n$ and $m$ (Fig. 1B). Applying standard statistical methods of polynomial regression fitting and discrimination (20, 21), one obtains that the statistically optimal fit of the red surface (corresponding to the PLSA) from Fig. 1B is given by a polynomial of the third degree in $n$ and $m$. Extrapolation to the typical physical problem sizes (e.g., $m=n={\mathrm{\hspace{0.17em}10}}^5$, $K=\mathrm{\hspace{0.17em}2}$) that, for example, emerge in biophysical applications like the protein molecules indicates that such an inference procedure based on the Expectation Maximization algorithm and PLSA would require approximately 1,450 years of computations on a single laptop personal computer. Detailed methodological description of the PLSA methodology and its relation to the reduced Bayesian model reduction methods is provided in SI Appendix, section S5.

In the following section, we will suggest several computational procedures for the scalable inference of reduced Bayesian relation model parameters (Eq. 2) directly from the observed data $\{X(1),X(2),\mathrm{\dots },X(S)\}$ and $\{Y(1),Y(2),\mathrm{\dots },Y(S)\}$. The optimal parameter estimates ${\widehat{\mathrm{\Gamma }}}^{*}$ and ${\widehat{\lambda }}^{*}$ that maximize the observation probability (called likelihood) of the given data in Eq. 2 can be obtained by solving the following log-likelihood maximization problem subject to equality and inequality constraints:

$$\widehat{L}=\sum _{i=1}^m\sum _{j=1}^n{N}_{ij}\log \left({\left\{\widehat{\lambda }\widehat{\mathrm{\Gamma }}\right\}}_{ij}\right)\to \underset{\widehat{\lambda },\widehat{\mathrm{\Gamma }}}{\max },$$ [3]

$${\widehat{\lambda }}_{ik}\ge 0,\sum _{i=1}^m{\widehat{\lambda }}_{ik}=1,\text{for all}\hspace{0.17em}i,k,$$ [4]

$${\widehat{\mathrm{\Gamma }}}_{kj}\ge 0,\sum _{k=1}^K{\widehat{\mathrm{\Gamma }}}_{kj}=1,\text{for all}\hspace{0.17em}k,j,$$ [5]

where $N_{ij}={\sum }_{s=1}^S\chi (Y(s)=y_i)\chi (X(s)=x_j)$ (with $\chi$ being an indicator function). It is straightforward to observe that, for any fixed $\widehat{\lambda }$, the original exact log-likelihood maximization problem (Eqs. 3–5) can be decomposed into $n$ optimization problems for the $n$ columns of $\widehat{\mathrm{\Gamma }}$—and each of the column problems with $(K-\mathrm{\hspace{0.17em}1})$ optimization arguments is concave and can be solved independently from the other column problems. This observation can help in designing a convergent algorithm requiring much less memory than the Expectation Maximization [$\mathcal{O}\left(K(m+n)+\min \{mn,S\}\right)$ instead of $\mathcal{O}\left((K+\mathrm{\hspace{0.17em}1})\cdot \min \{mn,S\}\right)$ for Expectation Maximization] and with computational iteration complexity of $\mathcal{O}\left({(m-\mathrm{\hspace{0.17em}1})}^3{K}^3+n{(K-\mathrm{\hspace{0.17em}1})}^3\right)$. It can be used for identification of the reduced Bayesian relation model parameters in the situations when $m$ and $K$ are relatively small and $n$ is large (e.g., as in the medical example 2 below). Detailed derivation of this algorithm is given in SI Appendix, section S4. However, when $m$ or $K$ is large (as in a case of the MSM inference in MD, where $m=n\approx {\mathrm{\hspace{0.17em}10}}^3-{\mathrm{\hspace{0.17em}10}}^9$), this scaling would not allow us to apply this method to large realistic systems.

It turns out that substituting the function $\widehat{L}$ with its lower-bound approximation $\widehat{L}\ge \widehat{l}$ $={\sum }_{i=1}^m{\sum }_{j=1}^n{\sum }_{k=1}^K{N}_{ij}{\widehat{\mathrm{\Gamma }}}_{kj}\log ({\widehat{\lambda }}_{ik})$ (which directly results from applying the Jensen’s inequality to Eq. 3) allows for providing a computational method that can solve this approximate model reduction problem with a much better scaling and allows analytically computable uncertainty estimates for the obtained reduced models.

Properties of this approximate model reduction procedure are summarized in the following theorem.

Theorem.

Given the two sets of categorical data $\{X(1),X(2),\mathrm{\dots },X(S)\}$ and $\{Y(1),Y(2),\mathrm{\dots },Y(S)\}$ (where for any $s,X(s)\in \{x(1),x(2),\mathrm{\dots },x(n)\}$ and $Y(s)\in \{y(1),y(2),\mathrm{\dots },y(n)\}$), the approximate maximum log-likelihood parameter estimates for $\widehat{\lambda }$ and $\widehat{\mathrm{\Gamma }}$ in the reduced model (Eq. 2) can be obtained via a maximization of the lower bound $\widehat{l}$ of the above log-likelihood function $\widehat{L}$ from Eq. 3:

$$\widehat{L}\ge \widehat{l}=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K{N}_{ij}{\widehat{\mathrm{\Gamma }}}_{kj}\log \left({\widehat{\lambda }}_{ik}\right)\to \underset{\widehat{\lambda },\widehat{\mathrm{\Gamma }}}{\max },$$ [6]

subject to the constraints (Eqs. 4 and 5). Solutions of this problem exist and are characterized by the discrete/deterministic optimal matrices $\widehat{\mathrm{\Gamma }}$ that have only elements zero and one. Solutions of Eqs. 4–6 can be found in a linear time by means of the monotonically convergent Direct Bayesian Model Reduction (DBMR) Algorithm shown below, with a computational complexity of a single-iteration scaling as $\mathcal{O}(K\cdot \min \{mn,S\})$ and requiring no more than $\mathcal{O}(K(m-1)+n+\min \{mn,S\})$ of memory. Asymptotic posterior uncertainty of the obtained parameters ${\widehat{\lambda }}^{*}$ (characterized in terms of the posterior parameter variance) can be computed analytically as $\text{Var}\{\mathbb{P}[{\widehat{\lambda }}_{ik}|{\widehat{\lambda }}^{*},{\widehat{\mathrm{\Gamma }}}^{*}X,Y]\}={\widehat{\lambda }}_{ik}^{*}(1-{\widehat{\lambda }}_{ik}^{*})/{\sum }_{i=1}^m{\sum }_{j=1}^n{N}_{ij}{\widehat{\mathrm{\Gamma }}}_{kj}^{*}$. The least biased estimate of the ratio $\rho$ for the expectations of posterior parameter variances from the resulting full and reduced models equals

$$\rho =\frac{{𝔼}_{ij}\mathrm{Var}\left\{\mathbb{P}[{\mathrm{\Lambda }}_{ij}|{\mathrm{\Lambda }}^{*},X,Y]\right\}}{{𝔼}_{ik}\mathrm{Var}\left\{\mathbb{P}[{\widehat{\lambda }}_{ik}|{\widehat{\lambda }}^{*},{\widehat{\mathrm{\Gamma }}}^{*}X,Y]\right\}}=\frac{n}{K}.$$ [7]

DBMR Algorithm.

• Choose a random ${\widehat{\lambda }}^{\left(\text{0}\right)}$ (e.g., from the least biased uniform prior), set I = 0.

• Set ${\mathrm{\Gamma }}_{\text{𝑘𝑗}}^{\left(\text{0}\right)}$ to 1 if $\text{𝑘}=\underset{\text{𝑘}\prime }{\text{argmax}}{\sum }_{\text{𝑖}=1}^{\text{𝑚}}{\text{𝑁}}_{\text{𝑖𝑗}}\text{log}({\widehat{\lambda }}_{\text{𝑖𝑘}\prime }^{\left(\text{0}\right)})$ and else to 0 for all j and k.

• Do until $\parallel \widehat{𝐥}({\mathrm{\Gamma }}^{\left(\text{𝐼}\right)},{\widehat{\lambda }}^{\left(\text{𝐼}\right)})-\widehat{𝐥}({\mathrm{\Gamma }}^{(\text{𝐼}-1)},{\widehat{\lambda }}^{(\text{𝐼}-1)})\parallel$ becomes less than a tolerance threshold.

  •  Step 1: set ${\widehat{\lambda }}_{\text{𝑖𝑘}}^{(\text{𝐼}+1)}=\frac{{\sum }_{\text{𝑗}=1}^{\text{𝑛}}{\text{𝑁}}_{\text{𝑖𝑗}}{\mathrm{\Gamma }}_{\text{𝑘𝑗}}^{\left(\text{𝐼}\right)}}{{\sum }_{\text{𝑖}=1}^{\text{𝑚}}{\sum }_{\text{𝑗}=1}^{\text{𝑛}}{\text{𝑁}}_{\text{𝑖𝑗}}{\mathrm{\Gamma }}_{\text{𝑘𝑗}}^{\left(\text{𝐼}\right)}}$ for all $\text{𝑖},\text{𝑘}$.

  •  Step 2: set ${\mathrm{\Gamma }}_{\text{𝑘𝑗}}^{(\text{𝐼}+1)}=1$ if $\text{𝑘}=\underset{\text{𝑘}\prime }{\text{argmax}}{\sum }_{\text{𝑖}=1}^{\text{𝑚}}{\text{𝑁}}_{\text{𝑖𝑗}}\text{log}\left({\widehat{\lambda }}_{\text{𝑖𝑘}\prime }^{(\text{𝐼}+1)}\right)$ and else ${\mathrm{\Gamma }}_{\text{𝑘𝑗}}^{(\text{𝐼}+1)}=\text{0}$ for all $\text{𝑗},\text{𝑘}$.

  •  $\text{𝐼}=\text{𝐼}+1.$

A proof is provided in SI Appendix, section S2.

As can be seen from Fig. 1A, the average number of DBMR iterations (green surface in Fig. 1A) (computed from a large ensemble of randomly generated Bayesian model reduction problems for $K=\mathrm{\hspace{0.17em}2}$) does not change with the dimensions $m$ and $n$. It implies that also the overall computational complexity of the DBMR is scaling as $\mathcal{O}\left(K\cdot \min \{mn,S\}\right)$. DBMR estimation of the reduced MSM for a medium-sized protein MD with $m=n={\mathrm{\hspace{0.17em}10}}^5$ and $K=\mathrm{\hspace{0.17em}2}$ takes 33 min (as mentioned above, the extrapolated estimate of the Expectation Maximization computational time was 1,450 years under the same optimization and hardware/software settings).

Fig. 1C represents the average relative log-likelihood differences between the results of exact iterative log-likelihood optimization of Eqs. 3–5 and the DBMR results (obtained under the same conditions). It reveals that the empirical average relative log-likelihood differences between the exact and the DBMR-approximated results converge to zero exponentially in $m$. This property implies that, for realistic high-dimensional applications, the log-likelihood difference between the reduced models obtained with the DBRM algorithm and those obtained with the optimization of the exact log-likelihood can be expected to become negligible—meaning that the reduced models obtained with the DBRM algorithm will have essentially the same posterior probability for explaining the observed full data as the exact reduced models.

The main feature of the two algorithms presented above is that they allow for obtaining the reduced model (Eq. 2) directly from the available observational data $\{X(1),X(2),\mathrm{\dots },X(S)\}$ and $\{Y(1),Y(2),\mathrm{\dots },Y(S)\}$—completely omitting a need for computation/estimation of the full relation matrix $\mathrm{\Lambda }$ in Eq. 1. The only tunable parameter in both of the algorithmic procedures introduced above (in the direct sequential optimization of the exact log-likelihood (Eqs. 4–6) and the DBMR algorithm) is the reduced process dimension $K$. The optimal integer value of $K$ can be obtained by performing the algorithms with different numbers of $K$ (i.e., $K=\mathrm{\hspace{0.17em}1},\mathrm{2,3},\mathrm{\dots }$) and then selecting the best reduced model (Eq. 2) according to one of the standard model selection criteria [e.g., cross-validation criterion, information criteria like Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC), or approaches like L curve] (22, 23). To select an optimal $K$ for the examples below, we have used the standard L-curve method (23) that identifies the optimal $K$ as the edge point of the curve that describes a dependence of the optimal value of the maximized function (Eq. 3 or 6 in our case) from $K$ (a practical example is in SI Appendix, Fig. S2).

When dealing with real-life applications, it is also important to have an option for adjusting a set of collective variables according to a physical intuition or some prior knowledge (1). For example, one could have some prior physical information that certain dimensions of the original problem have a higher relevance for the dynamics than some other physically less relevant dimensions. In SI Appendix, section S3, we present a computationally scalable way [with computational iteration complexity of $\mathcal{O}\left(mK+n(K-1)\log [n(k-1)]\right)$] to impose such a priori information—cast into a form of the weighted graph—on the DBMR algorithm. The resulting DBMR graph algorithm is presented in SI Appendix, section S4, and a practical application of this information-imposing clustering method to reduced Bayesian model inference is given in the breast cancer diagnostics example 2 below.

A MATLAB library of algorithms implementing the methods introduced in this manuscript—as well as different variants of the constrained Nonnegative Matrix Factorization (12, 24) and PLSA methods (13, 14)—can be found in SI Appendix and is available as open access via a general public license from https://github.com/SusanneGerber.

Results

Example 1: Reduced Model of the 10-Alanine Dynamics in Water.

First, we consider a colvar identification for a polypeptide molecule [deca-alanine (10-ALA)] from results of the MD simulation. This dataset represents an output of the 0.5-$\mu$s simulation (with a 2-fs time step) of a 10-ALA polypeptide in explicit water at the room temperature performed with the Amber99sb-ildn force field (25). These MD data were produced and provided by Frank Noe and Antonia Mey, Free University (FU) Berlin, Berlin. For additional analysis, the values of torsion angles ${\varphi }_i$ and ${\psi }_i$ ($i=\mathrm{\hspace{0.17em}1},\mathrm{\dots },8$) inside of the molecular backbone (i.e., ignoring the two end groups and the ${\omega }_i$ angles) are grouped into the Ramachandran states 1–3 for every $i$ (SI Appendix, Fig. S1, Left) with a time step resolution of 100 ps, resulting in eight categorical Ramachandran time series with 5,000 time points each. Based on these eight local junction time series, we create a series of global molecular states $X(s)$ ($s=\mathrm{\hspace{0.17em}1},\mathrm{\dots },5\text{,}000$), where every particular combination of eight Ramachandran states is assigned to a particular category; in our case, it is a categorical series with $n=\mathrm{\hspace{0.17em}531}$ of such eight-component combinations with $S=5\text{,}000$ time instances. As a 531D $X(s)$ variable to be reduced, we use this set of global states; as reference variables $Y_i$, we choose the individual Ramachandran series of junctions (i.e., with $m=\mathrm{\hspace{0.17em}3}$ each) at time $s+\mathrm{\hspace{0.17em}1}$. Thereby, we are casting the reduction problem to a setting of discrete Markov processes in time.

We start with setting $K=\mathrm{\hspace{0.17em}2}$ and comparing the practical performance of algorithms introduced in this paper with the PLSA method (13, 14). Results of this comparison are summarized in SI Appendix, Fig. S5. As can be seen from SI Appendix, Fig. S5, methods based on optimization of Eqs. 3 and 6 provide colvars that are better in terms of the log-likelihood measure as well as in terms of the information theoretical measures, like the robust AIC and BIC (22). AIC and BIC take into account the model quality and penalize model uncertainty—for the same quality (log-likelihood), these measures would provide smaller values for the models that are less uncertain (22).

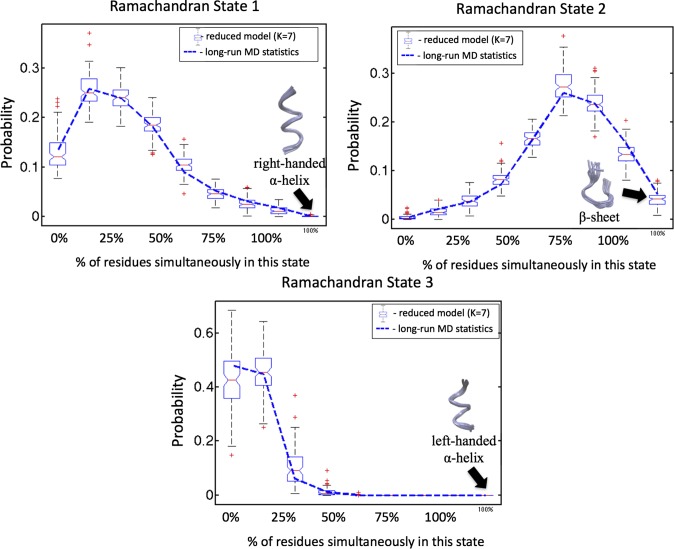
Second, we do the identification of reduced models (Eq. 2) for each of the peptide junctions ($i=\mathrm{\hspace{0.17em}1},\mathrm{\dots },8$). Values of the resulting optimal solutions for reduced log-likelihoods ${\widehat{𝐥}}_i$ ($i=\mathrm{\hspace{0.17em}1},\mathrm{\dots },8$) as functions of $K$ are shown in SI Appendix, Fig. S2. These results reveal that the reduced log-likelihood does not exhibit any nonnegligible increase for all $i$ when the number of colvars $K$ is becoming larger than three to seven, meaning that the maximal number of the nonredundant colvars is not greater than seven for this system. Next, we inspect the identified colvars for all of the $Y_i$. As can be seen from SI Appendix, Fig. S3 (as an example, representing a case of $Y_i$ being the Ramachandran time series of the junction 4 for $K=\mathrm{\hspace{0.17em}3}$), the three identified colvars almost perfectly—to 97%—coincide with the discretization that is solely based on this junction and disregard all other junctions in the peptide chain. In only 3% of the cases, the nonlocal information about the Ramachandran states of the peptide residues from other junctions is important. Therefore, relations in terms of temporal causality between the peptides MD dynamics can be almost (in 97% of the cases) described by a sequence of spatially independent Markov processes in each of the peptide junctions—for example, collected together in a form of the Ising model (26). To verify the validity of the obtained colvars as well as test the performance of the resulting reduced model (Eq. 2), we use these colvars to produce a long Monte Carlo time series of the reduced molecular simulation (Eq. 2) and compute statistics of the geometrical configurations for the entire molecule. As shown in Fig. 2, reduced dynamics based on just a few colvars can reliably represent the overall spatial statistics of molecular configurations in 3D—obtained from the full MD trajectory. These 3% of nonlocal dependence cases identified in SI Appendix, Fig. S3 seem to be crucial: without them, the corresponding box plot of the reduced Monte Carlo run is not capable of reproducing the true statistics of geometrical configurations from MD (SI Appendix, Fig. S4).

Fig. 2.

Probabilities for different proportions of the chain in the same local Ramachandran state; 100% means that all of the residues in the chain are in this Ramachandran state, and 0% means that there is not a single residuum in this state. The blue lines indicate the values of this distribution obtained from the full MD simulation data, and the box plots show the probability distribution and its 95% confidence intervals obtained from the optimal reduced model run with seven colvars ($K=\mathrm{\hspace{0.17em}7}$) and nonlocal causality boxes. Red points denote the statistical outliers of the reduced model (meaning that they are outside of the 99% confidence interval). Respective distributions for a completely independent model (i.e., for a model where 100% of causality boxes are local) are shown in SI Appendix.

Example 2: Reduced Model for the Breast Cancer Diagnostics Based on the Standard BI-RADS Data.

For the second example, we consider analysis and reduction of the standard Breast Imaging Reporting and Data System (BI-RADS) dataset for breast cancer diagnostics—available as an open access data file at the University of California Irvine (UCI) Machine-Learning Repository: mlr.cs.umass.edu/ml/datasets/Mammographic+Mass. This dataset contains information about 403 healthy (benign) and 427 malignant breast cancer patients. For each of the patient entries, the age and three categorical variables obtained from the mammography images are provided together with the basic result (“cancer”/“no cancer”) obtained from the invasive analysis of the tissue—as well as assessments based on the standard noninvasive mammography diagnostics procedure called BI-RADS. The three categorical variables provide qualitative characteristics of the mammographic image features used in BI-RADS—such as the shape of the intrusion (with four categories), characteristics of the intrusion margins (with five categories), and intrusion density (with four categories). This standard categorical dataset is widely used to access the quality of various computer-aided diagnostic (CAD) tools, with the general aim of identifying such a CAD tool that would use the noninvasive information of age and mammographic image features for the precise diagnostics of breast cancer and providing lower rates of false positive and false negative diagnoses than the standard BI-RADS procedure currently used by medical doctors (27). The widely used measure of CAD performance adopted in the medical literature is called area under curve (AUC) (28). The closer the AUC value is to $1.0$, the better the performance of the respective CAD tool and the lower the probability of false positive and false negative diagnoses. To compute the AUC values of different CAD tools together with the 99% confidence intervals of AUC, we use a methodology described in ref. 28 and available in the open source software library that can be downloaded at https://github.com/brian-lau/MatlabAUC. CAD tools based on the pattern recognition artificial neuronal networks (ANNs) have been reported to have the highest AUC for the breast cancer diagnostics issue (27). Training such ANNs on these data from 830 patients results in AUC of 0.85 with the 99% confidence interval of $[0.82,0.91]$, whereas we obtain AUC of 0.82 with the 99% confidence interval of $[0.78,0.87]$ for a standard BI-RADS diagnostics (on the same data and computed deploying the same methodology from ref. 28). Therefore, despite the fact that the AUC value of ANNs is somewhat larger than the AUC of BI-RADS, their confidence intervals are largely overlapping—meaning that, from the view point of statistics, this standard dataset does not reveal an advantage of the ANNs compared with BI-RADS. In addition, ANN has many free adjustable parameters (e.g., weights and biases of neurons, transfer functions, etc.), which increase the danger of overfitting for such relatively small data. The application of the categorical reduction procedure described in this paper results in an optimal set of just two collective variables that are both completely defined by information from a single categorical variable “margin.” Very unexpectedly, obtained optimal decomposition into two colvars turns out to be completely independent from all other variables and can be summarized in a very simple diagnostic rule: if the intrusion margin on the mammography image is circumscribed, then the risk of breast cancer is low (12%), and if not, the risk of breast cancer is high (72%). Applying the same open source methodology for AUC confidence intervals on the same standard data as above, we find that this very simple rule (with no free tunable parameters at all) has the AUC value of 0.835 with the 99% confidence interval of $[0.79,0.88]$ (i.e., in terms of the AUC performance, it is not worse than the ANN with approximately 20 free adjustable parameters).

Discussion

The most important features distinguishing the methodology presented in this paper from other approaches described in the literature are that it allows highly scalable (Fig. 1) identification of reduced Bayesian relation models, their uncertainty quantification, and inclusion of a priori physical information and does not rely on the prior knowledge or a necessity of estimation of the full matrix $\mathrm{\Lambda }$ (Eq. 1) of system’s relations in any step. It allows an identification of the colvars and the reduced relation models (Eq. 2)—as well as the MSMs—directly from the observational data.

According to the above theorem, the least biased estimate of the ratio $\rho$ for the expectations of posterior parameter variances from the resulting full and reduced models equals $n/K$—where $n$ is the number of the original dimensions, and $K$ is the reduced dimensionality. In application examples 1 and 2 shown above, $\rho$ is of the order of 100—meaning that the reduced models (Eq. 2) can be estimated from much shorter data series than those required for the full model without reduction. In the context of MD and other multiscale applications, this feature can be a used to bridge the gap toward longer time scales in simulations. In particular, in both examples, we have shown how the interpretation of the obtained colvars can provide clues about the locality or nonlocality of relations in the system. Application of this methodology in both examples revealed essentially local models (i.e., models where colvars mostly coincide with only one of the original systems dimensions). In example 1, we have shown that the relation between the local geometry changes of single peptide units in time is local to 97% and that, only in 3% of the original system’s states assembled to colvar, they are nonlocal (and distinctively defined by the peptide junction configuration farther away in the chain). In example 2, the two identified colvars were completely defined through only one of the original data dimensions and are entirely independent from all other information on the system. This seemingly oversimplification of the obtained reduced models could, however, be undermined by the comparison of results and predictions obtained for these very simple reduced models (Fig. 2 or the results of AUC comparison in example 2). The proposed methodology is very simple to implement and to use—we also provide a MATLAB toolbox with all of the methods from this manuscript as open access via the https://github.com/SusanneGerber. As was shown for two application examples, obtained results are straightforward to interpret and provide insights in the underlying systems as well as situations when the system’s dimension $n$ is large (e.g., $n=531$ for the example 1) and standard approaches may be subject to the overfitting issues.