Significance
How do apparently simple organisms coordinate sophisticated behaviors? The slime mold Physarum polycephalum solves complex problems, for example finding the shortest route between food sources, despite growing as a single cell and the lack of any neural circuitry. By carefully observing P. polycephalum’s response to a nutrient stimulus and using the data to develop a mathematical model, we identify a simple mechanism underpinning the slime mold’s behaviors: A stimulus triggers the release of a signaling molecule. The molecule is initially advected by fluid flows but also increases fluid flows, generating a feedback loop and enabling the movement of information throughout the organism’s body. This simple mechanism is sufficient to explain P. polycephalum’s emergent, complex behaviors.
Keywords: acellular slime mold, transport network, behavior, Taylor dispersion
Abstract
Complex behaviors are typically associated with animals, but the capacity to integrate information and function as a coordinated individual is also a ubiquitous but poorly understood feature of organisms such as slime molds and fungi. Plasmodial slime molds grow as networks and use flexible, undifferentiated body plans to forage for food. How an individual communicates across its network remains a puzzle, but Physarum polycephalum has emerged as a novel model used to explore emergent dynamics. Within P. polycephalum, cytoplasm is shuttled in a peristaltic wave driven by cross-sectional contractions of tubes. We first track P. polycephalum’s response to a localized nutrient stimulus and observe a front of increased contraction. The front propagates with a velocity comparable to the flow-driven dispersion of particles. We build a mathematical model based on these data and in the aggregate experiments and model identify the mechanism of signal propagation across a body: The nutrient stimulus triggers the release of a signaling molecule. The molecule is advected by fluid flows but simultaneously hijacks flow generation by causing local increases in contraction amplitude as it travels. The molecule is initiating a feedback loop to enable its own movement. This mechanism explains previously puzzling phenomena, including the adaptation of the peristaltic wave to organism size and P. polycephalum’s ability to find the shortest route between food sources. A simple feedback seems to give rise to P. polycephalum’s complex behaviors, and the same mechanism is likely to function in the thousands of additional species with similar behaviors.
One of the great challenges of unraveling biological complexity is understanding what kind of and how much computational power is required for an organism to generate sophisticated behaviors. Behaviors are typically associated with a nervous system, but many organisms without nervous systems integrate information and function as coordinated individuals (1); examples range from the ability of Escherichia coli to move up chemical gradients (2) to the ability of a multicellular fungus to sense and precisely explore unoccupied space (3). A recently published and striking example of a complex behavior involves bacteria within a biofilm: When a Bacillus subtilis biofilm is deprived of nutrients, bacteria are able to grow networks of channels and evaporatively pump flows, creating intricate structures that benefit the entire community (4).
Perhaps the archetypal example of an apparently simple organism able to generate sophisticated behaviors is the slime mold Physarum polycephalum, whose behaviors are repeatedly characterized as “intelligent.” This slime mold is able to navigate mazes by finding the shortest route between different food sources (5) and has used its ability to reconstruct the transportation maps of major cities (6). The organism can structure its connections to different nutrient sources to optimize its diet (7).
How the organism coordinates complex tasks in the absence of a nervous system remains unknown. P. polycephalum is unicellular, and as it forages the slime mold develops as a reticulated network of tubes. There is no obvious organizing center. Tubes are made of a gel-like outer layer and interior cytoplasmic fluids. The outer layer houses an actin–myosin cytoskeleton and the cytoskeleton generates periodic contractions of tube walls. Contraction amplitude and frequency generally increase or decrease organism-wide when encountering an attractant or repellant, respectively (8–11). Contractions drive periodic cytoplasmic fluid flows, and these extend across an entire individual. Intriguingly, the fluid flows are highly coordinated (12), and the phase of oscillations is tuned such that there is exactly one wavelength across an individual, regardless of an individual’s size. Data suggest P. polycephalum is somehow able to measure its size.
Although data also suggest P. polycephalum can communicate across its entire body (13), we have no knowledge of the nature of communication. Signals may propagate via elastic waves (14) or an advected molecular stimulus (15, 16) or electrical impulses (17). Our very recent work tentatively suggests the second hypothesis; flows generated from the coordinated contractions of tube walls are used to increase the effective dispersion of molecules substantially beyond their pure molecular diffusivity, a phenomenon known as Taylor dispersion (18). However, these different possibilities can be definitively distinguished by their velocities for signal propagation, which differ dramatically, and recognition of this fact opens up the possibility of understanding communication, the key to understanding behaviors.
Building on our previous observations (12, 18), we now report and characterize the mechanism of communication in P. polycephalum and demonstrate that a simple feedback between a signaling molecule and a propagating contraction front is sufficient to explain P. polycephalum’s sophisticated behaviors. The key experiment demonstrates that a localized nutrient stimulus triggers an increase in contraction amplitude initiating at the stimulus site. The amplitude front propagates across the organism with a velocity comparable to the dispersion of particles in cytoplasmic fluid flows. We use unrelated trace particles in the cytoplasm to measure flow velocities. We build a mathematical model based on these data and in the aggregate experiments and the model identify the mechanism of signal propagation across a body: The nutrient stimulus triggers the release of a signaling molecule. The molecule is advected by fluid flows but simultaneously hijacks flow generation by causing local increases in contraction amplitude as it travels. The molecule is initiating a feedback loop to enable its own movement. Although the chemical nature of the signaling molecule so far remains unidentified the discovery of the mechanism of signal propagation itself allows us to understand P. polycephalum’s complex dynamics. The mechanism implies that the peristaltic wave matches organism size, explaining our previous observation (12). Moreover the mechanism, working in tandem with tube radius adaptation in response to the increased flow, seems sufficient to explain how P. polycephalum is able to solve a maze and build efficient transport networks.
Results
P. polycephalum Responds to a Stimulus with a Propagating Change in Contraction Dynamics.
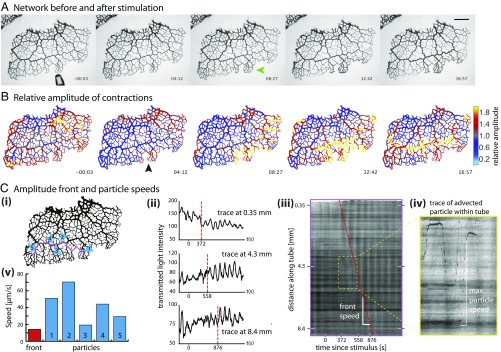
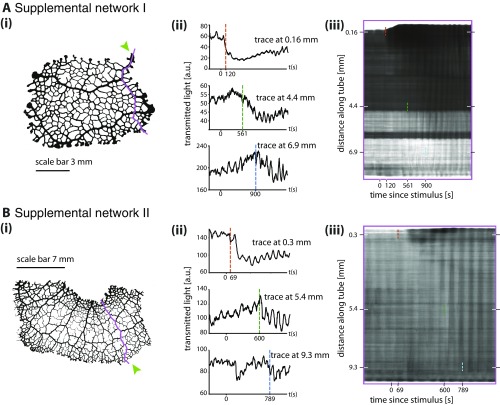
To follow the propagation of a stimulus throughout a P. polycephalum network we first observed networks before and after stimulation using bright-field microscopy over the course of 2 to 3 h. Data were analyzed to extract and track contractions along each tube (Materials and Methods). A nutrient stimulus gives rise to immediate changes in tube contraction dynamics and these propagate spatially over time (Fig. 1 and Movie S1). After a short delay, the response begins with a localized inflation of the tubes directly exposed to the nutritive liquid (green arrow in Fig. 1). A uniform reduction in tube volume elsewhere follows and is caused by the fixed amount of fluid within a network. Analysis of the wave patterns shows a clear increase in oscillation amplitude at the stimulation site (Fig. 1B and Movie S2); see ref. 22 for an independent dataset done in an entirely different context. Our dataset shows the change in amplitude subsequently propagates along the tubes with a speed of about 13 m/s (Fig. 1C, i and ii). The spread of the change is not symmetric in space around the stimulation site; instead, the change in amplitude obviously propagates more quickly along larger tubes compared with tubes with smaller radii. These observations are reproducible (Fig. S1).
Fig. 1.
Propagating amplitude front. (A) Bright-field images of a P. polycephalum network before (3 s, including approaching pipette) and after stimulation with a droplet of nutrient media. Droplet added at 0 s. Tubes swell where they make contact with the droplet (green arrow). (Scale bar, 2 mm.) (B) The same time points as in A showing contraction amplitude relative to the average over the last 10 periods before stimulation. Stimulation site marked by black arrow. The front (hot colors) spreads preferentially through tubes of larger radii. (C) Amplitude front and particle speeds extracted from bright-field dataset. (i) Locations of particle speed (blue) and front speed (magenta) measures. (ii) Contraction patterns at three different points further and further away from stimulation site. Dotted vertical lines mark sudden changes in contraction amplitude. (iii) Kymograph along trace in i showing change in contraction amplitude, observed as increased contrast during a contraction cycle. Front of increased amplitude propagates over time (red dashed line). (iv) Inset of iii: Particles advected along the tube appear as dark spotted trajectories. (v) Representative maximal speeds of particles (blue), located as pictured in i. Average front propagation speed (red) along trajectory in i as shown in iii.
Fig. S1.
Amplitude front propagation in two additional data sets. For both sets (A and B) i shows network morphology and stimulus site (green arrow). ii shows contraction patterns at three different points further and further away from stimulation site. Dotted vertical lines indicate a sudden change in contraction amplitude. iii shows a kymograph along the trace shown in i.
As we tracked contraction dynamics we simultaneously observed unrelated particles or vacuoles moving with shuttle flow within tubes. These appear as dark streaks in the kymograph (Fig. 1C, ii). Because of the ephemeral nature of the particles net transport velocity could not be calculated, but the streaks allow us to measure the maximal fluid flow velocity along a tube during a given contraction period. Fig. 1C, iii compares maximal flow speeds with speeds of the propagation front; the front propagation velocity is about two- to threefold slower than the maximal flow velocity and as such is likely to be similar to the net transport velocity within the cytoplasm (Fig. S2).
Fig. S2.
Maximal particle speed compared with net particle propagation speed. Shuttle flow of material can be seen in kymographs as sinusoidal patterns. Maximal particle speed (faster, yellow dashed line) corresponds to the steepest part of this sinusoid, whereas net propagation speed (slower, red dashed line) corresponds to incremental movements of the tips of the sinusoids along the tube.
Mechanism of Signal Propagation.
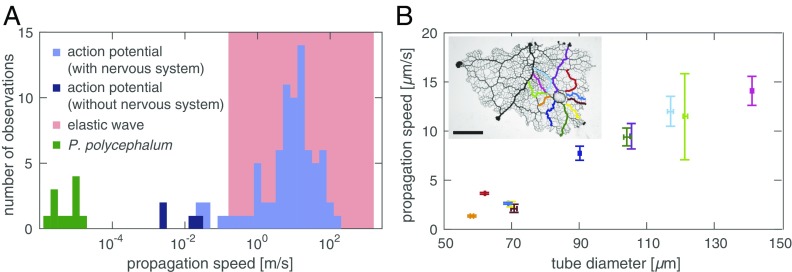
Experimentally we observe a propagating change in contraction amplitude triggered by a localized stimulus. The velocity of the amplitude front, m/s, is significantly slower than expected from propagation mechanisms involving elastic waves, m/s, or action potentials, mm/s, but is in the range expected from an internally advected signal (Fig. 2). Data also rule out the diffusive spread of a stimulus within the agar substrate: This mechanism would result in a radially symmetric increase in contraction amplitude around the stimulus site, but we observe an asymmetric spread along larger tubes with higher flow velocities. Experiments suggest a basic feedback mechanism: An initial stimulus triggers release of a signaling molecule and the molecule changes local wall contractions, increasing local fluid flow. Greater flow increases the dispersion of the signaling molecule away from its source, and the molecule continues to trigger wall contractions downstream. The process repeats itself and creates a self-propagating front across the entire organism.
Fig. 2.
Front speed identifies mechanism. (A) Propagation speeds for elastic waves (red), action potentials (blue), (19, 20), and P. polycephalum (green). Wave velocity in a fluid filled elastic tube varies between wave speed in the elastic wall (lower bound) and the fluid only (upper bound) (21). (B) Front speed increases with tube radius as predicted by the model. Amplitude fronts along tubes of a network centrally stimulated by nutrient droplet. Data show average speed and tube diameter with one SD error measured at five locations along the corresponding route (Inset). (Scale bar, 5 mm.)
To test whether this mechanism can explain experiments, we now translate it into a formal mathematical model, using parameters measured from the organism itself (Materials and Methods). Cytoplasmic flows are well described as a low-Reynolds-number (), incompressible fluid. The tube radius is much smaller than the oscillatory boundary layer thickness , defined by the ratio of kinematic viscosity and oscillation frequency . Thus, the flow velocity, , with the flow longitudinal and radial flow components in a cylindrical coordinate system, follows from the Stokes equations
| [1] |
where denotes fluid viscosity and pressure. The force represents force on the cell wall caused by the active tension generated by the actin–myosin cytoskeleton embedded in tube walls, as well as the elastic restoring force . We represent these effects through
| [2] |
so the force density is localized at the tube boundary where , oriented radially with the unit vector . Because the thickness of the tube wall is small compared with the base radius , we can approximate the elastic restoring force using the linear law
where characterizes the wall elasticity (23). The orientation of the restoring force is negative for , thus counteracting tension, while acting in parallel with tension for . Experiments have shown that the tension in the tube wall of P. polycephalum oscillates with a well-defined frequency (24, 25). A typical period is around s. Oscillations seem independent of cytoplasmic flows because they persist if cytoplasm is replaced by air (26), even though they become spatially uncorrelated if flows are stalled (26, 27). We incorporate this into our model by taking , where the tension strength depends on the concentration of the signaling molecule . We expect actin–myosin to respond to a time average of the signal concentration, so that , which for simplicity we assume to be linear, .
We note an important simplification of the fluid mechanics: Because the characteristic length scale of the contraction is much larger (i.e., organism size) than the radius of the tube, the Stokes equations (Eq. 1) simplify via lubrication theory (SI Text). This gives the flow velocity in the tube as a response to the forcing,
| [3] |
where is the cross-sectional average advection velocity in the tube. This equation is supplemented by the incompressibility condition, an equation for conservation of mass (Eq. 5), which holds throughout the closed tube.
Finally, to complete our model, we must specify the dynamics of the signaling molecule itself. This is given by
| [4] |
where is the molecular diffusivity. In the limit that the timescale for diffusion across the radius of the tube () is fast relative to a typical time for transport along the tube, the transport dynamics simplify to Taylor dispersion (Eq. 7) (28, 29). Specifying the dynamics of the cross-sectionally averaged concentration by Taylor dispersion shows that the quick diffusion across the tube cross-section augments diffusion proportional to the flow velocity.
Altogether the complete equations governing flow and transport are given by
| [5] |
| [6] |
| [7] |
| [8] |
where we omitted higher-order correction terms in Taylor dispersion due to nonuniform tube radius (30). Eq. 8 time-averages the concentration over a timescale . The precise value of does not affect model predictions as long as it is of the order of a period of contraction.
Amplitude Fronts Propagate by Taylor Dispersion.
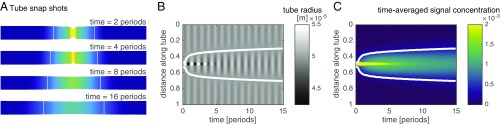
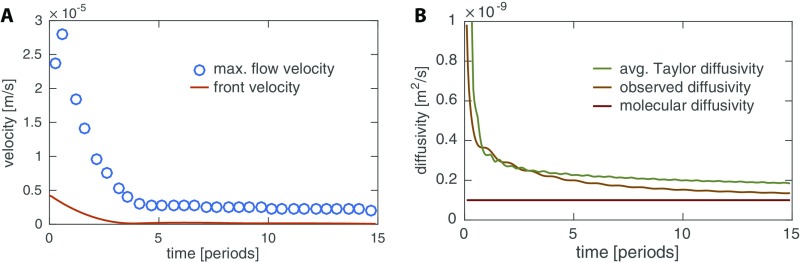
First we use our model (Eqs. 5–8) to explore the dynamics of flow and transport of a signal generated by a localized stimulus, as shown in Fig. 3. We find that the dynamics give rise to a self-propagating front of increased contraction amplitude. The localized signal’s concentration causes nonzero contraction amplitudes throughout the tube that peak with the peak in concentration. The contractions drive a shuttle flow and thus both signal concentration and increased contraction amplitude self-propagate with the flow through the tube. The propagation of the region of high amplitude is a diffusive process, because in a shuttle flow advective contributions cancel out over each period of contraction (Fig. S3A). The observed diffusivity of the concentration matches the Taylor dispersion coefficient (see Eq. 7), where flow velocity and radius are averaged in between the fronts of the centralized stimulus (Fig. S3B). The speed of the diffusively propagating front is therefore smaller than the maximal flow velocity within the tube, in agreement with experimental observations. Because the region of elevated contraction amplitude is diffusing and not being advected the speed of the increased amplitude front slows down over time. In experimental networks, the slowing-down effect is hard to observe because the front propagates with different speeds in tubes of different radii; exceptions showing slowing down are given in Fig. 1B, Movie S2, and Fig. S1A.
Fig. 3.
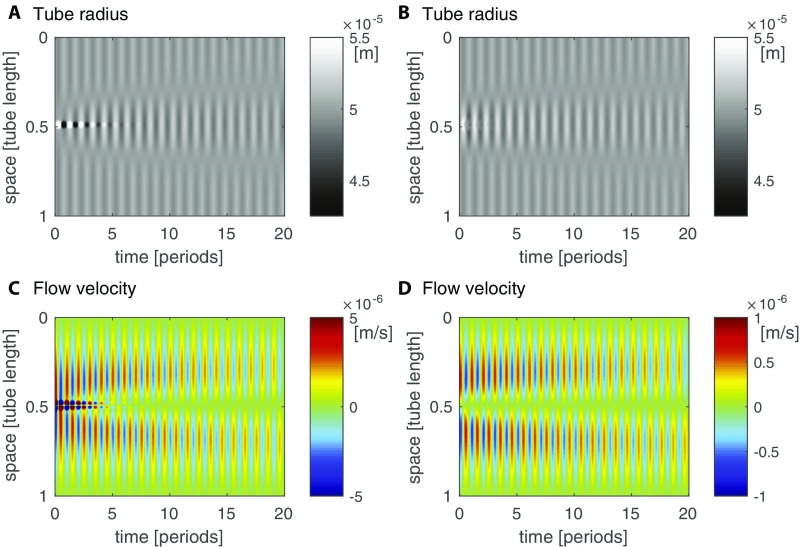
Signal propagation in a theoretical model. (A) Sketch of a tube and the concentration of a signaling molecule within the tube over time (color gradient, see legend of C). The signal increases the amplitude of radial contractions (smaller radius at high concentration) and so establishes a self-propagating front of increased signal concentration and contraction amplitude. When a region of large contraction amplitude contracts (between two white lines marking amplitude front location) surroundings expand, or vice versa. (B) Kymograph of tube radius along the tube over time. Amplitude front is marked by phase jump between stimulated region and surroundings (white line). (C) Map of the time-averaged signal concentration; spread is caused by flow. The location of the front as measured by the position of the phase jump coincides with the mean averaged concentration across the tube at every time point (white line).
Fig. S3.
Quantification of front propagation in model. (A) Comparison of maximal flow velocity and front velocity over the course of the initial 15 periods after a concentration stimulus in the center for a tube. (B) Comparison of observed front diffusivity calculated from the variance of the time-averaged concentration over time, , the absolute value of the effective Taylor diffusivity according to Eq. 7 averaged over the area within the two fronts spreading right and left of stimulation site, and the molecular diffusivity.
In simulations, we find that the front speed is strongly affected by parameters that control flow velocity according to Eq. 6. Specifically, an increase in tube radius , tension strength , and overall concentration increases front velocity, whereas fluid viscosity and tube length decrease it. In an experiment we then tested the model’s prediction that front velocities increase with tube radius. We stimulated a P. polycephalum network at its center and induced a propagating increase in amplitude along both larger and smaller tubes. We find the amplitude fronts to propagate more quickly within larger tubes compared with smaller tubes (Fig. 2).
Conservation of Mass Allows Calculation of Mean Concentration.
In simulations the region of greatest contraction amplitude is easily distinguished from its surroundings by a jump in the contraction phase of value (Fig. 3B). The phase jump is caused by conservation of fluid volume within a closed tube. An entire tube cannot contract (or expand) synchronously; instead, when one zone contracts the other must expand, and vice versa. In mathematical terms we can rationalize the observed phase jump from Eq. 6. Given that both tension and elastic forces are far bigger than the resulting small flow velocity, tension and elastic restoring force almost balance. Balanced forces imply tube dynamics of
| [9] |
marks the time-averaged signaling molecule concentration where the phase jump of occurs. Where concentrations are larger than this reference concentration the tube contracts, whereas for smaller concentrations the tube extends. The amplitude of the radial contractions is small compared the the tube’s base radius . From conservation of fluid volume in the tube, that is, , it follows that the reference concentration is just the spatial mean of the averaged concentration at a given time (SI Text). calculated from concentration dynamics exactly predicts the phase jump (Fig. 3). Contraction and flow dynamics are also well captured by Eq. 9 (Fig. S4). This finding implies that the mechanism of signal propagation enables the system to calculate the mean signaling molecule concentration.
Fig. S4.
Balance of tension and elastic forces approximates observed contraction and flow dynamics. Comparison of simulated (A) and calculated tube radius (B) according to Eq. 9 and the respective flow velocities (C and D). The calculated flow velocity follows from solving Eq. 5 given the approximated contractions. Note a fivefold decrease in scale for the flow velocities.
System Size Is Calculated by Contraction-Driven Gradient Generation.
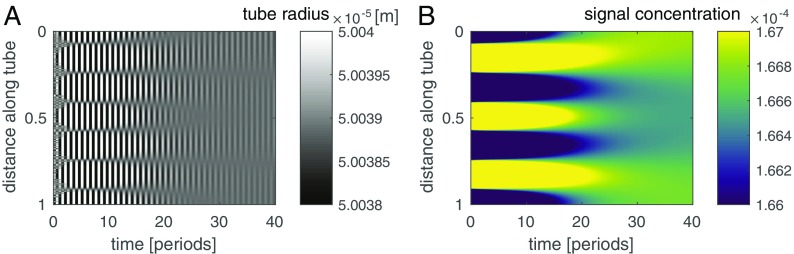
P. polycephalum adapts the wavelength of its contractions to match a network’s longest dimension, independent of network size (12). To test whether our model elucidates this adaptation we probe contraction dynamics and begin with a single tube encompassing three wavelengths of radial undulations coupled to a slightly randomized but otherwise constant concentration of signaling molecule (Fig. 4). Over time, undulations in the tube’s radius and the resulting perturbations in concentration die out in favor of a single contraction wavelength coupled to single concentration wavelength; this pattern persists through time. Although the ad hoc expected pattern would be a uniform concentration, uniformity would require homogeneous contractions of the tube and this would violate conservation of fluid volume. Thus, the closest state to a uniform concentration, namely a single wavelength, is observed, which itself entails a measure of system size and single wavelength in contractions.
Fig. 4.
Decay into a stationary state of a single wavelength matching organism size. The initial condition is set as three undulations in radius along a tube (A) and a slightly randomized but otherwise constant concentration of the signaling molecule concentration (B). The feedback between concentration and contraction amplitude drives the system to a single undulation in radius and concentration; the wavelength matches the tube length. Note that high and low concentrations and radii at early time points are not representing their true value to accommodate the range generated at final time points.
Signal Propagation Increases Flow Disproportionately Through Shorter Routes and Therefore Drives Selection of the Shortest Route.
P. polycephalum is notorious for its complex morphological dynamics; for example, the organism can find the shortest route through a maze connecting two food sources (5). Both food sources are external stimuli that would, according to our observations and model, trigger self-propagating fronts of increased contraction amplitude. Fronts would propagate into the network from both ends of the incipient route. Increases in contraction amplitude will increase the flow rate in a route proportional to the average amplitude increase along the entire route. Therefore, longer routes will experience a smaller increase in flow rate compared with shorter ones. Following the reasoning of Tero et al. (6) tube radii will grow because of an increased flow rate at the expense of tubes with less flow rate. Thus, the self-propagating amplitude fronts strengthen the shortest route between the two food sources by increasing the flow rate along it. The flow feedback-driven mechanism of signal propagation explains P. polycephalum’s ability to find the shortest route through a maze (5) and its ability to link multiple food sources into an efficient transport network (6, 31).
SI Text
Derivation: Lubrication Limit of Stokes Equation for a Long Tube.
To derive the dynamics of the cross-sectionally averaged flow velocity along a tube in response to an externally applied force we take the lubrication limit. First we write the continuity equation and the Stokes equation from Eq. 1 in dimensionless variables , and with and obtain
| [S1] |
| [S2] |
| [S3] |
In the limit where is small we find that the longitudinal flow velocity is far larger than any radial velocity and that the pressure driving this longitudinal flow has to be of order . Neglecting all terms of higher order in we arrive at
| [S4] |
| [S5] |
Integrating the second Stokes equation over and using the equation for the longitudinal component of the flow Poiseuille flow, , we find
| [S6] |
which gives the expression presented in Eq. 3
Derivation: Conservation of Mass Allows Calculation of Mean Concentration.
Here, we show the explicit derivation of how the calculation of the spatial mean of the time-averaged concentration follows from the balance of forces, which according to Eq. 9 implies the following function for the tube radius:
| [S7] |
Conservation of fluid volume requires
| [S8] |
Because the amplitude of contractions is small compared with the baseline tube radius, the volume of the tube is well approximated by
| [S9] |
Whereas the first term here is already a constant, conservation of mass requires the second term to be
| [S10] |
Here, time derivatives of the slowly changing time-averaged concentrations are neglected compared with the oscillation frequency. Therefore, conservation of mass implies that the reference concentration is equal the spatial mean concentration of the time-averaged concentration
| [S11] |
Discussion
The slime mold P. polycephalum coordinates complex behaviors using a simple feedback. An external stimulus triggers a change in contraction amplitude and the amplitude front propagates with a velocity equivalent to a particle’s diffusive transport. These experimental data and a model elucidate the mechanism of communication across the network: The stimulus triggers the release of a signaling molecule advected with cytoplasmic flows. The molecule hijacks flows by increasing local contraction amplitude and generating additional cytoplasmic flows to carry itself further into the network, where it again increases local contraction amplitude and again generates cytoplasmic flows. This mechanism explains the experimental observation of a self-propagating increase in contraction amplitude across a body; moreover, the model solves the puzzle of how an individual can measure its own size and match the wavelength of pulsatile contractions to its size. The mechanism also reveals how P. polycephalum finds the shortest route through a maze (5) or connects multiple food sources with shortest routes into an efficient transport network (6, 31).
The signaling molecule remains unidentified but among the molecules known to oscillate in P. polycephalum (ATP, cAMP, , and ), the most likely candidate is calcium. Calcium regulates actin–myosin dynamics and these dynamics drive network oscillations (25). Contrary to electron micrographs indicating calcium release during contraction and sequestering during relaxation (32), direct measurements observe calcium at low concentrations within contracting tubes of P. polycephalum, and at high concentrations in relaxed tubes (33). The latter is in agreement with the dynamics of our model’s signaling molecule. Calcium is a universal driver of metabolism (34), and it is fascinating to speculate that it also drives the rich and complex behavioral dynamics of slime molds.
P. polycephalum is a charismatic model and a tool to understand how other apparently simple organisms generate sophisticated behaviors. The mechanism of communication we identify involves basic features: a signaling molecule, fluid flows, and an interaction between the signal and fluid flows. These features may be common to thousands of species (35, 36) and even to species distantly related to slime molds, including, for example, fungi. The mechanism is likely to be a general one and may serve as a broad explanation for the complex behaviors of many organisms without nervous systems.
Materials and Methods
Preparation and Imaging of P. polycephalum.
Plasmodia of P. polycephalum (Carolina Biological Supply) were grown on 1.5% (wt/vol) agar without nutrients and fed every other day with oat flakes (Quaker Oats Co.). Twenty-four hours before imaging, newly colonized oat flakes were transferred to a new agar surface. Each plasmodium was allowed to explore the agar surface and form a mature network of well-defined tubes. Sections of network were prepared by scraping away excess tissue immediately before imaging so that the entire network would fit within the field of view. Networks were imaged using transmitted light on a Zeiss Axio Zoom V16 stereomicroscope. Images were taken every 3 s. A 1-L drop of medium was used to stimulate the network after approximately 1 h of recovery time and imaging continued for 2 to 3 h. The medium used for stimulus followed the recipe of Daniel and Rusch (37) with hematin (5 g per mL) replacing the chicken embryo extract (38). The medium gave a stronger and more reproducible response, compared with glucose (25) alone. Adding a source of protein, for example tryptone or yeast extract, to glucose worked best.
Image Analysis.
Key time-variant parameters were calculated from every point of a network using custom MATLAB (The MathWorks) code. Briefly, an image from a time series was thresholded to extract just the plasmodial tubes then skeletonized and separated into a connected map of nodes and edges. The skeleton was used to recover the tube radius at every point by finding the largest circle that would still entirely fit within a tube. Local amplitudes of contractions were extracted. Contraction amplitude was recovered by first detrending the oscillations and then using a windowed Hilbert transform. To record relative changes, amplitudes were normalized to values documented in the 10 periods immediately before the application of a stimulus. To visualize and measure propagation fronts, kymographs were created along tubes intersecting with the stimulation site. Kymographs were also used to measure typical, maximal particle speeds along the same routes of propagation.
Simulation.
Model Eqs. 5–8 were solved numerically using a custom, weighted Crank–Nicolson scheme using MATLAB (The MathWorks). Parameters chosen to model P. polycephalum include a base tube radius of m, wall height , tube length cm, contraction frequency s, dynamic viscosity of cytoplasm Ns/ m2 (39), and molecular diffusivity of a smaller molecule (i.e., ATP in cytoplasm) m2/s, resulting in . To estimate the elastic modulus we used the calculated value of myosin-generated elastic stress Pa during Dictyostelium discoideum cleavage (40) and for myosin activity in HeLa cells (41) to estimate Pa and a Poisson’s ratio of (42). Velocity of an elastic wave in tube wall follows using . For a fluid elastic wave water’s parameters are used. The averaging time window was chosen as about two periods s, and tension strength was chosen to be in the linear regime of the front velocity Pa.
Supplementary Material
Acknowledgments
We thank Mark Fricker for fruitful discussions. This work was supported by the Human Frontiers Science Program through Grant RGP0053/2012, the National Science Foundation through Harvard Materials Research Science and Engineering Center Grant DMR1420570 and Division of Mathematical Sciences Grant DMS-1411694, and the Deutsche Akademie der Naturforscher Leopoldina (K.A.). M.P.B. is an Investigator of the Simons Foundation.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1618114114/-/DCSupplemental.
References
- 1.Bonner JT. The Evolution of Culture in Animals. Princeton Univ Press; Princeton: 1980. [Google Scholar]
- 2.Berg HC. Chemotaxis in bacteria. Ann Rev Biophys Bioeng. 1975;4:119–136. doi: 10.1146/annurev.bb.04.060175.001003. [DOI] [PubMed] [Google Scholar]
- 3.Boddy L, Hynes J, Bebber DP, Fricker MD. Saprotrophic cord systems: Dispersal mechanisms in space and time. Mycoscience. 2009;50:9–19. [Google Scholar]
- 4.Wilking JN, et al. Liquid transport facilitated by channels in Bacillus subtilis biofilms. Proc Natl Acad Sci USA. 2013;110:848–852. doi: 10.1073/pnas.1216376110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nakagaki T, Yamada H, Tóth A. Maze-solving by an amoeboid organism. Nature. 2000;407:470. doi: 10.1038/35035159. [DOI] [PubMed] [Google Scholar]
- 6.Tero A, et al. Rules for biologically inspired adaptive network design. Science. 2010;327:439–442. doi: 10.1126/science.1177894. [DOI] [PubMed] [Google Scholar]
- 7.Dussutour A, Latty T, Beekman M, Simpson S. Amoeboid organism solves complex nutritional challenges. Proc Natl Acad Sci USA. 2010;107:4607–4611. doi: 10.1073/pnas.0912198107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ueda T, Kobatake Y. Chemotaxis in plasmodia of Physarum polycephalum. In: Aldrich HC, Daniel JW, editors. Cell Biology of Physarum and Didymium: Organisms, Nucleus, and Cell Cycle. Vol 1. Academic; New York: 1982. pp. 112–144. [Google Scholar]
- 9.Miyake Y, Tada H, Yano M, Shimizu H. Relationship between intracellular period modulation and external environment change in Physarum plasmodium. Cell Struct Funct. 1994;19:363–370. doi: 10.1247/csf.19.363. [DOI] [PubMed] [Google Scholar]
- 10.Wohlfarth-Bottermann KE. Oscillating contractions in protoplasmic strands of Physarum: Simultaneous tensiometry of longitudinal and radial rhythms, periodicity analysis and temperature dependence. J Exp Biol. 1977;67:49–59. doi: 10.1242/jeb.67.1.49. [DOI] [PubMed] [Google Scholar]
- 11.Durham AC, Ridgway EB. Control of chemotaxis in Physarum polycephalum. J Cell Biol. 1976;69:218–223. doi: 10.1083/jcb.69.1.218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Alim K, Amselem G, Peaudecerf F, Brenner MP, Pringle A. Random network peristalsis in Physarum polycephalum organizes fluid flows across an individual. Proc Natl Acad Sci USA. 2013;110:13306–13311. doi: 10.1073/pnas.1305049110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Natsume K, Miyake Y, Yano M, Shimizu H. Information propagation by spatio-temporal pattern change of Ca concentration throughout Physarum polycephalum with repulsive stimulation. Cell Struct Funct. 1993;18:111–115. doi: 10.1247/csf.18.111. [DOI] [PubMed] [Google Scholar]
- 14.Teplov VA, Romanovsky YM, Pavlov DA, Alt W. Auto-oscillatory processes and feedback mechanisms in Physarum plasmodium motility. In: Alt W, Deutsch A, Dunn GA, editors. Dynamics of Cell and Tissue Motion. Springer; Basel: 1997. pp. 83–92. [Google Scholar]
- 15.Korohoda W, Shraideh Z, Baranowski Z, Wohlfarth-Bottermann KE. Energy metabolic regulation of oscillatory contraction activity in Physarum polycephalum. Cell Tissue Res. 1983;231:675–691. doi: 10.1007/BF00218125. [DOI] [PubMed] [Google Scholar]
- 16.Ueda T, Mori Y, Nakagaki T, Kobatake Y. Changes in cAMP and cGMP concentration, birefringent fibrils and contractile activity accompanying UV and blue light photoavoidance in plasmodia of an albino strain of Physarum polycephalum. Photochem Photobiol. 1988;47:271–275. [Google Scholar]
- 17.Kessler D. Plasmodial structure and motility. In: Aldrich HC, Daniel JW, editors. Cell Biology of Physarum and Didymium: Organisms, Nucleus, and Cell Cycle. Vol 1. Academic; New York: 1982. pp. 145–210. [Google Scholar]
- 18.Marbach S, Alim K, Andrew N, Pringle A, Brenner MP. Pruning to increase Taylor dispersion in Physarum polycephalum networks. Phys Rev Lett. 2016;117:178103–178105. doi: 10.1103/PhysRevLett.117.178103. [DOI] [PubMed] [Google Scholar]
- 19.Bullock TH, Horridge GA. Structure and Function in the Nervous Systems of Invertebrates. Freeman; San Francisco: 1965. [Google Scholar]
- 20.Leys SP, Mackie GO, Meech RW. Impulse conduction in a sponge. J Exp Biol. 1999;202:1139–1150. doi: 10.1242/jeb.202.9.1139. [DOI] [PubMed] [Google Scholar]
- 21.Fuller CR, Fahy FJ. Characteristics of wave-propagation and energy-distributions in cylindrical elastic shells filled with fluid. J Sound Vib. 1982;81:501–518. [Google Scholar]
- 22.Hejnowicz Z, Wohlfarth-Bottermann KE. Propagated waves induced by gradients of physiological factors within plasmodia of Physarum polycephalum. Planta. 1980;150:144–152. doi: 10.1007/BF00582358. [DOI] [PubMed] [Google Scholar]
- 23.Takagi D, Balmforth NJ. Peristaltic pumping of viscous fluid in an elastic tube. J Fluid Mech. 2011;672:196–218. [Google Scholar]
- 24.Rieu JP, Delanoë-Ayari H, Takagi S, Tanaka Y, Nakagaki T. Periodic traction in migrating large amoeba of Physarum polycephalum. J Roy Soc Interface. 2015;12:20150099. doi: 10.1098/rsif.2015.0099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ueda T. Intracellular oscillations and pattern formation in the cell behavior of Physarum. In: Rensing L, editor. Oscillations and Morphogenesis. Dekker; New York: 1993. pp. 167–181. [Google Scholar]
- 26.Samans K, Hinz I, Hejnowicz Z, Wohlfarth-Bottermann K. Phase relation of oscillatory contraction cycles in Physarum plasmodia: I. A serial infrared registration device and its application to different plasmodial stages. J Interdiscip Cycle Res. 1984;15:241–250. [Google Scholar]
- 27.Achenbach U, Wohlfarth-Bottermann K. Synchronization and signal transmission in protoplasmic strands of Physarum. Planta. 1981;151:584–594. doi: 10.1007/BF00387438. [DOI] [PubMed] [Google Scholar]
- 28.Taylor G. Dispersion of soluble matter in solvent flowing slowly through a tube. Proc R Soc A. 1953;219:186–203. [Google Scholar]
- 29.Aris R. On the dispersion of a solute in a fluid flowing through a tube. Proc R Soc A. 1956;235:67–77. [Google Scholar]
- 30.Mercer GN, Roberts AJ. A complete model of shear dispersion in pipes. Jpn J Ind Appl Math. 1994;11:499–521. [Google Scholar]
- 31.Bonifaci V, Mehlhorn K, Varma G. Physarum can compute shortest paths. J Theor Biol. 2012;309:121–133. doi: 10.1016/j.jtbi.2012.06.017. [DOI] [PubMed] [Google Scholar]
- 32.Kuroda R, Kuroda H. Relation of cytoplasmic calcium to contractility in Physarum polycephalum. J Cell Sci. 1982;53:37–48. doi: 10.1242/jcs.53.1.37. [DOI] [PubMed] [Google Scholar]
- 33.Yoshimoto Y, Matsumura F, Kamiya N. Simultaneous oscillations of Ca2+ efflux and tension generation in the permealized plasmodial strand of Physarum. Cell Motil. 1981;1:433–443. doi: 10.1002/cm.970010404. [DOI] [PubMed] [Google Scholar]
- 34.Krebs J, Michalak M, editors. Calcium: A Matter of Life or Death. 1st Ed Elsevier; New York: 2007. [Google Scholar]
- 35.Stephenson SL, Stempen H. Myxomycetes: A Handbook of Slime Molds. Timber; Portland, OR: 1994. [Google Scholar]
- 36.Walker LM, Stephenson SL. The species problem in myxomycetes revisited. Protist. 2016;167:319–338. doi: 10.1016/j.protis.2016.05.003. [DOI] [PubMed] [Google Scholar]
- 37.Daniel JW, Rusch HP. The pure culture of Physarum polycephalum on a partially defined soluble medium. J gen Microbiol. 1961;25:47–59. doi: 10.1099/00221287-25-1-47. [DOI] [PubMed] [Google Scholar]
- 38.Daniel JW, Kelley J, Rusch HP. Hematin-requiring plasmodial myxomycete. J Bacteriol. 1962;84:1104–1110. doi: 10.1128/jb.84.5.1104-1110.1962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Swaminathan R, Hoang CP, Verkman AS. Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cells: Cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion. Biophys J. 1997;72:1900–1907. doi: 10.1016/S0006-3495(97)78835-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Robinson DN, Kee YS, Luo T, Surcel A. Understanding how dividing cells change shape. In: Egelman EH, Wirtz D, editors. Comprehensive Biophysics. Vol 7. Elsevier; New York: 2012. pp. 48–73. [Google Scholar]
- 41.Sedzinski J, et al. Polar actomyosin contractility destabilizes the position of the cytokinetic furrow. Nature. 2011;476:462–466. doi: 10.1038/nature10286. [DOI] [PubMed] [Google Scholar]
- 42.Schmidt FG, Ziemann F, Sackmann E. Shear field mapping in actin networks by using magnetic tweezers. Eur Biophys J. 1996;24:348–353. doi: 10.1007/BF00180376. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.