Abstract
This paper concerns the generation of distributed vector representations of biomedical concepts from structured knowledge, in the form of subject-relation-object triplets known as semantic predications. Specifically, we evaluate the extent to which a representational approach we have developed for this purpose previously, known as Predication-based Semantic Indexing (PSI), might benefit from insights gleaned from neural-probabilistic language models, which have enjoyed a surge in popularity in recent years as a means to generate distributed vector representations of terms from free text. To do so, we develop a novel neural-probabilistic approach to encoding predications, called Embedding of Semantic Predications (ESP), by adapting aspects of the Skipgram with Negative Sampling (SGNS) algorithm to this purpose. We compare ESP and PSI across a number of tasks including recovery of encoded information, estimation of semantic similarity and relatedness, and identification of potentially therapeutic and harmful relationships using both analogical retrieval and supervised learning. We find advantages for ESP in some, but not all of these tasks, revealing the contexts in which the additional computational work of neural-probabilistic modeling is justified.
Keywords: semantic predications, distributional semantics, word embeddings, predication-based semantic indexing, literature-based discovery, pharmacovigilance
Graphical abstract
1. Introduction
Methods for the generation of semantic vector representations of biomedical terms and concepts have been an active area of research over the past two decades, with applications that include information retrieval, literature-based discovery and text categorization (for a review, see [1]). Recently, there has been a surge in popularity in the application of neural network based language models as a means to obtain such vectors, with encouraging empirical results in both the general [2, 3, 4] and biomedical domains [5, 6, 7]. These results are part of a larger trend in machine learning research, where considerable progress has been made by learning vector representations of entities from large unlabeled data sets, obviating the need for extensive feature engineering [8, 9]. Though approaching the problem from a different perspective, the current crop of neural language models have much in common with methods of distributional semantics that preceded them (for reviews, see [1, 10, 11]), and it has been argued that the performance of preexisting distributional models on certain tasks can be improved using insights derived from their neurologically-inspired counterparts [12].
In this paper, we evaluate the extent to which such insights might be applied to improve upon an approach we have developed for representing structured information, called Predication-based Semantic Indexing (PSI) [13, 14]. PSI differs from traditional distributional models in that it attempts to derive high-dimensional vector representations of concepts from concept-relationship-concept triplets, such as “haloperidol TREATS schizophrenia”, known as semantic predications. In the biomedical domain, large numbers of such predications have been extracted from the biomedical literature by SemRep [15], a natural language processing (NLP) system, and have been made publicly available to the research community [16]. PSI derives vector representations of concepts from the predications in which they occur, using reversible vector transformations to encode the nature of the relationship between these concepts. This permits the resulting vector space to be searched for concepts that relate to a cue concept in particular ways, or for the nature of the relationship between a pair of concepts.
Nonetheless, PSI has much in common with the vector representations obtained through neural embeddings, as well as with prior approaches such as Latent Semantic Analysis (LSA) [17]. SemRep’s predications are extracted from mentions in text, so are often repeated. Because of this, PSI is a distributional model, in the sense that the distribution of the contexts that a particular concept occurs in determine its vector representation - concepts that occur in similar contexts with similar frequency will have similar vector representations. These vector representations are also distributed representations [18, 19], in the sense that the information they encode is distributed as a pattern of continuous values spread across the components of a vector, rather than through identification of a particular feature of the underlying data (such as the presence of a term) with a unique vector component.
In this paper we adapt the skipgram-with-negative-sampling (SGNS) algorithm of Mikolov and his colleagues [3] to develop a novel variant of the PSI approach to representing concept-relationship-concept triples, an approach we call Embedding of Semantic Predications (ESP). We evaluate this approach for its ability to retrieve encoded information, the correlation of similarity between the resulting vectors with human judgment, and as a means to facilitate the prediction of both therapeutic and harmful relationships between drugs and medical conditions. The paper proceeds as follows. First we describe RI, the distributional model that provides the basis for PSI. We then describe the SGNS approach, and highlight the similarities and differences between it and RI. We then proceed to describe the origin and implementation of the reversible vector transformations that are used to encode the nature of the relationships between concepts, how these are applied in PSI and ESP, and our empirical experiments in which we compare PSI to ESP across a number of tasks. We conclude with a discussion of our results, related work in the field, and directions of interest for future research.
2. Background
2.1. Random Indexing
RI emerged during the 1990’s as a scalable alternative to LSA, on account of its ability to construct a reduced-dimensional approximation of a term-by-context matrix without the need to explicitly represent the full matrix [20]. This approximation procedure is motivated by the Johnson-Lindenstrauss Lemma, which provides bounds on the extent to which distance relationships between points in high-dimensional space are distorted, when they are projected into a randomly-selected subspace [21]. In the current discussion, we focus on the sliding-window variant of RI introduced in [22]. This variant of RI considers proximal relationships within a sliding window moved through the text. Consider, for example, the phrase “management of psychosis in schizophrenia”. A “2+2” sliding window centered on the term “psychosis” is shown in Table 1.
Table 1.
2+2 sliding window. F=focus term. Numbers denote position relative to F.
| −2 | −1 | +1 | +2 | |
| management | of | in | schizophrenia |
The goal is to generate similar vector representations for terms that occur in similar contexts. In RI, this is accomplished by initializing a semantic vector for each term in the corpus (stoplists or frequency thresholds may be applied to limit this vocabulary), and also initializing a context vector for each of these terms. Semantic vectors are initialized as zero vectors, of a dimensionality specified by the modeler (a value on the order of 1,000 is typical). Context vectors are initialized stochastically. A typical scheme involves initializing a zero vector, and setting a small number (a value on the order of 10 is typical) of the components of this vector to +1 or −1 at random. On account of their sparsity, and the statistical properties of high-dimensional space, these vectors have a high probability of being mutually orthogonal, or close-to-orthogonal (see [13, 23, 24] for further discussion of this point). Once initialization has occurred, a sliding window is moved through the text, and the semantic vector for the focus term (F) is updated by adding to it the context vectors for the surrounding terms in the window. In symbols, with S(term) and C(term) as the semantic and context vectors for terms in the corpus, F as the focus term, and t ∈ T as the other terms in the window, the update process for a single sliding window proceeds as follows:
| (1) |
These superposition operations may be weighted in accordance with the position within the window such that proximal context terms receive greater emphasis [22]. Other weighting metrics may also be applied. For example, Inverse Document Frequency (IDF) may be applied such that context terms that occur less frequently in the corpus receive greater emphasis.
2.2. Neural Embeddings and SGNS
Current approaches to generating neural word embeddings extend earlier work on probabilistic language modeling using neural networks [25, 26]. These models share with other distributional models the aim of deriving distributed vector representations of words from their occurrence in natural language text. However, in neural models, this goal is framed probabilistically — the purpose is to derive a model that can predict the presence of a term given the terms that appear nearby to it, or vice versa.
Recent approaches, including the skip-gram with negative sampling (SGNS) approach developed by Mikolov and his colleagues [3], provide scalable solutions to the problem of inferring parameters for such models. The presentations in [27] and [28] provide deliberately more accessible accounts of the SGNS algorithm. However, the presentation below differs from previous descriptions of SGNS, as it attempts to elucidate the relationship between SGNS and RI, in order to reveal the features of SGNS we adapt for the purposes of the current research.
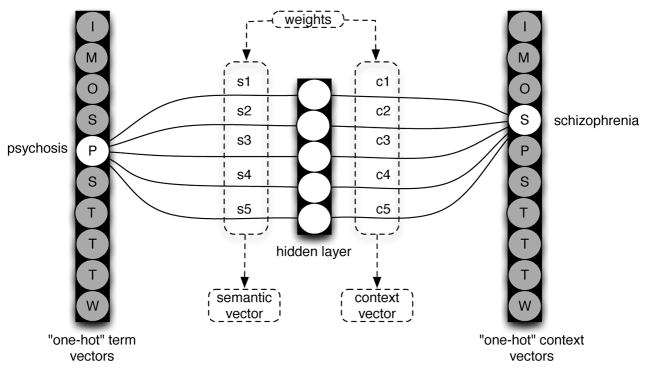
Consider the neural network architecture illustrated in Figure 1, which has an input layer, a hidden layer and an output layer (black rectangles) each containing a number of nodes that are connected by weights. This provides an illustration of a SGNS architecture to derive five-dimensional word embeddings from a small corpus with a vocabulary of ten unique words. On the left of the diagram is a so-called “one-hot” vector representation for the word “psychosis”. These vectors exist for each word in the vocabulary-to-be-represented, and have a dimensionality of the number of unique words in this vocabulary (in this case, 10). The designation “one-hot” refers to the fact that each vector has only one non-zero activation value. So, though the network is fully-connected in theory, the only connection weights that will not be nullified during the feed-forward phase are those connecting the single non-zero activation node for this word to the hidden layer. The hidden layer has k nodes, where k is the preassigned dimensionality of the word vectors to-be-generated. The single k-dimensional vector of weights that will not be nullified is the word embedding, or the semantic vector representation of this word – weight vectors are word vectors, and are initialized stochastically (a typical scheme involves initializing each weight from a uniform zero mean distribution, scaled by the dimensionality of the weight vectors). The weights connecting the hidden layer to the output layer, which also consists of “one hot” vectors, constitute the context vector for each word. In Figure 1 the semantic vector for “psychosis” and the context vector for “schizophrenia” are shown.
Figure 1.
Illustration of the SGNS architecture to generate 5-dimensional embeddings for a 10-word vocabulary.
The goal of SGNS is to predict context words (wc) given an observed word (wo). Ideally, in the example shown in Figure 1 and the sliding window shown in Table 1, P(schizophrenia|psychosis) ≈ 1, where P(context word|observed word) = σ(S(wo).C(wc)). That is to say, the probability of a context word given an observed word is estimated as the sigmoid function of the scalar product between the semantic vector of the observed word and the context vector of the context word. The normalized scalar product, or cosine metric, is the most widely-utilized metric of similarity within the distributional semantics community. Words that have a high probability of occurring together in context should have a high degree of similarity between their semantic and context vectors, as measured by this metric. The sigmoid function derives from the (unnormalized) scalar product a value between zero and one, which can be interpreted probabilistically.
It is also desirable that the predicted probability of words that do not occur in the context (w¬c) of the observed word be close to zero. As adjusting the parameters of the context vector for every out-of-context word each time a word is observed would be computationally inconvenient, SGNS instead takes a sample of these unobserved words (a negative sample), drawn at random from the rest of the words in the corpus with a probability derived from their frequency in the corpus (usually around 5–15 such words are drawn with a probability of where Z is the sum of the value of the numerator across all terms available for sampling). Words that do not occur in the context of the observed word should have a low predicted probability, which means that the scalar product between the word and context vectors concerned should be low. The optimization objective is then as follows [27]:
| (2) |
The first term in this equation is the sum of the logarithms of the predicted probabilities for words that occur together within a sliding window moved through the corpus, (wo, wc) ∈ D. The second term is the sum of the logarithms of one minus the predicted probabilities for words that (probably) do not occur together in such windows, (wo, w¬c) ∈ D′ (as σ(−x) = 1 − σ(x)). In SGNS, this objective is optimized by gradient descent. For each observed word pair, the incoming weight vectors, or semantic vectors (the word embeddings), are updated with the following step:
| (3) |
where α is the learning rate, which decreases linearly as the dataset is processed, and the term (1 − σ(S(wo).C(wc))) is the derivative of the first term in equation 2.1 So the update step involves adding C(wc) to S(wo).2 This superposition operation is weighted by the learning rate, α, and the difference between the ideal probability of 1 for this observed word-context pair, and the estimated probability of σ(S(wo) · C(wc)). For an entire sliding window, the update step for the semantic vector of the focus term, S(F), proceeds as follows:
| (4) |
As is the case in RI, the context vector C(t) for every other term in the window is added to the semantic vector for the focus term S(F). However, unlike RI, this superposition operation will favor those context vectors that are not already similar to the evolving semantic vector for the focus term. In addition, this semantic vector will stabilize over time, with observations that occur early in training resulting in greater changes than those that occur later. Another important difference from RI is that the context vectors are also updated.3
| (5) |
In our view, this is a particularly important difference from sliding-window based RI, as the context vectors that are added are updated over time, resulting in a second set of trained word vectors, which are usually discarded but have been leveraged to improve performance in some experiments [12]. A consequence of this is that, once the initial rounds of training are complete, semantic vectors are generated as superpositions of meaningful context vectors, rather than as superpositions of random context vectors in RI. These permits a form of similarity-based inference: the semantic vectors for terms that occur in the context of similar, but not necessarily identical terms, will be somewhat similar to one another.4
In addition, the semantic vector for the observed term and each randomly drawn context vector C(w¬c), representing a term that is unlikely to have been observed in this context window, are moved further apart from one another. In this case, the update procedures are as follows:
| (6) |
| (7) |
Which is to say, for negative samples, context vectors are subtracted from semantic vectors in proportion with the sigmoid function of the scalar product between them, and vice versa.5
In summary, though RI and SGNS are usually presented from different perspectives, they are both online training algorithms that generate semantic vector representations of words by superposing stochastically generated context vector representations of other words that occur in proximity. However, in the case of SGNS, these superposition operations are weighted in accordance with the learning rate, and the distance between these vector representations at this point in the training procedure. Furthermore, the context vector representations are also trained, which permits a form of similarity-based inference. Negative samples are used which accentuates the distinction between co-occurring and non-co-occurring terms, resulting in a more efficient use of available space.
With these additional features comes additional computational expense — the scalar product must be measured before each superposition operation, and the number of superposition operations is (2 + 2n) per observed pair, where n is the number of negative samples. So implementations of SGNS tend to be parallelized, which is readily permitted by the online nature of the algorithm. Optionally, this computational cost is offset to a degree using subsampling, which involves skipping over terms in the text with some probability. These serves the purpose usually fulfilled by weighting metrics in prior distributional models. For example, the size of the sliding window in SGNS is probabilistically determined, which results in proximal context terms being processed more frequently. This serves the purpose of a “weighted” sliding window, emphasizing terms that occur in closer proximity to the focus term. Similarly, terms that occur above some frequency threshold may be skipped over with a probability derived from the extent to which they exceed this threshold, approximating the way in which weighting metrics such as IDF limit the emphasis of frequently occurring terms. In contrast, with RI a single superposition operation is required for each pair. Also superposition itself can be very efficient on account of the sparse nature of the context vectors, as only the non-zero values need to be considered. So implementations of RI tend not to utilize parallelization, though this would be easy to implement if needed as like SGNS, each context is considered independently.
2.3. Vector Symbolic Architectures and PSI
In this section, we describe Predication-based Semantic Indexing or PSI, an approach to encoding concept-relation-concept triples that uses the same underlying representational approach as Random Indexing. We will then describe how we modified this approach, incorporating features of the SGNS algorithm to develop ESP.
PSI was developed in order to encode the nature of the relationships between biomedical concepts into a distributed vector representation. The main idea is that a reversible vector transformation is associated with the nature of the relationship concerned. So, given a semantic predication of the form subject-predicate-object, the context vector for the object C(object) is added to semantic vector for the subject S(subject) only after undergoing a transformation that indicates the nature of the predicate.
The reversible vector transformations used in current implementations of PSI originated in the connectionist cognitive science community in the late 1980’s [32], as a way to represent composite structures such as variable-value pairs, using distributed vector representations. Initially, the tensor product was used for this purpose [33]. In an effort to circumvent the combinatorial explosion in dimensionality that would occur with sequential tensor operations, a number of authors developed alternative binding operators [34, 35, 36, 37, 38], resulting in a family of representational approaches that have come to be known collectively as Vector Symbolic Architectures (VSAs) [39, 40]. In our work with PSI, the VSA we have employed most frequently is known as the Binary Spatter Code (BSC) [34], and it is also the VSA we employ for the current experiments.
The BSC uses high-dimensional binary vectors (on the order of 10,000 bits) as a fundamental unit of representation. These are initialized at random, with a .5 probability of any component being initialized as 1. Binding, which we will denote with the symbol ⊗, is accomplished using the pairwise exclusive OR operator (XOR). This operator is its own inverse, but as this is not the case for all VSA implementations, we will denote the inverse of binding with the symbol ⊘, to maintain a consistent description across VSAs. Weighted superposition (+) is implemented using weighted voting for each dimension with probabilistic tie-breaking, including some tradeoff between floating point accuracy and computational efficiency [41].
With both predications and concepts represented as distributed vectors, the update step for the semantic vector for “haloperidol” to encode the predication “haloperidol TREATS schizophrenia”, with P(PREDICATE) indicating the randomly generated vector representing a particular predicate, is:
| (8) |
This superposition operation is usually weighted with a global weighting metric that limits the influence of frequently occurring concepts (or predicates), and a local weighting metric that tempers the influence of repeated predications, though the weighting metrics used vary across experiments. The net result is a set of randomly generated context vectors for each concept, a randomly generated vector for each unique predicate, and a trained semantic vector for each concept. The vector space so constructed can be queried for concepts that relate to one another in particular ways, and for the nature of the relationship (or relationships) between pairs of concepts. Some illustrative searches are provided in Table 2, which shows how the space can be searched for concepts that relate to one another in particular ways, and Table 3 which shows how the relationships between pairs of concepts can be inferred from their vector representations.
Table 2.
Example searches for concepts in a 32,000-dimensional binary PSI space derived from version 25.1 of the SemMedDB database, containing 82,239,652 extracted predications. The “Results” column shows the nearest neighboring concept vectors to the “Cue” vector. The score is the number of standard deviations above the mean of ( ) for all vectors in the search vector store. ASSOC=ASSOCIATED_WITH. INV indicates the inverse of a predicate - if “subject PRED object” then “object PRED-INV subject”.
| Cue | Target | Results | Comments |
|---|---|---|---|
| S(haloperidol) | Semantic vectors | 93.37:haloperidol 30.43:clozapine 26.91:risperidone 26.74:antipsychotic_agents 25.92:sulpiride |
Other antipsychotic agents (and this drug class). |
|
S(haloperidol) ⊘ P(TREATS) |
Context vectors | 8.61:delirium 8.35:schizophrenia 7.72:chronic_schizophrenia 7.63:mania acute 7.37:agitation |
Therapeutic applications of haloperidol. |
|
S(haloperidol) ⊘ P(CAUSES) |
Context vectors | 11.46:catalepsy 7.66:akinesia 6.37:adverse_effects 6.00:hyperactive_behavior 5.50:vomiting |
Side effects of haloperidol. |
|
S(haloperidol) ⊘ P(TREATS) ⊗ (ASSOC) |
Semantic vectors | 8.39:syt4 8.38:calb2 8.38:gulp1 8.38:mir138-2 8.38:mir137hg |
Genes associated with conditions treated by haloperidol. |
Table 3.
Retrieval and reapplication of relational structure with PSI. Data, derivation and presentation as in Table 2. Up to five results >= 4SD above the mean of ( ) are shown. ASSOC=ASSOCIATED_WITH.
| Cue | Target | Results | Comments |
|---|---|---|---|
|
S(haloperidol) ⊘ C(schizophrenia) |
Predicate vectors | 8.16: TREATS | Haloperidol is a treatment for schizophrenia. |
|
S(haloperidol) ⊘ S(schizophrenia) |
Products of predicate vector pairs | 6.74: COMPARED WITH-INV ⊘ TREATS-INV 4.53: INTERACTS WITH ⊘ ASSOC-INV |
Haloperidol has been compared with another drug that schizophrenia is treated by, and interacts with a biological entity that is associated with schizophrenia. |
|
S(docetaxel) ⊘ P(COMPARED WITH-INV) ⊗ P(TREATS-INV) |
Semantic vectors | 14.79:non-small_cell lung_cancer_recurrent 13.58:small_cell lung_cancer_recurrent 12.35:non_small_cell lung_cancer_metastatic 11.27:oesophageal adenocarcinoma_stage_iii 9.7034:esophageal neoplasm_metastatic |
Applying a two-predicate path inferred from haloperidol::schizophrenia to docetaxel returns potential therapeutic applications of this drug. |
As both concepts and predicates are represented as vectors in the same high-dimensional space, this provides a simple mechanism for solving proportional analogies of the form “a is to b as c is to ?”. For example, the nearest semantic vector to the bound product S(haloperidol) ⊘ C(schizophrenia) ⊗ C(major depressive disorder) in this space represents the antidepressant “lexapro”. The capacity to model analogy in this way has been an important point of focus of VSA-related research since these models were first introduced (see for example [42, 43, 44]). It also relates to one of the well-known features of neural word embeddings, which is that word embeddings trained on free text can be used to solve proportional analogy problems using addition and subtraction (famously , but also more subtle analogies such as and (john) (coleman)). Unlike this work, however, work on analogical retrieval using VSAs, including PSI, tends to involve encoding the nature of the relationships between concepts explicitly.
With PSI, the explicit encoding of predicates has the desirable effect that analogical inference can proceed along longer paths, consisting of more than one predicate [45]. For example, applying the vector representation of the two-predicate path P(COMPARED_WITH) ⊘ P(TREATS-INV) to the semantic vector for the drug docetaxel results in the composite search cue S(docetaxel) ⊘ P(COMPARED_WITH) ⊗ P(TREATS-INV), which is closest in the PSI space used to generate Table 2 to the semantic vectors for potential therapeutic applications of docetaxel. The logic in this case is that if a drug has been compared with other drugs that treat a condition (for example, in a clinical trial or cell line experiment), it may be a potential treatment for this condition itself. The two-predicate path P(COMPARED_WITH) ⊘ P(TREATS-INV) was inferred from the example concept pair haloperidol::schizophrenia, so potential therapeutic applications of one drug have been identified using a reasoning pathway inferred from another.
This procedure, which we call Discovery-by-Analogy, has been applied successfully to recover held-out TREATS relationships in SemMedDB [46], identify relationships between drugs and adverse events [47], and predict the results of high-throughput screening evaluations against cancer cell lines [48]. It has been found that the accuracy of such predictions can be improved by combining multiple reasoning pathways to increase the breadth of the search [49], and extending the length of the pathways to increase search depth [50]. In the former case, this is accomplished by using the span of vectors to model logical disjunction (OR), following the approach developed in [51]. In the latter case, this is accomplished by superposing the semantic vectors representing concepts associated with the initial cue (e.g. superposing the vectors for all entities ASSOCIATED_WITH prostate carcinoma). For a comprehensive review of PSI-related work up until 2014, we refer the interested reader to [13].
2.4. Embedding of Semantic Predications
In this section we will describe a novel variant of PSI, called Embedding of Semantic Predications (ESP), that adapts elements of the SGNS algorithm to the task of modeling large stores of semantic predications. The following list enumerates these elements, and provides a high-level description of their implementation within ESP.
Gradient descent: Superposition operations are weighted by the extent to which they contribute to an error function, and by a linearly decreasing learning rate.
Evolving context vectors: Context vectors are similarly altered.
Negative sampling: For each encoded predication, a set of k negative subjects and k negative objects are drawn. These are concepts of the same UMLS semantic type as the positive subject and object for this predication, and are encoded in a manner analogous to the way in which negative samples are treated in SGNS.
Subsampling: Frequency thresholds are assigned for both concepts and predications. If a concept or predication occurs with a frequency greater than their respective threshold (e.g. more than 1 in 10,000 predications) the predication concerned will be ignored with a probability of , where T is the threshold and F is the frequency of the concept or predication.
Our hypotheses were that using gradient descent and negative sampling would lead to more efficient utilization of the available vector space, which should be further accentuated by the additional capacity to encode information provided by trained (rather than immutable) context vectors, and that these trained context vectors should permit a novel form of similarity-based inference. For example, S(haloperidol) ⊘ P(TREATS) should also be similar to the context vectors for entities that are similar to those entities that occur in a TREATS relationship with haloperidol explicitly. So, we anticipated ESP would better retain its performance as dimensionality decreased, and that ESP would have better performance in predictive modeling tasks with shorter reasoning pathways. In the section that follows we provide a more granular account of the binary vector based implementation of ESP that was evaluated in our experiments.
2.5. Binary Vector ESP
Our current implementation of ESP uses the Binary Spatter Code, described in Section 2.3, as a VSA. Both semantic vectors (e.g. S(haloperidol)) and context vectors (e.g. C(haloperidol)) vectors for each represented concept are stochastically initialized, with a .5 probability of a 1 or 0 in each dimension. For each encoded predication “s P o”, a set of k negative subjects (¬s) and k negative objects (¬o) are drawn, and updating of the semantic and context vectors occurs through the following steps:
| (9) |
| (10) |
| (11) |
| (12) |
where
The first of the preceding steps draws the semantic vector for the subject closer to the bound product of the vector representing the predicate and the context vector for the object. Conversely, the context vector of the object is moved closer to the results of applying the “release” operator (the inverse of the bind operator) to the semantic vector of the subject and the vector representing the predicate. The subsequent two steps (Equations 11 and 12) are applied to each of the k negative objects — random samples of concepts of the same UMLS semantic type as the actual object, that (probably) do not occur in a predication of this type with the subject. The bound product P(P) ⊗ C(¬o) is subtracted from the semantic vector for the subject. Similarly, the product S(s) ⊘ P(P) is subtracted from the context vector for the randomly drawn negative object, ¬o. These subtractions are weighted by the similarity between the vectors concerned, as estimated by the the non-negative normalized Hamming Distance (NNHD). So negative samples that are somewhat similar to the relevant bound products will exert a greater effect. This procedure is repeated to encode the predication in the opposite direction, “o PINV s”.
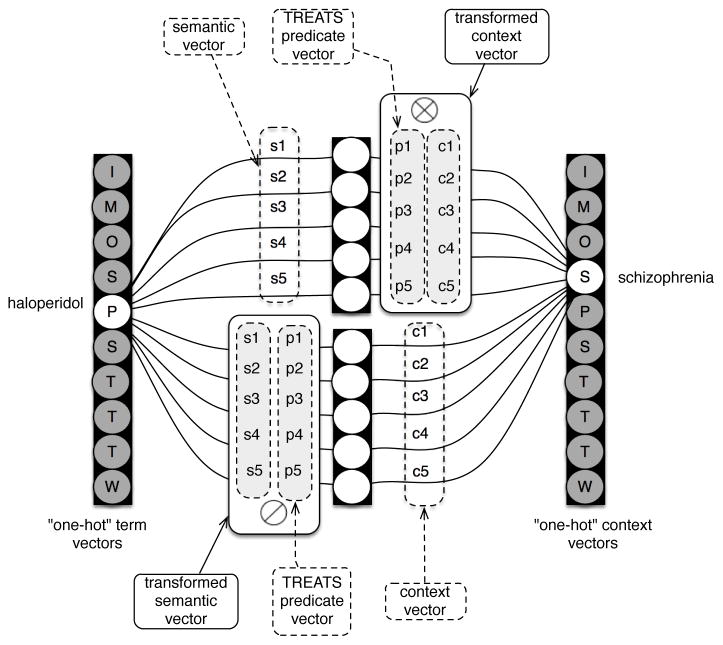
The full procedure essentially follows the same form as SGNS. With SGNS and terms that are observed together, their semantic and context vector representations are drawn together. In the case of a randomly drawn negative sample, the distance between its context vector and the semantic vector of the observed concept is increased, by modifying both of these vectors. However, in the case of ESP these modifications occur after a transformation of the vectors concerned to indicate the nature of the encoded relationship, as illustrated in Figure 2.
Figure 2.
Illustration of the ESP architecture to generate 5-dimensional embeddings for a 10-concept vocabulary. In SGNS, an objective is to raise the scalar product between the semantic and context vectors of words that are observed together. With ESP, we aim to raise the — between the semantic vector for the subject of a predication, and the bound product (⊗) of the predicate vector for the predicate concerned and the context vector of the object of this predication. In addition, we aim to raise the NNHD between the context vector of the object of the predication and the product of releasing (⊘) the predicate from the semantic vector of the subject.
With each predication ( s P o ) expanded to accommodate its inverse ( o P-INV s ), the optimization objective is as follows: 6
A number of other differences emerge on account of the use of binary vectors as a fundamental representational unit. As is evident from the preceding equations, we have replaced the sigmoid unit in the output layer with a regularized linear (RELU) unit, as the distance metric employed returns a result between −1 and 1, with a result of 0 indicating orthogonality, and results less than zero usually indicating close-to-orthogonality in the context of the binary spatter code. In addition, subtraction of one vector from another is implemented by adding the complement of this binary vector to the voting record concerned. Also, the bit matrix representation of the voting record (described in further detail in [41]) must be tallied before this comparison occurs, which is not prohibitively time consuming as it can be accomplished efficiently with parallel bitwise operations. In an effort to stay within the limits of floating point precision imposed by this representation, the initial and minimum learning rates are an order of magnitude higher than is customary with SGNS, at 0.25 and 0.001 respectively. Finally, reduction of the influence of frequently occurring concepts is accomplished with a subsampling strategy, such that predications containing a concept that occurs with a frequency, f, of more than a threshold of t = 10−5 (i.e. a concept occurring in more than one in 100,000 predications), and predications that occur with a frequency above t = 10−7 (i.e. predications that make up more than of the total number), will be ignored with a probability of . Our implementations of PSI and ESP are available as components of the open source Semantic Vectors software package [52, 53, 54].
As is the case with PSI, the vector space so constructed can be queried for concepts that relate to one another in particular ways, and for the nature of the relationship (or relationships) between pairs of concepts. Some illustrative searches are provided in Table 4 and Table 5.
Table 4.
Example searches for concepts in a 32,000-dimensional binary ESP space derived from version 25.1 of the SemMedDB database, containing 82,239,652 extracted predications. The “Results” column shows the nearest neighboring concept vectors to the “Cue” vector. The score is the number of standard deviations above the mean of ( ) for all vectors in the search vector store. ASSOC=ASSOCIATED_WITH. SV=Semantic Vectors. CV=Context Vectors. * = predication not in SemMedDB. RA=renin-angiotensin. SNS=sympathetic nervous system.
| Cue | Target | Results | Comments |
|---|---|---|---|
| S(haloperidol) | SV | 6.34:haloperidol 5.50:clozapine 5.43:sulpiride 5.13:fluphenazine 5.10:flupenthixol |
Other antipsychotic agents. |
|
S(haloperidol) ⊘ P(TREATS) |
CV | 17.52:general_mental_state* 16.62: mania_acute 16.40: undertaker* 16.06:alcohol_withdrawal_acute* 16.01: post-episiotomy pain* |
Some results similar to predications in the database - e.g. haloperidol TREATS pain. |
|
S(haloperidol) ⊘ P(CAUSES) |
CV | 19.89: noncompetitive inhibition* 17.95: catalepsy 17.70: right-shifted WBC* 17.50: behavioral syndromes AW physiological disturbances*... 17.47: drug-related alopecia* |
There are numerous reports of alopecia with haloperidol use, so this is an example of an accurate inference. |
|
S(haloperidol) ⊘ P(TREATS) ⊗ (ASSOC) |
SV | 16.31 anapolon_50 15.22:slc6a11 14.55: gh1 14.23: ahn_1055 17.21: premenstrone |
The gene slc6a11 and drug ahn1055 affect neurotransmitters associated with schizophrenia. |
Table 5.
Retrieval and reapplication of relational structure in ESP. Data, derivation and presentation as in Table 4. Up to five results >= 4SD above the mean of ( ) are shown. * indicates a predication that does not occur in SemMedDB. ASSOC=ASSOCIATED_WITH. CW=COMPARED_WITH
| Cue | Target | Results | Comments |
|---|---|---|---|
|
S(haloperidol) ⊘ C(schizophrenia) |
Predicate vectors | 18.26: TREATS 16.77:ASSOC* 9.77:AFFECTS 8.24:PREDISPOSES* 7.91:CAUSES* |
Haloperidol is a treatment for schizophrenia. |
|
S(haloperidol) ⊘ S(schizophrenia) |
Products of predicate vector pairs | 9.80:CW-INV ⊘ TREATS-INV 8.44:CW ⊘ TREATS-INV 7.39:INTERACTS_WITH ⊘ TREATS-INV 6.99:INTERACTS_WITH -INV ⊘ TREATS-INV 6.60:ISA ⊘ TREATS-INV |
Haloperidol relates in several ways to (other) entities that treat schizophrenia. |
|
S(docetaxel) ⊘ P(CW-INV) ⊗ P(TREATS-INV) |
Semantic vectors | 14.51:view waters 12.53: prostate non-hodgkin’s lymphoma 12.21:anaplastic giant cell thyroid carcinoma 12.06:stage iii mesothelioma 11.96:childhood supratentorial primitive neuroectodermal tumors |
Most represent potential therapeutic applications for docetaxel. |
Some differences between the models are apparent in these search results. For example, PSI tends to retrieve information that is explicitly encoded, while ESP tends to generalize. This can have positive effects, such as the identification of alopecia (hair loss) as an adverse effect of haloperidol. However, in other instances this ability to generalize can lead to the retrieval of results that suggest tenuous connections that may be detrimental for predictive modeling purposes. To a first approximation, PSI has better precision and ESP has better recall.
3. Methods
In these sections that follow we proceed to evaluate these models more formally, in order to characterize the differences between PSI and ESP as they pertain to retrieval of encoded information, representation of domain semantics, and inference.
3.1. Generation of Vector Spaces
We generated two pairs of 32,000-dimensional ESP and PSI spaces for our experiments from SemMedDB version 25.1, which contains 82,239,652 predications extracted from 25,027,441 MEDLINE citations. The first pair of spaces encodes all predications involving a set of predicates we have used in our pharmacovigilance related work [47], the set PV . The second pair of spaces encodes a smaller set of predications, involving the set of predicates we have utilized for our drug-repurposing related work [48], the set DR. The permitted predicates in each case are shown in Table 6. Both ESP spaces were trained for five epochs, using 5 negative samples per encoded predication, and a subsampling threshold of 10−5 for concepts, and 10−7 for predications. For consistency with the PSI models, we also excluded any concept that occurred more than 106 times. In addition to imposing this maximum frequency threshold, each superposition operation during generation of the PSI spaces was weighted as follows 7 :
| (13) |
| (14) |
| (15) |
| (16) |
Table 6.
Predicates used to generate the vector spaces for each experiment. Note that the set PV includes all elements of the set DR, ∈ DR.
| Set | Experiments | Permitted Predicates |
|---|---|---|
| DR | 3,4 | {AFFECTS; ASSOCIATED_WITH; AUGMENTS; CAUSES; COEXISTS_WITH; DISRUPTS; INHIBITS; INTERACTS_WITH; ISA; PREDISPOSES; PRE-VENTS; SAME_AS; STIMULATES; TREATS } |
| PV | 1,2,3,4 | {∈ DR; COMPARED_WITH; COMPLICATES; CONVERTS_TO; DIAGNOSES; LOCATION_OF; MANIFESTATION_OF; METHOD_OF; PART_OF } |
In order to asses performance at different dimensionalities, we truncated the vectors for each of the four spaces, which is a reasonable approach with binary vectors as information is evenly distributed across them. To facilitate inference across extended reasoning pathways, we also generated second-order semantic vectors, by superposing the semantic vectors of concepts that relate to a cue concept (ci) in particular ways. Three sets of second order semantic vectors were generated (S2(concept)), such that:
| (17) |
| (18) |
| (19) |
3.2. Experiment 1: Retrieval of Encoded Information
In order to evaluate the extent to which each model can accurately retrieve encoded information, we drew at random 17,204 predications from SemMedDB, with the constraints that the subject of each of these predications should appear in at least ten (not necessarily unique) predications, and that vector representations for both the predicate and object exist. We then applied the release operator and the random vector for the predicate to the semantic vector for the subject (S(subj) ⊘ P(PREDICATE)), and evaluated the proportion of the ten nearest neighboring context vectors represented the objects of predications in SemMedDB involving this subject and predicate. The resulting metric is the precision at k=10, pk10.
3.3. Experiment 2: Correlation with Human Judgment
As an initial assessment of the representational power of the resulting vectors, we evaluated the correlation between the pairwise distance between the resulting semantic vector representations, and human judgments of the semantic relatedness and similarity between pairs of UMLS concepts. We used the UMNSRS data set, developed by Pakhomov and his colleagues [56], which consists of 725 clinical term pairs, together with human estimates of their semantic relatedness and similarity. 588 of these have been judged for their semantic relatedness, and 567 have been judged for their semantic similarity. Similarity is a tighter constraint than relatedness — for example, haloperidol and chlorpromazine are both related and similar, while haloperidol and schizophrenia are related but dissimilar. (These differences are sometimes referred to respectively as paradigmatic and syntagmatic relationships [57].) The evaluation metric used for this evaluation is Spearman’s rank correlation coefficient, which we used to estimate the correlation between the rankings of the average score assigned to each pair by human annotators, and those assigned by each of the models.
3.4. Experiment 3: Discovery by Analogy
Discovery by Analogy (DbA) is an approach we have developed that leverages the analogical processing capabilities of VSAs to identify associations between biomedical entities. It involves a two-stage procedure. The first stage involves inferring the most strongly associated double-predicate pathways from a set of examples of the relationship type of interest. For example, we may infer the most strongly associated double predicate pathways connecting drugs in TREATS relationships with diseases, to those diseases. An example query might be S(haloperidol) ⊘ S(schizophrenia). This cue would be compared to vectors representing each of the permitted double-predicate pathways, such as P(INTERACTS_WITH) ⊘ P(ASSOCIATED_WITH-INV). We call these double-predicate pathways reasoning pathways, and they can be used as components of discovery patterns, as introduced in [58]. The most strongly-associated reasoning pathway for each cue pair is retrieved, and those pathways that occur most frequently across the set of cues are retained. Triple-predicate pathways are inferred using an identical procedure, but with a second-order semantic vector as the cue for one of the two concepts. Once identified, these pathways can be used to retrieve concepts related to another concept in the same way as the cue pair relate to one another, to solve proportional analogies of the form “what is to a as x is to y”.
To simplify matters for the current experiments, we used the sets of double and triple-predicate reasoning pathways inferred from cue pairs during our prior pharmacovigilance[47] and drug repurposing [48] related experiments, as shown in Table 7. In the former case these reasoning pathways were inferred from 90,787 drug/ADE pairs from the SIDER2 database [59], which were extracted from medication package inserts using NLP. In the latter case, they were inferred from TREATS relationships in SemMedDB between pharmaceutical substances and cancers other than prostate cancer. In addition, we evaluated the extent to which a single-predicate pathway (TREATS or CAUSES) could be used to identify relationships of interest.
Table 7.
Reasoning pathways utilized in Experiment 3. These pathways were applied in three configurations. Single predicate paths (1) were used alone exclusively. Double-predicate paths (2) were used alone, as well as in combination with triple-predicate paths (3).
| Pharmacovigilance Reasoning Pathways | |
|---|---|
| Predicates | Pathways |
| 1 | CAUSES-INV |
| 2 | INTERACTS_WITH:CAUSES-INV ASSOCIATED_WITH:COEXISTS_WITH COMPARED_WITH:CAUSES-INV ASSOCIATED_WITH:INTERACTS_WITH ISA:CAUSES |
| 3 | COMPARED_WITH:INTERACTS_WITH:ASSOCIATED_WITH-INV INTERACTS_WITH:INTERACTS_WITH:ASSOCIATED_WITH-INV INTERACTS_WITH:ASSOCIATED_WITH:COEXISTS_WITH-INV COMPARED_WITH:COEXISTS_WITH:ASSOCIATED_WITH-INV |
| Repurposing Reasoning Pathways | |
| Predicates | Pathways |
| 1 | TREATS-INV |
| 2 | ASSOCIATED_WITH:ISA INTERACTS_WITH:ASSOCIATED_WITH-INV COEXISTS_WITH:ASSOCIATED_WITH-INV INTERACTS_WITH:ASSOCIATED_WITH-INV INHIBITS:ASSOCIATED_WITH-INV |
| 3 | INTERACTS_WITH:COEXISTS_WITH-INV:ASSOCIATED_WITH INTERACTS_WITH:INTERACTS_WITH-INV:ASSOCIATED_WITH AUGMENTS:DISRUPTS:ASSOCIATED_WITH AUGMENTS:AFFECTS:ASSOCIATED_WITH DISRUPTS:AFFECTS:ASSOCIATED_WITH |
Relatedness across a reasoning pathway is estimated by binding the semantic vector for one concept to the elemental vector, or vectors, representing the reasoning pathway concerned. Then this bound product is compared to the vector representing the other concept of interest. For example the similarity between S(haloperidol) ⊘ P(INTERACTS_WITH) ⊗ P(ASSOCIATED_WITH-INV) and S(schizophrenia) gives an estimate of the extent to which these concepts are connected to one another across this pathway 8. Similarly, the hamming distance between S(haloperidol) ⊘ P(TREATS) and C(schizophrenia) provides an estimate of the extent to which this particular TREATS relationship contributes toward the semantic vector representation of haloperidol. Relatedness across multiple pathways is estimated by summing the relatedness across each individual pathway 9.
For the drug repurposing experiments, we evaluated these estimates of relatedness against empirical results documenting the effects of pharmaceutical agents against the PC3 line of prostate cancer cells. Of these agents, 1398 could be mapped to concepts in SemMedDB, and only 68 met the threshold used to indicate activity (a cellular growth rate of <= 1.5SD below the mean). Further details of this dataset are available in [48]. The target concept in this case was “prostate carcinoma”. For the pharmacovigilance experiments, we evaluated these estimates of relatedness using a reference set developed by Ryan and his colleagues [61]. This set contains 399 test cases of potential drug/ADE relationships, with 165 positive and 234 negative controls. The adverse events concerned are acute kidney injury, acute liver injury, acute myocardial infarction and gastrointestinal bleeding. The vector representations of these concepts were constructed by superposing the semantic vectors for concepts corresponding to ICD-9 codes provided in the Observation Medical Outcomes Partnership (OMOP) definitions of these health outcomes (http://omop.org/HOI) with expansion to include hyponyms, where vector representations of these concepts were available. In both experiments, drugs were rank ordered with respect to their relatedness across the reasoning pathways concerned, and the metric of evaluation utilized was the Area Under the Receiver Operating Characteristic (AUROC) curve.
3.5. Experiment 4: Classification by Analogy
In our recent work, we have developed an approach we call Classification-by-Analogy (CbA), using PSI. This approach applies supervised machine learning methods to the bound products of vectors representing concept pairs of interest [62]. For example, a data point in the drug repurposing set is the vector product S(docetaxel) ⊘ S(prostate carcinoma), with the label “1”, as this is a positive example of a drug with activity against the PC3 prostate cancer cell line. In our recent work, we have shown that the performance of CbA with PSI vectors and a Support Vector Machine (SVM), Logistic Regression model and k-nearest neighbor classifiers during five-fold cross-validation experiments using the pharmacovigilance data set exceed those achievable using DbA, with AUROCs of 0.94 and 0.93 for logistic regression and SVM respectively, and comparable F1 scores across the three methods. As good accuracy was achieved with CbA representations across a range of algorithms, this suggests that PSI vector representations provide an effective basis for supervised machine learning. For the current experiments, as our goal is to evaluate the underlying representations, we use a simple k-nearest neighbor approach, with k = 1 and a leave one out cross-validation scheme. So each example CbA bound product (such as S(docetaxel) ⊗ S(prostate carcinoma)) is assigned the label of the nearest neighboring labeled bound product. For the pharmacovigilance set, which is reasonably well-balanced with respect to positive and negative examples, we report the accuracy. In addition for both sets we estimate the AUROC by rank-ordering the examples with respect to the difference between their similarity to the nearest positive neighbor and their similarity to the nearest negative neighbor. We report this metric for both the pharmacovigilance set, and the drug repurposing set. However, for this latter set we do not report the accuracy, as this is spuriously inflated by the large number of negative examples.
4. Results and Discussion
4.1. Retrieval of encoded information
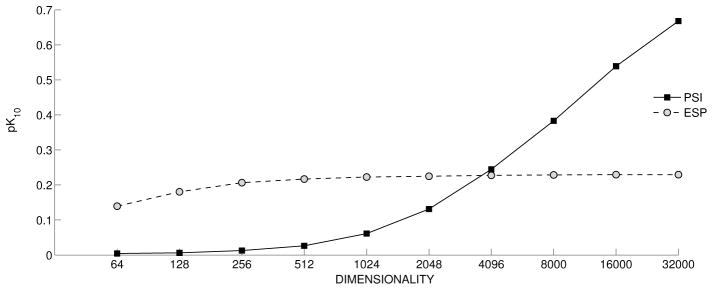
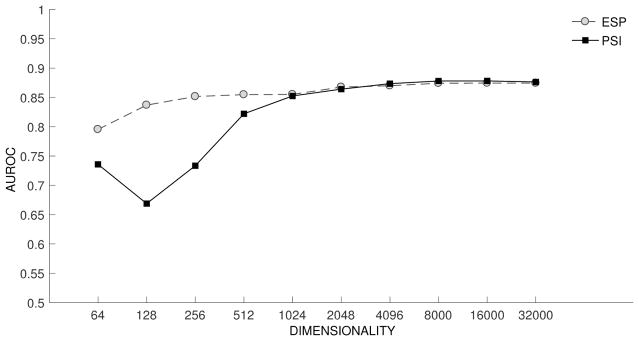
The results of experiments evaluating the capacity for retrieval of explicitly encoded information are shown in Figure 3. The performance of PSI is initially poor, but improves as dimensionality increases, with pk10 of around .7 at 32000 dimensions. In contrast, ESP is remarkably consistent across dimensionalities evaluated, with pk10 of around .2 even with 256 bit vectors, and .23 at the highest dimensionality evaluated. This suggests that ESP has reached a balance between explicit retrieval and similarity-based inference that is consistent with the examples presented in Table 4.
Figure 3.
Retrieval of Explicit Relationships. pk10: precision at k=10.
4.2. Correlation with human judgment
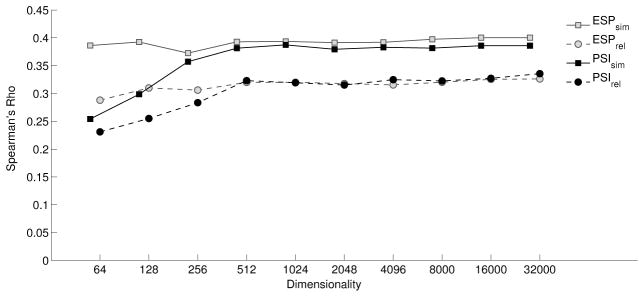
The tendency for the performance of ESP to stabilize at low dimensionality is also apparent in Figure 4, which displays the correlation between each model’s estimates of the association between pairs of UMLS concepts, and the average of estimates of relatedness and similarity provided by human raters. At the highest dimensionality evaluated, PSI exhibits slightly better correlation with respect to relatedness, and ESP exhibits slightly better correlation with respect to similarity. However these differences are marginal. We note that this level of performance on this evaluation set does not approach the best of those reported previously. For example, Pakhomov and his colleagues report correlations of .58 and .62 for relatedness and similarity respectively, with neural embeddings trained on full text articles from PubMed central [6]. Though their evaluation was conducted on a smaller subset, it seems likely that on this task the performance of neural embeddings trained on full text would exceed that of embeddings trained on predications. SemRep is optimized for precision over recall, and the approximately 80 million triples upon which our models were trained contain far less information than is present in the approximately 3 billion word corpus from which they were extracted. Nonetheless, it is interesting to note that the similarity and relatedness results at high dimensions either approach or exceed the best reported when applying ontology-based metrics to subsets of these evaluation sets in prior experiments [63]. As the predications SemRep is permitted to extract are constrained by UMLS semantic relations, both ESP and PSI can be considered as hybrid methods of semantic representation, with both distributional and ontological properties.
Figure 4.
Correlation with Human Judgment
4.3. Discovery by Analogy
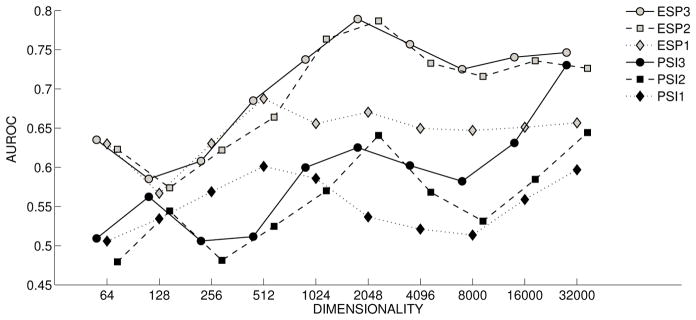
Figure 5 shows the Discovery-by-Analogy (DbA) results for the drug/ADE relationships described in [61]. The single-predicate results for PSI (◆) are generally not predictive, with an AUROC of below .6 at most dimensionalities, indicating the limits of the performance on this task that can be obtained by ranking drugs that occur in direct CAUSES relationships with the ADEs in question higher than those that do not. In contrast, the single-predicate results for ESP (
 ) begin to exceed this limit at a dimensionality of around 256 bits, and proceed to exceed all but one of the PSI results, stabilizing at an AUC of around .65. This illustrates the capacity of ESP to perform similarity-based inference across single predicate paths, such that drugs with similar properties to those that occur in explicit CAUSES relationships with an ADE will be ranked higher than those that are unrelated to these explicitly asserted exemplars. With PSI, two-predicate pathways (■) are predictive at higher dimensionalities, and performance improves substantially with the inclusion of three-predicate pathways (●), with a peak AUC of around .73 at 32,000 dimensions. In contrast, with ESP two-predicate paths (
) begin to exceed this limit at a dimensionality of around 256 bits, and proceed to exceed all but one of the PSI results, stabilizing at an AUC of around .65. This illustrates the capacity of ESP to perform similarity-based inference across single predicate paths, such that drugs with similar properties to those that occur in explicit CAUSES relationships with an ADE will be ranked higher than those that are unrelated to these explicitly asserted exemplars. With PSI, two-predicate pathways (■) are predictive at higher dimensionalities, and performance improves substantially with the inclusion of three-predicate pathways (●), with a peak AUC of around .73 at 32,000 dimensions. In contrast, with ESP two-predicate paths (
 ) begin to exhibit productivity at lower dimensionalities, with an AUC of around .76 with 1024-bit vectors. In addition, though adding three-predicate pathways (
) begin to exhibit productivity at lower dimensionalities, with an AUC of around .76 with 1024-bit vectors. In addition, though adding three-predicate pathways (
 ) does improve performance, the difference is less pronounced than when adding three-predicate pathways in PSI. This suggests that ESP is making better use of the capacity of the vector space, and also that similarity-based inference offers some of the benefits of explicit encoding of longer pathways.
) does improve performance, the difference is less pronounced than when adding three-predicate pathways in PSI. This suggests that ESP is making better use of the capacity of the vector space, and also that similarity-based inference offers some of the benefits of explicit encoding of longer pathways.
Figure 5.
Adverse Drug Reaction: Discovery by Analogy
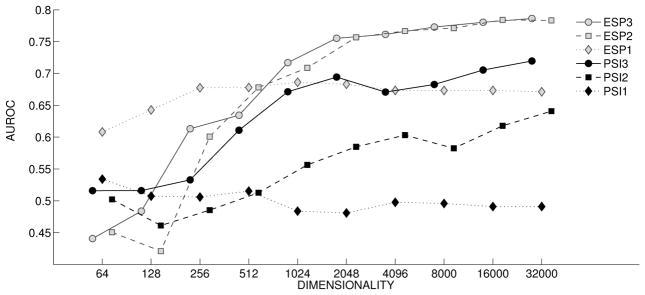
Figure 6 shows the DbA results for the prostate cancer evaluations, which exhibit similar patterns to those shown in Figure 5, despite the different nature of this data set (only around 5% of the examples are positive). The single-predicate pathway, using the predicate TREATS in this case, is unproductive for PSI (◆), but with ESP (
 ) exceeds the productivity of all PSI pathways, except at the highest dimensions evaluated. Once again, PSI performance improves considerably with inclusion of three-predicate pathways (●), this time with a peak AUC of around .72. With ESP, the advantage of three-predicate pathways (
) exceeds the productivity of all PSI pathways, except at the highest dimensions evaluated. Once again, PSI performance improves considerably with inclusion of three-predicate pathways (●), this time with a peak AUC of around .72. With ESP, the advantage of three-predicate pathways (
 ) over two-predicate pathways (
) over two-predicate pathways (
 ) is again less pronounced. However ESP’s improvement in performance over PSI, apparent at a dimensionality of 1024 bits and above, is more pronounced with a peak AUC of .786 with triple-predicate pathways at 32,000 dimensions.
) is again less pronounced. However ESP’s improvement in performance over PSI, apparent at a dimensionality of 1024 bits and above, is more pronounced with a peak AUC of .786 with triple-predicate pathways at 32,000 dimensions.
Figure 6.
High-throughput Screen: Discovery by Analogy
4.4. Classification by Analogy
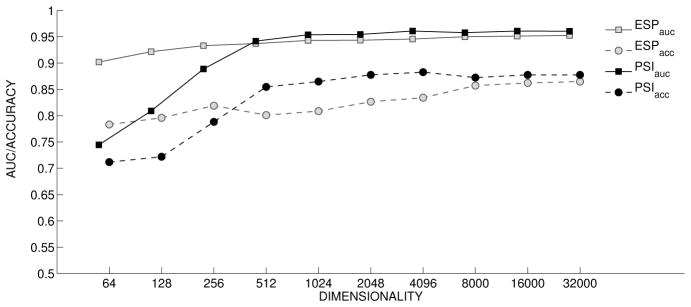
Classification-by-Analogy (CbA) results are shown in Figures 7 and 8. Both figures show the results of kNN classification with k=1. In Figure 7, both the AUROC and the accuracy are reported. In figure 8, only AUROC is reported, as the accuracy is inflated on account of the large number of negative examples (around 95% of the set). In both figures, we see that ESP performs best at lower dimensionalities. However, at highest dimensionalities PSI performs slightly better, with a more marked difference in the case of the ADE experiments in Figure 7, which also shows substantive improvements in performance with PSI at dimensions 512–4096 bit range. One interpretation of this finding is that the advantage with ESP in the DbA experiments, which may be attributable to similarity-based inference, is lost when applying a layer of supervised machine learning as this would provide PSI with the capacity for similarity-based inference also. This is clearly the case in the PCA experiments, where there is only one target concept (prostate carcinoma). This means that all vectors undergo an identical transformation, so the only information available for classification purposes is the similarity between drug vectors. In contrast, in the ADE experiments the vector representation used to classify a particular drug will differ across ADEs, and information concerning abstract predicate pathways is available for classification purposes also.
Figure 7.
Adverse Drug Reaction: Classification by Analogy
Figure 8.
Drug Repurposing: Classification by Analogy
4.5. Improvement across iterations
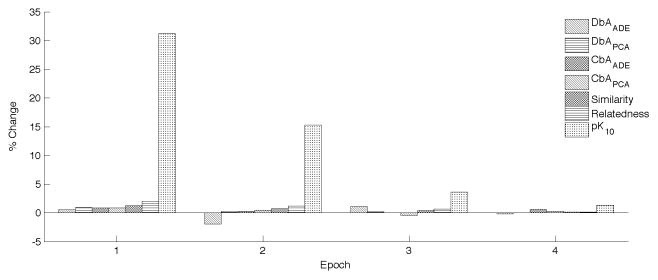
Figure 9 shows the percent change in performance for each evaluation across the five epochs as training. Epoch 0, representing the first epoch, is not shown. For all subsequent epochs, the percent change in each performance metric relative to the previous epoch is shown. In all but one case (DbAADE), there is a generally consistent pattern of improvement across iterations, with the greatest benefit with respect to retrieval of explicit relationships. Though the rate of improvement is clearly decreasing, the majority of peak performances (4/7) occurred in epoch 4, suggesting that further improvements may be obtained with larger numbers of training cycles.
Figure 9.
Percent change in performance from previous iteration. DbA=Discovery-by-Analogy. CbA=Classification-by-Analogy. ADE=Adverse Drug Event set. PCA=Prostate Cancer set. The metric illustrated is the AUROC for all of these aside from CbAADE, where changes in accuracy are shown instead. Similarity and Relatedness show changes in Spearman RhO, measuring correlation to the relevant UMNSRS set. pk10= precision at k=10, for retrieval of explicit relationships.
4.6. Summary of results
The results suggest that ESP and PSI have different strengths. ESP has better performance at lower dimensionalities in all tasks, which is consistent with our initial hypothesis that the incorporation of negative sampling would lead to more efficient utilization of the vector space, with ESP exhibiting comparable correlation with human judgment across all dimensionalities tested. The capacity to perform well at low dimensionality may be advantageous in some applications, such as those requiring semantic hashing, as it leads to much faster nearest neighbor calculation. At higher dimensions (>= 4096 bits) PSI exhibits better ability to retrieve explicit relationships, and as such is arguably the better choice for applications involving navigation of the large pool of explicit assertions in SemMedDB. However, the DbA results reveal that ESP offers a number of advantages for inferring relationships that are not stated explicitly. These include obtaining a level of prediction with cues consisting of a single predicate and cue concept (e.g. TREATS prostate carcinoma) only, on account of the similarity between context vectors that represent concepts that occur in similar predications. However, across experiments and models the performance with single-predicate pathways is worse than that where dual-predicate reasoning pathways are provided, and including triple-predicate pathways further improves performance. Unlike PSI, the advantage of including triple-predicate pathways is slight with ESP. Consequently, there is less motivation to go through the additional steps of producing second-order semantic vectors for concepts of interest. For each configuration (single, double or double- and triple-predicate pathways) ESP performance is generally better than PSI performance, suggesting it may be the better choice for predictive modeling. The CbA experiments show that this advantage is lost when a layer of supervised machine learning is applied to the resulting vector representations of entity pairs of interest, other than at low dimensionalities. However, we do not believe that this negates the advantages of ESP for predictive modeling. We would not anticipate the kNN classifiers generalizing to other test sets, and from a practical perspective it is often desirable to draw inferences in situations where a manually annotated reference set is unavailable (for example, to draw inferences concerning ADEs other than the four included in this reference set), or before the generation of empirical data (for example, to guide selection of a panel of agents for high-throughput screening experiments). From the perspective of literature-based discovery, an implication of these differences is that ESP may be better equipped to support open-ended discovery scenarios, such as the search for potential therapies for an otherwise poorly treatable disease. In contrast, PSI may be more useful as a means to retrieve explicit assertions that support a novel therapeutic hypothesis, or explain an observed relationship. These discovery scenarios have been referred to as open and closed discovery, respectively [64].
4.7. Related work
Inspired by both recent work on neural language models and prior work demonstrating the feasibility of learning distributed representations of relational data [65, 66], a number of authors have recently developed methods through which distributed representations can be derived from subject-predicate-object triples. Though this work tends not to reference the literature on VSAs, there is a common goal of deriving distributed representations from triples, which leads to a degree of overlap in the methodological approaches used to generate composite representations — a reversible transformation of the vector for an entity may be used to indicate the nature of a predicate.
For example, the TransE model developed by Bordes and his colleagues [67] attempts to minimize the distance between ( ) and , while maximizing this distance for corrupted triples in a manner analogous to the application of negative sampling in SGNS. Alternatively, a matrix may be assigned to each predicate, such that multiplication by this matrix affects a transformation on the vector representing a single entity [68, 69], or this matrix serves as a component of a bilinear tensor product with the subject and object vectors [70, 71]. The practical goal of these efforts is generally posed as a problem of knowledge graph completion. Models are trained on multi-relational data such as the collaboratively-created Freebase database of manually curated structured knowledge [72] and evaluated for their ability to recover held-out triples.
One relevant distinction between this task and the task of drawing inference from SemMedDB is that knowledge graphs contain a single instance of each relationship, while with extracted knowledge information concerning the frequency with which a relationship is repeated is also available for modeling. Another is that knowledge graphs tend to contain many more relationship types than the 30 predicates extracted by SemRep (for example, more than 7,000 in Freebase). As a consequence models emerging from this domain tend to learn parameters for representations of predicates. (By contrast, with PSI and ESP vector representations of predicates are held constant.) With the exception of TransE, predicate representations also have a dimensionality of d2 with d-dimensional concept vectors, which would make drawing inference across longer predicate pathways computationally cumbersome. Though this does not present a problem for knowledge graph completion per se, it constrains the utility of these models for analogical discovery. TransE, which uses vector representations of predicates, seems most readily adaptable to this purpose, though one would anticipate complications arising from the application of vector addition to implement both the generation of predicate-argument vectors and the updating of weights during the process of training.
In some cases, attempts have been made to incorporate unstructured data, for example by initializing concept vectors using word vectors trained on unstructured text [71]. Of particular relevance to the current work, Hyland and her colleagues recently reported a model that combines SemMedDB with unstructured Electronic Health Record (EHR) data by deriving triples from these data using an “appears in sentence with” relationship to indicate co-occurrence, after application of concept extraction and normalization procedures [69]. The results in both cases suggest that incorporating such unstructured information can result in modest improvements in performance on knowledge graph completion tasks.
Most recently, Nickel and his colleagues have proposed Holographic Encoding (HolE) as a method for knowledge graph embedding [73]. HolE is the first model to emerge from this community to make explicit use of a VSA -Plate’s Holographic Reduced Representations (HRR) [74] - to generate composite vector representations of predicate-argument pairs with promising results on knowledge-graph completion tasks. On account of its use of a VSA, HolE shares ancestry with both PSI and ESP, and is perhaps most closely related to ESP on account of its use of gradient descent during training. Though we have used the Binary Spatter Code as the VSA for the current work, we have evaluated HRR-based implementations of PSI in previous work [49, 41, 60], and anticipate developing HRR-based implementations of ESP in the future. Like other models emerging from this community, HolE differs from both ESP and PSI as it learns parameters for predicate representations. Another important difference has to do with our assignment of two vectors for each concept, corresponding to the random and semantic vectors used for terms in Random Indexing. These are fundamental to learning in PSI, and a consequence of ESP’s lineage. Though they are not essential when learning concept representations with gradient descent, they offer advantages for analogical retrieval such as the ability to isolate reasoning pathways that indicate implicit relationships.
4.8. Limitations and future work
The findings presented in this paper suggest that ESP offers advantages for analogical retrieval, but that ESP and PSI are on equal footing as a representational basis for supervised machine learning. To evaluate their utility for this purpose in the current paper, we have considered a single machine-learning algorithm only, and have not explored the parameter space of this algorithm in an effort to optimize performance. It may be the case that more sophisticated machine-learning approaches are able to leverage the additional information encoded by ESP to improve performance further. In addition, it seems likely that fixing the context vectors (output weights) in ESP, or slowing their learning rate, would result in a model with greater accuracy for retrieval of explicit relationships, that retains performance at lower dimensionalities. These are both possibilities we plan to explore in future work.
During the course of the work described in this paper, it has come to our attention that ESP can facilitate inference across triple-predicate paths without the need for the generation of second-order semantic vectors. Though some of the results from the current paper may be explained by this capability, we have yet to explore the extent to which the inference and application of triple-predicate and other paths from ESP vectors directly may be useful in DbA-type models. Also, though the current implementation of ESP uses binary vectors as a fundamental representational unit, we have also developed PSI implementations using both real and complex-valued vectors [41, 14, 60]. With PSI, binary vector spaces are generally slower to generate, but more space-efficient and faster to search. We anticipate this will be the case with ESP also, but further work will be required to develop real and complex vector based variants.
Our models use UMLS concepts, rather than terms, as a fundamental representational unit. An advantage of this is that synonyms and morphological variants are resolved by SemRep before distributed representations are generated. To the extent that NLP is accurate, this means that all information pertinent to a particular concept should be encoded in its unique vector representation, and that no two concepts will share a vector (as may occur when representing a polysemous term in term-based distributional models). However, on account of the granularity of the UMLS it is often the case that concepts that should arguably be collapsed are represented by a group of vectors. A common example is the assignment of separate UMLS concepts to the generic and trade names of the same drug. In the pharmacovigilance-related experiments described in this paper we developed an ad-hoc solution this problem that involved superposition of the vector representations of clinical conditions that are taxonomically related to a side effect of interest. Faruqi and his colleagues provide a more general solution [75], which we are currently exploring as a means to integrate information from taxonomies into distributional models of biomedical concepts [76], and seems readily applicable to vectors generated using ESP or PSI. In addition, as our distributed representations encode semantic information only, our models do not have access to orthographic information. For example, while it is obvious to the human reader that the terms “depressive disorder” and “major depressive disorder” are related to one another, the vector representations of the UMLS concepts corresponding to these terms will be similar only to the extent that they occur in similar contexts in SemMedDB. Methods exist to encode such orthographic information into distributed representations [77], including our own [78]. However, the utility this additional information for semantic and predictive modeling remains to be determined. Finally, the work of Hyland and her colleagues suggests that integrating unstructured information with SemMedDB may lead to better predictive models [69], a possibility we plan to evaluate in future work also.
5. Conclusion
This paper describes the development and evaluation of ESP, a novel approach to encoding semantic predications that combines compositional operators used in VSAs with a neural-probabilistic approach to training. We compared ESP to PSI, our previous approach to encoding semantic predications, across several tasks. The results suggest that both models can provide effective unsupervised pre-training of feature vectors for downstream machine learning tasks. However, ESP offers advantages for analogical retrieval, and in tasks where constraining the dimensionality of the vector space is desirable. In these circumstances in particular, the additional computational work required by ESP seems well justified.
Highlights.
We develop a neural-probabilistic approach to represent semantic predications.
This is compared to a prior representational approach across a number of tasks.
Application areas are pharmacovigilance and drug repurposing.
The neural-probabilistic model performs better at lower dimensions.
The neural-probabilistic model adds similarity-based inference.
Acknowledgments
This research was supported by US National Library of Medicine [grant number R01 LM011563], and Cancer Prevention and Research Institute of Texas [grant number RP150578]. The authors would also like to thank Tom Rindflesch and his team for extracting and sharing the predication database, and the Intramural Research Program of the US National Institutes of Health, National Library of Medicine for supporting his work in this area. We would also like to acknowledge Ning Shang, for sharing the terminological expansions used in our pharmacovigilance experiments.
Footnotes
From the perspective of backpropagation, this superposition corresponds to adjusting the incoming weights in accordance with their influence on the error function. Each incoming weight (a component of S(wo)) is multiplied by the corresponding outgoing weight (a component of C(wc)) to generate the scalar product S(wo) · C(wc). So the influence of a coordinate in S(wo) on the error is proportional to its counterpart in C(wc), and vice versa.
This update procedure is usually described before the update of the semantic vectors, in accordance with the propagation of the error function from output node to input vectors as prescribed by the back-propagation algorithm. However, in both cases the superposition involves the pre-update state of the other vector concerned. We have chosen to proceed in the opposite direction to emphasize the relationship with RI.
The superposition of partially-trained context vectors is similar in some respects to the superposition of iteratively trained context vectors in Reflective Random Indexing (RRI), an iterative variant of RI we developed to promote this sort of inference [29].
Interestingly, aside from the learning rate, this expression corresponds to orthogonal projection (i.e. rendering S(C) orthogonal to C(¬w)) in quantum logic [30], which has been used in information retrieval to isolate documents that relate to a specific sense of a cue term [31].
Once tallying of the voting record has occurred, NNHD S(s), P(P) ⊗ C(o) = NNHD(S(s) ⊘ P(P), C(o)).
ENT is a simplification of the standard expression for entropy weighting (see e.g. [55]), permitted because concept-role combinations occur once per predication only.
In probabilistic PSI [60], the estimated relatedness corresponds to the probability of traversing this path, in accordance with the rules of quantum probability
This straightforward approach produces marginally better performance across models than our prior method of measuring the length of the projection of a subspace constructed from the vector representing each reasoning pathway.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Cohen T, Widdows D. Empirical distributional semantics: methods and biomedical applications. Journal of biomedical informatics. 2009;42(2):390–405. doi: 10.1016/j.jbi.2009.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Mikolov T, Chen K, Corrado G, Dean J. Efficient estimation of word representations in vector space; Proceedings of the First International Conference on Learning Representations (ICLR); Scottsdale, Arizona. 2016. [Google Scholar]
- 3.Mikolov T, Sutskever I, Chen K, Dean J. Distributed representations of words and phrases and their compositionality. Proceedings of the 26th International Conference on Neural Information Processing Systems; Advances in Neural Information Processing Systems. NIPS’13; pp. 3111–3119. [Google Scholar]
- 4.Pennington J, Socher R, Manning CD. Glove: Global vectors for word representation. EMNLP. 2014;14:1532–43. [Google Scholar]
- 5.De Vine L, Zuccon G, Koopman B, Sitbon L, Bruza P. Medical semantic similarity with a neural language model. Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management, ACM; 2014; pp. 1819–1822. [Google Scholar]
- 6.Pakhomov SV, Finley G, McEwan R, Wang Y, Melton GB. Corpus domain effects on distributional semantic modeling of medical terms. Bioinformatics. 2016;32(23):3635–3644. doi: 10.1093/bioinformatics/btw529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Choi E, Schuetz A, Stewart WF, Sun J. Medical concept representation learning from electronic health records and its application on heart failure prediction. arXiv preprint arXiv:1602.03686. [Google Scholar]
- 8.Bengio Y, Courville A, Vincent P. Representation learning: A review and new perspectives. IEEE transactions on pattern analysis and machine intelligence. 2013;35(8):1798–1828. doi: 10.1109/TPAMI.2013.50. [DOI] [PubMed] [Google Scholar]
- 9.Bengio Y, Goodfellow IJ, Courville A. Deep learning. MIT Press; 2016. [Google Scholar]
- 10.Lenci A. Distributional semantics in linguistic and cognitive research. Italian journal of linguistics. 2008;20(1):1–31. [Google Scholar]
- 11.Turney PD, Pantel P, et al. From frequency to meaning: Vector space models of semantics. Journal of artificial intelligence research. 2010;37(1):141–188. [Google Scholar]
- 12.Levy O, Goldberg Y, Dagan I. Improving distributional similarity with lessons learned from word embeddings. Transactions of the Association for Computational Linguistics. 2015;3:211–225. [Google Scholar]
- 13.Widdows D, Cohen T. Reasoning with vectors: a continuous model for fast robust inference. Log J IGPL. 2015;23(2):141–173. doi: 10.1093/jigpal/jzu028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cohen T, Schvaneveldt RW, Rindflesch TC. Predication-based semantic indexing: Permutations as a means to encode predications in semantic space. AMIA Annual Symposium Proceedings, Vol. 2009, American Medical Informatics Association; 2009; p. 114. [PMC free article] [PubMed] [Google Scholar]
- 15.Rindflesch TC, Fiszman M. The interaction of domain knowledge and linguistic structure in natural language processing: interpreting hypernymic propositions in biomedical text. Journal of biomedical informatics. 2003;36(6):462–477. doi: 10.1016/j.jbi.2003.11.003. [DOI] [PubMed] [Google Scholar]
- 16.Kilicoglu H, Shin D, Fiszman M, Rosemblat G, Rindflesch TC. Semmeddb: a pubmed-scale repository of biomedical semantic predications. Bioinformatics. 2012;28(23):3158–3160. doi: 10.1093/bioinformatics/bts591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Landauer T, Dumais S. A solution to Plato’s problem: The latent semantic analysis theory of acquisition. Psychological Review. 1997;104(2):211–240. [Google Scholar]
- 18.Hinton G, McClelland J, Rumelhart D. Parallel distributed processing: explorations in the microstructure of cognition. Vol. 1. MIT Press; 1986. Distributed representations; pp. 77–109. [Google Scholar]
- 19.Kanerva P, et al. Fully distributed representation. Proceedings of 1997 Real World Computing Symposium; RWC ’97, Tokyo; Jan. 1997; Tsukuba-city, Japan. pp. 358–365. [Google Scholar]
- 20.Kanerva P, Kristofersson J, Holst A. Random indexing of text samples for latent semantic analysis. Proceedings of the 22nd Annual Conference of the Cognitive Science Society; 2000. [Google Scholar]
- 21.Johnson WB, Lindenstrauss J. Extensions of Lipschitz mappings into a Hilbert space. Contemporary Mathematics. 1984;26:189–206. [Google Scholar]
- 22.Karlgren J, Sahlgren M. In: From words to understanding. Foundations of Real-World Intelligence. Uesaka Y, Kanerva P, Asoh H, editors. Stanford: CSLI Publications; pp. 294–308. [Google Scholar]
- 23.Kanerva P. Sparse distributed memory. The MIT Press; 1988. [Google Scholar]
- 24.Sandin F, Emruli B, Sahlgren M. Incremental Dimension Reduction of Tensors with Random Indexing. arXiv preprint arXiv:1103.3585. 2011 Mar 18; [Google Scholar]
- 25.Xu W, Rudnicky AI. Can artificial neural networks learn language models?. International Conference on Statistical Language Processing; Beijing, China. 2000. pp. M1–13. [Google Scholar]
- 26.Bengio Y, Ducharme R, Vincent P, Jauvin C. A neural probabilistic language model. journal of machine learning research. 2003;3(Feb):1137–1155. [Google Scholar]
- 27.Goldberg Y, Levy O. word2vec explained: deriving mikolov et al.’s negative-sampling word-embedding method. arXiv preprint arXiv:1402.3722. [Google Scholar]
- 28.Rong X. word2vec parameter learning explained. arXiv preprint arXiv:1411.2738. [Google Scholar]
- 29.Cohen T, Schvaneveldt R, Widdows D. Reffective random indexing and indirect inference: A scalable method for discovery of implicit connections. Journal of Biomedical Informatics. 2010;43(2):240–256. doi: 10.1016/j.jbi.2009.09.003. [DOI] [PubMed] [Google Scholar]
- 30.Birkhoff G, von Neumann J. The logic of quantum mechanics. Annals of Mathematics. 1936;37:823–843. [Google Scholar]
- 31.Widdows D. Orthogonal negation in vector spaces for modelling word-meanings and document retrieval. Proceedings of the 41st Annual Meeting of the Association for Computational Linguistics (ACL); Sapporo, Japan. 2003. [Google Scholar]
- 32.Smolensky P. Connectionism, constituency, and the language of thought. University of Colorado; Boulder: 1988. [Google Scholar]
- 33.Smolensky P. Tensor product variable binding and the representation of symbolic structures in connectionist systems. Artificial intelligence. 1990;46(1):159–216. [Google Scholar]
- 34.Kanerva P. Binary spatter-coding of ordered k-tuples. Artificial Neural Networks—ICANN. 1996;96:869–873. [Google Scholar]
- 35.Plate TA. Holographic Reduced Representations: Distributed Representation for Cognitive Structures. CSLI Publications; 2003. [Google Scholar]
- 36.Gayler RW, Wales R. Connections, binding, unification and analogical promiscuity. In: DG, Holyoak BKK, editors. Advances in analogy research: Integration of theory and data from the cognitive, computational, and neural sciences. Sofia, Bulgaria: New Bulgarian, New Bulgarian University, Sofia; 1998. [Google Scholar]
- 37.Rachkovskij DA, Kussul EM. Binding and normalization of binary sparse distributed representations by context-dependent thinning. Neural Computation. 2001;13(2):411–452. [Google Scholar]
- 38.Gallant SI, Okaywe TW. Representing objects, relations, and sequences. Neural computation. 2013;25(8):2038–2078. doi: 10.1162/NECO_a_00467. [DOI] [PubMed] [Google Scholar]
- 39.Gayler RW. In: Slezak Peter., editor. Vector symbolic architectures answer Jackendoff’s challenges for cognitive neuroscience; ICCS/ASCS International Conference on Cognitive Science; Sydney, Australia. University of New South Wales; 2004. pp. 133–138. [Google Scholar]
- 40.Levy SD, Gayler R. Vector symbolic architectures: A new building material for artificial general intelligence. Proceedings of the 2008 conference on Artificial General Intelligence 2008: Proceedings of the First AGI Conference; IOS Press; 2008. pp. 414–418. [Google Scholar]
- 41.Widdows D, Cohen T. Real, complex, and binary semantic vectors. In: Busemeyer JR, Dubois F, Lambert-Mogiliansky A, Melucci M, editors. Quantum Interaction. QI 2012. Lecture Notes in Computer Science. Vol. 7620. Springer; Berlin, Heidelberg: [Google Scholar]
- 42.Eliasmith C, Thagard P. Integrating structure and meaning: A distributed model of analogical mapping. Cognitive Science. 2001;25(2):245–286. [Google Scholar]
- 43.Plate TA. Analogy retrieval and processing with distributed vector representations. Expert systems. 2000;17(1):29–40. [Google Scholar]
- 44.Kanerva P. What we mean when we say “What’s the dollar of mexico?”: Prototypes and mapping in concept space. 2010 AAAI Fall Symposium Series. 2010 [Google Scholar]
- 45.Cohen T, Widdows D, Schvaneveldt R, Rindflesch T. Finding schizophrenia’s prozac: Emergent relational similarity in predication space. Proceedings of the Fifth International Symposium on Quantum Interaction; 2011. [Google Scholar]
- 46.Cohen T, Widdows D, Schvaneveldt RW, Davies P, Rindflesch TC. Discovering discovery patterns with predication-based semantic indexing. Journal of biomedical informatics. 2012;45(6):1049–1065. doi: 10.1016/j.jbi.2012.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Shang N, Xu H, Rindflesch TC, Cohen T. Identifying plausible adverse drug reactions using knowledge extracted from the literature. Journal of biomedical informatics. 2014;52:293–310. doi: 10.1016/j.jbi.2014.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Cohen T, Widdows D, Stephan C, Zinner R, Kim J, Rindflesch T, Davies P. Predicting high-throughput screening results with scalable literature-based discovery methods. CPT: pharmacometrics & systems pharmacology. 2014;3(10):1–9. doi: 10.1038/psp.2014.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Cohen T, Widdows D, Vine LD, Schvaneveldt R, Rindflesch TC. Many paths lead to discovery: Analogical retrieval of cancer therapies. In: Busemeyer JR, Dubois F, Lambert-Mogiliansky A, Melucci M, editors. Quantum Interaction. QI 2012. Lecture Notes in Computer Science. Vol. 7620. Springer; Berlin, Heidelberg: [Google Scholar]
- 50.Cohen T, Widdows D, Schvaneveldt RW, Rindflesch TC. Discovery at a distance: farther journeys in predication space. Bioinformatics and biomedicine workshops (BIBMW), 2012 IEEE international conference on, IEEE; 2012; pp. 218–225. [Google Scholar]
- 51.Widdows D, Peters S. Word vectors and quantum logic. Proceedings of the Eighth Mathematics of Language Conference; Bloomington, Indiana. 2003. [Google Scholar]
- 52.Widdows D, Ferraro K. Semantic vectors: a scalable open source package and online technology management application. LREC; Citeseer: 2008. [Google Scholar]
- 53.Vine LD, Bruza P. Semantic oscillations: Encoding context and structure in complex valued holographic vectors. Proceedings of the AAAI Fall Symposium on Quantum Informatics for Cognitive, Social, and Semantic Processes (QI 2010); 2010. [Google Scholar]
- 54.Semantic vectors. https://github.com/semanticvectors/semanticvectors.
- 55.Martin DI, Berry MW. Mathematical foundations behind latent semantic analysis. In: Landauer TK, McNamara DS, Dennis S, Kintsch W, editors. Handbook of latent semantic analysis. Lawrence Erlbaum Associates, Inc.; 2007. pp. 35–56. [Google Scholar]
- 56.Pakhomov S, McInnes B, Adam T, Liu Y, Pedersen T, Melton GB. Semantic similarity and relatedness between clinical terms: an experimental study. AMIA annual symposium proceedings, Vol. 2010, American Medical Informatics Association; 2010; p. 572. [PMC free article] [PubMed] [Google Scholar]
- 57.Sahlgren M. PhD dissertation. Department of Linguistics, Stockholm University; 2006. The Word-Space Model, Using distributional analysis to represent syntagmatic and paradigmatic relations between words in high-dimensional vector spaces. [Google Scholar]
- 58.Hristovski D, Friedman C, Rindflesch TC, Peterlin B. Exploiting semantic relations for literature-based discovery. AMIA; 2006. [PMC free article] [PubMed] [Google Scholar]
- 59.Kuhn M, Campillos M, Letunic I, Jensen LJ, Bork P. A side effect resource to capture phenotypic effects of drugs. Molecular systems biology. 2010;6(1):343. doi: 10.1038/msb.2009.98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Cohen T, Widdows D. Embedding probabilities in predication space with hermitian holographic reduced representations. In: Atmanspacher H, Filk T, Pothos E, editors. Revised Selected Papers; Quantum Interaction, 2015, 9th International Conference, QI 2015; Filzbach, Switzerland. July 15–17; Springer; 2015. pp. 245–257. [Google Scholar]
- 61.Ryan PB, Schuemie MJ, Welebob E, Duke J, Valentine S, Hartzema AG. Defining a reference set to support methodological research in drug safety. Drug safety. 2013;36(1):33–47. doi: 10.1007/s40264-013-0097-8. [DOI] [PubMed] [Google Scholar]
- 62.Mower J, Subramanian D, Cohen T. Classification-by-analogy: using vector representations of implicit relationships to identify plausibly causal drug/side-effect relationships. AMIA Annu Symp Proc; American Medical Informatics Association; 2016. pp. 1940–1949. [PMC free article] [PubMed] [Google Scholar]
- 63.Mencıa EL, de Melo G, Nam J. Medical concept embeddings via labeled background corpora. LREC; 2016. [Google Scholar]
- 64.Weeber M, Klein H, de Jong-van den Berg L, Vos R, et al. Using concepts in literature-based discovery: Simulating swanson’s raynaud–fish oil and migraine–magnesium discoveries. Journal of the American Society for Information Science and Technology. 2001;52(7):548–557. [Google Scholar]
- 65.Hinton GE. Learning distributed representations of concepts. Proceedings of the eighth annual conference of the cognitive science society; Amherst, MA. 1986. p. 12. [Google Scholar]
- 66.Paccanaro A, Hinton GE. Learning distributed representations of concepts using linear relational embedding. IEEE Transactions on Knowledge and Data Engineering. 2001;13(2):232–244. [Google Scholar]
- 67.Bordes A, Usunier N, Garcia-Duran A, Weston J, Yakhnenko O. Translating embeddings for modeling multi-relational data. Advances in Neural Information Processing Systems. 2013:2787–2795. [Google Scholar]
- 68.Bordes A, Weston J, Collobert R, Bengio Y. Learning structured embeddings of knowledge bases. Conference on Artificial Intelligence, no. EPFL-CONF-192344; 2011. [Google Scholar]
- 69.Hyland SL, Karaletsos T, Rätsch G. Knowledge transfer with medical language embeddings. arXiv preprint arXiv:1602.03551. [Google Scholar]
- 70.Sutskever I, Tenenbaum JB, Salakhutdinov RR. Modelling relational data using bayesian clustered tensor factorization. Advances in neural information processing systems. 2009:1821–1828. [Google Scholar]
- 71.Socher R, Chen D, Manning CD, Ng A. Reasoning with neural tensor networks for knowledge base completion. Advances in Neural Information Processing Systems. 2013:926–934. [Google Scholar]
- 72.Bollacker K, Evans C, Paritosh P, Sturge T, Taylor J. Freebase: a collaboratively created graph database for structuring human knowledge. Proceedings of the 2008 ACM SIGMOD international conference on Management of data; ACM; 2008. pp. 1247–1250. [Google Scholar]
- 73.Nickel M, Rosasco L, Poggio T. Holographic embeddings of knowledge graphs. Thirtieth AAAI Conference on Artificial Intelligence.AAAI Publications; [Google Scholar]
- 74.Plate TA. Holographic reduced representations. IEEE Transactions on Neural Networks. 1995;6(3):623–641. doi: 10.1109/72.377968. [DOI] [PubMed] [Google Scholar]
- 75.Faruqui M, Dodge J, Jauhar SK, Dyer C, Hovy E, Smith NA. Retrofitting word vectors to semantic lexicons. Proc. of NAACL; 2015. [Google Scholar]
- 76.Yu Z, Cohen T, Bernstam EV, Wallace BC. Retrofitting word vectors of mesh terms to improve semantic similarity measures. EMNLP. 2016;2016:43. [Google Scholar]
- 77.Kachergis G, Cox G, Jones M. OrBEAGLE: integrating orthography into a holographic model of the lexicon. Artificial Neural Networks and Machine Learning–ICANN. 2011;2011:307–314. [Google Scholar]
- 78.Cohen T, Widdows D, Wahle M, Schvaneveldt R. Orthogonality and orthography: introducing measured distance into semantic space. In: Atmanspacher EKKRD, Haven H, editors. Selected Papers; Quantum Interaction. 7th International Conference. QI 2013; Leicester, UK. July 25–27; Springer; 2013. pp. 34–46. [Google Scholar]