Extremely thick cell walls and low mesophyll conductance: welcome to the world of ancient living!

Highlight

Low mesophyll conductance was the most important limiter of photosynthesis in the majority of evolutionarily old species and resulted from thick cell walls and low exposed chloroplast area.

Abstract

Mesophyll conductance is thought to be an important photosynthetic limitation in gymnosperms, but they currently constitute the most understudied plant group in regard to the extent to which photosynthesis and intrinsic water use efficiency are limited by mesophyll conductance. A comprehensive analysis of leaf gas exchange, photosynthetic limitations, mesophyll conductance (calculated by three methods previously used for across-species comparisons), and the underlying ultra-anatomical, morphological and chemical traits in 11 gymnosperm species varying in evolutionary history was performed to gain insight into the evolution of structural and physiological controls on photosynthesis at the lower return end of the leaf economics spectrum. Two primitive herbaceous species were included in order to provide greater evolutionary context. Low mesophyll conductance was the main limiting factor of photosynthesis in the majority of species. The strongest sources of limitation were extremely thick mesophyll cell walls, high chloroplast thickness and variation in chloroplast shape and size, and the low exposed surface area of chloroplasts per unit leaf area. In gymnosperms, the negative relationship between net assimilation per mass and leaf mass per area reflected an increased mesophyll cell wall thickness, whereas the easy-to-measure integrative trait of leaf mass per area failed to predict the underlying ultrastructural traits limiting mesophyll conductance.

Introduction

The 36-fold variation of net photosynthetic rate across C3 species (Wright et al., 2004) cannot be explained only by stomatal restrictions and biochemical potentials, because the CO₂ diffusion efficiency from substomatal cavities to chloroplasts (mesophyll diffusion conductance; g_m) plays an important role in shaping photosynthetic capacities and leaf resource-use efficiency across Earth’s ecosystems (Warren et al., 2003; Niinemets et al., 2009b, 2011; Terashima et al., 2011; Tosens et al., 2012b, 2016). The general consensus is that ignoring g_m in carbon gain calculations prevents the correct simulation of photosynthesis due to biased maximum velocity of carboxylation especially in stressful field environments (Manter and Kerrigan, 2004; Niinemets et al., 2011). Still, g_m has been ignored in carbon gain calculations because of our lack of knowledge about its various causes and the main drivers of its variation across species (Niinemets et al., 2009a).

Mesophyll conductance has now been estimated for more than 100 species from all major plant groups. Available data show that considerable variation of g_m between plant groups exists and it is larger than that of stomatal conductance (g_s) (Flexas et al., 2012; Tosens et al., 2016). g_m depends on the length and characteristics of the CO₂ diffusion path from substomatal cavities to chloroplasts (Evans et al., 2009; Hassiotou et al., 2009; Terashima et al., 2011; Tosens et al., 2012b). The main limitations to CO₂ diffusion are in the mesophyll liquid phase. Two traits, mesophyll cell wall thickness (T_cwm) and chloroplast surface area exposed to intercellular airspace (S_c/S), have been highlighted as the strongest limiting factors of g_m, but these anatomical traits are highly variable among species (Evans et al., 2009; Terashima et al., 2011; Tosens et al., 2012b). In addition, recent studies suggest that chloroplast thickness is also an important barrier limiting diffusion of CO₂ to Rubisco (Tosens et al., 2012a,b, 2016; Peguero-Pina et al., 2012; Tomás et al., 2013). The reduction of photosynthesis due to g_m can be about 25% for mesophytic species and up to 75% in evergreen species (Niinemets et al., 2011). The latter have more robust leaves, e.g. thicker cell walls due to their adaptations to their specific environmental stressors (Niinemets, 2016). Contrarily, ferns and allies have seemingly soft leaves and low leaf mass per area (LMA), but the extent of the photosynthetic limitation by g_m and net assimilation are in a similar range to that reported for sclerophyllous angiosperms due to their very thick mesophyll cell walls and very low S_c/S (Niinemets et al., 2009,b,c; Tosens et al., 2016). That is, g_m and its underlying traits cannot be simply extended across plant groups, and additional factors such as evolutionary age can play an important role in its determination.

Across spermatophytes g_m is lowest in gymnosperms (Flexas et al., 2012). Six-fold variation in g_m has been shown among the 13 conifer species studied so far (Warren et al., 2003; De Lucia et al., 2003; Manter and Kerrigan, 2004; Black et al., 2005; Mullin et al., 2009; Peguero-Pina et al., 2012, 2016). Collectively, the available data suggest that g_m is an important limiting factor of photosynthesis across and within conifer species. Despite its undoubted importance, only Peguero-Pina et al. (2012, 2016) have investigated g_m together with the underlying structural correlates. Therefore, integrative approaches are needed to characterize the nature of g_m and its importance in controlling realized photosynthesis rates in gymnosperms.

The leaf economics spectrum (LES) is a dimension of ecological variation reflecting differences across species in the cost of the investment in a unit of leaf area and the return on that investment (Wright et al., 2004). Despite the broad use of LES relationships in generalizing global leaf structure–function relationships, the morpho-physiological basis underlying given trade-offs are poorly understood, especially for species placed at the low-return end (Shipley et al., 2006; Niinemets et al., 2009a,b). These species are characterized by high LMA and robust structure, and therefore the realized photosynthetic rates are modified in an important way by leaf morphology (Flexas et al., 2008; Hassiotou et al., 2009; Niinemets et al., 2011; Tosens et al., 2012b). For example, high LMA could be associated with high net assimilation rate (A_area) if its main driver is great thickness of mesophyll and high S_c/S, or with low A_area if it is connected with its underlying anatomical variations such as thick mesophyll cell walls (Hassiotou et al., 2009; Tomás et al., 2013). However, the integrative trait of LMA may fail for species like Australian Proteaceae, which have mesophytic mesophyll tissue embedded in highly sclerophytic tissue, or in ferns and allies, which have low LMA but high T_cwm resulting in low photosynthesis (Niinemets et al., 2009c; Tosens et al., 2012b, 2016). Understanding the underlying ultrastructural traits controlling the global LMA–photosynthesis–nitrogen relationships is inescapable for understanding photosynthetic patterns across Earth’s ecosystems.

The reasons for lower photosynthesis rates and intrinsic water use efficiency (WUE_i) in gymnosperms are currently poorly known due to lack of studies separating mesophyll and stomatal diffusional and mesophyll biochemical photosynthetic limitations. Information about g_m with its underlying structural traits is especially limited. Here we set out to characterize the spectrum of photosynthetic strategies and related physiological and morphological traits in gymnosperms positioned at the lower return end of the leaf economics spectrum based on 11 gymnosperm and two evolutionarily older species, Psilotum nudum and Selaginella uncinata, in order to enhance the evolutionary context. Overall, the included species are evolutionarily old with a phylogenetic age extending from 306 million years for Psilotaceae to 75 million years for the genus Podocarpus (Pryer et al., 2004; Biffin et al., 2012). Metasequoia glyptostroboides, Cycas revoluta, Macrozamia riedlei and Araucaria heterophylla can even be regarded as living fossils as their morphology and habitat have a high resemblance to fossils dated to the Mesozoic (>110 My ago) and even to the late Paleozoic (300 My ago) (e.g. Norstog and Nicholls, 1997; Rydin et al., 2004; Zhang et al., 2015). The specific aims of the study were (i) to analyse the photosynthetic limitations to understand if diffusional limitations, especially g_m, are the most substantial constraints in evolutionarily old plants; (ii) to assess which structural traits are responsible for low CO₂ diffusion conductance in evolutionarily old species; and (iii) to understand the morpho-physiological basis underlying LES traits in evolutionarily old species.

Materials and methods

Plant material and growth conditions

Thirteen evolutionarily old species (Fig. 1 and Supplementary Table S1 at JXB online) with widely varying shape, size, longevity and structure of photosynthetic organs covering a broad range of evolutionary ages were included in the analysis. Out of the selected species, 11 (Araucaria heterophylla, Cupressus sempervirens, Cycas revoluta, Ephedra minuta, Macrozamia riedlei, Metasequoia glyptostroboides, Picea abies, Pinus sylvestris, Podocarpus alpinus, Podocarpus nivalis and Taxus baccata) were gymnosperms from three of the four gymnosperm divisions. Two primitive herbaceous plant species (a whisk fern, Psilotum nudum, and a clubmoss, Selaginella uncinata) were also included.

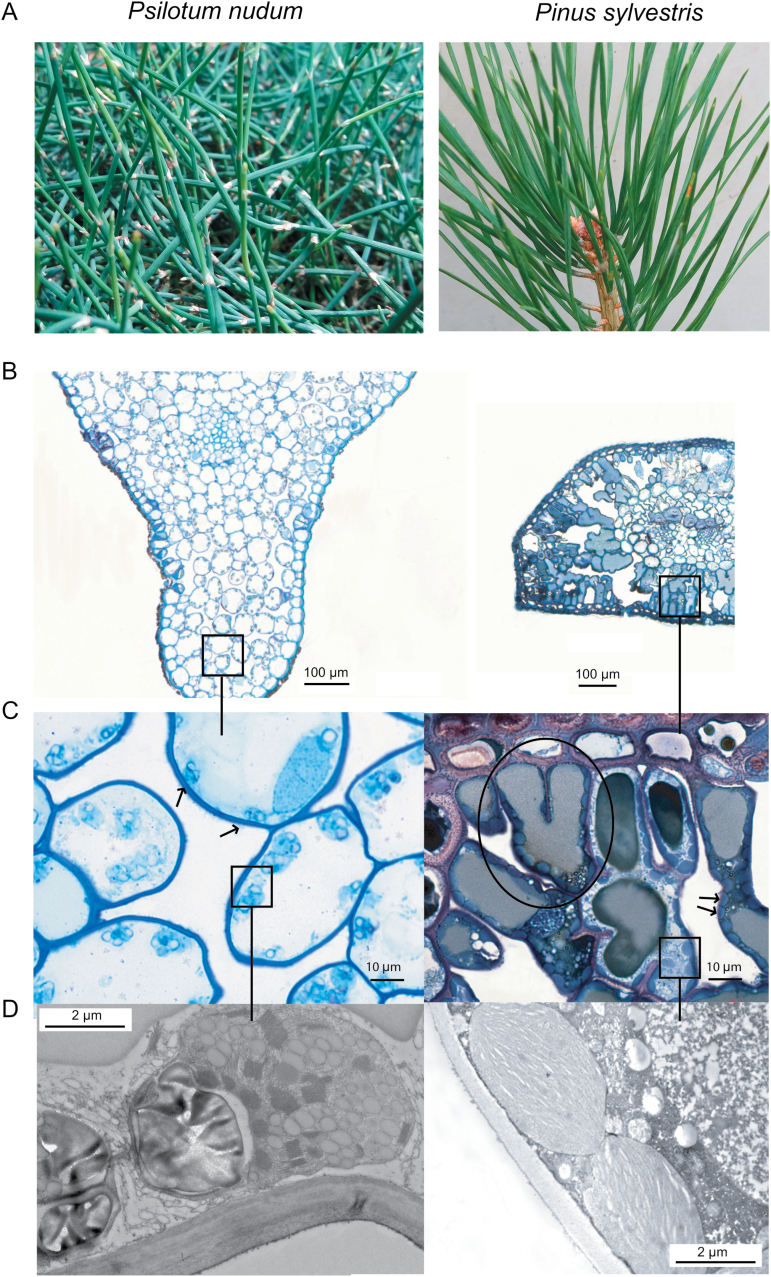
Fig. 1.

(A, B) Photographs (A) and cross-sections (B) of Psilotum nudum (left) and Pinus sylvestris (right) to illustrate different leaf internal anatomies. (C,D) Low (P. nudum, left) and high (P. sylvestris, right) chloroplast area exposed to intercellular airspace (S_c/S). Arrows in (C) indicate sparsely (left) and tightly packed chloroplasts (right). The P. sylvestris cross-section exhibits lobed cells (circled in C).

Five-month-old saplings of M. glyptostroboides, P. alpinus, P. nivalis, S. uncinata and T. baccata were obtained in October 2014 from a local nursery and transferred to a controlled-conditions phytotron, where they grew for 2–4 months before the measurements were begun. Other species were grown in the phytotron from seeds or seedlings brought from their country of origin (see Supplementary Table S1). All measured leaves emerged and matured in the phytotron conditions. Relative humidity was maintained at 60% and air temperature at 25 °C/22 °C (day/night). Light was provided by high pressure sodium lamps (400 W, E40 tubular clear, Beijing Luxram Lighting Ltd, China) for a 13 h photoperiod. The photosynthetic photon flux density (Q) incident to the plants was maintained at 1000 µmol m^–2 s^–1 reflecting the natural growth light conditions of the species (Supplementary Table S1). Plants were watered every second day with tap water and fertilized with soluble fertilizer once a week (Substral Miracle for evergreens, N:P₂O₅:K₂O:MgO 23:9:12:2 with microelements). In all cases, fully mature non-senescent foliage was used for the measurements.

Foliage gas exchange measurements and estimation of mesophyll conductance

Simultaneous gas exchange and fluorescence measurements were conducted with a GFS-3000 portable photosynthesis system (Walz GmbH, Germany). Foliage elements were arranged side by side in the leaf chamber to avoid any overlap and a digital photograph was taken for estimation of the exact projected foliage area enclosed in the chamber after its closure. In all measurements, vapor pressure deficit was kept at ca 1.5 kPa, and leaf temperature, measured with a thermocouple, at 25 ºC. Leaf net photosynthesis, the steady-state net photosynthesis rate under saturating Q of 1000 µmol m^–2 s^–1 (90% red and 10% blue light) and 400 µmol CO₂ mol^–1 (atmospheric CO₂ concentration, C_a), was recorded after the stomata opened and leaf gas exchange rates reached maximum steady state, 30–60 min after the enclosure of foliage in the chamber. Net assimilation vs. ambient CO₂ response curves were measured at a Q of 1000 µmol m^–2 s^–1 by varying C_a between 50 and 2000 µmol CO₂ mol^–1. After each steady-state net assimilation rate had been estimated, the steady-state fluorescence level (F) was recorded and a saturating pulse was given by the leaf chamber fluorimeter of the GFS-3000 system (PAM-fluorometer 3055-FL) to measure the maximum fluorescence yield (F_m′) and estimate the effective photosystem II quantum yield (Φ_PSII) as (F_m′–F)/F_m′ (Genty et al., 1989). The area of the leaf chamber was 8 cm². Once the measurements for a CO₂ response curve were completed, the light was switched off and the mitochondrial respiration rate (R_n) was measured after a minimum of 30 min of dark adaptation. g_s and intercellular CO₂ concentration (C_i) were calculated according to von Caemmerer and Farquhar (1981).

Mesophyll conductance was calculated according to Harley et al. (1992):

$$g_{\text{m}}=\frac{A_{\text{area}}}{C_{\text{i}}-\frac{\Gamma *J_{\text{ETR}}+8(A_{\text{area}}+R_{\text{d}})}{J_{\text{ETR}}-4(A_{\text{area}}+R_{\text{d}})}}$$ (1)

where A_area is the net assimilation rate, J_ETR is the rate of photosynthetic electron transport derived from chlorophyll fluorescence measurements, C_i is the CO₂ concentration in sub-stomatal cavities, R_d is the rate of non-photorespiratory respiration in the light and Γ* is the hypothetical CO₂ compensation point without R_d. R_d was estimated as half of R_n (Niinemets et al., 2005). This common adaptation is supported by previous experimental observations (Villar et al., 1995; Piel et al., 2002). Γ* was taken as 42.9 μmol mol^–1 at 25 °C (Bernacchi et al., 2001) as it has been shown before on vastly variable plant functional groups and g_m values that there is no significant difference between g_m calculated with Γ* according to Galmés et al. (2005) and Bernacchi et al. (2001) (Tomás et al., 2013). J_ETR was estimated from non-photorespiratory conditions (2% oxygen) from an A–C_i curve, although the calculations of g_m were relatively insensitive to moderate variations in J_ETR (<0.5%; see Niinemets et al., 2005). Therefore, the main assumption of Harley’s variable J method was not breached. The data were corrected for chamber leaks according to Flexas et al. (2007a) and Rodeghiero et al. (2007) using empty chamber measurements. Leaf absorption was measured with an integrating sphere (leaf absorption coefficient varied between 0.84–0.90). Gaskets were changed regularly, and modelling paste and paraffin film were used with thick leaves to ensure no leakage. Mesophyll conductance was calculated from measurements of net assimilation rate over the C_i range of 150–350 μmol mol^–1, because the g_m values are stable over this range and its estimates are relatively insensitive to minimal Γ*, R_d and A errors (Harley et al., 1992; Niinemets et al., 2006). WUE_i was defined as A_area/g_s (Flexas et al., 2013). As some plants studied here have small leaves or needles growing on several sides of the branch, not all of these were perpendicular to the light source. However, this is also the case for when they are growing in natural conditions as the branches were positioned in the same direction to the light source as they had grown.

Additionally, the one-dimensional within-leaf gas diffusion model of Niinemets and Reichstein (2003) was applied to provide an anatomically based estimate of g_m as in Tosens et al. (2012b) and from A–C_i curves as in Ethier and Livingston (2004).

Quantitative limitation analyses of A_area and partial limitations of g_m

The relative controls on A_area imposed by stomatal conductance (l_s), mesophyll conductance (l_m), and biochemical capacity (l_b) were calculated following the Grassi and Magnani (2005) approach, as has been successfully used for a large number of highly variable species from lycophytes, horsetails and ferns to Australian sclerophylls in Tomás et al. (2013) and Tosens et al. (2012b, 2016). These three values sum to 100% and characterize the extent to which any of the three limitations curbs photosynthesis at the given values of the other two. The contribution of different components of cellular resistance to total cellular resistance to CO₂ diffusion was estimated from the anatomical model following Tosens et al. (2016). This share of limitation (l_i) by different liquid phase components was calculated as:

$$l_{\text{i}}=\frac{g_{\text{m}}}{g_{\text{i}}\cdot \frac{S_{\text{c}}}{S}}$$ (2)

where l_i is the limitation by the cell wall, the plasmalemma, cytosol, chloroplast envelope and stroma, and g_i refers to the diffusion conductance of each corresponding diffusion pathway. The limitation of each cellular component was scaled up with S_c/S.

Estimation of leaf dry mass per area and nitrogen content

Foliage used for gas exchange measurements was further used for anatomical, morphological and chemical measurements. Individual foliage elements (leaves, needles or scales) were removed from the twigs and scanned at 300 dpi. The foliage was thereafter oven-dried at 70 °C for 48 h, and its dry mass was determined. Leaf projected area was determined from scanned images with ImageJ 1.48v software (Wayne Rasband/NIH, Bethesda, MD, USA) or calculated from the measured length and widths of sides measured with digital precision calipers (Mitutoyo CD-15DC, Mitutoyo Ltd, Andover, UK) for needles and cladodes (Niinemets et al., 2007). From these measurements, LMA and density (D_leaf=LMA/T_leaf) were calculated (Niinemets, 1999; Poorter et al., 2009). Nitrogen content per dry mass (N_mass) was determined by the dry combustion method with a Vario MAX CNS elemental analyser (Elementar, Hanau, Germany), and leaf nitrogen content per area as N_mass/LMA.

Light and electron microscopy

A sub-sample of leaves used for gas exchange measurements was taken for leaf anatomical measurements. Light and electron microscopy sample preparation and analyses followed Tosens et al. (2012b). Six samples were taken from three specimens of each species. Foliage cuts of approximately 6 × 4 mm (or width of the needle or cladode according to species) were taken from intercostal areas. In C. sempervirens scales and in S. uncinata whole leaves were stripped from the branches with tweezers. The plant material was infiltrated in a fixation buffer (3% glutaric aldehyde and 2% paraformaldehyde in 0.1 M phosphate buffer, pH 6.9) under vacuum in a syringe. The samples were post-fixed for 1 h in an osmium tetroxide solution (2%) and dehydrated in a series of increasingly stronger ethanol solutions and embedded in LR white resin (Electron Microscopy Sciences, Hatfield, PA, USA) according to standard procedures (Tosens et al., 2012b). Subsequently, the samples were polymerized in an oven at 60 °C for 26 h. Semi-thin cross-sections of 1 µm for light microscopy, and ultra-thin cross-sections of 70 nm were prepared by an ultramicrotome (Leica EM UC7, Leica Vienna, Austria) for transmission electron microscopy (TEM). The semi-thin sections were stained with toluidine blue for light microscopy, and the sections for TEM were stained with lead citrate and then mounted on formvar–carbon covered copper meshes (Electron Microscopy Sciences). Stained semi-thin sections were viewed in bright field ensuring that all sections were ideally straight with a Nikon Eclipse E600 microscope with phase contrast at magnifications of ×100, ×200 and ×400 and photographed with a Nikon 5 MP digital microscope camera DS-Fi1 (Nikon Corp., Kyoto, Japan). A Philips Tecnai 10 TEM (FEI, Eindhoven, Netherlands) was used to view the ultra-thin sections with the accelerating voltage of 80 kV and magnification between ×1800 and ×14 000. Between five and seven fields of view per sample were measured.

From digital images the following parameters were measured: fraction of intercellular airspace (F_ias), leaf thickness from adaxial to abaxial cuticle (T_leaf), mesophyll thickness excluding vascular bundles (T_mes), cytoplasm thickness (T_cyt), chloroplast thickness (T_chl), mesophyll cell wall thickness (T_cwm), chloroplast and mesophyll cell wall area from which S_c/S and mesophyll area exposed to intercellular airspace (S_m/S) were calculated according to Evans et al. (1994) (Table 2). These characteristics were measured for at least ten spongy and ten palisade parenchyma cells and tissue-volume weighted averages were calculated in the species with distinctive separation of mesophyll to spongy and palisade parenchyma. Thirty cells were analysed for every specimen. Light and electron micrographs were analysed with ImageJ 1.48v software.

Table 2.

Leaf anatomical parameters

Data are ±SE; n=3–5. F_ias, average fraction of intercellular airspace; T_cwm, mesophyll cell wall thickness; T_cyt, cytoplasm thickness; T_chl, chloroplast thickness.

Species	F ias	T cwm (μm)	T cyt (μm)	T chl (μm)
Selaginella uncinata	0.30 ± 0.03	0.22 ± 0.03	0.382 ± 0.033	2.359 ± 0.050
Psilotum nudum	0.15 ± 0.01	1.074 ± 0.074	0.177 ± 0.043	4.1 ± 0.3
Araucaria heterophylla	0.37 ± 0.09	0.67 ± 0.08	0.09 ± 0.01	2.727 ± 0.092
Cycas revoluta	0.20 ± 0.01	0.34 ± 0.05	0.215 ± 0.093	5.36 ± 0.10
Macrozamia riedlei	0.20 ± 0.03	0.37 ± 0.02	0.218 ± 0.009	3.918 ± 0.041
Ephedra minuta	0.21 ± 0.04	0.731 ± 0.010	0.299 ± 0.065	3.19 ± 0.12
Metasequoia glyptostroboides	0.29 ± 0.02	0.26 ± 0.05	0.091 ± 0.020	1.97 ± 0.06
Pinus sylvestris	0.21 ± 0.02	0.32 ± 0.08	0.089 ± 0.005	2.25 ± 0.22
Picea abies	0.18 ± 0.04	0.58 ± 0.05	0.070 ± 0.024	2.79 ± 0.11
Taxus baccata	0.30 ± 0.02	0.876 ± 0.042	0.087 ± 0.003	3.1 ± 0.2
Podocarpus alpinus	0.223 ± 0.008	1.18 ± 0.09	0.088 ± 0.009	2.09 ± 0.11
Podocarpus nivalis	0.26 ± 0.06	1.22 ± 0.09	0.092 ± 0.002	2.1 ± 0.2
Cupressus sempervirens	0.063 ± 0.003	0.91 ± 0.08	0.30 ± 0.09	2.81 ± 0.25

Statistical analyses

For each species, all measurements were replicated at least with three individual plants. Linear and non-linear regression analyses, t-tests and ANCOVA were used to examine the relationships among the traits and test for trait differences among species using Statistica 10.0 (StatSoft Inc., Tulsa, OK, USA). The choice between linear and non-linear models depended on the shape of the relationships, degree of explained variance and normality of data and residuals, and models providing the greatest r² and lowest deviations from normality of residuals were used. Due to high variability of foliage shapes and structures, individual species were occasionally outliers in statistical relationships, especially in relationships exploring the effects of individual underlying traits on composite variables. For instance, some correlations were significant when the gymnosperms were considered, but not when the spore-bearing species were included. We denote these and analogous outliers separately in bivariate statistical relationships.

Phylogenetic analyses

Sequences of the plant barcode genes maturase K (matK; a gene that encodes an intron splicing protein) and RbcL (a gene that encodes the large subunit of Rubisco; both genes are in the chloroplastic DNA; Hollingsworth et al., 2009) were extracted from NCBI GenBank (www.ncbi.nlm.nih.gov, last accessed July 2015). This information was not available for Macrozamia riedlei, so the closest available relative, M. moorei, was used. Phylogenetic analyses were conducted and phylogenetic trees were created by the neighbor-joining method using standard procedures in MEGA6 (Tamura et al., 2013). The maximum composite likelihood model was used for estimates of evolutionary divergence (Tamura et al., 2004), and the maximum likelihood method based on the Tamura–Nei model (Tamura and Nei, 1993) was used to create phylogenetic topology with the superior log-likelihood value. The evolutionary age of genera was based on previously published literature (Table 1: smaller numbers indicate evolutionarily closer species). This information was correlated with the study parameters using t-tests and ANCOVA. The Akaike information criterion was used as a measure of the relative quality of the multiple linear models used here.

Table 1.

Phylogenetic ages of the genera, growth form, leaf habit and distances of studied taxa and estimates of evolutionary divergence

Species are in the order of their evolutionary age. Evolutionary divergence is defined as the number of base substitutions per site between sequences.

Species (abbreviation)	Family	Evolutionary age of genus (My)	Growth form	Evolutionary divergence
Selaginella uncinata (S.u.)	Selaginellaceae	405 (Lang et al., 2010)	Herb	S.u.	Ps.n.	A.h.	C.r.	Ma.r.	E.m.	Me.g.	Pin.s.	Pic.a.	T.b.	Po.a.	Po.n.
Psilotum nudum (Ps.n.)	Psilotaceae	306 (Pryer et al., 2004)	Herb	0.87
Araucaria heterophylla (A.h.)	Araucariaceae	197 (Knapp et al., 2007)	Tree	0.76	0.61
Cycas revoluta (C.r.)	Cycadaceae	175 (Magallón and Sanderson, 2005)	Tree	0.69	0.59	0.23
Macrozamia riedlei (Ma.r.)	Zamiaceae	175 (Magallón and Sanderson, 2005)	Tree	0.67	0.61	0.23	0.094
Ephedra minuta (E.m.)	Ephedraceae	168 (Rydin et al., 2004)	Shrub	1.23	0.85	0.68	0.67	0.70
Metasequoia glyptostroboides (Me.g.)	Cupressaceae	146 (Hemsley and Poole, 2004)	Tree	0.87	0.66	0.18	0.27	0.27	0.71
Pinus sylvestris (Pin.s.)	Pinaceae	140 (Wang et al., 2000)	Tree	0.80	0.77	0.22	0.30	0.29	0.67	0.25
Picea abies (Pic.a)	Pinaceae	130 (Wang et al., 2000)	Tree	0.79	0.69	0.19	0.27	0.26	0.68	0.23	0.080
Taxus baccata (T.b.)	Taxaceae	120 (Cheng et al., 2000)	Tree	0.84	0.65	0.15	0.26	0.24	0.73	0.14	0.26	0.22
Podocarpus alpinus (Po.a.)	Podocarpaceae	75 (Biffin et al., 2012)	Shrub	0.88	0.71	0.20	0.29	0.29	0.75	0.24	0.32	0.31	0.25
Podocarpus nivalis (Po.n)	Podocarpaceae	75 (Biffin et al., 2012)	Shrub	0.87	0.71	0.20	0.28	0.29	0.75	0.24	0.31	0.30	0.24	0.004
Cupressus sempervirens (Cu.s.)	Cupressaceae	75 (Stewart, 1993)	Tree	0.88	0.70	0.19	0.25	0.29	0.70	0.085	0.28	0.26	0.16	0.26	0.26

Results

Variation in leaf anatomy and morphology in evolutionarily old species

In order to understand the mesophyll diffusional limitations to photosynthesis, a complete structural and ultrastructural analysis was performed of the photosynthetic organs of all the species. A large variability was observed in their macroscopic anatomy (Fig. 1A), but also structural and ultrastructural parameters (Figs 1B–D and 2), e.g. a P. sylvestris cross-section exhibited lobed cells, increasing mesophyll surface area exposed to the intercellular airspace (Fig. 1C). LMA varied about 7-fold between species, from 45 ± 12 g m^–2 in S. uncinata to 308 ± 22 g m^–2 in C. sempervirens. Leaf density (D_leaf) and thickness varied 16- and 24-fold, respectively. T_cwm varied 5.5-fold (from 0.2 ± 0.05 µm in S. uncinata to 1.2 ± 0.37 µm in P. nivalis), S_c/S varied 3.5-fold (from 4.9 ± 0.47 m² m^–2 in S. uncinata to 17.1 ± 0.62 m² m^–2 in P. sylvestris), and S_m/S varied 2.9-fold (6.1 ± 0.18 to 17.5 ± 0.72 m² m^–2). The variation in LMA was attributed to variation in both of its components, but there was a stronger positive relationship with D_leaf (excluding S. uncinata due to its extremely thin leaves) than T_leaf (Fig. 3A, B). However, there was no correlation between LMA and mesophyll cell wall thickness (Fig. 3C). There was a strong positive relationship between S_c/S and S_m/S (see Supplementary Fig. S1A), but neither of them was related to LMA (Fig. 3D for S_c/S; r²=0.077, P=0.36 for the correlation with S_m/S). Similarly, S_m/S was not correlated to fraction of intercellular airspaces, F_ias (r²=0.007; P=0.78). S_c/S was unrelated to T_mes (Supplementary Fig. S1B), but S_m/S had a positive correlation (Supplementary Fig. S1C). However, this correlation was not significant when only gymnosperms were included (r²=0.068; P=0.37).

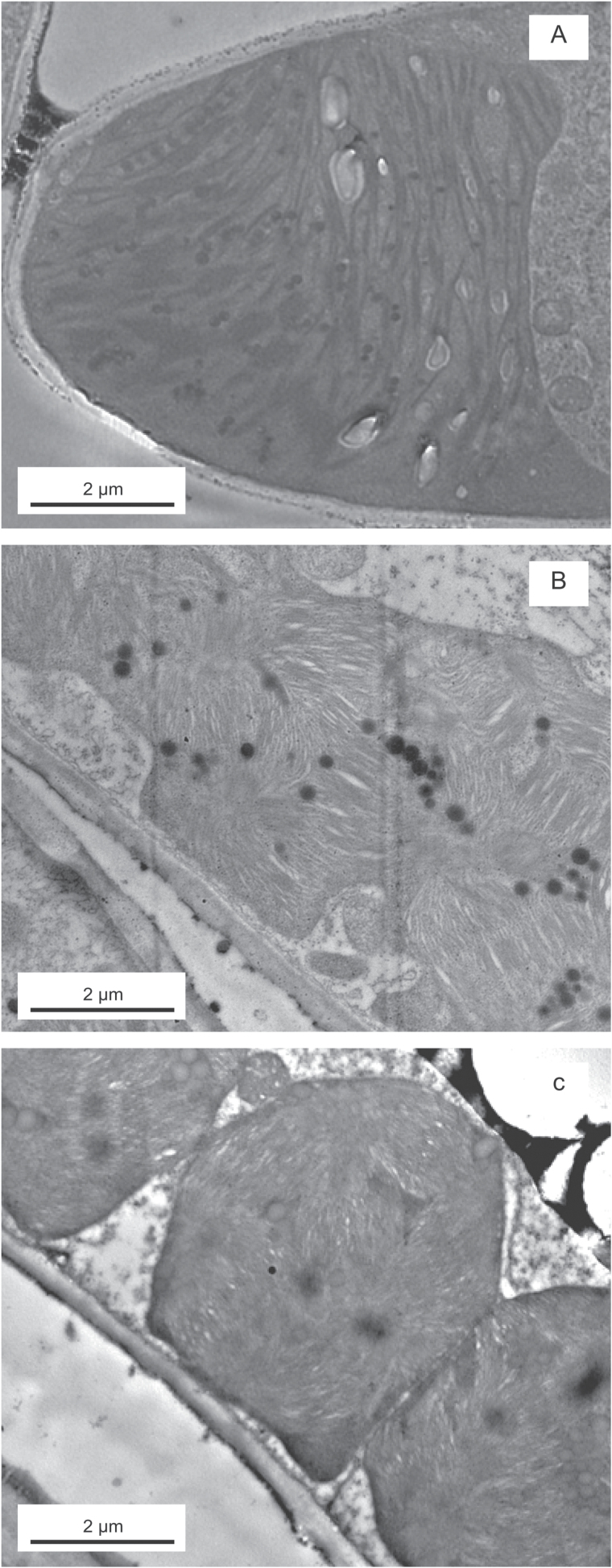
Fig. 2.

Ultrathin transmission electron microscopy cross-sections showing species with atypical chloroplast shapes and sizes: (A) Selaginella uncinata, (B) Cycas revoluta and (C) Macrozamia riedlei.

Fig. 3.

Leaf dry mass per area (LMA) in relation to (A) leaf density (D_leaf), (B) leaf thickness (T_leaf), (C) mesophyll cell wall thickness (T_cwm), and (D) chloroplast surface area exposed to intercellular airspaces (S_c/S). Each data point corresponds to one species (n=3–5). The non-gymnosperms are marked as open circles, while the only deciduous conifer, Metasequoia glyptostroboides, is marked as a filled square. Excluded species are marked with the species’ name. Error bars show average±SE of all presented species. Note that some standard errors are so small that they are not visible under the data points. Data were fitted by linear regression (all are significant at P<0.05).

Interspecific variation in photosynthetic capacity and its relationships with diffusional and structural determinants

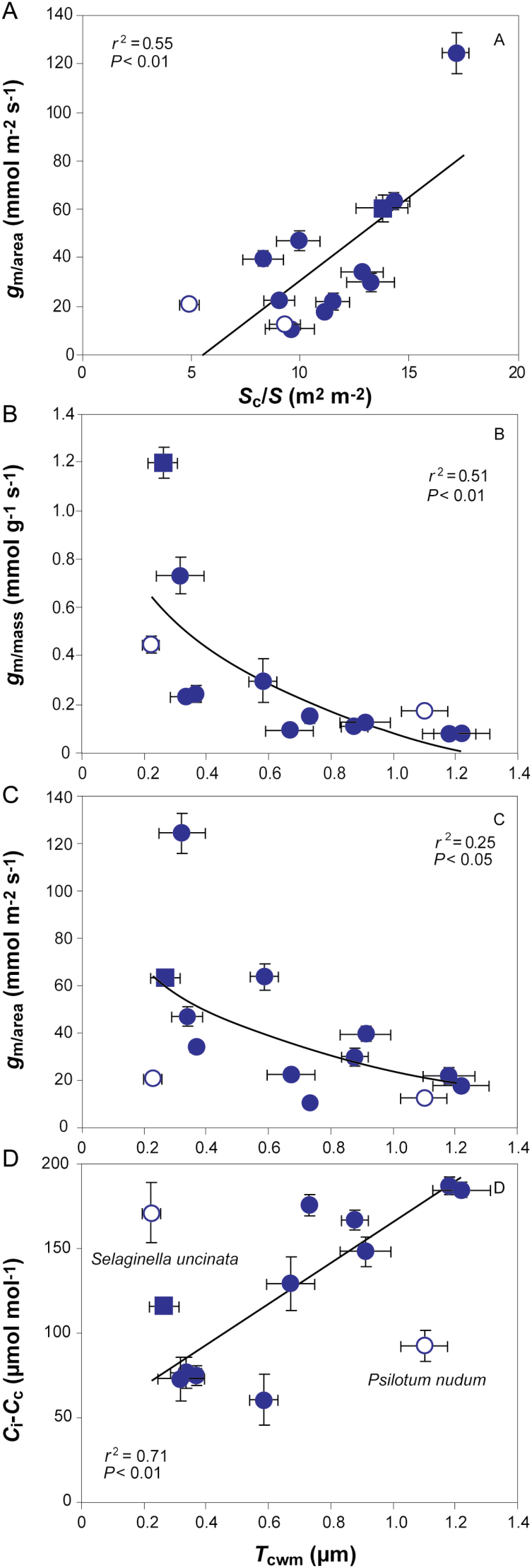
Area- and mass-based net assimilation (A_mass) varied about 5- and 8-fold, respectively (from 2.1 ± 0.34 µmol m^–2 s^–1 in P. nudum to 11.0 ± 0.78 µmol m^–2 s^–1 in P. sylvestris, and from 21 ± 3.9 nmol m^–2 s^–1 in C. revoluta to 165 ± 9 nmol m^–2 s^–1 in M. glyptostroboides). Mesophyll conductance per unit leaf area (g_m/area) varied over 12-fold (from 10 ± 2.1 mmol m^–2 s^–1 in Ephedra minuta to 124 ± 9 mmol m^–2 s^–1 in P. sylvestris) and mass-based g_m (g_m/mass) over 15-fold (from 0.08 ± 0.005 mmol g^–1 s^–1 in P. nivalis to 1.20 ± 0.06 mmol g^–1 s^–1 in M. glyptostroboides).

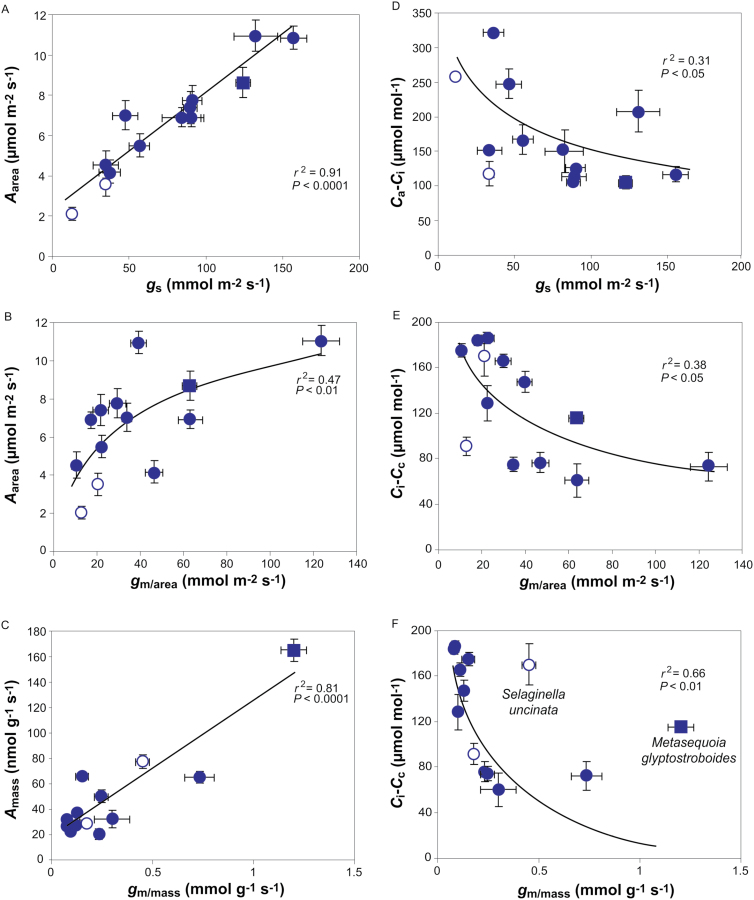
A _area depended strongly on g_s (Fig. 4A). Importantly, A_area scaled positively with g_m/area (Fig. 4B), but there was stronger positive correlation between A_mass and g_m/mass (Fig. 4C), which was significant even with the exclusion of M. glyptostroboides (r²=0.42; P=0.016). A similar strength negative curvilinear relationship was found between C_a–C_ivs g_s (Fig. 4D) and the CO₂ drawdown from the intercellular airspace to chloroplasts (C_i–C_c) vs g_m/area (Fig. 4E). However, a stronger relationship was found between C_i–C_cvs g_m/mass when S. uncinata and M. glyptostroboides were excluded (Fig. 4F).

Fig. 4.

(A, B) Area-based net assimilation (A_area) in relation to (A) stomatal conductance (g_s) and (B) mesophyll conductance per area (g_m/area). (C) Mass-based photosynthesis (A_mass) in relation to mass-based mesophyll conductance (g_m/mass). (D) The draw-down from the atmosphere to the intercellular airspaces (C_a–C_i) in relation to g_s. (E, F) The draw-down from intercellular airspaces to chloroplasts (C_i–C_c) in relation to (E) g_m/area and (F) g_m/mass. Data in (B) were fitted by non-linear regression of the form y=2.73ln(x)–2.81; data in (D) of the form y=–53ln(x)+389; data in (E) of the form y=–36ln(x)+252; and data in (F) of the form y=–30ln(x)+80. Data are presented as in Fig. 3.

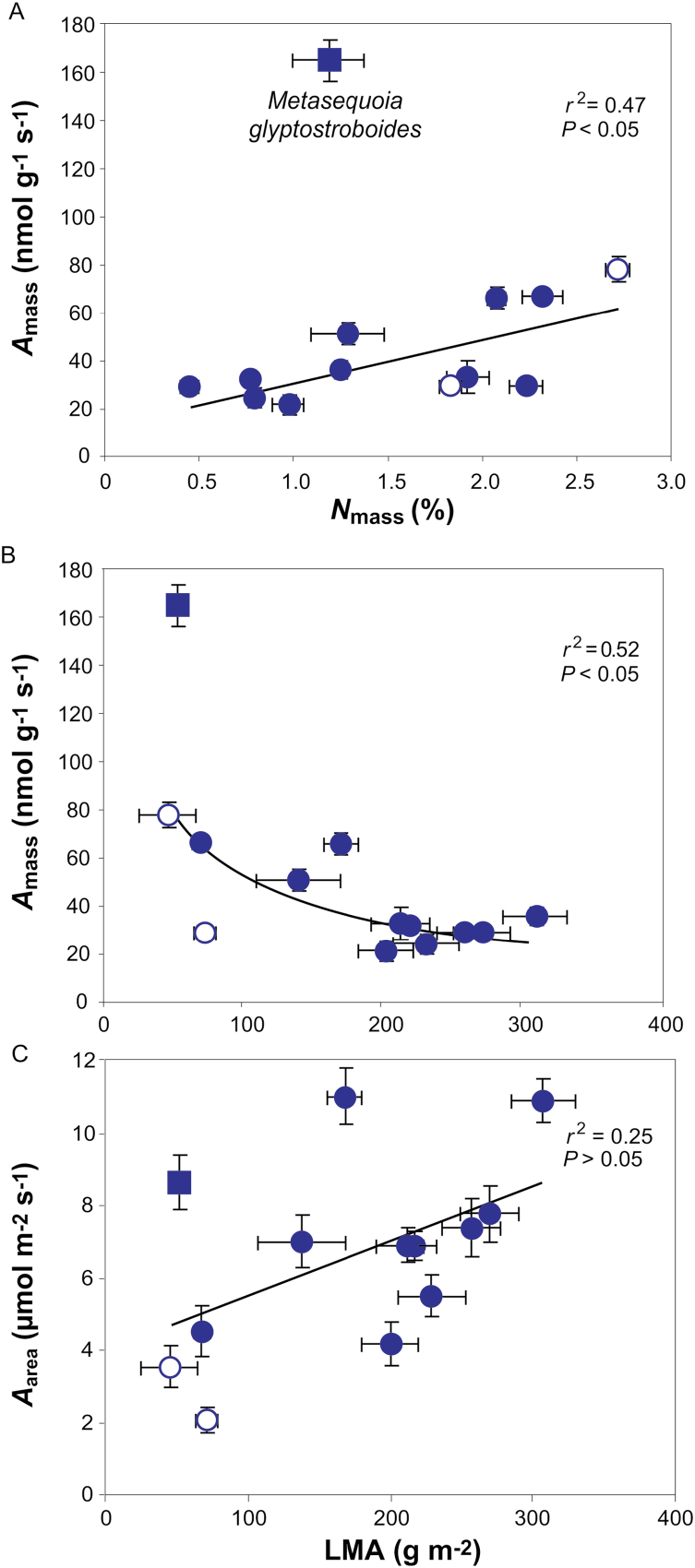
In addition to large variations in LMA and its components, nitrogen content per dry mass (N_mass) varied 6-fold (from 0.45 ± 0.02% to 2.72 ± 0.07%) and area-based nitrogen (N_area) varied 12-fold (0.6 ± 0.01 to 6.1 ± 0.09 g m^–2). A_mass scaled positively with N_mass, but the only deciduous conifer in this study, M. glyptostroboides, diverged from this relationship by having higher A_mass (Fig. 5A). There was no relationship between N_area and A_area (r²=0.20; P=0.12). Similarly, A_mass was negatively correlated with LMA, while there was no relationship between A_area and LMA (Fig. 5B, C).

Fig. 5.

Mass- and area-based net assimilation (respectively A_mass and A_area) in relation to (A) mass-based nitrogen content (N_mas) and (B, C) LMA. The data in (B) were fitted with a curvilinear regression of the form y=896x^–0.63. Data presentation and fitting in (A, C) are as in Fig. 3.

Analysis of the ultra-anatomical controls on g_m demonstrated that g_m/area was positively correlated with S_c/S. On the other hand, g_m/mass and g_m/area were negatively associated with T_cwm. C_i–C_c scaled positively with T_cwm across gymnosperms, but not across the whole sample (Fig. 6). T_cwm did not correlate with density (r²=0.030; P=0.55).

Fig. 6.

(A) The influence of chloroplast surface area exposed to intercellular airspaces (S_c/S) on mesophyll conductance (g_m/area). (B–D) The influence of cell wall thickness (T_cwm) on (B) mesophyll conductance per mass (g_m/mass), (C) mesophyll conductance per area (g_m/area), and (D) the draw-down from intercellular airspaces to chloroplasts (C_i–C_c). The data in (B) were fitted with a non-linear regression of the form y=–0.37ln(x)+0.09 and data in (C) of the form y=–26ln(x)+25. Data presentation and fitting are as in Fig. 3.

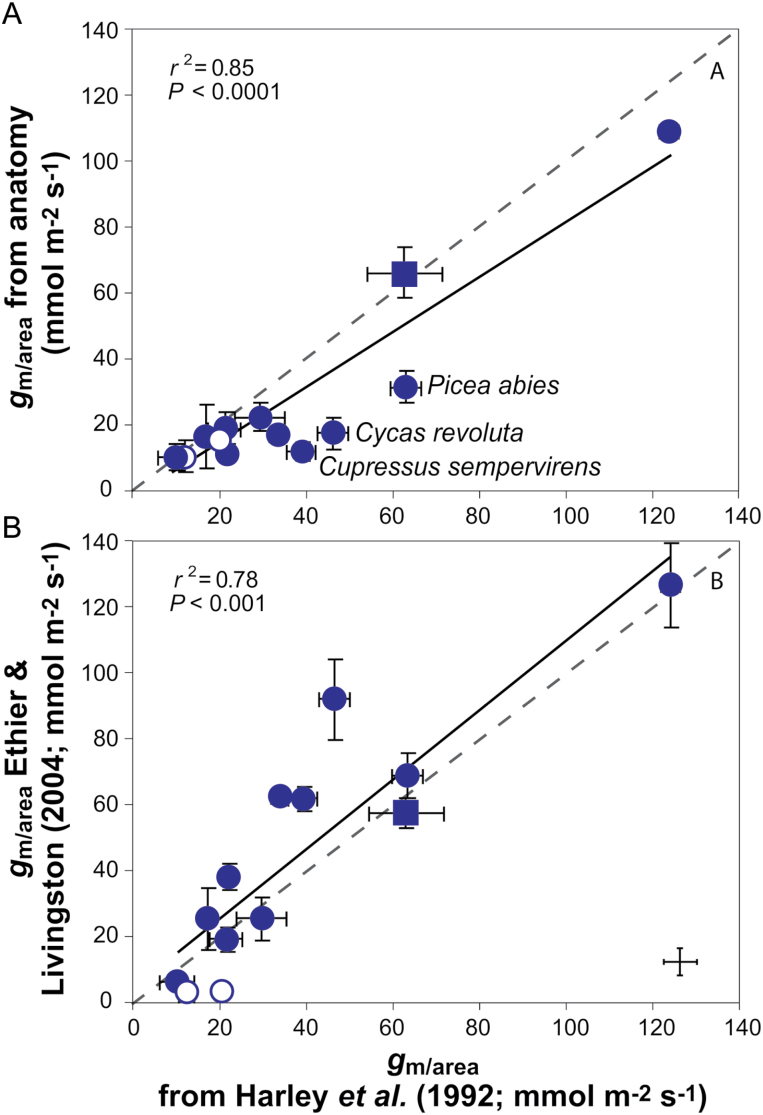
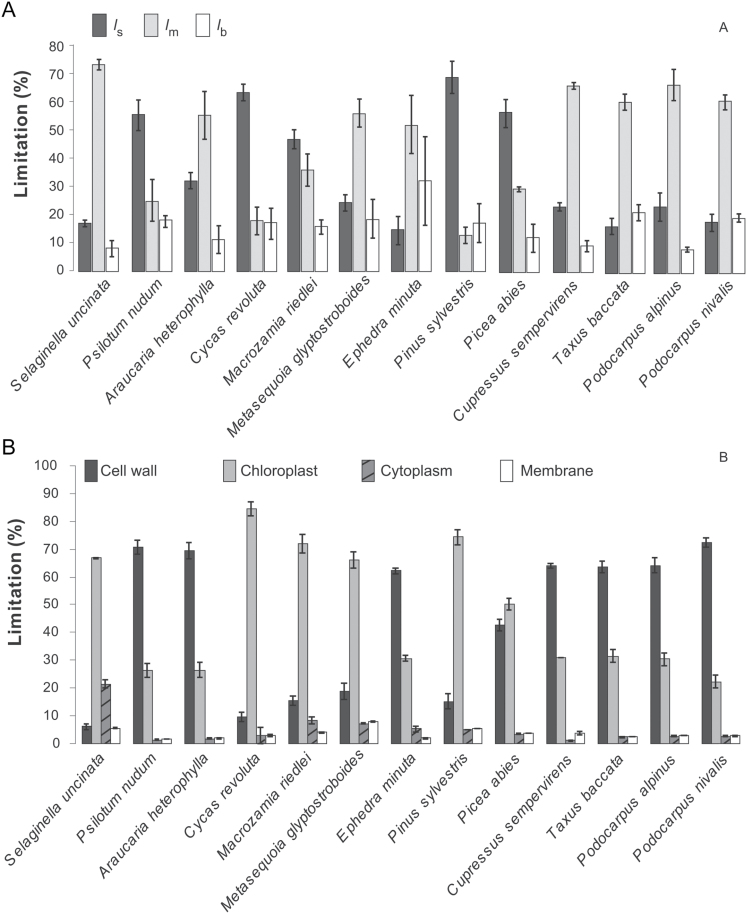
In addition to gas exchange–fluorescence methodology, g_m was estimated by two alternative methods: it was modeled from mesophyll anatomical traits by using the anatomical model of Niinemets and Reichstein (2003) and from A–C_i curves (Ethier and Livingston, 2004, Fig. 7). g_m calculated from anatomical measurements correlated better with the estimates obtained from gas exchange–fluorescence measurements than g_m obtained from A–C_i curves (average discrepancy between g_m from gas exchange–fluorescence was 27% with g_m from anatomy and 33% with g_m from Ethier and Livingston (2004)). Based on the quantitative limitation analysis, the photosynthetic capacity was strongly limited by both g_s (range 15–70%) and g_m/area (range 12–74%), while limited biochemical capacity (range 8–33%) restricted A_area less than stomata and mesophyll (Fig. 8A). With respect to the structural limitations of g_m, the estimated gas phase limitation inside the leaf was <1% of the total limitations for all the species (data not shown). Among all the components of liquid phase limitations, cytoplasm and membrane limitations played a minor role, whereas the predominant limitation was exerted by cell walls and chloroplast stroma (Fig. 8B and Table 2).

Fig. 7.

Comparison of g_m/area calculated based on Harley et al. (1992) with (A) g_m/area calculated from anatomical measurements according to Niinemets and Reichstein (2003) and (B) g_m/area calculated based on Ethier and Livingston (2004). Dashed lines represent 1:1 correlation. Data presentation and fitting are as in Fig. 3, but all species are included in the analyses. C. revoluta, C. sempervirens and P. abies were underestimated by the anatomical model.

Fig. 8.

(A) The percentage of assimilation limited by stomatal conductance (l_s), mesophyll conductance (l_m) and biochemistry (l_b). (B) The percentage of mesophyll conductance per area limited by liquid phase components: cell wall, chloroplast, cytoplasm and membrane. Error bars denominate standard errors (n=3–5). The species are in the order of evolutionary age.

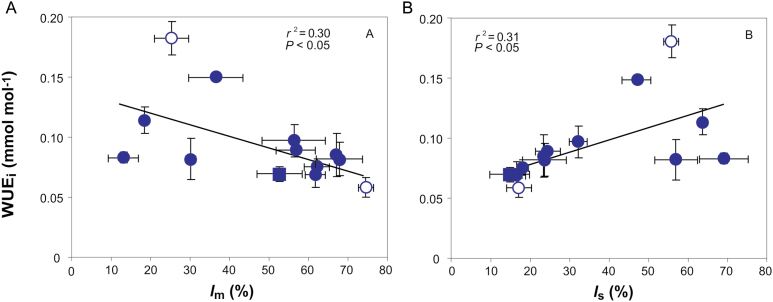
The intrinsic water use efficiency (WUE_i) varied ca 3-fold across species. It was negatively correlated with the share of photosynthesis limited by g_m/area (Fig. 9A). WUE_i also scaled positively with the photosynthesis limitation by stomata (Fig. 9B). When considered together, the interspecific variation in WUE_i was driven by both l_s and l_m (see Supplementary Table S2).

Fig. 9.

Correlations of intrinsic water use efficiency (WUE_i) with (A) the share of photosynthesis limited by mesophyll conductance (l_m) and (B) share of photosynthesis limited by stomatal conductance (l_s). Data presentation and fitting are as in Fig. 3.

The effect of divergence time on structure and physiology

In the given dataset, LMA and A_area were negatively correlated with the estimated evolutionary age of the genus (Supplementary Fig. S2 and Supplementary Table S3a; r²=0.45; p=0.012). However, g_m/area itself was not related to plant evolutionary age (r²=0.055; p=0.44) and g_m/area influenced A_area regardless of evolutionary age (Supplementary Table S3b). Nevertheless, the lowest mesophyll conductances were observed for the oldest genera (Ephedra: 10.3 mmol m^–2 s^–1; Psilotum: 12.5 mmol m^–2 s^–1; Selaginella: 20.5 mmol m^–2 s^–1). However, the highest average g_m/area was recorded for Pinus (124 ± 9 mmol m^–2 s^–1), although this genus is older than four others (Picea, Podocarpus, Taxus, Cupressus) in this study. In addition, g_s correlated negatively with the age of the genus (r²=0.41; P=0.017), but there was no significant correlation of WUE_i with the evolutionary age of the genus (r²=0.083; P=0.34).

Discussion

Structural and ultrastructural traits determining LES relationships in evolutionarily old species

LMA in our study depended on leaf density while its relationship with T_leaf was weaker (Fig. 3A, B) as shown by Tomás et al. (2013) across a variety of genera. Contrarily, LMA was more strongly related to T_leaf than to D_leaf in Australian sclerophylls (Niinemets et al., 2009c). The median value of LMA for evergreen gymnosperms is higher (230 g m^–2) than what was found here (214 g m^–2), but the minimum and maximum values here fall into the gymnosperm range (Poorter et al., 2009) placing them at the low end of LES characterized by overall robust foliage and low photosynthetic capacity (Wright et al., 2004).

Prior this study the highest T_cwm was recorded in ferns and allies: 0.81 µm (Tosens et al., 2016). The species here had even thicker mesophyll cell walls: up to 1.22 µm in P. nivalis. Both the average across the sample and across the gymnosperms (0.68 µm) were also very high compared with what has been previously found for non-stressed fully expanded leaves: from approximately 0.1–0.2 µm in annual to 0.4–0.5 µm in sclerophyllous species (Hanba et al., 2001; Terashima et al., 2006; Hassiotou et al., 2009; Tosens et al., 2012b, 2016; Tomás et al., 2013). On the other hand, values of S_c/S in our study were average in the majority of species as it varies from 1.6 to 32 m² m^–2 worldwide (Terashima et al., 2006; Peguero-Pina et al., 2012; Tosens et al., 2016) and the lowest values have been recorded in ferns (in the majority of species S_c/S<8) (Tosens et al., 2016), but across evergreen gymnosperms S_c/S had only been measured in Abies alba and A. pinsapo (17 and 32 m² m^–2, respectively) (Peguero-Pina et al., 2012). However, CO₂ diffusion to Rubisco is greatly enhanced if the cell walls are fully lined with chloroplasts, with S_c/S_m=1, a condition that in practice is rare (Terashima et al., 2011). The ratio was remarkably high in the gymnosperms studied here, being over 0.96 for five species (see Supplementary Fig. S1A).

The LMA components thickness and density alter leaf photosynthetic capacity in opposite directions (Niinemets, 1999). Leaf thickness often reflects a greater number of chloroplasts, higher S_c/S and S_m/S for CO₂ diffusion, and greater concentration of photosynthetic machinery, while greater density is associated with lower net assimilation due to increased cell wall resistance (Hanba et al., 1999; Niinemets, 1999; Terashima et al., 2006). Contrarily, Slaton and Smith (2002) studied a wide range of genera, but did not find a correlation between S_m/S and T_mes. Similarly, no relationship was found between S_c/S or S_m/S and T_mes across Australian sclerophylls (Tosens et al., 2012b). However, across the evolutionarily old species studied in this work, T_mes correlated positively with S_m/S, but regardless of the positive trend was not correlated with S_c/S (Supplementary Fig. S1B, C). However, the species with high S_m/S also had higher S_c/S (Supplementary Fig. S1A). This somewhat counterintuitive outcome results from the variability of S_c/S due to the spore-bearing plants in the sample as their S_c/S_m ratio was lower than average. These relationships were not significant, when these two species were excluded from the analyses. S_m/S and S_c/S depended on mesophyll architecture rather than T_mes or F_ias due to variability in density, size and shape of mesophyll cells (e.g. lobes; Fig. 1C) at a given thickness as was previously suggested by Tosens et al. (2012a). Likewise, this resulted in LMA not correlating with S_c/S (Fig. 3D).

Additionally, T_cwm was not related to LMA (Fig. 3C) or density as is often assumed (e.g. Syvertsen et al., 1995) showing that T_cwm may not vary with total leaf tissue density or other leaf tissue’s cell wall thicknesses (Tosens et al., 2012b). Collectively, these results suggest that widely varying combinations of leaf anatomical traits occur at given values of LMA, and detailed anatomical studies are needed to relate g_m to mesophyll structure.

Structural modifications of photosynthesis and mesophyll diffusion conductance

A _area and g_s were correlated and comparable to those found in spore-bearing plants and gymnosperms (James et al., 1994; Equiza et al., 2006; Franks, 2006; La Porta et al., 2006; Pardo et al., 2009; Zhang et al., 2015; Tosens et al., 2016). Flexas et al. (2012) set an average g_m slightly above 100 mmol m^–2 s^–1 for conifers, and studies have shown a wide variation from as low as 18 up to 110 mmol m^–2 s^–1 in evergreen gymnosperms (Warren et al., 2003; De Lucia et al., 2003; Manter and Kerrigan, 2004; Black et al., 2005; Mullin et al., 2009; Peguero-Pina et al., 2012, 2016). Accordingly, g_m varied from 10 to 124 mmol m^–2 s^–1 in this study. The values of C_i–C_c here fell in the higher part of the range found for angiosperms and were higher than previously found for conifers (Niinemets et al., 2005, 2009b; Warren, 2008; Hassiotou et al., 2009; Tosens et al., 2012b; Peguero-Pina et al., 2012). Importantly, g_m influenced both C_i–C_c and photosynthesis significantly with stronger mass-based relations (Fig. 4).

Nitrogen content was similar to that previously found in conifers and positively related to A_mass, as was also shown by Reich et al. (1995). M. glyptostroboides diverged in the analysis, which can be explained by its deciduous nature (Wright et al., 2002). A negative relationship between LMA and A_mass has been shown previously for evergreens while area-based photosynthesis seems not to correlate with LMA, which is contrary to deciduous species, where higher LMA has been shown to correlate with higher A_area (Reich et al., 1995; Wright et al., 2004). Accordingly, the same was found here (Fig. 5). Altogether, this illustrates strong investment in supportive structure (Niinemets et al., 2009c; Hassiotou et al., 2009).

Similarly to recent studies, the most important anatomical correlations with g_m were S_c/S and T_cwm (Terashima et al., 2011; Tosens et al., 2012b, 2016; Peguero-Pina et al., 2012; Tomás et al., 2013) (Fig. 6). The significance of each depends on foliage structure, e.g. in sclerophylls higher T_cwm overshadows the influence of S_c/S on g_m (Tomás et al., 2013). The g_m/mass–T_cwm correlation was stronger than the area-based one (Fig. 6B, C) as g_m/mass indicates the investment in cell walls and g_m/area in the mesophyll area (Niinemets et al., 2009b).

The importance of structure as a limiting factor of photosynthesis

In order to overcome the various uncertainties related to g_m estimations, it was additionally modelled from anatomy and estimated from A–C_i curves (Ethier and Livingston, 2004). All three methods show similarly wide variation in g_m across evolutionarily old species (Fig. 7). However, g_m from anatomy tended to underestimate, whereas the A–C_i curve method overestimated, g_m for some species. When both methods were considered, g_m from the variable J method was more strongly correlated with g_m obtained from anatomy than from A–C_i curves. Likewise, Tomás et al. (2013) found this across species exhibiting a wide variation of leaf morphologies. Yet, the model tends to over- or underestimate at the lower or higher end of g_m (Tosens et al., 2012a,b; Peguero-Pina et al., 2012; Tomás et al., 2013; Fini et al., 2016). In this sample, g_m from anatomy mostly underestimated for C. revoluta, C. sempervirens and P. abies (Fig. 7), while the model estimations where in strong agreement with g_m from gas exchange for species with thick mesophyll cell walls and low g_m. This is different from Tosens et al. (2016), where the model overestimated for evolutionarily old Ophioglossum and Lycopodium species exhibiting very high T_cwm (0.7–0.81 µm). The discrepancy between measured and modelled g_m may arise from various uncertainties associated with both estimates. As for combined gas exchange–fluorescence estimation, g_m is not the only component to affect C_c: the amount of respiratory and photorespiratory CO₂ should be considered as an independent source of CO₂ (Tholen et al., 2012). Concerning the predictive power of the anatomical model for species exhibiting a wide variation in T_cwm, heterogeneous chloroplast thickness and morphology (Figs 1 and 2), the strongest uncertainties are related to the unknown variation of mesophyll cell wall porosity and the actual determinants of stroma resistance including the role of carbonic anhydrase (CA). Nobel (1991) proposed an upper value of cell wall porosity of 0.3 and that it varies linearly with T_cwm. Indeed, 0.3 was used to calculate g_m for Populus tremula with low T_cwm and it gave good results (Tosens et al., 2012a). In a multispecies context the relationship between g_m from anatomy and gas exchange was improved when porosity was modelled varying between 0.04 and 0.095 and being negatively correlated with T_cwm (Tosens et al., 2012b; Peguero-Pina et al., 2012; Tomás et al., 2013). Some species here and in Tosens et al. (2016) exhibited very high T_cwm compared with prior research, and therefore lower porosity values were used for species where T_cwm>0.5 μm. However, as was emphasized by Tosens et al. (2012b), the linear decline of porosity with T_cwm is hypothetical and the discrepancy between modelled and measured g_m could be resolved by some other trait.

Quantitative limitation analysis further confirmed that the mesophyll gas phase limitation to CO₂ diffusion is negligible as it accounted for less than 1% of the total limitation. This is even less than previously observed in a wide range of sclerophyllous angiosperm genera or in spore-bearing plants (Tosens et al., 2012a,b; Tomás et al., 2013). Using limitation analysis to further separate the contribution of the components of the liquid phase revealed that the limitation of T_cwm and T_chl had the greatest span, ranging from 6 to 72% and from 22 to 84%, respectively (Fig. 8B). This is in agreement with the negative correlation between g_m/mass and T_cwm (Fig. 6B). CO₂ faces the longest diffusion distance in the liquid phase after entering the chloroplasts (Evans et al., 2009). In this set of species, T_chl varied between 1.97 and 5.36 μm (Fig. 2), which is thicker than previously reported explaining the high limitation by T_chl. It is debated whether the CO₂ diffusion efficiency in the chloroplast stroma is mainly controlled by CA activity in the chloroplast (Flexas et al. 2012) and if it varies across species (at normal cytosolic pH), being higher in evergreen sclerophylls in order to compensate for the low CO₂ diffusion efficiency through thick mesophyll cell walls (Gillon and Yakir, 2000), or whether CA is always sufficient and CO₂ interconversion is not a limiting factor of g_m. Equally, this analysis adds to the evidence that CO₂ diffusion is importantly controlled by the physical diffusion distance within the chloroplasts (Tosens et al., 2012a,b; Peguero-Pina et al., 2012; Tomás et al., 2013).

Overall, the good fit between g_m calculated from anatomy and gas exchange confirms that g_m is explained to a large extent by inherent variations in mesophyll anatomy, while mesophyll cell walls and chloroplasts are the most important structural determinants of liquid phase conductance in species exhibiting high T_cwm, T_chl and heterogeneous chloroplast morphology. However, the limitation amplitude was large implicating versatility in its importance among different species (Fig. 8A). The smallest limitation on A_area on average was biochemistry, which is similar to previous interspecies studies by Tomás et al. (2013) and Tosens et al. (2016). As the mesophyll and stomatal conductances were low, especially compared with maximal values measured so far (Wright et al., 2004; Flexas et al., 2012), it is expected that biochemistry plays a smaller role in limitations, because the photosynthetic enzymes are not saturated with CO₂ due to constraints on the previous parts of the pathway (Terashima et al., 2011; Niinemets et al., 2011). The limitations by stomata and mesophyll were similarly significant in the control of WUE_i showing again that leaf mesophyll structure plays an important role in realized WUE_i (Fig. 9).

The effect of divergence time on structure and physiology

The rate of photosynthesis depended on the age of the genera. This, however, was mostly due to the inclusion of spore-bearing plants reflecting the evolutionary increase in photosynthetic capacity from early plants to angiosperms (Brodribb et al., 2009; Carriquí et al., 2015; McAdam and Brodribb, 2015). However, when broad taxonomic groups are considered, species’ evolutionary adaptation to light and water conditions can actually drive photosynthetic capacity more strongly than their evolutionary age (Tosens et al., 2016). In this regard, it is important that A_area depended on g_m/area positively regardless of evolutionary age, showing that this correlation remained significant including the effect of divergence time in the model (see Supplementary Table S3a, b).

Analogously to A_area, it has been suggested that there is an increase in g_m/area through the evolution and diversification of embryophytes (Carriquí et al., 2015). While indeed gymnosperms studied here had a very low average g_m/area, much lower than angiosperms with comparably tough foliage structure (e.g. Flexas et al., 2012), g_m/area did not significantly depend on evolutionary age. As with within-group variability in ferns (Tosens et al., 2016) and angiosperms (Flexas et al., 2007b), this likely reflects individual species adaptation to specific habitat conditions.

Notwithstanding the lack of within-group evolutionary signal, low average g_m/area and A_area and the corresponding thick mesophyll cell walls for species with widely contrasting ecological strategies do support the preservation of old traits through evolution, suggesting apparent constraints on evolution. Different CO₂/O₂ selection pressures at the time of divergence for ferns and angiosperms have been hypothesized to be the reason for lower average A_area values for the former (Carriquí et al., 2015) as ferns evolved in several-fold higher CO₂ and slightly lower O₂ concentrations than angiosperms (Brodribb et al., 2009; Carriquí et al., 2015). In fact, in the high-CO₂ atmosphere where several of the thick-cell-walled species evolved (about 65–200 My ago), diffusional limitations exercised a lower control on the rate of photosynthesis. However, while this ancient trait has been preserved through evolution, g_m has started to exercise an increasingly stronger control on foliage assimilation rates. Yet, this might be inevitable given the inefficient dynamic stomatal control under water-limited conditions potentially leading to excess plant water loss until hydraulic constraints force stomatal closure (Brodribb et al., 2005; Carnicer et al., 2013).

Conclusions

This study demonstrates important relationships between mesophyll structure and physiology in evolutionarily old plants. A large variability was found in ultrastructural traits determining LES relationships. Although LMA depended on leaf density and thickness, they were not correlated with T_cwm or S_c/S illustrating that LMA cannot be used as a universal explanation for photosynthetic structural constraints.

Mesophyll anatomy exerted major control on net assimilation rates. The three methods used in previous studies for interspecies comparisons were used to confirm g_m values from gas exchange–fluorescence measurements and their anatomical nature. Although high variation was uncovered between species in g_m, it was on average very low. This resulted mainly from the exceptionally thick cell walls, large chloroplasts, and low S_c/S. The role of stroma deserves further attention.

These characteristics in evolutionarily older taxa support the preservation of ancient traits in evolution, although the role of functional adaptation and evolutionary constraint in leaf anatomy continues to be debated.

Glossary

Abbreviations:

A_area

net assimilation rate per area

A_mass

net assimilation rate per dry mass

C_a

atmospheric CO₂ concentration

CA

carbonic anhydrase

C_a–C_i

CO₂ drawdown from atmosphere to intercellular airspace

C_i

intercellular CO₂ concentration

C_i–C_c

CO₂ drawdown from intercellular airspace to chloroplasts

D_leaf

leaf density

F_ias

fraction of intercellular airspace

LMA

leaf dry mass per area

l_b, l_m and l_s

photosynthetic limitation by biochemistry, mesophyll and stomatal conductance, respectively

N_area

nitrogen content per area

N_mass

nitrogen content per mass

g_m

mesophyll diffusion conductance

g_m/area and g_m/mass

mesophyll conductance per area and per mass

g_s

stomatal conductance

S_c/S and S_m/S

chloroplast and mesophyll area exposed to intercellular airspace

T_chl

chloroplast thickness

T_cwm

mesophyll cell wall thickness

T_leaf

leaf thickness

T_mes

mesophyll thickness

WUE_i

intrinsic water use efficiency.