OpenRBC: A Fast Simulator of Red Blood Cells at Protein Resolution

Abstract

We present OpenRBC, a coarse-grained molecular dynamics code, which is capable of performing an unprecedented in silico experiment—simulating an entire mammal red blood cell lipid bilayer and cytoskeleton as modeled by multiple millions of mesoscopic particles—using a single shared memory commodity workstation. To achieve this, we invented an adaptive spatial-searching algorithm to accelerate the computation of short-range pairwise interactions in an extremely sparse three-dimensional space. The algorithm is based on a Voronoi partitioning of the point cloud of coarse-grained particles, and is continuously updated over the course of the simulation. The algorithm enables the construction of the key spatial searching data structure in our code, i.e., a lattice-free cell list, with a time and space cost linearly proportional to the number of particles in the system. The position and the shape of the cells also adapt automatically to the local density and curvature. The code implements OpenMP parallelization and scales to hundreds of hardware threads. It outperforms a legacy simulator by almost an order of magnitude in time-to-solution and >40 times in problem size, thus providing, to our knowledge, a new platform for probing the biomechanics of red blood cells.

Main Text

The red blood cell (RBC) is one of the simplest, yet most important cells in the circulatory system due to its indispensable role in oxygen transport. An average RBC assumes a biconcave shape with a diameter of 8 μm and a thickness of 2 μm. Without any intracellular organelles, it is supported by a cytoskeleton of a triangular spectrin network anchored by junctions on the inner side of the membrane. Therefore, the mechanical properties of an RBC can be strongly influenced by molecular level structural details that alter the cytoskeleton and lipid bilayer properties.

Both continuum models (1, 2, 3, 4) and particle-based models (5, 6, 7, 8) have been developed with the aim to help uncover the correlation between RBC membrane structure and property. Continuum models are computationally efficient, but require a priori knowledge of cellular mechanical properties such as bending and shear modulus. Particle models are useful for extracting RBC properties from low-level descriptions of the membrane structure and defects. However, it is computationally demanding, if not prohibitive, to simulate the large number of particles required for modeling the membrane of an entire RBC. To the best of our knowledge, a bottom-up simulation of the RBC membrane at the cellular scale using particle methods remains absent.

Recently, a two-component coarse-grained molecular dynamics (CGMD) RBC membrane model that explicitly accounts for both the cytoskeleton and the lipid bilayer was proposed (9). The model could potentially be used for particle-based whole-cell RBC modeling because its coarse-grained nature can drastically reduce computational workload while still preserving necessary details from the molecular level. However, due to the orders-of-magnitude difference in the length scale between a cell and a single protein, a total of about four million particles is still needed to represent an entire RBC. In addition, the implicit treatment of the plasma in this model eliminates the overhead for tracking the solvent particles, but also exposes a notable spatial density heterogeneity because all CG particles are exclusively located on the surface of a biconcave shell. The space inside and outside of the RBC membrane remains empty. This density imbalance imposes a serious challenge on the efficient evaluation of the pairwise force using conventional algorithms and data structures, such as the cell list and the Verlet list, which typically assume a uniform spatial density and a bounded rectilinear simulation box.

In this article, we present OpenRBC—a new software tailored for simulations of an entire RBC using the two-component CGMD model on multicore CPUs. As illustrated in Fig. 1, the simulator can take as input a triangular mesh of the cytoskeleton of a RBC and reconstruct a CGMD model at protein resolution with explicit representations of both the cytoskeleton and the lipid bilayer. This type of whole cell simulation of RBCs can thus realize an array of in silico measurements and explorations of the following: 1) RBC shear and bending modulus, 2) membrane loss through vesiculation in spherocytosis and elliptocytosis (10), 3) anomalous diffusion of membrane proteins (11), 4) interaction between sickle hemoglobin fibers and RBC membrane in sickle cell disease (12, 13), 5) uncoupling between the lipid bilayer and cytoskeleton (14), 6) ATP release due to deformation (15), 7) nitric oxide-modulated mechanical property change (16), and 8) cellular uptake of elastic nanoparticles (17).

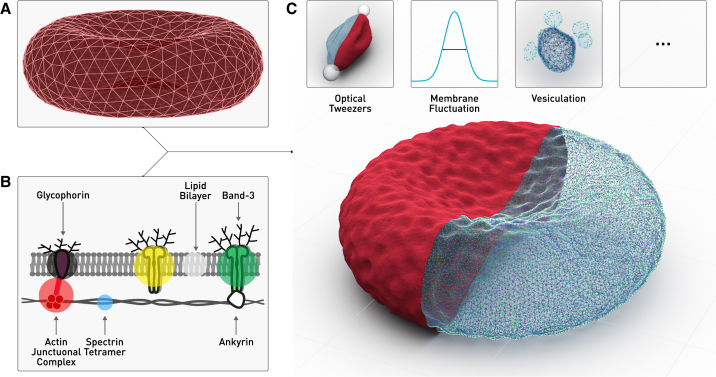
Figure 1.

(A) A canonical hexagonal triangular mesh of a biconcave surface representing the cytoskeleton network is used together with (B) the two-component CGMD RBC membrane model to reconstruct (C) a full-scale virtual RBC, which allows for a wide range of computational experiments. To see this figure in color, go online.

Software overview

OpenRBC is written in C++ using features from the C++11 standard. To maximize portability and allow easy integration into other software systems (18), the project is organized as a header-only library with no external dependencies. The software implements SIMD vectorization (19) and OpenMP shared memory parallelization, and was specifically optimized toward making efficient use of large numbers of simultaneous hardware threads.

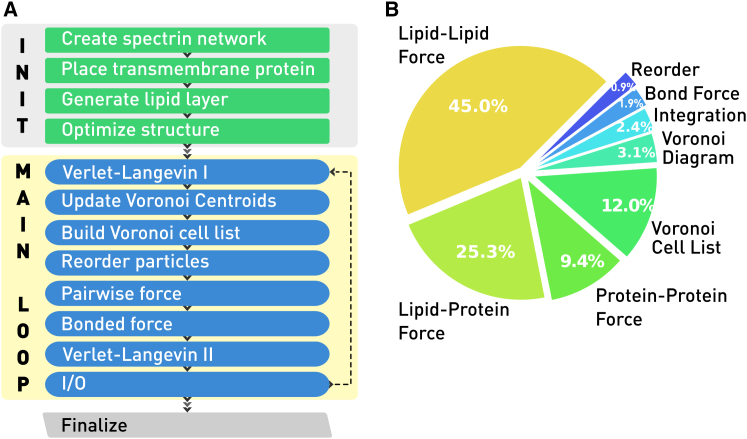
As shown in Fig. 2 A, the main body of the simulator is a time-stepping loop, where the force and torque acting on each particle is solved for and used for the iterative updating of the position and orientation according to a Newtonian equation of motion. The time distribution of each task in a typical simulation is given in Fig. 2 B. The majority of time is spent in force evaluation, which is compute-bound. This makes the code capable of utilizing the high thread count of modern CPUs with the shared memory programming paradigm.

Figure 2.

Shown here is the (A) flow chart and (B) typical wall time distribution of OpenRBC. To see this figure in color, go online.

Initial structure generation

As shown in Fig. 1, a two-component CGMD RBC system can be generated from a triangular mesh, which resembles the biconcave shape of a RBC at equilibrium. Note that the geometry may be alternatively sourced from experimental data using techniques such as optical image reconstruction because the algorithm itself is general enough to adapt to an arbitrary triangular mesh. This feature can be useful for simulating RBCs with morphological anomalies. Actin and glycophorin protein particles are placed on the vertices of the mesh, whereas spectrin and immobile band-3 particles are generated along the edges. The band-3-spectrin connections and actin-spectrin connections can be modified to simulate RBCs with structural defects. Lipid and mobile band-3 particles are randomly placed on each triangular face by uniformly sampling each triangle defined by the three vertices (20). A minimum interparticle distance is enforced to prevent clutter between protein and lipid particles. The system is then optimized using a velocity quenching algorithm to remove collision between the particles.

Spatial searching algorithm

Pairwise force evaluation accounts for >70% of the computation time in OpenRBC as well as other molecular dynamics softwares (21, 22). To efficiently simulate the reconstructed RBC model, we invented a lattice-free spatial partitioning algorithm that is inspired by the concept of Voronoi diagram. The algorithm, at the high level, can be described as the following:

• 1.Group particles into a number of adaptive clusters,
• 2.Compute interactions between neighboring clusters, and
• 3.Update cluster composition after particle movement. Then
• 4.Repeat from Step 2.

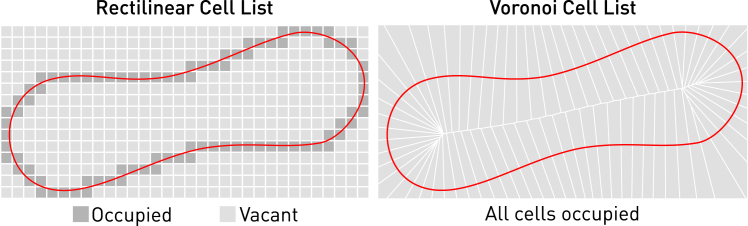
As illustrated in Fig. 3, the algorithm adaptively partitions a particle system into a number of Voronoi cells that are approximately equally populated. In contrast, a lattice-based cell list leaves many cells vacant due to the density heterogeneity. Thus, the algorithm can provide very good performance in partitioning the system, maintaining data locality and searching for pairwise neighbors in a sparse three-dimensional space. It is implemented in our software using a k-means clustering algorithm, which is, in turn, enabled by a highly optimized implementation of the k-d tree searching algorithm, as explained below.

Figure 3.

(Left) Only cells in dark gray are populated by CG particles in a cell list on a rectilinear lattice. This results in a waste of storage and memory bandwidth. (Right) All cells are evenly populated by CG particles in a cell list based on the Voronoi diagram generated from centroids located on the RBC membrane. To see this figure in color, go online.

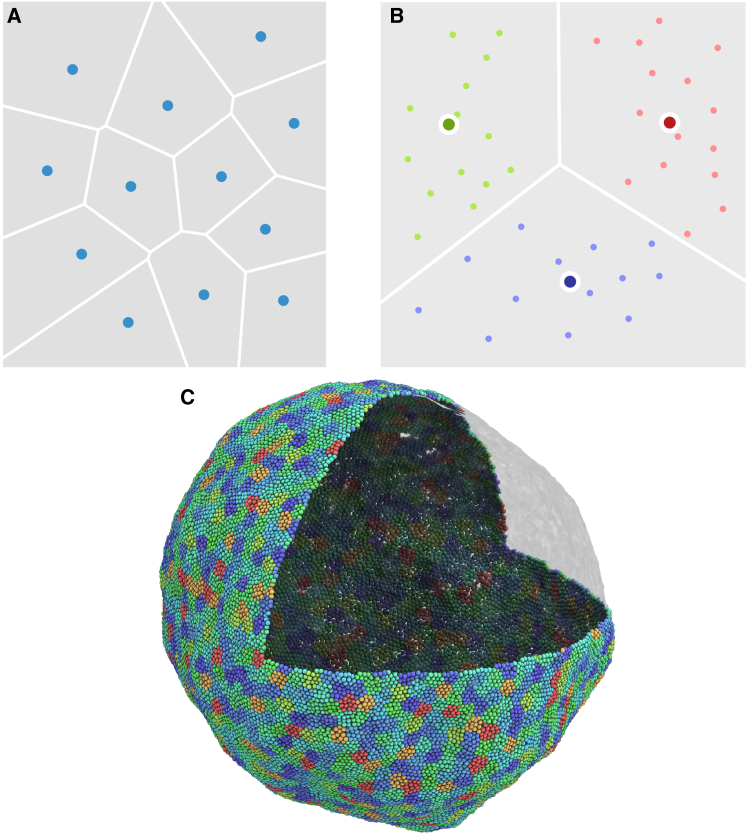
A Voronoi tessellation (23) is a partitioning of an n-dimensional space into regions based on distance to a set of points called the “centroids”. Each point in the space is attributed to the closest centroid (usually in the L2 norm sense). An example of a Voronoi diagram generated by 12 centroids on a two-dimensional rectangle is given in Fig. 4 A.

Figure 4.

(A) Shown here is a Voronoi partitioning of a square as generated by centroids marked by the blue dots. (B) Shown here is a k-means (k = 3) clustering of a number of points on a two-dimensional plane. (C) Shown here is a vesicle of 32,673 CG particles partitioned into 2000 Voronoi cells. To see this figure in color, go online.

The k-means clustering (24) is a method of data partitioning that aims to divide a given set of n vectors into k clusters in which each vector belongs to the cluster whose center is closest to it. The result is a partition of the vector space into a Voronoi tessellation generated by the cluster centers as shown in Fig. 4 B. Searching for the optimal clustering that minimizes the within-cluster sum of square distance is NP-hard, but efficient iterative heuristics based on, e.g., the expectation-maximization algorithm (25), can be used to quickly find a local minimum.

A k-d tree is a spatial partitioning data structure for organizing points in a k-dimensional space (26). It is essentially a binary tree that recursively bisects the points owned by each node into two disjoint sets as separated by an axial-parallel hyperplane. It can be used for the efficient searching of the nearest neighbors of a given query point in O(logN) time, where N is the total number of points, by pruning out a large portion of the search space using cheap overlap checking between bounding boxes.

The k-means/Voronoi partitioning of a point cloud adapts automatically to the local density and curvature of the points. As such, we exploit this property to create a generalization of the cell list algorithm using the Voronoi diagram. The algorithm can be described as a two-step procedure: 1) clustering all the particles in the system using k-means, followed by an online expectation-maximization algorithm that continuously updates the system’s Voronoi cells centroid location and particle ownership; and 2) sorting the centroids and particles with a two-level data reordering scheme, where we first order the Voronoi centroids along a space-filling curve (a Morton curve, specifically) and then reorder the particles according to the Voronoi cell that they belong to. The pseudocode for the algorithm can be found in the Supporting Material. The reordering step in updating the Voronoi cells ensures that neighboring particles in the physical space are also statistically close to each other in the program memory space. This locality can speed up the k-d tree nearest-neighbor search by allowing us to use the closest centroid of the last particle as the initial guess for the next particle. This heuristic helps to further prune out most of the k-d tree search space and essentially reduces the complexity of a nearest-neighbor query from O(logN) to O(1). In practice, this brings ∼100 times acceleration when searching through 200,000 centroids. As shown by Fig. 4 C, the Voronoi cells generated from a k-means clustering of the CG particles are uniformly distributed on the surface of the lipid membrane.

Force evaluation

Lipid particles accounts for 80% of the population in the whole-cell CGMD system. The Voronoi cells can be used directly for efficient pairwise force computation between lipids with a quad loop that ranges over all Voronoi cell v_i, all neighboring cells v_j of v_i, all particles in v_i, and all particles in v_j, as shown in the Supporting Material. Because the cytoskeleton of a healthy RBC is always attached to the lipid bilayer, its protein particles are also distributed following the local curvature of the lipid particles. This means that we can reuse the Voronoi cells of the lipid particles, but with a wider searching cutoff, to compute both the lipid-protein and protein-protein pairwise interactions. For diseased RBCs with fully or partially detached cytoskeletons, a separate set of Voronoi cells can be set up for the cytoskeleton proteins to compute the force. A list of bonds between proteins is maintained and used for computing the forces between proteins that are physically linked to each other.

A commonly used technique in serial programs to speed up the force computation is to take advantage of the Newton’s third law of action and reaction. Thus, the force between each pair of interacting particles is only computed once and added to both particles. However, this generates a race condition in a parallel context because two threads may end up simultaneously computing the force on a particle shared by two or more pairwise interactions.

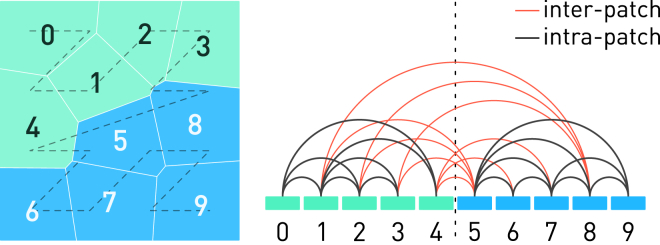
Our solution takes advantage of the strong spatial locality of the particles as maintained by the two-level reordering algorithm, and decomposes the workload both spatially and linearly-in-memory into patches by splitting the linear range of cells indices among OpenMP threads. Each thread will be calculating the forces acting on the particles within its own patch. As shown in Fig. 5, force accumulation without triggering racing condition can be realized by only exploiting the Newton’s third law on pairwise interactions where both Voronoi cells belong to a thread’s own patch. Interactions involving a pair of particles from different patches are calculated twice (once for each particle) by each thread. The strong particle locality minimizes the shared contour length between two patches, and hence also minimizes the number of interpatch interactions.

Figure 5.

Thanks to the spatial locality ensured by reordering particles along the Morton curve (dashed line), we can simply divide the cells between two threads by their index into two patches each containing five consecutive Voronoi cells. The force between cells from the same patch is computed only once using Newton’s third law, whereas the force between cells from different patches is computed twice on each side. To see this figure in color, go online.

Validation and benchmark

In this section we present validation of our software by comparing simulation and experimental data. We also compare the program performance against that of the legacy CGMD RBC simulator used in Li and Lykotrafitis (9). The legacy simulator, which performs reasonably well for a small number of particles in a periodic rectangular box, was written in C and parallelized with the message passing interface using a rectilinear domain decomposition scheme and a distributed memory model. Three computer systems were used in the benchmark, each equipped with a different mainstream CPU microarchitecture, i.e., the Intel Haswell, the AMD Piledriver, and the IBM Power8 (27). The machine specifications are given in Table 1.

Table 1.

A Summary of Capability and Design Highlights of OpenRBC and the Specifications of the Computer Systems Used in the Benchmark

Capability and Design					Performance—Time Steps/Day
OpenRBC Legacy Improvement					Cores Particles OpenRBC Legacy Speedup
Maximum system size (number of particles)	>8 × 106	2 × 105	>40 times		20	8.34 × 106	3.90 × 105	—	—
Line of code	4677	7424	37% less		4	1.88 × 105	3.86 × 106	0.42 × 106	9.2
CPU	Architecture	Instruction set	Frequency (GHz)	Physical cores	Hardware threads	Total threads	Last level cache (MB)	GFLOPS (SP)	Achieved FLOPS by OpenRBC (%)	Memory bandwidth (GB/s)
IBM POWER 8 “Minsky”	Power8	Power	3.5	10 × 2	8	160	80 × 2	560.0	8.7	230
Intel Xeon E5-2695 v3	Haswell	x86–64	2.3	14 × 2	2	56	35 × 2	1030.4	4.6	136
AMD Opteron 6378	Piledriver	x86–64	2.4	16 × 4	1	64	16 × 4	614.4	4.5	204

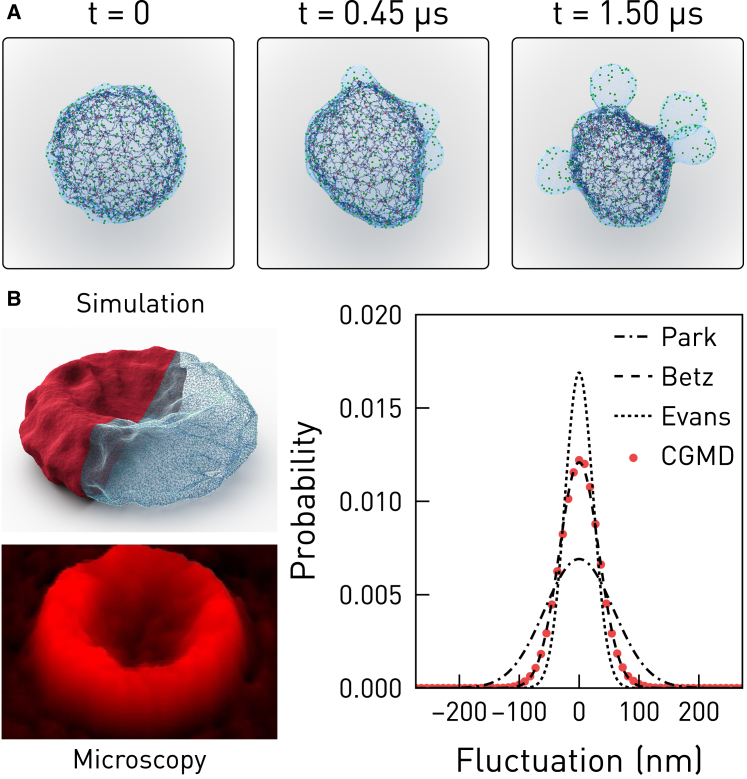
To compare performance between OpenRBC and the legacy simulator, the membrane vesiculation process of a miniaturized RBC-like sphere with a surface area of 2.8 μm² was simulated. The evolution of the dynamic process is visualized from the simulation trajectory and shown in Fig. 6 A. OpenRBC achieves almost an order-of-magnitude speedup over the legacy solver in this case on all three computer systems, as shown in Table 1.

Figure 6.

(A) Shown here is the vesiculation procedure of a miniature RBC. (B) The instantaneous fluctuation of a full-size RBC in OpenRBC compares to that from experiments (28, 29, 30). Microscopy image is reprinted with permission from Park et al. (28). To see this figure in color, go online.

Furthermore, OpenRBC can efficiently simulate an entire RBC modeled by 3,200,000 particles and correctly reproduce the fluctuation and stiffness of the membrane as shown in Fig. 6 B. The legacy solver was not able to launch the simulation due to memory constraint. The simulation was carried out by implementing the experimental protocol of Park et al. (28), which measures the instantaneous vertical fluctuation Δh(x,y) along the upper rim of a fixed RBC. In addition, a harmonic volume constraint is applied to maintain the correct surface-to-volume ratio of the RBC. We measured a membrane root-mean-square displacement of 33.5 nm, whereas previous experimental observations and simulation results range between 23.6 and 58.8 nm (28, 29, 30, 31).

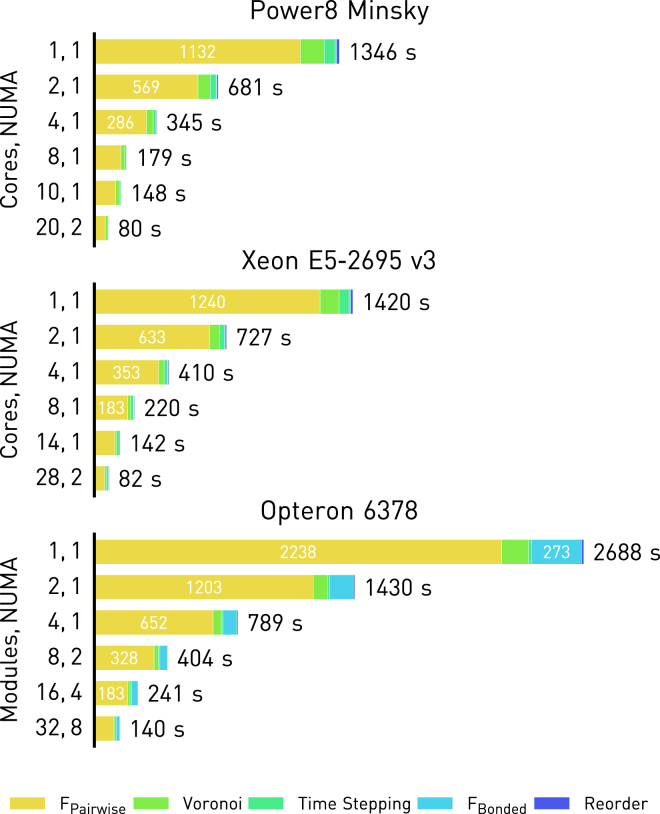
A scaling benchmark for the whole cell simulation on the three computer systems is given in Fig. 7. It can be seen that compute-bound tasks such as pairwise force evaluation can scale linearly across physical cores. Memory-bound tasks benefit less from hardware threading as expected, but thanks to thread pinning and a consistent workload decomposition between threads, there is no performance degradation from side effects such as cache and bandwidth contention.

Figure 7.

Shown here is the scaling of OpenRBC across physical cores and NUMA domains when simulating an RBC of 3,200,000 particles. To see this figure in color, go online.

It is also worth noting that Fu et al. (32) recently published an implementation of a related RBC model in LAMMPS, which can simulate 1.15 × 10⁶ particles for 10⁵ time steps on 864 CPU cores in 2761 s. However, the use of explicit solvent particles in their model generates difficulty in establishing a direct performance comparison between their implementation and OpenRBC. Nevertheless, as a rough estimate and assuming perfect scaling, their timing result can be translated into simulating 8.34 × 10⁶ particles for 0.41 × 10⁵ time steps per day on 864 cores. OpenRBC can complete roughly the same amount of time steps on 20 CPU cores. We do recognize that the explicit solvent model carries more computational workload, and that implementing nonrectilinear partitioning schemes may not be straightforward within the current software framework of LAMMPS. Nonetheless, this comparison does serve to demonstrate the potential of shared-memory programming paradigm on fat compute nodes with large numbers of strong cores and amounts of memory.

Summary

We presented a from-scratch development of a coarse-grained molecular dynamics software, OpenRBC, which exhibits exceptional efficiency when simulating systems of large density discrepancy. This capability is supported by an innovative algorithm that computes an adaptive partitioning of the particles using a Voronoi diagram. The program is parallelized with OpenMP and SIMD vector instructions, and implements threading affinity control, consistency loop partitioning, kernel fusion, and atomics-free pairwise force evaluation to increase the utilization of simultaneous hardware threads and to maximize memory performance across multiple NUMA domains. The software achieves an order-of-magnitude speedup in terms of time-to-solution over a legacy simulator, and can handle systems that are almost two orders-of-magnitude larger in particle count. The software enables, for the first time ever to our knowledge, simulations of an entire RBC with a resolution down to single proteins, and opens up the possibility for conducting many in silico experiments concerning the RBC cytomechanics and related blood disorders (33).

Author Contributions

Y.-H.T. designed the algorithm. Y.-H.T. and L.L. implemented the software. Y.-H.T. and C.E. carried out the performance benchmark. H.L. developed the CGMD model. H.L. and Y.-H.T. performed validation and verification. Y.-H.T., L.L., and H.L. wrote the manuscript. L.G., C.E., and V.S. provided algorithm consultation and technical support. G.E.K. supervised the work.

Editor: Nathan Baker.