Rich Dynamics Underlying Solution Reactions Revealed by Sampling and Data Mining of Reactive Trajectories

Abstract

Efficient sampling in both configuration and trajectory spaces, combined with mechanism analyses via data mining, allows a systematic investigation of the thermodynamics, kinetics, and molecular-detailed dynamics of chemical reactions in solution. Through a Bayesian learning algorithm, the reaction coordinate(s) of a (retro-)Claisen rearrangement in bulk water was variationally optimized. The bond formation/breakage was found to couple with intramolecular charge separation and dipole change, and significant dynamic solvent effects manifest, leading to the “in-water” acceleration of Claisen rearrangement. In addition, the vibrational modes of the reactant and the solvation states are significantly coupled to the reaction dynamics, leading to heterogeneous and oscillatory reaction paths. The calculated reaction rate is well interpreted by the Kramers’ theory with a diffusion term accounting for solvent–solute interactions. These findings demonstrated that the reaction mechanisms can be complicated in homogeneous solutions since the solvent–solute interactions can profoundly influence the reaction dynamics and the energy transfer process.

Short abstract

An efficient sampling protocol allows direct simulations of chemical reactions without preassumption of reaction pathways. Machine learning algorithms further extract rich dynamic observations of transition events beyond transition state theory.

Introduction

Condensed phase reactions are everywhere from science to industry, including organic synthesis in solution, enzymatic reactions in cells, and homogeneous catalysis, among which the solution reaction is of particular interest.¹⁻³ One widely applied approach in the study of reaction mechanism is to introduce reaction coordinate(s) (RC)⁴⁻⁶ and transition states (TS),⁷⁻¹⁰ giving rise to a simplified description of reduced dimensionality. However, the existence of solvent complicates the elucidation of reaction mechanisms considerably.^7,11,12 Foremost, chemical processes in solution take place in a high-dimensional space that include solvent coordinates apart from those delimiting reactants and products. Extracting the relevant factors that characterize such reactions can be difficult. Besides, for adiabatic reactions the energy-barrier crossing is driven by thermal fluctuations of the liquid solution.^13,14 Yet little is known about how the dynamics of the solvent fluctuations influence the proceeding of the reaction event. Being able to address these concerns will not only deepen our understanding of the most basic processes in chemistry, but help better manipulate the reaction environment for purposes like catalyzing or enhancing the regio-/stereoselectivity.

Quantum mechanics/molecular mechanics (QM/MM) molecular dynamics (MD) simulation is a powerful and widely used tool to study chemical reactions.^15,16 In spite of many successes, MD is limited by its inability to describe long-time scale dynamical processes when a high (free) energy barrier is involved. Some enhanced sampling methods^17,18 cope with this problem by introducing low-dimensional collective variables (CV) to capture the slowest motion along the reaction progression and focus the sampling on these projected dimensions. As a consequence, the solvent coordinates are hard to count due to the requirement of low dimensionality, and artifacts may arise if the CV is not properly chosen.¹⁹ On the other end, some methods are aimed to calculate dynamic properties, like transition path sampling (TPS)⁹ and milestoning,²⁰ etc. Rigorously the transition states should be defined as an ensemble.^8,10 To statistically define the RC and the TS one desires a thorough sampling of the transition paths and/or the equilibrium ensemble, without artificially a prior chosen CVs. An alternative and systematic way to achieve this goal is to use machine-learning methods to “learn” the RC based on statistical data rather than empirical assumptions.

In this paper, we adopted the enhanced sampling of reactive trajectories (ESoRT) protocol, which has previously been shown accurate and efficient in the study of organic reaction,²¹ to investigate a reversible unimolecular cyclization process (the reversibility allows us to connect and compare the kinetics calculation with equilibrium thermodynamics, so as to systematically validate the sampling protocol), named (retro-)Claisen rearrangement (Figure 1A)²² in aqueous solution. Unlike conventional Claisen rearrangement which is usually irreversible, the reaction here suffers intramolecular strain, which not only destabilizes the product, but also alters the molecular configurational space and reaction mechanisms. Besides, water is the most common solvent in nature, and the “in/on-water” reactions²³⁻²⁵ are important to biosynthesis, catalysis, and green chemistry. Understanding the profound water-acceleration effect in many organic reactions could lead to better design and manipulation of solvent conditions for organic synthesis. Here through QM/MM MD simulations, we were able to generate reactive trajectories and calculate the equilibrium thermodynamics properties including temperature-dependent parameters without the assumption of reaction mechanism or transition-state theory (TST). Optimizing the RCs via a data-based Bayesian learning algorithm, we could investigate how the solvent coordinates generate and contribute to varied reaction pathways. This study thus presents a unified strategy of deciphering the complex reaction mechanisms by unsupervised learning of both equilibrium and transition path ensembles. The kinetics of this in-water reaction can be well illustrated regarding Kramers’ theory. The current study revealed a number of interesting dynamical properties that are difficult to obtain without detailed analyses of reactive trajectories. Mechanistically, dynamic interactions between water and the reactant contribute to the water-acceleration effect. The hydrogen-bonding of water to the charge-enriched site of the reactant and the adapted parallelization of neighboring solvent dipoles during the reaction progression help stabilize the TS and facilitate this in-water reaction. By providing dynamic observations of transition events, this study puts the investigation of condensed phase reactions under molecular-detailed perspectives.

Figure 1.

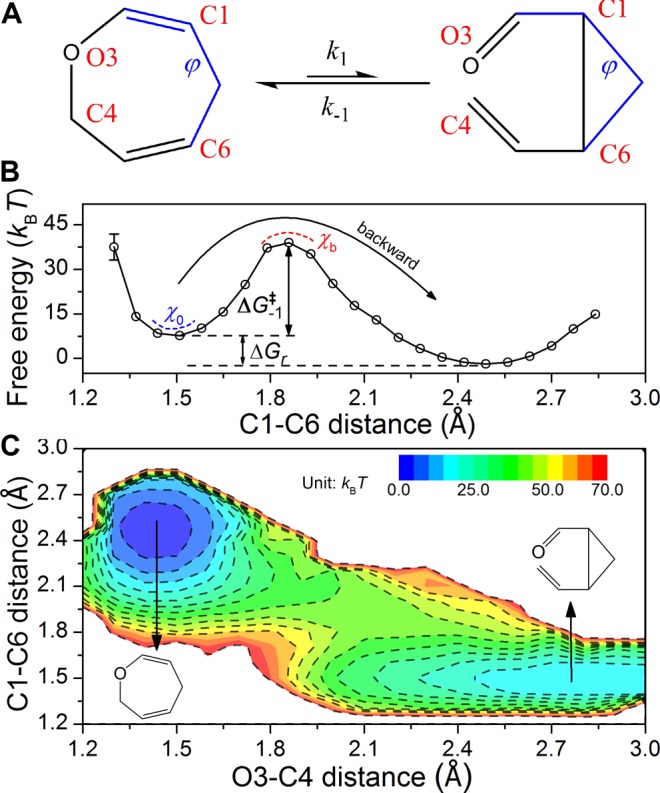
Calculating thermodynamics of (retro-)Claisen rearrangement using MITS. (A) Scheme of forward (k₁) and (k_–1) backward reactions: 2,5-dihydrooxepin (left) interconverts to cis-2-vinylcyclopropanecarboxaldehyde (right), with the bond forming/breaking sites indexed in red characters. Bonds defining characteristic dihedral angle φ are highlighted in blue. (B) Free-energy profile along the C1–C6 bond length. The dashed curves denote the curvature at the potential well (blue, χ₀) and the inverse curvature at the barrier top (red, χ_b ≈ 7 × 10² (k_BT)·Å^–2), respectively. ΔG^‡ is the free energy for activation (ΔG₁^‡ ≈ 25 kcal/mol, ΔG_–1 ≈ 19 kcal/mol, subscript 1/–1 stands for forward/backward reaction, respectively), and the free energy change of the forward reaction is ΔG_r = 5.9 kcal/mol. The arrow over the barrier top indicates the backward (retro) direction. (C) 2-D free-energy projection. The isovalue contours are drawn in dashed lines. Molecular configurations corresponding to each free-energy basin are shown.

Results

Multilevel Integrated Tempering Sampling (MITS)

The chemical reaction is characterized by a long waiting time inside the local minima (that define the reactant and product) and an ultrashort transition time over the in-between barrier.¹⁴ This feature leads to the over redundant sampling of conformational basins at the cost of insufficient sampling of the barrier region. A method is desired to enhance the sampling efficiency over the barrier region, meanwhile allowing the chemical reaction to almost spontaneously occur with the least artificial interference. To this end, we developed multilevel integrated tempering sampling (MITS) method, by which the chemical transition trajectories are sampled without imposing motions along any CVs. The thermal properties can be reweighted to different temperatures. This merit permits the calculation of temperature-dependent thermodynamics and kinetics properties. This method is based on the previous success of ITS²⁶ and SITS,^27,28 where we rescale the QM and non-QM Hamiltonians of QM/MM simulations and construct a generalized non-Boltzmann distribution by summing over the canonical distribution over a range of temperatures (see Supporting Information, Supplementary Text section II). As a single-copy and CV-free enhanced sampling method, MITS boosts the barrier transitions (Supporting Information, Figure S1) by attenuating the energy surface and effectively lowering the barriers (see Supporting Information, Supplementary Text II and Figure S2). Moreover, it does not prescribe the RCs or alter the TS properties, which allows thorough sampling of the phase space and automatic search for reaction mechanisms.

From Thermodynamics to Kinetics

We studied the well-known (retro-)Claisen rearrangement (Figure 1A), a reversible process through which the 2,5-dihydrooxepin (defined as reactant) interconverts to cis-2-vinylcyclopropanecarboxaldehyde (product, it is the three-member ring that renders this reaction reversible) in water.²² Such a [3,3]-sigmatropic reaction was previously thought to be concerted and undergo a six-member-ring transition state. Considering that the most commonly used RCs in earlier studies of Claisen rearrangement²⁹ are the C1–C6 (d(C1–C6), Figure 1B) and/or O3–C4 (d(O3–C4) bond length(s) (Supporting Information, Figure S3), we first calculated the free-energy profiles along these dimensions. Free-energy profiles along other dimensions can also be drawn, for instance, the d(C1–C6) × d(O3–C4) two-dimensional (2D) space (Figure 1C) and solvent coordinates (see Supporting Information, Figures S4 and S5). The two local basins are then separated at the barrier top on the one-dimensional (1D) free-energy profile, based on which we obtained the equilibrium constant K_eq and reaction free-energy change ΔG_r (Table 1). By virtue of MITS the thermodynamics can be reweighted to different temperatures within the sampling temperature range (see Supporting Information, Supplementary Text section III).²⁸ Therefore, from ΔG_r as a function of temperature T, one obtains directly the reaction entropy ΔS_r (see Supporting Information, Supplementary Text eq S21); similarly, the reaction enthalpy ΔH_r can be obtained through the Gibbs–Helmholtz equation (Table 1, Supporting Information, Supplementary Text eq S22, Figure S6).

Table 1. Summary of Reaction Thermodynamics and Kinetics (under 300 K, 1 atm).

thermodynamics		kinetics
Keq	(5.0 ± 0.2) × 10–5	k1a/s–1	(2.0 ± 0.2) × 10–7
		k–1/s–1	(4.3 ± 0.4) × 10–3
ΔGrb	5.90(0.07)c	ΔGr	5.9
ΔHr	12.3(0.5)	ΔH1‡	36(6)
ΔSr	21.5(0.7)	ΔH–1‡	23(4)

^aSubscript 1 or −1 stands for forward or backward reaction, respectively.

^bΔG_r, ΔH_r, and ΔH^‡ are in units of kcal/mol; ΔS_r in (cal·mol^–1·K^–1).

^cNumbers in parentheses are the statistical uncertainties.

Next, to retrieve the dynamics and kinetics of the chemical transition we conducted transition path shootings under the microcanonical ensemble.^21,30 A number of configurations were randomly selected from the equilibrium ensemble, each with known statistical weight, as the initial points for 2 ps forward and backward shootings on the original potential energy surface (see Supporting Information, Supplementary Text section IV). The pairwise trajectory was then judged to be reactive if the bidirectional shootings terminate in different basins. In this way, an ensemble of bidirectional reactive trajectories (along with many more nonreactive trajectories) were obtained (Supporting Information, Supplementary Movie). According to the flux-over-population theory,³¹ the forward/backward rate constant can be conveniently calculated by the probability of successful conversions among all shooting attempts in a given length of time (see Supporting Information, Supplementary Text section IV, eqs S23 and S24).²¹ This approach enjoys fast convergence (which was confirmed by comparison of transition path ensemble with equilibrium ensemble, see Supporting Information, Figure S7) and gives the forward and backward reaction rates, respectively (Table 1). The good agreement between kinetics and thermodynamics calculations (Table 1 and Supporting Information, Supplementary Text eq S27) shows the self-consistency and convergence of both configuration and trajectory sampling. Furthermore, the activation parameters (e.g., activation enthalpy ΔH^‡) are achieved using the rate coefficient obtained under different temperatures (see Supporting Information, Supplementary Text section IV). The Arrhenius plot was drawn accordingly, and the linear slope is known to be ΔH^‡ (Table 1, Supporting Information, Supplementary Text eq S30 and Figure S8). The activation enthalpies for forward and backward reactions roughly reproduce the overall reaction enthalpy (ΔH^‡ – ΔH_–1^‡ ≈ 13 kcal/mol), again demonstrating the reliability of the kinetics calculations.

Reaction Coordinates and Mechanisms

To identify the molecular mechanism one needs to define the RC(s) to effectively project the reaction event onto lower dimensions. But limited knowledge of the high-dimensional phase space and empirical biases are common origins for artificially chosen RCs to fail. Here we implemented the Bayesian measure^6,10 that enables a variational optimization of RCs. This approach draws on the relation between the equilibrium and transition-path ensembles, which not only defines and identifies the TS ensemble, but also leads to a quantitative metric for the quality of the candidate RC (r):

1

Three probabilities are introduced in eq 1: p(r|TP) is the probability density of r given that the system is on a transition path (TP), which can be easily obtained from the previous dynamic shootings, and p(TP) is the occupancy of transition path relative to the entire ensemble, which is a rate-relevant constant (see Supporting Information, Supplementary Text section VI, eq S38); the calculated p(TP|r) is the probability for being on a TP given that the system is in r. A good choice of r evokes a sharp high peak of p(TP|r), indicating infrequent recrossings around the identified transition state.⁶ Since p(TP) is an r-independent constant (estimated to be an order of magnitude between 10^–20 and 10^–19, see Supporting Information, Supplementary Text section VI), we replaced the p(TP|r) with p(TP|r)/p(TP). It should be noted here that this Bayesian method requires that the thermodynamics of chemical reactions can be projected onto arbitrary r (yielding the p_eq(r)), which severely impedes its practical usage in the absence of a CV-free sampling method like MITS.

Following this line, several generic and conventional RC candidates were assessed for this aqueous reaction. The C1–C6 bond length (d(C1–C6)) is judged to be a reasonably good RC with p(TP|r)/p(TP) ≈ 10¹⁷ (Figure 2A), characterizing the TS with d(C1–C6) ≈ 1.84 Å, although to a lesser extent a 1.95 Å O3–C4 bond length also describes the TS well (Figure 2B). These two coordinates agree with the kinetic isotope effect measurement for Claisen rearrangement.³² Noteworthy, the “breadth” of the TS region can be read from p(TP|r)/p(TP) (r = d(C1–C6)), which is ∼0.1 Å. Similarly, intrinsic molecular properties (Supporting Information, Figure S10) along with some representative solvent coordinates were examined (Supporting Information, Figures S11A and S12). Hydrogen bonding contributes moderately to the reaction coordinate, and particularly it helps improve the quality of d(O3–C4) as an RC (Supporting Information, Figure S11), indicating the coupling between these two motions. Interestingly, the solvation-shell dipoles randomly distributed in the reactant state tend to be antiparallel with the reactant dipole at the transition stage (Supporting Information, Figure S12A), which indicates a preference for more ordered electrostatic interactions at the TS. We further optimized the RC by linearly combining some important candidate RCs, e.g., d(C1–C6), d(O3–C4), and hydrogen bonding. A rising barrier height along the optimized RC was anticipated. The 0.82d(C1–C6)–0.18d(O3–C4) was found best among all trials (Figure 2C), which approximates the normal vector to the “separatrix” on the 2D (d(C1–C6) × d(O3–C4)) projected space. This combination hints at the predominance of the C1–C6 bond over the O3–C4, to some extent reflecting the breakdown of the ideal “concertedness”. We note here that the candidate RCs (or the “basis set”) may not be complete, whereas the local dimension of TS can be intricate and nonlinear. Nevertheless, the Bayesian optimization leads to a quantitative reduction of dimensionality and allows us to quantify the mechanistic difference of the reaction under different conditions.

Figure 2.

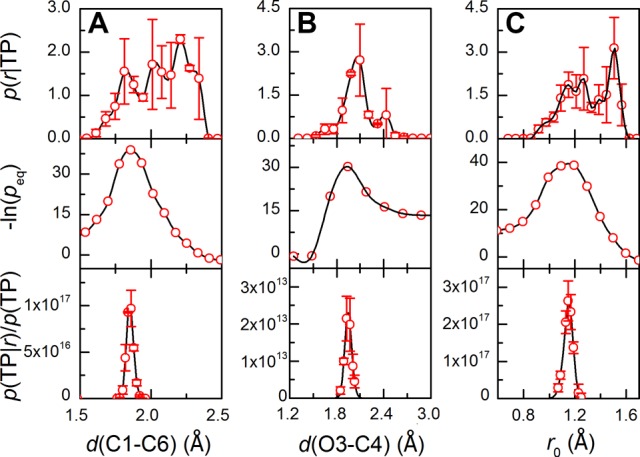
Quantitative assessment and optimization of the reaction coordinates (r) via Bayesian learning. (A) The C1–C6 bond length, d(C1–C6), as r (error bars too small to be displayed are not shown). (B) The O3–C4 bond length, d(O3–C4), as r. (C) The linear combination of d(C1–C6) and d(O3–C4), r₀ = 0.82 d(C1–C6)–0.18 d(O3–C4), is the optimized reaction coordinate. From top to bottom: the probability distribution of r on transition paths; the equilibrium probability distribution of r; the probability density of being on a transition path given the value of r (without normalization).

Solvation Effect and Inhomogeneous Dynamics

As a common practice, the rate constant is often calculated by TST along a selected RC. However, applying TST with the above optimized RC still leads to an overestimated rate constant (compared to the calculated absolute rate) by a factor of 20, yielding the transmission coefficient κ_TST ≈ 0.05 (see Supporting Information, Supplementary Text section VII). The nonunity κ_TST may result from two sources: the imperfection of the chosen RC, and/or the recrossing events caused by dynamic solvent effects.⁷ The dynamic solvent effects were historically addressed in terms of Kramers’ theory,^13,14 in which the reaction in solution is viewed as a thermally activated barrier crossing on a one-dimensional potential energy surface. The collisions with the solvent are included as a friction that affects the progress of the system along the RC. This theory expresses the rate constant as follows:^12,14

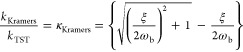2

k_Kramers and k_TST stand for the theoretical rate constant derived from Kramers’ theory and TST respectively, and κ_Kramers is the transmission coefficient; the friction damping frequency ξ is a metric of dynamic solvent effect on the reaction coordinate motion; ω_b is the barrier vibrational frequency which can be evaluated through Fourier analysis of the transition paths (ω_b ≈ 2 × 10¹³ s^–1, Supporting Information, Supplementary Text section IX). The diffusion constant (D*) along the chosen RC accounts for solute–solvent interactions and can be estimated through the transition path time (τ_TP):^10,33

3

where γ ≈ 0.577 is the Euler constant and χ is the curvature of the inverse parabola at the free-energy barrier top (Figure 1B); k_B and h are Boltzmann and Planck constants, respectively. T denotes the temperature. The average transition path length τ_TP is 88 ± 30 fs (Supporting Information, Figure S9). Given the curvature χ ≈ 7 × 10² (k_BT)·Å^–2 and the average barrier height ΔG^‡ ≈ 22 kcal/mol (Figure 1B), the diffusion constant D* approximates 7 × 10^–6 cm²·s^–1. This value corresponds to the 1D thermal diffusion length near the barrier top 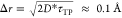, consistent with the TS breadth determined in Bayesian analysis (Figure 2A). After the Stokes–Einstein relation was applied, the friction coefficient was obtained, ξ = 3 × 10¹⁴ s^–1 ≫ ω_b (see Supporting Information, Supplementary Text section VII), indicating an overdamped solvent friction. Therefore, the Kramers’ transmission coefficient (evaluated according to eq 2) κ_Kramers ≈ ω_b/ξ ≈ 0.07, a value comparable to κ_TST. This small valued transmission coefficient suggests non-negligible recrossings and a lower pre-exponential factor (see Supporting Information, Supplementary Text section X).

Next, to obtain molecular details on the dynamic solvent effect, the reaction dynamics including both the intrinsic molecular properties (charges on O3, molecular dipole, etc.) and the solvent–solute interactions (hydrogen bond, excluded volume, etc.) were investigated following the reaction progression (reflected by d(C1–C6) as in Figure 3). This reaction is marked by a significant dipole change and charge separation (Figure 3A). The mutually coupled intrinsic molecular properties (e.g., d(C1–C6), molecular dipole and O3 charge) were also found strongly correlated with solvent DOFs including hydrogen bonding and solvent-excluded volume (Figure 3C, and Supporting Information, Figure S13).³⁴ The shrinkage of solvation shell (Figure 3C and Supporting Information, Figure S12B), reminiscent of the well-known “cage effect”, was observed during the reaction progression. Figure 3B further shows that the enrichment of charge on O3 position correlates strongly with the hydrogen-bonding from nearby water, which could help stabilize the charge separation during the transition, especially when the negative charge is enriched on O3 near the TS. These typical solvation effects could explain the acceleration of “in-water” Claisen rearrangement.^21,28

Figure 3.

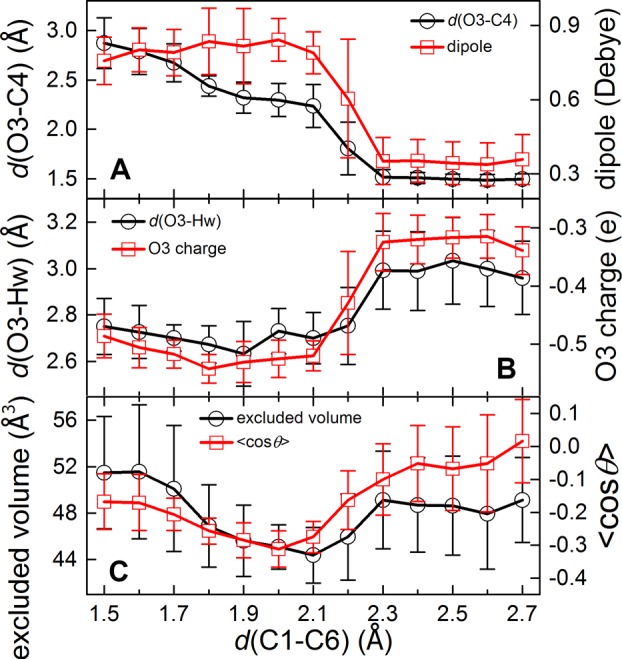
Dynamic changes of intramolecular properties and solute–solvent interactions along the reaction progression (d(C1–C6)). (A) O3–C4 distance d(O3–C4) (black) and molecular dipole (red) of the reactant; (B) the negative charge on O3 atom (red) and the hydrogen bond length (d(O3–Hw) (black); (C) the solvent-excluded volume (black) and the dipole orientation of the solvation shell codθ (red, see the definition in the Supporting Information, Text section V).

Additionally, the bond breaking and forming processes seem not consistently synchronic evidenced by the less-than-unity cross-correlation coefficient between d(C1–C6) and d(O3–C4) (Supporting Information, Figure S13), although this reaction is generally thought to be concerted (especially in gas phase). This cross-correlation coefficient is about −0.64, somewhere in between −1 (for an ideal concerted process) and 0 (for ideally stepwise mechanism), signing the mixed concerted and nonconcerted characteristics of the reaction pathways. The TS resembles the product so the backward reaction encounters an “early” TS, while the forward reaction is characterized by a “late” one. To illustrate the apparent nonconcertedness, we projected the “concerted transition state” (defined by d(C1–C6) and d(O3–C4) both), representative transition trajectories, and the “separatrix” region on to 2D diagrams (Figure 4A), respectively. Some trajectories indeed deviate far from the concerted transition state. Indeed, there exist more than one entry/outlet that connects the transition paths to the product basin (Supporting Information, Figures S7 and S17), which show the heterogeneity of reaction mechanisms. We hence employed a spectral clustering algorithm, proposed by Wang and Zhang³⁵ to deal with multivariate time series, on the transition path ensemble to test the mechanistic heterogeneity. Within the dimensions expanded by candidate RCs (associated with optimized coefficients from Bayesian learning), this approach yields the optimal cluster number which turns to be two (Supporting Information, Figures S15 and S16), and robustly clusters the transition paths accordingly (see Supporting Information, Supplementary Text section VIII). The consequential two clusters exhibit distinct features: paths in Cluster 1 are relatively short, passing nearby the concerted transition state with a relatively tight structure, while those in Cluster 2 are longer, more diffusive, and nonconcerted characterized by a loosened structure (Figure 4A). Coincidentally, transition paths in the two clusters enter/exit the product basin from different “entries/outlets” mentioned above (Supporting Information, Figure S18). Further analysis shows that the hydrogen bonds in Cluster 2 are shorter and stronger, with a more significant charge enrichment on O3 (Supporting Information, Figure S19).

Figure 4.

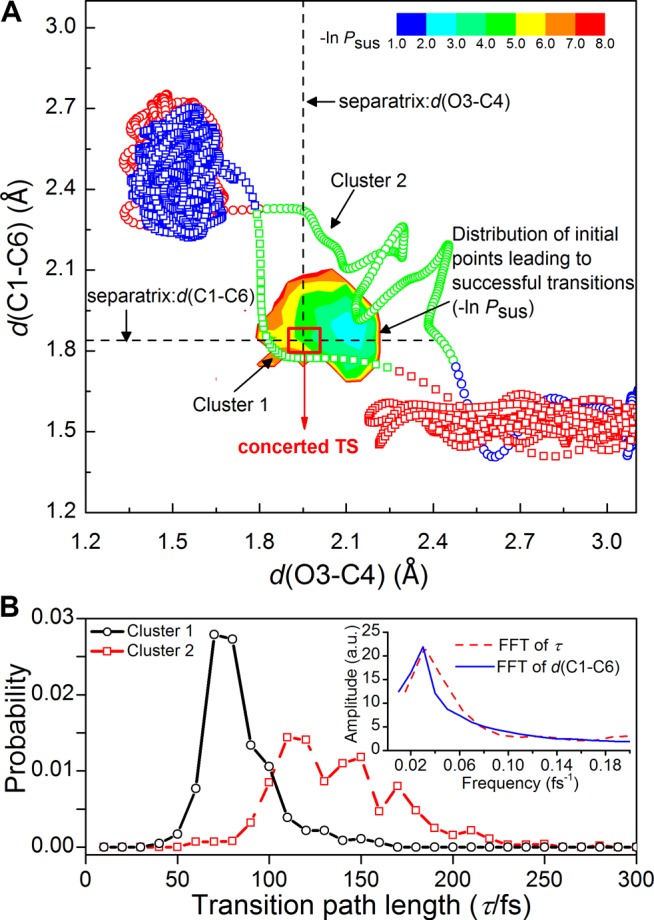
Inhomogeneous reaction pathways. (A) Two representative trajectories from Cluster 1 (hollow square symbol) and 2 (open circle symbol) are depicted in a 2-D diagram, respectively. Each trajectory starts from the red-colored basin, passing by the green-colored transition-path region and arrives at the blue-colored basin. The concerted TS locates at the cross point of the two separatrixes defined by d(C1–C6) and d(O3–C4). The probability distribution (−ln P_sus) of initial configurations for successful shootings is shown in a heat map, rendered according to the upper-right color scale. (B) Probability distributions of the transition path length for Cluster 1 (solid black, open circle) and Cluster 2 (red dashed, hollow square). (Inset) Fast Fourier transform (FFT) of the frequency of the oscillatory probability distribution of the transition path length in Cluster 2 (red dashed line), the vibrational frequency of d(C1–C6) during transition (solid blue line) with the amplitude in arbitrary units.

More intriguingly, the distributions of transition path lengths of these two trajectory clusters are distinctively different (Figure 4B). Cluster 1 has a very sharp Gaussian peak in the short-time region, while Cluster 2 exhibits a dispersed shape with multiple damping peaks. Fourier analysis indicates the occurrence frequency of the observed peaks is about 0.02–0.03 fs^–1, very close to the vibrational frequency of d(C1–C6) and d(O3–C4) in the transition path region (Figure 4B inset, and Supporting Information, Figure S22). In contrast, little resonance between bond-forming/-breaking motions was observed for the reactant/product or the nonreacting trajectories (Supporting Information, Figure S23). Such specific coupled oscillatory motions may reflect the energy transfer/dissipation during the reaction as recently observed for a gas phase reaction.³⁶ Our observations suggest that (i) the transition events may involve a varied number of vibrations of the breaking/forming bonds (Supporting Information, Figure S21); (ii) the transition is more (likely to be) concerted if crossing the TS region occurs within one vibration of the C1–C6 and O3–C4 bond; (iii) the breakdown of concertedness is subject to the strong solvent–solute interactions that allow the reactant lingering nearby the transition region for a longer time; and (iv) resonant collective vibrational modes are unique features for the transition state. Moreover, during the transition, the hydrogen bond length is strongly and dynamically correlated with the O3–C4 bond vibration that causes the translation of O3 position (Supporting Information, Figure S22). We also found that, compared with the failed reaction attempts, the variance of the hydrogen-bond lengths is much less in these successful transition trajectories (Supporting Information, Figure S25), and that the correlation between the hydrogen bond and the forming/breaking bonds is also more persistent (Supporting Information, Table S4). These observations imply that the transient dephasing of the hydrogen bond and O3–C4 vibration may be responsible for recrossing and transition failure (Supporting Information, Figure S26).

Discussion

Molecular bond breaking/forming defines chemistry. Although reactions in solution are among the most familiar events to chemists, many basic questions remain to be answered: how is the energy accumulated and dissipated during the chemical transition? How fast is the transition? How diverse is the transition pathway in solution? The understanding of solvation effects may add new insights or serve as a test to the transition-state theory and is thus essential for designing new reactions and catalysts, hence drawing the interest of many research fields. Usually a chemical reaction is too transient for high-resolution detection of the dynamics instrumentally. Complementarily, we applied efficient sampling strategies to successfully investigate these microscopic events using QM/MM MD simulations. The method presented in this paper enjoys several merits: (i) it avoids following any preselected CVs, being automatic and limiting subjective biases, while it is compatible with available a prior knowledge to further boost the efficiency;³⁷ (ii) it prioritizes the sampling effort on chemical transitions and meanwhile ensures sufficient sampling of solvent configurations; (iii) apart from the thermodynamics, it generates “true-dynamics” trajectories for kinetics and dynamics studies; (iv) it enables parallel comparison with experiments given that absolute rate constants and activation parameters can be conveniently calculated. Moreover, this sampling protocol enables us to systematically investigate and connect the thermodynamics, kinetics, and dynamics in a self-consistent manner (see Supporting Information, Supplementary Text section VI and eq S38). In addition to the improvement of sampling strategy, development in the methods is also needed for analyzing the mechanisms of chemical reactions in solution. In this study, based on high-dimensional data on the chemical transitions, information underlying both the equilibrium and transition path ensembles is analyzed using data-mining techniques, especially the Bayesian learning approach (or genetic neural network⁵ if one desires to introduce the nonlinearity). Given that the full-dimensional reactive trajectories can be projected onto arbitrary postselected reduced dimensions by virtue of MITS, seeking for RC is now cast as a dimension-reduction problem with possible variationally optimized solution, and the TS and “dividing surface” for (retro-)Claisen rearrangement are statistically defined on reduced dimensions through Bayesian learning. Clustering analysis of the dynamic transition paths further allows us to examine and identify different reaction pathways. Such a combination of CV-free sampling strategy and machine learning techniques maximize the ability to reveal and even predict chemical reaction mechanisms through MD simulations.

As barrier crossings in enzymatic reactions are thought to be subjective to protein dynamics,³⁸ the mechanistic and dynamics study of (retro-)Claisen rearrangement shows that reactions can also be complicated under solution conditions. Solvent coordinates play an important role in the reaction mechanism and dynamics: (i) specific water-reactant interactions facilitate the “in-water” reactions, (ii) overdamped solvent–solute frictions lead to the less-than-unity transmission coefficient and the diffusive barrier-crossing; (iii) the solvent configuration may also be closely related to microscopic energy transfer process in thermally activated reactions, resulting in, for instance, the observed “cage effect” and the resonant vibration of the hydrogen bond with the breaking/forming bonds and other possible collective modes of the TS complex. It is instructive to summarize the multiple roles of water played in the reactions. Water possesses specific collective properties: the high cohesive energy density, and strong dipoles, which give rise to the so-called hydrophobic effect and drives the extended solute (e.g., the product in Figure 1A) into more compact and reactive conformation thus accelerating the (backward) reaction rate.²⁸ Meanwhile water as individual molecules is small in size and capable of hydrogen bonding,²³ rendering water as a “catalyst” to facilitate the reaction. Taken altogether, the kinetic acceleration of this retro-Claisen rearrangement (the large k_–1) can be well understood. Compared to experimental neat conditions at room temperature (k_1,exp ≈ 10^–6 s^–1, k_–1,exp ≈ 10^–7 s^–1),²² the in-water context scarcely affects the forward reaction rate (where the less polar reactant is already very compact, and ether-oxygen is a weak hydrogen bond acceptor), but substantially accelerates the retro-Claisen rearrangement, by both promoting the accumulation of compact reactive conformation and forming stronger hydrogen bonds (with the carbonyl group) at the TS, and thus shifts the equilibrium toward the more compact ether. One may expect the choice of other nonpolar/aprotic solvents may alter or even reverse this thermodynamics effect.

Additionally, we identified inhomogeneous dynamics and mechanisms underlying this condensed phase reaction, which arise from different coupling modes and strengths between DOFs of the solvent and reactant. Concerted and nonconcerted transition pathways were both identified, which contribute to the overall rate constant differently (Supporting Information, Table S3). Noteworthy, the concept of “concertedness” depends on the time scale of observations. For instance, if one looks at this reaction at the resolution of 1 ps, the reaction is certainly concerted since most transient nonconcerted dynamics has been averaged out. However, with more details and higher resolution (e.g., smaller time steps) in dynamics as in this paper, it is more likely to find the mechanism to be nonconcerted, since the C1–C6 and O3–O4 vibration (and thus bond breaking/making) is very unlikely to be always in resonance. Moreover, it was found that the non-Markovian solvation configuration (i.e., the solvent configuration relaxation lags behind the rapid bond rearrangement process) may result in the asymmetry of this reversible reaction; hence the forward-bound and backward-bound trajectories favor different transition pathways (Supporting Information, Figure S20 and Table S3). Therefore, the solvation state subtly influences the transition pathways (and the TS), and such influence is likely to be linked with the regio-/stereoselectivity of organic reactions. For an outlook, the findings in this study will hopefully refresh and deepen our understanding of chemical reactions and dynamics in complex media. The methods used here, which can be further ameliorated by high-level electronic-structure calculations and corrections for nuclear quantum effect, will make more accurate molecular details of chemical reactions approachable.

Methods

QM/MM simulations were performed on the AMBER10 MD platform. Simulation details are included in Supporting Information, Text section I. For configurational and reactive trajectory sampling, the MD simulations were performed under an NPT ensemble (300 K, 1 atm). Transition path shootings were executed under an NVE ensemble (Supporting Information, Text section IV). Detailed methods and algorithms (including MITS, ESoRT, Bayesian learning, spectral clustering and Fourier transform, etc.) are included in Supporting Information Text.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.7b00037.

• Detailed methods, algorithms and data analyses with associated figures, and tables (PDF)

• Movie (MPG)

Author Contributions

^# J.Z. and Z.Z. contributed equally to this work. J.Z., Z.Z., Y.I.Y., L.Y. and Y.Q.G. designed the research; J.Z., Z.Z., L.Y., and Y.Q.G. performed the research; J.Z., Z.Z., S.L., and Y.Q.G. analyzed data; and J.Z., Z.Z., Y.I.Y., L.Y., and Y.Q.G. wrote the paper.

The authors declare no competing financial interest.