Best (but oft-forgotten) practices: mediation analysis^,

Abstract

This contribution in the “Best (but Oft-Forgotten) Practices” series considers mediation analysis. A mediator (sometimes referred to as an intermediate variable, surrogate endpoint, or intermediate endpoint) is a third variable that explains how or why ≥2 other variables relate in a putative causal pathway. The current article discusses mediation analysis with the ultimate intention of helping nutrition researchers to clarify the rationale for examining mediation, avoid common pitfalls when using the model, and conduct well-informed analyses that can contribute to improving causal inference in evaluations of underlying mechanisms of effects on nutrition-related behavioral and health outcomes. We give specific attention to underevaluated limitations inherent in common approaches to mediation. In addition, we discuss how to conduct a power analysis for mediation models and offer an applied example to demonstrate mediation analysis. Finally, we provide an example write-up of mediation analysis results as a model for applied researchers.

INTRODUCTION

Mediation is a third-variable effect that explains how or why 2 variables relate. By construction, mediation analysis implies a causal process that connects ≥2 variables. The mediation model considers the impact of an intervening variable (i.e., a mediator), M, which is posited to transmit the influence of an independent variable, X, onto an outcome, Y. Other terms used to describe mediator variables include intermediate variable and surrogate endpoint. One estimates parameters of interest in the statistical model within a theoretically defined, causal chain of variables. Investigators may conduct a mediation analysis to examine why an observed relation between variables exists or to help understand outcomes associated with prevention or intervention programs. In both scenarios, the impetus behind analyzing mediation effects is to illuminate the mechanism (or mechanisms) through which variables relate.

Mediation analysis has been used to examine relations among a wide range of predictor and outcome variables in nutrition research. Within the American Journal of Clinical Nutrition (the Journal), genomic, proteomic, and metabolomic variables (e.g., serum lipid concentrations, specific genetic polymorphisms or biomarkers, and BMI) have been tested as putative mediators underlying the impact of behavioral predictors (e.g., caloric intake, red meat consumption, regional diet, and coffee consumption) on a range of health outcomes: carotid atherosclerosis, diabetes risk, liver cancer risk, and pregnancy complications, respectively (1–4). Other research has considered how variables such as adiposity or previous falls may act as potential mediators of the impact of birth weight and diet on sedentary behavior and fracture risk, respectively (5, 6). Fewer studies have capitalized on the use of mediation analysis to evaluate intervention programs targeting health promotion and dietary outcomes (7, 8). Lockwood et al. (9) noted this latter point as well in an earlier review of the literature appearing in the Journal of the American Dietetic Association between January 2006 and May 2008. Only 11 of the 40 mediation studies Lockwood et al. identified came from randomized intervention trials, indicating that the lion’s share of randomized controlled trials in the nutrition area generally do not include mediation analysis as part of their evaluation plan.

The wide-ranging mediation research conducted in the nutrition literature mirrors the pervasive use of the technique in contemporary research more broadly. Baron and Kenny’s (10) seminal article on mediation and moderation effects has often been attributed to this focus on investigating mediation, because there was a rapid increase in the presence of mediation analyses across disciplines after the article’s publication. Although Baron and Kenny’s may be the most widely cited mediation publication, other essential references arguably provide more information on the basic tenets, rationale, and underlying foundations of mediation analysis (11–16). Judd and Kenny (11) describe mediation as a process analysis and emphasize the utility of examining mediation effects in intervention studies. Alwin and Hauser (12) and Wright (13) critically contributed to understanding how the estimation of mediation effects has roots in path analysis, which is a special case of structural equation modeling (SEM)³ that extends regression analysis and provides a framework for evaluating whether a set of data fits a causal model of interest.

An influx of additional methodological research on mediation analysis since the historical references cited above has further driven the accessibility of the method to substantive researchers (17–22). The utility of this access is useful, however, only if it is considered in tandem with critical theoretical considerations and assumptions underlying the statistical mediation model. This contribution in the “Best (but Oft-Forgotten) Practices” series thus focuses on discussing mediation analysis with the ultimate intention of helping nutrition researchers do the following: 1) clarify the rationale for examining mediation, 2) avoid common pitfalls when using the model, and 3) conduct well-informed analyses that can contribute to improving causal inference in evaluations of underlying mechanisms of effects on nutrition-related behavioral and health outcomes. We concentrate our attention on the single mediator model, to enhance focus on foundational concepts and theoretical matters. The topics discussed here extrapolate to more complex mediation models.

A BRIEF HISTORY OF MEDIATION

Revisiting the historical foundations of statistical mediation analysis affords an opportunity to understand the rationale for its intended use (12, 16, 23). Early references to mediation defined mediators as intervening variables that elaborated cause and effect between ≥2 other variables (14). Researchers often discussed mediation within the context of prevention and intervention studies, where they suggested that treatment effects could be further examined by conducting a “process analysis” of the data to probe how or why an effect occurred (11). In their narrative, Judd and Kenny (11) specified several requisite conditions to support evidence for mediation: 1) the independent variable must affect the outcome, 2) the independent variable must affect the mediating variable, 3) the mediating variable must affect the outcome, and 4) the independent variable must not affect the outcome when the mediating variable is controlled. Baron and Kenny (10) later recapitulated these conditions and went further to emphasize the distinction between mediation and moderation effects, as well as discussed examining the effects together. They additionally proposed that sufficient evidence for mediation could be shown if the relation between the independent variable and the outcome was simply reduced in magnitude once the mediator was controlled for, rather than requiring it to be zero as originally suggested by Judd and Kenny.

Kenny and colleagues’ (10, 11) conditions for mediation have been widely referred to as “causal steps” in the research literature. Although Judd and Kenny’s criteria specified that the independent variable should ideally cause the outcome variable, the authors acknowledged that an independent variable may not strongly relate to distal outcomes. This assertion laid the foundation for an argument presented later in the literature recommending that the requirement of a significant effect of the independent variable on an outcome for mediation should be relaxed (24). Indeed, diminished power to detect distal effects is not the only reason to consider relaxing this requirement; statistical suppression, competing mediators (in multiple mediator models), or unmodeled interactions may also compromise an examination of the effect. Perhaps more importantly, requiring a significant effect of the independent variable on a dependent variable in this context erroneously treats the relation as a population-level entity, rather than a statistical test that is subject to type 1 and type 2 error (21). Although the effect of an independent variable on an outcome is no doubt a key relation to test in a research study, it need not preclude the evaluation of mediation. Regardless of whether there is a significant effect of the independent variable on an outcome, conducting a mediation analysis can offer inherent value to a research study, particularly in prevention and intervention work (see section entitled “Mediation by design compared with mediation for explanation” below). Before delving further into details on mediation analysis, we first differentiate the effect from other third-variable models.

DIFFERENTIATING CONFOUNDER AND MEDIATION MODELS

Understanding the difference between confounder and mediator variables has often been a source of confusion for applied researchers. Certain approaches available to test statistical mediation propagate this misunderstanding by not emphasizing directionality of relations between variables in the mediation model. An inherent challenge in differentiating confounding and mediation effects is that the underlying statistical models are equivalent from a purely mathematical perspective (25, 26). It is helpful to consider the models within a path analysis context (12, 13, 27) to understand differences between them more clearly. For those unfamiliar with path analysis, one can view the framework as a multivariate extension of the general regression model for purposes of this discussion. In contrast to regression analysis, path analysis derives parameter estimates by maximizing how well a model reproduces the observed covariance structure of a set of data, rather than by minimizing the sum of the squared residuals as in ordinary least-squares regression (12). The utility of path analysis within the context of differentiating confounder and mediator models lies in the basic premise of the method—namely, that “Any correlation between variables in a network of sequential relations can be analyzed into contributions from all of the paths (direct or through common factors) by which the 2 variables are connected” (27).

For any path analysis, a corresponding path diagram illustrates hypothesized relations among variables in the model by denoting directionality with single-headed arrows connecting putative predictors with ≥1 outcomes. Every path diagram has a corresponding system of equations that delineates the statistical model underlying the diagram (13). Readers interested in learning more about the implementation of path analysis in nutrition research may benefit from reviewing Kirkegaard et al. (28), who applied path analysis in an article appearing in the Journal to investigate factors involved in the association between breastfeeding duration and BMI-adjusted waist circumference 7 y postpartum.

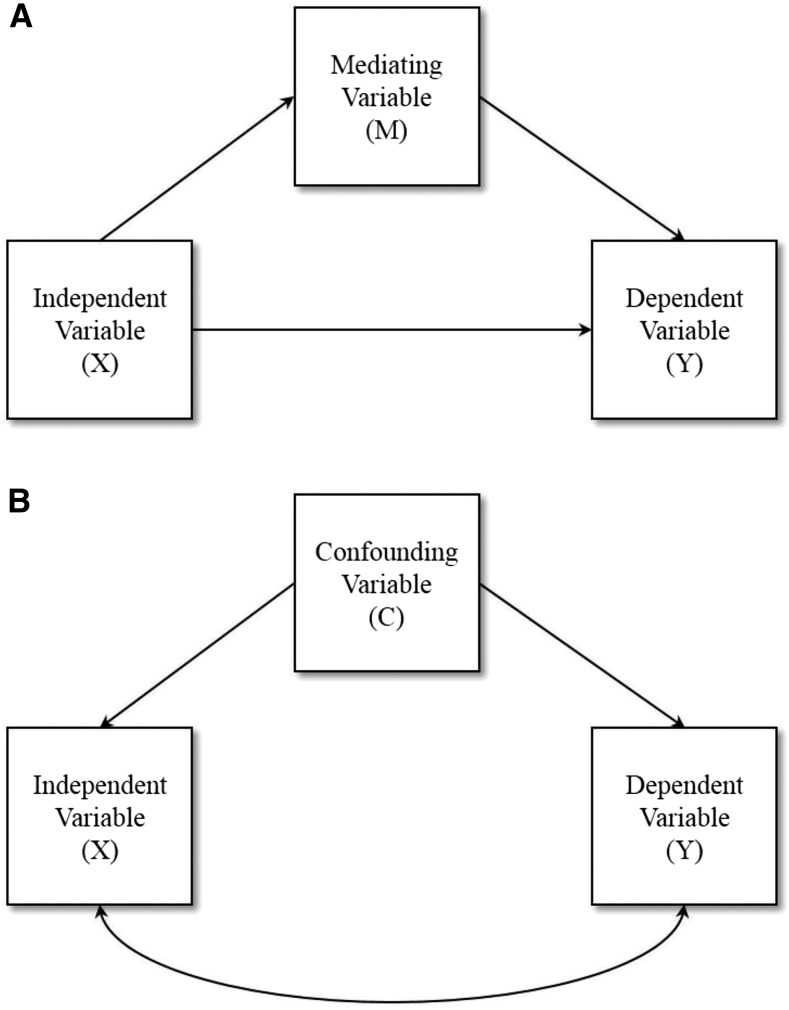
Figure 1 shows the path diagrams associated with the simplest mediation and confounding models, respectively. In these diagrams, boxes represent the variables in each model. Figure 1A shows a single mediator model, where the independent variable X is hypothesized to affect a third variable, M (i.e., the mediator), which in turn, is hypothesized to affect the ultimate outcome, Y. In contrast, Figure 1B shows a basic confounder model. This panel indicates that a third variable, C (i.e., the confounder), is hypothesized to simultaneously predict X and Y, artificially enhancing or suppressing their relation. Conceptually, the mediation model posits that a series of variables relates via a causal chain of effect, such that each variable in the model affects subsequent variables occurring later in the chain. No such causal chain of effect among the variables is posited in a confounding model; that is, C does not intercede in a causal chain between X and Y. Rather, the confounding model theorizes that X and Y relate given that they both have an underlying common cause, C; C causes X and C causes Y. This common cause (i.e., the confounder) introduces bias in estimating the causal effect of X on Y (29). We direct readers interested in learning more about confounding models in the context of causal effect estimation to Greenland et al. (29) and VanderWeele and Shpitser (30).

FIGURE 1.

A conceptual diagram differentiating mediation (A) and confounding (B) effects. Panels A and B are distinguished by a directional reversal of the arrow defining the relation between the independent variable and the “third” variable.

A classic confounding example is the relation between visual acuity and gray hair. If examined in isolation, there is often a bivariate relation observed between these 2 variables. However, once age (i.e., the confounding variable in this scenario) is controlled for, the relation between visual acuity and gray hair attenuates. This example is not demonstrative of mediation, because age is not theorized to be intermediate in a causal sequence between visual acuity and gray hair. Consider a second confounding example from the nutrition literature. Kris-Etherton et al. (31) reported that, although the Seven Countries Study (32) found a significant negative relation between fish consumption and 25-y mortality rates, the association was no longer significant when researchers controlled for smoking behavior (one of several referenced confounding variables). This example is not mediation, because smoking is not theorized to intervene in a causal sequence between fish consumption and mortality. The point shown in both examples can be clarified by the path diagrams in Figure 1, which shows that the third variable in a confounding model (i.e., the confounder) acts exclusively as an exogenous variable that is not predicted by other variables. In contrast, the third variable in a mediation model (i.e., the mediator) plays a dual role: it not only acts as predictor hypothesized to affect the ultimate outcome but also operates as an outcome, hypothesized to be affected by the independent variable.

Although conceptual distinctions among mediator and confounder variables can be shown with extreme substantive examples, the functions that variables play in real data are often less clear. Moreover, identifying the role of a variable as a confounder or as a mediator cannot be inferred by statistics alone. The literature on equivalency of path models helps elucidate this issue (33–36). Specifically, the posited causal structure between variables in a path analysis is not directly explained or verified by model estimation; different models may reproduce the observed covariance structure of data equally well with completely recursive path models, where the flow of causal relations in the model is one-way rather than bidirectional (35). In this case, although models may correspond to different causal structures and distinct substantive interpretations (such as the confounder and mediator models), they can be viewed equivalently from a statistical perspective (33, 34). This latter point stresses the importance of having a compelling theoretical rationale for examining mediation. Strong measurement and design features are also critical to strengthen support for hypothesized ordering of the variables.

MEDIATION BY DESIGN VERSUS MEDIATION FOR EXPLANATION

The notion that mediation effects may exist in the absence of a significant effect of the independent variable on an outcome may seem to belie the very foundation of the model. Yet, examining mediation in the presence of a nonsignificant overall effect of the independent variable on an outcome can shed light on key issues that illustrate utility of the analysis. The use of mediation by design as a tool in intervention studies may be the best exemplar to demonstrate this point.

Mediation analyses can be framed as mediation by design or mediation for explanation. In mediation for explanation studies, mediation analysis is conducted to probe underlying mechanisms for why a relation exists between a predictor and an outcome (18). Such analyses can lend insight into the etiology of different health and behavioral outcomes and help generate ideas for future mediation by design studies. Numerous mediation for explanation studies have been published in the Journal (1, 2, 5, 37–42).

In mediation by design studies, researchers identify mediator variables a priori and design an intervention to manipulate those variables with the ultimate intention of affecting an outcome (17, 43). If the mediator relates to the outcome as hypothesized, successful manipulation of that variable should yield change in the target behavior. Consider an intervention targeted to help individuals lose weight. One activity in such a program may be keeping a food journal, because research has shown that self-monitoring can result in positive behavioral change (44). The decision to target self-monitoring of dietary intake as part of the intervention is based on the concept that self-monitoring will affect weight loss by reducing individuals’ caloric intake. Mediation by design dually examines whether an intervention changed the targeted mechanism of action (i.e., the mediator) and whether changes in the mediator were associated with changes in the targeted outcome (20, 43). These entities are referred to as “action theory” and “conceptual theory,” respectively (45). The action theory of a model outlines program curriculum components related to a hypothesized mediator or mediators. The conceptual theory of a model defines how an intervening variable or variables relate to outcomes; relations examined in this part of the model are driven by theory or previous research.

Mediation by design analyses help interventionists understand how to proceed in the face of nonsignificant overall program effects, by identifying intervention aspects that contributed to success or failure (19, 43). If a mediation by design analysis indicates failure in the action theory of a program, stakeholders should focus efforts on identifying issues that may compromise effective program implementation and/or delivery. If the analysis indicates a breakdown in the conceptual theory of a program, practitioners should refine or reconsider the theory proposed to underlie the relation between the mediator and outcome. When both action and conceptual theories fail, practitioners may need to consider whether the program is worthwhile to pursue (45). Lockwood et al. (9) provide a useful table for nutrition researchers to reflect on different program effect possibilities through an action and conceptual theory lens, which may lend insight into interpretation of results and choices for future action, given particular scenarios.

Despite the valuable information that mediation by design studies provide, these types of analyses do not appear routinely in clinical nutrition research and represent a missed opportunity. Indeed, the impetus behind mediation by design analyses aligns well with the defined scope of this Journal that seeks, in part, to “describe scientific mechanisms [emphasis added] … of dietary interventions in the context of disease prevention.” A range of nutrition-based interventions lend themselves well to such analysis, and researchers would benefit from conducting mediation by design studies.

ESTIMATING MEDIATION EFFECTS

This article discusses statistical methods for testing mediation effects, in contrast to design approaches for testing mediation. We direct readers who are interested in learning more about experimental design approaches for examining mediation hypotheses to Pirlott and MacKinnon (46). With respect to statistical mediation analysis, MacKinnon and Dwyer (19) provided regression equations for the mediation model that remain in common use today:

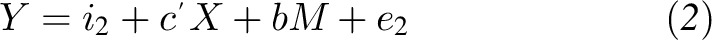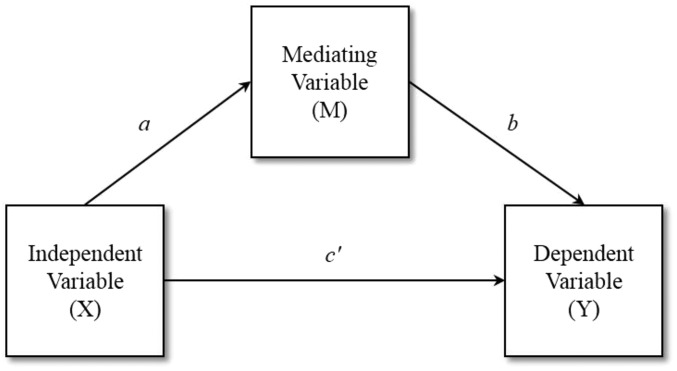
In the above equations, Y represents the outcome variable in an analysis, X represents the independent variable, and M represents the mediating variable. The c coefficient in Equation 1 defines the overall effect of the independent variable on the outcome and is called the total effect. The c′ coefficient in Equation 2 defines the effect of the independent variable on the outcome controlling for the mediating variable and represents the direct effect in a mediation analysis. The b coefficient in Equation 2 defines the effect of the mediating variable on the outcome controlling for the independent variable, and the a coefficient in Equation 3 defines the effect of the independent variable on the mediating variable. The intercepts for each equation are defined by i₁, i₂, and i₃, respectively, and e₁, e₂, and e₃ represent the corresponding residuals. Figure 2 provides an illustration of these regression equations in a path diagram, where the product of the a and b coefficients defines the indirect effect of X on Y through M given conventional path-tracing rules (12). Different approaches to testing statistical mediation make use of ≥2 of the equations above.

FIGURE 2.

Path diagram of a single mediator model, where the product of the a and b coefficients defines the indirect effect of X on Y through M. The c′ coefficient denotes the direct effect of X on Y, controlling for M. In linear models with continuous outcomes, an estimate of the total effect of X on Y is parameterized as follows: c = ab + c′.

Covariates can be incorporated into the equations as needed, and the model can be extended in a straightforward manner to incorporate additional X, M, or Y variables (18). Introducing >1 X, M, or Y variable in the equations yields a multiple mediator model, where >1 mediation effect is estimated. If multiple Y variables are considered, multivariate methods should be used. Software packages with SEM utilities can simultaneously estimate Equations 1, 2, and 3 (rather than having to estimate individual regression models) and can handle multivariate mediation models adeptly. To get a better understanding of how SEM may be of utility in nutrition research, we direct readers to Konttinen et al. (37), who, in the Journal, provide an applied example of SEM with latent variables to examine mediation effects.

Assumptions and causal inference

Assumptions underlying the statistical mediation model include those associated with regression analysis such as no omitted variables, no measurement error, and no correlated errors (47); correct causal ordering of the variables; no reverse causality effects; and no interaction between the predictor and mediator variables (18). The last assumption may be addressed by incorporating an interaction term between X and M in Equation 2, and by estimating separate mediation effects for each level of X. Including covariates in a mediation model, especially propensity scores, can help toward satisfying the no-omitted-variables assumption (48). One should avoid the use of posttreatment variables as covariates to minimize confounding (49).

The issue of causal inference in mediation has been extensively studied. Nonrandomized studies make interpretation of causal relations in the mediation model tentative without additional design considerations. Although the mediation model implies a causal structure among variables, causal effect estimation is not often possible if the sample is not also randomly assigned to levels of the mediating variable (50, 51). Randomizing X strengthens the assumption that the independent variable will not correlate with residual variance in M or Y. If M is not randomly assigned, it has the potential to be confounded with the assignment mechanism of X and may not be statistically independent from the outcome variable. Statistical solutions to causal inference problems in the mediation model have been proposed (52–55), and causality remains a large area of methodological study in mediation analysis today (56). Instrumental variable methods (57) and principal stratification from both frequentist and Bayesian perspectives (52, 58) provide frameworks to address causal inference in the mediation model. Methods for conducting sensitivity analyses via marginal structural models are also available to assess the robustness of mediated effects to omitted variables (59). Such analyses can also elucidate why a mediation relation may no longer hold after modeling applicable confounder variables. Finally, incorporating design features into a mediation analysis (e.g., matching) may be able to reduce alternative explanations of effects by promoting unit heterogeneity so that subjects are presumed to be equal on non–treatment-related aspects (60).

Approaches to testing mediation

Causal steps

Sample estimates of ĉ, b̂, and â must be significant to support evidence for mediation with the causal steps approach. In addition, ĉ′ must be reduced in magnitude relative to ĉ. If ĉ′ is not significant, the effect is said to be completely mediated, such that the effect of X on Y is conveyed entirely through the modeled mediator. If ĉ′ remains significant, the effect is said to be partially mediated. Although the causal steps procedure provides an elegant framework for conceptualizing mediation, there are critical limitations of the method when applied to real data analysis.

The first limitation is the conclusion that there needs to be a significant relation between the predictor and the outcome for mediation to occur. As described earlier, although this requirement may appear intuitive, the logic is fallible given the nature of null hypothesis significance testing and other statistical considerations. There can be instances in which X does not significantly predict Y but X significantly relates to M, and M significantly relates to Y (providing evidence for a causal chain). Such a possibility is likely to occur in inconsistent mediation models in which the direct effect and indirect effect are opposite in sign, potentially nullifying the overall effect (20, 21, 26). This may likewise occur in multiple mediator models, if different mediation effects vary in sign. The first limitation of the causal steps method heavily drives the second limitation; it is underpowered relative to other approaches for testing mediation (61, 62). Fritz and MacKinnon (61) indicate that if the direct effect is equal to zero, the causal steps approach requires 20,886 participants to detect mediation with 80% power when effect sizes of constituent paths are small (i.e., β = 0.14) in magnitude (63). Finally, although the method outlined by Kenny and colleagues (10, 11) delineates a series of logical steps that insinuate a mediational chain, the approach lacks a formal significance test of mediation. It yields neither a point estimate nor a SE of the mediated effect, precluding construction of CIs.

Joint significance

A related approach to the causal steps is the test of joint significance for mediation. In this method, one evaluates the statistical significance of the b̂ coefficient from Equation 2, and the â coefficient from Equation 3. If both coefficients are significant, there is evidence for mediation. Simulation studies have shown that the joint significance approach has reasonable power to detect effects when compared with other methods (61, 62), but the test does not provide a point or SE estimate for the mediated effect.

Difference in coefficients

The difference in coefficients approach compares the relation between the independent variable and the dependent variable before and after controlling for the mediator. The logic behind the estimator is to ascertain whether there is a significant reduction in the effect of the independent variable on the outcome once accounting for the mediator. Conceptualizing mediation in this way does not promote intentionally considering the implied causal direction of variables in the model and may facilitate conflation of mediation effects and confounding effects. This test of mediation has historically been applied in epidemiology and the medical sciences (19) and is commonly used to test mediation hypotheses in clinical nutrition research today (1, 2, 64, 65).

Mediation is quantified as the difference between the total effect of the independent variable on the outcome (i.e., c in Equation 1) and the direct effect of the independent variable on the outcome accounting for the mediator (i.e., c′ in Equation 2) by using this method. Statistical significance testing of the parameter estimate is conducted by dividing the ĉ – ĉ′ difference by its corresponding normal theory SE:

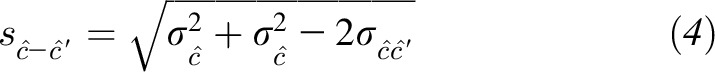Although the difference in coefficients approach provides a point and SE estimate for the mediated effect, the method does not easily extend to more complex models involving multiple mediators or models that include both mediation and moderation.

For example, only one mediated effect is calculated by using the difference in coefficients method in multiple mediator models. The parameter estimate obtained is a composite estimate that quantifies the reduction in the effect of X on Y, once all examined mediators are accounted for as a set. As such, the approach does not allow for examining individual mediated effects. This precludes investigating whether mechanisms of change show differential efficacy or significantly differ from one another. Moreover, the difference in coefficients approach has been shown to yield biased estimates of mediation when used with binary outcomes (66). Although implementing available scaling corrections can mitigate this bias, MacKinnon et al. (66) do not recommend using the difference in coefficients method to examine mediation in this context.

Product of coefficients

The product of coefficients approach for testing mediation derives from path analysis (12, 13, 27) and appears frequently in mediation analyses conducted in the social science literature. The method parameterizes mediation by using path-tracing rules to define the indirect effect of X on Y through the mediating variable, by multiplying the a coefficient from Equation 3 and the b coefficient from Equation 2 to yield ab (see Figure 2). By doing so, the impact of the independent variable on the mediator, as well as the subsequent influence of the mediator variable on the outcome (controlling for the independent variable), are both accounted for. The product of coefficients approach easily extends to complex models involving multiple mediators and/or outcomes, categorical outcomes, multilevel data, and conditional process models (67–71). Although the phrases “indirect effect” and “mediated effect” often have been used interchangeably, it may be useful to distinguish the terms as a means to differentiate cases of mediation in which there is no significant overall effect of X on Y compared with those in which there is a significant overall effect of X on Y, respectively.

Historically, statistical significance testing of the âb̂ estimate has been obtained by dividing the estimate by the square root of a normal-theory, asymptotic variance approximation for the product of 2 random variables:

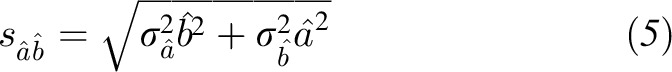The ratio presented in Equation 5 is often called the “Sobel test” for mediation, as the equation was derived by Sobel (72) with the use of the multivariate delta method. Alternative formulas for estimators of the exact (73) and unbiased (74) variance of 2 random variables are available and can also be used for hypothesis testing. Results that use these formulas tend to be trivially different from the Sobel approximation, however, and are thus less often used in applied work. Simulation studies have shown that statistical tests for mediation based on normal-theory variance estimators are unbiased and show tolerable type 1 error rates (62). The tests are often underpowered when used in small samples, however, because the variance estimators (inaccurately) assume normality of the ab sampling distribution (61, 75). This problem can be mitigated to some extent with a larger sample size, because the estimators are asymptotically efficient. For example, simulation work has shown that the Sobel test had sufficient (i.e., 0.80) power with n = 667, when there was a small-to-medium–sized direct effect (i.e., β = 0.14–0.39) in the model, and effect sizes of the a and b regression parameters were both small (61). It is difficult to advocate the use of these methods, however, given the wide availability of more modern procedures that do not impose distributional assumptions and that allow for the formation of asymmetric CIs to test significance of the mediated effect.

Asymmetric CIs

The sampling distribution of the product of 2 random normal variables, such as a and b, is nonnormal (76). When using a normal distribution for statistical inference, incorrect critical values will be referenced to ascertain P values of the mediated effect. This issue yields reduced power to detect mediation effects. Accounting for nonnormality of the ab sampling distribution in significance testing, by computing asymmetric confidence limits for the âb̂ estimate, references the correct critical value associated with a given α level set for a study and affords a more accurate and powerful approach to testing mediation, as compared with asymptotically efficient estimators (77).

A variety of methods exist to compute asymmetric CIs, including an approach based on the theoretical distribution of the product of 2 random, normal variables (76–78), resampling methods such as bootstrapping (79–81), and Markov chain Monte Carlo procedures (82). These methods are available across a range of software packages (e.g., SAS, STATA, SPSS, Mplus, R); researchers are encouraged to use existing code and packages to compute the CIs.

Effect sizes for mediation

Effect size estimates for mediation complement statistical significance testing by providing information on the magnitude of an effect. Characterizing the size of an effect can help researchers understand its practical, or clinical, significance. Most of the work that has been conducted on investigating effect size for the mediation model has focused on single mediator models, although it may be possible to extrapolate the methods to examine individual mediated effects in multiple mediator models. Several different effect size measures have been described: R²_mediated, the proportion mediated (PM), and κ² (83–85). None of the measures are without limitations.

MacKinnon (18) and Fairchild et al. (83) provided several r² effect size measures for individual paths in the mediation model based on squared and squared partial correlations. These measures quantify the amount of variance explained in the mediation model that is uniquely attributable to a single coefficient in the design and promote understanding of the relative contribution of different pieces in the model. They additionally described and evaluated an R²_mediated effect size measure for mediation that quantifies the proportion of variance in Y that is common to both X and M but is not attributable to either predictor alone:

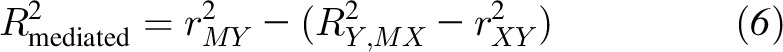The R²_mediated measure has been shown to be unbiased and can be used in sample sizes as small as n = 100, but it is possible that estimates from the measure can be negative in circumstances in which the direct effect is much larger in magnitude than the indirect effect due to a mathematical artifact of the equation (86).

The proportion mediated effect size is an intuitive measure that quantifies the proportion of a total effect that is mediated (84, 87), making a ratio of the mediated effect to the total effect:

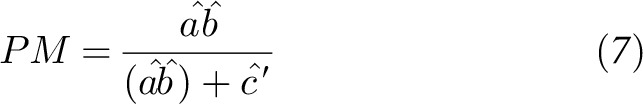Results yielded from the effect size are reported as a percentage. Statistical simulation work has shown that the proportion mediated should be used only with n ≥ 500, however, because of the instability of the estimate in smaller sample sizes (88).

Finally, Preacher and Kelley (85) presented κ² as an alternative to the R²_mediated and proportion mediated measures. The effect size characterizes the magnitude of a mediated effect as a proportion of its “maximum possible value.” Not only is interpretation of the measure difficult to understand (e.g., the maximum possible value varies as a function of the scale of the variables) but subsequent research has shown that the measure does not monotonically relate to the mediation parameter estimate with which it is associated (89). That is, κ² can decrease with increasing values of the mediated effect parameter estimate.

COMMON MISTAKES AND SUGGESTIONS FOR IMPROVED PRACTICE

Having covered foundational properties and theoretical aspects of the mediation model, we turn now to reflect on common mistakes made by applied researchers when conducting mediation analyses. These mistakes include the following: 1) examining mediation in cross-sectional data without sufficient rationale for the posited mediation process, 2) incomplete reporting of results, 3) inadequately handling missing data, and 4) failing to conduct power analyses. We consider each of these areas in the sections below and offer suggestions to improve practice.

Cross-sectional data

Various researchers conducting mediation analyses evaluate mediation effects in cross-sectional data; several examples of this practice have appeared in this Journal (3, 5, 38, 40, 42, 65). Although it may be possible that these instances are not all inappropriate, examining mediation in cross-sectional data that are observational (i.e., not experimental) is generally ill advised. A myriad of methodological work (90–94) cautions against this practice and emphasizes that examining mediation in cross-sectional data implicitly undermines an assumption of the statistical mediation model: the presumption that temporal ordering of variables in the causal chain of mediation is correct. Cross-sectional data preempt the evaluation of alternative temporal ordering of the variables to test the correct causal ordering assumption, and the nature of cross-sectional data lies in contradiction to examining a process that unfolds over time. To be clear, standardized coefficients from a mediation model conducted on observational, cross-sectional data reflect a series of correlation coefficients: 1 bivariate correlation coefficient (i.e., a) and 2 partial correlation coefficients (i.e., b and c′). Any estimations of a mediation effect in such data are thus correlational in nature. The notion that correlation coefficients do not infer causation, and cannot offer insight into directionality of a relation between variables, is a lesson taught early and often in statistics classrooms.

Methodologists have discussed inherent problems with cross-sectional data in mediation analyses, as well as have quantified the statistical bias observed when estimating longitudinal mediation effects in data of this type (90–92). Studies show not only that the sign and magnitude of bias observed in cross-sectional mediation models varies widely, making it unpredictable in practice, but also that cross-sectional sample data can indicate support for mediation effects when there is no true mediation process in the population (92). These findings are not to say that it is impossible to examine mediation hypotheses with data that are collected at one point in time; however, there is an onus on the researcher to provide a compelling rationale that temporal ordering of the examined variables is correct (93, 94). Indeed, Kenny and colleagues (10, 11) emphasized in early work that mediation analysis should not be conducted unless the temporal ordering of the variables is clear. Examining mediation hypotheses with cross-sectional data may be reasonable, for example, if measured variables can reflect nearly instantaneous processes, such as may be the case with some pharmacokinetics work, or imply timing by nature of their construction (18, 93). Consider a research scenario in which the mediating role of parental food monitoring during an individual’s adolescence (M) is posited to explain the impact of parental childhood obesity (X) on subjects’ current obesity status (Y). Although one may garner this information from participants at a single measurement occasion, it may be sensible to argue temporal precedence of the variables in a causal chain given the chronological nature of the constructs. Researchers should be mindful of potential retrospective reporting bias in these cases, however.

Reporting results

Failing to report sufficient information associated with an analysis propagates confusion for readers and precludes future researchers from using the results in a meaningful way (e.g., to conduct meta-analyses). Moreover, the practice undermines the replication of results. This latter point is especially pertinent considering the nationally recognized reproducibility crisis occurring in science (95). Indeed, the NIH and other federal agencies are amending research policies to support enhanced reproducibility of scientific findings, placing methodological rigor and transparent reporting at center stage.

At a minimum, mediation researchers should report the following: 1) the sample size associated with analysis; 2) the software, including version number, and statistical estimator used to conduct the analysis, unstandardized parameter estimates of individual coefficients, and mediated effects (alongside their associated SEs and/or CIs); 3) the effect size of model parameter estimates; and 4) how missing observations were handled in analysis. It is also useful to provide a path diagram of the model for readers to provide an illustration of the relations examined in analysis. This clarifies what roles each variable plays and provides a streamlined avenue for reporting parameter estimates in the model. With respect to estimating mediated effects, we further recommend that researchers use either the product of coefficients approach with asymmetric confidence limits (constructed via bootstrapping or another method), or one of the newer causal inference methods for testing mediation. When examining >1 mediator in a study, we encourage researchers to use multiple mediator models rather than examining several single mediator models individually; this approach is more parsimonious and facilitates the comparison of different mediated effects in the model. Note that if a researcher chooses to examine several single mediator models, it is necessary to invoke a correction for conducting multiple null hypothesis significance tests to control for type 1 error inflation (96). Below, we provide an abbreviated example of a multiple mediator model analysis (with a dichotomous predictor, 2 continuous mediators, and a continuous outcome variable) to serve as a template for applied researchers.

Abbreviated example write-up of mediation analysis results

We conducted a multiple mediator analysis on a longitudinal data set (n = 599) to enhance our understanding of the effects of a health-promotion program conducted in firefighters. The data come from a mediation by design study: Promoting Healthy Lifestyles: Alternative Models’ Effects (PHLAME) (7). Details on the trial are available elsewhere (7, 97, 98). Note that we provide this example as a means to show appropriate steps to conduct and report the results of a mediation analyses rather than to inform the literature in a substantive way.

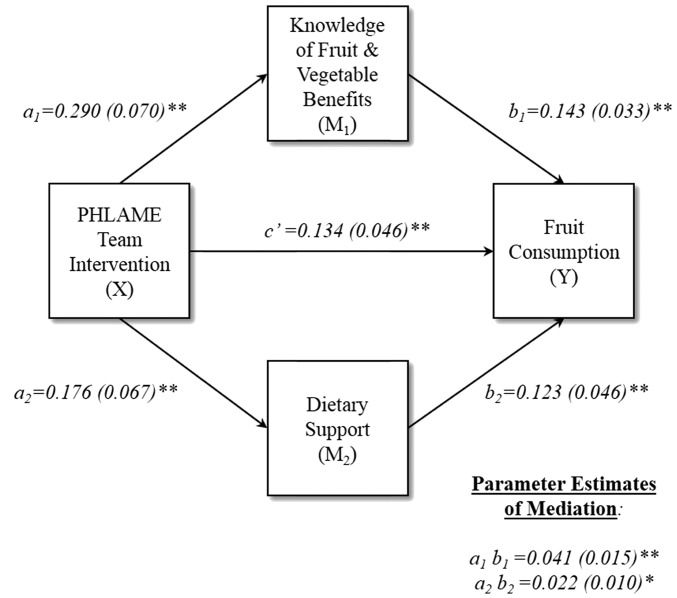
We examined how the PHLAME team program affected fruit consumption via 2 hypothesized mediators: knowledge of fruit and vegetable benefits and dietary support (see Figure 3). Previous research has suggested that knowledge and social support predict fruit and vegetable intake in adults (99). Different program modules targeted the respective mediators, supporting action theory for the intervention. The conceptual theory for the intervention was informed by social-cognitive theory (100) and the health belief model (101).

FIGURE 3.

An example path diagram presenting the results of a multiple mediator model. *P < 0.05, **P < 0.01. PHLAME, Promoting Healthy Lifestyles: Alternative Models’ Effects.

Data were collected at baseline and then after implementation of the 1-y intervention. The mediator and outcome variables were assessed via self-report surveys. Baseline measures of the mediator and outcome variables were incorporated as covariates in the design, and all continuous variables were mean-centered. The predictor, PHLAME team intervention assignment, was dichotomous with a value of 1, indicating that the participant was assigned to the intervention. We analyzed mediation within a path analysis framework by using an SEM software package, Mplus version 7 (102). We estimated mediation effects by using the product of coefficients approach and used a maximum likelihood estimator with SEs robust to violations of normality (in a path analysis framework, robust SE estimates can be used to determine significance of indirect, or mediated, effects). We used full-information maximum likelihood (FIML) to handle missing observations (103) and controlled for clustering to account for the multilevel nature of the data, because 599 firefighters were nested within 48 fire stations (104). The chi-square test of exact model fit suggested that the model-implied covariance matrix adequately reproduced the observed data: chi-square = 11.421, P = 0.326. Additional recommended fit indexes, such as the Root Mean Square Error of Approximation (RMSEA), the Standardized Root Mean Square Residual (SRMR), and the Comparative Fit Index (CFI), also met the criteria for close model fit (105): RMSEA = 0.015, SRMR = 0.022, CFI = 0.996.

Unstandardized parameter estimates for the model are shown in Figure 3, with all associated SE estimates following in parentheses. Regressing knowledge of fruit and vegetable benefits at time 2 on treatment assignment (controlling for knowledge at time 1) showed that the team intervention significantly increased knowledge of fruit and vegetable benefits [a₁ = 0.290 (0.070); P < 0.001; 95% CI: 0.154, 0.426]. Regressing dietary support at time 2 on treatment assignment (controlling for dietary support at time 1) showed that the team intervention also significantly increased dietary support [a₂ = 0.176 (0.067); P = 0.008; 95% CI: 0.046, 0.307]. Finally, regressing fruit consumption at time 2 on knowledge of fruit and vegetable benefits, dietary support, and treatment assignment (controlling for fruit consumption at time 1) showed that both mediators significantly increased the outcome, and that a significant direct effect of the program on fruit consumption remained after the mediators were modeled [b₁ = 0.143 (0.033); P < 0.001; 95% CI: 0.077, 0.208; b₂ = 0.123 (0.036); P = 0.001; 95% CI: 0.051, 0.194; c′ = 0.134 (0.046); P = 0.004; 95% CI: 0.044, 0.225].

Mediation analysis showed that both knowledge and dietary support significantly mediated the effects of the program on fruit consumption (see Figure 3) [a₁b₁ = 0.041 (0.015); P = 0.006; 95% CI: 0.012, 0.071; a₂b₂ = 0.022 (0.010); P = 0.036; 95% CI: 0.001, 0.042]. Overall, R² = 36.80% of the variance in fruit consumption at time 2 was explained by variables in the model. Proportion-mediated effect size estimates for the individual mediation pathways indicated that knowledge of fruit and vegetable benefits (PM = 21.09%) conveyed a larger portion of the program impact on fruit consumption, compared with dietary support (PM = 10.94%). Given the significant direct effect of the team program on fruit consumption, as well as the magnitude of the observed variance explained by the model, it is likely that there are additional mediators that could contribute to understanding the effect of the team program on fruit consumption.

Missing data

Despite the availability of modern methods to handle missing data observations, many researchers continue to use outdated methods, such as listwise deletion. This problem is not limited to the mediation area and is worth mentioning because it is manifest in several investigations of mediation published in the Journal (2, 4, 6, 38–40, 64, 65). Listwise deletion assumes data are missing completely at random (MCAR) and will provide unbiased estimates when the assumption is satisfied (106). Methodological research has quantified critical bias in sample estimates, however, when using listwise deletion with data that are not MCAR (103). Applied researchers should empirically test (and report) the tenability of the MCAR assumption to ensure unbiased estimates if seeking to listwise delete data (107).

Modern methods for handling missing observations do not require MCAR data. Rather, assumptions are relaxed to allow for data to be missing at random, such that the likelihood of missingness on a given variable is permitted to be conditional on ≥1 other observed variables (103). Multiple imputation (MI) and FIML procedures (108) afford greater flexibility in analyzing data with missing observations, and we advise researchers to adopt these methods. Note that there are different methods available to conduct MI, including, but not limited to, parametric methods such as MI by chained equations (109) and machine learning methods such as random forests (110). A variety of statistical software packages allow for the estimation of the techniques. Some examples of software that facilitate the use of FIML to handle missing data in mediation models are the “lavaan” R package (use the missing = “ML” argument), STATA [use the “sem” command with the “method(mlmv)” option], Mplus (FIML is the default estimation option), and SAS (use the method = fiml option in PROC CALIS). Finally, some examples of software that enable the use of MI to handle missing data in mediation models are the “mice” R package, STATA (use the “mi” suite of commands), SAS (use the PROC MI statement), and SPSS (available in the SPSS Missing Values add-on module). Although Mplus can conduct MI, the technique is more onerous (requiring Bayesian model estimation before imputation can be conducted), and users may encounter convergence problems. Readers should take note that estimating a mediation model in SAS or SPSS with the use of a variety of available macros (17, 70, 111) will not handle missing data in your data; they tacitly implement listwise deletion of missing observations. This includes the widely popular PROCESS utility in SPSS (17).

Power analyses

Many studies perform statistical mediation analysis without a sufficient sample size. Previous methodological work has indicated lower bounds to detect mediation effects with 80% power. If effect sizes of the a and b parameters in the mediation model are small (i.e., β = 0.14), nearly 500 subjects (i.e., n = 462) are required to detect mediation even when using the best of methods such as the bias-corrected bootstrap (58). Not all research studies may involve small effect sizes. If effect sizes of the a and b parameters in the mediation model are both medium or large (i.e., a and b are either both β = 0.39 or β = 0.59, respectively), and the bias-corrected bootstrap is used to test mediation, the required sample size to detect the mediated effect will be n = 71 and n = 34, respectively. Studies that include ≥1 path of the mediated effect that is small in magnitude, however, require a minimum of n = 377 participants for adequate power, even when using the powerful methods (61). This latter case likely represents the most common research scenario observed in practice and should be considered a conservative lower bound for testing mediation effects.

This recommendation is prudent for ≥2 reasons. First, applied researchers often may not know what effect sizes to expect due to the novel nature of their work or conflicting results in the literature. Second, although meta-analyses can help inform what effect sizes to expect, these studies regularly indicate that estimates vary widely depending on what variables are being examined. Consider some meta-analyses from the nutrition literature as an example. In a meta-analysis of 88 studies investigating the relation between soft drink intake and nutritional health outcomes, Vartanian et al. (112) found that the average effect size estimate across studies was r = 0.16. In contrast, Robinson et al. (113) reported that average effect size estimates across 24 studies examining the influence of attentive eating on energy intake ranged from d = 0.39 to d = 0.76. The divergent results of these studies should emphasize how critical it is to contemplate power to detect mediation effects in clinical nutrition studies. Our research indicates that this practice is scarce, however, identifying only one article published in the Journal that conducted a power analysis (albeit post hoc) on their mediation results (38). Depending on the specific content area, conducting a mediation analysis may, or may not, be viable. We recommend conducting a priori power analyses that consider a range of effect sizes (63) to provide upper and lower bound estimates for power to detect mediation effects in a study.

Conducting power analyses for advanced methods such as mediation can be challenging, but there are resources available to aid in the endeavor. Two approaches can be implemented: using information from tables in the literature or conducting a Monte Carlo study specific to the model under consideration. For some mediation models, researchers may be able to reference findings from existing studies that directly align with the model they intend to use. In other situations, it may be necessary to conduct a Monte Carlo study to garner appropriate power estimates. We consider each of these possibilities below.

Several methodological studies exist that provide tables of required sample size and/or empirical power estimates for different mediation models. The most comprehensively studied mediation model is the single mediator model with continuous predictor, mediator, and outcome variables. Fritz and MacKinnon (61) conducted a Monte Carlo simulation study to determine the sample size needed to detect mediation effects of varying sizes with 80% power in this model. They compared various approaches to test the significance of the indirect effect, including the causal steps, the test of joint significance, the Sobel method, the distribution of the product, the percentile bootstrap, and the bias-corrected bootstrap. Researchers can reference Fritz and MacKinnon’s tables of required sample size to ascertain how many participants would be required to detect mediation effects with adequate power in their proposed research.

Taylor et al. (71) conducted a Monte Carlo simulation study to provide power estimates to detect mediation effects in serial mediation models, in which 2 mediators act in a sequence to mediate the effect of X on Y (called a “3-path mediated effect”). The authors provide a table with power estimates at different mediated effect sizes, sample sizes, and continuous or dichotomous levels of X. Readers are encouraged to reference the Taylor et al. (71) tables for ascertaining power if they are examining a comparable model.

Ma and Zeng (114) conducted a Monte Carlo simulation study to examine power in multiple mediator models with 1 binary independent variable, 3 mediator variables, and 1 continuous dependent variable. They provide empirical power estimates for each individual mediated effect, as well as the overall mediation effect across a range of sample sizes and effect sizes of a and b. In addition, they report the required sample size needed to achieve adequate power for each combination of effect sizes. This is a helpful reference for researchers who seek to examine a multiple mediator model such as the one examined.

Finally, Pituch et al. (69, 115) evaluated power for single mediator models in multilevel mediation models. Pituch et al. (115) examined lower-level mediation models, in which all variables of interest were at the individual level and all parameter estimates were specified as fixed effects. Sample sizes at level 1 and level 2 were systematically varied, as were residual intraclass correlations and methods to test the indirect effect. Tables of empirical power estimates are provided across these conditions. In general, Pituch et al. (115) found that power increased with increasing sample sizes at level 1 and level 2 and with increasing effect sizes.

Pituch et al. (69) conducted a Monte Carlo study of mediation in cluster randomized trials across a range of sample and effect sizes. Two cluster randomized situations were explored. In both permutations, treatment assignment occurred at level 2 (i.e., the cluster level) and the outcome was measured at level 1 (i.e., the individual level). However, in 1 variation, the mediator was assessed at the cluster level, and in the other it was assessed at the individual level. Effects of X and M were fixed, and the size of the residual intraclass correlations and c′ were held constant. Results indicated that power estimates varied more in designs in which the mediator and outcome were measured at the individual level. Results for this design are provided by the authors in table form and may be used by researchers to inform power estimates for cluster randomized designs.

Although the above studies are helpful references if they closely align with the model a researcher intends to use, often there are no existing studies available to guide power estimates for mediation in more complex analyses. In these cases, it may be necessary for the researcher to conduct his or her own power analysis. Thoemmes et al. (116) discussed methods by which a researcher can conduct a Monte Carlo study to determine power for complex mediation models. In Monte Carlo studies, the researcher creates (i.e., simulates) population data by fixing parameters in the desired model to values supported by the extant literature. Effect size, sample size, and α level must be defined to estimate power (117). Alternatively, a researcher can fix effect size, power, and α-level values if they seek to identify the required sample size to detect the mediation effect for a given power level. Exogenous variables in the data are generated by a pseudo-random number generator from the appropriate distribution (e.g., a binomial distribution for dichotomous variables, or a Gaussian distribution for continuous variables), and endogenous variables are generated by estimating the specified population-level model. Subsequently, many random samples of a chosen size are drawn (with replacement) from the population data; the population model is then fitted to the resulting sample data sets. Parameter estimates in each sample will vary around the researcher-specified population values, due to naturally occurring sampling variation. Power estimates from these studies are garnered by calculating the proportion of times that the parameter estimate is statistically significant across the sample data sets (assuming nonzero parameter combinations). For 80% power, a parameter estimate must be significant in 80% of the sample draws.

This method of power analysis is very flexible and applies well to complex models. Thoemmes et al. (116) present a detailed discussion and syntax for running a Monte Carlo study in Mplus to determine the necessary sample size needed to achieve adequate power in a variety of mediation models. They cover a multiple mediator model with 2 mediators, a serial mediation model, a model that includes both mediation and moderation effects, and mediation in a latent growth curve modeling framework. Zhang (118) expanded the work of Thoemmes et al. (116) by using bootstrap methods to test for mediation in conducting a power analysis (rather than normal-theory variance estimators), as well as by presenting detailed descriptions and code for conducting power analyses in R. The freely available, open-source “bmem” R package works in conjunction with the “lavaan” R package to conduct power analyses with normal, robust, or bootstrapped CIs to test the significance of mediation effects. The authors describe how this program can be used to conduct power analyses for advanced mediation models, including conditional process models and mediation analysis with latent variables. See Table 1 for a summary of the power resources discussed for mediation models in this section.

TABLE 1.

Summary of resources available for assessing power in mediation models

Study	Application
Fritz and MacKinnon (61)	Power tables provided for the single mediator model
Ma and Zeng (114)	Power tables provided for select multiple mediator models
Pituch et al. (115)	Power tables provided for lower-level mediation models in select multisite designs
Pituch et al. (69)	Power tables provided for mediation models in select cluster-randomized designs
Taylor et al. (71)	Power tables provided for serial mediation models with a 3-path mediated effect
Thoemmes et al. (116)	Tutorial on running Monte Carlo studies in Mplus to assess power in complex mediation models
Zhang (118)	Tutorial on running Monte Carlo studies in R to assess power in complex mediation models

CLOSING THOUGHTS

We focused on describing only the simplest mediation model in this narrative, to promote foundational learning and to emphasize crucial issues to consider when conducting a mediation analysis. The topics considered here extrapolate to more sophisticated mediation models, with a variety of different data types (e.g., count data, survival data) and model structures (e.g., hierarchical models). The use of SEMs that incorporate latent variables to estimate mediation effects may be of special interest, because measurement error can be modeled in analysis and myriad longitudinal designs can be considered that allow for the evaluation of latent heterogeneous populations within a single sample. Although other procedures may suffice in limited situations, we recommend that applied researchers use the product of coefficients to test mediation with the bias-corrected bootstrap or Monte Carlo CIs if not applying one of the newer causal inference methods. Although navigating the newer causal inference methods may appear daunting, the increasing generalizability and power of the procedures relative to other approaches may make the trip worthwhile.