The Evolutionary Interplay between Adaptation and Self-Fertilization

Abstract

Genome-wide surveys of nucleotide polymorphisms, obtained from next-generation sequencing, have uncovered numerous examples of adaptation in self-fertilizing organisms, especially regarding changes to climate, geography, and reproductive systems. Yet existing models for inferring attributes of adaptive mutations often assume idealized outcrossing populations, which risks mischaracterizing properties of these variants. Recent theoretical work is emphasizing how various aspects of self-fertilization affects adaptation, yet empirical data on these properties are lacking. We review theoretical and empirical studies demonstrating how self-fertilization alters the process of adaptation, illustrated using examples from current sequencing projects. We propose ideas for how future research can more accurately quantify aspects of adaptation in self-fertilizers, including incorporating the effects of standing variation, demographic history, and polygenic adaptation.

Trends

Analysis of large-scale next-generation sequencing datasets are finding more examples of adaptive evolution at the genomic level.

Advances in theoretical work has demonstrated how self-fertilisation affects different aspects of adaptation in these organisms, compared to outcrossers.

Current software and statistical methods do not take different mating systems into account, which risks mischaracterising the presence or strength of adaptive mutations from genome scans.

Development of new mathematical and statistical methods that explicitly consider self-fertilization and associated demographic effects will enable researchers to more accurately quantify adaptation in these organisms.

Why the Mating System Matters When Studying Adaptation

Adaptive mutations are the fuel of evolution. Appearance of novel genotypes with reproductive advantages allows populations to persist in the face of continual and threatening changes. The ubiquity of cheap genome sequencing makes it possible to uncover a greater number of adaptive mutations than before. In addition, many researchers are enacting large-scale sequencing projects of organisms capable of self-fertilization (see Glossary), especially plants. For example, in the Ensembl database, 17 of 36 angiosperm species and four of 11 nematodes are listed as preferentially selfing. As these organisms are spread across large geographic ranges, genomic studies of self-fertilizing organisms are proving fruitful in determining the evolutionary history of species following ancient climatic events (such as the last glacial maximum), and how they respond to local geographic and climatic changes ^{1, 2}. The majority of crop plants also self-fertilize to some degree [3]; finding adaptive variants in them plays a key role in agricultural genomic studies.

Many theoretical predictions regarding the genetic basis of adaptation, and the majority of statistical methods used to detect loci that have been subject to selection, were developed for populations assumed to be completely outcrossing. Yet self-fertilization strongly affects the setting on which adaptation takes place. Under selfing, two gametes are inherited from the same parent, increasing homozygosity and reducing haploid gene flow (e.g., pollen gene flow in plants). Increased homozygosity also weakens the mixing effects of recombination because it takes place between highly similar chromosomes [4]. Selfing also increases genetic drift as it reduces the number of independent alleles sampled at reproduction [5]. Dominance values of mutations contributing to adaptation will also depend on the mating system [6], yet most selection inference methods implicitly assume additive selection. In some cases, predictions on the dynamics of adaptation under selfing can be obtained by rescaling relevant population genetics parameters to incorporate these effects (see mathematical details in Box 1). Yet under more complex scenarios (such as polygenic adaptation), selfing also qualitatively changes adaptation dynamics compared to outcrossing.

Box 1. How Self-Fertilization Affects Genetic Evolution.

Reduction in Effective Population Size, Ne

The selective strength acting on mutations is proportional to Ne × s, where Ne is the effective population size and s the selective advantage of a beneficial variant [66]. Ne in self-fertilizing organisms is generally scaled by a factor α/(1 + F). Here F = σ/(2 − σ) is the inbreeding rate, given self-fertilization occurs with probability σ [5], and α accounts for the effect of background selection. Hence Ne is reduced by at least a half with complete self-fertilization [67], weakening selection overall. A lower Ne can also inhibit adaptation from standing variation through limiting neutral diversity from which beneficial variants could arise from [34].

Reduced Recombination

Self-fertilization also lessens the impact of recombination in generating novel haplotypes, if identical haplotypes were inherited from the same parent. For tightly linked loci, the recombination rate is reduced by a factor (1 − F) [4]. The exact rescaling becomes more complex over long map distances with high self-fertilization [68].

Altered Emergence Probabilities

If the beneficial variant is initially present as a single copy, it is most likely to go extinct by genetic drift [19]. If the selective advantage of homozygote mutations is 1 + s for s ≪ 1, and heterozygote mutations have advantage 1 + hs (h being the dominance coefficient), the emergence probability for a mutation to escape early extinction by drift equals [19]:

$$\frac{2s\left(h+F-hF\right)}{1+F}$$ (I)

With complete outcrossing (F = 0), the emergence probability equals 2hs and thus increases with higher dominance, h. In contrast, with complete self-fertilization (F = 1) the fixation probability equals s; dominance does not affect emergence. Recessive mutations (h < 0.5) are thus more likely to fix with higher rates of self-fertilization, while dominant mutations (h > 0.5) are less likely to fix.

Different Adaptation Trajectories

For weak selection coefficients, the rate of change in variant frequency p over time can be given by [19]:

$$\frac{dp}{dt}=sp\left(1-p\right)\left[F+h-Fh+\left(1-F\right)\left(1-2h\right)p\right]$$ (II)

Hence the level of self-fertilization affects the fixation time [19]. The level of dominance and self-fertilization also interact to affect the genetic history of the adaptive variant, which can influence how its properties are inferred (see Figure 1 in main text).

Alt-text: Box 1

Looking beyond genetic consequences, selfing species often exhibit specific biological and ecological traits that affect a species’ demography. In particular, ‘Baker’s Law’ states that organisms capable of self-fertilization (or any other uniparental reproduction) are more likely to establish new populations following long-distance dispersal than outcrossing relatives ^{7, 8}. Selfing is thus often associated with weedy habitats [9], invasiveness [10], and range expansions [11]. Selfers also tend to exhibit frequent bottlenecks, rapid population growth, and extinction-recolonization dynamics [12]. These demographic regimes induce strong local genetic drift, which shapes patterns of genetic diversity in combination with high within-individual genetic relatedness, low haploid gene flow, and reduced effective recombination rates. Hence selfing species often exhibit strong genetic structure, with one or a few multilocus genotypes locally predominating ^{13, 14, 15, 16}. As a consequence, adaptation, population structure, and demography become more entwined than they would otherwise be in outcrossing species, and are more difficult to tease apart [17].

Here we review and discuss empirical population genomics studies of adaptation in self-fertilizing species, in the light of classical and recent theory predicting how self-fertilization affects the genetic basis, rates, and genomic signatures of adaptation. This synthesis highlights the specificities of selfing species in studying adaptation, and how future research can best utilise emerging sequence data to accurately quantify adaptation in organisms undergoing self-fertilization.

Selfing Can Limit Adaptation

No ‘Haldane’s Sieve’ in Selfers

In outcrossing organisms, beneficial variants are more likely to emerge in a population from low frequency if dominant (h > ½). This is the original formulation of ‘Haldane’s Sieve’ [18]. Higher rates of self-fertilization are more likely to create homozygote copies of beneficial alleles, meaning recessive types have a higher fixation probability compared to outcrossers [19]. However, this prediction only holds at a single locus when genetic drift is solely affected by selfing (Box 1). Additional drift, due to demographic history or background selection (see below), should reduce the dominance threshold for which selfing favours the fixation of beneficial alleles.

Strong Selective Interference in Selfers

Selection interference can further reduce the efficacy of selection in low-recombining genetic regions ^{20, 21} and is expected to be pervasive in self-fertilizing organisms that exhibit reduced effective recombination rates (Box 1). High rates of self-fertilization makes it likelier that linked deleterious alleles hitch-hike to fixation with selective sweeps, compared to outcrossing populations [22]. This phenomenon is a consequence of a reduction in both the net recombination rate, and a weakened overall efficacy of selection due to a reduced effective population size. For similar reasons, an adaptive allele will also be less likely to fix if a first sweeping allele is already present, if self-fertilization is more frequent [23]. Multilocus models similarly show that high selfing rates amplifies background selection, reducing the effective population size by one or possibly several orders of magnitude, adversely affecting the fixation probability of beneficial mutations [24].

Except for strongly beneficial recessive mutations, self-fertilization should reduce the overall efficacy of selection acting on individual mutations. However, while there have been many comparative studies between outcrossing and self-fertilizing sister species focusing on background selection ^{25, 26, 27}, there are few studies comparing adaptation rates between sister species, with the exception of a few well-analysed taxa including Arabidopsis and Capsella [28]. One problem is that if species split relatively recently, there could not have been sufficient time for differences in adaptation rates to manifest themselves in nucleotide data. Furthermore, demography associated with the species split, such as bottlenecks, could remove diversity that would otherwise be under selection ^{26, 29}. Another problem is that the stronger effects of linked selection in selfers, caused by reduced recombination, should be accounted for as they are expected to substantially bias estimates of adaptation rates. Despite these challenges, comparisons were obtained between the outcrossing snail Physa acuta, which displayed evidence of adaptive substitution (as measured using the McDonald–Kreitman test) and the self-fertilizer Galba truncatula, which showed no evidence for adaptation [30].

Selection interference models also predict different outcomes than those expected by ‘Haldane’s Sieve’ ^{22, 23}. In particular, if adaptive mutations are recessive (h < 0.5) then intermediate self-fertilization rates, as opposed to complete selfing, leads to the highest emergence probabilities of novel beneficial alleles. Here, partial selfing combines the best of both worlds: some degree of outcrossing and recombination reduces selection interference, while selfing reveals recessive beneficial mutations when rare. To our knowledge, these predictions have not yet been tested. Model species exhibiting varying degrees of selfing, such as Mimulus [31] and Arabis alpina [32], would be ideal candidates to test these theories.

Adaptation from Standing Variation Is Less Likely in Selfers

It has become apparent in recent years that many adaptations arise from pre-existing neutral (or deleterious) variation, or from recurrent mutation, so adaptive variants are initially found on multiple genetic backgrounds [33]. Adaptation from standing variation can be less likely with selfing, since both neutral diversity and population-wide mutations rates are reduced as a consequence of a lower effective population size [34]. In addition, Haldane’s sieve applies less strongly when adaptation proceeds from pre-existing variation, because both homozygote and heterozygote genotypes can segregate in the population when the beneficial allele is already present in several copies ^{35, 36}. As a consequence, even recessive mutations are more likely to fix in outcrossers than in selfers [27]. Reduction in genetic diversity can also prevent self-fertilizing organisms from adapting quickly in an unfavourable environment. Yet if the mutations needed for evolutionary rescue are present before the harmful environment arose, these rescuing mutations can be more readily selected under selfing by quickly creating fitter homozygote genotypes [37].

Detecting the Genetic Basis of Adaptations in Selfers

Fixation Trajectories and Effect on Nucleotide Diversity

Numerous statistical tests exist for inferring adaptation from genomic data. Table 1 outlines some key methods used, along with how their outcomes can be altered under self-fertilization. One popular method for detecting recent adaptation involves tracking footprints of selective sweeps, where the spread of a beneficial variant reduces sequence diversity at neutral markers linked to the selected site. Box 2 outlines the basic theory used to predict patterns of diversity around a selective sweep. Selective sweeps can be easier to detect in selfers than outcrossers for two reasons. First, self-fertilization reduces fixation times of beneficial alleles, as homozygote mutations arise earlier, exposing the mutant to selection [6]. Second, reduced effective recombination under selfing means that recombinant haplotypes are less common, making it easier to detect sweeps [38]. Unfortunately, the exact locus undergoing adaptation will be less easy to pinpoint as large genomic regions fix alongside targets of selection.

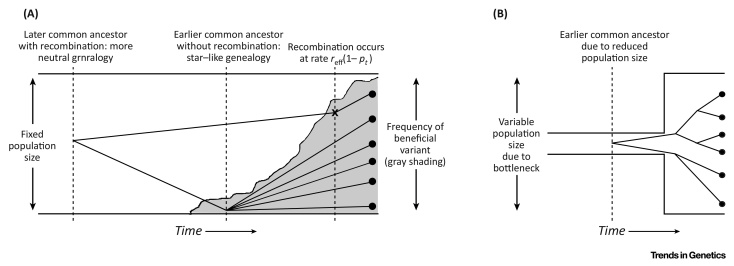
Figure I.

Schematics of Effect of Demographic History on Genealogies. (A) Genealogies for a selective sweep in a fixed-size population. The effective recombination rate r_eff depends on the level of self-fertilization (Box 1). The point when the top lineage was affected by recombination is marked ‘×’. (B) Genealogies where the population experienced a bottleneck in the recent past

Table 1.

Overview of Methods for Detecting Selection Footprints in Data from Genome-wide Re-sequencing Studies

Type of method	Summary of method	Data needed	How does selfing affect the method?	Refs
McDonald–Kreitman (MK) test	Detects abnormally high nonsynonymous over synonymous divergence ratio, relative to nonsynonymous over synonymous polymorphism ratio	SNP data, unlinked, and divergence to an outgroup (e.g., a related sister-species)	Linked selection could be more prevalent with selfing, which can alter estimates of the distribution of fitness effects of deleterious mutations. This distribution usually has to be accurately calculated to correctly infer the proportion of adaptive substitutions.	[74]
Site–frequency spectrum (SFS) tests	SFS in sweep regions consists of elevated low- and high-frequency variants compared to neutral case	SNPs data, unlinked, unphased	Selfing will affect expectation for SFS under soft and hard sweeps (Figure 1). SFS methods inferring selection assume invariably unlinked SNPs; this assumption is much more likely to be violated in selfers.	75, 76
Neutrality tests based on SFS (Tajima’s D, Fay and Wu’s H, etc.)	These tests measure the excess or deficit of rare alleles in the SFS compared to neutral expectations	SNPs data, unlinked, unphased	Should work; selfing per se unlikely to sway these tests. Yet they are sensitive to demography, whose effect could be more difficult to remove in selfing species (Box 2).	[77]
Linkage disequilibrium (LD)	Increase in linkage disequilibrium at loci flanking a sweep	SNPs data, linked and phased	A decrease in effective recombination rate might further amplify the effect of selective sweeps and expand the width of high LD regions.	[78]
Fst-based tests	Tracks local adaptation between two geographic regions by finding highly differentiated loci, as measured using the Fst statistic	SNP frequencies from two or more populations	Fst scans for excess differentiation will be robust to selfing when using a background genomic distribution as a null neutral distribution. Fst scans relying on a model-based approach to derive a neutral distribution might be sensitive to misspecification of population structure. Selfing species often have complex population structures that are hard to model accurately.	[1]
Haplotype tests	Average number of haplotypes around sweep is reduced; mean haplotype length is increased	SNPs data, linked and phased	Haplotype tests relying on detecting abnormal haplotype length surrounding a focal SNP should be robust to any levels of selfing. Strong levels of selfing will amplify the signal of extended haplotypes.	[41]
Singleton density score	The physical distance between singletons is increased in regions that have recently experienced a sweep	SNPs data, linked but unphased	Currently unclear. Since a sweep still reduces average number of singletons with self-fertilization, this test should work.	[65]

Box 2. Genetic Diversity Expected under Scenarios Involving Adaptation and Demographic Changes.

The expected diversity in genome samples following a selective sweep can be determined by studying gene genealogies of derived haplotypes using coalescent theory. Coalescent models calculate the expected time in the past to the most recent common ancestor of haplotypes; this elapsed time also determines the level of genetic divergence between samples.

For neutral sites in a constant-sized population, coalescent times are on the order of the effective population size, which depends on the level of self-fertilization as N_e = N (1 – σ/2) for selfing probability σ [5]. Conversely, sites that are tightly linked to adaptive variants have much lower coalescence times than unlinked neutral sites, and will therefore harbour reduced levels of genetic diversity. With looser linkage, genetic variants are likely to recombine onto neutral backgrounds, restoring genetic diversity and weakening the selective sweep pattern (Figure 1B). ‘Soft’ sweeps are caused by genetic variants whose expected coalescence times are longer than the time under which selection was acting ^{33, 40}.

Certain demographic changes, especially a recent increase in population size, will generate coalescent histories similar to those experienced by adaptive variants that rapidly rose to high frequency (Figure I). This process can confound genomic scans for beneficial alleles [69]. A simulation study [70] found that inferring demographic history over loci recently subjected to a selective sweep would predict the presence of a population bottleneck, even if the population size remained constant over time. Recurrent selective sweeps also caused a popular method to quantify past population sizes [71] to spuriously infer recent reductions in population size from simulated data when none existed.

It remains a long-standing problem in evolutionary genetics to reliably disentangle selection from demographic changes. However, given that long-range linkage disequilibrium is induced following a sweep in selfers, it will be even more important to account for demographic history when inferring adaptive sites as the two will become even more strongly intertwined. One solution is to simulate baseline levels of genetic diversity caused only by expected demography, and subsequently search for regions exhibiting discrepant patterns relative to this background [47]. Because sweeps in selfers can affect wider chromosomal regions ^{46, 49}, this will magnify risks of inferring recent population expansions even if none existed [70]. Recent advances in machine-learning methods that detect selective sweep patterns under different demographic histories [72] could prove promising in jointly measuring adaptation and demography under high selfing rates.

Alt-text: Box 2

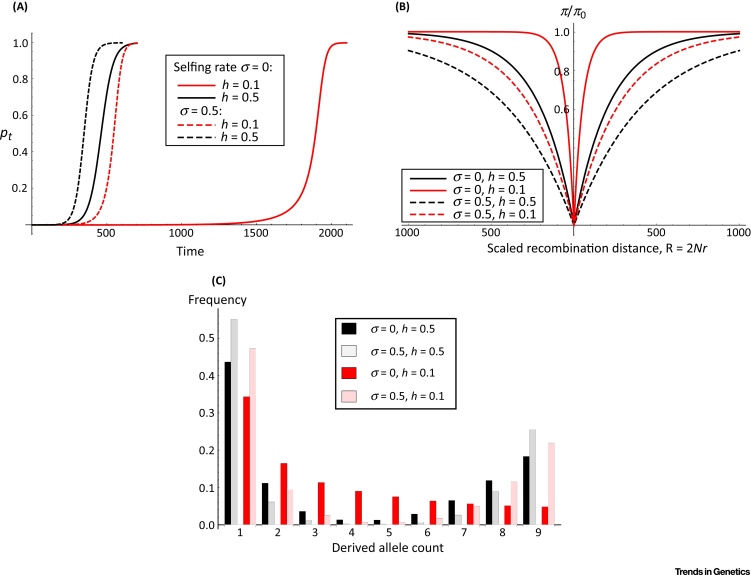
Under outcrossing, recessive mutations spend most of their time at a low frequency before going to fixation; while codominant mutations reach high frequencies more quickly (Figure 1A). Sweep trajectories become similar with higher rates of self-fertilization, as more mutations are present as homozygotes irrespective of their dominance levels (Figure 1A). As recessive mutations spend a long time at a low frequency, they exhibit weaker signatures of beneficial selection than dominant ones, with a weaker reduction in neutral diversity at linked sites [39] (Figure 1B). There is also more time for recombination to act, creating a greater number of intermediate-frequency variants (Figure 1C).

Figure 1.

Self-Fertilization, Dominance, and Signatures of Adaptive Mutation. (A) Different allele trajectories over time. Curves are obtained by numerically evaluating Equation (II) in Box 1, with initial frequency p₀ = 1/2N (with N = 50 000). The beneficial allele has selective advantage s = 0.05; dominance (h) and self-fertilization (σ) parameters are as shown in the legend. (B) Pairwise diversity (π) relative to neutral expectations (π₀) will be reduced close to the sweep, and recover further from the sweep. This sweep signature is weakened if the beneficial variant is recessive (h = 0.1, dashed lines), but is strengthened with increased self-fertilization due to reduced recombination and quicker fixation times (Boxes 1 and 2). (C) Expected site frequency spectra following a selective sweep, based on 10 genetic samples. A sweep is characterised by many variants at low and high frequencies (1 and 9 respectively, in this example), with more pronounced signatures with higher rates of self-fertilization. Values used in (B) and (C) were obtained using Equations 7 and 15 respectively from [73], modified to account for self-fertilizing trajectories

There are two main sweep types. Hard sweeps are created from the spread of a single new beneficial mutation. Soft sweeps are caused by variants that are present on multiple genetic backgrounds before being subject to selection, either because the variant was previously neutral or it was introduced by recurrent mutation onto different haplotypes ^{33, 40}. It is unclear how feasible it will be to discern soft sweeps from hard ones under heightened self-fertilization. While theory predicts that the potential for adaptation from standing variation is reduced under self-fertilization, any soft sweeps that do occur will potentially be easier to detect due to reduced recombination rates and quicker fixation times. However, some methods to detect soft sweeps are based on detecting genetic regions consisting of multiple common haplotypes segregating at high frequencies ^{41, 42}. These signatures could be more difficult to extract from neutral backgrounds (or from hard sweeps) in highly selfing populations, if only a few haplotypes are initially present that subsequently sweep to high frequencies.

Controlling for Population Structure and Demography When Finding Candidate Loci for Adaptation

Despite the fact that adaptation rates are reduced in self-fertilizing organisms, there is clear evidence for adaptive evolution, especially in genes related to flowering time, immunity, and environmental stresses ^{28, 43, 44}. Many studies have been carried out in the model organism Arabidopsis thaliana, for which evidence of adaptation is accumulating ^{28, 45}. Yet precautions must be taken when looking for signatures of adaptation in selfers, because the confounding effects of population structure and demography are expected to be more pronounced than in outcrossers (Box 2).

A study of A. thaliana populations from northern Sweden [46] found global selective sweep footprints stretching over large areas of the genome due to reduced recombination (Figure 1). Subsequent research found signatures for local sweeps in southern Sweden, however it was necessary to first account for demographic history by determining the likely population history in northern and southern Sweden, including subpopulation sizes and migration rates. Expected neutral diversity under this model was then used as a baseline for finding loci exhibiting site-frequency spectra consistent with selective sweeps [47]. In the model legume Medicago truncatula, both global and local selective sweeps were found after controlling for population structure [48], but no explicit demographic model was inferred [48]. Strong support for species-wide and chromosome-wide selective sweeps was also obtained in the self-fertilizing nematode Caenorhabditis elegans. Nucleotide data was compared to simulation scenarios with different demography and population structure; the best-fitting models included a global selective sweep [49]. Another noteworthy example of a genome-wide selective sweep is provided by triazine herbicide resistance in A. thaliana populations along the British railway network [50]. Resistance is conferred by a chloroplast mutation, yet surveys of resistant individuals from the UK revealed that the whole nuclear genome also ‘hitch-hiked’ to fixation along with the adaptive mutation.

While signatures of selective sweeps provide evidence for adaptive evolution, we currently know little about the strength of selection underlying these signatures, or whether adaptation involved pre-existing variants. Studies of A. thaliana in Sweden [47] suggest that selection was stronger in the north than the south. This conclusion was based on simulation results; in the absence of a defined statistical model, no actual inference regarding the strength of selection could be made. It remains challenging to directly estimate selection coefficients from sweep signatures.

A Complex Interplay between Demography and Selection

The examples discussed above highlight how selection and demography become strongly intertwined with self-fertilization, which can complicate genetic scans for adaptive traits (Box 2). The prevalence of cheap sequencing means it is now possible to sequence self-fertilizing organisms on a large enough scale to jointly infer demographic and selective history. However, it remains difficult to disentangle the two when considering the invasion of self-fertilizing organisms into new regions. Genotype-dependent colonization should leave different signatures from selection events occurring independently of the establishment process [51]. Yet it is unclear if the two scenarios can be reliably distinguished in selfing species.

Consistent with Baker’s Law, several selfing species have exhibited genomic signatures of a strong bottleneck followed by demographic expansion, which is behaviour associated with colonization events [11]. North American populations of A. thaliana offer a striking example where many samples appear to have originated from a single haplotype. Several SNPs were detected that may have contributed to adaptation to the newly-colonized environment, including some involved in root development [52]. Data from 1135 A. thaliana genomes sampled across Eurasia have shown that ancestral samples from refugia populations in southern Europe and Asia migrated north over time, as new environments were made accessible following the last glacial maximum [53]. A second invasion wave across Eurasia was then inferred, which originated from northern Balkan regions, and subsequently replaced a majority of ancestral groups with the extant population [54]. The perennial herb A. alpina, which is mostly (but not always) highly selfing throughout its range [32], also shows potential evidence for strong selection for migration ability into northern Europe [55].

Genomic data can also inform on bottleneck size following an invasion. It was initially thought that the self-fertilizing plant Capsella rubella recently arose from a single colonising individual, because European samples were found to include at most two distinct haplotypes [56]. Follow-up studies identified several haplotypes that potentially founded the selfing population, with diversity likely being lost after the transition to self-fertilization [57]. This analysis revealed a more nuanced version of Baker’s Law; rather than colonisation occurring by a single individual, a tiny subpopulation of the outcrossing ancestor (on the order of tens of individuals) founded the new population. Recent invasions can also be caused by human-mediated long-distance dispersal. A unique genotype of the freshwater snail Pseudosuccinea columella was found in eight worldwide regions, which could have spread due to the global trade of aquarium-related plants and seawater [58]. However, for these two examples we still do not know whether the colonizing genotypes possessed exceptional invasive ability, or were simply the luckiest ones.

Polygenic Adaptation in Selfers

So far, we have discussed examples of adaptation involving specific targets (genes or genomic regions). A more challenging issue is to understand and detect adaptation on polygenic traits. The rescaling procedures from outcrossing models that were successful when considering evolutionary trajectories at one or two loci usually no longer apply here, because selfing induces multilocus behaviours that cannot merely be thought of as rescaled instances of outcrossing behaviour.

Under partial selfing, individuals are not inbred by the same amount on average. Instead the population is best viewed as stratified in cohorts of individuals that have experienced zero, one, two, or more generations of selfing in their recent history. Response to selection on quantitative traits needs to account for structure that results in different inbreeding classes ^{59, 60}. This structure generates genome-wide associations both among alleles (linkage disequilibrium) and genotypes (identity disequilibrium). In contrast, progress on understanding the multilocus population genetics of polygenic adaptation in outcrossing populations has often been obtained under the assumption of ‘quasi-linkage equilibrium’, where linkage disequilibrium rapidly equilibrates to low values due to high recombination, ensuring that it does not build up between loci involved in polygenic adaptation. A recent model of stabilizing selection on quantitative traits [61] showed how genetic associations influence long-term adaptation. Below a given selfing threshold, a population reaches an ‘outcrossing-like equilibrium’ where highly inbred individuals are quickly eliminated, and only lineages with no or little selfing in their recent history persist. In this regime, classical predictions (with some rescaling when necessary) do apply. Above the threshold, genetic associations cannot be neglected and the population reaches a ‘purged equilibrium’ where the genome mostly ‘congeals’ with very high linkage disequilibrium and selection of the few best haplotypes strongly reducing genetic variation.

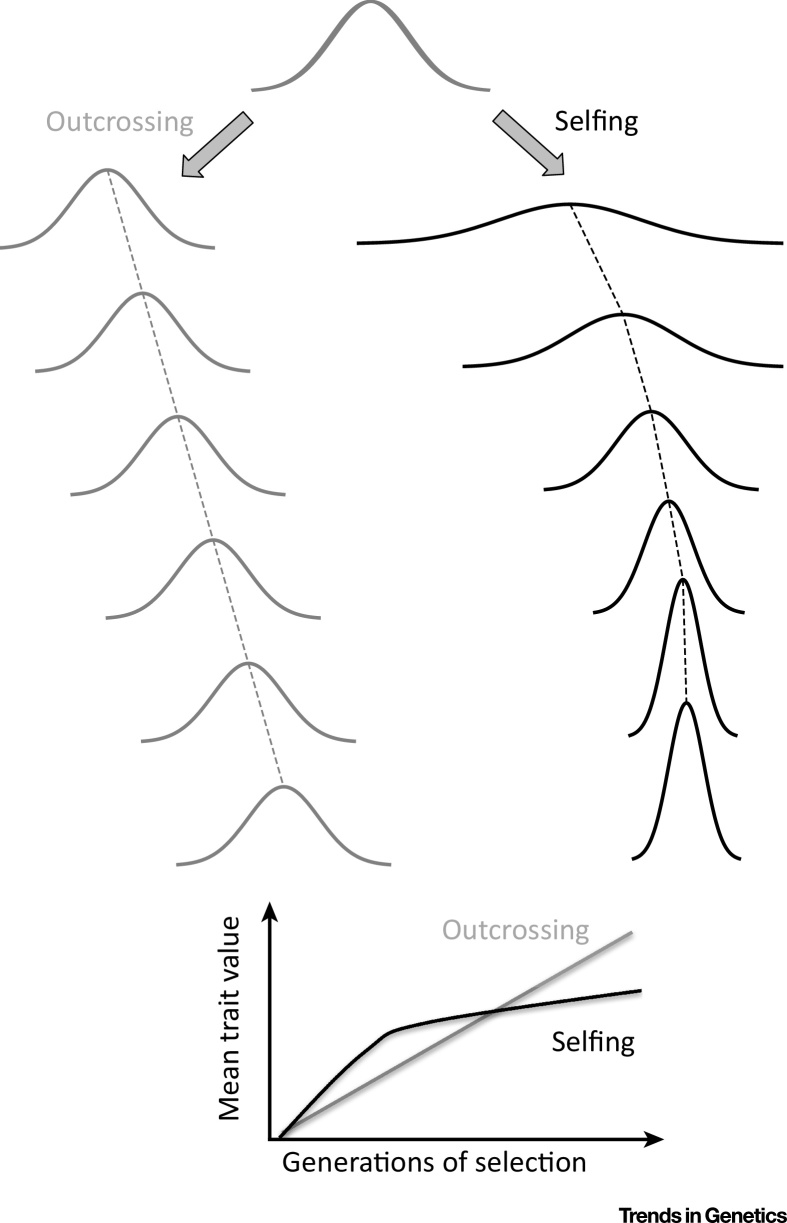
Imposing a selfing regime on a population at outcrossing equilibrium (e.g., through experimental inbreeding or when a modifier gene for increased selfing invades an outcrossing population) is predicted to initially convert dominance and epistatic variance into additive genetic variance, thereby increasing responses to selection [62]. Once populations have reached the purged equilibrium, long-term responses to selection might in turn be compromised due to the lack of available genetic variation (Figure 2). These dynamics have recently been characterized in freshwater snails where outcrossing rates were experimentally manipulated, with the surprising result that genetic variance can be eroded in a few generations under a selfing regime [63]. Yet studies documenting similar dynamics in natural populations are currently lacking. Furthermore, under the high-linkage regime where selected loci become strongly associated with each other, selection could act on sets of competing clones composed of co-adapted allelic combinations, instead of weakly correlated loci [64]. Any subsequent outcrossing will then create unfavourable allele combinations, which could enforce further selfing. While this process requires further exploration, we propose that this phenomenon could be pervasive in highly selfing populations.

Figure 2.

Response to Selection on a Polygenic Trait under Outcrossing and Selfing. Evolution of additive genetic variance is shown for a quantitative trait under directional selection with outcrossing or selfing. We assume both scenarios start from the same initial outcrossing population. Under outcrossing, genetic variance is mostly conserved and the trait mean changes linearly through time, at least on short time scales if selection is not too strong. Under selfing, genetic variance initially increases much more rapidly than in the outcrossing population. Here, more extreme phenotypes (i.e., those with very high or low values) are generated due to creating homozygotes at multiple loci, speeding up the response to selection. Genetic variance can then be quickly eroded because only a few haplotypes are retained after selection, and new combinations cannot be readily created because of a lack of effective recombination. The trait mean can therefore rapidly plateau

While detecting the dynamics of polygenic adaption in selfing populations is expected to be a challenging task, whole-genome sequencing opens up the possibility of detecting subtle coordinated changes in allele frequencies at multiple loci. Recent work on the detection of recent temporal changes of allelic frequency using large scale resequencing [65] demonstrated that the density of singletons around candidate SNPs provides information on recent selection occurring in their vicinity. Scrutinizing singleton densities around regions harbouring quantitative trait loci, even those that may fail a statistical test for genome-wide significance, now offers a powerful way to uncover instances of polygenic selection. We expect this strategy will be powerful when applied to selfers, although further research is needed into how these statistics behave under partial selfing.

Concluding Remarks and Future Perspectives

The democratisation of genome sequencing means we are uncovering adaptive mutations in greater number than before. Yet if we ultimately wish to quantify the origins and selective effects of adaptive mutations from genomic data, it will be important to create new theoretical, statistical, and computational tools that explicitly take this reproductive mode into account (see Outstanding Questions). Given the importance that self-fertilizing organisms play in ecological research, it will also prove fruitful to consider the impact of multiple SNPs that correlate with environmental adaptation, how mechanisms of polygenic adaptation operate under this particular reproductive mode, and what impact it has on evolving in rapidly-changing environments. Introducing mating-system effects into genome analyses will yield a more accurate picture of the mechanisms underlying adaptation in these organisms, and how they differ compared to outcrossing species. It will also encourage researchers to think more deeply about what other traditional modelling assumptions may be violated in their studies.

Outstanding Questions.

Can we estimate selection and dominance coefficients of adaptive mutations in partially self-fertilizing organisms? Is there a clear difference compared to outcrossing species?

Is there any evidence for ‘soft sweeps’ in selfing organisms?

How strongly entwined are demography and adaptive effects in self-fertilizers? How possible is it to disentangle the two?

What is the genetic basis behind traits appearing over short timespans?

Can we detect if quantitative trait evolution in natural populations differs between selfing and outcrossing species?

How extensive is polygenic adaptation in selfers? Can it be detected?

Glossary

Additive genetic variance

genetic variation in genes with additive effects on a trait. Additive variation represents the fraction of heritable variation underlying response to selection in sexually reproducing organisms. Epistatic and dominance variance are not directly available for responding to selection.

Background selection

process by which the removal of deleterious mutations can in turn result in the removal of linked neutral variation.

Baker’s Law

the hypothesis, formulated originally by Herbert G. Baker in 1955, that organisms capable of self-fertilization (or any uniparental reproduction) are more able to establish new populations following long-distance dispersal.

Coalescent theory

a mathematical theory for predicting the causes of observed diversity in genome sequences, as determined by an underlying demographic or selection model, based on modelling genealogical relationships among samples.

Dominance

with regard to a single mutation, this is a measure of the relative fitness of heterozygote mutations compared to homozygote mutations (usually denoted by the dominance coefficient, h). If heterozygotes confer half the advantage of homozygotes, the mutation is said to be codominant.

Evolutionary rescue

when a population genetically adapts to an altered environment where it would otherwise go extinct.

Genetic drift

changes in allele frequencies solely arising by sampling of a finite number of individuals each generation. Drift effects are expected to be stronger under self-fertilization.

Hard sweep

when a beneficial mutation appears from a single copy to fix in the population. Contrast with soft sweep.

Identity disequilibrium

a measure of statistical non-random associations between genotypes at different loci. Positive identity disequilibrium means that the frequency of double homozygotes or double heterozygotes is higher than expected, based on the product of individual genotype frequencies.

Linkage disequilibrium

a measure of statistical nonrandom associations between alleles at different loci.

McDonald–Kreitman test

a statistical test contrasting levels of polymorphism and divergence at both neutral and potentially selected sites. Often used to estimate the fraction of divergence at selected sites driven by positive selection.

Selection interference

when selection acting on one locus is affected by simultaneous selection at a linked locus.

Selective sweep

when neutral diversity spreads through the population, due to tight linkage to a locus containing an adaptive allele.

Self-fertilization

a reproductive mode where individual parents produce both male and female sex cells, which can fertilize one another.

Singleton

a polymorphism where the derived allele is present in only one copy among the sampled individuals.

Site frequency spectrum (SFS)

a count of how many polymorphisms are present at set frequencies in a population sample.

Soft sweep

when a beneficial mutation appears from either recurrent mutation, or from neutral standing variation. Contrast with hard sweep.