Moment-to-Moment BOLD Signal Variability Reflects Regional Changes in Neural Flexibility across the Lifespan

Abstract

Variability of neuronal responses is thought to underlie flexible and optimal brain function. Because previous work investigating BOLD signal variability has been conducted within task-based fMRI contexts on adults and older individuals, very little is currently known regarding regional changes in spontaneous BOLD signal variability in the human brain across the lifespan. The current study used resting-state fMRI data from a large sample of male and female human participants covering a wide age range (6–85 years) across two different fMRI acquisition parameters (TR = 0.645 and 1.4 s). Variability in brain regions including a key node of the salience network (anterior insula) increased linearly across the lifespan across datasets. In contrast, variability in most other large-scale networks decreased linearly over the lifespan. These results demonstrate unique lifespan trajectories of BOLD variability related to specific regions of the brain and add to a growing literature demonstrating the importance of identifying normative trajectories of functional brain maturation.

SIGNIFICANCE STATEMENT Although brain signal variability has traditionally been considered a source of unwanted noise, recent work demonstrates that variability in brain signals during task performance is related to brain maturation in old age as well as individual differences in behavioral performance. The current results demonstrate that intrinsic fluctuations in resting-state variability exhibit unique maturation trajectories in specific brain regions and systems, particularly those supporting salience detection. These results have implications for investigations of brain development and aging, as well as interpretations of brain function underlying behavioral changes across the lifespan.

Introduction

BOLD signal variability is often considered as a source of unwanted noise. This is in contrast to theories proposing that biological variability is necessary for optimal brain function (McIntosh et al., 2010; Garrett et al., 2013b; Tognoli and Kelso, 2014). For example, the coordination dynamics theory proposes that networks fluctuate among integration, segregation, and metastable configurations (Tognoli and Kelso, 2014). Metastability requires a balance between integration and segregation where signal variability within a network facilitates shifting between integration and segregation. That is, networks demonstrating high integration or segregation without variability cannot flexibly shift between configurations. Conversely, networks with high variability can shift flexibly through integrative and segregative configurations. Another approach highlighting the importance of neural variability is the “Bayes optimal theory,” which proposes that, if neurons fired identically to stimuli over time, then systems would not adapt to that stimulus in different circumstances (Beck et al., 2008). These perspectives posit that variability in neuronal response is a critical component of brain function.

Accumulating research has demonstrated differences in BOLD variability between older adults compared with younger adults in a number of task-based fMRI contexts. BOLD variability in the majority of brain regions decreases during task-based fixation periods (i.e., task-absent) in older adults compared with younger adults (Garrett et al., 2010). Increased BOLD variability has also been linked to younger individuals, with faster reaction time and more consistent performance in perceptual matching and attentional cueing tasks (Garrett et al., 2011). Greater BOLD variability during the fixation period of a task is also associated with more efficient behavioral performance in younger adults compared with older adults (Garrett et al., 2013a). Such studies generally demonstrate that BOLD variability decreases across development, with fewer regions demonstrating increased variability across development. Nonetheless, both increases and decreases in variability have been found throughout the frontal, parietal, and temporal brain areas. In addition, increased left inferior frontal junction variability has been linked to improved performance on a cognitive flexibility task, but impaired performance on an inhibition task (Armbruster-Genç et al., 2016). This suggests that the beneficial impact of regional BOLD variability may be task and circuit dependent. Finally, increased variability in the nucleus accumbens has been associated with greater financial risk taking in older age (Samanez-Larkin et al., 2010). Together, these studies demonstrate that greater variability is associated with younger individuals, faster and more consistent performance, and cognitive flexibility, demonstrating its importance as a neural signature of optimal task performance.

The aforementioned studies have mainly examined the effects of BOLD variability within task-based fMRI contexts in younger adults (20–35 years old) and older adults (65–80 years old). However, no studies to date have characterized resting-state BOLD variability or variability across the entire lifespan. This is important for two reasons: First, although previous studies analyzed fixation periods within task-based fMRI paradigms, fixation periods are short in duration and may be influenced by task-based processing demands (Northoff et al., 2010). Resting-state fMRI offers temporal continuity across the time series and is unaffected by possible task-based influences that could affect individuals at varying ages differentially. Second, exploring variability across the lifespan allows for characterization of both linear and quadratic effects. This is important because such effects are present in lifespan resting-state fMRI studies charting functional connectivity trajectories (Betzel et al., 2014; Cao et al., 2014).

To explore these questions, the current study used two groups of resting-state fMRI data (n = 187 and n = 191; age range, 6–85 years) to examine lifespan trajectories of BOLD variability and to demonstrate replicability of findings across different multiband acquisition parameters. Based on predictions from the previous task-based fMRI studies examining fixation periods between task blocks (Garrett et al., 2010), we expected to find that a majority of voxels would demonstrate decreases in variability across the lifespan and that a minority of voxels would demonstrate increases in variability across the lifespan.

Materials and Methods

Participants.

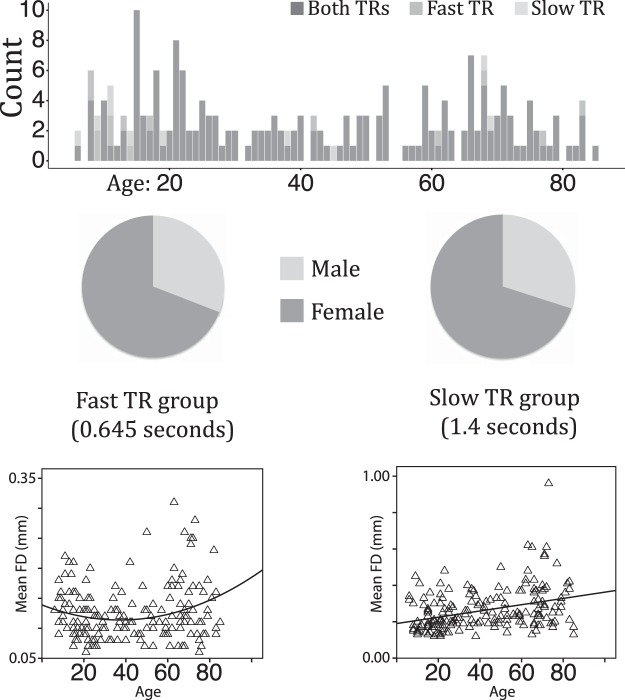
Two resting-state fMRI datasets (fast TR group: n = 191, TR = 0.645 s; slow TR group: n = 187, TR = 1.4 s), each containing 10 minutes of data, were downloaded from the Nathan Kline Institute (NKI)-enhanced database (Nooner et al., 2012) (Fig. 1). Both groups included participants from a wide age range (6–85 years of age) and differed principally in multiband TR acquisition time. Group 1, the “fast TR group” (TR = 0.645 s), included 191 participants [132 female; mean age = 42.26 years old, SD = 23.60; mean full-scale IQ = 104.31, SD = 14.06; mean framewise displacement (FD) = 0.12, SD = 0.04]. Handedness was assessed using the Edinburgh Handedness Questionnaire (EHQ) (Oldfield, 1971) on a scale of −100 to 100; 19 participants had negative scores. Group 2, the “slow TR group” (TR = 1.4 s), included 187 participants (131 female; mean age = 42.46 years old, SD = 23.30; mean full-scale IQ = 104.54, SD = 13.75; mean FD = 0.26, SD = 0.12; 20 participants had negative EHQ scores). We included both datasets with different TRs in our analyses to ensure the robustness and reliability of any mean square successive difference (MSSD) effects as a function of age. This procedure mitigates concerns regarding the unknown influence on the reliability of MSSD results from data acquired using recently developed multiband EPI protocols (Smith et al., 2013).

Figure 1.

Age (top row) and gender (middle row) distribution in the fast and slow TR groups. Scatterplots for each TR group that represent the relationship between age and FD are pictured in the bottom row.

Inclusion criteria for both data sets were the following: subjects had no current or past DSM diagnosis for psychiatric disorders, and <3 mm in translational head movement and/or 3° of rotational head movement. There were 177 subjects who appeared in both groups. Subjects appeared in one group but not the other because of poor/missing functional scans in one dataset or the other. There were no significant differences in age (t₍₃₇₆₎ = 0.08, p = 0.93) or in IQ (t₍₃₇₆₎ = 0.16, p = 0.87) in the two TR groups because most subjects contributed data to both groups. However, there was a significant difference in FD (t₍₃₇₆₎ = 15.46, p = 4.31 × 10⁻⁴²) between the groups. Larger FD for the slow TR group was expected: head movement would be naturally smaller for the fast TR group because there is less time to move between successive volume acquisitions. Because of these differences in head movement between TR groups and the stringent head motion analysis corrections that we used, we reasoned that any MSSD effects that replicated across both groups would ameliorate concerns that head movement influenced the results.

Imaging was performed on a Siemens Trio 3.0 T scanner that collected a T1 anatomical image and multiband (factor of 4) EPI sequenced resting-state images (low TR group: 3 × 3 × 3 mm, 40 interleaved slices, TE = 30 ms, flip angle = 60 degrees, field of view = 222 mm, 900 volumes; high TR group: 2 × 2 × 2 mm, 64 interleaved slices, TE = 30 ms, flip angle = 65 degrees, field of view = 224 mm, 404 volumes). Participants were instructed to keep their eyes open and fixate on a central cross in the middle of the screen (http://fcon_1000.projects.nitrc.org/indi/enhanced/mri_protocol.html).

Image preprocessing.

Resting-state scans were preprocessed using FSL, AFNI, and SPM 8 functions through DPARSF-A (http://rfmri.org/DPARSF). The first five volumes were removed to allow the MRI signal to reach equilibrium. Several steps were undertaken to remove motion artifacts and other sources of noise from the data before analysis. Resting-state data were realigned (FSL) and smoothed (FSL: 6 mm) before individual independent component analyses (ICA) were conducted for all data sets using automatic dimensionality estimation (FSL's MELODIC). Noise components were then classified for 20 subjects in the fast TR group and 20 subjects in the slow TR group (random sampling by choosing subjects separated by ∼5 years of age) by transforming independent component maps into MNI space (3 mm for the fast TR group and 2 mm for the slow TR group to match their respective acquisition parameters). The resulting component classifications were then fed into FMIRB's ICA-FIX classification algorithm (Griffanti et al., 2014) to classify noise and non-noise components from both groups before conducting nuisance regression of classified noise components from the resting-state scans in subject space. The ICA-FIX cleaned data were then normalized into MNI space (DPARSF-A) using an EPI template from SPM (3 mm for the low TR group and 2 mm for the high TR group to match each group's respective acquisition parameters). The data were then despiked using AFNI's 3dDespike (“New”) algorithm, subjected to nuisance covariance regression (Friston 24 motion parameters, WM, CSF), linear detrended, and band-pass filtered (0.01–0.10 Hz) to isolate low-frequency fluctuations that characterize resting-state BOLD signals (Damoiseaux et al., 2006).

Experimental design and statistical analysis.

The current study examined the relationship between bold variability and age using a voxelwise within-subjects measure called MSSD. MSSD was calculated on a voxelwise basis for all subjects using custom MATLAB scripts. For more details, see the section “BOLD signal variability.”

The voxelwise relationship between MSSD and age was tested using an ordinary least-squares (OLS) regression model in FSL using a repeated-measures design with linear age and quadratic age as regressors of interest and handedness, FD, and IQ as nuisance regressors. To account for multiple voxelwise comparisons, spatial maps from the OLS analysis were subjected to a voxelwise threshold of p < 0.002 (uncorrected) and a cluster-wise threshold of p < 0.5 (corrected using Gaussian Random Field theory). For more details on the OLS analysis, see the section “BOLD signal variability.”

Post hoc testing of significant cluster corrected effects using a linear regression analysis in SPSS 24 was conducted to further examine linear and quadratic effects identified from the OLS analysis. This was done to ensure that significant effects identified from the voxelwise analysis remained significant when averaging MSSD across a number of voxels and to account for possible influences of gray matter probability (GMP) and gender. For more details, see section “Post hoc analysis of GMP and gender, linear, and quadratic effects.”

Additional post hoc testing consisted of examining the relationship between MSSD values for only the 177 subjects present in both TR groups. Spearman's rank-order correlations were conducted in SPSS 24 on the effects examined in the previously described post hoc regression analyses. For more details, see section “Linear relationship between MSSD values for subjects in both TR groups.”

BOLD signal variability analysis.

Preprocessed time series were converted to z statistics (zero mean, unit SD) before calculating MSSD scores for each voxel (Von Neumann et al., 1941). MSSD was used in the current study because of the temporal continuity afforded by resting-state data and because it avoids the influence of auto-correlation that is exacerbated by multiband EPI acquisition parameters (Smith et al., 2013) on measures such as the SD (Arbabshirani et al., 2014). MSSD was calculated by subtracting time point t from time point t + 1, squaring the result, and then averaging all resulting values acquired from the entire voxel time course as follows:

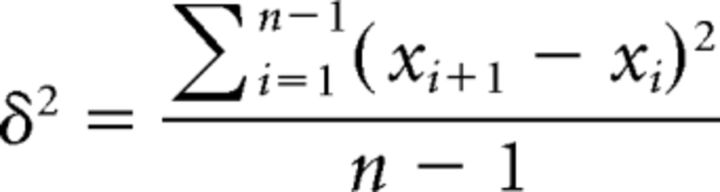Associations between MSSD and age were calculated in FSL using OLS. Age regressors included the linear (mean centered) and quadratic age (squared mean centered age). Full-scale IQ, EHQ handedness scores, and FD were included as nuisance regressors. The resulting t-maps were first examined using a liberal voxelwise correction (uncorrected p < 0.40) without cluster size correction. These more general results demonstrated the reliability of the effects across the two different acquisition times (Fig. 1).

T-maps were then examined by using stricter voxel wise (uncorrected at p < 0.002 for linear effects and at p < 0.05 for quadratic effects; see Results for additional details) and cluster size (corrected at p < 0.05) correction to identify results less susceptible to type 1 errors (Eklund et al., 2016). Spatial maps identifying brain areas with significant overlapping effects across both TR groups were produced to further isolate replicable effects. Overlapping effects across TR groups were identified by resampling the slow TR group results to have the same voxel resolution as the fast TR group results (down-sampling the slow TR group cluster-corrected spatial t-maps to 3 mm³). We then overlaid the fast TR group cluster-corrected results on corresponding cluster-corrected maps for the slow TR group to identify cluster-corrected effects present in both TR groups. MSSD values from each TR group for overlapping significant cluster corrected voxels were then extracted and converted to z statistics to create scatterplots for visualization of lifespan trajectories.

Post hoc analysis of GMP and gender, linear, and quadratic effects.

Three regression analyses were run to rule out the influence of GMP and gender and also to further explore linear and quadratic voxelwise effects. The primary goal of these follow-up tests was to account for differences in gray matter and gender and to confirm that voxelwise effects persisted when averaging MSSD across a group of voxels. Following previous work accounting for changes in gray matter (Damoiseaux et al., 2008), we used ROIs of the overlapping cluster-corrected results from the previous voxelwise analysis to calculate individual subject estimates of GMP. GMP and gender were then used in subsequent analyses as nuisance regressors. GMP was assessed by segmenting the T1 structural images into gray matter, white matter, and CSF probability maps in SPM and taking the mean GMP in the ROI. A secondary goal of further exploring linear and quadratic effects was also performed through these three post hoc regression analyses.

Three post hoc regression models were run. The first post hoc regression model tested whether the MSSD linear effects indeed extend across the lifespan without the quadratic predictor in the model, and to confirm that these linear effects persisted when accounting for GMP and gender. As with previous regression tests, this model used linear age (mean centered) as a regressor of interest along with handedness, IQ, FD, GMP, and gender as nuisance covariates. This model was run on ROIs representing significant group-overlapping linear effects from the cluster-corrected voxelwise analysis.

A second post hoc regression model was used to test whether a quadratic effect better explained the MSSD trajectory than the linear effect from the first regression model. This model used linear age (mean centered) and quadratic age (squared mean centered age) as regressors of interest, along with handedness, IQ, FD, GMP, and gender as nuisance covariates. As with the first model, this model was run solely on ROIs representing significant group-overlapping linear effects from the cluster-corrected voxelwise analysis. We determined that a quadratic model was a better fit compared with the linear model if the quadratic term was statistically significant (p < 0.05).

Finally, a third post hoc regression model was used to confirm that voxelwise quadratic effects persisted when controlling for GMP and gender. This model used linear age (mean centered) and quadratic age (squared mean centered age) as regressors of interest, along with handedness, IQ, FD, GMP, and gender as nuisance covariates. This model was run on ROIs representing group-overlapping quadratic effects from the voxelwise analysis.

Results

Associations between MSSD and linear effects of age

The average whole-brain MSSD value across all subjects was 0.2073 (SD = 0.0102, range: 0.1734 - 0.2359) for the fast TR group and 0.443 (SD = 0.0194, range: 0.3916-0.4886) for the slow TR group, indicating significantly smaller MSSD for the fast TR group (t(376) = 148.581, p < 0.0001). This mirrored differences in head motion metrics across TR groups and was also expected because there should be less difference between the BOLD signal for consecutive volumes when they are acquired closer together in time. Therefore, any effects replicating across both TR groups should not be due to the absolute size of MSSD, but rather to the contrasts of interest.

Within-subject voxel-wise whole-brain group average correlations between z-score normalized MSSD (zMSSD), non-normalized SD (SD), percent-change normalized MSSD with a mean of 100 (%MSSD), and percent-change normalized SD with a mean of 100 (%SD) showed that SD, %MSSD, and %SD were strongly positively correlated with each other (rs > 0.98) (Table 2) and negatively correlated with zMSSD (rs < -0.25).

Table 2.

Within-subject voxelwise whole-brain group average correlations between zMSSD, non-normalized SD, percentage-change normalized MSSD with a mean of 100 (%MSSD), and percentage-change normalized SD with a mean of 100 (%SD)

	Fast TR group				Slow TR group
	zMSSD	SD	%MSSD	%SD	zMSSD	SD	%MSSD	%SD
zMSSD	—	—	—	—	—	—	—	—
SD	−0.392				−0.44
%MSSD	−0.251	0.9811			−0.314	0.9838
%SD	−0.392	1	0.9811		−0.439	0.9999	0.9839

SD, %SD, and %MSSD are strongly correlated with each other and negatively correlated with zMSSD.

Previous research has demonstrated that MSSD and SD are strongly correlated (r > 0.97) within the context of a task-based fMRI study (Garrett et al., 2011). To determine how MSSD and SD are related in the context of a resting-state fMRI study, voxelwise estimates of SD were calculated on non-normalized time courses for all gray matter voxels. Average correlations between MSSD and SD for gray matter voxels across the whole brain were then calculated across all subjects in each TR group. Strong positive correlations were present for both the fast (mean r = 0.73, SD = 0.037) and slow (mean r = 0.72, SD = 0.046) TR groups, replicating previous findings of strong correspondence between MSSD and SD.

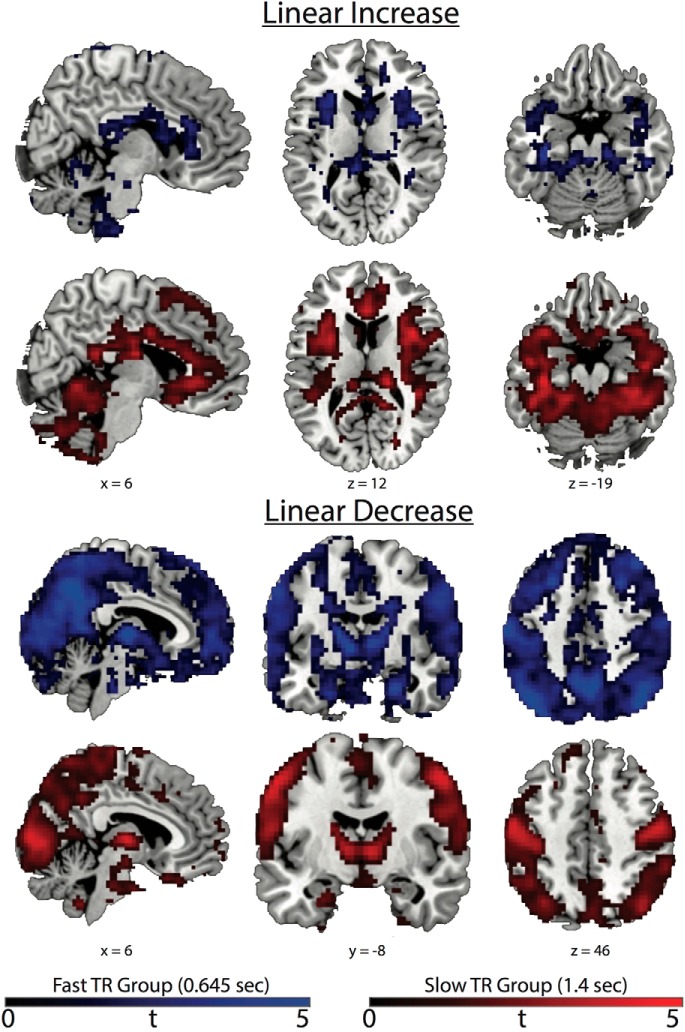
General linear age MSSD effects revealed both increases and decreases in functionally distinct cortical and subcortical brain areas. Spatial maps for each TR group with a liberal voxelwise criteria (p < 0.40) and no cluster size correction (Fig. 2) demonstrate that MSSD increases linearly across the lifespan in salience network (SN) nodes (bilateral anterior insula) and bilateral ventral temporal cortices. Linear decreases in MSSD as a function of age appear in the thalamus and basal ganglia and brain networks representing visual, sensorimotor, central executive network (CEN), and nodes of the default mode network (DMN). These results demonstrate that an intrinsic brain pattern of BOLD variability related to maturation across the lifespan is characterized by an increase in SN and ventral temporal cortex (VTC) variability and a decrease in variability for most every other brain area, including nodes in the CEN and DMN, along with brain areas in visual, sensorimotor, and subcortical areas. These general results were replicated across both TRs, providing evidence for the robustness of the observed effects.

Figure 2.

Liberal voxelwise corrected (p < 0.40 uncorrected) t-maps without cluster correction. Blue represents the fast TR group and red represents the slow TR group. General linear MSSD increases can be seen in SN nodes such as the bilateral anterior insula and anterior cingulate cortex and also in the VTC. General linear MSSD decreases can be seen in subcortical, visual, sensorimotor, DMN (posterior cingulate and medial prefrontal cortex), and CEN (supramarginal gyrus and dorsal–lateral prefrontal cortex) brain areas. Colored bars represent t values.

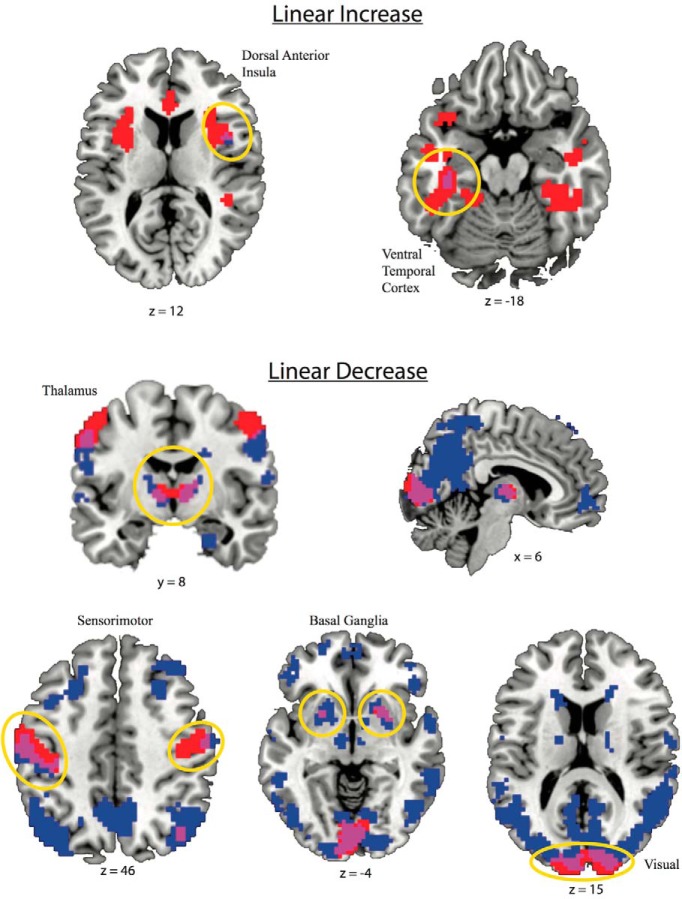
Spatial maps (Fig. 3) and scatterplots (Fig. 4) are presented from brain regions where there was a significant cluster-corrected association with age in both TR groups. This included a linear MSSD increase across the lifespan in the right dorsal anterior insula (dAI) and left VTC and a linear MSSD decrease across the lifespan in bilateral visual and sensorimotor networks, as well as the bilateral thalamus and basal ganglia regions.

Figure 3.

Spatial maps showing brain areas surviving voxelwise (p < 0.002 uncorrected) and cluster size (p < 0.05 corrected) associations between MSSD and age. Red indicates the slow TR group (1.4 s), blue is the fast TR group (0.645 s), and violet is the voxel overlap between fast and slow TR groups, neuroscientific convention. Significant cluster-corrected voxels overlapping across both TR groups demonstrate linear increases in the right anterior cingulate and left VTC and linear decreases in thalamus, sensorimotor cortex, and in the primary visual cortex.

Figure 4.

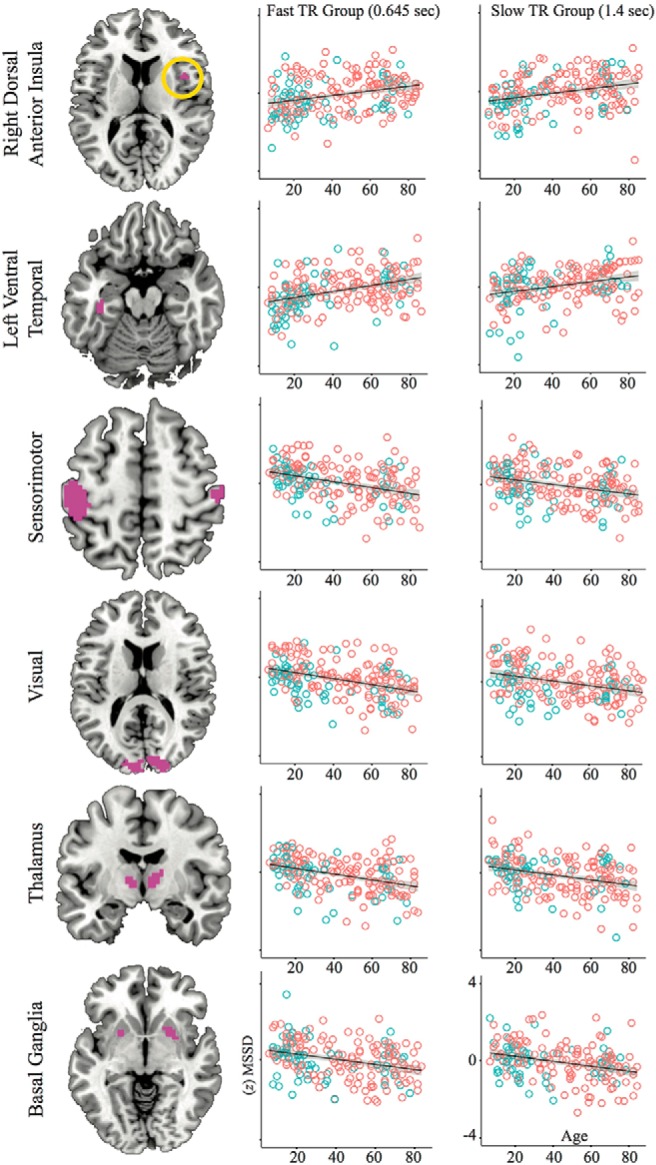
Scatterplots depicting linear MSSD effects across the lifespan. ROIs were taken from areas of cluster-corrected TR group overlap (violet colors) in Figure 3. Blue circles are males and red circles are females.

Associations between MSSD and nonlinear effects of age

There were no quadratic effects of age that survived stringent voxelwise (p < 0.002, Fast TR group df = 189, Slow TR group df = 185) and cluster wise (p < 0.05) correction. There were two quadratic effects that survived a more liberal voxelwise (p < 0.05) and cluster wise (p < 0.05) correction. Although these effects in isolation are more susceptible to type I errors (Eklund et al., 2016), the overlap across two different TR acquisitions provides some evidence for the reliability of these effects. There was a positive quadratic effect for the thalamus in the slow TR group and a negative quadratic effect for the right lateral VTC in both TR groups. The positive quadratic cluster-corrected effect in the slow TR group did overlap with a positive quadratic effect in the fast TR group that was not cluster corrected (voxelwise p < 0.05; Fig. 5). This demonstrates that an area of the thalamus had high MSSD in young and old age but low MSSD in middle age. The positive quadratic-overlapping TR group effect was in a more dorsal–anterior portion of the thalamus compared with the linear MSSD decrease effect, which was in a more ventral posterior portion of the thalamus. The negative quadratic effect in both groups was in the right lateral VTC (Fig. 5). This demonstrates that an area in the right VTC had low MSSD in young and old age, but high MSSD in middle age.

Figure 5.

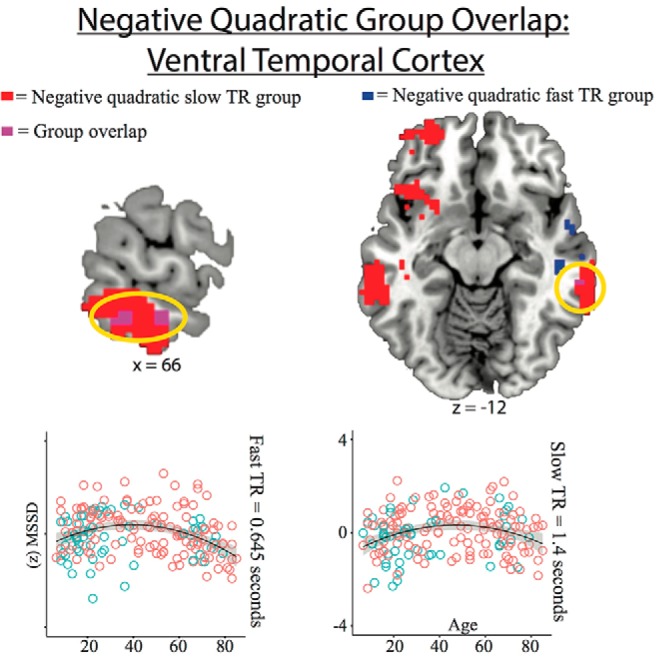
Negative quadratic effect overlap for both TR groups with scatterplots showing MSSD effects (voxelwise at p < 0.05 and cluster corrected at p < 0.05 for both TR groups). Blue circles are males and red circles are females. Scatterplots show MSSD values for the fast TR group effect (voxelwise at p < 0.05) and slow TR group effect (voxelwise at p < 0.05 and cluster corrected at p < 0.05).

Post hoc analysis of GMP and gender, linear, and quadratic effects

To examine the specificity of the voxelwise effects, we performed three follow-up post hoc tests to determine whether these relationships could be accounted for by age-related changes in GMP or gender and to further explore linear and quadratic effects. The first post hoc regression model used linear age as the regressor of interest, and handedness, IQ, FD, GMP, and gender as nuisance regressors. This test produced significant post hoc effects for linear age for all overlapping ROIs across both TRs except for the sensorimotor ROI in the slow TR group, which produced a marginally significant effect (Table 1). This demonstrates that significant linear effects persisted across the lifespan after accounting for GMP and gender in the absence of a quadratic regressor.

Table 1.

Results from post hoc regression analyses

	Fast TR group, 0.645 s					Slow TR group, 1.4 s
		R2	(df) F	βlinear (p value)	βquadratic (p value)		R2	(df) F	βlinear (p value)	βquadratic (p value)
Left VTC linear increase	M1	0.189	(6, 184) 7.15	0.389 (4.3463 × 10−7)	—	M1	0.163	(6, 180) 5.83	0.323 (0.000061)	—
	M2	0.204	(7, 183) 6.71	0.410 (1.2892 × 10−7)	−0.140 (0.063)	M2	0.170	(7, 179) 5.24	0.335 (0.000037)	−0.091 (0.214)
Right insula linear increase	M1	0.143	(6, 184) 5.13	0.308 (0.00013)	—	M1	0.114	(6, 180) 3.86	0.3 (0.00039)	—
	M2	0.144	(7, 183) 4.40	0.312 (0.000125)	−0.034 (0.663)	M2	0.147	(7, 179) 4.40	0.325 (0.000112)	−0.195 (0.009)
Sensorimotor linear decrease	M1	0.168	(6, 184) 6.17	−0.352 (0.002)	—	M1	0.120	(6, 180) 4.09	−0.356 (0.000092)	—
	M2	0.180	(7, 183) 5.72	−0.382 (0.001)	0.125 (0.102)	M2	0.121	(7, 179) 3.52	−0.358 (0.000088)	0.033 (0.660)
Visual linear decrease	M1	0.222	(6, 184) 8.78	−0.429 (1.9072 × 10−7)	—	M1	0.173	(6, 180) 6.28	−0.360 (0.000009)	—
	M2	0.226	(7, 183) 7.65	−0.436 (1.408 × 10−7)	0.069 (0.345)	M2	0.177	(7, 179) 5.51	−0.367 (0.000007)	0.069 (0.346)
Thalamus linear decrease	M1	0.174	(6, 184) 6.48	−0.433 (1.9711 × 10−7)	—	M1	0.123	(6, 180) 4.21	−0.256 (0.005)	—
	M2	0.183	(7, 183) 5.84	−0.431 (2.1183 × 10−7)	0.139 (0.065)	M2	0.138	(7, 179) 4.08	−0.257 (0.005)	0.132 (0.083)
Basla ganglia linear decrease	M1	0.116	(6, 184) 4.03	−0.376 (0.000006)	—	M1	0.113	(6, 180) 3.83	−0.368 (0.00001)	—
	M2	0.127	(7, 183) 3.79	−0.387 (0.000004)	0.116 (0.136)	M2	0.115	(7, 179) 3.33	−0.373 (0.000008)	0.048 (0.528)
Right VTC negative quadratic	M3	0.197	(7, 183) 6.40	−0.203 (0.015)	−0.233 (0.003)	M3	0.093	(7, 179) 2.63	−0.078 (0.354)	−0.270 (0.001)

Model 1 investigated whether linear effects persisted across the lifespan in the absence of a quadratic regressor when averaging MSSD across a group of voxels and accounting for gray matter probability and gender. Model 2 ruled out that a quadratic effect better explained the linear effect from Model 1 when averaging MSSD across a group of voxels and accounting for gray matter probability and gender. Model 3 investigated whether quadratic effects persisted across the lifespan when averaging MSSD across a group of voxels and accounting for gray matter probability and gender. Beta coefficients are reported in standardized form.

The second post hoc regression model added quadratic age as a factor of interest back into to the first post hoc regression model and produced a significant negative quadratic effect for the right dAI in the slow TR group, a marginally significant positive quadratic effect of the basal ganglia in the fast TR group, a marginally significant positive quadratic effect for the sensorimotor ROI in the fast TR group, and marginally significant positive quadratic effects for the thalamus in both the fast TR and slow TR groups (Table 1). No other quadratic effects were significant. This confirms that a model including a quadratic factor generally does not outperform a model including the linear factor for most linear effects (except for the dAI in the slow TR group) after accounting for gray matter and gender. This also demonstrates slight U-shaped influences on sensorimotor and basal ganglia ROIs for the fast TR group and on the thalamus for both TR groups.

The third post hoc regression model showed that the positive voxelwise quadratic effect in the thalamus remained significant in both the fast TR group and the slow TR group (Table 1). One outlier from the fast TR group and one outlier from the slow TR group were removed for the quadratic thalamus effect (SD > 4). The negative voxelwise quadratic effect in the right VTC also remained significant in both the fast TR group and slow TR group. This demonstrates that voxelwise quadratic effects still persist after accounting for GMP and gender.

Linear relationship between MSSD values for subjects in both TR groups

To determine the consistency of MSSD values for subjects present in both TR groups, Spearman's rank-order correlations were recalculated using MSSD values for the 177 subjects common to both groups for all post hoc analyses. Significant positive correlations were replicated for all post hoc regression effects as in the original manuscript (left VTC linear increase: ρ₍₁₇₅₎ = 0.291, p = 0.000085; right dAI linear increase: ρ₍₁₇₅₎ = 0.470, p = 3.9022 × 10⁻¹¹; sensorimotor linear decrease: ρ₍₁₇₅₎ = 0.634, p = 2.7058 × 10⁻²¹; visual linear decrease: ρ₍₁₇₅₎ = 0.685, p = 6.9544 × 10⁻²⁶; thalamus linear decrease: ρ₍₁₇₅₎ = 0.595, p = 2.5408 × 10⁻¹⁸; basal ganglia linear decrease: ρ₍₁₇₅₎ = 0.361, p = 7.8534 × 10⁻⁷; right VTC negative quadratic: ρ₍₁₇₅₎ = 0.425, p = 3.7767 × 10⁻⁹). This demonstrates that MSSD values were similar in both the fast and slow TR analyses for each subject that was present in both TR groups.

Age–FD and age–sample size relationships

One possible concern with the current study is related to how the association between age and head motion may affect measures of MSSD across the lifespan. To further investigate the relationship between age and head motion (e.g., FD), linear regression models were run using age (mean centered) and age squared (squared mean center age) as regressors in a stepwise model. In the fast TR group, we observed a positive quadratic relationship between age and FD (F_(2,188) = 3.99, p = 0.02, R² = 0.04; β_linear = 0.092, p = 0.209; β_qaudratic = 0.164, p = 0.025), whereas in the slow TR group, we observed a positive linear relationship between age and FD (F_(1,185) = 25.22, p = 0.000001, R² = 0.12; β_linear = 0.0346, p = 0.000001). Adding a quadratic term to the linear model for the slow TR group failed to produce a significant change in the F statistic (F_change = 0.756). Scatterplots visualizing the age–FD relationship for both TR groups can be found at the bottom of Figure 1. Despite the significant relationships between age and FD, the voxelwise and post hoc regression analyses used FD as a nuisance regressor that accounted for such relationships while still demonstrating significant effects across both analyses.

Another possible concern related to the current study could be that there was an unequal age distribution of participants: this dataset includes more subjects in early and old age compared with middle age. To determine whether this unequal distribution led to overfitting for young and older individuals compared with middle age individuals, we investigated whether there was a relationship between age and the unstandardized residuals for each post hoc regression analysis. Visual inspection of these scatterplots demonstrated that residuals were evenly distributed across the entire age range, suggesting that analysis did not overfit the regression line systematically at young and old age.

Discussion

Brain signal variability has been linked to optimal neural function (Garrett et al., 2013b) and has been hypothesized to help facilitate shifts between integrative and segregative brain networks (Tognoli and Kelso, 2014). Previous studies have focused on identifying differences in BOLD variability between younger and older adults within the context of task-based fMRI paradigms (Garrett et al., 2010, 2011, 2012). The current study investigated resting-state BOLD variability across the lifespan for the first time. We find linear and quadratic changes in lifespan BOLD variability trajectories in distinct brain areas similar to lifespan changes in resting-state functional connectivity (Betzel et al., 2014) and task-related univariate activity (Kennedy et al., 2015). The current study also complements research demonstrating developmental maturation of structural brain properties such as total cerebral volume and white/gray matter maturation (Giedd et al., 1999).

Overall, we found that variability increases linearly in SN nodes (anterior insula) and the VTC across the lifespan. In contrast, brain signal variability decreases across the lifespan in most every other brain area, including subcortical, visual, sensorimotor, DMN, and CEN regions. Cluster corrected results across two TRs demonstrated BOLD signal variability linearly increased across age in the right dAI and left VTC, whereas linear decreases were localized bilaterally in visual, sensorimotor, thalamic, and basal ganglia areas. Last, we demonstrate preliminary support for a positive quadratic thalamus effect that was spatially distinct from the linear decrease thalamus effect and a negative right VTC quadratic effect.

Brain variability across the lifespan

The current results align with research demonstrating that BOLD variability mostly decreases in old age: fewer brain regions show increased variability with old age (Garrett et al., 2010, 2011). However, the current results do not align with previous evidence for a general cortical–subcortical dichotomy where subcortical areas increase in variability across age compared with cortical areas (Garrett et al., 2013b). Instead, the current study found different MSSD trajectories based on functional systems (e.g., SN vs the rest of the brain) rather than a cortical–subcortical dichotomy. These data also conflict with previous results showing both increases and decreases in BOLD variability across age in frontal, temporal, and parietal areas (Garrett et al., 2010; Garrett et al., 2013b). The current study also conflicts with previous EEG results (McIntosh et al., 2008) and BOLD variability studies (Garrett et al., 2011) that led researchers to propose an inverted U-shaped trajectory in which brain variability is low in children and older adults, but high in middle age (Garrett et al., 2013b).

One explanation for the divergent findings is that we used resting-state data, whereas previous studies focused on fixation and task periods within the context of task performance. Previous research indicates that completing task-based fMRI affects resting-state BOLD fMRI (Northoff et al., 2010). Therefore, preceding task trials in task-based fMRI may affect variability analyzed during fixation periods. Furthermore, it is typical to isolate low-frequency fluctuations in resting-state data through band-pass filtering (0.01–0.10 Hz), something typically not done in task-based fMRI BOLD variability analyses. Finally, the current study used multiband acquisition data whereas previous studies did not. Additional research should explore how interspersed task blocks affect BOLD variability during fixation periods compared with rest, how BOLD variability may differ when isolating specific frequency bands, and the influence of multiband acquisition parameters on BOLD variability.

Functional connectivity across the lifespan

Two previous studies using the NKI database (age range 7–85 years old, TR = 2.5) demonstrate that modularity (how well major networks are partitioned into smaller integrative and segregative communities, e.g., SN, DMN) generally shows a linear decrease across the lifespan, indicating reduced functional subnetwork autonomy (Betzel et al., 2014; Cao et al., 2014). Betzel et al. (2014) also demonstrated general within-network node functional connectivity decreases alongside general between-network node functional connectivity increases for the DMN, CEN, visual, and sensorimotor networks. In the current study, general decreases in MSSD across the lifespan for most networks (except the SN) may be related to decreased modularity because increased variability is thought to enhance functional specificity by facilitating flexibly switching between integrative and segregative states (Tognoli and Kelso, 2014).

In addition, Betzel et al. (2014) found that salience/ventral attention network nodes (including the right dAI) demonstrated positive quadratic trajectories for within-network node comparisons. They also found increased lifespan between-node connectivity involving the dorsal attention network, DMN, and CEN. Therefore, the dAI demonstrated functional connections in different directions from the general decreased connectivity found between most other brain areas. Cao et al. (2014) conducted ROI-to-whole-brain functional connectivity analyses and demonstrated linear decreases of whole-brain functional connectivity metrics for nodes within salience (including the right dAI), default, attention, visual, and subcortical regions; positive quadratic effects were found for the parahippocampus and thalamus, whereas negative quadratic effects were found in the frontal, temporal, and parietal areas.

The current results demonstrating differential variability patterns in the right dAI compared with other brain areas are consistent with Betzel et al. (2014), who found that the right dAI showed differential patterns of functional connectivity across the lifespan compared with the rest of the cortex. The positive thalamic quadratic effect and the negative quadratic effect for the VTC in the current study align with Cao et al. (2014), who found a positive thalamic quadratic effect and negative temporal quadratic effect for functional connectivity. Other work indicates that dorsal–anterior portions of the thalamus strengthen their functional connections to frontal areas, whereas ventral–posterior portions of the thalamus weaken their functional connections to temporal areas from childhood to adulthood (Fair et al., 2010). These dissociations in thalamic connectivity mirror the spatially distinct thalamic variability results in the current study, in which a dorsal–anterior thalamic area demonstrates a positive quadratic effect and a ventral–posterior thalamic area a negative linear effect. These studies, in conjunction with the current study, suggest that the right dAI, thalamus, and temporal cortex present with unique types of variability and functional connectivity lifespan trajectories compared with other brain areas. Future work is needed to explore the relationship between BOLD variability and functional connectivity across the lifespan.

Behavioral relevance of MSSD lifespan trajectories

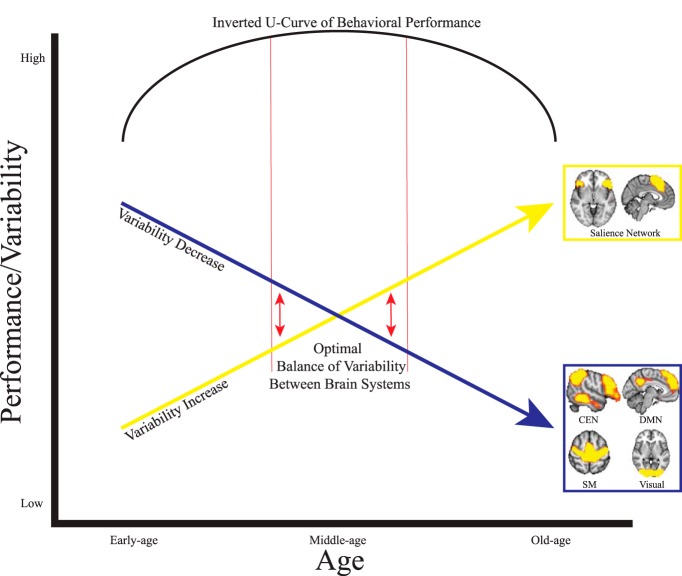
On a systems level, different brain networks interacting with varying degrees of variability may reflect the inverted U-curve trajectories (see Fig. 6) present across the lifespan for various behavioral measures (Cepeda et al., 2001; Hommel et al., 2004; Li et al., 2004; Tran and Formann, 2008). The right dAI within the SN in particular has been identified as a “hub” that participates in a myriad of cognitive processes including network switching, salience detection (Menon and Uddin, 2010), and integrating sensory networks (Nomi et al., 2016). Therefore, increased variability in the right dAI is notable because of its dynamic interaction with almost every brain system and its involvement in nearly every cognitive process (Uddin et al., 2014; Uddin, 2015). Speculatively, it is possible that large differences in variability between SN nodes and other brain areas/systems could produce the suboptimal behavioral performance seen in early childhood and old age. In middle age, variability between different brain areas/systems may reach more of an equilibrium, resulting in optimal behavioral performance—an idea consistent with theories proposing that a balance between excitation and inhibitory neuronal processes facilitates optimal brain function (Shew et al., 2011). Additional studies that characterize the relationship between resting-state and task-based fMRI BOLD variability across the lifespan are crucial for understanding the behavioral significance of the current findings.

Figure 6.

Speculative model describing the proposed relationship between linear increases and decreases in BOLD variability across the lifespan and the inverted U-shaped curve of lifespan behavioral performance characterizing many behavioral tasks. The yellow arrow indicates linear increases in BOLD variability for SN nodes and the blue arrow indicates linear decreases in BOLD variability for CEN, DMN, sensorimotor (SM), and visual areas. In early and old age, large differences in variability between brain networks leads to suboptimal behavioral performance. The red arrows indicate that optimal behavioral performance may come from the intrinsic balance between high and low variability between different brain networks in middle age.

Physiological influences on the BOLD signal across the lifespan

A concern in lifespan neuroimaging studies is neurovascular coupling; that is, how neural activity interacts with brain vasculature across age to influence the BOLD signal artificially (D'Esposito et al., 2003). Although it is difficult to completely rule out physiological confounds, previous work suggests that vascular changes are not responsible for the BOLD variability trajectories observed in the current study. First, previous developmental BOLD variability research argued that global unidirectional vascular-coupling age effects cannot explain multidirectional BOLD variability trajectories (Garrett et al., 2010). Second, whereas early studies demonstrated an influence of vascular coupling on BOLD signal activity in aging research (D'Esposito et al., 1999), recent studies claim that these effects were driven by the inclusion of voxels biased toward younger subjects' task activation in statistical analyses (Aizenstein et al., 2004) and by using task designs that produce attentional and motor differences in older individuals compared with younger individuals (Grinband et al., 2017). Because the current study found multidirectional trajectories of BOLD variability (increases, decreases, and quadratic effects), avoided analyzing voxels biased toward any age range by focusing analyses on only voxels with significant age trajectories, and used resting-state fMRI data that were not influenced by task design, vascular coupling influences across age should be minimized.

Summary

The current study identified general lifespan trajectories of resting-state BOLD variability that complements previous research showing structural and functional lifespan changes within the brain. We demonstrate that variability in SN nodes increases linearly across the lifespan, whereas variability from most other large-scale networks decreases linearly over the lifespan. We also demonstrate a positive quadratic thalamic effect and a negative quadratic right VTC effect. These findings add to a growing literature demonstrating the contributions of neural variability to flexible cognition.