The neocortical microcircuit as a tabula rasa

Abstract

The neocortex has a high capacity for plasticity. To understand the full scope of this capacity, it is essential to know how neurons choose particular partners to form synaptic connections. By using multineuron whole-cell recordings and confocal microscopy we found that axons of layer V neocortical pyramidal neurons do not preferentially project toward the dendrites of particular neighboring pyramidal neurons; instead, axons promiscuously touch all neighboring dendrites without any bias. Functional synaptic coupling of a small fraction of these neurons is, however, correlated with the existence of synaptic boutons at existing touch sites. These data provide the first direct experimental evidence for a tabula rasa-like structural matrix between neocortical pyramidal neurons and suggests that pre- and postsynaptic interactions shape the conversion between touches and synapses to form specific functional microcircuits. These data also indicate that the local neocortical microcircuit has the potential to be differently rewired without the need for remodeling axonal or dendritic arbors.

Ahallmark of the neocortex is its sensitivity to environmental conditions that can drive profound structural and functional changes (1-4). At the microcircuit level, these changes include the creation, elimination, and modification of synaptic connections between neurons (5-10). To understand the mechanisms and full potential of cortical plasticity, it is essential to answer a fundamental question: How does a neuron choose to connect to only a small fraction of its neighboring neurons in a cortical volume packed with intertwined dendrites? This question has been debated extensively for more than a decade (11-15). At the heart of the debate is the question of whether recurrent synapses between pyramidal neurons, which are the vast majority of neocortical synapses (14, 16), are placed randomly to form an arbitrary functional microcircuit or deterministically to form a highly specific functional microcircuit.

Theoretical work suggests that it is essentially impossible for an axon of a pyramidal neuron to avoid touching any other pyramidal neuron within the local microcircuit (up to ≈150 μm from the soma) (see Fig. 1C) (14, 17, 18). However, experimental studies with paired recordings clearly indicate that pyramidal neurons are synaptically connected to only a small fraction of their neighboring neurons (19-24). Even more puzzling is that when a functional connection is established, multiple synaptic contacts are observed (22, 23, 25, 26). Furthermore, there are only enough synaptic boutons on a local pyramidal axon (≈1,000-1,500) to form multiple synaptic contacts with a small fraction of the 1,000-2,000 neighboring pyramidal neurons (14, 27). A form of target neuron selection must therefore take place at some level. To resolve this question, we undertook a combined multineuron recording and confocal study to compare structural and functional properties of connections between neocortical thick tufted pyramidal neurons in layer V.

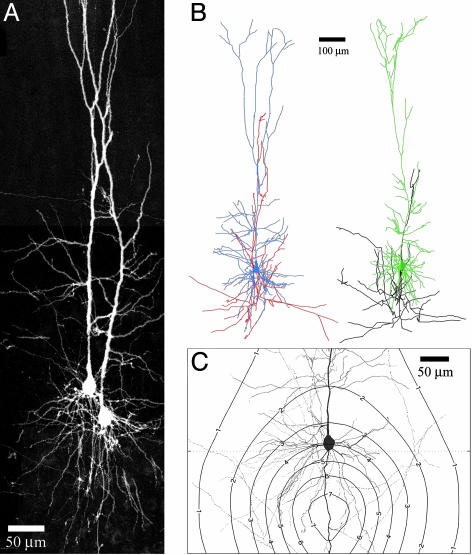
Fig. 1.

Confocal imaging and 3D reconstructions of pairs and triplets of layer V pyramidal neurons. (A) Flattened representation from 3D image stacks of a pair of pyramidal neurons in layer V, as acquired by confocal microscopy. The entire span of the neurons is captured, allowing for a detailed investigation of all apposition points between axons and dendrites. (B) The high resolution of confocal imaging allowed for unambiguous tracing of axons and dendrites to create detailed 3D reconstructions. The higher neuron is colored blue for soma and dendrites and red for the axon. The lower neuron is colored green for soma and dendrites and black for the axon. (C) Geometrical connectivity between pyramidal neurons of layer V can be predicted from their characteristic morphology. We assumed a setting of two layer V pyramidal neurons with any spatial separation between their somata. The contour plot shows the expected number of touch sites as a function of the relative somatic location of the two neurons when one of them is located at the center. The plot was calculated from the neuronal morphologies obtained from the 3D reconstructions (18) and corrected for neuropil volume.

Our results show that the axon of any pyramidal neuron is not biased toward the dendrites of particular neighboring pyramidal neurons. The axons and dendrites are sufficiently branched so that at least one “touch” (a direct apposition between axonal and dendritic membranes) is observed for every pair of pyramidal neurons sharing the same cortical column. However, we found that synaptic boutons are formed at existing touches between functionally connected pyramidal neurons, as revealed by paired recordings. We show that the amplitudes of the recorded synaptic responses were correlated to the numbers of observed synaptic boutons but not to the numbers of touch sites. Based on these findings, we propose a cortical model, which states that the anatomical structure of the neocortical microcircuit is like a tabula rasa, from which a multitude of functional microcircuits may be formed. These functional microcircuits are likely to be continuously reshaped by the relative activity of their constituent neurons, reflecting the ongoing interactions with the environment.

Materials and Methods

Slice Preparations and Recordings. Simultaneous multineuron recordings were obtained from neuronal pairs and triplets in neocortical slices (sagittal, 300 μm thick) from the somatosensory cortex of Wistar rats (postnatal day 14-16). Slices were incubated for 30 min at 35°C and then at room temperature (≈20-22°C) until transferred to the recording chamber (35 ± 0.5°C). The slice was visualized by IR-differential interference contrast microscopy optics with a Zeiss Axioscope and IR camera (Hamamatsu Photonics, Hamamatsu City, Japan). The bathing solution consisted of 125 mM NaCl, 25 mM NaHCO₃, 25 mM glucose, 2.5 mM KCl, 2 mM CaCl₂, 1.25 mM NaH₂PO₄, and 1 mM MgCl₂. Whole-cell recordings were made by using patch pipettes (5-10 MΩ), containing 110 mM K-gluconate, 10 mM KCl, 10 mM Hepes, 10 mM phosphocreatine(Na), 4 mM MgATP, 0.3 mM NaGTP, and 4 mg/ml biocytin. Thick tufted pyramidal neurons in layer V of the somatosensory cortex were selected for recording according to the morphology of their somata and proximal dendrites. Somata of recorded neurons were located at least 70 μm below the slice surface to enable reliable morphological reconstruction, and distances between somata of recorded pairs or triplets were at <150 μm. Voltage recordings were obtained by using axopatch 200/B amplifiers (Axon Instruments, Union City, CA). The existence of a functional connection between neuron pairs was assessed by the average of at least 30 postsynaptic responses to action potential trains in the presynaptic neuron (see Fig. 3B). In triplets, each experiment resulted in six tested connections. Autaptic connections were analyzed exactly as pairs in terms of their morphological properties but were not studied in terms of their electrophysiological properties.

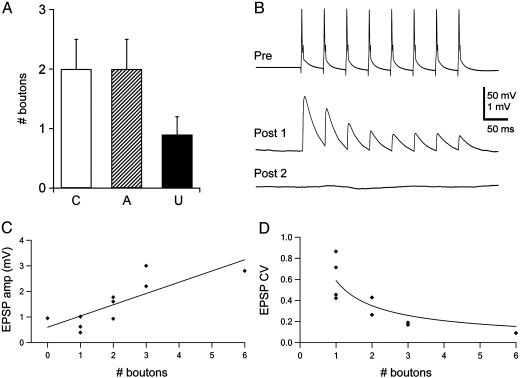
Fig. 3.

Functional connectivity. (A) Synaptic boutons found between pairs of neurons after analysis of high-magnification confocal images and classified according to the functional connectivity of the neuronal pairs. C, connected; A, autapses; U, unconnected. (B) Example of functional connectivity between layer V pyramidal neurons. The presynaptic action potential train (Top) elicited synaptic responses in the first postsynaptic neuron (Middle) but not in the second (Bottom). The postsynaptic traces represent an average of 30 individual trials. (C) Correlation between EPSP amplitudes and the numbers of boutons in connected pairs. Amplitudes of unitary EPSPs (first EPSP in a train) are plotted against the number of boutons, as identified by confocal microscopy. The correlation coefficient is 0.77, and the slope of the linear fit is 0.41 ± 0.12 mV per bouton. (D) Negative correlation between the CV of EPSP amplitudes and the number of boutons. The CV was calculated as SD divided by the mean of EPSP amplitudes from at least 30 individual responses. The continuous line represents a fit to the inverse square function, which is predicted from models of CV analysis of quantal synaptic transmission.

Confocal Microscopy and 3D Computer Reconstructions. After being recorded, slices were fixed with 0.1 M phosphate-buffered solution containing 2% paraformaldehyde and 2% glutaraldehyde for a period of 24-48 h. Each slice was then washed with phosphate-buffered solution, embedded in a gelatin block, and resectioned into four to five thinner slices with a final thickness of 70-80 μm. The sections were then incubated for 3 h in phosphate-buffered solution with 1:100 fluorescent FITC-streptavidin (Sigma) and 0.1% Triton X-100. After being stained, sections were washed in phosphate-buffered solution, flattened on glass slides in ImmuGlo mounting medium (Immco Diagnostics, Buffalo, NY), and cover-slipped for confocal imaging. Each group (pair or triplet) was subjected to confocal imaging (Zeiss LSM 510; excitation, 488-nm argon laser line; detection, 505- to 560-nm band-pass filter). Three-dimensional image stacks of the entire dendritic span and local axon collaterals were acquired by using a 40× objective (Plan-Neofluar, Zeiss). The z distance between successive images in each stack was 1 μm. The stacks were aligned correctly relative to each other to form a continuous 3D representation of the entire neuronal span (Fig. 1 A).

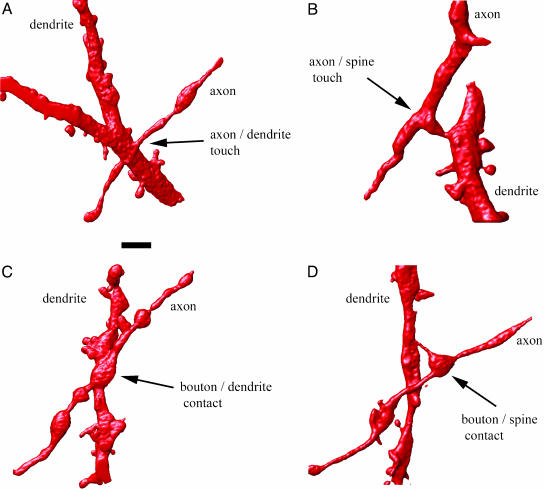
The imaged neurons were fully reconstructed by a 3D-reconstruction software developed in our lab for this purpose. Because of the high resolution of confocal microscopy, in all cases the axonal and dendritic processes could be unambiguously traced to their somatic origin (Fig. 1B). After reconstruction, all sites where an axon passed <2 μm to a dendrite were visually inspected. Unless visual inspection of the images unambiguously discarded any contact between the axon and dendrite, the coordinates of the passing site were saved for higher-magnification imaging. To this end, a 100× objective was used with a 4× scan zoom factor and a narrow pinhole setting. A 3D image stack of each putative contact site was taken with z spacing of 0.2 μm. The quality of the resulting images allowed clear identification of spines, filopodia, and boutons (Fig. 2). Each stack was analyzed for the exact nature of the contact it contained. Criteria for classification were as follows. Geometrical contacts were considered wherever there was no significant decrease in the fluorescence intensity between the axonal and dendritic sites. The criteria for a bouton touch was a geometrical contact that also showed significant swelling of the axon (defined as a bouton) of at least 3-fold the average axonal width. The postsynaptic target was classified as being a spine or a dendritic shaft. The criterion for contacts on spines was the existence of a dendritic protrusion of at least 0.5 μm touching the axon. Examples of each touch type are given in Fig. 2. To avoid any bias in the analysis, all high-zoom stacks were analyzed without knowledge of the functional connectivity. Only after they were classified into touches with or without boutons were they sorted according to the connected, unconnected, and autaptic cases.

Fig. 2.

Geometrical connectivity. (A) Three-dimensional rendering of confocal microscope images of a close apposition between an axon and dendritic shaft in which no presynaptic bouton is observed. (B) Three-dimensional rendering showing a touch without synaptic bouton between an axon and a dendritic spine. (C) Three-dimensional rendering showing a putative synaptic contact between an axon and a dendritic shaft. (D) Three-dimensional rendering showing a putative synaptic contact between an axon and a dendritic spine. (Scale bar, 2 μm.)

Statistical Analysis. Because the existence of a bouton in a touching site is a binary value (either there is a bouton or not), we used binomial distributions of individual bouton/touch ratios to calculate the probability of bouton formation in touch sites. The binomial distribution derived from the connected and autaptic axodendritic pairs was used to estimate the probability for obtaining the ratios observed in unconnected pairs. The significance of difference between the groups was assessed according to the binomial estimate. In all other significance tests, single-factor ANOVA was used.

Results

Simultaneous whole-cell recordings from pairs and triplets of thick tufted layer V pyramidal neurons were obtained from slices of rat somatosensory cortex. For each pair of neurons, two reciprocal connections were tested and classified as functionally connected according to the existence of synaptic responses (see Materials and Methods and Fig. 3B). Recordings were accompanied by injection of biocytin, which enabled subsequent fluorescence avidin staining of the neurons. Neuron pairs and triplets, in which at least one functional synaptic connection was observed, were selected for detailed morphological analysis. A total of 38 axodendritic pairs were morphologically analyzed independently in a blind study in which the neurons that were functionally connected were not indicated. Each neuron pair was scanned systematically with a confocal microscope (see Materials and Methods) and then 3D reconstructed with computer software (Fig. 1 A and B). After reconstruction, all locations in which any axonal segment passed <2 μm by any dendritic process were isolated. We found that the axon of every pyramidal neuron makes as many as 10 such close passes by the dendrites of any neighboring pyramidal neuron or its own dendrites.

We then reimaged these close passes at high magnification for a higher-resolution analysis to determine the number of touch sites (see Materials and Methods). Touch sites were classified into touches with and without synaptic boutons (Fig. 2). After classification, all touch-sites were sorted according to the functional connectivity (synaptically connected versus unconnected). In addition, autaptic axodendritic contacts were also classified as such.

Geometrical Connectivity. We use the term geometrical connectivity to describe close axodendritic appositions and touch sites, regardless of the existence of a functional synapse. The average number of axodendritic touches between any pair of pyramidal neurons was 5.6 ± 3.57 (mean ± SD; n = 38 pairs; range, 0-16, with 37/38 making at least one touch). This result indicates that each pyramidal neuron physically touches every other neighboring pyramidal neuron in the local microcircuit and that in most cases multiple touches are made.

The numbers of touches for connected pairs (6.6 ± 1.5, n = 10), unconnected pairs (4.5 ± 0.8, n = 12) and for autaptic axodendritic pairs (5.8 ± 0.8, n = 16) were not significantly different (see Table 1, which is published as supporting information on the PNAS web site) (P = 0.38, single-factor ANOVA; P = 0.16 for comparison between connected and autaptic versus unconnected axodendritic pairs), indicating that touches occur in a manner that is not significantly biased toward neurons with which functional synapses are formed. Furthermore, the number of touches between neighboring pyramidal neurons agree with the values predicted by theoretical studies (17, 18), assuming randomly distributed touch sites resulting only from geometrical considerations (Fig. 1C). The geometrical predictions validated by the above results indicate that several touch sites are likely to be present between any two pyramidal neurons <300 μm apart, i.e., sharing the same cortical column. This “all-to-all” geometrical connectivity is in sharp contrast to the much sparser functional connectivity observed for the different neuron pairs.

Functional Connectivity. A total of 63 bouton touches were observed, of which 53 were formed on basal dendrites and 10 on oblique dendrites. All of the boutons observed for connected pairs were located on basal dendrites (n = 20). We compared the numbers of boutons observed for connected, unconnected, and autaptic axodendritic pairs. A total of 52 boutons at 159 touches (33%) with a mean ratio (mean of boutons/touches for all neuron pairs) of 0.30 were found for the connected and autaptic cases, compared with 11 boutons at 54 (20%) touches with a mean ratio of 0.19 in the unconnected cases. There was a significant difference between the unconnected pairs and the connected and autaptic axodendritic pairs (P < 0.025, binomial probability estimate) (see Materials and Methods), indicating that putative synaptic boutons had significantly higher probability to exist at touch sites of connected and autaptic axodendritic pairs, compared with the unconnected pairs.

Bouton numbers were >2-fold higher for connected (boutons per pair expressed as mean ± SE, 2 ± 0.5; range, 0-6) and autaptic (boutons per pair, 2 ± 0.5; range, 0-8) connections than for unconnected pairs (boutons per pair, 0.9 ± 0.3; range, 0-3) (Fig. 3A). The mean numbers for bouton-spine contacts were 1.5 ± 0.3 and 0.58 ± 0.22 for the connected and unconnected cases, respectively. This almost 3-fold difference is statistically significant (P < 0.02, single-factor ANOVA), unlike the contacts of boutons on dendritic shafts. In this case, the means were 0.5 ± 0.3 and 0.33 ± 0.14 for the connected and unconnected directions, and the difference is insignificant (P > 0.6, single-factor ANOVA). These data strongly suggest that the bouton-spine appositions are indeed functional synapses. The above bouton numbers are underestimates because they were defined according to a strict cutoff criterion (3-fold swelling of the axon) for the specific purpose of being more sensitive toward any differences between populations. Assuming a Gaussian distribution of bouton size, the actual bouton numbers might therefore be as much as 2-fold greater, which is consistent with previous experimental estimates (23, 25, 28, 29). It is interesting to note that we observed bouton-spine appositions also between unconnected pairs (5 of 12 pairs), with possible reasons for this being (i) that the observed contacts were synapses at different maturation states (before or after being electrically functional), (ii) they could be “silent” synapses (30-32), and (iii) it may be that these observed spines and boutons formed synaptic contacts with unlabeled elements of other neurons.

The probability to find a functional connection was ≈15% (65 of 407 tested pairs), similar to previously reported values (23). The amplitudes of excitatory postsynaptic potentials (EPSPs) recorded in connected pairs (first EPSP evoked by a train of action potentials; see Fig. 3B) were highly correlated to the number of identified synaptic boutons (Fig. 3C), with a correlation coefficient of 0.77 (0.67 for boutons on spines only). The slope of the linear fit of EPSP amplitudes as a function of bouton numbers yielded a value of 0.41 ± 0.12 mV per bouton (0.64 ± 0.24 mV for boutons on spines). When the linear fit was constrained to pass through the axes origin (zero point), the slope was higher, yielding a value of 0.62 ± 0.09 mV per bouton (0.91 ± 0.13 for boutons on spines). These values are within the range reported for the same type of connection (23) and are higher than the value of 0.14 mV per contact reported for connections between layer IV spiny-stellate cells to layer III pyramidal neurons (26). In contrast, the correlation between EPSP amplitudes to the number of axodendritic touch sites was significantly lower, with a correlation coefficient of 0.17 and the slope of the linear fit yielding a value of 0.03 ± 0.06 mV per touch. Distances between bouton touches and somata ranged between 9.4 and 138.6 μm, with a mean of 75.7 ± 30.9 μm. No significant correlation was observed between the distance of individual bouton touches from the soma and the EPSP amplitude after normalizing for the number of boutons per pair (data not shown). The release probability and time constant of recovery from depression, as derived from the model for synaptic dynamics (33), ranged from 0.30 to 0.56 (mean, 0.45 ± 0.09), and from 0.45 to 0.96 s (mean, 0.59 ± 0.16), respectively, and were not correlated to the number of bouton touches. The coefficient of variation (CV) of EPSP amplitudes ranged from 9% to 86% and was negatively correlated to the number of bouton touches (Fig. 3D), which is in agreement with predictions derived from models of quantal synaptic transmission (34), indicating that bouton touches are indeed correlated with the existence of functional synapses.

Discussion

Our results reveal an all-to-all geometrical connectivity matrix between neighboring thick tufted pyramidal neurons in layer V of the rat somatosensory cortex. The statistics of the axodendritic appositions are consistent with random connectivity governed by neuronal geometrical properties, providing direct evidence that the axon of one neuron is not structurally biased toward the dendrites of any preselected target neuron. Increased probability for synaptic boutons formed onto dendritic spines is the morphological indicator distinguishing between functionally connected and unconnected pyramidal neurons. We suggest that modifications at axodendritic touch sites by the creation and elimination of functional synaptic contacts can account for the dynamic formation of functional networks between neighboring pyramidal neurons of the neocortical microcircuit.

Touches Versus Synapses. To avoid any ambiguity in touch-site classification, we used strict criteria to define the existence of a bouton at a given touch site (see Materials and Methods). Our observations of geometrical contacts exhibiting boutons at touch sites, in particular those formed on spines, are very likely to be real synaptic sites for the following reasons. (i) We observed a marked (3-fold) difference between connected and unconnected pairs when comparing boutons on spines but no difference at all when comparing boutons on shafts. This finding is in accord with the fact that >90% of the pyramidal excitatory synapses occur on spines rather than shafts (35, 36). (ii) Other studies combining biocytin staining, light microscopy, and electron microscopy (23, 25, 26) showed that the observation of a bouton on a spine in light microscopy is highly indicative of the existence of a synaptic site. (iii) The high resolution of fluorescent staining with confocal microscopy guarantees that boutons and spines are clearly visible and well defined. (iv) Electrophysiological measurements of EPSP amplitude and CV were highly correlated to numbers of boutons between connected neurons.

The number of synaptic sites participating in a functional connection was shown in this study to be lower than observed in previous studies (23, 25, 37) involving avidin-horseradish per-oxidase staining and regular light microscopy. This difference could be attributed to the different experimental techniques and the criterion for classification. The resolution achieved in this study was such that the definition of boutons and spines was almost always conclusive. In regular light microscopy and staining, the resolution is reduced, and occasional misclassifications of contacts may occur. Also, the quantitative criterion for bouton definition in this study (a 3-fold increase of axon thickness) is stringent and might cause an underestimation in the number of synapses. The validity of bouton definition in our study is further supported by the high correlation observed between the EPSP amplitude and the number of boutons (Fig. 3C), compared to the low correlation observed between EPSP amplitude and the number of touch sites. It is important to note that autaptic innervation was similar to that of connected pairs, in agreement with previous reports for the same cortical area and developmental stage (25).

All-to-All Geometrical Connectivity. In this study we showed that layer V pyramidal neurons are sufficiently branched to ensure multiple touch points between axons and dendrites of all neighboring neurons. The axonal and dendritic arborization of pyramidal neurons therefore provides the geometrical solution for all-to-all connectivity of densely packed cortical microcircuit. We suggest that our findings may be generalized to other cortical areas because of the stereotypic form of pyramidal neurons (11, 23, 38) and the common constraints to which they are all subjected, such as cortical wiring optimization (14, 39-42). Similar results, albeit with a different technique, were also obtained for pyramidal neurons in layer 2/3 of the rat visual cortex (17). Cortical pyramidal neurons are, however, not a homogenous population (11, 43, 44), and it is yet to be shown whether connectivity properties we observed for layer V thick tufted pyramidal neurons will indeed hold true for connectivity within and between other subclasses of pyramidal neurons. In a recent study (45), it was shown that the connectivity between GABAergic interneurons and pyramidal neurons is highly specific compared with the connectivity between pyramidal neurons, suggesting a qualitative difference in microcircuit wiring for different neuronal populations. It is also expected that other brain structures, for example, the cerebellum, which displays an entirely different topographic organization, may obey very different connectivity rules than what we report here for the neocortical microcircuit.

As revealed by paired recordings, only a small fraction of the geometrical contacts is used to form functional connections. How, then, are geometrical contacts important? We propose that the importance of all-to-all geometrical connectivity is primarily to enable the dynamic rewiring of the cortical microcircuit without the need for major axonal and dendritic remodeling. All-to-all geometrical connectivity therefore allows for any two pyramidal neurons in the cortical column to form a reliable synaptic connection without arbor remodeling by simply using the existing fiber infrastructure. Any learning process that might require two specific neurons in the column to be functionally connected could therefore occur by the transformation of existing geometrical touches into a synaptic contact between a bouton and spine. Such transformations are probably faster (8, 9) and metabolically cheaper than any process requiring axonal or dendritic growth. Secondly, although the mechanisms triggering and enhancing formation and modification of synapses are only partially understood, it is likely that some form of “molecular handshaking” between the neurons, reflecting their relative activity, is required (46-49). Because most pairs of pyramidal neurons in the column are geometrically connected, they can relay molecular signaling between them in a truly parallel manner. The fact that multiple contacts are observed between synaptically connected neuronal pairs may be explained by the hypothesis that molecular interactions at axodendritic touch sites are driven by the electrical activity of the pre- and postsynaptic neurons. If the molecular signaling is considered to be a computational process ending in a decision to create, modify, or remove a functional synapse, it significantly enhances parallel information processing in the neocortex. One may also speculate that an intermediate state of such transformations is the silent synapse (30-32). Finally, the fact that only a small fraction of potential touch sites are used to form functional connections endows the microcircuit with a vast number of possible connectivity configurations (50, 51). The “filling fraction” (51), which denotes the ratio between the actual and potential connectivity, is used to assess the information content of the cortical tissue in terms of information bits per synapse, as a function of the possible network configurations. According to this formalism, the low filling fraction (≈0.1) implied in our study suggests a high information content of ≈4-5 bits per synapse (51).

Geometrical Role of Dendritic Spines. Most excitatory cells in the cortex are covered with dendritic spines, which have long been suggested to be enhancers of connectivity between neurons (see ref. 52 for a review). Specifically, spines have been suggested to play a morphological role by allowing axon collaterals to grow through the cortical gray matter in a remarkably straight course (53). Swindale (53) argued that axons need not zigzag between neurons, because the existence of spines relaxes the distance constrains between axonal and dendritic centers. Stepanyants et al. (51) suggested that the existence of spines decreases the filling fraction in cortical tissues by increasing the number of potential synaptic sites. This decrease of the filling fraction causes a further elevation of the information content per synapse.

We wish to highlight another aspect of the morphological role of spines, from the topological point of view of connectivity. As predicted from the model for geometrical connectivity (18), any enlargement of the dendritic diameter leads to a larger number of axodendritic touch sites. In this study, we observed that 3.3 contacts on average are formed between axons and dendritic shafts. When contacts onto dendritic spines are also regarded, the average number of contacts increases to 5.6. In the model framework, this is equivalent to adding 70% to the “effective diameter” of the dendrite. Spines and filopodia could therefore be considered to be devices that increase the geometrical connectivity between neurons. This possibility is further suggested by high spine and filopodia motility in comparison to negligible axonal and dendritic arbor remodeling (54-56).

Conclusion

Geometrical connectivity that does not underlie functional synaptic contacts is not commonly discussed in studies of the neocortical microcircuit. Our findings suggest that geometrical contacts are probably not mere by-products of cortical wiring but are a prevalent and important microcircuit property that is crucial for plasticity and computation. The physical proximity between axons and dendrites enables signaling between neurons to guide synaptic formation, elimination, and modification triggered by reciprocal neuronal activity and manifested by spine and filopodia motility. The tabula rasa geometrical connectivity therefore provides the potential for complete reconfiguration of the local microcircuit without any arbor remodeling, simply by the creation and elimination of synapses at existing geometrical contacts. The small fraction of functionally connected pyramidal neurons in the neocortical microcircuit at a given moment constitutes only one of a virtually infinite number of possible configurations. The conditions and time courses required for functional reconfiguration of the microcircuit are still unknown and present important challenges for further experiments.