Abstract
A simple model combining leaf hydraulics and abscisic acid sensitivity can predict stomatal dynamics to short-term changes in plant water status in a conifer.
The ability of plants to dynamically regulate water loss through stomata under conditions of changing evaporative demand or water availability is paramount for avoiding excessive desiccation, hydraulic failure, and plant death under conditions of water stress. Despite apparently similar functional demands on stomatal evolution, not all lineages employ the same mechanism of controlling water loss, but rather show a directional shift from passive hydraulic control in ferns and lycophytes to active metabolic control mediated by the phytohormone abscisic acid (ABA) in angiosperms (Brodribb and McAdam, 2011; McAdam and Brodribb, 2014). Phylogenetically midway between the ferns and angiosperms are the gymnosperms, which appear to employ passive hydraulic control for short-term perturbations in leaf water status, in common with earlier lineages, but are also capable of switching to ABA-mediated control following extended water stress (Brodribb and McAdam, 2013; McAdam and Brodribb, 2014; Martins et al., 2016).
The proposed evolutionary trajectory from simple to more complex mechanisms of stomatal control of leaf water status may provide a useful framework for the general modeling of stomatal control, starting from passive hydraulic models in ferns and lycophytes, with the end goal of modeling stomatal control in angiosperms where both hydraulics and metabolism are important (Buckley et al., 2003; Brodribb and McAdam, 2011). Of the many hydraulic models proposed (e.g. Tuzet et al., 2003; for review, see Damour et al., 2010), including models combining both metabolic and hydraulic components (Buckley et al., 2003), most do not describe stomatal dynamics to short-term perturbations, nor do they specifically include the effect of ABA. Older hydraulic models that do describe stomatal dynamics were principally interested in the “wrong-way” response or stomatal oscillations (e.g. Cowan, 1972; Delwiche and Cooke, 1977). Models that do include ABA (Tardieu and Davies, 1993; Dewar, 2002) rely on the hypothesis that ABA is produced in the roots following water stress and is transported via xylem sap to the shoots, where it accumulates in leaves (Davies and Zhang, 1991). However, the root-derived ABA hypothesis has been challenged on multiple fronts, with recent data supporting leaf-synthesized ABA as the source of stomatal control (Holbrook et al., 2002; Christmann et al., 2007; Manzi et al., 2015; McAdam et al., 2016). Moreover, the sensitivity of stomatal conductance (gs) to ABA level in current stomatal models is highly empirical, with no obvious mechanistic basis (Tardieu and Davies, 1993; Gutschick and Simonneau, 2002). ABA acts to close stomata through the activation of outward-rectifying anion channels, including SLAC1 in guard cells (Kollist et al., 2014). Modeling stomatal movements on the basis of ion fluxes into and out of guard cells will provide the ultimate mechanistic basis for changing aperture, and although Hills et al. (2012) developed a model of stomatal movement based on known ion channel behavior from electrophysiological studies, the intention of their model at this stage is not to predict leaf-level stomatal behavior. In light of recent developments, modeling the effect of ABA on stomatal conductance needs re-evaluation.
Dynamic stomatal responses to changes in plant water status are well described by a passive hydraulic model in ferns and lycophytes due to ABA insensitivity (Brodribb and McAdam, 2011; Martins et al., 2016), and in gymnosperms over short intervals of water stress due to a limited influence of ABA, which is synthesized slowly in conifers (McAdam and Brodribb, 2014). However, over longer periods of water stress, the synthesis of ABA leads to an uncoupling of stomatal conductance from bulk water potential in gymnosperms (McAdam and Brodribb, 2014). Here, we developed an analytic passive hydraulic model based on leaf water relations, augmented by a simple, semimechanistic ABA effect at the guard cell. The model was tested on the gymnosperm Metasequoia glyptostroboides Hu and Cheng, first fitting to steady-state behavior, then perturbing the plant water status by: (1) excising branches in air to stop hydraulic supply and allowing stomata to close as the leaves dry out, before recutting underwater to reconnect the hydraulic supply; and (2) droughting plants to allow branches to experience longer periods of water stress and accumulate ABA, before rehydrating leaves by recutting underwater to reconnect the hydraulic supply.
THE ABA HYDRAULIC MODEL
The dual ABA hydraulic model for dynamic stomatal conductance was based on simple water relations, augmented by osmotic changes in the guard cell to include an ABA effect. The rate of change of leaf water content (W, mol m−2) is given by the difference between the incoming liquid flux (J, mol m−2 s−1) and the outgoing vapor flux from transpiration (E, mol m−2 s−1; Jones, 1982)
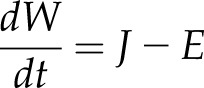 |
(1) |
Assuming an Ohm’s law approximation for both liquid and vapor fluxes, the definition of leaf capacitance (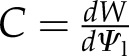 , mol m−2 Pa−1), and the chain rule, Equation 1 can be expressed in terms of leaf water potential (Ψl, Pa) as
, mol m−2 Pa−1), and the chain rule, Equation 1 can be expressed in terms of leaf water potential (Ψl, Pa) as
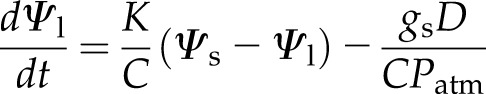 |
(2) |
where K is the leaf hydraulic conductivity (mol m−2 s−1 Pa−1), gs is stomatal conductance (mol m−2 s−1), Ψs is the source water potential (Pa) in the petiole of the leaf, D is the vapor pressure difference (Pa) between the leaf and surrounding air, and Patm is the atmospheric pressure (Pa). Here, it is assumed the air surrounding the leaf is well mixed so that the boundary layer resistance is negligible.
Ignoring mechanical advantage, which is not significant in conifers (Franks and Farquhar, 2007; McAdam and Brodribb, 2012), stomatal conductance was assumed to be a linear function of guard cell turgor pressure, a common assumption valid over a range of physiologically relevant stomatal conductances and guard cell turgor pressures (Cowan, 1972; Dewar, 1995, 2002; Franks et al., 1998; Franks and Farquhar, 2001; Buckley et al., 2003; Buckley, 2005):
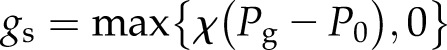 |
(3) |
where P0 is the guard cell turgor pressure where stomatal conductance is zero and χ is the constant of proportionality.
In the light, guard cell turgor is higher than leaf turgor due to active pumping and accumulation of solutes in the guard cell (Kollist et al., 2014). Here, guard cell turgor pressure was assumed to be above the turgor pressure of the rest of the leaf by an actively generated osmotic pressure πa (Pa). In addition, it was also assumed: (1) there was negligible hydraulic resistance between the guard cell and the bulk leaf; and (2) no peristomatal transpiration occurred, i.e. the site of evaporation in the leaf occurred in the mesophyll and not directly from the guard cells. Both assumptions are consistent with a previous iterative hydraulic model that successfully predicted dynamics to changes in water status in ferns and conifers (Brodribb and McAdam, 2011; McAdam and Brodribb, 2014; Martins et al., 2016). Moreover, the above assumptions together imply guard cell water potential equilibrated instantaneously with bulk leaf water potential and that no water potential gradient exists between the guard cells and the bulk leaf.
Interchanging between turgor pressure, osmotic pressure, and water potential (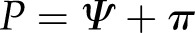 ), Equation 3 can be expressed as
), Equation 3 can be expressed as
| (4) |
where 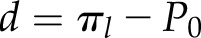 and πl is the bulk osmotic pressure of the leaf (Pa).
and πl is the bulk osmotic pressure of the leaf (Pa).
Given assumptions 1 and 2, Equation 4 can be used to test the assumption of gs being a linear function of Pg. Under conditions of constant light and no ABA accumulation, any change in gs is expected to be due to changes in Ψl and not to changes in πa, so the relationship between gs and Ψl is expected to be linear with a slope equal to χ if the above assumption holds.
To test this assumption and to get an estimate of χ, excised branches were allowed to slowly desiccate over a time period of less than 4.5 h to avoid the threshold time of 6 h for ABA biosynthesis in M. glyptostroboides leaves (McAdam and Brodribb, 2014). Stomatal conductance was periodically sampled on short shoots using an infrared gas analyzer (LI-6400; LI-COR Biosciences) with chamber conditions of 22°C, light intensity 1,000 μmol m−2 s−1 photosynthetically active radiation (PAR; above light saturation for gs in M. glyptostroboides), and D of 1.5 kPa, the same as external conditions. Short shoots outside the chamber were illuminated using a customized fiber-optic light shower. Leaf water potential was measured concurrently on a neighboring short shoot using a Scholander pressure chamber (see Supplemental Methods S1). Linearity in the relationship between gs and Ψl was found to be the case over physiologically relevant Ψl and gave an estimate of χ of 0.0995 mol m−2 s−1 MPa−1, essentially identical to the estimate of Buckley et al. (2003) of 0.1 mol m−2 s−1 MPa−1 for Vicia faba (Supplemental Fig. S1; Table I).
Table I. Parameters used in the dual ABA hydraulic model and the source of the values.
| Parameter | Name | Value and Source |
|---|---|---|
| K | Leaf hydraulic conductivity | 4.1 mmol m−2 s−1 MPa−1 (Martins et al., 2016); 1.77 mmol m−2 s−1 MPa−1 for [ABA] = 5,951 ng g−1 fresh weight (McAdam and Brodribb, 2014) |
| C | Leaf hydraulic capacitance | 1,022 mmol m−2 MPa−1 (Martins et al., 2016) |
| χ | Sensitivity of gs to changes in turgor pressure | 0.0995 mol m−2 s−1 MPa−1 (fitted, Fig. 1) |
| D | Leaf vapor pressure difference | 1.2 kPa (known) |
| M | Maximum active component of osmotic pressure in the guard cell | 3.427 MPa (fitted) |
| d | Guard cell offset | 0.00844 MPa (fitted) |
| [ABA]0 | [ABA] where guard cell osmotic pressure is half-maximum | 593 ng g−1 (fitted) |
| t1/2 hydraulic | Hydraulic half-time | 75 s (calculated 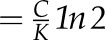 ; Eq. 10) ; Eq. 10) |
| t1/2 evaporative | Evaporative half-time | 260 s (calculated 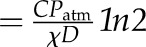 ; Eq. 11) ; Eq. 11) |
| t1/2 total | Half-time taking into account both hydraulic and evaporative components | 58 s (calculated 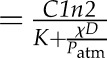 ; Eq. 9) ; Eq. 9) |
The active metabolic control of stomatal aperture occurs through πa. A complete description in terms of ion channels is difficult (Hills et al., 2012), even without considering the complex signaling pathways involved (Li et al., 2006). Instead, a simplified approach was taken, with steady-state guard cell osmotic pressure governed by the balance between inward and outward fluxes of solutes. For short-term changes in plant water status, both inward and outward fluxes of solutes, and hence the net balance of solutes, were assumed constant. The flux of solute into the guard cell was assumed to be proportional to the difference between a target solute concentration in the absence of ABA, set by photosynthetic and metabolic conditions, and the current solute concentration (Kirschbaum et al., 1988; Haefner et al., 1997). The flux of solutes out of the guard cell was assumed to be dependent on the level of ABA in the leaf ([ABA], g g−1 fresh weight) and the solute concentration of ions responsive to ABA in the guard cell, by simple mass action. Expressed in terms of osmotic pressure, the above flux balance gives
| (5) |
where M is the light-dependent osmotic pressure of the guard cell in the absence of ABA and k1 and k2 are the rate constants for the inward and outward fluxes, respectively. Rearranging, Equation 5 becomes
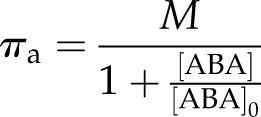 |
(6) |
where [ABA]0 is the ratio of inward and outward rate constants and represents the [ABA] where πa is half the maximum value.
Rearranging Equation 4 and eliminating Ψl from Equation 2, noting πa is assumed constant over short-term changes in plant water status, gives
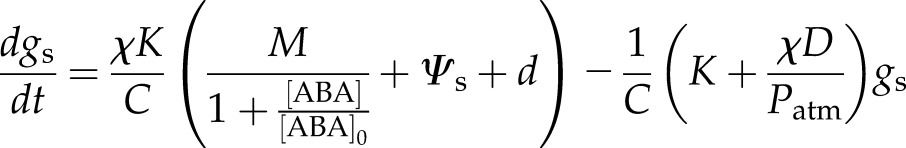 |
(7) |
Steady-state solutions for gs can be obtained by letting 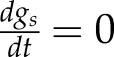 . For the case of plant parameters being constants and the plant hydraulic supply uncompromised, steady-state stomatal conductance becomes
. For the case of plant parameters being constants and the plant hydraulic supply uncompromised, steady-state stomatal conductance becomes
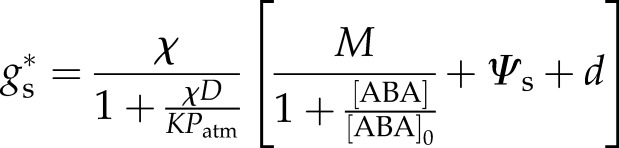 |
(8) |
The overall form of Equation 8 is identical to equation 1 of Buckley et al. (2003) and shows the Leuning (1995) form for D dependence. Importantly, however, gs is predicted to be an offset hyperbolic function of ABA level. For the case of hydraulic supply completely disrupted (K = 0), as is the case for excision in air, it is easy to see steady-state gs is zero.
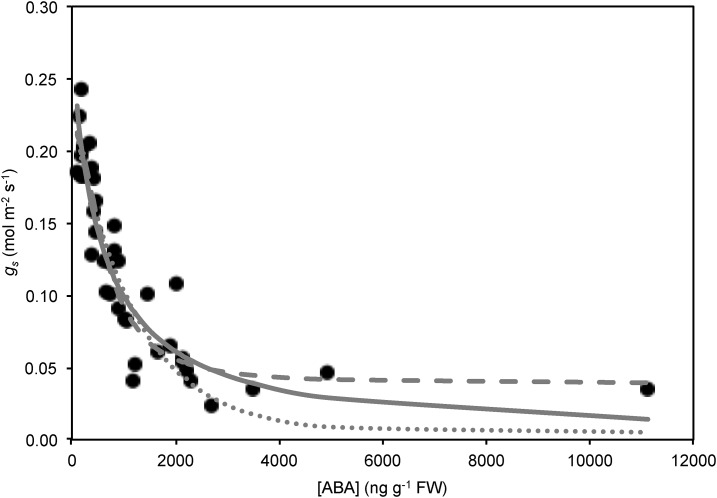
To test how well Equation 8 could describe steady-state gs dependence on [ABA], Equation 8 was fitted to gs versus [ABA] data from McAdam and Brodribb (2014). In McAdam and Brodribb (2014), stomatal sensitivity to ABA was determined by four independent methods: (1) feeding ABA into the transpiration stream of fully hydrated, excised shoots; (2) rehydrating excised shoots previously allowed to slowly bench dry up to 24 h to stimulate ABA synthesis; (3) rehydrating excised shoots of plants undergoing drought stress; and (4) examining in vitro response of stomatal aperture to ABA in solution and calculating gs using the formula of Parlange and Waggoner (1970; see Supplemental Methods S1). In fitting Equation 8 to observed data, the above estimate of χ was used, along with K taken from Martins et al. (2016). In all cases Ψs was essentially zero, D was approximately 1.2 kPa for gas exchange measurements, and Patm assumed 101 kPa. All measurements were undertaken under light saturation of gs for M. glyptostroboides. Allowing the remaining plant parameters to be unconstrained, Equation 8 could reasonably fit the observed data given the scatter in the data (Fig. 1; R2 = 0.86). The fitted value for M of 3.4 MPa was within the range of reasonable turgor pressure versus aperture relationships of guard cells (Franks et al., 1998), while d was estimated at 0.008 MPa, i.e. close to zero as expected for complete closure when all active osmolytes in the guard cell are removed (Table I). [ABA]0 was estimated as 593 ng g−1 (Table I). That Equation 8 could fit the observed gs versus [ABA] relationship with physiologically believable parameters given the scatter in the data suggests the hydraulic model augmented by a simple flux balance at the guard cell was functional.
Figure 1.
Equation 8 (solid line), a variation of Equation 8 using Hill equation kinetics for ABA-driven efflux of solutes (Eq. S19 in Supplemental Model Development S1; dashed line), and the Tardieu and Davies model (Eq. S20 in Supplemental Model Development S1; dotted line) fitted to data from McAdam and Brodribb (2014), showing the dependence of fully hydrated stomatal conductance on leaf ABA levels. Known parameters were fixed, while unknown parameters were fitted. The hyperbolic dependence of stomatal conductance on leaf ABA level predicted by Equation 8 provides a reasonable fit to the observed data and was comparable to the other model fits (Eq. 8 R2 = 0.86; Hill variation R2 = 0.89; Tardieu and Davies R2 = 0.84), suggesting the simple input-output view of solutes across the guard cell membrane was functional. Parameter values for the fits were as follows: Hill variation, d = 0.23 MPa, M = 2.55 MPa, k3/k1 = 8.35, KA = 1,992 ng g−1, n = 2.03; and Tardieu and Davies, gmin = 0.005 mol m−2 s−1, α = 0.223 mol m−2 s−1, β = −0.00082 g ng−1, δ = 0 MPa−1.
To see how the ABA dependence of the model compared with other possible forms, an ABA model where the solute efflux exhibited Hill equation kinetics and the currently accepted Tardieu and Davies (1993) sensitivity of gs to [ABA] were both fitted to the experimental data (Fig. 1). The sensitivity of gs to Ψl in the Tardieu and Davies model (δ) was set at zero. Both alternative models produced fits that were comparable to the observed data despite both requiring one more parameter to be fitted than the ABA hydraulic model (Fig. 1; Hill model R2 = 0.88; Tardieu and Davies model R2 = 0.84), indicating the model developed here was at least on par with other similar forms and the currently used form of ABA dependence, despite requiring the fitting of fewer parameters.
Analytic dynamic solutions for gs can easily be obtained for constant plant parameters from Equation 7 and give exponentials. The total half-time for leaf water potential and thus for gs in the absence of dynamic changes in ABA level
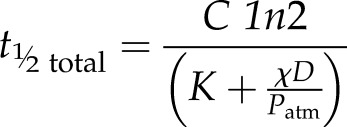 |
(9) |
is the combined half-time for a step change in hydraulic supply or demand where neither is completely inhibited, as is typical for a plant. Thus, step changes in hydraulic supply or demand yield half-times for gs that are composed of two component half-times describing the dynamics of leaf water potential: one related to plant hydraulic supply, denoted here as the hydraulic half-time, and one related to evaporative demand, denoted here as the evaporative half-time.
The hydraulic half-time (s)
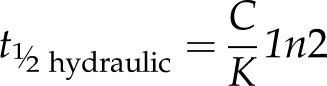 |
(10) |
is the half-time predicted for water potential in a leaf where hydraulic supply is connected but there is no transpiration (i.e. D = 0), such as observed in the rehydration method for determining K and C (Blackman and Brodribb, 2011).
The evaporative half-time (s)
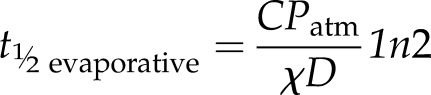 |
(11) |
is the half-time predicted for water potential in a leaf where leaf water potential is a linear function of transpiration and hydraulic supply is not connected (i.e. K = 0), such as a leaf excised in air allowed to dehydrate. Note that the total half-time is faster than the two component half-times.
Shown analytically here and experimentally by Martins et al. (2016), a half-time in stomatal response to a step change in D that is proportional to leaf hydraulic capacitance is indicative of hydraulic control. Equation 9 also shows why half-times for transitions under hydraulic control would be more strongly proportional to C but perhaps weakly proportional to the hydraulic characteristic time 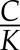 : checking the approximate order of magnitude of both
: checking the approximate order of magnitude of both 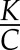 and
and 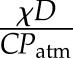 gives both on the order of magnitude of 10−2 s−1 (or characteristic times of the order of 100 s), showing in general both terms contribute approximately equally to the predicted half-time. Although a larger K, χ, or D would result in faster stomatal dynamics, all else being equal, the effect of varying one of these parameters by less than an order of magnitude might thus be expected to be small compared with changing C. When the leaf is isolated from hydraulic supply (K = 0), the response time for stomatal closure is predicted to be slower compared with that for stomatal opening when a leaf is fully connected to hydraulic supply.
gives both on the order of magnitude of 10−2 s−1 (or characteristic times of the order of 100 s), showing in general both terms contribute approximately equally to the predicted half-time. Although a larger K, χ, or D would result in faster stomatal dynamics, all else being equal, the effect of varying one of these parameters by less than an order of magnitude might thus be expected to be small compared with changing C. When the leaf is isolated from hydraulic supply (K = 0), the response time for stomatal closure is predicted to be slower compared with that for stomatal opening when a leaf is fully connected to hydraulic supply.
The dual ABA hydraulic model was tested under two dynamic scenarios. In the first, fully hydrated excised branches were excised in air to stop hydraulic supply and stomata allowed to close as the leaves dried out, before recutting underwater to reconnect the hydraulic supply. Stomatal conductance was tracked by enclosing a short shoot in the chamber of an infrared gas analyzer with chamber conditions 22°C, light intensity 1,500 μmol m−2 s−1 PAR, and D maintained at approximately 1.2 kPa. Short shoots outside the chamber were illuminated using a customized fiber-optic light shower. Leaf [ABA] was quantified before excision in air, at the point of re-excision underwater and once gs regained a steady state (see Supplemental Methods S1).
If the leaf was excised in air at time t = 0 and recut underwater at time t = tr, the model predicts
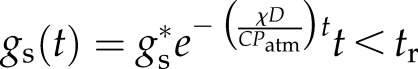 |
(12a) |
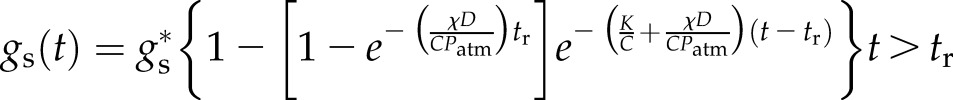 |
(12b) |
Either solution is valid at t = tr.
In the second test, an individual plant was droughted by withholding water and branches sampled at 6, 10, 14, and 21 d post cessation of watering, after which time the [ABA] in the leaves was 175, 604, 1,835, and 5,951 ng g−1 fresh weight, respectively. Branches were rehydrated by recutting underwater to reconnect the hydraulic supply, while stomatal conductance was again tracked by enclosing a short shoot in the chamber of an infrared gas analyzer, with conditions as above except at a light intensity of 1,000 μmol m−2 s−1 PAR. Leaf [ABA] was quantified on a neighboring short shoot when gs reached a steady state (see Supplemental Methods S1). If the initial gs was gs0 and recutting underwater occurred at time t = 0, the model predicts
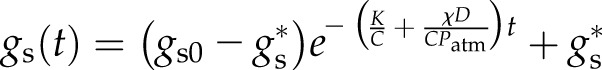 |
(13) |
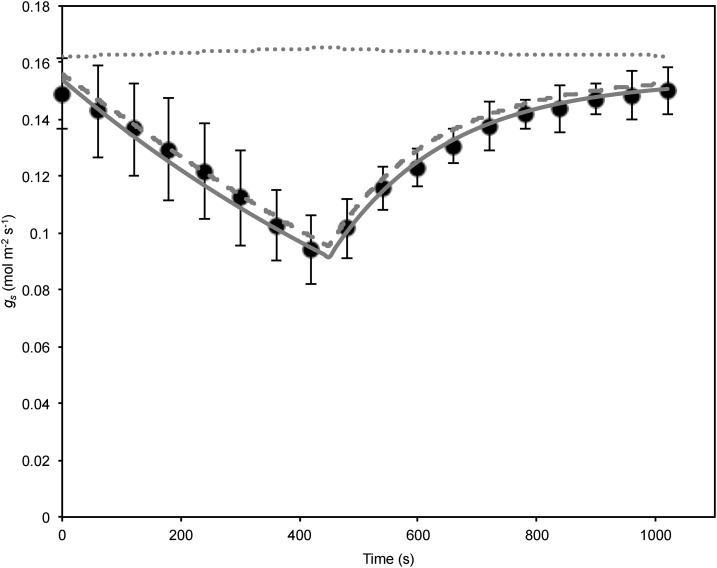
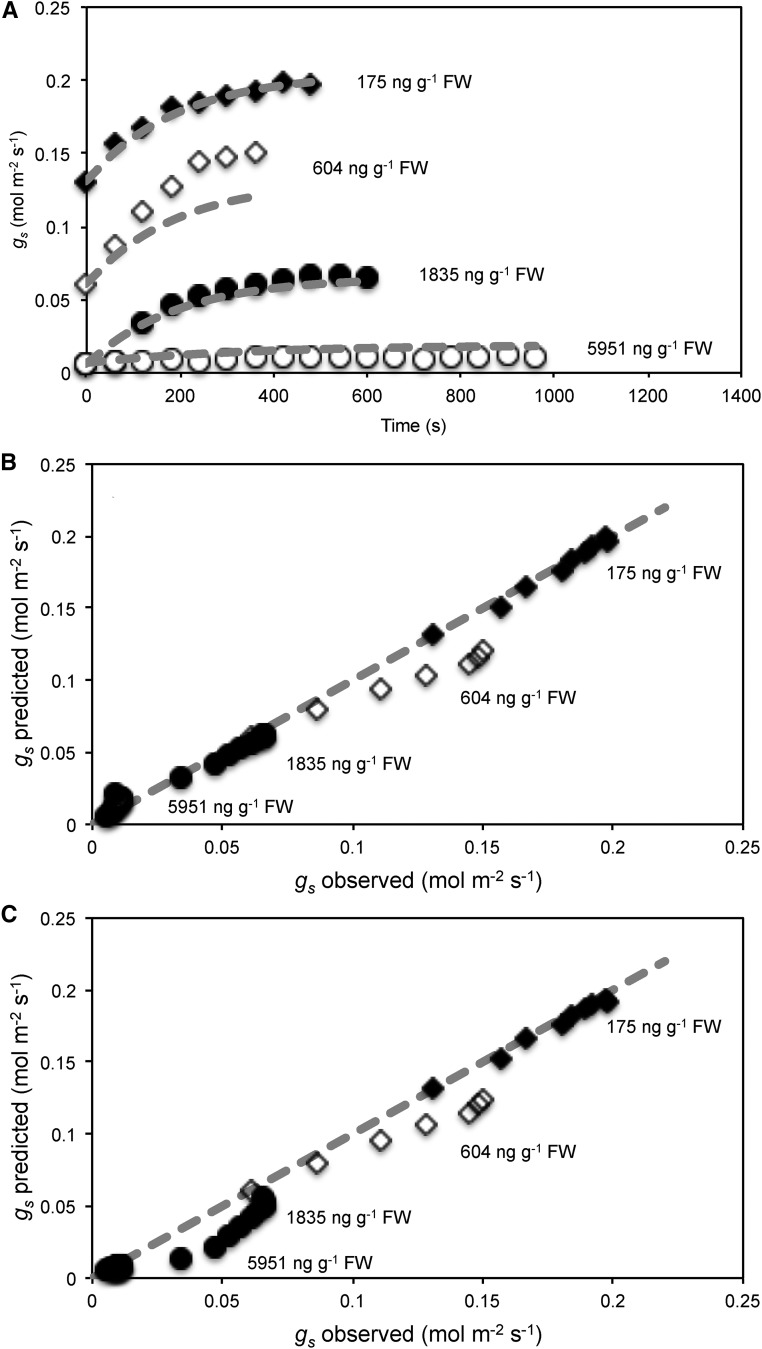
The model predicted closely the observed dynamics when simulated for the two experimental tests using the plant parameters as above, C from Martins et al. (2016; Table I) and [ABA] as measured experimentally (Figs. 2 and 3). The model predicted a hydraulic half-time of 75 s, while the evaporative half-time at a D of 1.2 kPa was predicted to be slower at 260 s (Table I). For the case of a transpiring leaf with hydraulic supply, the total half-time for rehydration and stomatal opening at a D of 1.2 kPa was predicted to be 58 s, faster than the individual half-times alone (Table I). Both the predicted magnitude and half-times of the responses were similar to those observed for the two tests (Figs. 2–4). The model strongly accounted for excision and rehydration dynamics (Fig. 2) and dynamics for rehydration following prolonged dehydration for [ABA] of 175 ng g−1 and 1,835 ng g−1 (Fig. 3). Rehydration kinetics at [ABA] of 604 ng g−1 were predicted to be slightly slower than observed, perhaps due to individual variation in leaf hydraulic parameters. In the most desiccated leaf where [ABA] was 5,951 ng g−1, leaf water potential prior to rehydration was sufficiently low to cause a significant loss in hydraulic conductivity. Consequently, the model was simulated with the appropriate loss in hydraulic conductivity expected from vulnerability curves (McAdam and Brodribb, 2014). Despite a reduced hydraulic conductivity, predicted recovery of gs was higher than observed; the absolute error however was small compared with the magnitude of gs at lower levels of ABA (Fig. 3).
Figure 2.
Stomatal conductance observed in M. glyptostroboides during excision in air at time t = 0 s, cutting off hydraulic supply, followed by recutting underwater to reconnect hydraulic supply at t = 450 s, from McAdam and Brodribb (2014) and the model predictions (gray curves) using the ABA hydraulic (solid line), and the Tardieu and Davies model without sensitivity to leaf water potential (δ = 0 MPa−1; dotted line) and with sensitivity to leaf water potential set at δ = −1.2 MPa−1 (dashed line). [ABA] was set at 430 ng g−1 fresh weight, very close to the measured ABA level from McAdam and Brodribb (2014; 430 ng g−1 prior to excision, 409.5 ng g−1 at minimum gs, 432 ng g−1 fully hydrated post reconnection of hydraulic supply). Points and error bars are means and ses, respectively, for three replicates.
Figure 3.
A, Stomatal conductance recovery upon recutting underwater, following drought to increase leaf ABA levels. In most cases the ABA hydraulic model (dashed gray lines) predicted the expected dynamics given the previously prescribed parameters and known leaf [ABA]. B, Comparison of predicted gs against observed gs during rehydration dynamics for the ABA hydraulic model at the different ABA levels. C, Comparison of predicted gs against observed gs during rehydration dynamics for the Tardieu and Davies model. In general, the ABA hydraulic model fitted observed stomatal dynamics better than the Tardieu and Davies model.
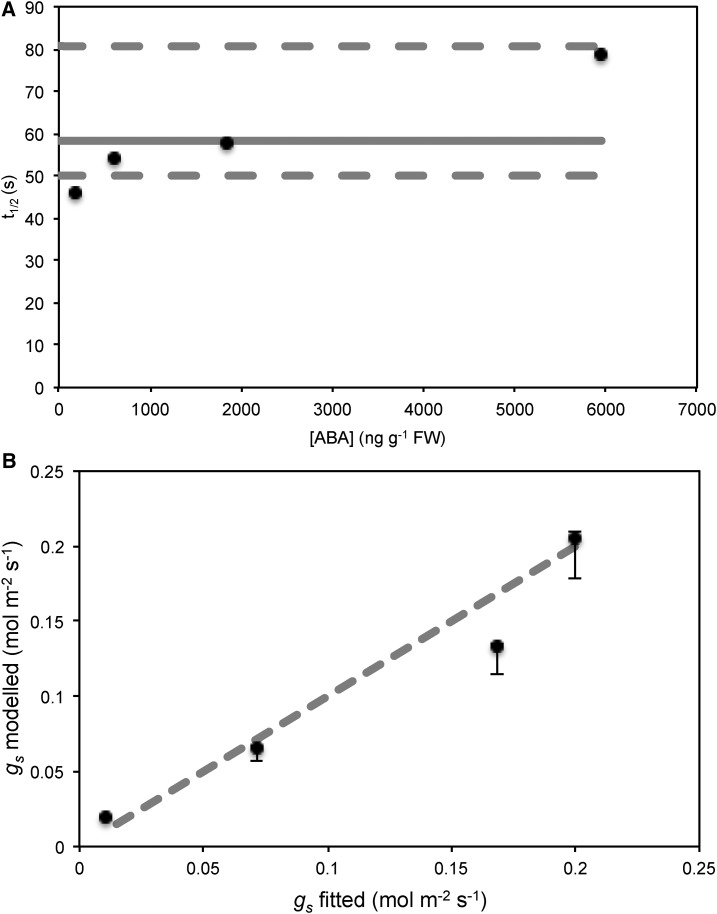
Figure 4.
A, Half-times calculated from exponential fits to kinetics of stomatal conductance recovery upon recutting underwater, following drought to increase leaf ABA levels. Dashed lines represent bounds of half-times expected for the model based on hydraulic parameters for the maximum and minimum cases of C/K observed within branches, while the solid line represents the half-time calculated from the model using mean hydraulic parameters. Although there is an apparent ABA dependence on half-times of rehydration kinetics, almost all are within the expected bounds of hydraulic parameters, while an increase in half-times may be expected if K decreased with drought. B, Steady-state gs modeled using mean parameters compared with that fitted assuming exponential kinetics. The dashed line is the 1:1 line. Error bars represent the range of steady-state gs calculated using the range of observed K between branches.
To test whether the dynamics observed could be described by exponentials as predicted in the model and whether discrepancies were due to variation in hydraulic parameters, exponential curves were fitted to the observed dynamics. All dynamics could be strongly fitted by exponential curves (Supplemental Fig. S2; R2 > 0.97 for [ABA] = 175, 604, and 1,835 ng g−1; R2 = 0.81 for [ABA] = 5,951 ng g−1) and produced half-times largely within that expected for the observed range of hydraulic parameters within measured branches (Fig. 4). Although there appeared to be some ABA dependence on observed half-times, a similar behavior may also be expected if K also decreased with drought. The modeled steady-state gs was not significantly different from the steady state predicted from the exponential fits as determined from a paired t test of residuals (Fig. 4; P = 0.62). Comparisons with the exponential fits of observed dynamics suggest the model can reasonably describe both dynamics and steady states within the bounds of expected hydraulic parameters.
To see how the model compared dynamically with the Tardieu and Davies model, a modified Tardieu and Davies model was developed and simulated for excision-rehydration and rehydration kinetics (see Supplemental Model Development S1). Simulating the model without sensitivity to Ψl produced wrong-way kinetics. However, fitting the Tardieu and Davies model with δ = −1.2 MPa−1 produced kinetics that were indistinguishable from the hydraulic ABA model for dehydration-rehydration kinetics (Fig. 2; Supplemental Fig. S3). The Tardieu and Davies model was similar to the ABA hydraulic model for some rehydration kinetics but was overall a poorer fit (Fig. 3; Supplemental Fig. S4). However, dynamic stomatal behavior predicted by the Tardieu and Davies model was clearly being driven by changes in Ψl and not the flux of ABA in the xylem, with the strongest correspondence with the ABA hydraulic model occurring when the gs versus Ψl relationship was approximately linear and similar in slope to that used for the ABA hydraulic model (Supplemental Fig. S5). The corresponding change in [ABA] predicted was small. By being grounded in a combined hydraulic-metabolic semimechanistic framework and possessing fewer parameters to fit, the ABA hydraulic model developed here has potential advantages over the purely empirical form of Tardieu and Davies (1993), currently the most popular form for relating [ABA] to gs. The ABA hydraulic model is also consistent with ABA synthesis to water stress occurring predominantly in the leaves and not translocated from the roots, and provides a simpler mechanism for how Ψl drives stomatal dynamics to short-term changes in water status.
CONCLUSION
The dual ABA-hydraulic model reconciles the dynamics of hydraulic stomatal responses to perturbations in plant water status as seen in ferns, lycophytes, and gymnosperms with the ability of gymnosperms to metabolically regulate maximum gas exchange over longer timescales through ABA. In predicting steady-state gs as a function of leaf ABA and short-term dynamics to changes in plant water supply in the gymnosperm M. glyptostroboides, the model was successful. Currently, the model cannot predict wrong-way responses to rapid changes in water status often observed in angiosperms, caused by the mechanical advantage of the epidermis. It also assumes steady-state ABA levels to be known and cannot predict dynamics under conditions where leaf ABA levels change. Rapid synthesis of ABA in the leaf is paramount for angiosperms to overcome the wrong-way opening response to increased D (McAdam et al., 2016). Until recently, little was known about the time dynamics for ABA biosynthesis, even though early studies suggested the water potential trigger for ABA synthesis occurred when leaf turgor approached zero (Pierce and Raschke, 1980, 1981). The role of guard cell biosynthesis of ABA in responses to humidity is also unclear (Bauer et al., 2013). However, by providing a way to predict the effect of constant leaf [ABA] on stomatal conductance on the backbone of a hydraulic model, the model here provides an important stepping stone for working toward a dynamic model including both water relations and ABA dynamics. Despite the limited test here in a species in which a substantial set of hydraulic and stomatal data are available (McAdam and Brodribb, 2014), the model may also act as a bridge to go from the current purely empirical models of how ABA affects gs toward a mechanistic view of the effect of ABA at the ion channel level, and further tests in other species will be necessary to confirm the generality of this approach. New work characterizing leaf turgor thresholds to ABA biosynthesis and ABA synthesis dynamics (McAdam and Brodribb, 2016) will greatly enhance the ability of future models to incorporate dynamics of both ABA and leaf water potential, as will further model development and incorporation of processes at the ion channel level (Hills et al., 2012), leading to the goal of a holistic model of plant water relations and plant gas exchange.
An apparent shift in the mechanism of stomatal control of leaf water potential through evolutionary time presents new opportunities for modeling stomatal behavior. Transitions from passive hydraulic control, to passive hydraulic with long-term ABA control, to rapid ABA biosynthesis to overcome mechanical advantage on top of a hydraulic base provide a logical pathway to understanding not only the most derived lineages but also stomatal control in all vascular plants.
Supplemental Data
The following supplemental materials are available.
Supplemental Figure S1. The linear range of dependence of stomatal conductance on leaf water potential for M. glyptostroboides.
Supplemental Figure S2. Exponential fits to observed kinetics of stomatal conductance recovery upon recutting underwater, following drought to increase leaf ABA levels.
Supplemental Figure S3. Tardieu and Davies model (Eq. S20 in Supplemental Model Development S1) showing the dependence of fully hydrated stomatal conductance on leaf ABA levels.
Supplemental Figure S4. Stomatal conductance recovery upon recutting underwater, following drought to increase leaf ABA levels.
Supplemental Figure S5. Plotted dependence of stomatal conductance on leaf water potential for the Tardieu and Davies model.
Supplementary Material
Acknowledgments
We thank Samuel Martins for useful discussion, Roderick Dewar for discussions on the Tardieu and Davies model, and two anonymous reviewers for their comments that greatly improved the manuscript. R.M.D. would also like to thank the University of Tasmania University Club for financial support through The University Club Honours Scholarship.
Footnotes
Articles can be viewed without a subscription.
References
- Bauer H, Ache P, Lautner S, Fromm J, Hartung W, Al-Rasheid KAS, Sonnewald S, Sonnewald U, Kneitz S, Lachmann N, et al. (2013) The stomatal response to reduced relative humidity requires guard cell-autonomous ABA synthesis. Curr Biol 23: 53–57 [DOI] [PubMed] [Google Scholar]
- Blackman CJ, Brodribb TJ (2011) Two measures of leaf capacitance: insights into the water transport pathway and hydraulic conductance in leaves. Funct Plant Biol 38: 118–126 [DOI] [PubMed] [Google Scholar]
- Brodribb TJ, McAdam SAM (2011) Passive origins of stomatal control in vascular plants. Science 331: 582–585 [DOI] [PubMed] [Google Scholar]
- Brodribb TJ, McAdam SAM (2013) Abscisic acid mediates a divergence in the drought response of two conifers. Plant Physiol 162: 1370–1377 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckley TN. (2005) The control of stomata by water balance. New Phytol 168: 275–292 [DOI] [PubMed] [Google Scholar]
- Buckley TN, Mott KA, Farquhar GD (2003) A hydromechanical and biochemical model of stomatal conductance. Plant Cell Environ 26: 1767–1785 [Google Scholar]
- Christmann A, Weiler EW, Steudle E, Grill E (2007) A hydraulic signal in root-to-shoot signalling of water shortage. Plant J 52: 167–174 [DOI] [PubMed] [Google Scholar]
- Cowan IR. (1972) Oscillations in stomatal conductance and plant functioning associated with stomatal conductance: observations and a model. Planta 106: 185–219 [DOI] [PubMed] [Google Scholar]
- Damour G, Simonneau T, Cochard H, Urban L (2010) An overview of models of stomatal conductance at the leaf level. Plant Cell Environ 33: 1419–1438 [DOI] [PubMed] [Google Scholar]
- Davies WJ, Zhang JH (1991) Root signals and the regulation of growth and development of plants in drying soil. Annu Rev Plant Physiol Plant Mol Biol 42: 55–76 [Google Scholar]
- Delwiche MJ, Cooke JR (1977) An analytical model of the hydraulic aspects of stomatal dynamics. J Theor Biol 69: 113–141 [DOI] [PubMed] [Google Scholar]
- Dewar RC. (1995) Interpretation of an empirical model for stomatal conductance in terms of guard cell function. Plant Cell Environ 18: 365–372 [Google Scholar]
- Dewar RC. (2002) The Ball-Berry-Leuning and Tardieu-Davies stomatal models: synthesis and extension within a spatially aggregated picture of guard cell function. Plant Cell Environ 25: 1383–1398 [Google Scholar]
- Franks PJ, Cowan IR, Farquhar GD (1998) A study of stomatal mechanics using the cell pressure probe. Plant Cell Environ 21: 94–100 [Google Scholar]
- Franks PJ, Farquhar GD (2001) The effect of exogenous abscisic acid on stomatal development, stomatal mechanics, and leaf gas exchange in Tradescantia virginiana. Plant Physiol 125: 935–942 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franks PJ, Farquhar GD (2007) The mechanical diversity of stomata and its significance in gas-exchange control. Plant Physiol 143: 78–87 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutschick VP, Simonneau T (2002) Modelling stomatal conductance of field-grown sunflower under varying soil water content and leaf environment: comparison of three models of stomatal response to leaf environment and coupling with an abscisic acid-based model of stomatal response to soil drying. Plant Cell Environ 25: 1423–1434 [Google Scholar]
- Haefner JW, Buckley TN, Mott KA (1997) A spatially explicit model of patchy stomatal responses to humidity. Plant Cell Environ 20: 1087–1097 [Google Scholar]
- Hills A, Chen ZH, Amtmann A, Blatt MR, Lew VL (2012) OnGuard, a computational platform for quantitative kinetic modeling of guard cell physiology. Plant Physiol 159: 1026–1042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holbrook NM, Shashidhar VR, James RA, Munns R (2002) Stomatal control in tomato with ABA-deficient roots: response of grafted plants to soil drying. J Exp Bot 53: 1503–1514 [PubMed] [Google Scholar]
- Jones HG. (1982) Plants and Microclimate. Cambridge University Press, Cambridge, UK [Google Scholar]
- Kirschbaum MUF, Gross LJ, Pearcy RW (1988) Observed and modeled stomatal responses to dynamic light environments in the shade plant Alocasia macrorrhiza. Plant Cell Environ 11: 111–121 [Google Scholar]
- Kollist H, Nuhkat M, Roelfsema MRG (2014) Closing gaps: linking elements that control stomatal movement. New Phytol 203: 44–62 [DOI] [PubMed] [Google Scholar]
- Leuning R. (1995) A critical appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant Cell Environ 18: 339–355 [Google Scholar]
- Li S, Assmann SM, Albert R (2006) Predicting essential components of signal transduction networks: a dynamic model of guard cell abscisic acid signaling. PLoS Biol 4: e312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manzi M, Lado J, Rodrigo MJ, Zacarías L, Arbona V, Gómez-Cadenas A (2015) Root ABA accumulation in long-term water-stressed plants is sustained by hormone transport from aerial organs. Plant Cell Physiol 56: 2457–2466 [DOI] [PubMed] [Google Scholar]
- Martins SCV, McAdam SAM, Deans RM, DaMatta FM, Brodribb TJ (2016) Stomatal dynamics are limited by leaf hydraulics in ferns and conifers: results from simultaneous measurements of liquid and vapour fluxes in leaves. Plant Cell Environ 39: 694–705 [DOI] [PubMed] [Google Scholar]
- McAdam SAM, Brodribb TJ (2012) Fern and lycophyte guard cells do not respond to endogenous abscisic acid. Plant Cell 24: 1510–1521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAdam SAM, Brodribb TJ (2014) Separating active and passive influences on stomatal control of transpiration. Plant Physiol 164: 1578–1586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAdam SAM, Brodribb TJ (2016) Linking turgor with ABA biosynthesis: implications for stomatal responses to vapour pressure deficit across land plants. Plant Physiol 171: 2008–2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAdam SAM, Sussmilch FC, Brodribb TJ (2016) Stomatal responses to vapour pressure deficit are regulated by high speed gene expression in angiosperms. Plant Cell Environ 39: 485–491 [DOI] [PubMed] [Google Scholar]
- Parlange JY, Waggoner PE (1970) Stomatal dimensions and resistance to diffusion. Plant Physiol 46: 337–342 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierce M, Raschke K (1980) Correlation between loss of turgor and accumulation of abscisic acid in detached leaves. Planta 148: 174–182 [DOI] [PubMed] [Google Scholar]
- Pierce M, Raschke K (1981) Synthesis and metabolism of abscisic acid in detached leaves of Phaseolus vulgaris L. after loss and recovery of turgor. Planta 153: 156–165 [DOI] [PubMed] [Google Scholar]
- Tardieu F, Davies WJ (1993) Integration of hydraulic and chemical signalling in the control of stomatal conductance and water status of droughted plants. Plant Cell Environ 16: 341–349 [Google Scholar]
- Tuzet A, Perrier A, Leuning R (2003) A coupled model of stomatal conductance, photosynthesis and transpiration. Plant Cell Environ 26: 1097–1116 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.