Abstract
We present a new framework for calculating coupled cluster (CC) excitation energies at a reduced computational cost. It relies on correlated natural transition orbitals (NTOs), denoted CIS(D′)-NTOs, which are obtained by diagonalizing generalized hole and particle density matrices determined from configuration interaction singles (CIS) information and additional terms that represent correlation effects. A transition-specific reduced orbital space is determined based on the eigenvalues of the CIS(D′)-NTOs, and a standard CC excitation energy calculation is then performed in that reduced orbital space. The new method is denoted CorNFLEx (Correlated Natural transition orbital Framework for Low-scaling Excitation energy calculations). We calculate second-order approximate CC singles and doubles (CC2) excitation energies for a test set of organic molecules and demonstrate that CorNFLEx yields excitation energies of CC2 quality at a significantly reduced computational cost, even for relatively small systems and delocalized electronic transitions. In order to illustrate the potential of the method for large molecules, we also apply CorNFLEx to calculate CC2 excitation energies for a series of solvated formamide clusters (up to 4836 basis functions).
I. INTRODUCTION
Nowadays, coupled cluster (CC) theory,1,2 together with the response function3–7 or the equation-of-motion8–11 formalisms, is well-established as the method of choice for the calculation of electronic transition properties of molecules dominated by a single electronic configuration. However, the steep computational scaling with a system size of CC theory limits its application to molecules with a few tens of atoms. For the calculation of transition properties of large molecules, more affordable but less reliable methods, such as time-dependent density-functional-theory (TDDFT), are generally preferred.12 The limitations of DFT methods are well-known,13,14 and it is therefore important to provide more robust alternatives for large-scale calculations of transition properties.
The steep computational scaling of CC theory can be attributed to the fact that highly delocalized canonical Hartree-Fock (HF) orbitals are used to describe electron correlation effects that are of local nature.15,16 For the calculation of CC ground state energies, many methods have been developed to take advantage of the locality of correlation effects to reduce the cost of CC calculations, and some efficient linear-scaling algorithms are now available.17–22 We note that the ground state correlation energy is a size-extensive quantity, and, by definition, CC algorithms that target size-extensive properties have to scale at least linearly with the system size. The key to achieving a reduction in computational cost without affecting significantly the accuracy of the calculated quantities is to formulate the CC equations in a basis where the inherent locality of electron correlation can be efficiently exploited. While orthogonal localized occupied orbitals are universally used,23–26 the virtual space has been described by local orthogonal virtual orbitals26–28 or non-orthogonal alternatives, such as projected atomic orbitals (PAOs),29 orbital-specific virtuals (OSVs),30 or pair-natural orbitals (PNOs).31–33
More recently, some attention has also been given to CC algorithms with reduced scaling for the determination of excitation energies and other frequency-dependent properties. In this context, it is important to realize that electronic transition properties are size-intensive. For local electronic transitions, it should therefore be possible to devise a procedure where the computational cost depends only on the character of the electronic transition and not on the system size. However, unlike ground state correlation effects, some electronic transitions are not of local nature, and it is therefore not straightforward to use the same locality approximations for the calculation of transition properties as for the ground state energy.
In the design of approximated CC methods for excitation energy calculations, the size-intensivity of electronic transitions has often been ignored. Instead, the local approximations for ground state calculations have been extended to take into account the potential delocalized character of electronic transitions by relying on information from low-level calculations34–43 [often from the configuration interaction singles (CIS) model]. Such a strategy allows for a more uniform description of size-intensive and size-extensive properties but limits significantly the potential computational savings. On the other hand, some approaches have been designed specifically for the calculation of size-intensive properties44–49 and cannot be used to obtain, e.g., correlation energies. Finally, we note that computational savings can be obtained by simply truncating the virtual orbital space in the canonical orbital basis.50,51
In a previous publication, we have introduced a local framework for calculating CC excitation energies (LoFEx),49 which provides a general approach for calculating excitation energies at a reduced computational cost. The orbital space in the LoFEx approach is a mixed space containing natural transition orbitals (NTOs) determined from a time-dependent Hartree-Fock (TDHF) calculation and localized molecular orbitals (LMOs). A subset of this mixed orbital space is then determined in a black-box manner to ensure the error control of the calculated quantities. In Ref. 49, it was shown that a compact description of electronic transitions could be obtained for transitions that are localized to a small part of the considered molecular system. However, for transitions that are delocalized over a large part of the molecule, no computational savings can be obtained with LoFEx.
In this paper, we investigate alternative orbital spaces that can be used to efficiently describe all types of transitions (including delocalized ones) and avoid the need for an optimization of the reduced orbital space. The new orbital spaces are made of generalized NTOs that include correlation effects such that an optimal reduced orbital space can be chosen solely based on the NTO eigenvalues as described in Secs. II and III. The new method entitled CorNFLEx (Correlated Natural transition orbital Framework for Low-scaling Excitation energy calculations) is tested on a set of spectroscopically interesting medium-sized molecules to calculate excitation energies at the second-order approximated CC singles and doubles (CC2) level (Sec. IV). We also calculate excitation energies of solvated formamide clusters of increasing size to illustrate the capabilities of the new method.
II. NATURAL TRANSITION ORBITALS
Our overall goal is to obtain computational savings by carrying out a standard CC excitation energy calculation within a reduced orbital space composed of transition-specific orthogonal molecular orbitals (MOs). In this section, we describe and compare different choices of NTOs that may be used for this purpose. Throughout the paper, we consider closed-shell molecules and spin-free orbitals using the following index convention (unless otherwise noted):
-
•
i, j, k, l: occupied canonical MOs;
-
•
a, b, c, d: virtual canonical MOs;
-
•
I, J, K, L: occupied MOs in the CIS-NTO basis;
-
•
A, B, C, D: virtual MOs in the CIS-NTO basis;
-
•
: occupied MOs in the occupied correlation domain (OCD);
-
•
: virtual MOs in the virtual correlation domain (VCD);
-
•
p, q, r, s: MOs of unspecified nature and occupation;
-
•
: atomic orbitals;
-
•
: projected atomic orbitals.
In Sec. II A, we summarize how NTOs are obtained at the CIS level. In Secs. II B and II C, we generalize the concept of NTOs to include correlation effects at the CC2 and CIS(D)52 levels of theory, while an approximation to CIS(D)-NTOs is introduced in Sec. II D.
A. CIS-NTOs
NTOs are usually obtained from a singular-value-decomposition (SVD) of one-particle excitation vectors.53,54 At the CIS level, the excitation vector associated with a given electronic transition is obtained from the following eigenvalue problem:55
| (1) |
where is the CIS Hamiltonian, is the HF ground-state energy, and the eigenvalue is the associated excitation energy. An SVD of is equivalent to the diagonalization of the following hole and particle density matrices:
| (2a) |
| (2b) |
CIS-NTOs are thus obtained by solving the eigenvalue equations,
| (3a) |
| (3b) |
where and are diagonal matrices with eigenvalues and on the diagonal. The / matrices represent the transformation from the occupied/virtual canonical MO basis to the occupied/virtual CIS-NTO basis. In the following discussion, it is assumed that the eigenvalues in Eq. (3) are listed in order of decreasing magnitude and that the number of virtual orbitals is larger than the number of occupied orbitals (), which is the case in all practical applications. In order to simplify the following discussion, we note that the rank of a matrix equals the number of non-zero singular values and that the following relations hold for a real matrix B of dimension (m, n):
| (4) |
Thus, from Eq. (2), it follows that
| (5a) |
| (5b) |
which implies that the last (V − O) eigenvalues of are zero. Furthermore, the first O virtual eigenvalues equal the occupied eigenvalues , i.e.,54
| (6a) |
| (6b) |
We also note that normalizing the CIS excitation vector is equivalent to requiring the sum of the eigenvalues to equal one,
| (7) |
The magnitude of the eigenvalues can be related to the importance of a given pair of CIS-NTOs for describing the transition of interest at the CIS level of theory. It would thus be convenient to choose a subset of CIS-NTOs based on their eigenvalues and then carry out a correlated CC calculation within this reduced orbital space in order to decrease the computational effort of the CC calculation. However, such a strategy is not useful in practice since it discards at least all the virtual CIS-NTOs with zero eigenvalues. This would result in unacceptable errors in the subsequent CC calculation and make it impossible to approach the full CC result in a systematic manner. In Secs. II B–II D, we generalize the concept of NTOs to include correlation effects with the objective of calculating accurate CC excitation energies within a reduced orbital space composed of correlated NTOs.
B. CC2-NTOs
In order to include the effects of CC2 doubles excitations in the NTOs, we consider the following generalized hole and particle density matrices at the CC2 level of theory:
| (8a) |
| (8b) |
where and are the singles and doubles components of the solution vector of the right CC2 eigenvalue problem,56
| (9) |
and A and are the CC2 Jacobian and CC2 excitation energies, respectively. We note that the density matrices in Eq. (8) (with a slightly different convention for the off-diagonal elements) were first introduced by Høyvik, Myhre, and Koch in connection with the multilevel CC scheme57 and that when the vector is normalized. In analogy with Eq. (3) for the CIS density matrices, the CC2-NTOs are obtained by diagonalizing and ,
| (10a) |
| (10b) |
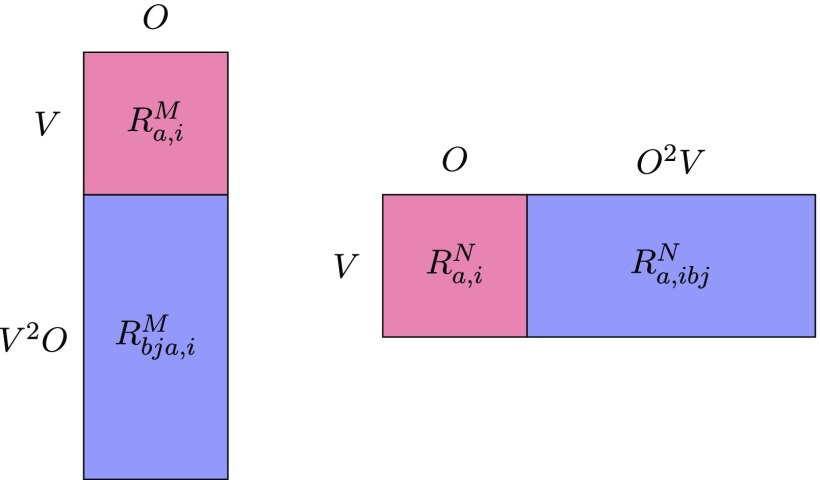
For the following analysis, it is convenient to interpret the total eigenvector entering Eq. (8a) as a matrix RM with a singles block of dimension (V,O) and elements and a doubles block of dimension (V2O, O) and elements (see Fig. 1, left). This enables us to write the matrix in Eq. (8a) as
| (11) |
Similarly, we consider a matrix RN with a singles block of dimension (V,O) and elements and a doubles block of dimension (V,O2V) and elements (see Fig. 1, right) and write the matrix in Eq. (8b) as
| (12) |
FIG. 1.
Representation of the RM (left) and RN (right) matrices used to calculate generalized transition density matrices.
Using the general identity in Eq. (4) and the dimensions of the RM and RN matrices, it then follows that
| (13a) |
| (13b) |
This should be put in contrast with the ranks of the CIS density matrices in Eqs. (5). Comparing Eqs. (2) and (8), we thus see that the inclusion of the doubles excitation vector component enables the existence of nonzero eigenvalues for all of the CC2-NTOs generated by the diagonalization of and . We also note that in contrast with the CIS case in Eq. (6), the occupied and virtual CC2-NTO eigenvalues are generally different, .
The generation of the CC2-NTOs requires the determination of the CC2 excitation vector for the full molecular system, and the CC2-NTOs are therefore primarily of analytical interest if CC2 excitation energies are targeted. It is thus instructive to look at the explicit expression for the CC2 doubles excitation vector in order to consider approximations in Secs. II C and II D that could be invoked in practical calculations of CC2 excitation energies. From Ref. 58, the CC2 doubles excitation vector is given by
| (14) |
where the transformed integrals are written as
| (15) |
with
| (16) |
and
| (17a) |
| (17b) |
| (17c) |
| (17d) |
where C is the standard (canonical) MO coefficient matrix and tai are the ground state CC2 singles amplitudes, while and represent the occupied and virtual orbital energies, respectively. The expensive part of the CC2-NTO procedure is the calculation of the doubles excitation vector components in Eq. (14) and their contraction in Eq. (8), both of which scale as where N is a measure of the size of the molecular system. In particular, the determination of requires the iterative solution of both the ground state CC2 equations (to determine tai) and the subsequent iterative solution of the CC2 eigenvalue problem in Eq. (9).
C. CIS(D)-NTOs
As a first approximation to the CC2-NTOs, we consider NTOs generated from the simpler CIS(D) model.52 In Eq. (14), this effectively corresponds to setting the ground state singles amplitudes to zero () and using the CIS excitation energy and excitation vector instead of the corresponding CC2 quantities. Thus, within the CIS(D) model, the amplitudes may be determined in a non-iterative process according to
| (18) |
where the transformed integrals are given by
| (19) |
| (20a) |
| (20b) |
The CIS(D)-NTOs are then obtained by diagonalizing the CIS(D) hole and particle density matrices, which are constructed analogously to Eqs. (8),
| (21a) |
| (21b) |
D. CIS(D′)-NTOs
The generation of CIS(D)-NTOs is a non-iterative process, and it is therefore prohibitively expensive for large molecular systems. In this section, we describe a strategy for determining approximate CIS(D)-NTOs by using CIS information and locality arguments to approximate the doubles terms in Eq. (21).
The occupied and virtual CIS-NTO bases are defined by the and transformation matrices in Eq. (3). We now consider two mixed bases—one where the occupied orbitals are canonical and the virtual orbitals are expressed in the CIS-NTO basis, and vice versa—leading to the following approximate doubles vectors:
| (22a) |
| (22b) |
where we have used capital letters to denote the CIS-NTO basis and made the diagonal Fock matrix approximation in the CIS-NTO basis. The use of Eq. (22) alone does not reduce the computational effort compared to Eq. (18). However, we now invoke a procedure where we freeze the most important CIS-NTOs and transform the remaining orbitals to a local basis in which the number of important doubles vector elements can be reduced. The philosophy behind this approach is that the frozen CIS-NTOs describe the main character of the transition at the CIS level of theory, while the remaining local orbitals allow for an efficient description of correlation effects. In the remainder of this section, we describe the technical details of this procedure which is also summarized in Figs. 2 and 3.
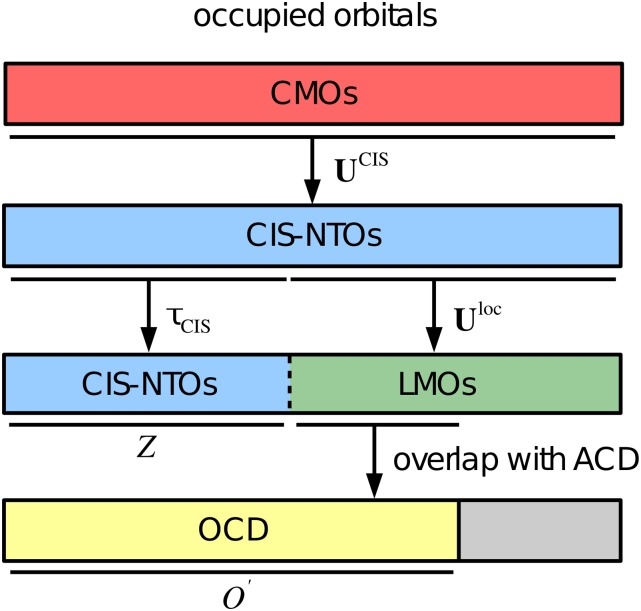
FIG. 2.
Schematic representation of the generation of the occupied correlation domain (OCD). The matrix transforms from occupied canonical molecular orbitals (CMOs) to the CIS natural transition orbital (CIS-NTOs) basis. A subset of Z CIS-NTOs is selected using [see Eq. (23)], while the matrix transforms the remaining CIS-NTOs to a local basis (LMOs). The atomic correlation domain (ACD) is constructed as a list of atoms located in the same part of space as the important CIS-NTOs. Finally, LMOs are included in the OCD if their atomic extents overlap with any of the atoms in the ACD, see text for details.
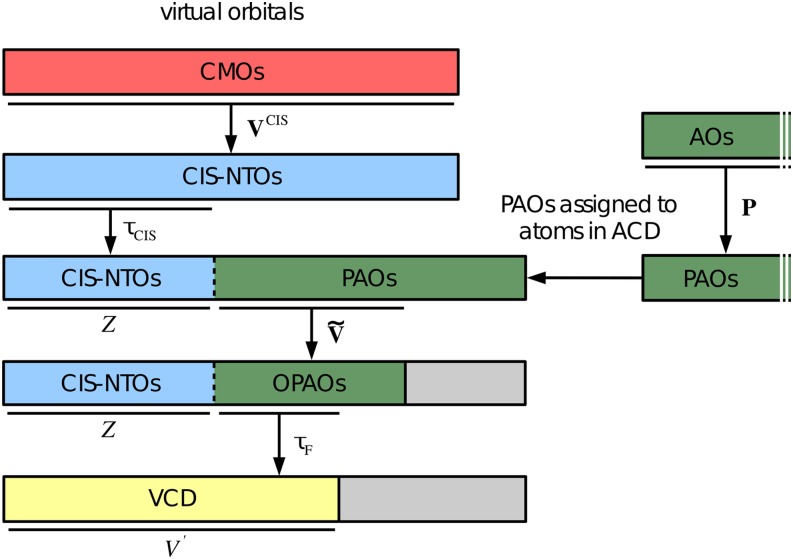
FIG. 3.
Schematic representation of the generation of the virtual correlation domain (VCD). The matrix transforms from virtual canonical molecular orbitals (CMOs) to the CIS natural transition orbital (CIS-NTO) basis. A subset of Z CIS-NTOs is selected using [see Eq. (23)], while the P matrix is used to generate projected atomic orbitals (PAOs), see Eq. (25). The atomic correlation domain (ACD) is constructed as a list of atoms located in the same part of space as the important CIS-NTOs. A subset of PAOs assigned to atoms in the ACD is then orthonormalized using the matrix [see Eq. (29)], and redundant PAOs are discarded to arrive at a set of non-redundant orthogonal PAOs (OPAOs). Finally, all OPAOs with a diagonal matrix element are discarded. The remaining OPAOs and the Z important CIS-NTOs then constitute the VCD.
As a first step, we define a subset of Z occupied and Z virtual CIS-NTOs for which the eigenvalues add up to one minus some threshold ,
| (23) |
where p refers to either occupied (p = I) or virtual (p = A) CIS-NTOs. In practice, we set . In order to account for correlation effects associated with the (2Z) important CIS-NTOs defined by Eq. (23), we define an atomic correlation domain (ACD), which is a list of atoms that represent the part of the molecular system where the important CIS-NTOs are located. Specifically, for each important CIS-NTO (p), we determine an orbital extent as the smallest possible reduced set of atomic orbitals (AOs) for which the accumulated Löwdin charge is above 0.95, i.e.,
| (24) |
where is the Löwdin charge of CIS-NTO p on AO . An atomic site is then included in the ACD if at least one of its AOs is contained in one of the orbital extents for the important CIS-NTOs.
Once the important CIS-NTOs have been identified and the ACD has been defined, we localize the remaining (O − Z) occupied orbitals and determine the orbital extent for each of these as described above. We then define the occupied correlation domain (OCD), which contains the Z important occupied CIS-NTOs and those localized occupied orbitals for which the orbital extent contains at least one AO assigned to an atom in the ACD. The OCD is thus a mixed occupied CIS-NTO/local basis {} of dimension with . As a localization function, we use the second power of the second moment of the orbitals,26 which provides a good compromise between the locality and computational cost.28 The generation of the OCD is illustrated in Fig. 2.
A similar but slightly more involved procedure is used to obtain a reduced virtual correlation domain (VCD). We first define a set of projected atomic orbitals (PAOs) where all occupied orbitals and the Z important virtual CIS-NTOs have been projected out,
| (25) |
where the projection matrix P is given by
| (26) |
| (27) |
| (28) |
We note that in Eq. (27), the i-summation runs over all occupied orbitals (both core and valence orbitals), while the A-summation runs only over the set of important virtual CIS-NTOs defined by Eq. (23). The PAOs in Eq. (25) are thus a redundant and nonorthogonal set of local orbitals that spans the part of the virtual space, which is orthogonal to the Z important virtual CIS-NTOs. Note that the PAOs defined by Eq. (25) are different from conventional PAOs29 due to the second term in Eq. (27).
We now construct a reduced set of PAOs by considering only PAOs spatially local to the important CIS-NTOs, i.e., if atomic orbital does not belong to the ACD, then PAO is discarded. All the remaining PAOs are then orthonormalized and redunancies are removed, i.e., we diagonalize the PAO overlap matrix,
| (29) |
| (30) |
and generate orthogonalized PAOs (OPAOs) using the transformation matrix. OPAOs with small eigenvalues () are removed from the set, and the remaining non-redundant OPAOs are normalized. Furthermore, from Eq. (22a), we note that large diagonal virtual Fock matrix elements will generally lead to small doubles excitation vector elements. We therefore propose to reduce the set of OPAOs further by considering only the OPAOs for which the diagonal Fock matrix elements are above a certain threshold , which we set to 50 eV. To summarize, the Z important CIS-NTOs and the reduced set of OPAOs define the VCD {}, which is an orthonormal set of virtual orbitals of dimension with . The generation of the VCD is illustrated in Fig. 3.
Using the occupied {} and virtual {} correlation domains defined above, we may now approximate the doubles excitation vectors in Eq. (22) in the following manner:
| (31a) |
| (31b) |
where the prime denotes the occupied and virtual correlation domains of reduced dimensions and , while the summations in the canonical basis run over the full set of orbitals. We refer to and as the CIS(D′) hole and particle density matrices. In analogy with Eq. (10), the CIS(D′)-NTOs may then be obtained by diagonalizing and . We note that while the primed indices are generally reduced compared to the full dimensions, and always have full molecular dimensions, and the diagonalization procedure therefore leads to O occupied and V virtual CIS(D′)-NTOs with a priori nonzero eigenvalues. This may be seen explicitly by considering the ranks of the CIS(D′) density matrices, which—in analogy with Eq. (13)—obey the following equations:
| (32a) |
| (32b) |
It is seen that all the CIS(D′)-NTOs generally have nonzero eigenvalues, which can be used to quantify the physical significance of each orbital for describing the targeted transition.
The generation of CC2-NTOs and CIS(D)-NTOs is an iterative and a non-iterative process, respectively. An algorithm for generating CIS(D′)-NTOs is given in the Appendix where it is shown that the generation of CIS(D′)-NTOs has a formal scaling behaviour (assuming that the reduced dimensions and are independent of the system size for a given type of electronic transition). CIS(D′)-NTOs can thus be calculated for much larger molecular systems than CC2-NTOs or CIS(D)-NTOs.
We emphasize that even though the generation of CIS(D′)-NTOs described in this section and the Appendix is a bit technical, the end result is a set of prioritized orthogonal MOs that span the full molecular orbital space. A subset of CIS(D′)-NTOs can thus be chosen based on their eigenvalues. Furthermore, we may transform such a subset to a pseudo-canonical basis by diagonalizing the corresponding occupied-occupied and virtual-virtual blocks of the Fock matrix. These pseudo-canonical orbitals can be straightforwardly used in a standard CC code to calculate CC excitation energies. The main complexity compared to a conventional CC implementation thus occurs during the orbital generation rather than in the actual CC calculation.
E. Comparison of NTOs
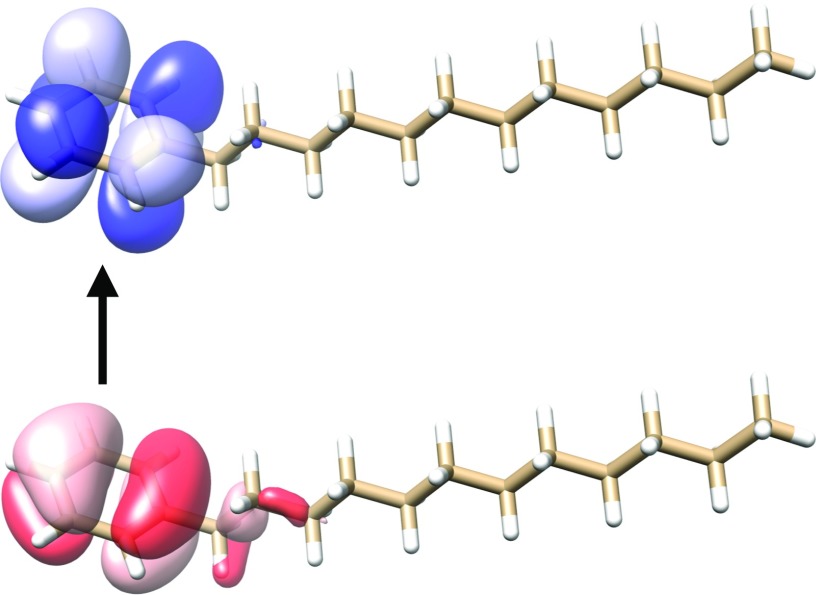
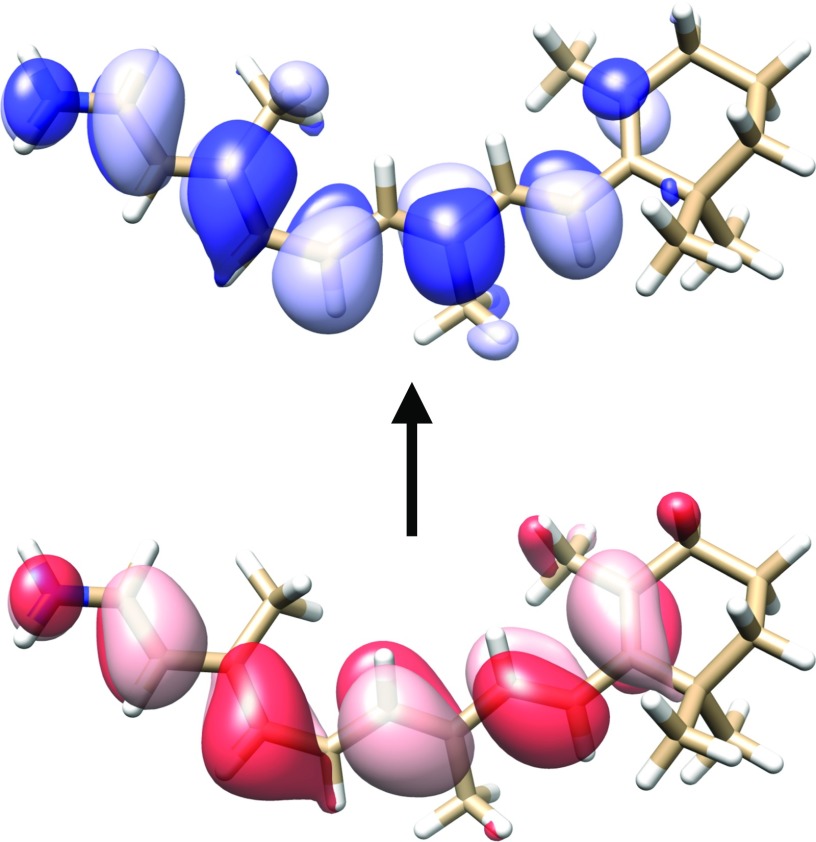
In this section, we compare the different sets of NTOs introduced above. We consider dodecylbenzene and 11-cis-retinal protonated Schiff base (CRPSB), which are depicted in Figs. 4 and 5, respectively, together with the dominant pair of CIS-NTOs for the lowest electronic transition. All the calculations were performed using augmented basis sets of double- quality as described in Sec. IV. For dodecylbenzene, it is clear that the transition is localized in a relatively small region of the molecule, while the transition in CRPSB involves almost the entire molecule. The dodecylbenzene and CRPSB cases are thus typical examples of a localized transition and a delocalized transition, respectively.
FIG. 4.
Illustration of the lowest electronic transition in dodecylbenzene in terms of the dominant occupied (red, bottom) and virtual (blue, top) CIS-NTOs (aug-cc-pVDZ′ basis). The contour plot value was set to 0.02 a.u.59
FIG. 5.
Illustration of the lowest electronic transition in the 11-cis-retinal protonated Schiff base in terms of the dominant occupied (red, bottom) and virtual (blue, top) CIS-NTOs (aug-cc-pVDZ′ basis). The contour plot value was set to 0.02 a.u.59
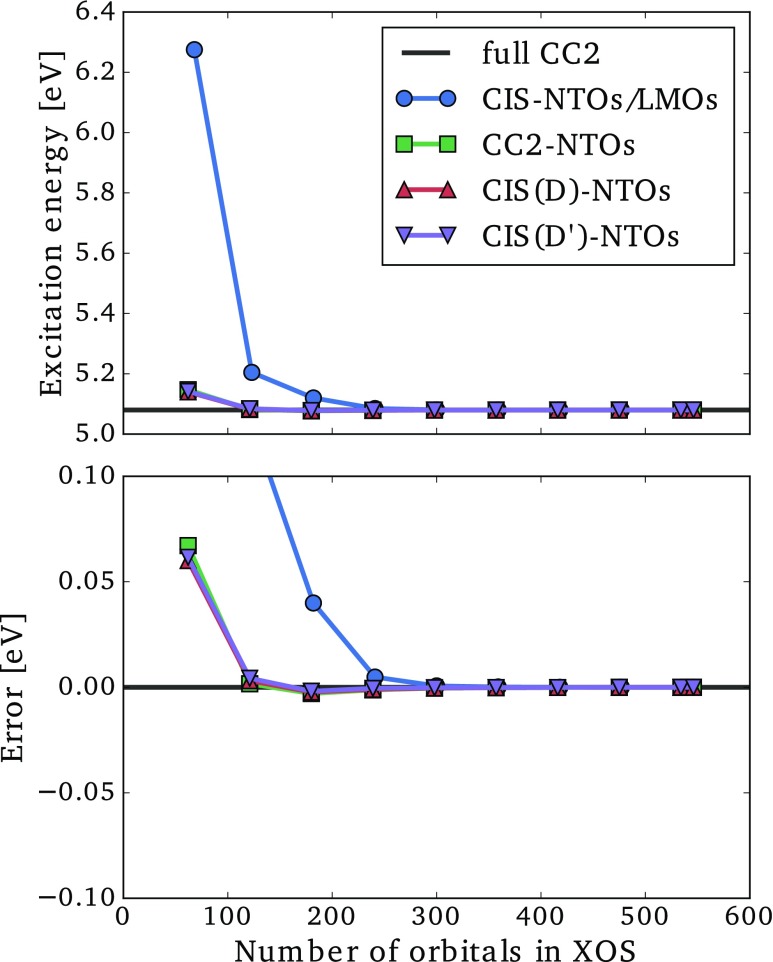
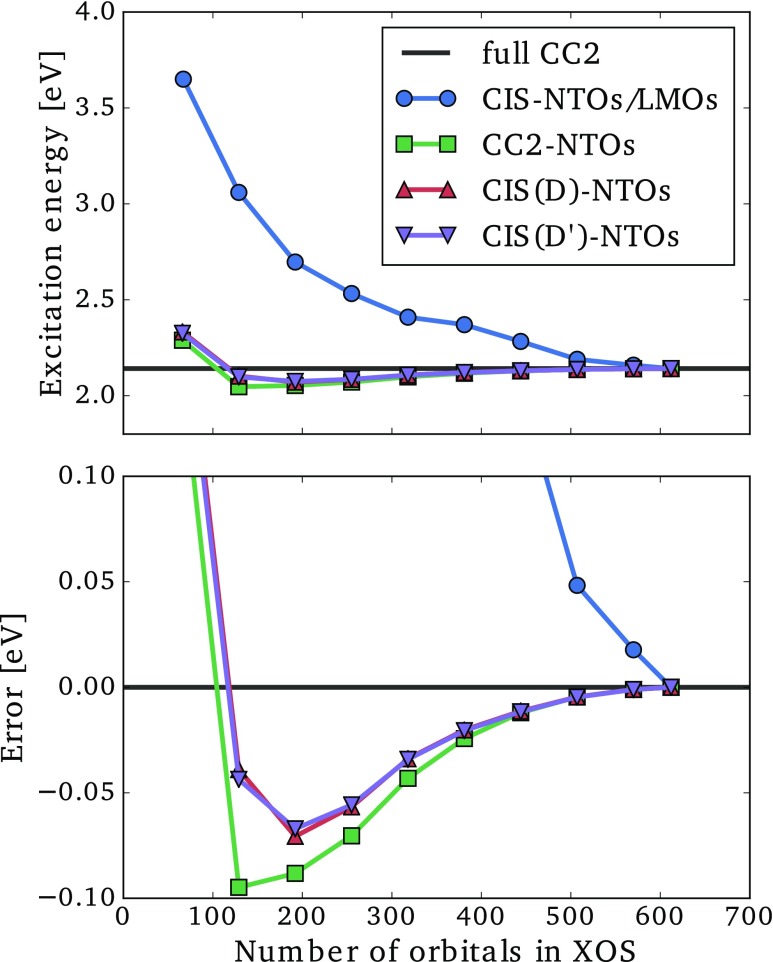
For the CC2-, CIS(D)-, or CIS(D′)-NTOs (collectively referred to as correlated NTOs), we may list the orbitals in order of descending NTO eigenvalues. We then select a given number of orbitals from this list to generate an excitation orbital space (XOS), in which the CC2 ground state amplitude equation and CC2 eigenvalue equation are solved to yield an approximate CC2 excitation energy. In Figs. 6 and 7, we present the lowest CC2 excitation energies and associated errors for the dodecylbenzene and CRPSB molecules as a function of the number of MOs included in the XOS for the correlated NTOs. For comparison, we also give results for the mixed CIS-NTO/LMO space, which was defined in Refs. 49 and 60.
FIG. 6.
Lowest CC2/aug-cc-pVDZ′ excitation energy (top) and error (bottom) as a function of the size of the excitation orbital space (XOS) for dodecylbenzene using different choices of orbital spaces.
FIG. 7.
Lowest CC2/aug-cc-pVDZ′ excitation energy (top) and error (bottom) as a function of the size of the excitation orbital space (XOS) for the 11-cis-retinal protonated Schiff base using different choices of orbital spaces.
For a given XOS, errors compared to the full CC2 calculation arise since (i) the ground state amplitude equations and (ii) the CC2 eigenvalue problem in Eq. (9) are solved in the restricted XOS. We note that the errors of type (i) affect the errors of type (ii) indirectly, since the Jacobian matrix A in Eq. (9) is determined from ground state amplitudes.56 All in all, the complex interplay of these two error sources ultimately leads to the errors observed in Figs. 6 and 7.
The CIS-NTO/LMO space behaves markedly different for the two molecules. For dodecylbenzene, the excitation energy error is below 0.1 eV when about 150 orbitals have been included in the XOS [see Fig. 6 (bottom)], while almost 500 orbitals are required to achieve the same accuracy for CRPSB [see Fig. 7 (bottom)]. This difference can be rationalized as follows. For the local transition in dodecylbenzene (Fig. 4), the use of LMOs leads to a significant reduction of the XOS, since a large region of the molecule is unaffected by the transition. On the other hand, for the delocalized transition in CRPSB (Fig. 5), the transition induces changes in the electronic structure throughout the molecular system, and the use of LMOs offers very modest reductions of the XOS. These two examples clearly show the strength and weakness of the CIS-NTO/LMO approach introduced in Ref. 49, i.e., significant computational savings are possible for local transitions, while a delocalized transition essentially requires the full molecular CC calculation to be carried out.
For the local transition in Fig. 6, the use of any of the correlated NTOs leads to much smaller errors than the CIS-NTO/LMO mixed space for a given number of XOS orbitals. The correlated NTOs thus allow for a more compact representation of correlation effects than the LMOs. Even more striking is the behavior of the correlated NTOs for the delocalized transition in Fig. 7, where errors below 0.1 eV are observed with only around 100 orbitals, which is in stark contrast to the CIS-NTO/LMO curve. Thus, using correlated NTOs, it seems possible to obtain a compact representation of the orbital space for both localized and delocalized transitions.
The results in Figs. 6 and 7 obtained using the different correlated NTOs are very similar, indicating that all three sets of NTOs contain the basic information about correlation effects. This is a very important result, since the CIS(D′)-NTOs are much cheaper to generate than the CIS(D)- and CC2-NTOs (Sec. II D and the Appendix). The curves for CIS(D)- and CIS(D′)-NTOs are almost identical, and the approximations introduced in Sec. II D thus appear to be negligible for practical purposes. Both negative and positive errors occur for the correlated NTOs, and it is notable that the CIS(D′)- and CIS(D)-NTOs often yield smaller absolute errors than the CC2-NTOs even though the excitation energy is calculated at the CC2 level. This can happen due to error cancellations between the error sources (i) and (ii) mentioned above.
In summary, the dodecylbenzene and CRPSB results presented here indicate that the CIS(D′)-NTOs can be used to generate a reduced orbital space that may significantly lower the computational cost of CC2 calculations for both localized and delocalized transitions.
III. COUPLED CLUSTER EXCITATION ENERGIES USING CorNFLEx
In this section, we introduce a general framework for calculating CC excitation energies at a reduced computational cost using the concept of CIS(D′)-NTOs. We consider excitation energies calculated using the CC2 model introduced by Christiansen et al.,56 where the resolution-of-the-identity (RI) approximation is used for the two-electron repulsion integrals, as introduced by Hättig and Weigend.58 We refer to Refs. 56 and 58 for a detailed description of the CC2 model.
The main algorithm is presented in Sec. III A, while the treatment of multiple excitation energies is detailed in Sec. III B. In Sec. III C, we describe how the number of auxiliary functions in the XOS may be reduced.
A. The main CorNFLEx algorithm
The results in Sec. II E indicate that the CIS(D′)-NTOs provide a compact representation of electronic transitions at the CC level. After solving the CIS eigenvalue problem for the full molecule, we thus propose the following procedure to reduce the computational cost of CC excitation energy calculations:
-
1.
Perform an SVD of the CIS eigenvectors to determine the CIS-NTOs according to Eqs. (3).
-
2.
Calculate CIS(D′) density matrices from Eqs. (31) as detailed in Sec. II D.
-
3.Diagonalize the CIS(D′) density matrices to determine the and transformation matrices that define the occupied and virtual CIS(D′)-NTOs,
(33a) (33b) -
4.List the CIS(D′)-NTO eigenvalues in descending order and scale them such that they add up to one (equivalent to normalizing the CIS(D′) excitation vectors),
(34) -
5.Choose a subset of occupied and virtual CIS(D′)-NTOs based on the threshold,
(35a)
This subset of orbitals containing Zo occupied CIS(D′)-NTOs and virtual CIS(D′)-NTOs is denoted the excitation orbital space (XOS).(35b) -
6.
For the chosen CC model (CC2 in this work), solve the ground state amplitude equation and the Jacobian eigenvalue equation within the XOS to obtain the CC excitation energy corresponding to the CIS excitation vector used to generate the XOS.
We denote the approach defined by these six steps as the Correlated Natural transition orbital Framework for Low-scaling Excitation energy calculations (CorNFLEx). We stress that is our main threshold which controls the accuracy of the CorNFLEx calculation, e.g., in the limit where all orbitals are included and the full CC result is reproduced. The CorNFLEx procedure should be applied to each electronic transition of interest, and additional technical details related to the determination of multiple excitation energies are discussed in Sec. III B.
The use of CIS(D′)-NTOs implies that only single-replacement dominated electronic transitions that are described at the CIS level of theory can be addressed with CorNFLEx. However, many transitions of interest in typical organic and biological molecules are of this type. Furthermore, for the CC2 model, which is the target model in the present study, single-replacement dominated transitions are correct through second order in the fluctuation potential, while double-replacement dominated transitions are correct only to zeroth order.61 The CC2 model thus provides accurate results only for transitions dominated by single-electron replacements. The fact that our CIS(D′)-NTOs can be generated only for such transitions is therefore not a limitation from a practical point of view.
B. Multiple excitation energies
When several excitation energies are requested, the CorNFLEx algorithm defined by the six steps in Sec. III A is applied to each CIS excitation vector of interest, starting with the lowest CIS excitation energy. For example, if the three lowest CIS vectors are determined , we may calculate the corresponding three CC2 vectors, , which, of course, do not necessarily correspond to the three lowest excitation energies at the CC2 level of theory. In CorNFLEx, it is thus implicitly assumed that there is a one-to-one correspondence between each CIS vector and the determined CC2 vector and care must be exercised if the CIS vectors mix considerably at the CC2 level of theory. For this reason, we consider the overlap, , between the CIS target vector, , and the final CC2 singles vector, , as a measure of the reliability of the results,
| (36) |
If and are both normalized in the singles space, then . Thus, if is much smaller than one, we recommend to reduce (increase the XOS) and repeat the calculation to check the validity of the calculated CC2 excitation energy. We return to this issue in Sec. IV and now turn our attention to some technical details regarding the determination of several excitation energies.
First, it is necessary to ensure that the solution of each CC2 eigenvalue equation (step 6 in Sec. III A) converges to the CC2 vector that has the largest overlap with the CIS target vector. A root homing procedure62 is therefore applied to track the CIS vector of interest when the CC2 eigenvalue problem is solved using Davidson techniques.63–65 Thus, in the Davidson procedure, we calculate the overlap () between the CIS target vector and each of the optimal CC2 vectors generated in the current iteration. The optimal CC2 vector with the largest overlap is then used to calculate the residual vector and to extend the Davidson subspace with a new direction if the norm of the residual vector is above a convergence threshold.
Second, as an additional precaution, we project out the k − 1 previously determined CC2 vectors from the CIS target vector k, i.e., we transform in the following manner:
| (37a) |
| (37b) |
| (37c) |
This projection strategy is important when two or more CIS vectors mix considerably at the CC level of theory. For such cases, the use of Eq. (37) effectively ensures that any given CC2 vector is only determined once.
All in all, the root homing and projection strategies described in this section provide a way to calculate several excitation energies within independent XOSs.
C. Natural auxiliary functions
In Sec. III A, we have detailed a procedure to construct a reduced space of orthogonal occupied and virtual orbitals (the XOS). The MOs in the XOS are in principle expressed as a linear combination of all AOs which puts severe limitations on the performance of the method. However, as detailed in Appendix B of Ref. 66, the number of AOs in the XOS can be reduced by removing molecular orbital tails using a least squares fitting procedure. Similarly, for the RI approximation, we consider only the subset of auxiliary functions that are assigned to the subset of atoms defined by the AOs in the XOS (see Ref. 67 for details).
Once the XOS has been defined and the atomic and auxiliary functions have been reduced, a standard CC calculation is performed in that space. Our implementation of the CC2 model for excitation energies closely follows the RI specific algorithm described in Ref. 58 with the exception that the required tensors of dimension are kept in the core memory instead of a disk (where denotes the number of auxiliary functions). It is thus very important to reduce the auxiliary dimension as much as possible. For that purpose, we invoke the use of natural auxiliary functions (NAFs) as introduced by Kállay in Ref. 68.
Using the RI approximation, the two-electron integrals involved in the CC2 algorithm can be written as follows:
| (38) |
| (39) |
where and denote the auxiliary basis functions. In our implementation, we calculate NAFs by diagonalizing the following symmetric matrix:
| (40) |
where the summation runs over all possible pairs of MO indices (ai, ia, ab, ij). In Ref. 68, NAFs were obtained in a similar way but using or (depending on the targeted model) instead of . In a standard CC2 calculation, it might be more appropriate to use the tensor instead of since it avoids the contraction of the integrals with the MO coefficients. However, in the context of CorNFLEx, the number of MOs in the XOS is significantly smaller than the number of AOs, and using enables a larger reduction of the number of auxiliary functions. In our CC2 implementation, the integrals are thus stored in the form
| (41) |
where the coefficients —which transform a standard auxiliary function () to the corresponding NAF ()—are obtained as described in Ref. 68. The number of NAFs is significantly reduced compared to the number of auxiliary functions by considering only those functions that correspond to an eigenvalue of W larger than a truncation threshold, . For the calculation of CC2 excitation energies, our test calculations indicate that a truncation threshold of can be used without affecting the results (see Sec. IV A). This is particularly useful in the context of CorNFLEx where the number of NAFs and the memory requirements can be greatly reduced.
IV. RESULTS
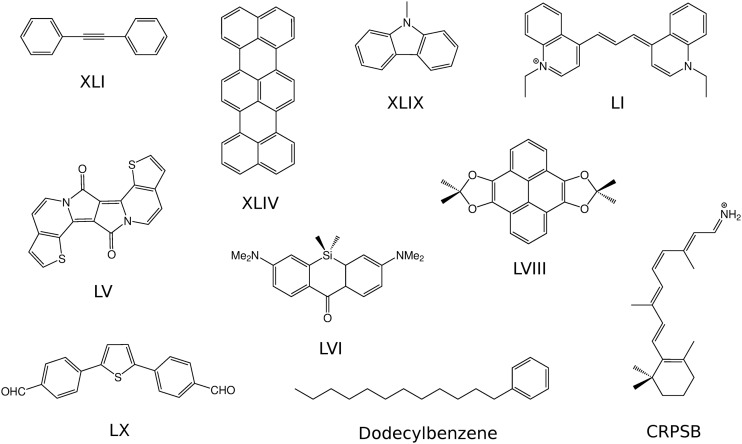
In this section, we present numerical results and applications of the CorNFLEx procedure to real-life compounds and assess the performance and accuracy of the method when targeting CC2 excitation energies. As a test set, we consider the five lowest CIS transitions and the corresponding CC2 excitation energies of the following ten molecules, which are shown in Fig. 8:
-
•
The molecules XLI, XLIV, XLIX, LI, LV, LVI, LVIII, and LX from the test set presented in Ref. 69.
-
•
Dodecylbenzene optimized at the MP2/cc-pVDZ level using the ORCA program70 (Cartesian coordinates are available in the supplementary material).
-
•
11-cis-retinal protonated Schiff base (CRPSB) using the geometry from Ref. 43.
FIG. 8.
Molecules contained in the test set used in Sec. IV A.
The CorNFLEx CC2 excitation energies and timings for those systems are compared to full CC2 calculations in Sec. IV A. All calculations have been performed with a local version of the LSDalton program,71,72 using the frozen core approximation. The correlation consistent aug-cc-pVDZ′ and aug-cc-pVTZ′ basis sets73,74 were used with the corresponding auxiliary basis sets aug-cc-pVDZ-RI′ and aug-cc-pVTZ-RI′ for the RI approximation.75 The prime in the basis set notation indicates that diffuse functions have been removed from the hydrogen atoms.
Finally, in order to demonstrate the potential of CorNFLEx, we also consider molecular clusters of solvated formamide containing up to 144 water molecules in Sec. IV B. The structures were obtained by the modification of a single snapshot taken from Ref. 76 and are available in the supplementary material.
A. Performance of CorNFLEx for the test set
In this section, we consider the five lowest excited states for the test set in Fig. 8 to compare the accuracy and computational cost of the CorNFLEx procedure described in Sec. III with full (canonical) CC2 calculations. In total, we thus consider 50 singlet electronic transitions using both augmented double- and triple- quality basis sets.
In order to evaluate the convergence of the excitation energies with the size of the XOS, we have performed calculations using and 10−5. In the supplementary material (Tables SI-SX), we report the individual errors in the excitation energies, , while we present the mean absolute error,
| (42) |
the maximum absolute error,
| (43) |
the mean error,
| (44) |
and the standard deviation,
| (45) |
for the aug-cc-pVDZ′ and aug-cc-pVTZ′ basis sets in Tables I and II, respectively. Here, n = 50 is the number of excitation energies calculated from the 10 molecules in the test set.
TABLE I.
Statistical analysis of CC2 excitation energies for the test set using the aug-cc-pVDZ′ basis set. The mean absolute error (), the maximum absolute error (), the mean error (), and the standard deviation () are reported. We also consider the same measures for the subset of CC2 states with (see text for details). All measures are given in eV.
| All errors | |||
|---|---|---|---|
| 0.07 | 0.02 | 0.00 | |
| 0.37 | 0.22 | 0.02 | |
| −0.01 | −0.01 | 0.00 | |
| 0.10 | 0.04 | 0.01 |
| Errors () | |||
|---|---|---|---|
| 0.06 | 0.01 | 0.00 | |
| 0.22 | 0.08 | 0.02 | |
| 0.00 | −0.01 | 0.00 | |
| 0.08 | 0.02 | 0.01 |
TABLE II.
Statistical analysis of CC2 excitation energies for the test set using the aug-cc-pVTZ′ basis set. The mean absolute error (), the maximum absolute error (), the mean error (), and the standard deviation () are reported. We also consider the same measures for the subset of CC2 states with (see text for details). All measures are given in eV.
| All errors | |||
|---|---|---|---|
| 0.11 | 0.05 | 0.01 | |
| 0.43 | 0.40 | 0.05 | |
| −0.04 | −0.05 | −0.01 | |
| 0.16 | 0.08 | 0.01 |
| Errors () | |||
|---|---|---|---|
| 0.11 | 0.04 | 0.01 | |
| 0.43 | 0.16 | 0.05 | |
| −0.04 | −0.04 | −0.01 | |
| 0.15 | 0.05 | 0.01 |
In general, we observe that the excitation energy errors decrease systematically with decreasing values for both basis sets. For example, the mean absolute errors are 0.11 eV, 0.05 eV, and 0.01 eV for and 10−5 when the aug-cc-pVTZ′ basis set is used. The mean absolute errors are small compared to typical CC2 errors, which are typically of the order of 0.2 eV.58,77–79
The maximum absolute errors reveal that there are some outliers. For example, using and the aug-cc-pVTZ′ basis set, the maximum absolute error is 0.40 eV. This error is associated with the third state of the XLIV molecule (Table SII in the supplementary material). As discussed in Sec. III B, the CorNFLEx procedure can only be expected to yield very accurate results when the CC2 singles vector is dominated by a single CIS vector. This is the case if the measure in Eq. (36) is larger than 0.5. For the third state of XLIV molecule in the aug-cc-pVTZ′ basis set, we find that . It is therefore not surprising that the associated error is rather large. However, by decreasing from 10−4 to 10−5, the error for the considered state is effectively removed. In the lower parts of Tables I and II, we present the different error measures calculated from a subset of the 50 excitation energies where states with (k = 1, 2, 3, 4, 5) have been removed. This corresponds to removing between 2 and 4 states (out of the 50 states) and reduces most of the maximum errors quite dramatically, e.g., from 0.40 eV to 0.16 eV using and the aug-cc-pVTZ′ basis set.
All in all, we conclude that the CorNFLEx procedure allows us to calculate excitation energies of CC2 quality. One should, however, check the diagnostics when analyzing the results. If for a given state k, it is recommended to decrease for that state to validate the calculated excitation energy. The exact CC2 result is obtained by reducing the threshold, and we will refer to the values of 10−3, 10−4, and 10−5 as loose, standard, and tight, respectively.
In order to evaluate the computational cost of the CorNFLEx scheme, we consider the mean, maximum, and minimum speed-ups compared to a state-specific full calculation calculated as
| (46) |
For each of the 10 molecules, is the time for the correlated part of the CC2 calculation, i.e., the determination of the CC2 ground state amplitudes and solution of the Jacobian eigenvalue problems for the five excited states in the complete canonical basis using the root homing procedure.62 includes both the time spent in the generation of the CIS(D′)-NTOs and the time spent in the CC2 calculation within the restricted XOS determined by .
The timing results obtained using the aug-cc-pVDZ′ and aug-cc-pVTZ′ basis sets are given in Table III. It is seen that computational savings are obtained with all of the tested thresholds although the speed-ups of course decrease with decreasing . The largest speed-ups are observed for dodecylbenzene where the XOS is very small compared to the full orbital space, since the transitions are localized on the benzene ring (see Fig. 4 for an illustration of the lowest transition). However, significant speed-ups are also obtained for the delocalized transitions. The CorNFLEx procedure thus cures the main flaw of our recently proposed LoFEx scheme where speed-ups were only obtained for localized transitions. In summary, CorNFLEx generally yields excitation energies of CC2 quality at a reduced computational cost for both localized and delocalized transitions.
TABLE III.
Relative speed-ups of CorNFLEx calculations compared to canonical CC2 calculations for the test set using the aug-cc-pVDZ′ and aug-cc-pVTZ′ basis sets.
| Basis | Measure | Loose | Standard | Tight |
|---|---|---|---|---|
| aug-cc-pVDZ′ | Mean | 5.9 | 3.3 | 1.8 |
| Max | 19.0 | 11.3 | 5.0 | |
| Min | 1.9 | 1.5 | 1.1 | |
| aug-cc-pVTZ′ | Mean | 7.5 | 4.4 | 2.5 |
| Max | 26.4 | 13.8 | 7.6 | |
| Min | 2.9 | 2.1 | 1.4 |
Finally, we note that the CorNFLEx results in Tables I and II used the NAF approximation described in Sec. III C with . In Tables SXI and SXII in the supplementary material, we present errors introduced by the NAF approximation in CorNFLEx calculations for CRPSB and dodecylbenzene. We note that the NAF errors are generally at least an order of magnitude smaller than the corresponding CorNFLEx errors (Tables SIX and SX in the supplementary material). We thus conclude that the main threshold controls the accuracy of a CorNFLEx calculation, while the NAF error is negligible. Finally, from Tables SXIII and SXIV in the supplementary material, we see that the use of NAFs reduces the number of auxiliary functions in the CorNFLEx CC2 calculations considerably compared to a full calculation.
B. Solvated formamide
In order to investigate the potential of CorNFLEx for large molecular systems, we now consider the lowest excitation energy in a series of solvated formamide clusters with an increasing number of water molecules. All the calculations have been performed using the aug-cc-pVDZ′ basis set, and the CorNFLEx strategy has been applied with the loose, standard, and tight thresholds for clusters including up to 144 water molecules (4836 basis functions). Reference calculations using a conventional CC2 implementation have also been performed for clusters containing up to 63 water molecules (2163 basis functions).
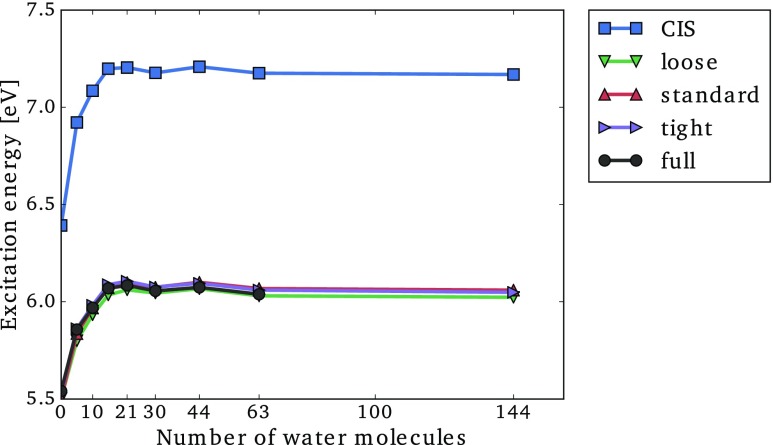
In Fig. 9, we have plotted the convergence of the excitation energy as a function of the number of water molecules included in the cluster using the loose, standard, and tight CorNFLEx thresholds (explicit values are given in the supplementary material). The excitation energies obtained with conventional CIS and CC2 algorithms are also reported. Figure 9 shows that the solvation effects result in a blueshift of eV at the CIS level, while the blueshift is lowered to around 0.5 eV at the CC2 level. Most of the solvation effects are already included with only 15 water molecules, and adding more waters results in small oscillations of around 0.03 eV. We note that the observed solvatochromatic shift is consistent with Ref. 76 but that a conformational sampling is required to obtain reliable results.
FIG. 9.
Lowest excitation energy of a series of solvated formamide with an increasing number of water molecules using the aug-cc-pVDZ′ basis set. CC2-CorNFLEx results are reported using the loose, standard, and tight thresholds. For comparison, the CIS and full CC2 results are also reported.
The excitation energies calculated using CorNFLEx are effectively of CC2 quality, even with the loose threshold. A closer look at the (absolute) errors for the different structures shows that they are at most 0.06 eV, 0.04 eV, and 0.02 eV for the loose, standard, and tight thresholds (see Table SXIII in the supplementary material). This is in accordance with the errors observed for the test set in Sec. IV A. The main correlation effect (i.e., a lowering of the blueshift compared to the CIS result) is thus well described with all of the tested thresholds.
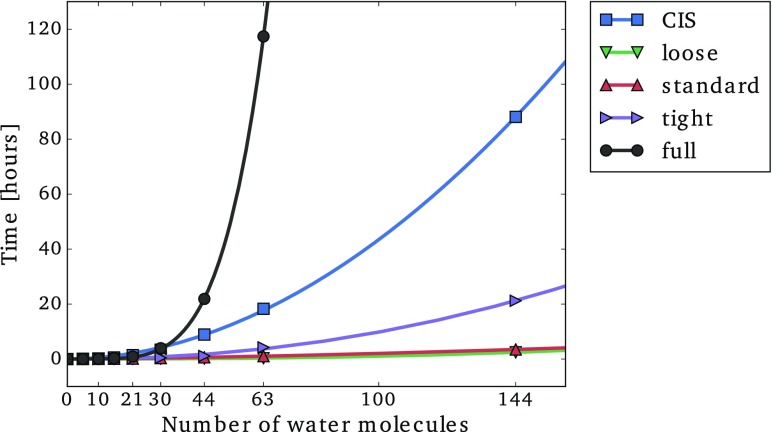
In order to analyze the performance of the CorNFLEx strategy compared to a conventional algorithm, we report timings for the CIS calculation and for the correlated parts of the CC2 calculations in Fig. 10. For CorNFLEx, the time plotted includes the generation of the CIS(D′)-NTOs and the solution of the CC2 equations in the restricted XOS, while only the time for the solution of the CC2 equations is considered for the full calculation. Figure 10 shows that the CorNFLEx calculations (with all three thresholds) are systematically faster than the conventional CC2 calculations, and the speed-up grows rapidly as a function of the molecular cluster size. For example, for the cluster with 63 water molecules, the CorNFLEx calculation with the standard threshold is 111 times faster than the conventional CC2 calculation. The largest presented CorNFLEx calculations correspond to a molecular cluster containing 4836 basis functions, which is out of reach using our conventional CC2 implementation. It is also notable that the CorNFLEx calculation constitutes only a small fraction of the CIS time for the larger clusters.
FIG. 10.
Time spent in the calculation of the lowest excitation energy of a series of formamide-water clusters of increasing size using the aug-cc-pVDZ′ basis set. CIS: time spent in the HF ground state and CIS excitation energy calculations (prior to the CorNFLEx or full CC2 calculation). Loose/standard/tight: time spent in the CorNFLEx algorithm (generation of the CIS(D′)-NTOs and solution of the CC2 equations in the XOS). Full: solution of the CC2 equations in the full canonical basis. All calculations were performed on a single Lenovo nx360 M5 node with 28 cores @ 2.4 GHz and 256 GB memory.
V. CONCLUSION
In this work, we have introduced a new method for the calculation of CC excitation energies on large molecules denoted CorNFLEx. It relies on the generalization of the concept of NTOs to include correlation effects. The resulting CIS(D′)-NTOs are obtained based on an approximation to the CIS(D) model, and their generation formally scales cubically with the system size. Once the CIS(D′)-NTOs have been generated, a reduced orbital space can be determined by discarding a subset of occupied and virtual CIS(D′)-NTOs with low eigenvalues, and a conventional CC excitation energy calculation can then be performed in that reduced space. We have defined the reduced orbital space in terms of the loose, standard, and tight thresholds, which ultimately define the precision of a CorNFLEx calculation compared to a conventional CC2 calculation.
The CorNFLEx algorithm has been tested for the calculation of CC2 excitation energies on a set of 50 singlet electronic transitions resulting in mean absolute errors of 0.11 eV, 0.05 eV, and 0.01 eV (triple- basis) with the loose, standard, and tight thresholds, respectively. Even though some of the considered molecules were of limited size and many of the transitions were nonlocal, significant computational savings were systematically obtained. We have also applied CorNFLEx to a series of solvated formamide clusters of increasing size (up to 4836 basis functions). The results indicate that our new scheme allows CC2 excitation energies to be determined at the cost of a CIS calculation and thus further extends the application range of the CC2 model.
The use of CIS(D′)-NTOs implies that only electronic transitions that are described at the CIS level of theory can be addressed (single-replacement dominated transitions). However, these include most transitions of interest in typical organic and biological molecules. We also note that the presented developments are not specific to the CC2 model as such, and more accurate CC models might also benefit from using the CorNFLEx scheme. Finally, we note that while our previously proposed LoFEx scheme only allows for computational reductions when the transitions of interest are local, the CorNFLEx procedure yields computational savings for both localized and delocalized transitions.
SUPPLEMENTARY MATERIAL
See supplementary material for the excitation energies of the test set and formamide clusters, the NAF results, and the Cartesian coordinates of dodecylbenzene and solvated formamide clusters.
ACKNOWLEDGMENTS
The research leading to these results has received funding from the European Research Council under the European Unions Seventh Framework Programme (No. FP/2007-2013)/ERC Grant Agreement No. 291371. The numerical results presented in this work were performed at the Centre for Scientific Computing, Aarhus (http://phys.au.dk/forskning/cscaa/).
APPENDIX: ALGORITHM FOR GENERATING CIS(D′) DENSITY MATRICES
In this appendix, we present an algorithm for calculating the CIS(D′) density matrices in Eqs. (31). First, we note from Eq. (22) that the doubles excitation vectors occurring in Eq. (31) are given by
| (A1a) |
| (A1b) |
where the two-electron integrals can be written as
| (A2a) |
| (A2b) |
The lowercase indices refer to MOs in the full canonical basis, the primed capital indices denote the reduced CIS-NTO/local basis (OCD and VCD), and the barred indices are transformed with the matrices in Eqs. (20), e.g.,
| (A3) |
As mentioned in Sec. III C, we employ the RI approximation to reduce the cost of the generation of the four-center integrals. For example, the integral in Eq. (A3) may be written as
| (A4) |
We note that NAFs are not used in the generation of the CIS(D′)-NTOs, and the set of auxiliary basis functions is therefore not reduced.
Using Eqs. (A2) and (A4), the doubles excitation vectors in Eq. (A1) may be written as
| (A5a) |
| (A5b) |
where the action of the permutation operator is defined in Eq. (16). From Eq. (A5), we see that the following integrals are required to evaluate the doubles contributions to the hole density matrix in Eq. (31a):
-
•
, , and ,while the particle density matrix in Eq. (31b) can be determined from the following integrals:
-
•
, , and .
We recall that the primed indices denote reduced sets of occupied and virtual orbitals of dimensions and , respectively. The size-intensivity of excitation energies implies that and are independent of the system size for a given type of electronic transition. This will be assumed in the following.
In our current implementation, we first calculate the six integrals listed above and store them in memory. The construction of the integrals is detailed in Table IV. The first step is the construction of the integrals, which formally scales as where and denote the number of atomic and auxiliary basis functions, respectively. However, this scaling is effectively only quadratic with the system size if efficient integral screening techniques are employed. In step 2, one of the AO indices is transformed to a reduced MO index. These steps scale as with pre-factors or . In steps 3 and 4, the second AO index is transformed to an occupied and a virtual index, respectively, leading to formal scalings of and . Finally, in steps 5 and 6, the auxiliary index is transformed with the matrix to provide the desired three-center integrals listed above. These last steps scale as or depending on the type of integrals. In summary, since the reduced dimensions or are independent of the system size for a given type of electronic transition, all steps involved in the generation of the integrals in Table IV scale cubically with the system size.
TABLE IV.
Generation of two-electron RI integrals required for constructing CIS(D′) hole and particle density matrices. Batching of integrals and reordering of tensors have been omitted for clarity.
| Step | Operation | Prefactor | Scaling |
|---|---|---|---|
| 1 | Calculate integrals | ||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
Once the integrals have been generated from Table IV, the doubles excitation vectors are calculated according to Eq. (A5). It is seen that the determinations of and scale as and with pre-factors and , respectively. Finally, the density matrices are evaluated according to Eq. (31) where the evaluation of and scales as O3 and with pre-factors and , respectively. In order to reduce the memory requirements, one may calculate the doubles excitation vectors in batches and contract them on the fly. Specifically, we batch over the k-index in Eq. (31a) and the c-index in Eq. (31b).
All in all, we conclude that the generation of the hole and particle density matrices scales cubically with the size of the molecular system for a given type of electronic transition. The pre-factor depends on the dimensions of the OCD and VCD ( and ), which depend on the type of electronic transition under consideration.
REFERENCES
- 1.Čížek J., J. Chem. Phys. 45, 4256 (1966). 10.1063/1.1727484 [DOI] [Google Scholar]
- 2.Shavitt I. and Bartlett R. J., Many-Body Methods in Chemistry and Physics: Many-Body Perturbation Theory and Coupled-Cluster Theory (Cambridge University Press, Cambridge, UK, 2009). [Google Scholar]
- 3.Monkhorst H. J., Int. J. Quantum Chem. 12, 421 (1977). 10.1002/qua.560120850 [DOI] [Google Scholar]
- 4.Dalgaard E. and Monkhorst H. J., Phys. Rev. A 28, 1217 (1983). 10.1103/physreva.28.1217 [DOI] [Google Scholar]
- 5.Olsen J. and Jørgensen P., J. Chem. Phys. 82, 3235 (1985). 10.1063/1.448223 [DOI] [Google Scholar]
- 6.Koch H. and Jørgensen P., J. Chem. Phys. 93, 3333 (1990). 10.1063/1.458814 [DOI] [Google Scholar]
- 7.Kondo A. E., Piecuch P., and Paldus J., J. Chem. Phys. 104, 8566 (1996). 10.1063/1.471546 [DOI] [Google Scholar]
- 8.Emrich K., Nucl. Phys. A 351, 397 (1981). 10.1016/0375-9474(81)90180-9 [DOI] [Google Scholar]
- 9.Sekino H. and Bartlett R. J., Int. J. Quantum Chem. 26, 255 (1984). 10.1002/qua.560260826 [DOI] [Google Scholar]
- 10.Stanton J. F. and Bartlett R. J., J. Chem. Phys. 98, 7029 (1993). 10.1063/1.464746 [DOI] [Google Scholar]
- 11.Krylov A. I., Annu. Rev. Phys. Chem. 59, 433 (2008). 10.1146/annurev.physchem.59.032607.093602 [DOI] [PubMed] [Google Scholar]
- 12.González L., Escudero D., and Serrano-Andrés L., ChemPhysChem 13, 28 (2012). 10.1002/cphc.201100200 [DOI] [PubMed] [Google Scholar]
- 13.Cohen A. J., Mori-Sanchez P., and Yang W., Science 321, 792 (2008). 10.1126/science.1158722 [DOI] [PubMed] [Google Scholar]
- 14.Dreuw A. and Head-Gordon M., J. Am. Chem. Soc. 126, 4007 (2004). 10.1021/ja039556n [DOI] [PubMed] [Google Scholar]
- 15.Nesbet R. K., Adv. Chem. Phys. IX, 321 (1965). 10.1002/9780470143551.ch4 [DOI] [Google Scholar]
- 16.Sæbø S. and Pulay P., Annu. Rev. Phys. Chem. 44, 213 (1993). 10.1146/annurev.pc.44.100193.001241 [DOI] [Google Scholar]
- 17.Riplinger C., Pinski P., Becker U., Valeev E., and Neese F., J. Chem. Phys. 144, 024109 (2016). 10.1063/1.4939030 [DOI] [PubMed] [Google Scholar]
- 18.Werner H.-J., Knizia G., Krause C., Schwilk M., and Dornbach M., J. Chem. Theory Comput. 11, 484 (2015). 10.1021/ct500725e [DOI] [PubMed] [Google Scholar]
- 19.Rolik Z., Szegedy L., Ladjánszki I., Ladóczki B., and Kállay M., J. Chem. Phys. 139, 094105 (2013). 10.1063/1.4819401 [DOI] [PubMed] [Google Scholar]
- 20.Nagy P. R., Samu G., and Kállay M., J. Chem. Theory Comput. 12, 4897 (2016). 10.1021/acs.jctc.6b00732 [DOI] [PubMed] [Google Scholar]
- 21.Li W., Ni Z., and Li S., Mol. Phys. 114, 1447 (2016). 10.1080/00268976.2016.1139755 [DOI] [Google Scholar]
- 22.Kjærgaard T., Baudin P., Bykov D., Eriksen J. J., Ettenhuber P., Kristensen K., Larkin J., Liakh D., Pawłowski F., Vose A., Wang Y. M., and Jørgensen P., Comput. Phys. Commun. 212, 152 (2017). 10.1016/j.cpc.2016.11.002 [DOI] [Google Scholar]
- 23.Pipek J. and Mezey P. G., J. Chem. Phys. 90, 4916 (1989). 10.1063/1.456588 [DOI] [Google Scholar]
- 24.Boys S. F., Rev. Mod. Phys. 32, 296 (1960). 10.1103/revmodphys.32.296 [DOI] [Google Scholar]
- 25.Edmiston C. and Ruedenberg K., Rev. Mod. Phys. 35, 457 (1963). 10.1103/revmodphys.35.457 [DOI] [Google Scholar]
- 26.Jansík B., Høst S., Kristensen K., and Jørgensen P., J. Chem. Phys. 134, 194104 (2011). 10.1063/1.3590361 [DOI] [PubMed] [Google Scholar]
- 27.Høyvik I.-M., Jansík B., and Jørgensen P., J. Chem. Phys. 137, 224114 (2012). 10.1063/1.4769866 [DOI] [PubMed] [Google Scholar]
- 28.Høyvik I.-M. and Jørgensen P., Chem. Rev. 116, 3306 (2016). 10.1021/acs.chemrev.5b00492 [DOI] [PubMed] [Google Scholar]
- 29.Pulay P., Chem. Phys. Lett. 100, 151 (1983). 10.1016/0009-2614(83)80703-9 [DOI] [Google Scholar]
- 30.Yang J., Kurashige Y., Manby F. R., and Chan G. K.-L., J. Chem. Phys. 134, 044123 (2011). 10.1063/1.3528935 [DOI] [PubMed] [Google Scholar]
- 31.Löwdin P.-O., Phys. Rev. 97, 1474 (1955). 10.1103/physrev.97.1474 [DOI] [Google Scholar]
- 32.Edmiston C., J. Chem. Phys. 45, 1833 (1966). 10.1063/1.1727841 [DOI] [Google Scholar]
- 33.Neese F., Wennmohs F., and Hansen A., J. Chem. Phys. 130, 114108 (2009). 10.1063/1.3086717 [DOI] [PubMed] [Google Scholar]
- 34.Crawford T. D. and King R. A., Chem. Phys. Lett. 366, 611 (2002). 10.1016/s0009-2614(02)01639-1 [DOI] [Google Scholar]
- 35.Korona T. and Werner H.-J., J. Chem. Phys. 118, 3006 (2003). 10.1063/1.1537718 [DOI] [Google Scholar]
- 36.Kats D., Korona T., and Schütz M., J. Chem. Phys. 125, 104106 (2006). 10.1063/1.2339021 [DOI] [PubMed] [Google Scholar]
- 37.Kats D., Korona T., and Schütz M., J. Chem. Phys. 127, 064107 (2007). 10.1063/1.2755778 [DOI] [PubMed] [Google Scholar]
- 38.Kats D. and Schütz M., J. Chem. Phys. 131, 124117 (2009). 10.1063/1.3237134 [DOI] [PubMed] [Google Scholar]
- 39.Helmich B. and Hättig C., J. Chem. Phys. 139, 084114 (2013). 10.1063/1.4819071 [DOI] [PubMed] [Google Scholar]
- 40.Helmich B. and Hättig C., Comput. Theor. Chem. 1040-1041, 35 (2014). 10.1016/j.comptc.2014.03.004 [DOI] [Google Scholar]
- 41.Crawford T. D., in Recent Progress in Coupled Cluster Methods: Theory and Applications, edited by Cársky P., Paldus J., and Pittner J. (Springer, Netherlands, Dordrecht, 2010), Vol. 53, Chap. 2, pp. 37–55. [Google Scholar]
- 42.Mata R. A. and Stoll H., J. Chem. Phys. 134, 034122 (2011). 10.1063/1.3522881 [DOI] [PubMed] [Google Scholar]
- 43.Dutta A. K., Neese F., and Izsák R., J. Chem. Phys. 145, 034102 (2016). 10.1063/1.4958734 [DOI] [PubMed] [Google Scholar]
- 44.Myhre R. H., Sánchez de Merás A. M. J., and Koch H., Mol. Phys. 111, 1109 (2013). 10.1080/00268976.2013.798435 [DOI] [Google Scholar]
- 45.Myhre R. H., Sánchez de Merás A. M. J., and Koch H., J. Chem. Phys. 141, 224105 (2014). 10.1063/1.4903195 [DOI] [PubMed] [Google Scholar]
- 46.Myhre R. H. and Koch H., J. Chem. Phys. 145, 044111 (2016). 10.1063/1.4959373 [DOI] [PubMed] [Google Scholar]
- 47.Caricato M., Vreven T., Trucks G. W., and Frisch M. J., J. Chem. Phys. 133, 054104 (2010). 10.1063/1.3474570 [DOI] [PubMed] [Google Scholar]
- 48.Caricato M., Vreven T., Trucks G. W., and Frisch M. J., J. Chem. Theory Comput. 7, 180 (2011). 10.1021/ct1006289 [DOI] [PubMed] [Google Scholar]
- 49.Baudin P. and Kristensen K., J. Chem. Phys. 144, 224106 (2016). 10.1063/1.4953360 [DOI] [PubMed] [Google Scholar]
- 50.Send R., Kaila V. R. I., and Sundholm D., J. Chem. Phys. 134, 214114 (2011). 10.1063/1.3596729 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kumar A. and Crawford T. D., J. Phys. Chem. A 121, 708 (2017). 10.1021/acs.jpca.6b11410 [DOI] [PubMed] [Google Scholar]
- 52.Head-Gordon M., Rico R. J., Oumi M., and Lee T. J., Chem. Phys. Lett. 219, 21 (1994). 10.1016/0009-2614(94)00070-0 [DOI] [Google Scholar]
- 53.Luzanov A. V., Sukhorukov A. A., and Umanskii V. E., Theor. Exp. Chem. 10, 354 (1976). 10.1007/bf00526670 [DOI] [Google Scholar]
- 54.Martin R. L., J. Chem. Phys. 118, 4775 (2003). 10.1063/1.1558471 [DOI] [Google Scholar]
- 55.Foresman J. B., Head-Gordon M., Pople J. A., and Frisch M. J., J. Phys. Chem. 96, 135 (1992). 10.1021/j100180a030 [DOI] [Google Scholar]
- 56.Christiansen O., Koch H., and Jørgensen P., Chem. Phys. Lett. 243, 409 (1995). 10.1016/0009-2614(95)00841-q [DOI] [Google Scholar]
- 57.Høyvik I.-M., Myhre R. H., and Koch H., J. Chem. Phys. 146, 144109 (2017). 10.1063/1.4979908 [DOI] [PubMed] [Google Scholar]
- 58.Hättig C. and Weigend F., J. Chem. Phys. 113, 5154 (2000). 10.1063/1.1290013 [DOI] [Google Scholar]
- 59.Pettersen E. F., Goddard T. D., Huang C. C., Couch G. S., Greenblatt D. M., Meng E. C., and Ferrin T. E., J. Comput. Phys. 25, 1605 (2004). 10.1002/jcc.20084 [DOI] [PubMed] [Google Scholar]
- 60.In Ref. 49, we used TDHF-NTOs instead of CIS-NTOs, but this difference has a very minor effect on the presented results.
- 61.Hald K., Jørgensen P., Olsen J., and Jaszuński M., J. Chem. Phys. 115, 671 (2001). 10.1063/1.1379332 [DOI] [Google Scholar]
- 62.Butscher W. and Kammer W. E., J. Comput. Phys. 20, 313 (1976). 10.1016/0021-9991(76)90084-x [DOI] [Google Scholar]
- 63.Davidson E. R., J. Comput. Phys. 17, 87 (1975). 10.1016/0021-9991(75)90065-0 [DOI] [Google Scholar]
- 64.Davidson E. R., Comput. Phys. Commun. 53, 49 (1989). 10.1016/0010-4655(89)90147-1 [DOI] [Google Scholar]
- 65.Murray C. W., Racine S. C., and Davidson E. R., J. Comput. Phys. 103, 382 (1992). 10.1016/0021-9991(92)90409-r [DOI] [Google Scholar]
- 66.Ettenhuber P., Baudin P., Kjærgaard T., Jørgensen P., and Kristensen K., J. Chem. Phys. 144, 164116 (2016). 10.1063/1.4947019 [DOI] [PubMed] [Google Scholar]
- 67.Baudin P., Ettenhuber P., Reine S., Kristensen K., and Kjærgaard T., J. Chem. Phys. 144, 054102 (2016). 10.1063/1.4940732 [DOI] [PubMed] [Google Scholar]
- 68.Kállay M., J. Chem. Phys. 141, 244113 (2014). 10.1063/1.4905005 [DOI] [PubMed] [Google Scholar]
- 69.Jacquemin D., Duchemin I., and Blase X., J. Chem. Theory Comput. 11, 5340 (2015). 10.1021/acs.jctc.5b00619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Neese F., Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2, 73 (2012). 10.1002/wcms.81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.See http://daltonprogram.org for LSDalton, a linear-scaling molecular electronic structure program, Release Dalton 2016 (2015).
- 72.Aidas K., Angeli C., Bak K. L., Bakken V., Bast R., Boman L., Christiansen O., Cimiraglia R., Coriani S., Dahle P., Dalskov E. K., Ekström U., Enevoldsen T., Eriksen J. J., Ettenhuber P., Fernández B., Ferrighi L., Fliegl H., Frediani L., Hald K., Halkier A., Hättig C., Heiberg H., Helgaker T., Hennum A. C., Hettema H., Hjertenaes E., Høst S., Høyvik I.-M., Iozzi M. F., Jansík B., Jensen H. J. A., Jonsson D., Jørgensen P., Kauczor J., Kirpekar S., Kjærgaard T., Klopper W., Knecht S., Kobayashi R., Koch H., Kongsted J., Krapp A., Kristensen K., Ligabue A., Lutnaes O. B., Melo J. I., Mikkelsen K. V., Myhre R. H., Neiss C., Nielsen C. B., Norman P., Olsen J., Olsen J. M. H., Osted A., Packer M. J., Pawłowski F., Pedersen T. B., Provasi P. F., Reine S., Rinkevicius Z., Ruden T. A., Ruud K., Rybkin V. V., Sałek P., Samson C. C. M., Sánchez de Merás A. M. J., Saue T., Sauer S. P. A., Schimmelpfennig B., Sneskov K., Steindal A. H., Sylvester-Hvid K. O., Taylor P. R., Teale A. M., Tellgren E. I., Tew D. P., Thorvaldsen A. J., Thøgersen L., Vahtras O., Watson M. A., Wilson D. J. D., Ziółkowski M., and Ågren H., Wiley Interdiscip. Rev.: Comput. Mol. Sci. 4, 269 (2014). 10.1002/wcms.1172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.T. Dunning, Jr., J. Chem. Phys. 90, 1007 (1989). 10.1063/1.456153 [DOI] [Google Scholar]
- 74.Kendall R., T. Dunning, Jr., and Harrison R. J., J. Chem. Phys. 96, 6769 (1992). 10.1063/1.462569 [DOI] [Google Scholar]
- 75.Weigend F., Köhn A., and Hättig C., J. Chem. Phys. 116, 3175 (2002). 10.1063/1.1445115 [DOI] [Google Scholar]
- 76.Sneskov K., Schwabe T., Kongsted J., and Christiansen O., J. Chem. Phys. 134, 104108 (2011). 10.1063/1.3560034 [DOI] [PubMed] [Google Scholar]
- 77.Koch H., Christiansen O., Jørgensen P., and Olsen J., Chem. Phys. Lett. 244, 75 (1995). 10.1016/0009-2614(95)00914-p [DOI] [Google Scholar]
- 78.Silva-Junior M. R., Sauer S. P. A., Schreiber M., and Thiel W., Mol. Phys. 108, 453 (2010). 10.1080/00268970903549047 [DOI] [Google Scholar]
- 79.Send R., Kaila V. R. I., and Sundholm D., J. Chem. Theory Comput. 7, 2473 (2011). 10.1021/ct200215d [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See supplementary material for the excitation energies of the test set and formamide clusters, the NAF results, and the Cartesian coordinates of dodecylbenzene and solvated formamide clusters.