Assessing Quantile Prediction With Censored Quantile Regression Models

Summary

An important goal of censored quantile regression is to provide reliable predictions of survival quantiles, which are often reported in practice to offer robust and comprehensive biomedical summaries. However, formal methods for evaluating and comparing working quantile regression models in terms of their performance in predicting survival quantiles have been lacking, especially when the working models are subject to model mis-specification. In this paper, we proposes a sensible and rigorous framework to fill in this gap. We introduce and justify a predictive performance measure defined based on the check loss function. We derive estimators of the proposed predictive performance measure and study their distributional properties and the corresponding inference procedures. More importantly, we develop model comparison procedures that enable thorough evaluations of model predictive performance among nested or non-nested models. Our proposals properly accommodate random censoring to the survival outcome and the realistic complication of model mis-specification, and thus are generally applicable. Extensive simulations and a real data example demonstrate satisfactory performances of the proposed methods in real life settings.

1. INTRODUCTION

Quantile regression (Koenker and Bassett, 1978) has emerged as a useful approach to analyzing survival data. It permits comprehensive explorations of covariate effects across different segments of an event time distribution. Moreover, it serves as a major tool for predicting survival quantiles. Quantiles of a survival time have been frequently reported in biomedical studies; they have many appealing features including straightforward interpretations and invariance to monotone transformations. Moreover, while the mean of a survival time is often not identifiable when censoring presents, the quantiles of a survival time can still be estimated at a range of quantile levels. Accurate predictions of survival quantiles can provide valuable biomedical insights, and constitute a fundamental goal of applying quantile regression to survival data.

Most of research efforts on quantile regression with survival data have been oriented to developing estimation and inference procedures for models assumed to perfectly conform to the underlying data mechanism (Ying et al. 1995; Portnoy 2003; Zhou 2006; Peng and Huang 2008; Wang and Wang 2009; Huang 2010; among others). However, very limited attention was paid to the evaluation of quantile regression models as well as the comparison among a set of candidate models.

Existing methods for assessing quantile regression models are generally focused on models’ goodness-of-fit or lack-of-fit. For example, Koenker and Machado (1999) proposed a goodness-of-fit criterion based on the check loss function ρ_τ (u) = u{τ − I(u ≤ 0)}, which is analogous to the R² statistic in classical least squares regression. He and Zhu (2003) proposed an omnibus lack-of-fit test for linear or nonlinear quantile regression models. Wang (2008) studied a nonparametric test for checking the lack-of-fit of censored quantile regression. All these methods assess models based on their fit to existing data.

The perspective we take in this paper is to evaluate or compare quantile regression models based on their capacity in predicting quantiles of future outcomes. Further, we do not assume that we know the form of the true model that explains the underlying relationship between covariates and response. This means, we view any adopted quantile regression model as a working model. Similar model evaluation frameworks have been studied in other settings, where the quantities to predict do not relate to quantiles. For example, Tian et al. (2007) used absolute prediction error to assess the predictive performance of working linear transformation models for an uncensored continuous response. With survival data, Uno et al. (2007) developed a framework for evaluating a model’s predictive performance for t-year survival status. Tian et al. (2014) considered evaluating the prediction performance for the restricted mean event time (RMET), where the RMET can be estimated either semi-parametrically or non-parametrically. Such works shed useful insight for our proposals in this paper, which target the prediction of quantiles.

To assess the prediction of quantiles, an intuitive idea is to evaluate the squared or absolute difference between true and predicted conditional quantiles. However true conditional quantiles are not directly observable. This adds subtlety to the assessment of the predictive performance of quantile regression models. Moreover, to evaluate quantile prediction with survival data, censoring is an important feature that needs to be appropriately handled, like in the model estimation setting. Noh et al. (2013) made a precursor effort for the uncensored setting by studying the properties of Koenker and Machado (1999)’s model adequacy measures in the presence of model mis-specification. Their work provided an approach to comparing two nested linear quantile models regardless of whether the linear specification of the conditional quantile functions is correct or not. It is tempting to develop a formal framework for assessing quantile prediction that is suitable for censored responses and allows for more general types of quantile predictions and model specification.

In this paper, we fill in this gap by developing model evaluation and comparison procedures regarding the predictive performances of censored quantile regression models. We only consider models with a finite number of covariates, which can be models obtained after an appropriate variable selection procedure is applied. The thrust of this work is to adapt and generalize the available model evaluation/validation framework to censored quantile regression, which is a major tool for predicting survival quantiles in practice. To this end, the foremost step is to construct and justify a sensible predictive performance measure. Given the flexibility of quantile regression in modeling a spectrum of quantiles simultaneously, we will also investigate the proposed predictive performance measure as a function of quantile index. Our methods provide valid statistical evidences to compare the predictive capacity of working censored quantile regression models through an easily implementable procedure.

In Section 2, we outline the proposed framework for evaluating a quantile regression model regarding its performance in predicting quantiles. In particular, we introduce predictive performance measures and illustrate their interpretations. In Section 3, we propose the estimation and inference procedures for our predictive performance measures, which appropriately account for censoring without assuming a correct model specification. In Section 4, we focus on model comparisons based on the predictive performance measures presented in Section 2. Our proposals are not limited to comparing nested models and can also handle comparisons among non-nested models. Numerical studies are presented in Sections 5–6.

2. THE PROPOSED FRAMEWORK

2.1 Expected check loss for quantifying the prediction loss

To illustrate our methods, we first consider assessing quantile prediction for uncensored data. Let T be a continuous outcome, and Z̄ ≡ (1, Z₁, …, Z_p) be a 1 × (p + 1) covariate vector that includes all covariates collected from a subject, where p is a finite integer. To develop a predictor for Q_T (τ|Z̄) = inf{t : Pr(T ≤ t|Z̄) ≥ τ}, τ ∈ (0, 1), suppose that one applies a working model, such as a quantile regression model, to a dataset 𝒟_m that includes m i.i.d. representative observations of (T, Z̄) from the study population of interest. Let Z denote the vector of covariates in the working model, which can be a subset of Z̄, or Z̄ itself. After one fits a working model to 𝒟_m, the estimated model parameters can be used to construct a quantile predictor, denoted by ξ̂_τ(Z). It maps a covariate vector Z to a predicted τ_th quantile. Note that ξ̂_τ(Z) is fixed given 𝒟_m, Z and the working model.

To ascertain the performance of ξ̂_τ(Z), we consider the check loss function ρ_τ{T⁰ − ξ̂_τ(Z⁰)}. It is important to note that here T⁰ and Z⁰ denote T and Z of a new subject from the same study population and thus are independent of data 𝒟_m where ξ̂_τ(·) is derived. This represents a crucial distinction between using the check function as a loss function for evaluating model predictive performance versus using the check function as a model goodness-of-fit criterion.

The expected check loss, Eρ_τ{T⁰ − ξ̂_τ(Z⁰)|𝒟_m}, can be justified as a sensible measure for assessing the discrepancy between predicted quantiles and true quantiles. To see this, let ${\xi }_{\tau }^0\equiv Q_{T^0}(\tau |{\overline{\mathit{Z}}}^0)$ denote the true conditional quantile of T⁰ of the new subject. Following the arguments in Koenker (2005) (Section 2.9) and Angrist et al. (2006) and temporarily suppressing ξ̂_τ(Z⁰) to ξ̂_τ, we can show that

$$E\{{\rho }_{\tau }(T^0-{\hat{\xi }}_{\tau })-{\rho }_{\tau }(T^0-{\xi }_{\tau }^0)|{\overline{\mathit{Z}}}^0,{𝒟}_m\}={\int }_0^{{\hat{\xi }}_{\tau }-{\xi }_{\tau }^0}\{F({\xi }_{\tau }^0+s|{\overline{\mathit{Z}}}^0)-\tau \}ds,$$ (1)

where F(·|Z̄⁰) is the conditional distribution function of T⁰ given Z̄⁰. Let $d_{{\overline{\mathit{Z}}}^0}({\xi }_{\tau })={\int }_0^{{\xi }_{\tau }-{\xi }_{\tau }^0}\{F({\xi }_{\tau }^0+s|{\overline{\mathit{Z}}}^0)-\tau \}ds$, which is always non-negative. Let f(·|Z̄⁰) be the conditional density function of T⁰ given Z̄⁰. When f(·|Z̄⁰) is bounded, $d_{{\overline{\mathit{Z}}}^0}({\xi }_{\tau })=\frac{1}{2}f({\xi }_{\tau }^0|{\overline{\mathit{Z}}}^0){({\xi }_{\tau }-{\xi }_{\tau }^0)}^2+o\{{({\xi }_{\tau }-{\xi }_{\tau }^0)}^2\}$. Let E_Z̄⁰ denote expectation taken over Z̄⁰, we see that

$$E_{{\overline{\mathit{Z}}}^0}\{{\rho }_{\tau }(T^0-{\hat{\xi }}_{\tau })-{\rho }_{\tau }(T^0-{\xi }_{\tau }^0)|{𝒟}_m\}=E_{{\overline{\mathit{Z}}}^0}\{d_{{\overline{\mathit{Z}}}^0}({\hat{\xi }}_{\tau })|{𝒟}_m\},$$

and approximates $E_{{\overline{\mathit{Z}}}^0}\{\frac{1}{2}f({\xi }_{\tau }^0|{\overline{\mathit{Z}}}^0){({\hat{\xi }}_{\tau }-{\xi }_{\tau }^0)}^2|{𝒟}_m\}$, which may be viewed as a weighted squared difference between the predicted quantile ξ̂_τ and the true quantile ${\xi }_{\tau }^0$ with weight $\frac{1}{2}f({\xi }_{\tau }^0|{\overline{\mathit{Z}}}^0)$. Note that the true quantile ${\xi }_{\tau }^0$ and so $E\{{\rho }_{\tau }(T^0-{\xi }_{\tau }^0)\}$ are generally unknown in practice but are fixed. Hence assessing E{ρ_τ (T⁰ − ξ̂_τ)|𝒟_m} allows us to evaluate how well ξ̂_τ predicts ${\xi }_{\tau }^0$ relatively to predictors from other models.

The ultimate goal here is to assess the capacity of a working model in predicting the true quantiles. To this end, we propose to take a further step by considering lim_m→∞ Eρ_τ{T⁰ − ξ̂_τ(Z⁰)|𝒟_m}. For a working model to serve as a reliable prediction tool, it is desirable that the estimated parameters in the model converge in probability to deterministic values when m increases, even under potential model mis-specification. As a result, the predictor ξ̂_τ(·) will also converge in probability to a deterministic function ξ̃(·) uniformly in Z⁰, and thus lim_m→∞ Eρ_τ{T⁰ − ξ̂_τ(Z⁰)|𝒟_m} = Eρ_τ{T⁰ − ξ̃_τ(Z⁰)}. This quantity essentially captures the predictive capacity of a working model at the τ_th quantile.

2.2 Quantile prediction loss with censored outcomes

We now consider right-censored survival data. Let T represent the log survival time and C be the log censoring time. In the presence of censoring, the identifiability of Eρ_τ{T⁰ − ξ_τ (Z⁰)} is often of concern. This is particularly true when the upper bound of the censoring support is less than that of T’s support in the observed data. It is natural to consider a modified check loss measure for censored data as E [ρ_τ{T^0u − ξ_τ(Z⁰)}], where T^0u = T⁰ Λ u and u is a prespecified deterministic constant that is less than the upper bound of C’s support. For example, in many clinical studies, u can be chosen to be slightly smaller than the planned follow-up time in the study protocol. Similar truncation techniques have been adopted in many other survival settings, for example, studying restricted mean (Zucker, 1998; Chen and Tsiatis, 2001; Goldberg and Kosorok, 2012) and evaluating predictive performance (Tian et al., 2014; Lawless and Yuan, 2010). When τ = 0.5, L(τ, β) = 0.5|T^0u − ξ_τ(Z⁰)| and is quite similar to the absolute prediction loss in Tian et al. (2014) for the RMET.

Write Y = T Λ C and δ = I(T ≤ C). Suppose that ξ̂_τ (·) is an estimated quantile predictor for Q_T(τ|Z̄), derived under a working model using dataset ${𝒟}_m\equiv {(Y_i,{\delta }_i,{\overline{\mathit{Z}}}_i)}_{i=1}^m$. In this work, we consider linear quantile regression models as the working models to obtain ξ̂_τ(·). Standard survival models, including the Cox proportional hazards model, can also serve as reasonable working models. For example, under a Cox proportional hazards model, ξ̂_τ(Z) can be defined as log [inf {t : exp{−Ĥ₀(t) exp(Zb̂)} ≤ 1 − τ}], where Ĥ₀(t) and b̂ are the estimated baseline cumulative hazard function and the Cox regression coefficient respectively. Methods we propose below can be easily adapted to situations with such choices of ξ̂_τ(·).

A common linear quantile regression model takes the form,

$$Q_T(\tau |\overline{\mathit{Z}})=\mathit{Z}{\mathit{\beta }}_0(\tau ),\tau \in [{\tau }_L,{\tau }_U],$$ (2)

where Z is a subvector of Z̄ or Z̄ itself, including 1 as the first component, and 0 < τ_L ≤ τ_U < 1. Using the dataset 𝒟_m well representing the study population of interest, one may implement an existing quantile regression procedure to obtain an estimator of β₀(τ), denoted by β̂(τ). For a new subject from the same population with Z̄ = Z̄⁰, based on model (2), a prediction of the τ_th quantile of the potential log survival time T⁰ is given by ξ̂_τ(Z⁰) = Z⁰β̂(τ). In this work, we shall focus on the log survival times, but the methods can also handle the original survival times with minor modifications.

Under model (2), the quantile prediction loss becomes L(τ, β̂), where

$$L(\tau ,\mathit{\beta })\equiv E[{\rho }_{\tau }\{T^{0u}-{\mathit{Z}}^0\mathit{\beta }(\tau )\}],$$ (3)

is a continuous function of β(τ) at a fixed τ. When sample size increases, a desirable β̂(τ) is expected to converge in probability to a deterministic function of τ, denoted by β̃(τ). Consequently, L(τ, β̂) will also converge in probability to its limiting value L(τ) ≡ L(τ, β̃), which may be more precisely expressed as L(τ, β̃) = E [ρ_τ{T^0u − Z⁰β̃(τ)}]. In addition, we hope that the the selected β̂(τ) can lead to an L(τ, β̃) with meaningful interpretations. That is, the resulting L(τ, β̃) can capture the capacity of the working model in predicting conditional quantiles. As such, L(τ, β̃) provides a sensible approach to evaluating and comparing models. Based on the arguments in Section 2.1 on $E\{{\rho }_{\tau }(T^0-{\hat{\xi }}_{\tau })-{\rho }_{\tau }(T^0-{\xi }_{\tau }^0)\}$, one should interpret L(τ, β̃) in a relative scale, for example, through comparisons between different working models.

In this work we particularly investigate the case with β̂(τ) chosen as Zhou (2006)’s estimator of β₀(τ) for a working model of form (2), which minimizes

$${\hat{L}}_m(\tau ,\mathit{b})=m^{-1}\sum _{i=1}^m\frac{{\mathrm{\Delta }}_i}{Ĝ(Y_i^u|{\mathit{Z}}_i)}{\rho }_{\tau }\{Y_i^u-{\mathit{Z}}_i^T\mathit{b}\},$$ (4)

where $Y_i^u=T_i^u\wedge C_i=Y_i\wedge u,{\mathrm{\Delta }}_i=I(T_i^u\le C_i)=I(Y_i>u)+I(Y_i\le u,{\delta }_i=1)$, and Ĝ(t|Z) is a consistent estimator for Pr(C > t|Z). The validity of (4) requires C⊥T given Z, where ⊥ stands for statistical independence. In addition, it only relies on the conditional quantile modeling at the single quantile level τ, not all quantile levels in [τ_L, τ_U]. When it is reasonable to assume the independence between C and Z, Ĝ(·|Z) can reduce to Ĝ(·), the Kaplan-Meier estimator of the unconditional survival function of C. When C and Z are dependent, one may obtain Ĝ(·|Z) after imposing a proper regression model for C given Z, such as the Cox proportional hazards model. It is worth noting that the validity of the proposed estimation procedure requires a correct specification of the assumed regression model for C. Adopting an inadequate regression model for C may lead to biased Ĝ(·|Z) and consequently biased estimation of L(τ, β̃). For presentation simplicity, we assume that C⊥(T, Z) in the sequel.

As we discuss in Supplemental Material A.1, this β̂(τ) can be shown to converge in probability to a deterministic value β̃(τ) even under model mis-specification, where β̃(τ) coincides with the minimizer of E{ρ_τ(T − Zb)} regarding b. Thus, Zβ̃ (τ) can be viewed as the theoretically best predictor under the working model (2). In the rest of the paper, we focus on the utility of the L(τ, β̃) discussed above as a predictive performance measure.

2.3 Summary measure of prediction performance

Let L(τ) be the shorthand notation for L(τ, β̃), which captures the prediction loss locally at the τ_th quantile. If we have multiple working models, a comparison of the resulting L(τ)’s can reveal the relative prediction loss of these models at the τ_th quantile. One caveat with L(τ) is that its magnitude generally depends on τ, making it difficult to compare L(τ)’s over different τ’s. To address this limitation, we propose coefficient of determinant measure, R¹(τ), for censored data. The measure is analogous to the R² coefficient for least squares regression, and has been studied for uncensored data (Koenker and Machado, 1999; Noh et al., 2013). With censored data, we propose to use

$$R^1(\tau ,\tilde{\mathit{\beta }})=1-\frac{E{\rho }_{\tau }(T^{0u}-{\mathit{Z}}^0\tilde{\mathit{\beta }})}{E{\rho }_{\tau }(T^{0u}-{\zeta }_{\tau })}=\frac{L_0(\tau )-L(\tau ,\tilde{\mathit{\beta }})}{L_0(\tau )},$$ (5)

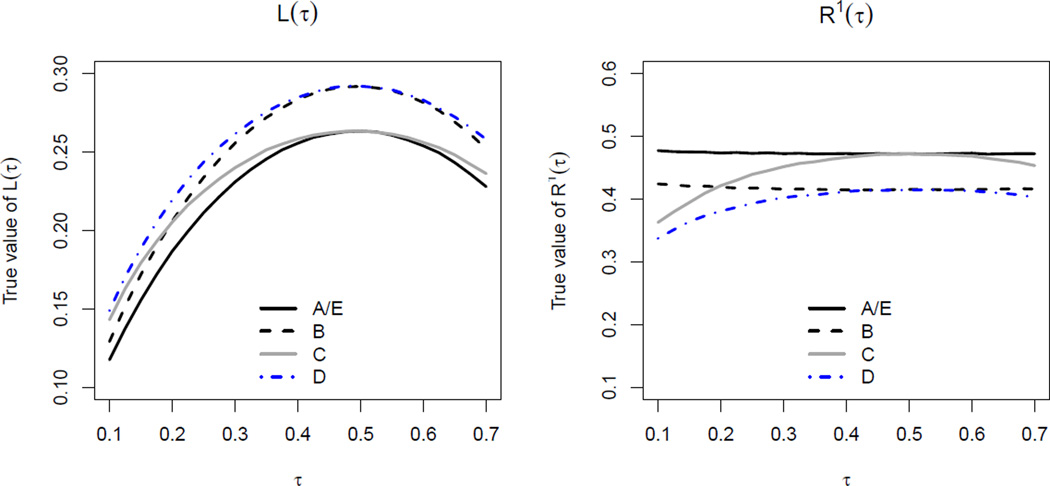
where ζ_τ denotes the true unconditional τ_th quantile of T⁰, and L₀(τ) ≡ Eρ_τ(T^0u − ζ_τ). It is worth noting that this measure is different from existing goodness-of-fit measures, because T⁰ and Z⁰ denote data from a new subject. Unlike L(τ), the scale of R¹(τ) ≡ R¹(τ, β̃) does not vary across τ and R¹(τ) always lies between 0 and 1. An illustrative example of L(τ) and R¹(τ) is provided in Figure 1 of Section 5. Note that R¹(τ) quantifies the extent to which model (2) improves quantile prediction at the τ_th quantile, when compared to a degenerated model with only the intercept term. Therefore, R¹(τ) can serve as a sensible measure of the performance in predicting the τ-th quantile. We also propose a summary measure as $R^1={({\tau }_U-{\tau }_L)}^{-1}{\int }_{{\tau }_L}^{{\tau }_U}{R}^1(\tau )d\tau$, which represents the overall prediction performances of a model across τ ∈ [τ_L, τ_U].

Figure 1.

Values of L(τ) and R¹(τ) under different working models.

3. ESTIMATION AND INFERENCE

3.1 The proposed estimators of L(τ, β̃) and R¹(τ, β̃)

In this section, we study the estimation of L(τ, β̃) and R¹(τ, β̃), which are justified as appropriate predictive performance measures in Section 2. We first consider a plug-in type estimator for L(τ) ≡ L(τ, β̃). Suppose that the observed data consist of n i.i.d. observations ${(Y_i,{\delta }_i,{\overline{\mathit{Z}}}_i)}_{i=1}^n$, which contain the data 𝒟_m used to derive β̂. The plug-in estimator is

$${\hat{L}}_n(\tau ,\hat{\mathit{\beta }})=n^{-1}\sum _{i=1}^m\frac{{\mathrm{\Delta }}_i}{Ĝ(Y_i^u|{\mathit{Z}}_i)}{\rho }_{\tau }\{Y_i^u-{\mathit{Z}}_i\hat{\mathit{\beta }}(\tau )\}.$$ (6)

where β̃(τ) is the estimator in Zhou (2006) using all observed data. The remarks about the censoring mechanism and Ĝ(·) in Section 2.2 also apply to the Ĝ(·) here. In the following, we adopt the Kaplan-Meier estimator Ĝ(·) under the C⊥(T, Z) assumption for the purpose of illustration. The plug-in estimator for R¹(τ) is ${\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})=1-{\hat{L}}_n(\tau ,\hat{\mathit{\beta }})/{\hat{L}}_n(\tau ,{\hat{\zeta }}_{\tau })$, where ζ̂_τ represents Zhou (2006)’s estimator in an intercept-only model.

Assume that (T⁰, Z̄₀) in the definition of L(τ, β̃) comes from the same population. In Supplementary Materials A.1, we use empirical process techniques to show that L̂_n(τ, β̂) and ${\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})$ are uniformly consistent to L(τ) and R¹(τ) respectively. The simpler notation L(τ) and R¹(τ) are adopted for L(τ, β̃) and R¹(τ, β̃) unless confusions occur. The results are formally stated in Theorem 1, where ‖x‖ denotes the Euclidean norm of a vector x.

Theorem 1

Under regularity conditions C1–C4 in Supplementary Materials A, we have ${\text{sup}}_{\tau \in [{\tau }_L,{\tau }_U]}\Vert \hat{\mathit{\beta }}(\tau )-\tilde{\mathit{\beta }}(\tau )\Vert \stackrel{p}{\to }0$, where β̃(τ) is the solution to E[Z′{Pr(T ≤ Zb|Z) − τ}] = 0. Furthermore,

$$\underset{\tau \in [{\tau }_L,{\tau }_U]}{\text{sup}}|{\hat{L}}_n(\tau ,\hat{\mathit{\beta }})-L(\tau )|\stackrel{p}{\to }0;\hspace{1em}\underset{\tau \in [{\tau }_L,{\tau }_U]}{\text{sup}}|{\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})-R^1(\tau )|\stackrel{p}{\to }0.$$ (7)

To estimate L(τ, β̃), the plug-in estimator L̂_n(τ, β̂) uses the entire observed dataset twice; the first use is to use it as 𝒟_m for estimating β̃(τ) via (4) and the second use is for approximating the check loss function in (6). The downward bias caused by using the same data twice can be shown to be of order O_p(n⁻¹), which is not of concern with a reasonably large n such as n = 400. With a small n, a bias correction procedure can be implemented. More details and justifications for the bias correction is provided at the end of Section 4.1.

Alternatively, we consider a cross validation (CV) type estimator, where different subsets of the data are utilized for estimating β̃(τ) and L(τ, β̃). Specifically, one may split the observed data randomly into K disjoint subsets, with approximately equal sample sizes close to n/K. Here, K is a small fixed integer that does not grow with n. In practice, we suggest using K = 10 or K = 5. Let V_i ∈ {1, 2, …, K} denote the subset membership of the ith observation. For each subset k, let β̂_(−k)(τ) represent the estimator of β₀(τ) based on all observations except those in the k_th subset. We define

$${\hat{L}}^k\{\tau ,{\hat{\mathit{\beta }}}_{(-k)}\}=\frac{K}{n}\sum _{i=1}^n\frac{{\mathrm{\Delta }}_{i}I(V_i=k)}{Ĝ(Y_i^u)}{\rho }_{\tau }\{Y_i^u-{\mathit{Z}}_i{\hat{\mathit{\beta }}}_{(-k)}(\tau )\},k=1,2,\dots ,K.$$

This loss function averages across the check loss among subjects in the k^th subset, where the predicted quantile is obtained via β̂_(−k). Finally, the proposed the CV-type estimator of L(τ, β̃) can be calculated as ${\hat{L}}_{CV}(\tau ,\hat{\mathit{\beta }})=K^{-1}{\sum }_{k=1}^K{\hat{L}}^k\{\tau ,{\hat{\mathit{\beta }}}_{(-k)}\}$, and a corresponding estimator for R¹(τ) is ${\hat{R}}_{CV}^1(\tau ,\hat{\mathit{\beta }})=1-{\hat{L}}_{CV}(\tau ,\hat{\mathit{\beta }})/{\hat{L}}_{CV}(\tau ,{\hat{\zeta }}_{\tau })$. Similar to the plug-in estimators, L̂_CV(τ, β̂) and ${\hat{R}}_{CV}^1(\tau ,\hat{\mathit{\beta }})$ provides uniformly consistent estimations for L(τ) and R¹(τ). The proof is provided in Supplementary Material A.3.

3.2 Distributional properties of the proposed estimators

It is also important to examine the distributional properties of the estimators, so as to enable statistical inferences on the predictive capacity measures. We derived the following theorem:

Theorem 2

Under conditions C1–C4 in Supplementary Materials A, we have

$$\sqrt{n}\{{\hat{L}}_n(\tau ,\hat{\mathit{\beta }})-L(\tau )\}=n^{-1/2}\sum _{i=1}^n{\pi }_i(\tau ,\tilde{\mathit{\beta }})+o_p^{\tau }(1),$$ (8)

where $o_p^{\tau }(1)$ stands for a function of τ converging to 0 in probability uniformly in τ ∈ [τ_L, τ_U]. Furthermore, $\sqrt{n}\{{\hat{L}}_n(\tau ,\hat{\mathit{\beta }})-L(\tau )\}$ converges weakly to a zero-mean Gaussian process.

The detailed proof of Theorem 2 and the form of the influence function π_i(τ, β̃) are deferred to Supplementary Materials A.2. We further establish in Supplementary Materials A.3 that the distribution of $\sqrt{n}\{{\hat{L}}_{CV}(\tau ,\hat{\mathit{\beta }})-L(\tau )\}$ is asymptotically equivalent to that of $\sqrt{n}\{{\hat{L}}_n(\tau ,\hat{\mathit{\beta }})-L(\tau )\}$. As a result, $\sqrt{n}\{{\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})-R^1(\tau )\}$ and $\sqrt{n}\{{\hat{R}}_{CV}^1(\tau ,\hat{\mathit{\beta }})-R^1(\tau )\}$ are also asymptotically equivalent and converge weakly to a zero-mean Gaussian process. Their influence functions are provided in Supplementary Materials A.2.

For covariance and interval estimation, we also develop a perturbation resampling scheme similar to those in Jin et al. (2001). We consider a perturbed objective function, defined as

$${\hat{L}}_n^{*}(\tau ,\mathit{b})=n^{-1}\sum _{i=1}^n{\omega }_i\frac{{\mathrm{\Delta }}_i}{G^{*}(Y_i^u)}{\rho }_{\tau }(Y_i^u-{\mathit{Z}}_i\mathit{b})$$

where ${\{{\omega }_i\}}_{i=1}^n$ are i.i.d. unit exponential random variates. Here G*(t) is a perturbed version of the Kaplan-Meier estimator using the same set of weights. That is, G*(t) = 𝒫_s∈[0,t]{1 − dN*(t)/Y*(t)}, where $N^{*}(t)=n^{-1}{\sum }_{i=1}^n{\omega }_{i}I(Y_i\le t,{\delta }_i=1)$ and $Y^{*}(t)=n^{-1}{\sum }_{i=1}^n{\omega }_{i}I(Y_i\ge t)$, and 𝒫 is the product-integral operator. Define β̂*(τ) as the minimizer of ${\hat{L}}_n^{*}(\tau ,\mathit{b})$ with respect to b. In Supplementary Materials A.4, we show that the unconditional distribution of $\sqrt{n}\{{\hat{L}}_n(\tau ,\hat{\mathit{\beta }})-L(\tau )\}$ is asymptotically the same as the conditional distribution of $\sqrt{n}\{{\hat{L}}_n^{*}(\tau ,{\hat{\mathit{\beta }}}^{*})-{\hat{L}}_n(\tau ,\hat{\mathit{\beta }})\}$. In practice, one may generate B perturbed samples of ${\hat{L}}_n^{*}(\tau ,{\hat{\mathit{\beta }}}^{*})$ for a large number B, denoted by ${\{{\hat{L}}_n^{*b}(\tau ,{\hat{\mathit{\beta }}}^{*})\}}_{b=1}^B$. The standard error estimates for the proposed estimators of L(τ) and the confidence intervals for L(τ) can be obtained from the empirical standard deviations and the empirical percentiles of $\sqrt{n}\{{\hat{L}}_n^{*b}(\tau ,{\hat{\mathit{\beta }}}^{*})-{\hat{L}}_n(\tau ,\hat{\mathit{\beta }})\}$.

4. THE PROPOSED MODEL COMPARISON PROCEDURES

In practice, there are often more than one candidate models under consideration. Based on the arguments in Section 2, we can formally compare the predictive performance between two working models by comparing their respective L(τ)’s. Let Z_A and Z_B be two subvectors of Z̄ and both of them include 1 as the first element. The working model (2) with Z = Z_A and the working model (2) with Z = Z_B are referred to as model A and model B, respectively. Their corresponding prediction loss L(τ)’s are denoted by L_A(τ) and L_B(τ). Likewise, in the sequel, subscripts, such as A and B, will be used to differentiate quantities for different working models. From the arguments in Section 2, L_A(τ) − L_B(τ) can be used to capture the relative prediction loss of two working models at the τ_th quantile level. This motivates us to compare the predictive capacity of two candidate models based on their difference in L(τ).

4.1 Model comparisons at a fixed τ

When the interest lies in a single quantile at level τ, we formulate the predictive capacity comparison as a hypothesis testing problem regarding L_A(τ) − L_B(τ), which, by Theorem 1, can be consistently estimated by 𝒯_AB(τ) ≡ L̂_nA(τ, β̂_A) − L̂_nB(τ, β̂_B). However, a notable complication is that the limiting distribution of 𝒯_AB(τ) under the null, H₀ : L_A(τ) = L_B(τ), is different under the nested model scenario and the non-nested model scenario. Thus, the hypothesis testing method needs to be designed differently for these two scenarios.

When the two models are non-nested, in the sense that Z_A contains covariates not contained in Z_B and vice versa, we consider the following two-sided hypothesis testing problem:

$$H_0:L_A(\tau )=L_B(\tau )\text{ vs}.\hspace{1em}{H}_1^{nn}:L_A(\tau )\ne L_B(\tau ),$$ (9)

where H₀ corresponds to the scenario when models A and B have equivalent predictive capacity for the τ_th quantile. Naturally, we adopt 𝒯_AB(τ) as the test statistics. Based on Theorem 1, we have

$${𝒯}_{AB}(\tau )-\{L_A(\tau )-L_B(\tau )\}=n^{-1}\sum _{i=1}^n\{{\pi }_{iA}(\tau ,{\tilde{\mathit{\beta }}}_A)-{\pi }_{iB}(\tau ,{\tilde{\mathit{\beta }}}_B)\}+o_p(n^{-1/2}).$$ (10)

From the definition of π_i․(τ, β̃) in Supplementary Materials A.2., we see that π_iA(τ, β̃_A) − π_iB(τ, β̃_B) is not degenerate provided Z_Aβ̃_A(τ) ≢ Z_Bβ̃_B(τ), which is a reasonable assumption for the non-nested case. When this holds, we can show that 𝒯_AB(τ) is of order O_p(n^−1/2) under H₀, and that $\sqrt{n}{𝒯}_{AB}(\tau )$ converges to a zero-mean Normal distribution. We employ a resampling procedure to approximate the limit distribution of 𝒯_AB(τ) under H₀. Let

$${𝒯}_{AB}^{nn*}(\tau )-\{{\hat{L}}_{nA}^{*}(\tau ,{\hat{\mathit{\beta }}}_A^{*})-{\hat{L}}_{nA}(\tau ,{\hat{\mathit{\beta }}}_A)\}-\{{\hat{L}}_{nB}^{*}(\tau ,{\hat{\mathit{\beta }}}_B^{*})-{\hat{L}}_{nB}(\tau ,{\hat{\mathit{\beta }}}_B)\},$$

where ⁿⁿ stands for non-nested. By the arguments in Supplementary Materials A.4, we see that the conditional distribution of $\sqrt{n}{𝒯}_{AB}^{nn*}$ given the observed data is asymptotically equivalent to the unconditional distribution of $\sqrt{n}{𝒯}_{AB}$ under H₀. Therefore, one may obtain distribution cut-off values for 𝒯_AB(τ) based on its perturbed samples, ${\{|{𝒯}_{AB}^{nn*b}(\tau )|\}}_{b=1}^B$, and reject H₀ when |𝒯_AB(τ)| is greater than the cut-off value.

We next consider the more complicated scenario that involves two nested models. Suppose Z_A is a subvector of Z_B and thus L_B(τ) ≤ L_A(τ). We assume that the elements in Z_B are linearly independent with each other, in the sense that there does not exist a non-zero vector α satisfying Z_Bα ≡ 0. We formulate a one-sided hypothesis test,

$$H_0:L_A(\tau )=L_B(\tau )\text{ vs}.\hspace{1em}{H}_1^n:L_B(\tau )<L_A(\tau ).$$ (11)

Rejecting H₀ would imply a significant improvement by adopting model B (versus model A) in predicting the τth-quantile, which may lead to a decision of adopting model B instead of model A in constructing the quantile predictor. In the nested case, H₀ corresponds to the situation when Z_Aβ̃_A ≡ Z_Bβ̃_B. Note that the asymptotic representation in (10) is not useful, because π_iA(τ, β̃_A) − π_iB(τ, β̃_B) ≡ 0. As a result, 𝒯_AB(τ) is no longer of order O_p(n^−1/2) under H₀ but has a faster convergence rate to 0. The faster convergence to 0 was also noted in Demler et al. (2012) for comparing area under curve between nested models.

To address this difficulty, we develop a different perturbation scheme by extending the method in Chen et al. (2008). Specifically, we propose the following perturbed test statistics,

$${𝒯}_{AB}^{n*}(\tau )=\{{\hat{L}}_{nA}^{*}(\tau ,{\hat{\mathit{\beta }}}_A^{*})-{\hat{L}}_{nA}^{*}(\tau ,{\hat{\mathit{\beta }}}_A)\}-\{{\hat{L}}_{nB}^{*}(\tau ,{\hat{\mathit{\beta }}}_B^{*})-{\hat{L}}_{nA}^{*}(\tau ,{\hat{\mathit{\beta }}}_B)\},$$

where ⁿ stands for nested. Note that ${𝒯}_{AB}^{n*}(\tau )$ differs from ${𝒯}_{AB}^{nn*}(\tau )$ by including ${\hat{L}}_{nA}^{*}(\tau ,{\hat{\mathit{\beta }}}_A)$ and ${\hat{L}}_{nB}^{*}(\tau ,{\hat{\mathit{\beta }}}_B)$ as the second and fourth term, in place of L̂_nA(τ, β̂_nA) and L̂_nB(τ, β̂_nB). This minor modification allows us to achieve a fine enough approximations to 𝒯_AB(τ), which is of order O_p(n⁻¹) under H₀. Specifically, Theorem 3 provides the crucial result for justifying the use of ${𝒯}_{AB}^{n*}(\tau )$. Our proof for this theorem in Supplementary Materials B.1. follows the lines of Rao and Zhao (1992)(see Lemma 2.2) and Chen et al. (2008).

Theorem 3

Define $\mathit{J}(\tau )=\frac{\partial }{\partial b}E\{\mathit{Z}I(T\le \mathit{Z}\prime \mathit{b})\}{|}_{\mathit{b}=\tilde{\mathit{\beta }}(\tau )}$. Under conditions C1–C4,

$$n\{{\hat{L}}_n(\tau ,\hat{\mathit{\beta }})-{\hat{L}}_n(\tau ,\tilde{\mathit{\beta }})\}=-\frac{n}{2}\{\hat{\mathit{\beta }}(\tau )-\tilde{\mathit{\beta }}(\tau )\}\prime \mathit{J}(\tau )\{\hat{\mathit{\beta }}(\tau )-\tilde{\mathit{\beta }}(\tau )\}+o_p(1);$$ (12)

Similarly, for the perturbed counterpart of the loss function, we have

$$n\{{\hat{L}}_n^{*}(\tau ,{\hat{\mathit{\beta }}}^{*})-{\hat{L}}_n^{*}(\tau ,\hat{\mathit{\beta }})\}=-\frac{n}{2}\{{\hat{\mathit{\beta }}}^{*}(\tau )-\hat{\mathit{\beta }}(\tau )\}\prime \mathit{J}(\tau )\{{\hat{\mathit{\beta }}}^{*}(\tau )-\hat{\mathit{\beta }}(\tau )\}+o_p(1).$$ (13)

It is worth noting that the J(τ) matrix equals E[Z^⊗2f{Zβ̃(τ)|Z}]. Due to the unknown conditional density f, it is rather hard to directly estimate matrix J(τ) in practice. Based on Theorem 3, we derived the asymptotic distribution of n𝒯_AB(τ) and the limit conditional distribution of $n{𝒯}_{AB}^{n*}(\tau )$ given the observed data; see Supplementary Materials B.2. Our results justify the use of ${𝒯}_{AB}^{n*}$ for approximating the distribution of ${𝒯}_{AB}^{n*}(\tau )$.

Remark

Theorem 3 also allows us to correct for the small bias in L̂_n(τ, β̂). From (12), we see that the bias in L̂_n(τ, β̃) due to using the entire observed dataset twice is asymptotically $-\frac{1}{2}\{\hat{\mathit{\beta }}(\tau )-\tilde{\mathit{\beta }}(\tau )\}\prime \mathit{J}(\tau )\{\hat{\mathit{\beta }}(\tau )-\tilde{\mathit{\beta }}(\tau )\}$, which is non-positive and of order O_p(n⁻¹). According to (13), we propose to use

$${\hat{L}}_{\mathit{\text{adj}}}(\tau ,\hat{\mathit{\beta }})={\hat{L}}_n(\tau ,\hat{\mathit{\beta }})-B^{-1}\sum _{b=1}^B\{{\hat{L}}_n^{*b}(\tau ,{\hat{\mathit{\beta }}}^{*})-{\hat{L}}_n^{*b}(\tau ,\hat{\mathit{\beta }})\},$$

where B is the total number of perturbations. The adjustment to L̂_n(τ, β̂) is of order O_p(n⁻¹); thus the influence functions for L̂_n(τ, β̂), π_i(τ, β̃), still apply to L̂_adj(τ, β̂). This adjustment can also be implemented in the test statistics 𝒯_AB(τ) when testing non-nested models, but not in the comparison of nested models.

4.2 Model comparisons across a range of τ

In practice, it is often desirable to compare two models by accounting for a range of quantiles, so as to identify an optimal model for predicting a range of quantiles simultaneously. A model comparison procedure that addresses a range of quantiles simultaneously can be achieved through the R¹ measure introduced in Section 2.3. Specifically, we propose to compare two candidate models, namely model A and B, by testing the hypotheses, $H_0^{nn}:R_A^1=R_B^1\text{ vs}.H_1:R_A^1\ne R_B^1$ when model A and model B are non-nested, and the hypothesis $H_0^n:R_A^1=R_B^1\text{ vs}.H_1:R_A^1<R_B^1$ in the nested case where Z_A is a subvector of Z_B.

Next, we notice that $R_A^1-R_B^1=\frac{1}{{\tau }_U-{\tau }_L}{\int }_{{\tau }_L}^{{\tau }_U}\frac{L_B(\tau )-L_A(\tau )}{E{\rho }_{\tau }(T^{0u}-{\zeta }_{\tau })}d\tau$. This motivates us to define

$${ℛ}_{AB}=\frac{1}{{\tau }_U-{\tau }_L}{\int }_{{\tau }_L}^{{\tau }_U}\frac{{\hat{L}}_{nB}(\tau ,{\hat{\mathit{\beta }}}_A)-{\hat{L}}_{nA}(\tau ,{\hat{\mathit{\beta }}}_B)}{{\hat{L}}_n(\tau ,{\hat{\zeta }}_{\tau })}d\tau .$$ (14)

Essentially, ℛ_AB is a weighted average of 𝒯_AB across τ. The distribution of ℛ_AB under H₀ can be approximated through the empirical distribution of ${ℛ}_{AB}^{n*}=-\frac{1}{{\tau }_U-{\tau }_L}{\int }_{{\tau }_L}^{{\tau }_U}\{{𝒯}_{AB}^{n*}/{\hat{L}}_n^{*}(\tau ,{\hat{\zeta }}_{\tau }^{*})\}d\tau$ in the nested case, and through ${ℛ}_{AB}^{nn*}=-\frac{1}{{\tau }_U-{\tau }_L}{\int }_{{\tau }_L}^{{\tau }_U}\{{𝒯}_{AB}^{nn*}/{\hat{L}}_n^{*}(\tau ,{\hat{\zeta }}_{\tau }^{*})\}d\tau$ in the non-nested case.

5. SIMULATIONS

5.1 Estimation of the prediction performance measures

Simulations were conducted to assess the finite-sample performances of the proposed methods. The first part of our simulations illustrates the proposed measures, L(τ) and R¹(τ), under various working prediction models, and furthermore examines whether they can be consistently estimated by the proposed estimators. We generated the survival times as

$$T^{*}=\text{exp}\{2\times Z_{10}+I(Z_2=1){\epsilon }_1+I(Z_2=0){\epsilon }_2+Z_3+{\epsilon }_3\},$$

where Z₁₀ follows a truncated normal distribution with mean 0, standard deviation 0.5, and truncation points ±1.5. The variable Z₂ follows a Bernoulli distribution with expectation 0.5, and Z₃ ~ Uniform(−0.5, 0.5). The ε₁, ε₂, and ε₃ are mutually independent and follow Normal(0, 1²), Normal(0, 0.2²) and Normal(0, 0.25²) respectively. Therefore, we have

$$Q_T(\tau |\mathit{Z})=q_{\epsilon 2+\epsilon 3}(\tau )+2\times Z_{10}+\{q_{\epsilon 1+\epsilon 3}(\tau )-q_{\epsilon 2+\epsilon 3}(\tau )\}\times Z_2+Z_3.$$ (15)

The coefficient of Z₂ is a monotone function of τ that crosses 0 at τ = 0.5. The censoring time C* = exp(C), where C = ζ_C × runif(−1.2, 2.5) + (1−ζ_C) × 2.5 and ζ_C ~ Bernoulli(0.8). The censoring rate is 28%, and we set u = 2.49.

Our goal is to assess the predictive capacity of several working models, namely (A) Z₁₀ + Z₂ + Z₃, (B) Z₁ + Z₂ + Z₃, (C) Z₁₀ + Z₃, (D) Z₁ + Z₃, and (E) Z₁₀ + Z₂ + Z₃ + Z₄ + Z₅ + Z₆. Here, each working model is represented by an addition sentence, the terms of which indicate the covariates included in Z. Each model can facilitate a quantile predictor ξ̂_τ (·). The covariate Z₁ = Z₁₀ + ε₄, where ε₄ ~ Uniform(−0.25, 0.25). Thus Z₁ represents a mis-measured version of Z₁₀. Also, Z₄ ~ Uniform(−1, 1), $Z_5=\mathit{\text{sign}}(Z_{10})·\sqrt{|Z_{10}|}$, and Z₆ ~ 2 × Beta(2, 2). Therefore, Model (A) represents the data generation model in (15). Model (B) corresponds to the situation where one covariate in the true model is subject to mis-measurement. In Model (C), one leaves out a covariate that explains the heteroscedasticity of the error terms. Model (D) is another mis-specified model that includes Z₁ instead of Z₁₀ and excludes Z₂. Finally, model (E) includes several redundant covariates. It exemplifies a working prediction model that is over-fitted and has the problem of collinearity.

To visualize the corresponding prediction loss and performance measures L(τ) and R¹(τ) under (A)–(E), we plot their theoretical values, which were obtained via large-sample approximations based on 10, 000 simulated uncensored data points. We observe in Figure 1 that the two measures effectively describe the predictive capacity of the working models. For example, we observe from the left panel of Figure 1 that model (A) and (E) always render the smallest L(τ). Model (B) leads to larger prediction loss, by including a mis-measured covariate Z₁ instead of the true Z₁₀. Model (C) yields the same prediction loss as (A) and (E) when τ = 0.5, for which the conditional quantile does not depend on Z₂. However, the quantile prediction is generally worse at other quantile levels. Model (D) is worse than (B) and (C) by deviating further away from the true model. In addition, we observe from the right panel of Figure 1 that R¹(τ) transforms the prediction loss into a predictive performance measure of unified scales, thereby facilitating comparisons across a range of τ.

We examined whether the proposed methods can provide adequate estimation and inference for the prediction loss/performance measures. For each working model, we conducted 2, 000 simulations under sample sizes n = 200, 400 and 600. We present the simulation results under model (A) and (B) in Table 1 for τ = 0.1, 0.3, 0.5 and 0.6. The results under other working models are similar and thus are not reported. The reported summary statistics include the empirical bias (EB), the empirical standard error (ESE), the average of influence function based standard error (ASE), and empirical coverage probabilities of 95% Wald-type confidence intervals (C95). To build a confidence interval for L(τ), we used a log transformation and the Delta method. The log{− log(x)} transformation was used to build a confidence interval for R¹(τ). The performance of the bias-adjusted estimators in Section 4.1 is also summarized. Table 1 suggests that L(τ) and R¹(τ) are estimated accurately by the proposed plug-in estimators L̂_n(τ,β̂) and ${\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})$. The standard errors are generally small. The coverage rates of the confidence intervals for L(τ) are slightly low when n = 200 but get closer to the nominal level for larger n’s. The bias-adjusted methods show some improvement when n = 200, but the improvement become negligible when n ≥ 400. The performances of the CV-estimators are similar and deferred to Supplementary Materials C, Table C.1.

Table 1.

Simulations: summary statistics for L̂_n(τ, β̂) and ${\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})$ at τ = 0.1, 0.3, 0.5, 0.6 under model A and model B. The expected number of events $E({\sum }_{i=1}^n{\delta }_i)$ equal 144, 288 and 432 when n = 200, 400 and 600 respectively. The results of the bias-adjusted estimators are also included.

n		Model A					Model B
	τ	TRUE	EB ×103	ESE ×103	ASE ×103	C95 (%)	TRUE	EB ×103	ESE ×103	ASE ×103	C95 (%)
						L̂n(τ, β̂)
200	0.1	0.117	−5	11	11	90.4	0.129	−5	11	11	90.6
	0.3	0.231	−6	21	20	92.3	0.255	−7	21	21	92.4
	0.5	0.263	−7	25	24	91.8	0.291	−8	25	24	91.3
	0.6	0.253	−7	25	23	91.0	0.281	−7	25	24	90.6
400	0.1	0.117	−2	8	8	93.2	0.129	−2	8	8	93.2
	0.3	0.231	−2	15	15	93.5	0.255	−3	15	15	93.9
	0.5	0.263	−3	18	17	92.9	0.291	−4	18	17	93.5
	0.6	0.253	−3	18	17	92.6	0.281	−4	18	17	93.0
600	0.1	0.117	−1	7	6	93.7	0.129	−1	7	7	93.9
	0.3	0.231	−1	12	12	94.6	0.255	−2	12	12	94.0
	0.5	0.263	−2	14	14	94.2	0.291	−2	14	14	93.6
	0.6	0.253	−2	14	14	93.6	0.281	−2	14	14	93.2
						${\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})$
200	0.1	0.478	11	52	51	93.3	0.425	11	53	52	93.4
	0.3	0.473	7	48	47	93.9	0.417	8	49	48	94.4
	0.5	0.472	7	51	49	93.2	0.415	8	51	50	93.8
	0.6	0.473	7	53	51	93.1	0.416	8	55	52	93.0
400	0.1	0.478	6	37	36	93.7	0.425	6	37	37	93.8
	0.3	0.473	4	34	33	93.7	0.417	5	34	34	93.8
	0.5	0.472	5	36	35	93.8	0.415	6	36	35	93.8
	0.6	0.473	5	37	36	93.5	0.416	6	38	37	93.6
600	0.1	0.478	5	30	29	94.1	0.425	4	30	30	94.2
	0.3	0.473	3	28	27	94.3	0.417	4	28	28	94.6
	0.5	0.472	3	29	28	94.0	0.415	4	29	29	94.4
	0.6	0.473	4	31	30	93.8	0.416	4	31	30	94.1
						L̂adj(τ, β̂)
200	0.1	0.117	−1	12	11	93.0	0.129	−1	12	11	92.4
	0.3	0.231	−2	21	21	93.9	0.255	−2	22	21	93.5
	0.5	0.263	−2	25	24	93.4	0.291	−2	25	24	93.2
	0.6	0.253	−2	25	23	92.4	0.281	−2	25	24	92.9
400	0.1	0.117	0	8	8	93.3	0.129	0	8	8	93.6
	0.3	0.231	−1	15	15	93.5	0.255	−1	15	15	93.9
	0.5	0.263	−1	18	17	93.1	0.291	−1	18	17	93.5
	0.6	0.253	−1	18	17	92.9	0.281	−1	18	17	93.3
600	0.1	0.117	0	7	6	93.6	0.129	0	7	7	93.9
	0.3	0.231	0	12	12	94.5	0.255	0	12	12	94.1
	0.5	0.263	0	14	14	94.5	0.291	0	15	14	94.2
	0.6	0.253	0	14	14	94.1	0.281	0	15	14	93.9
						${\hat{R}}_{\mathit{\text{adj}}}^1(\tau ,\hat{\mathit{\beta }})$
200	0.1	0.478	2	53	51	93.6	0.425	1	54	52	93.9
	0.3	0.473	0	49	47	93.8	0.417	−1	50	48	93.8
	0.5	0.472	−1	51	49	93.4	0.415	−1	52	50	93.7
	0.6	0.473	−1	54	51	93.2	0.416	−1	54	52	93.3
400	0.1	0.478	0	37	36	94.4	0.425	0	39	37	93.7
	0.3	0.473	0	35	33	94.0	0.417	0	35	34	93.4
	0.5	0.472	0	36	35	94.4	0.415	0	37	35	93.4
	0.6	0.473	0	37	36	94.0	0.416	1	39	37	93.4
600	0.1	0.478	−1	30	29	94.5	0.425	−1	30	30	94.7
	0.3	0.473	−1	28	27	94.8	0.417	−1	28	28	94.0
	0.5	0.472	−1	29	28	94.4	0.415	0	29	29	94.3
	0.6	0.473	−1	30	30	94.6	0.416	−1	31	30	94.4

We also conducted sensitivity studies by setting C = log{2.05ϖ*exp(0.25 × Z₂ + 0.25 × Z₃)}, where ϖ follow exponential distribution with rate 0.5. The censoring time exp(C) thus follows a Cox proportional hazards model, and the censoring rate remains 28%. We implemented the proposed methods with Ĝ(·) adopted, pretending C is still independent of Z. Under such a mis-specification of the censoring distribution, we observe from Table C.2 in supplemental material C that the bias of ${\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})$ are still very small. The empirical coverage rates may be slightly lower than the nominal level but are still reasonable.

5.2 Inferences on predictive capacity

In the second part of our simulations, we examine the utility of the proposed hypothesis testing method for comparing the quantile predictive performance between candidate prediction models, with the true predictive performance measures displayed in Figure 1. We considered five scenarios: (i) A vs. B, (ii) A vs. C, (iii) E vs. A, (iv) B vs. C, and (v) B vs. D. The one-sided hypothesis was adopted for evaluating (ii), (iii) and (v), while two-sided hypothesis was adopted for (i) and (iv). We considered two significance levels, α = 0.05 and α = 0.1, and set re-sampling sample size B = 1, 999. The results were summarized in Table 2. We observe that the empirical sizes are generally close to the nominal levels, no matter whether the working models under comparison are correctly specified or not. Furthermore, the empirical powers appear satisfactory. The influence functions we derive also facilitate Wald-type confidence intervals for the difference in R¹(τ) between two non-nested models. Some simulation results were provided in Table C.3 of Supplemental Material C.

Table 2.

Simulation results: empirical rejection rates (ERR) based on 𝒯_AB(τ) and perturbations, where the bolded cells are empirical sizes, and the remaining cells correspond to empirical power. The first row within each section presents the difference in R¹(τ) between the two models under comparison.

		α = 0.05				α = 0.1
		τ				τ
		0.1	0.3	0.5	0.6	0.1	0.3	0.5	0.6
(i) A vs. B	Diff	0.052	0.057	0.057	0.056	0.052	0.057	0.057	0.056
	ERR, n = 200	0.611	0.739	0.726	0.675	0.732	0.835	0.822	0.793
	ERR, n = 400	0.876	0.959	0.946	0.918	0.930	0.977	0.976	0.963
	ERR, n = 600	0.966	0.996	0.997	0.989	0.981	0.997	0.998	0.994
(ii) A vs. C	Diff	0.114	0.021	0.000	0.005	0.114	0.021	0.000	0.005
	ERR, n = 200	0.991	0.567	0.055	0.134	0.996	0.666	0.094	0.212
	ERR, n = 400	1.000	0.877	0.053	0.259	1.000	0.932	0.096	0.350
	ERR, n = 600	1.000	0.964	0.052	0.349	1.000	0.980	0.093	0.475
(iii) E vs. A	Diff	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	ERR, n = 200	0.059	0.041	0.038	0.048	0.125	0.087	0.090	0.103
	ERR, n = 400	0.052	0.047	0.052	0.052	0.110	0.093	0.098	0.105
	ERR, n = 600	0.048	0.046	0.051	0.051	0.101	0.096	0.101	0.103
(iv) B vs. C	Diff	0.062	−0.036	−0.057	−0.052	0.062	−0.036	−0.057	−0.052
	ERR, n = 200	0.290	0.221	0.570	0.452	0.431	0.333	0.711	0.593
	ERR, n = 400	0.527	0.426	0.910	0.767	0.674	0.546	0.948	0.839
	ERR, n = 600	0.714	0.574	0.979	0.904	0.818	0.682	0.991	0.945
(v) B vs. D	Diff	0.087	0.015	0.000	0.003	0.087	0.015	0.000	0.003
	ERR, n = 200	0.963	0.425	0.041	0.108	0.980	0.536	0.088	0.174
	ERR, n = 400	1.000	0.695	0.049	0.179	1.000	0.788	0.095	0.255
	ERR, n = 600	1.000	0.873	0.049	0.263	1.000	0.925	0.096	0.375

We next conducted model comparisons for τ ∈ [0.1, 0.6] based on ℛ_AB, the overall test statistic. Taking all quantiles into consideration, each pair of compared models do not have the same predictive performance except under scenario (iii), E vs. A. The results in Table C.4 of Supplementary Material C suggest that the hypothesis testing procedures maintained the sizes well when H₀ is true. The empirical power increases with the sample size as well as the expected model discrepancy. We also conducted sensitivity analysis to evaluate the hypothesis testing procedure under the aforementioned covariate-dependent censoring scenario, where Ĝ(·) is obtained using the Kaplan-Meier estimator. From Table C.5 of Supplementary Material C, we observe that the hypothesis testing procedure still performs adequately under moderate violations of the covariate-independent censoring assumption.

6. DATA ANALYSIS

We applied the proposed methods to a renal disease study, which examined dialysis mortality in a cohort of incident dialysis patients aged 20 years and older (Kutner et al., 2002). The primary endpoint was time to death since study enrollment, and the mean follow-up time was approximately 3 years. The mean age at baseline was 56 years. Covariates include severity of restless syndrome (LEGS), age in years (AGE), BMI, dialysis mordality (HDPD), hematocrit (HCT), mental health score (MH), ferritin level (FER), albumin level (ALB), primary diagnosis of diabetes at study start (PRIDIAB), presence of cardiovascular comorbidity (NEWCAR), higher education level (HIEDU), male sex (MALE), fish consumption (FISHH), and black race (BLACK) (Peng and Huang, 2008; Peng et al., 2014). The survival endpoint may be censored by renal transplantation or end of study follow-up, leading to an overall censoring rate of 35%. There were 191 observations with complete data in this dataset.

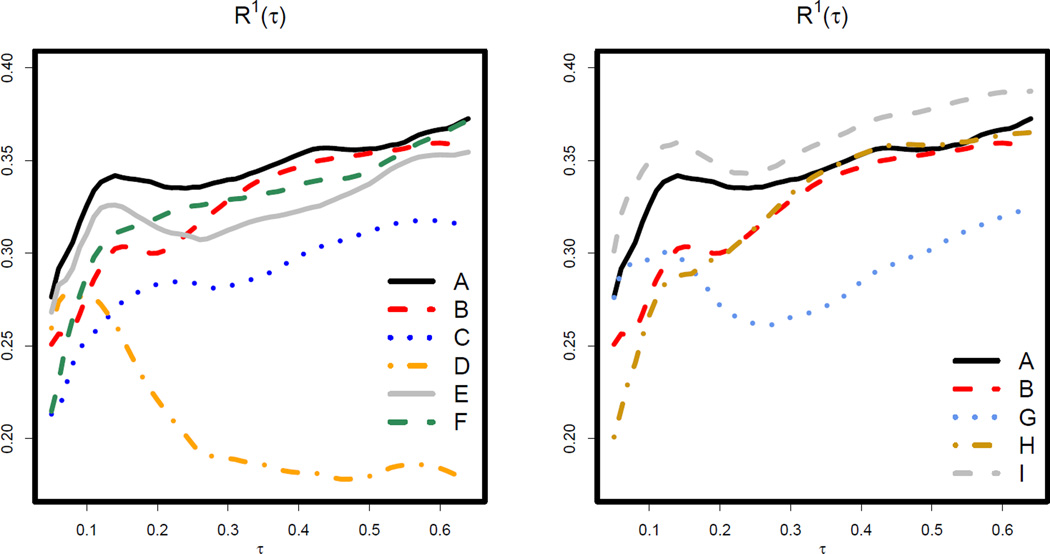
Our goal here is to evaluate and compare the predictive capacity of different working quantile regression models. Our preliminary results based on the proposed methods suggested two potential candidates, namely Model A: {AGE, BLACK, FISHH, HCT, LEGS}, and Model B: {AGE, BLACK, FISHH, HCT}. To have a more comprehensive illustration, we also considered several alternative models here, some of which have been studied in literature (Peng et al., 2014). See Table 3 for details. Specifically, Models B–F are sub-models of model A that includes one less covariate. In model G, AGE_B is a binary variable that indicates whether the patient was greater than or equal to 60 years of age. This is to illustrate whether the common practice of stratefying age makes any difference in this data analysis. Model H denotes the model selected by the adaptive-LASSO method under the accelerated failure time (AFT) model (Wang and Leng, 2007). Finally, Model I includes two additional covariates besides those in Model A. The overall prediction performance measure ${\hat{R}}^1=\frac{1}{{\tau }_U-{\tau }_L}{\int }_{{\tau }_L}^{{\tau }_U}{\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})d\tau$ for [τ_L, τ_U) = [0.05, 0.65) was also provided in Table 3. We plotted the pointwise ${\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})$ for τ ∈ [0.05, 0.65) in Figure 2. Table 4 displays the results of the formal hypothesis tests, either overall or at specific τ ’s.

Table 3.

Analysis of the dialysis data: list of models and the corresponding R̂¹’s.

	Covariates	R̂1
Model A	AGE, BLACK, FISHH, HCT, LEGS	0.345
Model B	AGE, BLACK, FISHH, HCT	0.327
Model C	AGE, FISHH, HCT, LEGS	0.289
Model D	BLACK, FISHH, HCT, LEGS	0.206
Model E	AGE, BLACK, HCT, LEGS	0.324
Model F	AGE, BLACK, FISHH, LEGS	0.328
Model G	AGEB, BLACK, FISHH, HCT, LEGS	0.290
Model H	AGE, BLACK, FISHH, HDPD, NEWCAR	0.326
Model I	AGE, BLACK, FISHH, HCT, LEGS, HDPD, HIEDU	0.362

Figure 2.

Analysis of the dialysis data: ${\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})$ under Models A–I.

Table 4.

Analysis of the dialysis data: results of model comparisons. Each cell corresponds to the p-value at a specific τ or for τ ∈ [0.05, 0.65). The p-values were based on 1,999 perturbed resamples.

		τ
Models	Nested	0.1	0.2	0.3	0.4	0.5	0.6	[0.05,0.65)
A vs. B	Yes	0.092	0.039	0.4	0.3	0.7	0.5	0.12
A vs. C	Yes	0.028	0.006	0.001	0.004	0.051	0.017	< .001
A vs. D	Yes	0.08	< .001	< .001	< .001	< .001	< .001	< .001
A vs. E	Yes	0.2	0.036	0.034	0.016	0.138	0.3	0.02
A vs. F	Yes	0.04	0.1	0.3	0.1	0.2	0.6	0.05
A vs. G	No	0.2	0.02	0.006	0.01	0.06	0.09	0.02
A vs. H	No	0.3	0.3	0.8	1	0.9	0.9	0.5
B vs. H	No	0.8	0.9	0.8	0.7	0.8	0.7	0.95
I vs. A	Yes	0.3	0.5	0.4	0.3	0.2	0.2	0.2
I vs. B	Yes	0.05	0.08	0.3	0.3	0.2	0.2	0.084

The left panel of Figure 2 and the top section of Table 4 compare model A to its several sub-models, models B–F. These results reveal the relative importance of each covariate. For example, we observe that dropping AGE from Model A resulted in the biggest decline in R¹(τ), suggesting that AGE is crucial for quantile prediction across τ. This is confirmed by the hypothesis testing results, where the p-values for comparing Model A vs. D were almost always < .001. By comparison, the decline in R¹(τ) by dropping LEGS from model A appears larger for smaller τ ’s but diminishes when τ increases. Coupled with the p-values for comparing Model A vs. B, this result may suggest that LEGS is non-negligible for lower quantiles but may be less important for upper quantiles. This finding is consistent with previous analysis of this dataset (Peng and Huang, 2008). Thus, one may prefer Model B when research interest lies only in the higher quantiles but may favor Model A when the lower quantiles, corresponding to the higher risks patients, are also of interest.

In the right panel of Figure 2 and the bottom session of Table 4, we illustrate more scenarios of model comparisons. When comparing Model A with Model G, we observe that the continuous AGE covariate served significantly better as a predictor, as compared to its dichotomized counterpart. Note that the proposed methods allow us to evaluate the influence of covariate transformations on quantile prediction. Next, we observe that the ${\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})$ of Model A generally lie above that of Model H, the model selected by the adaptive Lasso method under AFT model. Although the difference between Models A and H are not statistically significant, Model A may be preferred by rendering higher ${\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})$ with the same number of covariates. Finally, we observe that adding additional predictors, HDPD and HIEDU, into Model A does not lead to significant improvement in prediction performances. This bigger model, Model I, did outperformed Model B at lower quantiles, possibly by including LEGS.

Through these visual and formal comparisons, we conclude that Model A may be adopted if one wishes to achieve good quantile prediction for both the lower quantiles and the higher quantiles. Alternatively, Model B may be preferred in terms of overall prediction performance. The regression coefficient estimates under Model A are presented in Supplemental Material C. Using this data example, we demonstrate that the proposed methods allow us to evaluate the quantile prediction performance of various working models. It also facilitates comprehensive and rigorous comparisons in predictive capacity between various candidate models.

7. DISCUSSION

In this work, we have proposed a rigorous framework for evaluating the predictive capacity of working quantile regression models in predicting the quantiles of a survival outcome. The proposed framework allows for not only quantification of either local or global predictive performances, but also formal comparisons between two models that are either nested or non-nested. By its robustness to model mis-specification and straightforward interpretation, we believe that the proposed framework features high practical utility in biomedical studies.

The proposed framework bears a fundamental difference from the existing goodness-of-fit methods by targeting the performance in predicting the underlying survival quantiles of new patients. In contrast, goodness-of-fit methods typically evaluate how the observed existing data match the data expected under an assumed model. The key distinction is well reflected by the construction of the proposed prediction loss function, E[ρ_τ{T⁰−ξ_τ (Z⁰)}], which takes expectation over the data obtained from a new subject, (T⁰, Z⁰), rather than the data where the quantile prediction rule ξ_τ is derived from. Our proposals in Section 4 demonstrate a useful application of the proposed framework. That is, they provide formal inference procedures for conducting model comparison/selection based on the criterion formulated according to the proposed predictive performance measure.

The proposed framework is general and allows one to adopt other forms of quantile predictors. Employing a different ξ̂_τ (·) would only require moderate modifications to the inference procedures. One may need to adapt the components involving the variability of ξ̂_τ (·) in the derivation of the influence function π_i(τ). The asymptotic null distribution for the test of nested models would take a different form but can be derived by similar lines.

The proposed L(τ) is constructed based on log-transformed survival time T. Given the equivariance property of quantiles, which implies Q_T(τ|Z̄) = log{Q_exp(T)(τ|Z̄)}, L(τ) can be interpreted as a measure capturing the discrepancy in log survival quantiles. Note that censored quantile regression typically models a log-transformed survival time, and the resulting quantile predictions often present a skewed distribution across subjects. Assessing quantile prediction performance in the log-time scale can protect against such skewness.

In Section 2.1, one may want to rescale the summands of L_n (τ,β̂) by the inverse of the conditional density $f({\xi }_{\tau }^0|\overline{\mathit{Z}})$. However, direct estimation of $f({\xi }_{\tau }^0|\overline{\mathit{Z}})$ typically involves smoothing and can be unstable with small to moderate sample size. In practice, we recommend using ${\hat{R}}_n^1(\tau ,\hat{\mathit{\beta }})$, a scaled alternative to L_n (τ,β̂) which is also easy to interpret.

The proposed procedures assume that p is finite. When the number of covariates in a real dataset is large, one may first apply existing variable selection procedures for quantile regression models (Wu and Liu 2009; Li and Zhu 2008; Zou and Yuan 2008; Peng et al. 2014; among others) to reduce the model dimensionality. Our proposals in this work can provide an objective analytical tool to validate and compare the models resulted from various different selection procedures.