Evaluating Public Health Interventions: 6. Modeling Ratios or Differences? Let the Data Tell Us

Abstract

We provide an overview of the relative merits of ratio measures (relative risks, risk ratios, and rate ratios) compared with difference measures (risk and rate differences). We discuss evidence that the multiplicative model often fits the data well, so that rarely are interactions with other risk factors for the outcome observed when one uses a logistic, relative risk, or Cox regression model to estimate the intervention effect.

As a consequence, additive models, which estimate the risk or rate difference, will often exhibit interactions. Under these circumstances, absolute measures of effect, such as years of life lost, disability- or quality-adjusted years of life lost, and number needed to treat, will not be externally generalizable to populations other than those with similar risk factor distributions as the population in which the intervention effect was estimated. Nevertheless, these absolute measures are often of the greatest importance in public health decision-making.

When studies of high-risk study populations are used to more efficiently estimate effects, these populations will not be representative of the general population’s risk factor distribution. The relative homogeneity of ratio versus absolute measures will thus have important implications for the generalizability of results across populations.

In part one of this two-part commentary, the sixth in this series, we provide an overview of the considerations involved in the choice of the intervention effect estimator, primarily but not exclusively focusing on the relative merits of ratio measures (relative risks, risk ratios, or rate ratios), compared with difference measures (risk or rate differences). These terms are defined in the box on the next page.

Definitions and Models

The risk ratio, also known as the relative risk (RR), is the ratio of the risk, probability, or cumulative incidence of a health outcome of interest in the exposed, treated, or intervention group, r₁, divided by the same in the unexposed or control group, r₀. The risk difference (RD) subtracts the health outcome risk in the control group from the health outcome risk in the intervention group. That is,

As a relative measure of effect, the RR is most directly estimated by the multiplicative model when it fits the data. The risk difference is an absolute measure of effect, most directly estimated by the additive model when it fits the data. Cumulative incidences, risks, and proportions are synonyms. Rates, such as mortality rates or disease incidence rates, are used as outcome measures when censoring, staggered enrollment, or competing risks are in play. The interpretation of a risk depends critically upon the duration of follow-up over which it is calculated. Their primary disadvantage is more difficulty in interpretability, as they require units of person-time, which can be difficult to explain to nontechnical audiences.

In an individually randomized intervention of sufficient sample size, straightforward methods for a single 2 × 2 table can be used to estimate RRs and RDs, as there is no need to adjust for confounding. Alternatively, in an individually randomized intervention design, the risk ratio can be modeled on the multiplicative scale as

where Y_i is the binary outcome upon which the intervention is focused, X_i is 1 if the participant was randomized to the intervention and 0 otherwise, e^β₁ is the relative risk and greater than 1 otherwise, e^β₀ is the risk in the control group, and E[·] denotes the expected value, which for binary data are equivalent to the outcome model probability. If the difference measure is of interest, the risk difference can be modeled on the additive scale as

where the risk difference is α₁. The parameters of models 1 and 2 have a one-to-one correspondence; thus, from the point of view of validity, in individually randomized studies with no loss to follow-up, staggered entry, or competing risks, the choice between the ratio or difference measure—that is, the choice between model 1 and 2, does not matter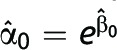, and and .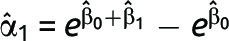

Things change when confounding needs to be considered. As discussed in a previous column in this series,¹ in cluster-randomized studies, unless there is a large number of clusters or outcome rates between clusters are relatively constant, residual between-cluster confounding is likely. Then, to validly estimate the intervention effects, models 1 and 2 need to be expanded:

where C_1ij, . . . , C_pij are the p covariates measured in the study that are needed to validly estimate the intervention effect, the relative risk, e^β₁, for the i^th participant in cluster j. A similar model could be fit if the risk difference were the parameter of interest:

Further details on definitions and models are given in the appendix, available as a supplement to the online version of this article at http://www.ajph.org.

Although models 1 and 2 are interchangeable in the sense that a simple algebraic transformation of one leads to the other as shown here, this is not the case when confounding needs to be adjusted for, as in models 3 and 4. In fact, if model 3 fits the data and the risk difference is of interest, except under the null, there will be modification of the risk difference by each of C_1ij, . . . , C_pij, not just individually but jointly by all of their higher order interactions. This is quite an undesirable situation because, as is well-known, when effect modification is present, it is desirable to report effects by each level of the jointly cross-classified modifiers, or some sort of averaging or standardization procedure must be used to obtain a marginal effect estimate.² Otherwise, if model 3 fits the data, but a difference measure is of primary interest, model 2 could be fit to the data and the average risk difference obtained would be applicable only to the study population at hand in a randomized trial and those with identical, or at least similar, joint distributions of the covariates, C_1ij, . . . , C_pij.

Nearly all studies we are aware of in population health, including public health evaluations, are designed to obtain accurate and precise measures of the primary measure of effect, which may sometimes mean forfeiting generalizability. By design, the distribution of the covariates will not be representative of any general population of interest, as it is through these distributions that a high-risk population is obtained. This principle has been exploited in epidemiology to often favor cohort and case–control studies in high-risk populations because of either high exposure levels or high background risk—for example, uranium miners in the study of the health effects of radon progeny³—or in populations in which loss to follow-up and misclassification can be expected to be minimized, such as the Nurses’ Health Study.⁴ Both of these strategies provide cost- and time-efficient means for obtaining high-quality effect estimates. This foundational epidemiological design principle has made it possible for an enormous amount of information about risk factors for most common diseases to have been obtained over the past 35 years.

The logistic regression model became quite popular in population sciences because it is very stable numerically and may give odds ratio parameter estimates that quite closely approximate the risk ratio when exponentiated. As is well established, the odds ratio is not a parameter of interest in public health research.⁵ However, in cohort studies aimed at estimating the cumulative incidence of disease by the end of follow-up and in cumulative-incidence-sampled case–control studies, if the disease risk is less than 10%, unless the intervention has a very strong effect, the odds ratio will well approximate the risk ratio; otherwise, it tends to overestimate it. When the intervention effect is weak or moderate, the logistic approximation to the risk ratio will often provide sufficient accuracy for disease risks even greater than 10%.^6,7 However, important examples in which the logistic approximation has led us astray have been given.^8,9 The rare disease assumption is obviated when rates are the measure of disease frequency in cohort studies and in incidence-density, or risk-set-sampled case–control studies. The appendix (available as a supplement to the online version of this article at http://www.ajph.org) contains a more in-depth overview of these points.

THE DOMINANCE OF THE MULTIPLICATIVE MODEL

Expressions for the additive and multiplicative models are provided in the box on the next page. Although models 1 and 2 in the box on the next page are interchangeable, this is not the case when one needs to adjust for confounding, as in models 3 and 4, located in the box on the next page. In fact, if model 3, the multiplicative model, fits the data and the risk difference is of interest, there will be modification of the risk difference by each of the confounders, except in the absence of an effect of the confounders or in the absence of an effect of the exposure itself. This is quite an undesirable situation because, as is well known, when effect modification is present, it is desirable to report effects by each level of the jointly cross-classified modifiers, or some sort of averaging or standardization procedure must be used to obtain an externally generalizable effect estimate.²

With these basic principles established and further elaborated in the appendix (available as a supplement to the online version of this article at http://www.ajph.org) we can now move to considerations driving the choice of the model within which the intervention effect is to be estimated. Our recommendation is simple—let the data tell us on which scale to fit the model. If the data fit the multiplicative model best—that is, by using the log or logistic link function—then that is what must be done, and similarly if the additive model provides the better fit. Methods for formal statistical determination of relative goodness of fit between nonnested models such as these are underdeveloped. An informal comparison of log-likelihoods of the fits of models 3 and 4 will indicate that the model associated with the largest log-likelihood is the one with the best fit.

Parsimony is an additional source of information: if the log-link function provides a model with no interaction terms, particularly none with the intervention variable, and the identity link function provides a model that needs many interaction terms, finite sample statistical stability will be obtained by choosing the former. Also of importance, the poor fit of additive models to most studies of binary health outcomes is underscored by the common experience that such models often fail to converge.

Although more formal quantitative work is needed, there is extensive anecdotal evidence that suggests that often in public health the multiplicative models fit the data well. The first author has published nearly 650 peer-reviewed scientific publications in a diverse range of substantive areas including chronic disease epidemiology, HIV/AIDS, and environmental health, and, for nearly all of these, her primary contribution to the research was that of the study statistician. In almost all of these, the multiplicative model fit the data consistently and extraordinarily well. The second author, who has devoted much of his methodological work to interaction, has numerous examples of interaction on additive scales but, in more than 230 articles, can think of only two examples of multiplicative interaction that replicated across studies (e.g., VanderWeele et al.¹⁰).

These impressions are further confirmed by other senior researchers: our department chair, Albert Hofman, has informed us that he cannot think of a single important multiplicative modifier uncovered during his long research career among his more than 2000 scientific articles. Similarly, Walter Willett, former chair of Harvard’s nutrition department, could think of four multiplicative modifiers among more than 1700 scientific publications.

Despite an enormous amount of research on gene–environment interactions on the multiplicative scale, very few have yet been found and replicated.^11,12 Recent careful modeling of potential gene–environment interaction in breast cancer research likewise indicated little evidence of multiplicative interaction.¹³ This is, of course, anecdotal evidence that could be confirmed with a more systematic and far-reaching study, but the anecdotal evidence comes from very many studies.

Summaries of meta-analyses have also reported higher rejection rates for risk difference homogeneity than risk-ratio homogeneity,^14,15 although it is unclear whether statistical power favors the heterogeneity test on one scale versus the other.^16,17 There may also be mathematical reasons for greater homogeneity of risk ratios than risk differences.¹⁷ Although further and more formal quantitative work evaluating the relative degree of heterogeneity for risk ratio versus risk differences may be important, the previously mentioned considerations do seem to provide some indication that, for whatever reason, risk ratio modification is uncommon. Importantly, this implies that risk difference modification is nearly universal, a point to which we will return, mostly in part two of this commentary, to appear in a future edition of this journal.

Air Pollution Exposure and All-Cause Mortality

To illustrate these points, we analyzed data from the Nurses’ Health Study looking at the relationship over time between fine particulate matter of 2.5 micrometers or less (PM_2.5) exposure, a constituent of air pollution that has been found to be particularly toxic, and all-cause mortality.¹⁸ Among 628 186 person-years between 2000 and 2006, 8617 deaths occurred among 108 767 nurses. A Poisson regression model with the identity link function, with adjustment for five-year age groups, was used to fit the additive model, and the Cox model was used to fit the multiplicative model, with age in months as the time scale. As is our typical experience fitting additive models, the model gave a warning message and it is uncertain if the results provided are indeed the maximum likelihood estimates, although they may be. Table 1 provides the results on the multiplicative and additive scales. A significant association is observed on the multiplicative scale, but not on the additive scale, consistent with an overall poor model fit on this scale. As is often the case, there is no evidence for any modification of the effect of PM_2.5 by either age or race on the multiplicative scale. As expected, therefore, there are substantial and significant additive interactions of the PM_2.5 by both age and race. To the extent that they are interpretable, the strong additive interactions will have important implications for the quantification and interpretation of absolute effects, which will be discussed in the next column in this series.

TABLE 1—

Exposure to Fine Particulate Matter Air Pollution in Relation to All-Cause Mortality in the Nurses’ Health Study: United States, 2000–2006

Model	% of Person-Years	Rate Ratio (95% CI)/10 µg/m3	P, Test for Multiplicative Interaction	Rate Difference (95% CI)/ 10 µg/m3/Person-Months	P, Test for Additive Interaction
Main effect only		1.13 (1.05, 1.22)		0.0044 (−0.0084, 0.0173)
Interaction by age, y			.34		< .001
< 60	13	1.35 (0.84, 2.16)		−0.0008 (−0.0291, 0.0275)
60 to < 70	42	1.02 (0.86, 1.21)		0.0007 (−0.0197, 0.0211)
≥ 70	45	1.16 (1.06, 1.26)		0.0079 (−0.0100, 0.0258)
Interaction by race			.76		< .001
White	94	1.12 (1.04, 1.22)		0.0037 (−0.0096, 0.0169)
Black	2	1.25 (0.94, 1.66)		0.0149 (−0.0326, 0.0624)
Other	4	1.26 (0.94, 1.68)		0.0129 (−0.0357, 0.0615)

Note. CI = confidence interval. Adjusted for age (months), calendar year, race, region, season, smoking status, pack-years, family history of myocardial infarction, body mass index, hypercholesterolemia, median family income in census tract of residence, median house value in census tract of residence, physical activity, alternate healthy eating index, nurses’ education, occupation of both parents, marital status, and husbands’ education.

It has proven difficult to find examples in the literature in which the additive model fit the data and (negative) interaction was evident on the multiplicative scale, but examples certainly do exist; two such recent examples can be found in Crump et al.¹⁹ and Colangelo et al.²⁰

The Search for Interactions

Best practice in the analysis of data, including data from randomized studies, involves investigation of modification of the effect of primary interest by the other strong determinants of the outcome and any other a priori suspected modifiers. This is recommended because there is no a priori reason to assume that the model chosen to fit to the data is linear in the chosen link function—that is, that there is no effect measure modification. The term “measure” is inserted here because effect modification is scale-dependent. Again, no effect modification of the risk ratio almost certainly suggests effect modification of the risk difference, and vice versa.

Nevertheless, a number of well-known pitfalls associated with statistical significance tests and related procedures complicate the implementation of this best-practice recommendation. First, there is the multiple comparisons problem, in which the probability of a chance significant finding increases as the number of statistical tests performed increases. Many chronic diseases and other health outcomes of interest to public health investigators have 20 or more known or suspected risk factors. Under the global null of no effect modification by any of these, in any given study, on average, one should manifest as a statistically significant modifier at the P less than or equal to .05 level of significance. Thus, it is additionally recommended that for exploratory investigation of effect modification among known and suspected risk factors for the outcome, any significant findings should be reported with caution, as is recommended for exploratory analysis in general.

Correcting for multiple comparisons can also often offset any optimism that an interaction has been detected. Often significant effect modification discovered through exploratory analysis will fail to be replicated. This phenomenon has been well-documented in the gene-by-environment interaction literature in which many such disappointments have occurred.¹¹ Sometimes, it appears that interactions associated with P values less than .05 occur less than 5% of the time. For example, in the Pooling Project of Diet and Cancer in Men and Women,²¹ we systematically worked through most of their hypothesized dietary causes of the major types of cancer—breast, colon, lung, ovarian, pancreatic, and renal. Pooling of initially eight studies to up to more than 30 presently, from around the world, we have diligently checked for effect modification on the multiplicative scale for each dietary exposure of interest with respect to the other major risk factors for the cancer, but Stephanie Smith-Warner, the leader of this project, recalls two among hundreds of diet–cancer endpoint associations investigated. What we mostly showed was that the effect modification reported in a small number of publications by individual studies was most likely attributable to random variation and failed to replicate in the pooled analysis, illustrative of the multiple comparison problem.

Next, there is the problem, in large studies and in pooled analyses, meta-analyses, and the analysis of data from consortia, that the tests for effect modification can be “overpowered,” whereby significant interactions can be observed for very small departures from the null hypothesis of no effect modification. For example, in a recent article on the population attributable risk of modifiable postmenopausal breast cancer risk factors among 8421 cases and 2 400 000 person-years of follow-up in the Nurses’ Health Study, among scores of possible two-way interactions among 13 well-established breast cancer risk factors, three were significant at P less than or equal to .05.²² Among these, none had any material importance whatsoever—that is, magnitudes of the differences between relative risks for one risk factor among levels of another were too small to be of any consequence. This is a judgment call that needs to be made by researchers leading large studies, including public health researchers in the context of evaluation of large-scale interventions.

Finally, there is the “underpowering” issue. As most evaluations are not designed with effect modification in mind, they are justifiably not powered to detect it. Given budgetary constraints, it is typically a struggle to design a sufficiently powerful evaluation aimed at accurate and reliable estimation of the main intervention effect. Powering subgroup analysis is simply prohibitive in most situations.^23,24

FUTURE DIRECTIONS AND CONCLUSIONS

In summary, it is best to estimate intervention effects on the scale that best fits the data, which seems very often to be the multiplicative scale. Importantly, whenever the results are internally valid, if effect modification is absent across measured and unmeasured confounders, then results are externally generalizable as well. The box on page 1090 provides definitions of internal and external validity. Even when ratio measures are used for modeling, various absolute measures will often be of interest for public health decision-making. In the next commentary in this series, we will discuss options for the selection of an absolute effect measure and methods for producing externally valid ones for public health and policy purposes. Questions of effect estimation for precision public health²⁵ also will be addressed in part two of this commentary.

Internal and External Validity

Internal validity occurs in the absence of bias attributable to confounding, measurement error or misclassification, and selection bias, such that the “in-sample” effect estimate accurately approximates its underlying true value.

External validity occurs when an estimate is both internally valid and applicable to a broader population to which it is thought to be relevant.