RNA primer–primase complexes serve as the signal for polymerase recycling and Okazaki fragment initiation in T4 phage DNA replication

Significance

The lagging-strand polymerase sometimes begins the synthesis of a new Okazaki fragment prior to finishing the previous fragment, creating a gap between the Okazaki fragments. The mechanism and signal that initiate this behavior have not been definitively identified. We demonstrate that primer–primase complexes left on the lagging ssDNA from primer synthesis have a residence time similar to the timescale of Okazaki fragment synthesis and the ability to block holoenzymes synthesizing DNA and stimulate the dissociation of the holoenzyme, triggering polymerase recycling. The collision with primer–primase complexes triggering early polymerase recycling has distinct advantages over previously proposed “signals.” Modeling of repeated cycles of Okazaki fragment initiation reproduced experimental data, providing insights into Okazaki fragment initiation and overall functioning of DNA replisomes.

Abstract

The opposite strand polarity of duplex DNA necessitates that the leading strand is replicated continuously whereas the lagging strand is replicated in discrete segments known as Okazaki fragments. The lagging-strand polymerase sometimes recycles to begin the synthesis of a new Okazaki fragment before finishing the previous fragment, creating a gap between the Okazaki fragments. The mechanism and signal that initiate this behavior—that is, the signaling mechanism—have not been definitively identified. We examined the role of RNA primer–primase complexes left on the lagging ssDNA from primer synthesis in initiating early lagging-strand polymerase recycling. We show for the T4 bacteriophage DNA replication system that primer–primase complexes have a residence time similar to the timescale of Okazaki fragment synthesis and the ability to block a holoenzyme synthesizing DNA and stimulate the dissociation of the holoenzyme to trigger polymerase recycling. The collision with primer–primase complexes triggering the early termination of Okazaki fragment synthesis has distinct advantages over those previously proposed because this signal requires no transmission to the lagging-strand polymerase through protein or DNA interactions, the mechanism for rapid dissociation of the holoenzyme is always collision, and no unique characteristics need to be assigned to either identical polymerase in the replisome. We have modeled repeated cycles of Okazaki fragment initiation using a collision with a completed Okazaki fragment or primer–primase complexes as the recycling mechanism. The results reproduce experimental data, providing insights into events related to Okazaki fragment initiation and the overall functioning of DNA replisomes.

During DNA replication, the opposite polarity of the two DNA strands necessitates that the leading DNA strand is copied continuously whereas the lagging DNA strand is copied in discrete segments known as Okazaki fragments. The initiation of each new Okazaki fragment involves the release of the current Okazaki fragment by the lagging-strand holoenzyme, the synthesis of a primer by primase, and the handoff of the primer to the recycled lagging-strand polymerase. Two mechanisms have been proposed to describe how and when these multiple events of Okazaki fragment initiation occur to maintain the coordinated replication of the leading and lagging DNA strands within a replisome, and evidence suggests that both mechanisms operate in the replisomes studied thus far [T4 (1), T7 (2), and Escherichia coli (3)]. In the collision mechanism, the lagging-strand holoenzyme is triggered to recycle whenever it collides with the previous Okazaki fragment (4, 5), possibly due to the absence of ssDNA template downstream of the polymerase (6, 7). In the signaling mechanism, the lagging-strand holoenzyme is triggered to stop the synthesis of the current Okazaki fragment short of the previous fragment, leaving a gap. This early recycling of the polymerase is believed to result from one or more events related to repetitive lagging-strand DNA synthesis, specifically the association of primase with the replisome (3, 8, 9), crosstalk between primase subunits within the replisome (10), primer synthesis (11), the loading of a clamp onto a primer by a clamp loader (1, 12), the release of a priming loop (12), or the tension-induced dissociation of the lagging-strand holoenzyme (13). However, the mechanism and the trigger underlying the signaling mechanism have not been definitively identified.

The primase from T4 bacteriophage uses two mechanisms to synthesize RNA primers (14). The first mechanism involves the disassembly of a primase subunit from the replisome with its newly synthesized RNA primer; the result is the formation of a primer–primase complex on the lagging DNA strand. In the second mechanism, a small ssDNA loop is formed between the helicase and primase within the replisome; the result is that primase remains with the replisome, and the naked RNA primer is available for the clamp loader to load a clamp protein. The percentage of primers used for Okazaki fragment synthesis compared with the total number of primers synthesized is low; in ensemble rolling circle studies on the T4 system, only between 20% and 40% are used to initiate Okazaki fragments (1). Therefore, many unused primers could build up ahead of the holoenzyme on the lagging DNA strand in the form of primer–primase complexes. This study investigates the possibility that these primer–primase complexes serve as blocks on the lagging strand and correspond to the “signal” that causes the lagging-strand polymerase to recycle.

Results and Discussion

Model System.

In these studies, it was necessary to use a small DNA substrate modeling the essence of the much larger lagging strand (Fig. S1). The substrate had template DNA with a 5′-GCT-3′ priming recognition site and an annealed DNA oligonucleotide to serve as the Okazaki fragment being extended by the holoenzyme. The ends of the substrate were blocked with biotin–streptavidin to prevent the holoenzyme from sliding off the ends of the DNA, which would impact the measured rate of holoenzyme dissociation. Either an annealed DNA oligonucleotide to mimic the previous Okazaki fragment in the collision mechanism or a primer–primase complex to evaluate its capacity to initiate premature recycling in the signaling mechanism were bound downstream of the holoenzyme on this substrate. Due to the stochastic nature of primer synthesis by the T4 primase at priming recognition sites and the extremely low priming rate in the absence of helicase, an exogenous primer was used in these experiments instead of a primer synthesized in situ by primase. We used T7 RNA polymerase and transcription runoff to generate the physiological 5-mer RNA primer including its 5′-triphosphate moiety of the T4 primase (Fig. S2). Here we designate pppRNA and HO-RNA as this 5-mer RNA primer with a 5′-triphosphate group and 5′-hydroxyl group, respectively.

Fig. S1.

Small DNA substrates modeling the essence of the much larger lagging strand. (A) Schematic of preassembled primer–primase complex on ssDNA used to measure complex stability. (B) Schematic of substrates used in Okazaki fragment extension assays to test the ability of a DNA oligonucleotide mimicking the previous Okazaki fragment in the collision model or a pppRNA–primase complex in the signaling model to block holoenzyme synthesis. We have used a 5′-OH DNA oligonucleotide to mimic the previous Okazaki fragment, whereas a physiological Okazaki fragment consists of a 5′-triphosphate RNA primer that has been extended with DNA. We believe that this change in the 5′ terminus does not significantly impact our conclusions because a previous study found both a 5′-OH DNA oligonucleotide and a 5′-triphosphate RNA oligonucleotide blocked a synthesizing holoenzyme and increased the dissociation rate of the holoenzyme 30–50-fold over the baseline rate without any block (5). (C) Schematic of substrates used to measure holoenzyme dissociation under conditions of no recycling, collision, or signaling.

Fig. S2.

Synthesis of a physiological RNA primer. (A) The physiological RNA primer (pppRNA) with the sequence 5′-ppp-rGrCrCrGrA-3′ with a 5′-triphosphate moiety was synthesized using a standard run-off transcription protocol with T7 RNA polymerase. The resulting RNA product was size fractionated on a 7.5 M urea–20% polyacrylamide gel. (B) Mass spectroscopy data acquired on a Waters Micromass LCT Premier time-of-flight mass spectrometer equipped with a Waters Alliance 2695 Separations Module and using electrospray ionization confirmed the pentaribonucleotide product by excellent agreement between the measured and calculated molecular masses.

Residence Time of pppRNA–Primase Complexes on ssDNA.

Primer–primase complexes must have a residence time on the lagging strand similar to the timescale of Okazaki fragment synthesis to block the holoenzyme during the synthesis of an Okazaki fragment and lead to its recycling. The fluorescence of a dye on the DNA substrate positioned 3 nt downstream from the priming recognition site (i.e., the primer–primase complex binding site) was found to be sensitive to the presence or absence of a primer–primase complex on the DNA (Fig. S1A). This environmental sensitivity of the fluorophore allowed us to study the kinetics of primer–primase complex dissociation from ssDNA by monitoring changes in the fluorescence of the dye as a function of time.

We preassembled in a stopped-flow instrument the primer–primase complex on the fluorescently labeled substrate and mixed it with unlabeled ssDNA trap to prevent rebinding. Extended time courses of the fluorescence signal displayed three distinct phases (Fig. S3A). Two of these phases displayed decreases in the fluorescence signal as a function of time, and control experiments demonstrated these phases to be related to photobleaching of the dye (Fig. S3B) and fluorescence quenching of the DNA substrate when mixed with a large excess of ssDNA trap (Fig. S3 C and D). The third phase, which was only observed in the presence of primase or primer–primase complexes, displayed an increase in the fluorescence signal over time and was assigned to the dissociation of primase or primer–primase complexes from the fluorescently labeled substrate.

Fig. S3.

Stability of pppRNA–primase complex to serve as a signal. (A) Extended time course of the fluorescence signal displayed three distinct phases for the kinetics of pppRNA–primase dissociation from ssDNA. Physiological pppRNA–primase complex (400 nM) preassembled on Cy5-labeled DNA substrate (400 nM) was mixed with ssDNA trap (2 mg/mL), and the fluorescence signal was monitored over time. The trace was fit to the sum of three exponentials with the residuals shown below. (B) The fluorescence signal was monitored in control experiments mixing Cy5-labeled DNA substrate (400 nM) with buffer. The traces were fit to an exponential equation determining the rate constant and relative amplitude of photobleaching of the Cy5 dye, which are reported in Table S1. Although the rate of dye photobleaching was constant (k_{photobleaching} = 0.0048 ± 0.0007 s⁻¹), its amplitude was dependent on the concentration of the pppRNA–primase complex, suggesting that the binding of the complex on DNA offered protection from photobleaching. (C) The fluorescence signal was monitored in control experiments mixing Cy5-labeled DNA substrate (400 nM) with ssDNA trap (2 mg/mL). The traces were fit to the sum of two exponentials determining the rate constants and relative amplitudes of quenching of the Cy5 dye by ssDNA trap and photobleaching of the Cy5 dye, which are reported in Table S1. Neither the amplitude nor the rate of fluorescence quenching upon mixing with ssDNA trap were strongly correlated to the concentration of the primer–primase complex. (D) Cy5-labeled DNA substrate (400 nM) was mixed with a concentration series of ssDNA trap (0.2–2 mg/mL), and the fluorescence signal was monitored over time. The traces were fit to the sum of two exponentials determining the rate constants and relative amplitudes of the quenching of the Cy5 dye by ssDNA trap and photobleaching of the Cy5 dye. The observed rate of the fluorescence quenching of the Cy5 dye was dependent on the concentration of the ssDNA trap. (E) A concentration series of physiological pppRNA–primase complex (0–500 nM) preassembled on Cy5-labeled DNA substrate (400 nM) were mixed with ssDNA trap (2 mg/mL), and the fluorescence signal was monitored over time. The traces were fit to the sum of three exponentials determining the rate constants and relative amplitudes of the dissociation of pppRNA–primase complex from ssDNA, quenching of the Cy5 dye by ssDNA trap, and photobleaching of the Cy5 dye, which are reported in Table S1. The amplitude of the complex dissociation phase (red circles) was directly proportional to the concentration of the pppRNA–primase complex up to a 1:1 ratio with the DNA substrate. The amplitude of the photobleaching phase (blue squares) was inversely proportional to the concentration of the pppRNA–primase complex up to a 1:1 ratio with the DNA substrate.

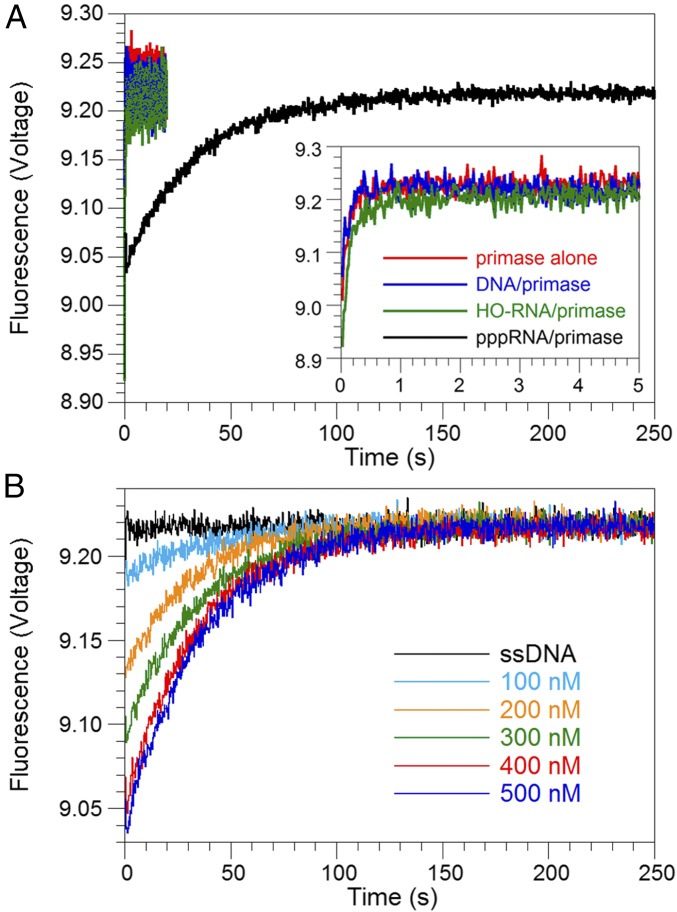
Kinetic traces displaying only the relevant exponential term for the dissociation phase using preformed complexes of primase alone, DNA primer–primase, or RNA primer lacking a 5′ triphosphate moiety (HO-RNA)–primase bound to the fluorescently labeled substrate show very rapid increases in fluorescence (Fig. 1A) with an average rate constant of k_dissociation = 7.3 ± 0.4 s⁻¹ (Table S1). These results indicate that the DNA or HO-RNA exogenous primers do not bind to primase subunits with high affinity and suggest that the observed changes in fluorescence reflect primase protein alone dissociating from the fluorescently labeled substrate in each of these experiments. The correspondingly short half-life of 0.095 ± 0.005 s indicates that primase protein alone on the lagging ssDNA cannot serve to initiate lagging-strand holoenzyme recycling.

Fig. 1.

Stability of pppRNA–primase complex to serve as a signal. Traces display only the relevant exponential term for the primer–primase complex dissociation phase extracted from the entire time traces that include phases related to fluorescence quenching due to mixing with ssDNA trap and photobleaching. (A) Time trace of pppRNA–primase complex (black trace) dissociation displays a sufficient half-life to serve as a signal for holoenzyme recycling. (Inset) Time traces of primase alone (red trace), DNA primer–primase (blue trace), and HO-RNA–primase (green trace) complex dissociation display a short half-life. (B) Time traces of pppRNA–primase complex dissociation over a series of complex concentrations demonstrate a stoichiometery of one primer and primase subunit per complex.

Table S1.

Rate constants and relative amplitudes for the dissociation of primer–primase complexes from Cy5-labeled DNA substrate

	Complex dissociation		Quenching due to trap		Photobleaching
Sample	Amplitude	Rate, s−1	Amplitude	Rate, s−1	Amplitude	Rate, s−1
0 nM complex (control)			0.0527 ± 0.008	0.073 ± 0.002	0.21 ± 0.02	0.0048 ± 0.0007
100 nM complex	−0.033 ± 0.004	0.028	0.043 ± 0.004	0.18 ± 0.03	0.161 ± 0.008	0.0048
200 nM complex	−0.091 ± 0.005	0.028 ± 0.001	0.031 ± 0.003	0.40 ± 0.05	0.09 ± 0.01	0.0048
300 nM complex	−0.128 ± 0.009	0.028 ± 0.001	0.07 ± 0.01	0.32 ± 0.05	0.07 ± 0.01	0.0048
400 nM complex	−0.167 ± 0.005	0.0305 ± 0.0004	0.07 ± 0.01	0.34 ± 0.06	0.04 ± 0.01	0.0048
500 nM complex	−0.18 ± 0.01	0.028 ± 0.001	0.08 ± 0.01	0.34 ± 0.02	0.034 ± 0.002	0.0048
Primase alone	−0.205 ± 0.007	7.2 ± 0.3	0.0383 ± 0.0003	0.073	0.2	0.0048
DNA primer	−0.1683 ± 0.0009	7.8 ± 1.4	0.05 ± 0.01	0.073	0.2	0.0048
HO-RNA primer	−0.31 ± 0.03	7.0 ± 0.1	0.018 ± 0.001	0.073	0.2	0.0048

Values given in italics were fixed when fitting the time traces to the sum of three exponentials.

In contrast, a physiological pppRNA primer formed a stable complex with primase subunits on the fluorescently labeled substrate (Fig. 1A), demonstrating the importance of the 5′-triphosphate moiety in the formation of a pppRNA–primase complex. The dissociation rate of a pppRNA–primase complex from the DNA substrate was constant, k_dissociation = 0.028 ± 0.001 s⁻¹ (t_1/2 = 24.8 ± 0.9 s) (Table S1), whereas the amplitude of the fluorescence increase was dependent on the concentration of the pppRNA–primase complex formed. Kinetic traces displaying only the relevant exponential term for the dissociation phase show an increase in amplitude up to a 1:1 ratio of pppRNA–primase complex to DNA substrate (Fig. 1B and Fig. S3E), suggesting a stoichiometry of one primase subunit in every pppRNA–primase complex, which dissociates in a first-order kinetic process.

Previously, we measured the lifetime of in situ pppRNA–primase complexes on ssDNA to be 4.2 ± 0.3 s while under pressure from a reannealing DNA hairpin in a magnetic tweezers assay (14), and we expect an even longer lifetime for the complex in the absence of a reannealing DNA hairpin. Our measured half-life of 24.8 ± 0.9 s, equal to a lifetime of 36 ± 1 s, for the pppRNA–primase complex on ssDNA is in good agreement with that expectation. At an average nucleotide incorporation rate of 150 nt/s for the lagging-strand holoenzyme, it would take 6–13 s to synthesize an Okazaki fragment of 1,000–2,000 bp in length. Therefore, a pppRNA–primase complex with a half-life of 24.8 ± 0.9 s on ssDNA would be sufficiently stable to create blocks on the lagging strand for a holoenzyme synthesizing Okazaki fragments.

pppRNA–Primase Complexes Block DNA Synthesis by Holoenzymes.

For a primer–primase complex to cause the holoenzyme to recycle, the complex must be capable of blocking the progress of a holoenzyme extending an Okazaki fragment. Using a ³²P-radiolabeled Okazaki fragment extension assay (Fig. S1B), Okazaki fragment synthesis can be monitored as the holoenzyme collides with an annealed DNA oligo (mimicking the previous Okazaki fragment in the collision model) or a primer–primase complex (the putative signal in the signaling model).

The annealed DNA oligonucleotide mimicking the previous Okazaki fragment blocked a large percentage (88 ± 9%, the average quantitated from three gels) of the holoenzyme from extending the primer to the end of the DNA template (Fig. 2A). This incomplete blocking may be the result of the holoenzyme extending a small percentage of the substrate lacking the annealed DNA oligonucleotide to the end of the template. The relatively broad band of blocked extension products indicates that the exonuclease-deficient polymerase is capable of strand-displacement synthesis, creating a small flap of ssDNA. These data are consistent with expectations from the collision model that the holoenzyme will recycle when it encounters the previous Okazaki fragment.

Fig. 2.

Blocking Okazaki fragment synthesis and rapid dissociation of holoenzyme upon collision with pppRNA–primase complex. (A) Denaturing PAGE analysis displays the percentage of holoenzyme synthesis blocked by an annealed DNA oligonucleotide (lane 3) and increasing concentration of pppRNA–primase complex (lanes 6–9). The amount of primase and/or pppRNA compared with the DNA substrate is given as a fold-excess (e.g., –10×) for each lane (entire gel shown in Fig. S4A). (B) Time traces of holoenzyme dissociation upon collision with an annealed DNA oligonucleotide (blue trace) or pppRNA–primase complex (red trace) display a population of holoenzyme with a faster dissociation rate compared with holoenzyme that does not recycle (black trace). P/T, primer/template DNA substrate.

We tested the ability of either a physiological pppRNA primer or a primase subunit alone to block the progress of a holoenzyme. Neither was able to impede Okazaki fragment synthesis, which is consistent with the weak binding of primase to ssDNA and the unstable annealing of a short pentaribonucleotide primer. We also tested the ability of several primer–protein complexes, including DNA and HO-RNA pentamers as the primer with primase and clamp–clamp loader combinations, to block holoenzyme extension (Fig. S4A); however, none were efficient blocks for a holoenzyme synthesizing an Okazaki fragment.

Fig. S4.

Blocking Okazaki fragment synthesis by holoenzyme upon collision with primer–protein complex. (A) Denaturing polyacrylamide gel analysis of Okazaki fragment extension assays testing the ability of the indicated primer–protein complexes to block Okazaki fragment synthesis by a holoenzyme. Holoenzyme was first loaded at the primer/template junction of the DNA substrate followed by the addition of the primer–protein complex. The amount of protein and/or primer compared with the DNA substrate is given as a fold-excess (e.g., –10×) for each lane. The reactions were initiated by the addition of dNTPs and ssDNA trap to prevent rebinding of the holoenzyme and quenched after 1 min. The resulting products were separated on a 7.5 M urea–12% polyacrylamide gel; the migration position of the starting primer, blocked product, and fully extended product are indicated. The amount of each product was quantitated using a Personal Molecular Imager (Bio Rad), and the percentage of blocked products was calculated in comparison with the sum of the products for each reaction. The quench and trap controls were performed by adding the EDTA/proteinase K solution or the ssDNA trap, respectively, to the DNA substrate before the holoenzyme was loaded. Neither a DNA nor a HO-RNA primer of the same length could form a stable complex with primase subunits to block the holoenzyme extension, again demonstrating the importance of the 5′-triphosphate moiety in the formation of a pppRNA–primase complex. Likewise, holoenzyme extension was not blocked by a pppRNA–clamp–clamp loader complex possibly because the loading of clamp proteins by clamp loader on a primer/template junction is unstable in the absence of polymerase to complete the formation of the holoenzyme (37). (B) Schematic of a short, mismatched, relatively unstable stem-loop structure that can form in the DNA substrate in the absence of the annealed DNA block oligonucleotide or bound pppRNA–primase complex. Stem-loop structures have been shown to block DNA synthesis of a holoenzyme (4); the position of this particular block is labeled as “Hairpin.” For simplicity, only the ssDNA portion of the DNA substrate is shown. (C) Schematic of a short, mismatched, relatively unstable stem-loop structure that can form in the DNA substrate in the absence of the annealed DNA block oligonucleotide or bound pppRNA–primase complex. The position of this particular block coincides with the blocking position caused by a pppRNA–primase complex. For simplicity, only the ssDNA portion of the DNA substrate is shown. P/T, primer/template DNA substrate.

Only a pppRNA–primase complex bound on the DNA substrate was able to block the progress of a holoenzyme from synthesizing to the end of the DNA template (Fig. 2A). The amount of blocked holoenzyme depended on the pppRNA–primase concentration (lanes 6–9) and reached a maximum of 45 ± 7% (the average quantitated from three gels) at a 10-fold excess of the pppRNA–primase complex (i.e., the holoenzyme is able to read through the pppRNA–primase block in ∼55% of the encounters). This is a lower bound for the ability of the pppRNA–primase complex to block the holoenzyme, as the ssDNA trap present in the assay appears to affect our saturation level of the pppRNA–primase complex on the DNA template. The footprint of the pppRNA–primase complex binding ssDNA is evident from the slightly shorter blocked extension products in the presence of the pppRNA–primase complex compared with the blocked extension products in the presence of a DNA oligonucleotide. These data are consistent with pppRNA–primase complexes causing the holoenzyme to recycle in the signaling model.

pppRNA–Primase Complexes Stimulate Holoenzyme Dissociation.

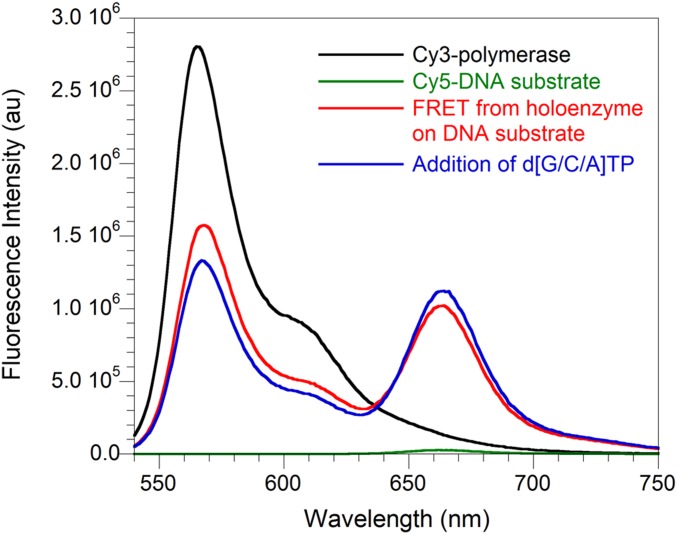
A pppRNA–primase complex must also increase the dissociation of the holoenzyme upon collision to serve as a signal for holoenzyme recycling and Okazaki fragment initiation. A distinct FRET signal between Cy3-labeled polymerase and Cy5-labeled DNA substrate is observed in the presence of clamp, clamp loader, and ATP (Fig. S5) and provides the basis for a FRET-based assay to monitor holoenzyme dissociation from the DNA substrate. The omission of dTTP in the assay stalls the holoenzyme on the DNA substrate and allows us to measure the holoenzyme dissociation rate in the absence of a collision or signal (Fig. S1C). The dissociation rate enhancement due to collision with an annealed DNA oligonucleotide to mimic the previous Okazaki fragment or due to encountering a primer–primase complex can then be determined.

Fig. S5.

FRET-based assay reporting on holoenzyme dissociation from the DNA. Fluorescence emission spectra were obtained by exciting the Cy3-labeled polymerase (black trace) and Cy5-labeled DNA substrate (green trace) separately at 514 nm. Cy5-DNA substrate can be excited through FRET from Cy3-polymerase only when the holoenzyme is bound to the DNA substrate (red trace). The addition of dGTP, dCTP, and dATP allowed the holoenzyme to synthesize DNA up to 3 nt from the Cy5 label on the DNA substrate; the small decrease in Cy3 emission and small increase in Cy5 emission (blue trace) indicate that the FRET signal is not very distance-dependent in this case. au, arbitrary units.

We preassembled in a stopped-flow instrument the holoenzyme on the fluorescently labeled substrate and mixed it with nucleotides (dGTP, dCTP, and dATP), ATPγS, and ssDNA trap to prevent rebinding. As previously observed (15, 16), the T4 holoenzyme dissociates slowly from a primer/template junction, displaying a half-life of almost 2.5 min (Fig. 2B and Table S2) in the absence of a collision or signal. Upon collision with a DNA oligonucleotide to mimic the previous Okazaki fragment, 15.6 ± 0.2% of the holoenzyme dissociated ∼180 times faster, with a half-life of 0.85 ± 0.03 s, whereas 84.4 ± 0.8% of the holoenzyme dissociated at a reduced rate with an extremely slow half-life of over 5 min (312 ± 1 s). This decrease in the dissociation rate of the holoenzyme encountering a DNA block compared with the no collision scenario is speculated to be an artifact of exonuclease-deficient polymerase performing strand-displacement synthesis, which creates a ssDNA flap that might stabilize the polymerase on the DNA substrate. The wild-type T4 polymerase is not capable of the strand-displacement synthesis, preventing the formation of a stabilizing DNA flap; therefore, we expect that all of the holoenzyme in a wild-type replisome would dissociate at the faster rate upon collision with the previous Okazaki fragment, consistent with previous studies (4, 5).

Table S2.

Rate constants and relative amplitudes for the dissociation of Cy3-labeled holoenzyme from Cy5-labeled DNA substrate

	Fast holoenzyme dissociation		Slow holoenzyme dissociation
Sample	Amplitude	Rate, s−1	Amplitude	Rate, s−1
No recycling			2.637 ± 0.004	0.0049
Collision model	0.415 ± 0.006	0.82 ± 0.03	2.245 ± 0.002	0.00222 ± 0.00001
Signaling model	0.84 ± 0.03	0.0241 ± 0.0007	1.08 ± 0.02	0.0040 ± 0.0002

Upon encountering a pppRNA–primase complex in the signaling model, 44 ± 2% of the holoenzyme dissociated approximately six times faster than the stalled holoenzyme with a half-life of 28.8 ± 0.9 s, whereas the remaining 56 ± 1% of the holoenzyme dissociated with a half-life of 2.87 min (172 ± 9 s). The former population of holoenzyme (∼45%) is the same percentage of holoenzyme that was blocked by a pppRNA–primase complex in the Okazaki fragment extension assays (45 ± 7%). These data suggest that this population of holoenzyme has been blocked by the pppRNA–primase complex and dissociated from the substrate. The dissociation rate of the latter ∼56% of the holoenzyme is similar to the rate observed in the stalled holoenzyme case and is the same percentage of holoenzyme that extended a primer to the end of the template in the Okazaki fragment extension assays containing pppRNA–primase complex (55 ± 7%). Taken together, these data suggest that this population of holoenzyme bypassed the pppRNA–primase complex. In the context of a complete T4 replisome, holoenzyme dissociation due to collision with a pppRNA–primase complex would be expected to entail subsequent recycling and initiation of a new Okazaki fragment—that is, the signaling model. Although the dissociation rate of a holoenzyme encountering a pppRNA–primase complex does not match the dissociation rate of a holoenzyme encountering an Okazaki fragment (0.0241 ± 0.0007 s⁻¹ vs. 0.82 ± 0.03 s⁻¹) and appears to be too slow to support coupled leading- and lagging-strand synthesis, other proteins and/or protein–protein interactions in the replisome, especially the dimerization between the leading- and lagging-strand polymerases (17), may accelerate the lagging-strand polymerase dissociation rate to a physiologically relevant level in a complete replisome.

pppRNA–Primase Complexes Act as Signals for Polymerase Recycling.

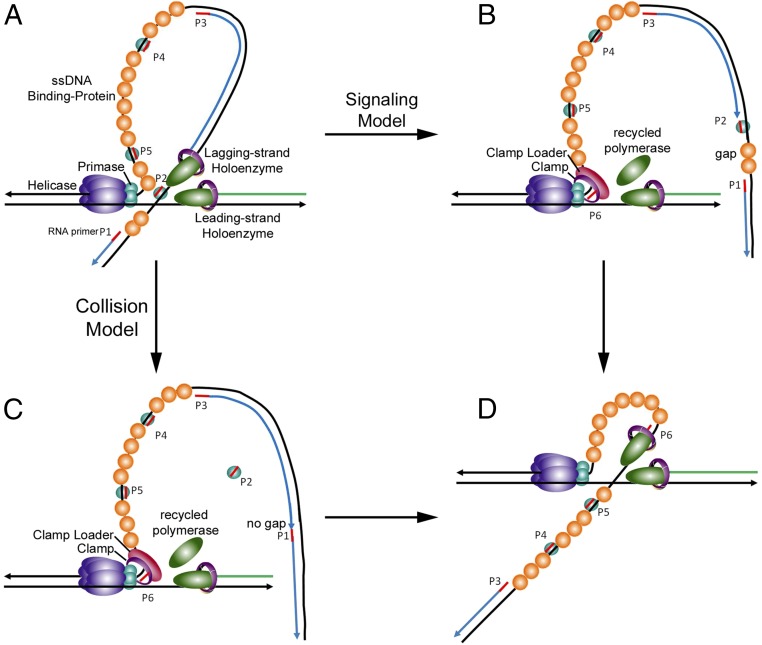
Our data suggest that the lagging-strand polymerase may be triggered to recycle to begin a new Okazaki fragment in the signaling model by collision with unused primer–primase complexes on the lagging-strand DNA (Fig. 3A). When the lagging-strand holoenzyme encounters a pppRNA–primase complex, either it can be blocked, which triggers the early recycling of the holoenzyme and creates a gap between the two Okazaki fragments as described in the signaling model (Fig. 3B), or it can read through this potential block, eventually colliding with the previous Okazaki fragment, which also triggers its release and recycling as described in the collision model (Fig. 3C). In either case, the polymerase is retained within the replisome and is recycled to initiate the next Okazaki fragment (18, 19) (Fig. 3D).

Fig. 3.

Proposed model for pppRNA–primase complex as the signal for lagging-strand initiation. (A) During the replication phase of Okazaki fragment synthesis, primase subunits within a replisome stochastically synthesize 5-mer RNA primers at priming sites along the lagging-strand DNA; these primers are stabilized on the DNA by primase subunits dissociated from the primosome. (B) A pppRNA–primase complex forms a block, triggering recycling of the lagging-strand polymerase in the signaling model, and results in a gap between Okazaki fragments. (C) Collision with the previous Okazaki fragment triggers recycling of the lagging-strand polymerase in the collision model and results in no gap between Okazaki fragments. (D) The holoenzyme is assembled on the new RNA primer to initiate the next Okazaki fragment.

There are several advantages of a pppRNA–primase complex serving as the “signal” in the signaling model over those previously proposed. First, the signal of holoenzyme encountering a pppRNA–primase complex directly involves the lagging-strand holoenzyme as opposed to requiring the lagging-strand holoenzyme to sense events happening at a distance through protein or DNA interactions, such as primase associating with the replisome, primer synthesis, or clamp loading at a new primer. Second, the mechanism for rapid dissociation of the holoenzyme is the same for both the collision and signaling mechanism—namely, the collision with a block (either the previous Okazaki fragment or a pppRNA–primase complex), as opposed to an unknown release mechanism acting at a distance as in the previously proposed signals. Third, no unique properties are assigned to either the leading- or lagging-strand holoenzyme, such as the lagging-strand holoenzyme being less processive or synthesizing DNA faster than an identical leading-strand holoenzyme.

Stochastic Simulations of Lagging-Strand Synthesis.

We used computational modeling to simulate lagging-strand synthesis in a T4 replisome to investigate the feasibility and ramifications of primer–primase complexes acting to initiate polymerase recycling. The model consists of a single helicase moving along a strand of DNA, primase proteins that bind to the helicase and synthesize primers, clamp–clamp loader complexes that bind to these primers, and a single lagging-strand polymerase that discontinuously synthesizes DNA. Our model takes into account the cellular concentration of the distributive T4 replisome proteins, the size of the T4 bacteriophage genome, and the mechanisms and associated kinetic parameters that are available in the literature and from this work for the steps involved in lagging-strand initiation. These simulations are stochastic in nature and allow us to observe a broad distribution of Okazaki fragment lengths, gap lengths, primer utilization, and the ratio of collision to signaling metrics. A complete description of the model and kinetic parameters used are given in SI Materials and Methods.

Fig. 4A shows the distribution of Okazaki fragment lengths from stochastic simulations where pppRNA–primase complexes serve as signals for holoenzyme recycling overlaid with the distribution of Okazaki fragment lengths obtained from the in vitro T4 replisome activity on M13 DNA (20). Both distributions indicate that the majority of Okazaki fragments are less than 4,000 bp in length, with a small population extending to lengths as long as 10,000 bp, and there is good agreement between these distributions at lengths >2,000 bp. However, the peak of the histogram from the simulations at ∼250 bp is shifted relative to the peak of the histogram from the experimental data at ∼1,800 bp. This shift toward shorter Okazaki fragment lengths in the simulations, relative to the experiments, may be explained by the resolution limitation of the experimental method to detect small Okazaki fragments and/or small gaps between Okazaki fragments. This limitation may lead to the misidentification of two shorter fragments as one longer fragment, consistent with the discrepancies between these two datasets. Fig. 4B shows the distribution of gap lengths from stochastic simulations, which is broadly consistent with the distribution of gap lengths observed for the E. coli DNA replication system in single-molecule experiments (21). The simulations also report on the initiation time, the amount of lagging strand replicated, primer utilization, and the ratio of collision to signaling metrics (SI Text and Table S3), which compare favorably with experimentally determined values. Furthermore, these data were affected in an expected manner due to changes in the initial conditions, such as lagging-strand polymerization rate, primer synthesis rate, and clamp–clamp loader concentrations.

Fig. 4.

Metrics from stochastically simulated lagging-strand synthesis. (A) The stochastically simulated (black) and electron microscopy (red) Okazaki fragment length distributions display reasonable agreement. The electron microscopy data were compiled from tables 1 and 2 of ref. 20. (B) Distribution of gap lengths. (C) Distribution of distances, relative to the position of the helicase, of the pppRNA–clamp–clamp loader complexes bound by the polymerase. (D) The accumulated probability of initiation time displays two populations of recycling polymerase.

Table S3.

Metrics obtained from stochastic simulations and their variation due to changes in the initial conditions

Parameter	Value*	Median fragment length, nt	Median gap length, nt	Median initiation time, s	DNA replicated†	Primer utilization, %	Collision, %
Holoenzyme procession rate, nt⋅s−1	300	2,250	2,194	6.2	80.1	11.0	70.0
	150	1,893	2,919	5.9	66.2	8.8	63.8
	75	2,833	6,917	5.7	56.2	2.9	68.6
	30	2,968	12,491	5.6	33.9	1.1	82.1
	15	1,845	22,051	5.0	14.9	0.7	89.8
Priming rate, s−1	0.750	1,893	2,919	5.9	66.2	8.8	63.8
	0.375	3,441	5,273	10.3	70.5	7.8	70.5
	0.150	9,854	13,476	22.8	78.9	7.1	82.6
	0.075	19,048	23,544	40.4	84.7	7.8	90.3
Clamp/clamp loader concentration, molecules	1,400	1,439	1,860	2.7	71.3	13.3	67.9
	700	1,893	2,919	5.9	66.2	8.8	63.8
	350	5,410	4,859	12.4	60.1	5.5	59.9
	140	3,101	9,585	29.8	52.3	2.7	57.7

^*The default value in each case is shown in bold face.

^†The percentage of DNA synthesis was calculated as the ratio between the number of bases synthesized and the sum of the total bases synthesized and total gaps. This is fundamentally a different measure and inherently lower than the total number of bases unwound by the helicase.

In addition to these data, the simulations can provide useful qualitative insights on replisome functioning not readily accessible to direct experimental observation or investigation. We previously observed that the disassembly mechanism was the predominant primer synthesis mechanism outside of a replisome (14); however, we knew that the looping mechanism would play a larger role in primer synthesis with the presence of ssDNA-binding protein (gp32) in the context of a replisome (12). Although coordinated leading- and lagging-strand DNA replication was observed with a fused helicase–primase protein, which can only synthesize primers via the looping mechanism and therefore lacks any primer–primase complexes to initiate holoenzyme recycling, the Okazaki fragments were abnormally long and the overall amount of DNA synthesized was low compared with a wild-type replisome (14). These studies further support our proposal that primer–primase complexes generated via the disassembly mechanism can initiate holoenzyme recycling and suggest that the T4 replisome uses both the disassembly and looping mechanisms to synthesize primers for DNA replication. To determine the optimal ratio of primers synthesized via the disassembly and looping mechanisms, we performed a series of simulations varying the percentage of primers made via the looping mechanism from 5–95%. Surprisingly, a relatively high, broad range of 65–85% of primers made via the looping mechanism was optimal to best reproduce the available experimental data (Table S4), and we have used the value of 75% in our simulations. We infer that the majority of primers are synthesized via the looping mechanism during T4 DNA replication.

Table S4.

Metrics obtained from a series of simulations varying the percentage of primers made via the looping mechanism

Looping,* %	Median Okazaki fragment length, nt	Median gap length, nt	DNA replicated,† %	Primer utilization, %	Collision to signal ratio, %
5	746	15,489	10.4	1.2	38.7
10	891	11,301	16.8	2.2	29.9
15	943	9,259	20.5	3.2	28.2
20	973	7,384	24.3	4.1	28.8
25	1,015	5,977	28.5	4.9	30.5
30	1,044	5,097	32.2	5.7	32.9
35	1,085	4,368	35.5	6.4	34.4
40	1,111	4,065	38.7	7.0	37.7
45	1,159	3,654	42.7	7.6	40.9
50	1,237	3,357	46.2	8.1	44.1
55	1,313	3,138	49.8	8.5	47.5
60	1,361	2,943	53.4	8.8	50.4
65	1,522	2,989	57.0	8.9	54.4
70	1,680	2,870	62.0	9.0	59.3
75	1,893	2,919	66.2	8.8	63.8
80	2,184	3,078	71.1	8.4	69.3
85	2,589	3,204	76.3	8.0	74.8
90	3,496	3,785	82.7	7.0	81.6
95	4,980	4,864	90.2	5.7	89.9

^*The default value is shown in bold face.

^†The percentage of DNA synthesis was calculated as the ratio between the number of bases synthesized and the sum of the total bases synthesized and total gaps. This is fundamentally a different measure and inherently lower than the total number of bases unwound by the helicase.

The presence of large numbers of pppRNA–primase complexes on the lagging strand suggests that these complexes might be used by the holoenzyme to initiate Okazaki fragment synthesis. We attempted to extend primers within pppRNA–primase complexes using either polymerase alone or the full holoenzyme; however, these attempts were largely unsuccessful on a timescale relevant to Okazaki fragment synthesis (Fig. S6). Based on these data, Okazaki fragments in our model of T4 replication originate only from primers synthesized via the looping mechanism. The implication of this is that the lagging-strand polymerase will recycle to bind a newly synthesized primer whose position behind the replication fork is dictated by the brief lifetime of a naked primer and the slightly longer lifetime of a pppRNA–clamp–clamp loader complex (Movie S1). We calculated the distribution of positions of the pppRNA–clamp–clamp loader complexes bound by the polymerase, relative to the position of the helicase at the time of recycling, in our simulations (Fig. 4C). These data indicate that the polymerase binds within 400 nt of the helicase in ∼90% of recycling events. This relatively narrow distribution of distances suggests that the lifetimes of primers and pppRNA–clamp–clamp loader complexes on the lagging DNA strand are all that are necessary for the replisome to effectively self-regulate the recycling of the lagging-strand polymerase to a position near the replication fork. This self-regulation of the replisome is essential for maintaining coordinated leading- and lagging-strand DNA synthesis and avoiding replication fork collapse.

Fig. S6.

Extension of the primer in pppRNA–primase complex by holoenzyme or polymerase. (A) Denaturing polyacrylamide gel analysis testing the ability of the holoenzyme or polymerase to use the primer of a pppRNA–primase complex to initiate Okazaki fragment synthesis. The pppRNA–primase complex was first bound to a ssDNA substrate containing a primer recognition site. The reactions were initiated by the addition of holoenzyme components or polymerase and dNTPs; the reactions were quenched at the indicated time points. The resulting products were separated on a 7.5 M urea–14% polyacrylamide gel; the migration positions of the starting primer, 40-mer product, and 70-mer template are indicated. The amount of each product was quantitated using a Persona Molecular Imager (Bio Rad), and the final concentration of product in each reaction was calculated using a standard curve of dCTP [α-³²P]. (B) The amount of primer in pppRNA–primase complexes extended by holoenzyme (red high–low bars) or polymerase (blue squares) is plotted over time. Linear least squares regression of the data yields a primer extension rate of 0.22 nM primer per second for holoenzyme and 0.0024 nM primer per second for polymerase under these conditions of 200 nM pppRNA–primase complex and 300 nM holoenzyme or polymerase. During the approximate 25-s half-life of the pppRNA–primase complex, holoenzyme was able to extend only 2.8% of the primers, indicating the unlikelihood that primers synthesized by the disassembly mechanism are used to initiate Okazaki fragment synthesis.

Concerning the temporal nature of holoenzyme recycling and Okazaki fragment initiation, the simulations demonstrate that a finite holoenzyme recycling and Okazaki fragment initiation time is important for establishing and maintaining a stable Okazaki fragment length distribution and processive DNA replication. In Alberts’ original trombone model (22), the polymerase recycles only upon collision with the previous Okazaki fragment. Assuming a finite initiation time, this behavior leads to continuously increasing lengths of Okazaki fragments rather than the stochastic distribution observed in experiments (20). This discrepancy could be explained by the replisome pausing during some step(s) of lagging-strand initiation (23) and/or the lagging-strand holoenzyme synthesizing DNA faster than the leading-strand holoenzyme (24); however, there is no evidence that either of these occur in T4 replication. In contrast, the previously proposed signals, in particular those featuring primer synthesis or clamp loading as the trigger, generally entail very short initiation times. In these models, primer synthesis and clamp loading steps may occur while the lagging-strand polymerase is still synthesizing an Okazaki fragment; this reduces the wait time for Okazaki fragment initiation considerably, assuming that intracomplex rebinding of polymerase to a new clamp is very fast. If the initiation time is too short, the Okazaki fragment length continuously shortens because less lagging-strand DNA template is unwound by the helicase each time the polymerase is signaled to recycle. The initiation time for the T7 DNA replication system was observed to follow a single-exponential dependence with a decay constant of 12.0 ± 0.4 s in single-molecule experiments (2) and was subsequently shown to be dependent on the rate of primer release from the primase active site (half-life of ∼7 s) (25). However, the initiation time for the E. coli DNA replication system has been estimated to be under 0.1 s to sustain the physiological rate of DNA synthesis (7). Fig. 4D displays the accumulated probability of initiation time from our simulations. Two populations of initiation times can be seen: one where ∼25% of recycling polymerase binds to an already available pppRNA–clamp–clamp loader complex in <1 s, and a second where ∼75% of recycling polymerase must wait a median time of 5.9 s for the formation of a pppRNA–clamp–clamp loader complex. Our simulations illustrate that the joint probabilities of synthesizing a primer, capturing this primer with clamp–clamp loader, and binding polymerase to this complex result in varying initiation times that naturally provide a mechanism for successive Okazaki fragments to lengthen, whereas the signaling events provide a mechanism for them to shorten (Movie S2). The interplay between these two processes leads to a semirandom distribution of Okazaki fragment lengths in our simulations, consistent with that observed experimentally (20).

SI Text

A pppRNA–primase complex serving as the signal is consistent with the effects of Okazaki fragment length previously observed by manipulating the rate of lagging-strand holoenzyme synthesis, primase concentration or priming rate, or clamp and clamp loader concentration. Slowing lagging-strand synthesis increases the time allowed for pppRNA–primase complexes to dissociate shifting the replisome to depend more on the collision model, resulting in longer Okazaki fragments. Likewise, decreasing the primase concentration or priming rate would result in fewer pppRNA–primase complexes on the lagging-strand DNA, again shifting the replisome to depend on the collision model and increase the Okazaki fragment length. Previously, increasing the clamp and clamp loader concentrations resulted in shorter Okazaki fragment lengths, leading to the proposal that clamp loading onto a primer served as the signal for polymerase recycling. We are not proposing a role for clamp and clamp loader in the signaling model; however, increasing the concentration of clamp and clamp loader will still result in shorter Okazaki fragments in our model because clamp and clamp loader are still required for efficient initiation of the new Okazaki fragment when the polymerase recycles.

Conclusions

Taken together, our experimental data and simulations demonstrate for the T4 bacteriophage DNA replication system that primer–primase complexes left on the lagging ssDNA from primer synthesis form blocks for the lagging-strand holoenzyme and that encounters with a pppRNA–primase complexes correspond to the signal that causes the lagging-strand polymerase to recycle early, leaving a gap between Okazaki fragments as described in the signaling model. Data from previous studies that suggest a long-distance protein trigger for the signaling model are also consistent with polymerase recycling being triggered by an encounter with a pppRNA–primase complex on the lagging strand as suggested here. It is possible that pppRNA–primase complexes could signal lagging-strand polymerase recycling in other replisomes that use an independent primase protein, such as E. coli (26) and eukaryotes (27).

Materials and Methods

SI Materials and Methods details pppRNA primer and substrate synthesis, protein purification, stopped-flow fluorescence and FRET measurements, radioactive assays, and stochastic modeling of lagging-strand synthesis; SI Text and figures are also available.

SI Materials and Methods

Synthesis of Physiological RNA Primer.

The physiological RNA primer with the sequence 5′-ppp-rGrCrCrGrA-3′ with a 5′-triphosphate moiety was synthesized using a standard run-off transcription protocol with the T7 RNA polymerase (Fig. S2A). The double-stranded DNA template containing the region from –17 to –1 of the class III T7 RNA polymerase promoter followed by the complement of the desired RNA sequence was prepared from synthetic DNA oligonucleotides (IDT; promoter, 5′-GAA ATT AAT ACG ACT CAC TAT A-3′; template, 5′-TCG GCT ATA GTG AGT CGT ATT AAT TTC-3′) annealed by heating at >80 °C for 3 min and cooling gradually in the presence of 0.1 M NaCl. The T7 RNA transcription was performed overnight at 37 °C in a reaction mixture containing 3.3 μM dsDNA template, 7.5 mM of each rNTP, 34 mM MgCl₂, 1 U/μL Recombinant RNasin Ribonuclease Inhibitor (Promega), 10 mM DTT, 0.1 U/μL inorganic pyrophosphatase, and 10 U/μL T7 RNA polymerase (New England Biolabs) in 1× RNAPol Reaction Buffer (40 mM Tris⋅HCl, pH 7.9, 6 mM MgCl₂, 2 mM spermidine, 10 mM DTT). The resulting RNA product was size fractionated on a 7.5 M urea–20% polyacrylamide (19:1) gel in 1× TBE and visualized under brief UV shadowing. The gel slice was crushed and soaked overnight at 4 °C in 10 mM Tris⋅HCl (pH 7.5) and 1 mM EDTA (1× TE) with constant rotary agitation. The gel mixture was filtered through a 0.22-μm filter, and the RNA product was desalted using Sep-Pak Classic C18 Cartridges (Waters), during which any metal cations were exchanged for NH₄⁺, eluted with 25% acetonitrile:water, and dried. The RNA product was dissolved in RNase-free water, quantified with UV spectroscopy, and stored at –20 °C.

Mass spectroscopy data were acquired on a Waters Micromass LCT Premier time-of-flight mass spectrometer equipped with a Waters Alliance 2695 Separations Module and using electrospray ionization (The Huck Institute of Life Sciences Proteomics and Mass Spectrometry Core Facility, The Pennsylvania State University) to confirm authenticity and purity of the RNA product; agreement between the calculated (1,807.156) and measured (1,805.141 for [M-2H]) molecular masses was excellent (Fig. S2B).

Synthesis of Lagging DNA Strand Substrate.

Custom DNA oligonucleotides were synthesized by IDT and were PAGE or HPLC purified. The template strands of the unlabeled and Cy5-labeled lagging DNA strand substrates were constructed from two shorter oligonucleotides [template A plus (Cy5–)template B] to ensure the presence of biotin on both the 3′ and 5′ ends. Template A (5′-AGG ACG TGC GGA AGG AGT-biotin-3′) was 5′-phosphorylated by T4 polynucleotide kinase (New England Biolabs) according to the manufacturer’s protocol. It was then ligated to template B (5′-biotin-GAA TGA GGA GTA GTA GTG AAT GTA GTG AGG TA/Cy5/ATA TCG GCT GGT CTG GTC TGT GCC AAG TTG CTG CAA AA-3′) with or without the Cy5 internal label using T4 DNA ligase (New England Biolabs) with the hybridized primer (5′-ACT CCT TCC GCA CGT CCT TTT TGC AGC AAC TTG-3′) serving to bridge the two template oligonucleotides. The duplex was then purified on a native 10% polyacrylamide (19:1) gel in 1× TBE and visualized under brief UV shadowing. The gel slice was crushed and soaked overnight at 4 °C in 1× TE with constant rotary agitation. The gel mixture was filtered through a 0.22-μm filter, and the substrate was desalted using Sep-Pak Classic C18 Cartridges (Waters), eluted with 25% acetonitrile:water, and dried. The lagging DNA strand substrate was dissolved in RNase-free 10 mM Tris⋅HCl, pH 8.0, buffer and quantified with UV-Vis spectroscopy, accounting for the single- and double-stranded portions of the molecule (ε₂₆₀ = 1,071,924 M^–1⋅cm⁻¹) for the unlabeled substrate and using the Cy5 absorbance (ε₆₄₈ = 250,000 M^–1⋅cm⁻¹) for the Cy5-labeled substrate.

Proteins.

Bacteriophage T4 replication proteins primase (gp61) (28), exonuclease-deficient polymerase [gp43(exo-)] (29), clamp loader (gp44/62) (30), and clamp (gp45) (31) were purified as described previously. The gp45 concentrations reported are for the homotrimeric clamp.

The gp43(exo-) protein was labeled predominately at the N terminus with an excess of monofunctional NHS-Ester Cy3 dye for 4 h at 4 °C in labeling buffer (20 mM Hepes, pH 6.8, 100 mM NaOAc, and 10% glycerol). Unreacted dye was removed by size exclusion chromatography using a Sephadex G-25 column (12 mm × 40 cm) with isocratic elution in storage buffer [10 mM Tris⋅HCl, pH 7.8, 25 mM KOAc, 5 mM Mg(OAc)₂, 20% glycerol]. Depending on the preparation, a labeling efficiency of ∼2 dye molecules per protein monomer was calculated using the visible absorbance of the dye and the Bradford protein quantitation assay (Bio Rad). The Cy3-labeled gp43(exo-) protein was found to be as active as unlabeled gp43(exo-) in standard primer extension assays.

Blocking Okazaki Fragment Synthesis Assay.

The primer of the unlabeled lagging DNA strand substrate was 5′-phosphorylated with [γ-³²P] ATP by T4 polynucleotide kinase (New England Biolabs) according to the manufacturer’s protocol. DNA Block, a 40-mer oligo complementary to the far end of the ssDNA region (5′-GCC GAT ATT ACC TCA CTA CAT TCA CTA CTA CTC CTC ATT C-3′), was annealed to create a block at the position of the primer–protein binding site as a mimic of the previous Okazaki fragment. A slight excess of streptavidin was added to bind the biotin molecules at either end of the substrate, thereby preventing the holoenzyme from slipping off the ends of the substrate.

The holoenzyme synthesis reactions were carried out in complex buffer containing 25 mM Tris–OAc (pH 7.5), 125 mM KOAc, and 10 mM Mg(OAc)₂. The standard conditions used in all reactions consisted of 300 nM lagging DNA strand substrate, 750 nM streptavidin, and 1 mM ATP; 330 nM each of gp44/62, gp45, and gp43(exo-); 100 μM dNTPs; and 2 mg/mL ssDNA from Salmon testes (Sigma) in a typical reaction volume of 8 μL. Blocking of holoenzyme synthesis in the collision model was simulated by the annealed DNA Block oligo to the lagging-strand substrate to mimic the previous Okazaki fragment. The ability of a pppRNA–protein complex to block holoenzyme synthesis was tested by adding a combination of 0–3 μM pppRNA, HO-RNA (5′-rGrCrCrGrA-3′), or DNA (5′-GCCGA-3′) primer and 0–3 μM gp61 or 0–3 μM each of gp45 and gp44/62 following holoenzyme assembly. The DNA polymerase holoenzyme proteins [gp43(exo-), gp45, and gp44/62] were first preincubated at 25 °C with the lagging DNA strand substrate in the presence of 2 mM ATP for 1 min followed by the addition of the primer (pppRNA, HO-RNA, or DNA)–protein (gp61 or gp45 and gp44/62) complex for 1 min. The DNA synthesis activity by the holoenzyme was initiated with the addition of dNTPs and ssDNA trap. After 1 min, the reaction was quenched with 4 μL of 0.25 M EDTA and 10 mg/mL proteinase K and incubated at 37 °C for more than 6 min. An equal volume of loading buffer (formamide, 1 μg/mL bromophenol blue, and 1 μg/mL xylene cyanol FF) was added, and samples were heated at 95 °C for 2 min. Reaction products were separated on a 7.5 M urea–12% polyacrylamide gel in 1× TBE buffer and analyzed using a Personal Molecular Imager (Bio Rad).

Primer Extension Assay.

The primer extension reactions were carried out in complex buffer containing 25 mM Tris–OAc (pH 7.5), 125 mM KOAc, and 10 mM Mg(OAc)₂ at 37 °C. The standard conditions used in all reactions consisted of 300 nM nonbiotinylated template B ssDNA substrate, 200 nM pppRNA primer, and 200 nM gp61 in a typical reaction volume of 50 μL. The ability of 300 nM gp43(exo-) or holoenzyme [300 nM gp43(exo-), 600 nM each gp45 and gp44/62, and 1 mM ATP] to extend the primer of a pppRNA–protein complex was tested by initiating the reaction with 100 μM dNTPs (including 12.5 μCi of [α-³²P] dCTP) and gp43(exo-) or holoenzyme. At the indicated time points, 10 μL aliquots of the reactions were quenched with an equal volume of quench solution (0.25 M EDTA, 50% formamide, 1 μg/mL bromophenol blue, and 1 μg/mL xylene cyanol FF), and samples were heated at 95 °C for 2 min. Reaction products were separated on a 7.5 M urea–14% polyacrylamide gel in 1× TBE buffer and analyzed using a Personal Molecular Imager (Bio Rad).

Steady-State FRET Measurements.

Equilibrium fluorescence measurements of the holoenzyme loaded on the lagging DNA strand substrate were carried out on a Horiba Jobin Yvon Fluoromax 4 spectrofluorometer at 25 °C with 200 nM Cy5-DNA substrate; 1 μM streptavidin; 200 nM each of gp44/62, gp45, and Cy3-gp43(exo-); 2 mM ATP; and 100 μM each of dGTP, dCTP, and dATP. The buffer contained 25 mM Tris–OAc (pH 7.5), 125 mM KOAc, and 10 mM Mg(OAc)₂. The sample was excited at 514 nm (2 nm slit width), whereas the emission spectra was recorded from 540–750 nm (5 nm slit width) with a 0.1-s integration time.

Stopped-Flow Fluorescence and FRET Measurements.

The presteady state fluorescence reactions were monitored on an Applied Photophysics SX20 stopped-flow apparatus equipped with a fluorescence detector. The buffer contained 25 mM Tris–OAc (pH 7.5), 125 mM KOAc, and 10 mM Mg(OAc)₂.

The kinetics of pppRNA–primase complex dissociation from DNA were measured by mixing equal volumes of preassembled 400 nM Cy5-labeled lagging DNA strand substrate; 1 μM streptavidin; 800 nM pppRNA, HO-RNA, or DNA primer; and 0–500 nM gp61 in syringe A with 2 mg/mL ssDNA trap in syringe B. Upon excitation of the Cy5 dye at 600 nm, the corresponding fluorescence emission (>645 nm using a long pass filter) was recorded on a logarithmic time scale. The resulting time traces displayed a decrease in fluorescence, followed by an increase in fluorescence and finally another decrease in fluorescence and were therefore fit to the sum of three exponentials. One phase, characterized by a decrease in fluorescence, was assigned as photobleaching of the Cy5 dye based on control experiments mixing 400 nM Cy5-labeled DNA substrate and 1 μM streptavidin in syringe A with buffer in syringe B. A second phase, also characterized by a decrease in fluorescence, was assigned as quenching of the Cy5 dye by ssDNA trap based on additional control experiments mixing 400 nM Cy5-labeled DNA substrate and 1 μM streptavidin in syringe A with 2 mg/mL ssDNA trap in syringe B. To confirm the assignment of this phase, we further characterized the quenching of the Cy5 dye by varying the ssDNA trap concentration in syringe B from 0.2–2 mg/mL and demonstrating that the rate of Cy5 fluorescence quenching is dependent on the concentration of the ssDNA trap. The last phase, uniquely characterized by an increase in fluorescence, was only observed in the presence of a preassembled primase and primer–primase complex on the Cy5-labeled DNA substrate and was assigned as the release of Cy5 dye quenching upon dissociation of the primase or primer–primase complex from the DNA.

The kinetics of holoenzyme dissociation were determined by mixing equal volumes of preassembled 400 nM Cy5-labeled DNA substrate, 1 μM streptavidin, 500 μM ATP, and 400 nM each of gp44/62, gp45, and Cy3-labeled gp43(exo-) in syringe A with 200 μM each of dGTP, dCTP, and dATP; 2 mM ATPγS; and 2 mg/mL ssDNA trap in syringe B. Dissociation of the holoenzyme in the collision model was simulated by the annealed DNA Block oligonucleotide to the lagging-strand substrate in syringe A to mimic the previous Okazaki fragment. The ability of a pppRNA–primase complex to trigger holoenzyme release was tested by adding 4 μM pppRNA and primase following holoenzyme assembly in syringe A. The addition of ATPγS in syringe B increased the effectiveness of the ssDNA trap by preventing clamp loader from reloading clamp and polymerase to reform the holoenzyme in an ATP-dependent process. Upon excitation of the Cy3 dye at 514 nm, the corresponding FRET emission (>645 nm using a long pass filter) between the holoenzyme on the DNA was recorded on a logarithmic time scale. The resulting time traces displayed a decrease in FRET emission and were fit to an exponential or the sum of two exponentials as appropriate.

Stochastic Modeling of Lagging-Strand Synthesis.

Our stochastic model sought to represent lagging-strand DNA synthesis as faithfully as possible to previously determined experimental data while making minimal assumptions regarding the behavior of the replisome. The helicase processes at a deterministic rate constant of 150 nt/s and is able to bind between zero and three primase proteins simultaneously. There are 170 independent copies of primase modeled, corresponding to the measured primase protein copy number per cell (32). These primases bind to the helicase at a stochastic rate constant (c) of 0.002 molecule⁻¹⋅s⁻¹ (c = k/n_A⋅V for a second order reaction, where k is the deterministic rate constant for primase binding ssDNA, n_A is Avogadro’s number, and V is the volume of a bacterial cell in liters) and can dissociate unproductively from the helicase at a rate of 0.1 s⁻¹ (the deterministic and stochastic rate constants are equal for a first-order reaction). Although the exact k_on and k_off for the primase binding to helicase are not known, these values are consistent with the K_d determined to be between 0.05 and 0.1 μM (28). When more than one primase is bound to the helicase, only one primase attempts to prime per time step, consistent with the expectation that only one primase is able to scan the template DNA for a priming sequence at any moment in time. When primase is bound to helicase, it synthesizes primers at a deterministic rate constant of 0.75 s⁻¹; built into that priming rate is the frequency of priming recognition sites on ssM13 DNA (28). Additionally, we have included a 10-nt footprint to disallow multiple priming events in nonphysically close proximity to each other. Primase subunits may synthesize primers either by a disassembly mechanism (whereby a primer–primase complex is left at the priming site) or by a looping mechanism (whereby a primer only is left at the priming site) (14). For primers synthesized by the looping mechanism, additional priming events were disallowed in a 170-nt region upstream of the priming site to represent the formation of a priming loop (14). Using our model, we have tested a range of percentages of primers synthesized by the looping versus the disassembly mechanism, as the physiological partitioning between these two mechanisms is not well known. This proportion is important, as in our model disassembly primers may constitute a signal to recycle whereas looping primers cannot.

If priming has occurred via disassembly, the resulting primer–primase complex may dissociate from the DNA at the measured rate of 0.03 s⁻¹ (this work). When primer–primase complexes dissociate, we have chosen to dissociate both the primer and primase rather than leaving the primer bound to DNA to independently bind the clamp or dissociate. This decision was based on the expectation that the pppRNA primer has a greater affinity for the primase than it does for the DNA. In addition, we have evidence that suggests the ability of clamp–clamp loader to bind the primer in a primer–primase complex and displace primase is very low (Fig. S6). Therefore, primers synthesized by the disassembly mechanism to create a primer–primase complex are not extended into Okazaki fragments in our model but contribute to the low primer utilization rate observed for the T4 replisome.

If priming has occurred via looping to create a primer/template junction, a clamp–clamp loader must capture the naked primer before it dissociates at an estimated rate of 1.2 s⁻¹ (33). We have represented clamp and clamp loader in this model through explicit representation of 700 equivalents of clamp–clamp loader complexes, corresponding to the measured limiting protein copy number of gp62 subunit per cell (32). Clamp–clamp loader complexes bind naked primer/template junctions at the stochastic rate constant of 0.0006 molecule⁻¹⋅s⁻¹, k = 0.6 μM⁻¹⋅s⁻¹ (34). Once clamp–clamp loaders have bound a primer, they may dissociate at a measured rate of 0.3 s⁻¹ (34) or productively bind polymerase with an arbitrary rate of 10.0 s⁻¹ to form a holoenzyme. The clamp loader recycles once polymerase has bound, forming a holoenzyme with the clamp rather than after completion of the Okazaki fragment when clamp and polymerase recycle.

Once the holoenzyme is formed, it begins to synthesize an Okazaki fragment at the deterministic rate constant of 150 nt⋅s⁻¹. The holoenzyme will unbind immediately if it collides with the previous Okazaki fragment or the beginning of the DNA strand. If the holoenzyme encounters a primer–primase complex, it will unbind immediately according to the 45% probability to signal holoenzyme recycling or continue synthesizing the current Okazaki fragment according to the 55% probability to bypass a primer–primase complex bound to DNA (this work). If the holoenzyme encounters a pppRNA or pppRNA–clamp–clamp loader complex, these species will unbind and the holoenzyme will continue with a 100% bypass probability, as indicated by the experiments. When the holoenzyme unbinds due to signaling, all primer–primase complexes and primer–clamp–clamp loader complexes in the resulting gap are forcibly unbound to prevent nonphysical depletion of these species from the free store of unbound proteins in the simulation.

All species begin the simulation in an unbound state, with the exception of the helicase, which begins bound to DNA and remains so throughout the simulation. The dynamic binding and unbinding of various replication machinery throughout the simulation occurs at discrete time steps according to stochastic dynamics governed by random number generation and rate constants, either measured in this work, obtained directly from the literature, or estimated from the literature to the best of our abilities. We did not require a minimum template length before allowing the holoenzyme to form and begin synthesizing the first Okazaki fragment. We have tested the effects of variations of these parameters to illustrate the robustness of the model and have generally observed only modest effects due to these perturbations.

Simulations were performed in discrete time steps of 0.005 s, corresponding to ∼1 nt per step procession rate, based on the 150 nt/s procession rates of the helicase and the polymerase in the model. For variation of the ratio of looping versus disassembly, 1,000 trajectories, each 1,000 s in length, were performed, whereas for the default model and for tests of other parameters, 10,000 trajectories, each 1,000 s in length, were performed for each condition. Random numbers were generated using the double-precision SIMD-oriented Fast-Mersenne Twister algorithm (35). Videos were created using Visual Molecular Dynamics and rendered with Tachyon (36). For analysis purposes, the first and last fragment generated in each trajectory were omitted to prevent possible artifacts that these might create.