Fundamental trade-offs between information flow in single cells and cellular populations

Significance

The function of signal transduction networks is to detect changes in the extracellular environment and combine this with information on intracellular state and thereby control cell-fate decisions. Recent evidence suggests that high levels of biochemical noise in eukaryotic signaling networks interfere with information transmission, making it unclear how cell fate is correctly controlled. Here, we show that high noise levels are advantageous when a system needs to regulate the behavior of populations of cells using noisy biological signals. In contrast, when the key biological unit is a single cell, we show that the impact of noise on cellular responses is much less pronounced. Understanding how noise is generated and exploited advances our understanding of information processing in cells.

Abstract

Signal transduction networks allow eukaryotic cells to make decisions based on information about intracellular state and the environment. Biochemical noise significantly diminishes the fidelity of signaling: networks examined to date seem to transmit less than 1 bit of information. It is unclear how networks that control critical cell-fate decisions (e.g., cell division and apoptosis) can function with such low levels of information transfer. Here, we use theory, experiments, and numerical analysis to demonstrate an inherent trade-off between the information transferred in individual cells and the information available to control population-level responses. Noise in receptor-mediated apoptosis reduces information transfer to approximately 1 bit at the single-cell level but allows 3–4 bits of information to be transmitted at the population level. For processes such as eukaryotic chemotaxis, in which single cells are the functional unit, we find high levels of information transmission at a single-cell level. Thus, low levels of information transfer are unlikely to represent a physical limit. Instead, we propose that signaling networks exploit noise at the single-cell level to increase population-level information transfer, allowing extracellular ligands, whose levels are also subject to noise, to incrementally regulate phenotypic changes. This is particularly critical for discrete changes in fate (e.g., life vs. death) for which the key variable is the fraction of cells engaged. Our findings provide a framework for rationalizing the high levels of noise in metazoan signaling networks and have implications for the development of drugs that target these networks in the treatment of cancer and other diseases.

Signaling networks allow cells to sense intra- and extracellular concentrations of cytokines, nutrients, ions, and so on and control both discrete and continuous changes in cell state (1–5). Apoptosis and the commitment to cell division are typical of binary responses, whereas directed cell movement and induced gene expression are typical of continuously variable responses (2, 4, 6). Dysregulation of intracellular signaling has been implicated in a wide range of diseases including cancer, chronic inflammation, neurodegeneration, and others (7). Understanding how information is processed in cells will be essential to developing rational therapies for treating such diseases (5, 8). Although signaling networks have long been the subject of intense experimental and theoretical study, it has only recently become possible to monitor signal transduction at the level of individual cells (1, 9, 10). These studies have shown that signaling networks are subject to significant noise, which manifests itself as stochastic fluctuations in the activities of signaling proteins and as cell-to-cell variability among genetically identical cells in a population (1, 3, 8, 11–15). Such noise is ubiquitous and, although its physiological impact remains unclear (16–18), variability has been shown to reduce the effectiveness of drugs that inhibit oncogenic and inflammatory signaling (8).

Information theory (19) provides a powerful analytical framework for quantifying the impact of noise on the ability of a system to transmit information. Levchenko and coworkers pioneered the application of information theory to signaling in mammalian cells (9) with the concentration of an extracellular ligand (e.g., the inflammatory cytokine TNF-α) serving as the input to a (potentially noisy) intracellular signaling network (or channel), leading to a downstream response that can be experimentally measured (the nuclear translocation of NF-κB). They estimated a channel capacity (which is the maximum information a system can transmit) of less than 1 bit for TNF-induced NF-κB translocation to the nucleus based on single-cell data (Table 1, entries 1–4 and 12) (9, 20–22). Because the number of distinct signal values that can be resolved approaches 2^C asymptotically (23), this analysis implies that intracellular signaling networks are barely able to distinguish between the presence or absence of TNF.

Table 1.

Estimated channel capacity for experimental data

Signal, response	Signal	Response	${\widehat{C}}_{S,P}$ (bits)	Data source	Calculation source
Molecular, molecular	1. TNF	NF-κB	0.92 ± 0.01	9	9
	1.1. TNF	ATF-2	0.85 ± 0.02	9	9
	1.2. TNF	NF-κB & ATF-2	1.05 ± 0.02	9	9
	2. PDGF	NF-κB	0.67 ± 0.01	9	9
	2.1. PDGF	ATF-2	0.74 ± 0.01	9	9
	2.2. PDGF	NF-κB & ATF-2	0.81 ± 0.02	9	9
	3. EGF	Erk (fold-change)	0.60 ± 0.03	21	9
	4. UDP	Peak Ca2+	1.22 ± 0.03	20	9
	4.1. UDP	Integrated Ca2+	1.07 ± 0.02	20	9
	5. TNF	A20 transcripts	0.84 ± 0.10	24	This work
	6. TRAIL	Casp-8 activity	1.01 ± 0.01	This work	This work
	7. TRAIL	Casp-8 activity (live cells)	1.01 ± 0.01	This work	This work
	8. TRAIL	Casp-3 activity	0.56 ± 0.01	This work	This work
	9. Casp-8 activity	Casp-3 activity	1.23 ± 0.01*	This work	This work
	10. Casp-8 activity	Cell decision	0.63 ± 0.01	This work	This work
	11. α-Factor	pFUS1-GFP	2.26 ± 0.04	6	This work
Position, molecular	12. Embryo perimeter	Phosphorylated Erk	1.61 ± 0.05	22	9
Position, motion	13. Bacterium	Neutrophil motion	1.82 ± 0.11		This work
	14. cAMP	Dictyostelium motion	2.19 ± 0.08	Firtel laboratory	This work
Molecular, population	15. TRAIL	% dead (HeLa; resampled)	2.44 ± 0.02	This work	This work
	16. TRAIL	% dead (HeLa; FACS)	3.41 ± 0.03	This work	This work
	17. TRAIL	% dead (MCF10A)	3.38 ± 0.01	This work	This work

The estimated channel capacity for population-level response in HeLa cells was calculated using 1,000 cells per TRAIL concentration and all population-level channel capacities were calculated using 100 independent populations. Ranges on values in the table represent 95% confidence intervals, calculated using the robust variance estimator (see Materials and Methods and SI Appendix). Bootstrap estimates of the confidence intervals result in similar values (Table S1 and SI Appendix).

^*Indicates that the value is an underestimate (the optimal number of bins for estimation was not reached due to computational limitations).

More recent research has focused on characterizing strategies that cells might use to achieve higher levels of information transfer. Lee et al. (24) argued that detecting the fold change between a steady-state and induced signal reduces the impact of noise, although we found that fold-change detection in the TNF system still transmits less than 1 bit of information (entry 5, Table 1). Wollman and coworkers (10) recently demonstrated that using multiple time points from the trajectory of a molecular response (e.g., Erk activation over time) significantly increases estimated channel capacities. However, for a cell to use dynamics to increase C requires biochemical circuits for storing and retrieving information, which would themselves be subject to noise (10).

It is difficult to interpret the physiological significance of low channel capacities in published work on signaling because the outputs being measured (e.g., nuclear localization of the NF-κB transcription factor or Erk activation) do not correspond directly to well-defined changes in cell fate (9, 24). We therefore focused on an unambiguous phenotype: life or death as regulated by TNF-related apoptosis-inducing ligand (TRAIL). TRAIL induces apoptosis by binding to cell surface receptors and initiating the formation of death-inducing signaling complexes (DISCs). These complexes then initiate a sequence of biochemical events resulting in mitochondrial outer membrane permeabilization (MOMP), activation of the effector caspases (ECs), and cell death (Fig. 1A). Dramatic cell-to-cell variability has been observed in the responses of clonal cells to TRAIL (and other death ligands): a subset of cells dies within 2–8 h of ligand exposure, whereas others survive indefinitely. When these survivors are reassayed for TRAIL sensitivity following outgrowth the same fractional killing is observed, showing that variability is a stable property of the cell population. Molecular studies have shown that this variability arises from extrinsic noise in receptor-to-caspase signaling networks (1, 11, 12).

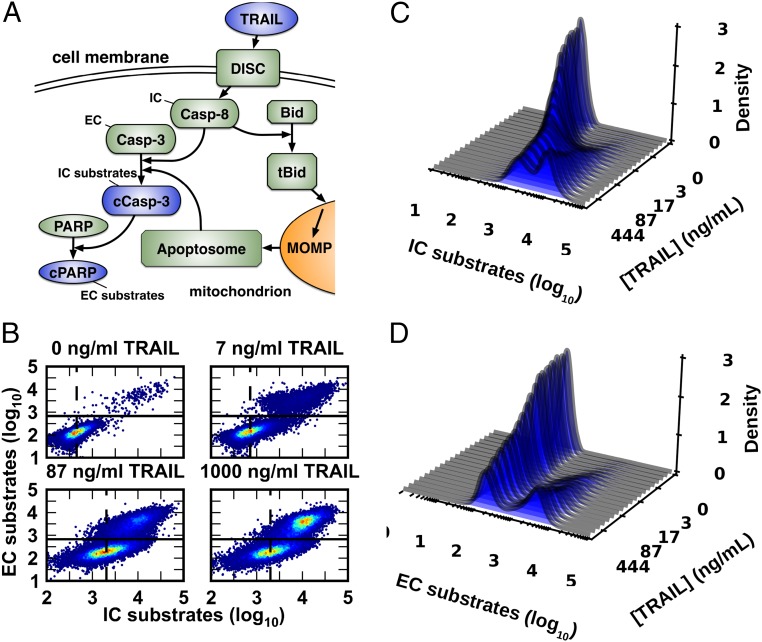
Fig. 1.

Cell-to-cell variability in response to a range of TRAIL doses. (A) TRAIL activates the IC Casp-8 via DISCs. Active Casp-8 then activates the EC Casp-3 via two mechanisms: direct cleavage and MOMP, which induces formation of the apoptosome, another activator of Casp-3 (13). (B) Measurement of cleaved EC and IC substrates by flow cytometry (13) shows that HeLa cells have a highly variable response to TRAIL across a wide range of doses (n = 60,000 cells per TRAIL dose). The solid line is the minimum density in the bimodal EC response (∼2.8 in log₁₀ units) and acts as a threshold for apoptosis, whereas the dashed line marks the average IC response for nonapoptotic cells. We used kernel density estimators to estimate TRAIL-dependent response distributions for IC (C) and EC (D) activity.

In this paper we show that noise in cell signaling has different effects at the level of single cells and cell populations. When the key physiological output is the behavior of a single cell (as in chemotaxis or mating), high levels of information transfer are observed, implying that noise is likely suppressed (10, 16–18, 24). However, when the key physiological output is the fraction of cells in a tissue or population committing to apoptosis, increased noise reduces information transfer at the level of single cells while increasing it at the level of cell populations. This trade-off between single-cell and population-level information flow is particularly significant when the input signal (e.g., ligand concentration) itself exhibits even small amounts of noise.

Results

Estimating Channel Capacities.

The information carried by a channel is quantified by the mutual information, I:

$$I\left(X;Y\right)={\displaystyle \sum _X{\displaystyle \sum _{Y}p\left(x,y\right)\log \frac{p\left(x,y\right)}{p\left(x\right),p\left(y\right)}}},$$ [1]

where X is the random variable representing the signal and Y is the variable representing the response (9, 19). The base of the logarithm determines the units of the mutual information: the conventional base 2 quantifies information in “bits” (25). Because the value of I depends on the input distribution, the mutual information of a signaling channel represents a combination of the properties of the signal and the intrinsic limits of the channel itself. Therefore, using mutual information to evaluate information flow in cell signaling networks necessitates an analysis of the properties of input signal distributions in vivo, which are rarely known.

The maximum possible information that a channel can carry, the channel capacity, C, is

$$C=\underset{p_X\left(x\right)}{\sup }I\left(X:Y\right),$$ [2]

where the supremum (the least upper bound) is evaluated over all possible choices of the probability distribution of the input. C is an inherent feature of the channel: the larger the value, the more information that a channel can theoretically transmit (9, 19).

Although Eqs. 1 and 2 seem straightforward, estimation of mutual information and channel capacity from experimental data is a nontrivial challenge. Recent algorithms make it possible to estimate the channel capacity between cellular signals and the downstream responses they control (9). These approaches use empirical dose–response data to estimate p(y|x) and then search over a finite set of input distributions P = {p_X(x)} to find the one that maximizes I. Although the resulting values are reported as “channel capacities” (9, 10), with a finite set of possible input signals S and a finite set of probability distributions P, one cannot find the supremum as defined in Eq. 2 (25, 26). We therefore refer to the maximum mutual information calculated in this manner as the “estimated channel capacity given S and P” (Ĉ_S,P) or simply the “estimated channel capacity” (Ĉ).

To facilitate comparison between our calculations and those performed by Cheong et al. (9) we designed a software package to estimate mutual information based on the binning procedure they applied in their work (see Materials and Methods and SI Appendix for further details). This software is freely available (https://github.com/ryants/EstCC).

Individual Cells Responding to TRAIL Exhibit a Low Channel Capacity.

To estimate the channel capacity of the extrinsic apoptosis signaling cascade, HeLa cells were treated with TRAIL for 11 h over a range of ligand concentrations from sub- to superphysiological, and molecular responses in single cells were then measured by flow cytometry (12). The level of cleaved caspase-3 (cC3) served as a measure of the time-integrated activity of initiator caspases (ICs) and cleaved PARP (cPARP) served as a measure of downstream EC activity (Fig. 1A). Previous studies have shown that TRAIL exposure results in a dose-dependent increase in IC activity that varies significantly from cell to cell; in any single cell, when IC activity exceeds a threshold set by antiapoptotic Bcl-2 proteins, ECs are activated and the cell proceeds inexorably to death (Figs. 1 B–D) (1, 12).

Using the distributions of IC and EC activity in single cells, we calculated an estimated channel capacity between TRAIL dose and IC activity of Ĉ ∼1.01 bits and between TRAIL and EC activity of Ĉ ∼0.56 bits (entries 6 and 8, Table 1). Previous studies in our groups using identical experimental methods show high correlations between technical and biological repeats, suggesting that low estimated channel capacities are unlikely to reflect noise in the instrument or errors in experimental technique (27). We considered the possibility that dead or dying cells (those with EC levels above the death threshold) would exhibit apparently increased levels of IC activity due to feedback by ECs (28), masking or degrading the signal contributed directly by the upstream TRAIL/receptor axis. We therefore estimated channel capacity between TRAIL and IC activity in surviving cells that did not activate ECs and observed similarly low values (entry 7, Table 1 and SI Appendix, Figs. S3 and S4).

To determine whether noise was introduced primarily by the upstream (receptor to IC) or downstream (IC to EC) step, we calculated the channel capacity between IC and EC activity and obtained Ĉ = 1.23 bits (entry 9, Table 1). The larger Ĉ for the downstream step compared with both the upstream step (TRAIL to IC, Ĉ = 1.01 bits) and the overall process (TRAIL to EC, Ĉ = 0.56 bits) indicates that, whereas activation of ICs by a given TRAIL dose is highly variable among cells, IC activity itself is predictive of cellular responses, consistent with our previous work (1, 29).

Populations of Cells Responding to TRAIL Exhibit High Channel Capacity.

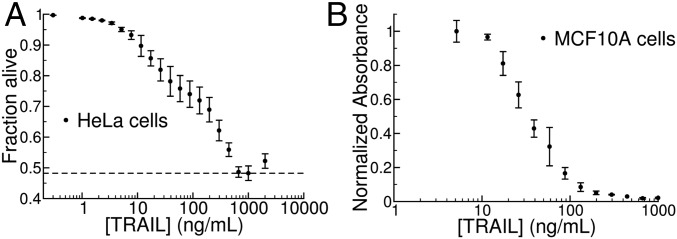
When we examined the channel capacity between TRAIL dose and phenotypic response at the population level we obtained a very different result. The combination of noise and a threshold causes the fraction of cells that die to vary smoothly with TRAIL concentration (1, 13–15, 30). For either of two cell types (transformed HeLa and nontransformed MCF10a cells) we found that the fraction of cells surviving exposure to TRAIL gradually decreased as the concentration of ligand increased over a 10³-fold range, with comparatively little variance between replicate experiments (Fig. 2). As a result, the estimated channel capacity between TRAIL dose and the fraction of cells undergoing apoptosis was much higher than that observed for the molecular response in single cells, Ĉ ∼3.4–4 bits depending on the population size (entries 15 and 16 in Table 1 and Fig. 3). This finding suggests that low information transfer at the single-cell level is accompanied by high rates of transfer in cell populations, allowing TRAIL dose to control the fraction of cells that die without precisely specifying which cells in the population cross the IC activity threshold.

Fig. 2.

Population-level dose–response relationship for TRAIL-mediated apoptosis. (A) We used the threshold described in Fig. 1B to map data from HeLa cells to fractional survival at varying TRAIL doses. We recorded a maximal effect at [TRAIL] = 1,000 ng/mL (indicated by the dashed line); higher doses of TRAIL lead to less fractional killing in a “ligand squelching” effect that we have consistently observed for this system. Because the channel capacity represents a supremum over all possible probability distributions of input signals, we removed the final point ([TRAIL] = 2,000 ng/mL) from our analysis without loss of generality. Error bars indicate sample standard deviation across three replicates of 20,000 cells each. (B) Fraction of MCF10A cells surviving TRAIL treatment as assayed by methylene blue staining (SI Appendix) (12) shows a graded response similar to that of the HeLa population in A.

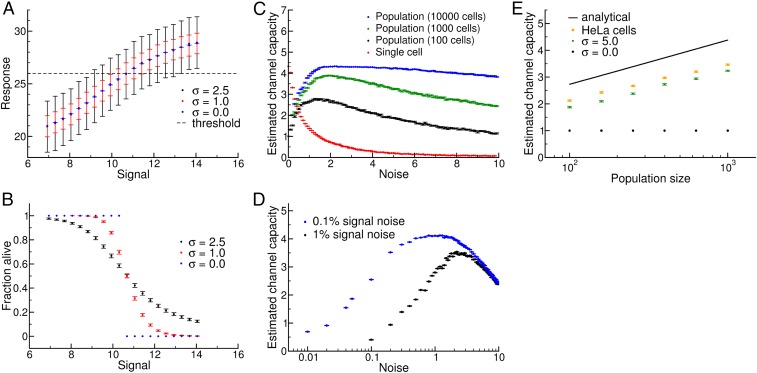
Fig. 3.

Relationship between single-cell and population-level channel capacity. (A) Single-cell dose–response behavior for the model described in Eq. 3 (see SI Appendix for model parameters). The mean response and standard deviation of 1,000 independent simulated “cells” is shown for various noise values, relative to a cell death threshold (dashed line). (B) Population dose–response behavior from P = 100 independent populations with n = 1,000 cells per signal. Individual cells’ response map to either death or survival according to the threshold in A. (C) Increasing noise decreases information transmission in single cells and simultaneously increases the population-level channel capacity up to an optimal noise value. (D) Estimated channel capacity for the model in Eq. 3, but extended to include noise in the signal. Here, the x axis is the noise in the response as in C and the points represent two levels of relative signal noise (1% and 0.1%; SI Appendix). Even with arbitrarily high signal resolution, relatively high levels of single-cell noise are required to compensate for realistic levels of noise in signal values. (E) Scaling of channel capacity with population size. The black curve is our analytical prediction, C ∼ 1/2 log N. The orange points were obtained by resampling our experimental data for HeLa cells at the indicated population sizes, and the green points are results from our Gaussian signal-response model. Note that Ĉ is slightly lower in both cases, and there is a slight deviation in the scaling relationship at higher values of N; both of these phenomena derive from limited sampling of signals (i.e., a particular ΔS; SI Appendix).

A Trade-Off Between Single-Cell and Population-Level Information Transfer.

To understand how noise in single cells contributes to high channel capacity at a population level (3, 13–15) we created a series of simple models of intracellular signaling. In the first model, the response R of individual cells to a signal dose S is related by a Hill function modified to account for noise:

$$R=\left(R_{\max }-R_{\min }\right)\mathrm{\cdot }\frac{S^n}{S^n+K^n}+R_{\min }+\epsilon ,$$ [3]

where K is the concentration of an input ligand that results in a half-maximal response, n is the Hill exponent (a measure of ultrasensitivity in the dose–response relationship), R_min and R_max represent the range of average responses, and ε is a noise term sampled from a Gaussian distribution with mean μ = 0 and variable standard deviation, σ (12). We used this model to generate a series of single-cell dose–response curves with different levels of noise (Fig. 3A) and estimated Ĉ(S;R) using the same approach we applied to the experimental data (Figs. 1 and 2). To map individual cell responses to a binary decision, we introduced a threshold θ (dashed line in Fig. 3A): individual cells with R < θ survive, whereas those with R ≥ θ die. This mimics the MOMP threshold set by antiapoptotic Bcl-2 proteins (12). Using this threshold, we can obtain population-level transitions in the percentage of cells that die as a function of S (Fig. 3B).

For simulated populations of n = 10² to 10⁴ cells, this model revealed a striking trade-off between the estimated channel capacity for single cells and populations. In this case, we used an evenly spaced set of signal values characterized by a minimal signal resolution ΔS, similar to experimental systems (Figs. 1 and 2) (9, 10). When noise is low, the entire population-level transition happens between two neighboring S values, leading to a step-like response in the population (Fig. 3 A and B, blue). At higher levels of noise, the response of individual cells becomes more variable, and the fraction of cells that die gradually increases (Fig. 3 A and B, black and red) (1, 13–15, 30). Low noise thus leads to high estimated channel capacities between S and R measured at the single-cell level (5 bits or more) but low estimated channel capacities between S and the fraction of cells that die (∼1 bit or less, Fig. 3C).

Although the trade-off observed in Fig. 3C is suggestive, it is important to note that the minimal step size ΔS used for this calculation is arbitrary. If, instead, we use the principle of gain adaptation (i.e., adjusting ΔS so that signal values are finely sampled when R varies most rapidly) (25, 26), we find that population-level channel capacities become insensitive to noise below a certain ΔS value (SI Appendix, Figs. S12 and S13). To better characterize the relationship between single-cell noise and population-level information transfer we developed an analytical framework for the S/R model (SI Appendix, sections 5–7). Although the channel capacities for the original model with Gaussian-distributed noise could not be expressed in closed form, a simplified model with a uniform distribution of noise proved to be analytically tractable. In this simplified model, if we consider the limit of continuous signals (i.e., ΔS →0), we find that the estimated population-level channel capacity follows:

$$C\mathrm{\sim }\frac{1}{2}\log N$$ [4]

for any nonzero value of noise below a certain threshold (SI Appendix, section 7).

The question then becomes: why might cells evolve networks with high levels of noise to maximize population-level information flow, if even a very small amount of noise would suffice to accurately control the population? The answer to this question likely lies in the fact that, at the local level at which they act in paracrine regulation, cytokines such as TRAIL are not present at uniform, precise concentrations. Rather, they are synthesized and catabolized locally, and therefore subject to Poisson-style birth–death noise (31, 32). To get a sense of the scale of these fluctuations, consider a tissue compartment with volume similar to that of an intestinal crypt (33, 34). In this case, the concentrations of TRAIL used in our in vitro experiments correspond to ∼10² to 10⁴ molecules per compartment. Cells must maintain these concentrations by synthesizing TRAIL to make up for cytokine loss from the compartment due to degradation or dilution, and so we can expect relative fluctuations in TRAIL concentrations to approach 1–10% (SI Appendix).

We found that, even with 1% fluctuation in the input signal, population-level estimated channel capacities drop dramatically at low levels of noise, even when ΔS is taken to be arbitrarily small (Fig. 3D). This occurs because when single-cell noise levels are low the population-level transition becomes very sharp (Fig. 3B), and ΔS must be very small to capture that transition (SI Appendix). In this case, noise in the signal generates “confusion” from nearby signals, which makes it difficult to control the population. In contrast, if levels of noise in individual cells are relatively high, the population-level transition occurs across a wide range of signal values, and the impact of small fluctuations in signal value becomes less important and population level control increases.

As mentioned above, our analytical calculations indicated that population-level channel capacity should increase as 1/2 log N. To examine the effect of population size on estimated channel capacity using experimental data, we randomly sampled subpopulations of the ∼6 × 10⁴ HeLa cells analyzed at each TRAIL dose. We found exactly the predicted dependence of population-level information transfer on population size in both our experimental data and our Gaussian model (Fig. 3E).

Low Channel Capacities Likely Do Not Represent Intrinsic Biophysical Limits.

We next explored whether the noise observed in TNF and TRAIL signaling represents a physical limit for eukaryotic signal transduction circuits. To do this, we considered two cases in which individual cells (rather than cell populations) must respond accurately to environmental stimuli. During Saccharomyces cerevisiae mating, haploid a and α cells must determine whether a suitable mating partner is sufficiently close for conjugation to be successful. Cells sense the local concentration of the mating pheromone α factor via a G protein-coupled cell surface receptor and a downstream MAP kinase cascade; when a suitable partner is available for conjugation they reorient their cytoskeleton and initiate a complex transcriptional program (4, 6). The decision to mate results in cell-cycle arrest (35) and is highly consequential for yeast cell fate, and so we expect there would evolutionary pressure for individual cells to acquire accurate information about the availability of a mating partner. We calculated Ĉ ∼2.26 bits between pheromone dose and transcriptional output as measured by a fluorescent reporter (entry 11, Table 1). This value is achieved even though we consider only single-cell data on the status of the pheromone-sensing network (6), and not the prior history of signaling, as did Doncic et al. (16−17) and Doncic and Skotheim (18); consideration of this historical information would likely increase our channel capacity estimate (10).

Another situation in which individual cells are the key biological actors is eukaryotic chemotaxis. We therefore analyzed a classic movie of a human neutrophil “hunting” a bacterial cell and a movie of a single Dictyostelium cell responding to cAMP emanating from a micropipette (https://www.youtube.com/watch?v=Kb-m1uDoWfU and Movie S1, respectively) (36). Because migrating cells are polar, it is possible to define a cell-based coordinate system using standard tracking software (CellTrack) (37). Following the lead of others working on distributions of directional movement (38), we defined the input as the angle between the chemoattractant (bacterium or micropipette) and the cell axis and the output as the angle of the subsequent motion (SI Appendix). For neutrophils and Dictyostelium we computed Ĉ ∼1.8 and C ∼2.2 bits (entries 13 and 14, Table 1), which is almost certainly a lower bound given that we simplify a 3D problem as a 2D search (Discussion). Nonetheless, we conclude that signaling networks in single cells can likely encode more than 2 bits of information.

Discussion

Our findings touch on two distinct and complementary aspects of information transfer in signal transduction: single-cell and population-level information processing. In the case of regulatory networks that control apoptosis, the key physiological variable is the fraction of cells responding at a given dose (14, 30). In this case, low estimated channel capacity at a single-cell level (Ĉ < 1) results in high capacity at a population level (Ĉ ∼3–4). We might therefore expect that when a binary cell-fate decision is the output of a signaling system, heterogeneity in the population induced by noise allows precise control of the fraction of cells above (or below) a decision threshold (1, 2, 13–15, 30).

Our analysis indicates that variability in the input signal is a key factor in understanding the interplay between single-cell noise and population-level control. With cell culture experiments in which a ligand is added at specified concentration, it is reasonable to assume that the input signal is uniform among cells. In an organism, however, the distribution of the signal is likely to be much more complex. The levels of soluble ligands are subject to fluctuation in rates of synthesis and degradation in tissue compartments of limited size. From the point of view of calculating channel capacities, a key insight of our work is that noise in the input signal limits the ability to achieve high levels of population-level control when there is high fidelity in single-cell signaling. In contrast, increasing single-cell noise allows cells to optimize population control in the face of an unpredictable and noisy environment. Although our results are suggestive, further experimental work will be needed to characterize the signal distributions that control population-level responses in vivo.

A different situation arises when individual cells must precisely resolve signals to make decisions in a continuous response space. For eukaryotic chemotaxis, we found that the single-cell channel capacity is significantly higher than has hitherto been observed (Ĉ ∼2, Table 1, entries 13 and 14). As mentioned above, we expect that this value is likely a lower bound; for instance, the data for the Dictyostelium calculation (Ĉ ∼2.2, Table 1, entry 14) exhibits tight distributions around ∼6 input angles, producing a maximum input entropy (and thus an upper limit on Ĉ) of slightly less than log₂ (6) = 2.6 bits. Because the estimated channel capacity is close to this value, we suspect that the calculated spatial channel capacity in this case is limited by insufficiently fine sampling of signaling space (i.e., the relative angle between the source of the signal and the cell).

Another prototypical example of a cell-fate decision that is critical for an individual cell but not a population is cell-cycle arrest by yeast in response to pheromone secreted by cells of the opposite mating type (35). We found that the pheromone signaling network can transmit over 2 bits of information to transcriptional responses in single yeast cells (Table 1, entry 11). Interestingly, Doncic et al. (17) thoroughly characterized the molecular mechanisms controlling this decision-making process, and they found that events such as nuclear export of Whi5 accurately predict whether a cell will arrest or commit to division. The decision to arrest the yeast cell cycle thus involves signaling motifs that integrate information over multiple time scales, from rapid sensing of pheromone gradients on the order of seconds to signaling events from multiple past generations (a timescale of many hours), enhancing control over cell-fate decisions (16, 18).

These findings suggest that low channel capacities at a single-cell level (Ĉ < 1) do not reflect an inherent limit in the biochemistry of signal transduction, but rather a natural trade-off between the knowledge that individual cells have about their environment and the ability of multicellular organisms to control responses reliably at the population level. With respect to noise levels in these systems, two nonexclusive possibilities exist. The first is that networks that control cellular populations simply exploit noise that arises from stochastic fluctuations in transcription, protein synthesis, and related processes whereas chemotactic and mating networks have evolved to suppress it (10, 16–18). The second is that some signaling networks have actually evolved higher levels of noise than the underlying biophysics might dictate (39–42). Expression of T-cell receptors seems to be one case in which regulatory networks are structured to increase cell-to-cell variability (13). In either case, the physiological importance of noise may explain why drugs that target cellular decision networks have difficulty eliciting complete population-level responses (8). Understanding and ultimately exploiting biological noise is thus likely to be as important for therapy as it is for understanding metazoan signaling.

Materials and Methods

Experimental Methods.

See SI Appendix, section 8 for details on the experimental methods used in this work.

Calculating Mutual Information.

Our method for calculating channel capacities was based on the approach described in Cheong et al. (9). As in their case, we randomly resampled the data across a range from 60 to 95% to extrapolate the mutual information at infinite sample size. The error ranges reported in Table 1 are the 95% confidence intervals for the estimate of mutual information extrapolated to infinite sample size. The source code can be found at https://github.com/ryants/EstCC and a complete description of the estimation procedure is given in SI Appendix.