Estimation of the Optimal Regime in Treatment of Prostate Cancer Recurrence from Observational Data Using Flexible Weighting Models

Summary

Prostate cancer patients are closely followed after the initial therapy and salvage treatment may be prescribed to prevent or delay cancer recurrence. The salvage treatment decision is usually made dynamically based on the patient's evolving history of disease status and other time-dependent clinical covariates. A multi-center prostate cancer observational study has provided us data on longitudinal prostate specific antigen (PSA) measurements, time-varying salvage treatment and cancer recurrence time. These data enable us to estimate the best dynamic regime of salvage treatment, while accounting for the complicated confounding of time-varying covariates present in the data. A Random Forest based method is used to model the probability of regime adherence and inverse probability weights are used to account for the complexity of selection bias in regime adherence. The optimal regime is then identified by the largest restricted mean survival time. We conduct simulation studies with different PSA trends to mimic both simple and complex regime adherence mechanisms. The proposed method can efficiently accommodate complex and possibly unknown adherence mechanisms, and it is robust to cases where the proportional hazards assumption is violated. We apply the method to data collected from the observational study and estimate the best salvage treatment regime in managing the risk of prostate cancer recurrence.

1. Introduction

Usually after initial treatment, patients with clinically localized prostate cancer are actively monitored for possible cancer recurrence by measuring prostate-specific antigen (PSA). A noticeable rise in the levels of PSA is considered as an indicator for increased risk of cancer recurrence and in these situations salvage androgen deprivation therapy (SADT) would typically be applied to delay the recurrence. The reduction in the hazard of recurrence due to SADT has been estimated using various regression approaches (Kennedy et al., 2010; Taylor et al., 2014). Clinically, “when to start SADT” is hard to determine because early initiation of SADT has both benefits and harms. If SADT is given too early when PSA values are still low, it is wasted during the time when the patient is at low risk, while later on the beneficial effect may wear off as the patient develops resistance. On the other hand if the patient waits to start SADT until PSA is very high, it becomes less effective because by that time the cancer is already well established and may have already spread to other sites.

In this paper, we try to directly address the above question and make recommendations on when would be the optimal time to start SADT in terms of prolonging a patient's cancer recurrence free survival. We use flexible weighting models based on longitudinally collected PSA data to estimate an optimal regime. This situation can be framed as a dynamic treatment regime (DTR) (Murphy, 2003; Robins, 2004), in which dose or treatment is frequently modified according to a patient's current history and disease status. Identifying such optimal dynamic decision rules offers an effective vehicle for personalized management of chronic diseases, for which a patient typically has to be treated at multiple stages.

Although data from sequential multiple assignment randomized trials (SMARTs) are desirable (Murphy, 2005) to evaluate the performance of different DTRs, observational studies are the most common source of data. Careful formulation and assumptions are required to make valid causal inference, especially on how the observational data may restrict the set of DTRs that can be assessed, which are called the feasible (Robins, 1994) or viable (Wang et al., 2012) DTRs. A variety of estimation approaches have been developed for this situation. Murphy (2003) and Robins (2004) generalized the G-estimation method of structural nested models (Robins, 1986) for optimal treatment regime estimation. Furthermore, Q-learning (Watkins, 1989; Watkins and Dayan, 1992; Murphy et al., 2007) and advantage learning (A-learning, Murphy, 2003; Robins, 2004; Blatt et al., 2004) became more and more popular in this field, which are closely related to reinforcement learning methods (Sutton and Barto, 1998) for sequential decision-making in computer science. However, the computational burden of these methods also increases substantially as the number of decision-making stages increases. For chronic diseases, it is common to have a long follow-up period with many clinical visits where new treatment could be initiated dynamically. In these situations, methods based on inverse probability weighting (IPW) are easier to conduct and provide certain robustness against model mis-specifications (Hernán et al., 2006; Robins et al., 2008). But the validity of these approaches still relies on correct model assumptions of the treatment assignment mechanism. This is especially challenging in our prostate cancer study, because the treatment assignment in this observational study is not completely understood, and the nonlinear PSA trend makes it difficult to model the treatment time. Furthermore, the typical proportional hazard assumption is also likely to be violated when comparing different regimes; thus causal differences between regimes may not be well summarized by a single hazard ratio parameter.

The robustness of estimation and model selection for both treatment and outcome models have been discussed in the literature (Mortimer et al., 2005; Neugebauer et al., 2012; Zhang et al., 2013). Nonparametric modeling has been suggested for doubly robust estimators to increase model flexibility and stability (Stitelman et al., 2012). Among which, the successful implementation of Super Learner (Van der Laan et al., 2007) has suggested the potential of machine learning methods to account for the complexity in the underlying mechanism (Neugebauer et al., 2013, 2014). Following the spirit of these researches, we propose to use a flexible approach that imposes minimal model assumptions for the unknown and potentially complicated treatment assignment mechanism. Specifically, we focus on evaluating a class of pre-specified viable DTRs for a time-to-event outcome, with the goal of estimating, from the observational data, the optimal regime to initiate SADT for prolonging the time before cancer recurrence, and we compare different regimes without assuming that the hazards are proportional across regimes. We proceed by artificially censoring subjects when they become noncompliant with a specific regime under investigation (Robins, 2002; Hernán et al., 2006). This censoring potentially induces a bias which we correct using a modified Inverse Probability of Censoring Weighting (IPCW) (Robins, 1993). Then we employ a modified version of Nelson-Aalen estimator with a Random Forest based flexible data driven weighting scheme to (1) accurately estimate the survival distribution under a pre-defined DTR of interest; and (2) compare the survival distribution under different viable DTRs.

In Section 2, we describe the prostate cancer study. In Section 3, we introduce notation under the counterfactual framework of causal inference, followed by the description of the class of DTRs of clinical interest. In Section 4, we present our method of the weighted Nelson-Aalen estimator, where the weights are derived from Random Forest regression. In Section 5, we demonstrate the validity of the proposed method in various simulation scenarios that mimic different treatment/adherence mechanisms, and then we present the analysis results from the prostate cancer data example in Section 6, followed by a discussion in Section 7.

2. The prospective cohort study on prostate cancer recurrence

The data used in this paper come from a prospective study of prostate cancer recurrence. The study enrolled a total of 2781 patients with clinically localized prostate cancer, all of whom were initially treated with external beam radiation therapy (EBRT). Patients came from four cohorts: University of Michigan (Michigan, U.S.A.); Radiation Therapy Oncology Group; Peter MacCallum Cancer Center (Melbourne, Australia); and William Beaumont Hospital (Michigan, U.S.A.). Pretreatment prognostic factors PSA (ng/ml) and T-stages (with value 1-4) were recorded prior to initial EBRT, and then PSAs were monitored at periodic visits throughout follow-up. Each patient enrolled in the study was followed up for at least one year with a minimal of two visits. The median follow-up was 5.2 years, and the median number of PSA measurements (visits) prior to recurrence or SADT was 9. Further description of the data can be found in Proust-Lima et al. (2008). Overall, 11% of the patients received SADT and 12% experienced a recurrence of prostate cancer. A higher level of PSA is considered an important indicator of increasing risk of cancer recurrence; thus a typical regime in clinical practice would be to treat a patient with SADT when his PSA value is increasing and the first time it goes above a certain threshold. However, it is likely that different physicians will have different criteria for when to begin SADT treatment. Moreover, the typical PSA trajectories after initial treatment also have varying and complicated shapes over time, which contribute to the heterogeneity of the observed treatment times in the dataset. We will rely on statistical tools to connect the observed data to various regimes of clinical interest, and to find the optimal one that can be used to guide future clinical practice.

3. Notation and Dynamic Treatment Regimens

Consider a cohort of n patients at baseline t₀ = 0. Prior to the cancer recurrence or the patient's dropping out, each patient visits the clinic at regular intervals t₁, t₂, ⋯, t_k, ⋯ until the study end (t_K) and has their time-dependent covariates (the PSA level) measured. Treatment decisions, i.e. whether to start SADT, were made soon after each clinic visit and at no other time. Assume that the subjects in the cohort are a random sample from a large population of interest. For patient i at time t_k, with i = 1, ⋯, n and k = 0, ⋯, K, let L_k,i = PSA_k,i denote the time-dependent covariate observed at t_k. In particular, L_0,i = (PSA_0,i, V_0,i) includes baseline PSA as well as other baseline covariates V_0,i for patient i. In our study, V_0,i denotes indicators for the patient's baseline T-stage. Let R_k,i denote a binary indicator for event occurrence, which takes value 1 if the patient has experienced prostate cancer recurrence by time t_k and 0 otherwise. Let A_k,i denote the kth-specific SADT prescription which takes values in a finite set 𝒜_k = {0,1}. We further assume that a patient would stay on the treatment once initiated. Following the convention in the literature, we use overbars to denote the history of the variable up to the indexed time. Capital letters are used to refer to random variables or vectors, while lower-case letters are employed to denote the observed values of the corresponding random variables. For example, the observational data for a given patient i up to time t_k is denoted as Ō_k,i = (O_0,i, ⋯, O_k,i) = (R_0,i, L_0,i, R_1,i, L_1,i, R_2,i, ⋯, L_k−1,i, R_k,i) and a possible observed treatment history up to time t_k is denoted as ā_k,i = (a_0,i, ⋯, a_k,i) ∈ 𝒜₀ × ⋯ × 𝒜_k = 𝒜̄_k. For simplicity, we will suppress the patient index i in the future when no confusion exists.

Since our interest lies in the outcome when everyone follows the same regime, we define the treatment regime specific counterfactual outcomes under the framework of causal inference (Robins, 1986). For k = 1, ⋯, K, let $R_k^C({\overline{\mathit{a}}}_{k-1})$ denote the counterfactual event status that would be observed at time t_k were the patient to receive treatment history ā_k−1 regardless what treatment sequence he actually followed up to t_k, and similarly let $L_k^C({\overline{\mathit{a}}}_{k-1})$ denote the corresponding counterfactual covariate information at time t_k under treatment history ā_k−1. Then all the counterfactual random variables up to time t_K can be denoted as

$${\mathit{Z}}^C=\{{\mathit{O}}_0,{\mathit{O}}_1^C(a_0),\cdots ,{\mathit{O}}_{K-1}^C({\overline{\mathit{a}}}_{K-2}),R_K^C({\overline{\mathit{a}}}_{K-1}),\forall {\overline{\mathit{a}}}_{K-1}\in {\overline{\mathcal{A}}}_{K-1}\}=\{R_0,{\mathit{L}}_0,R_1^C(a_0),L_1^C(a_0),\cdots ,R_{K-1}^C({\overline{\mathit{a}}}_{K-2}),L_{K-1}^C({\overline{\mathit{a}}}_{K-2}),R_K^C({\overline{\mathit{a}}}_{K-1}),\forall {\overline{\mathit{a}}}_{K-1}\in {\overline{\mathcal{A}}}_{K-1}\}.$$

In our survival outcome setting, the counterfactual observation would only be meaningful up to the time when the counterfactual event occurs, if the counterfactual event happens before t_K. So we only include them in Z^c for ease of notation.

The SADT treatment process can be formulated as a dynamic treatment regime g = {g_k : k = 0, ⋯, K − 1}. The rule for determining the treatment prescription at each time t_k, g_k ∈ 𝒜_k, may depend on part or all of the recorded health information about the patient up to and including time t_k. The optimal regime would be a regime that maximizes the expected utility function if all patients in the population follow g. Note that the expected utility can depend on both the rule g as well as the subject-specific ō_k, thus it provides a personalized treatment decision. For time-to-event outcomes with right censoring, the Cox model (Cox, 1972) is the most popular choice. However, in our case, it may be unrealistic to expect the proportional hazard assumption to hold across all regimes. Thus, we propose to estimate each regime specific survival curve directly and use the restricted mean survival time (RMST) as the utility function. If we denote the survival time by T, then for some arbitrary time bound T_max, the RMST can be represented as μ ≡ E {min (T, T_max)} which equals the area under the survival curve up to T_max, $\mu ={\int }_0^{T_{max}}S(t)\mathit{\text{dt}}$. Here a large value is commonly chosen for T_max such as t_K. We consider a set of clinically relevant regimes as described earlier where a patient starts SADT when his PSA is increasing and the first time it goes above a threshold b. Practically, we define increasing PSA by its empirical slope, ${\text{PSA}}_k^{\prime }={\text{PSA}}_k-{\text{PSA}}_{k-1}>0$, for k = 1, ⋯, K, i.e. the current PSA value needs to be larger than the value at the previous visit. To formalize this, we consider the class of regimes indexed by b, $\mathcal{G}\equiv \{g^b:b\in \mathcal{R}\}=\{(g_0^b,\cdots ,g_{K-1}^b):b\in \mathcal{R}\}$ where at baseline t₀ = 0, no salvage treatment would be initiated, i.e. $g_0^b({\mathit{O}}_0)\equiv 0$. For t_k, k = 1, ⋯, K − 1, the treatment indicator is defined as

$$g_k^b({\overline{\mathit{O}}}_k^b,{\overline{\mathit{A}}}_{k-1}^b)=\{\begin{array}{cc}0& \text{if}{A}_{k-1}^b=0,R_k^b=1,{\text{PSA}}_k^{\prime b}\le 0,\text{or}{\text{PSA}}_k^b\le b,\\ 1& \text{if}{A}_{k-1}^b=0,R_k^b=1,{\text{PSA}}_k^{\prime b}>0,\text{and}{\text{PSA}}_k^b>b,\\ 1& \text{if}{A}_{k-1}^b=1,R_k^b=1.\end{array}$$ (1)

where again the superscript b is used to denote the regime g^b specific counterfactuals, ${\overline{\mathit{O}}}_k^b={\overline{\mathit{O}}}_k^C({\overline{\mathit{g}}}_{k-1}^b)$, ${\overline{\mathit{g}}}_{k-1}^b=(g_0^b,\cdots ,g_{k-1}^b)$, $A_{k-1}^b=g_{k-1}^b=g_{k-1}^b({\overline{\mathit{O}}}_{k-1}^b,{\overline{\mathit{A}}}_{k-2}^b)$, ${\text{PSA}}_k^{\prime b}={\text{PSA}}_k^{\prime C}({\overline{\mathit{g}}}_{k-1}^b)$ and ${\text{PSA}}_k^b={\text{PSA}}_k^{\mathrm{C}}({\overline{\mathit{g}}}_{k-1}^b)$. In this setting, a treatment regimen g^b is fully defined by cut-off value b. The counterfactual data used in the definition of $g_k^b$ in (1) is specific to the case where all patients follow g^b. If we denote the RMST under regime g^b to be μ^b, then the optimal regime is g^opt = arg max_{g^b∈𝒢} μ^b.

Definition (1) is based on the assumption that we observe the counterfactual data under all regimes g^b ∈ 𝒢. In practice, not all of them can be observed for each patient, because each patient is observed to experience one and only one treatment history. So instead of calculating μ^b from the counterfactual data ${\overline{\mathit{O}}}_K^b$, we need to estimate it from the observed data Ō_k. To make this possible, we follow Robins (1993) and make the following assumptions. (i) The consistency assumption: ${\mathit{O}}_k={\mathit{O}}_k^C({\overline{\mathit{A}}}_{k-1})={\sum }_{{\overline{a}}_{k-1}\in {\overline{\mathcal{A}}}_{k-1}}{\mathit{O}}_k^C({\overline{\mathit{a}}}_{k-1})I({\overline{\mathit{A}}}_{k-1}={\overline{\mathit{a}}}_{k-1})$ for k = 1, ⋯,K; that is, a patient's observed covariates and outcomes are the same as the potential ones in the counterfactual world as long as this person has the same treatment history he actually received. (ii) No unmeasured confounder assumption (NUCA) implies that A_k is independent of Z^C conditional on (Ō_k, Ā_k−1) for k = 1, ⋯, K. (iii) The positivity assumption: for a viable regime g^b ∈ 𝒢, $P\{A_k=g_k^b|{\overline{\mathit{O}}}_k={\overline{\mathit{O}}}_k^b({\overline{\mathit{a}}}_{k-1}),{\overline{\mathit{A}}}_{k-1}={\overline{\mathit{a}}}_{k-1}\}\ge \epsilon >0$ for k = 1, ⋯, K with probability 1 for an arbitrary small positive constant ε. This essentially guarantees that in the counterfactual world where everyone follows regime g^b, if there were patients with history ō_k and ā_k−1 who would be assigned to treatment $A_k^b=g_k^b({\overline{\mathit{o}}}_k,{\overline{\mathit{a}}}_{k-1})$, then, in the observational world, there must be some actual patients as counterparts who have the same history (ō_k and ā_k−1) and received treatment $a_k=g_k^b$. Because the treatment can only go from 0 to 1 in our case, we only need to assume the positivity when the patient is not on treatment until t_k−1. With the above assumptions, for k = 1, ⋯, K with any fixed ${\overline{\mathit{a}}}_{k-1}={\overline{\mathit{g}}}_{k-1}^b({\overline{\mathit{o}}}_{k-1},{\overline{\mathit{a}}}_{k-2})\in {\overline{\mathcal{A}}}_{k-1}$ under regime g^b, we have

$$\begin{array}{c}{p}_{R_k^b|{\overline{\mathit{L}}}_{k-1}^b,{\overline{\mathit{R}}}_{k-1}^b}(r_k|{\overline{\mathit{l}}}_k,{\mathit{r}}_{k-1})=p_{R_k|{\overline{\mathit{A}}}_{k-1}{\overline{\mathit{L}}}_{k-1},{\overline{\mathit{R}}}_{k-1}},(r_k|{\overline{\mathit{a}}}_{k-1},{\overline{\mathit{l}}}_{k-1},{\mathit{r}}_{k-1}),\\ p_{L_k^b|{\overline{\mathit{R}}}_k^b,{\overline{\mathit{L}}}_{k-1}^b}(l_k|{\overline{\mathit{r}}}_k,{\overline{\mathit{l}}}_{k-1})=p_{L_k|{\overline{\mathit{R}}}_k,{\overline{\mathit{A}}}_{k-1},{\overline{\mathit{L}}}_{k-1}}(l_k|{\overline{\mathit{r}}}_k,{\mathit{a}}_{k-1},{\overline{\mathit{l}}}_{k-1}),\end{array}$$

where p(·) denotes the probability function, and thus we are able to make inferences on μ^b using the observational data (Ō_k, Ā_k−1). The validity of this inference can be proved using the similar approach as for a continuous outcome (Robins, 1993; Pearl and Robins, 1995), and the details are provided in Web Appendix A.

4. Method

The assumptions from last section enable us to connect the observational data to the counterfactuals of interest. However, we usually do not know if the decision about treatment initiation was based on a pre-planned regime, instead, we can only judge whether their observed data are compatible with a certain regime at each longitudinal visit. Thus we need to use causal inference tools to estimate the counterfactual survival experiences that the whole cohort of patients would have had if they had truly been adherent to g^b.

4.1 Inverse Probability of Adherence Weighting

For a specific regime g^b, we proceed by artificially censoring patients at their first nonadherent visit. Let $C_k^b=A_k·g_k^b({\overline{\mathit{O}}}_k,{\overline{\mathit{A}}}_{k-1})+(1-A_k)·\{1-g_k^b({\overline{\mathit{O}}}_k,{\overline{\mathit{A}}}_{k-1})\}$ be the indicator of adherence at time t_k, k = 0, ⋯, K − 1, which is 1 if the patient's observed treatment status at time t_k is the same as the treatment assignment if he followed regime g^b (adherent), and 0 otherwise. The patient's data is compatible with regime g^b until time t_k if ${\overline{\mathit{C}}}_k^b=\overline{\mathbf{1}}$, where 1̄ is a vector of 1's with the same length as ${\overline{\mathit{C}}}_k^b$. The patient is censored at time $t={min}_{t_k}\{C_k^b=0\text{for}k=0,\cdots ,K\}$ to create the regime g^b adherence dataset, i.e. for a patient who partially follows the regime of interest, we will include him only up to the first time his data is not compatible with following that regime.

Following Robins (1993), we adjust for the bias induced from this artificial censoring by weighting each patient by their Inverse Probability of Adherence Weights as following:

$$w_{A,k}^b=\prod _{j=1}^k\frac{P(C_j^b=1|{\overline{\mathit{C}}}_{j-1}^b=\overline{\mathbf{1}},{\mathit{L}}_0={\mathit{l}}_0)}{P(C_j^b=1|{\overline{\mathit{C}}}_{j-1}^b=\overline{\mathbf{1}},{\overline{\mathit{O}}}_j={\overline{\mathbf{o}}}_j,{\overline{\mathbf{A}}}_{j-1}={\overline{\mathit{a}}}_{j-1})}$$ (2)

Each adhering patient is essentially weighted at each time point by the inverse probability that he remains adherent given his covariates history, and thus accounts for himself as well as other similar patients who were non-adherent and artificially censored. The probability of adherence for a patient at time t_k is calculated as the multiplication of the conditional probabilities of adherence at each time point t_j given that he remains adherent up to time t_j−1 (j = 1, ⋯, k). A numerator term, which modeled only with baseline covariates, is included to reduce the variability of the weights (Robins and Finkelstein, 2000; Cain et al., 2010).

4.2 Random Forest Regression

Traditionally, the probability models in the numerator and denominator of Equation (2) are estimated by fitting logistic regression models, and if there are multiple time points, the models are usually fitted by pooling data from all possible person-time pieces together (Hernán et al., 2006). In our case, the regime rules are defined based on the PSA value. The non-linear trajectory of PSA and the wide spectrum of regimes from different physicians and different centers leads to some complexity of the treatment mechanism. Although a time-dependent intercept is commonly used in such cases to provide more flexibility for the logistic regression models, it may fail to fully capture the association between adherence and covariates. To this end, we propose to use Random Forest regression to model the probability of treatment in our case and account for things like nonlinear dependence on PSA and interaction between PSA and time.

Random Forests (Breiman, 2001) is a non-parametric classification and regression method. It employs a combination of resampling and ensembles of single tree based models to give superior performance in both classification and regression. Compared to parametric logistic regression, the tree-based regression provides more flexibility in capturing the non-linear effects of the covariates. Furthermore, the resampling in Random Forests also helps to achieve smooth estimates and avoids very extreme probabilities, which is a common problem in using a logistic model to estimate the weights. As a relatively large number of decision points are considered in our case, the number of patients at risk decreases dramatically over time. Thus, it may not be efficient to fit separate conditional probability models at each time point. With Random Forest regression, we can follow the same strategy as in traditional approaches to pool the data of all person-time pieces together, and fit a single model for conditional probabilities at all stages by directly including time as a covariate to account for their variability over stages. Specifically, for the denominator in Equation (2), we fit the model for the observed treatment assignment mechanism, P(A_k = 1|Ō_k = ō_k, Ā_k−1 = 0̄), with all the observed data available up to the first time point when the patient is on treatment, i.e. person-time pieces up to t = max{t_k : A_k−1 = 0, k ≤ K}. The following property connects the treatment probabilities with the model for the adherence to regime g^b.

Property 1: For any patient i = 1, ⋯, n, and k = 1, ⋯, K − 1, we have

$$P(C_k^b=1|{\overline{C}}_{k-1}^b=\overline{\mathbf{1}},{\overline{\mathit{O}}}_k={\overline{\mathit{o}}}_k)=P(A_k=1|{\overline{\mathit{O}}}_k={\overline{\mathit{o}}}_k,{\overline{\mathit{A}}}_{k-1}={\overline{\mathit{a}}}_{k-1})I\{g_k^b({\overline{\mathit{o}}}_k,{\overline{\mathit{a}}}_{k-1})=1\}+P(A_k=0|{\overline{\mathit{O}}}_k={\overline{\mathit{o}}}_k,{\overline{\mathit{A}}}_{k-1}={\overline{\mathit{a}}}_{k-1})I\{g_k^b({\overline{\mathit{o}}}_k,{\overline{\mathit{a}}}_{k-1})=0\}$$

A brief derivation of Property 1 is outlined in Web Appendix B. It allows us to calculate the probability of regime adherence from the probabilities of initiating treatment. Since the treatment model for the observational data is the same regardless of which regime is under investigation, this allows us to obtain the probability of adherence for various regimes while only fitting a single pooled Random Forest model. Besides, the treatment model can incorporate information from all the pre-treatment person-time pieces available, which will be more efficient than modeling the regime specific censoring mechanism. However, for the numerator, we may not be able to do the same thing, or the numerator will also depend on the time-dependent confounder Ā_k. Thus, we proceed by directly modeling $P(C_j^b=1|{\overline{\mathit{C}}}_{j-1}^b=\overline{\mathbf{1}},{\mathit{L}}_0={\mathit{l}}_0)$ in the adherence cohort for each regime of interest. The Random Forest regression is done using the R function randomForest with all default settings except for the number of trees to grow (ntree) and number of candidate variables to include at each split (mtry). We set ntree = 1000, and perform a grid search for mtry from {1, 2, 4} based on the “out-of-bag” prediction error. In both simulation and data application, we end up using mtry = 2. Following the suggestion in Foster et al. (2011), we also include the two-way interactions of all variables in the model for better numerical performance. The treatment/adherence probability estimates are then obtained from the “out-of-bag” predictions.

4.3 Weighted Nelson-Aalen Estimator

For the regime g^b adherent cohort, we assign a time-dependent weight $w_{A,k,i}^b$ to each person-time piece. Then we define the following weighted number of events and the weighted number at risk at time t_k (k = 1, ⋯, K) as

$$d_k^b=\sum _{\{i:R_{k,i}=1,\&R_{k-1,i}=0\}}{w}_{A,k,i}^b\text{and}{Y}_k^b=\sum _{\{i:R_{k-1,i}=0\}}{w}_{A,k,i}^b$$

and employ the weighted Nelson-Aalen formula for the regime g^b-specific survival function as Ŝ^b(t) = exp{−Λ̂^b(t)}, where ${\widehat{\mathrm{\Lambda }}}^b(t)={\sum }_{t_j\le t}{d}_j^b/Y_j^b$ is the cumulative hazard function. The estimated counterfactual RMST is then given by ${\widehat{\mu }}^b={\int }_0^{t_K}{\widehat{S}}^b(t)\mathit{\text{dt}}$. Since we have discrete visit times, the integral can be written as ${\widehat{\mu }}^b={\sum }_{k=1}^K\{(t_k-t_{k-1}){\widehat{S}}^b(t_{k-1})\}$.

As a widely used flexible modeling approach, the theoretical properties of Random Forests have been intensively studied and discussed (Lin and Jeon, 2006; Biau and Devroye, 2010; Scornet et al., 2015). They have provided valuable insights on the consistency of the method. Based on the consistency results of Random Forest regression, we have the following property for the weight estimator ${\widehat{w}}_{A,k,i}^b$ in Section 4.2.

Property 2: The time-dependent weights estimated through Random Forests are consistent estimators of the true weights given the observed history Ō_k,i at t_k (k = 1, …, K). That is, ${\widehat{w}}_{A,k,i}^b\to w_{A,k,i}^b$ as n → ∞, where $w_{A,k,i}^b=d{\mathcal{P}}_{g^b,k}/d{\mathcal{P}}_k,{\mathcal{P}}_{g^b,k}$ denotes the measure generated by counterfactual variables observed until t_k under the given regime g^b, and 𝒫_k denotes the corresponding measure generated by observational data Ō_k,i up to time t_K.

With Properties 1 and 2, we can further investigate the consistency property of the proposed estimator for the counterfactual quantities of interest as following:

Proposition 1: Under assumptions (i) - (iii) and the following regularity conditions:

1. The observational data (Ō_k,i, Ā_K−1,i) are independent and identically distributed,

2. ${\int }_0^{t_K}{\lambda }_0^b(t)\mathit{\text{dt}}<\infty$ where ${\lambda }_0^b(t)$ is the true marginal hazard for any regime g^b ∈ 𝒢,

3. For the true marginal survival function $S_0^b(t)$, we assume there exist continuous first-order derivatives in t and bounded second partial derivatives (uniformly in t ∈ (0, t_K]). $S_0^b(t)$ can thus be consistently estimated by the proposed estimator Ŝ^b(t), and μ̂^b is a consistent estimator for true regime specific RMST ${\mu }_0^b$.

Web Appendix C provides a brief derivation of this proposition. Property 1, Property 2, and Proposition 1 assure that the weights are able to be consistently estimated through the proposed procedure, and then the weighted Nelson-Aalen estimator is consistent for the regime specific counterfactual survival function. Furthermore, the estimation of the utility ${\mu }_0^b$ is also consistent. Thus, we can identify the optimal DTR by maximizing μ̂^b within all the g^b's that are considered, that is, ${\widehat{g}}^{\text{opt}}=arg{max}_{g^b\in \mathcal{G}{\widehat{\mu }}^b}$.

So far we consider the data with only administrative censoring. For more complicated censoring mechanisms, inverse probability of censoring weights could be applied in addition to correct for the possible bias related to censoring. More specifically, one can first model the time-dependent censoring probability in the full dataset using similar strategy via Random Forest regression, then the overall weight for each person-time piece would be the product of the adherence weight and the censoring weight.

5. Simulation

In order to evaluate the performances of the proposed method, we conduct simulation studies where we explicitly model the relationship among time to recurrence, SADT free PSA, and treatment effect. In the simulation studies, we have the fully adherent data available for each defined regime, and thus we can use these simulated counterfactual data as the “gold standard”. Two scenarios are considered, one to mimic a simple case with linear PSA trajectories and the second with a more complicated but more realistic pattern of PSA trajectories. We compare the performance of our proposed method with a naive unweighted estimator and the logistic regression based estimator, where for the denominator of the weight in Equation (2), the treatment probabilities are estimated from

$$\text{logit}P(A_j=1|{\overline{\mathit{O}}}_j={\overline{\mathit{o}}}_j,{\overline{\mathit{A}}}_{j-1}=\overline{\mathbf{0}})=h_1(t_j)+{\mathit{\beta }}_1{\mathit{O}}_j+{\mathit{\beta }}_2^T{\mathit{V}}_0$$ (3)

and for the numerator, one fits the regime specific adherence model as

$$\text{logit}P(C_j^b=1|{\overline{\mathit{C}}}_{j-1}^b=\overline{\mathbf{1}},{\mathit{V}}_0={\mathit{\upsilon }}_0)=h_2(t_j)+{\mathit{\beta }}_3^T{\mathit{V}}_0.$$ (4)

Here, following Hernán et al. (2006), the time-dependent intercepts h₁(t_j) and h₂(t_j) are included in (3) and (4) to increase the modeling flexibility. We use cubic splines with 2 internal knots to non-parametrically estimate these intercept terms. The observational data, O_k, include PSA_k and the empirical slope ${\text{PSA}}_k^{\prime }$ at time t_k (for Scenario 1, we only consider PSA_k). Similar as in Proust-Lima et al. (2008), the PSA values are log-transformed. T-stage at baseline (V₀) is represented as a 2-dimensional vector of indicators V₀ = (I(T-stage = 2), I(T-stage ≥ 3))^T. For each scenario, we simulate 500 datasets each with 2000 subjects.

5.1 Simulation set-up of Scenario 1

5.1.1 Longitudinal PSA Values

During the follow-up period (0, t_K], each patient is repeatedly measured every year, and we choose t_K = 15 years. Let ${\text{PSA}}_{k,i}^0$ denote the observed PSA value for patient i measured at t_k (t_k = k = 0,1, …, 15) if he has not received any SADT treatment. We simulate ${\text{PSA}}_{k,i}^0$ from the following linear mixed model:

$${\text{PSA}}_{k,i}^0=X_i(t_k)+{\varepsilon }_{k,i}=({\alpha }_0+a_{0,i})+({\alpha }_1+a_{1,i})t_k+{\varepsilon }_{k,i},$$ (5)

where X_i(t) = (α₀ + α_0,i) + (α₁ + a_1,i)t models the underlying true SADT free PSA for t ∈ (0,t_K]. (α₀, α₁) = (−3.0, 0.3) are fixed effect parameters, (a_0,i, a_1,i) ∼ MVN(0,Σ) are subject-specific random effects, with $\sum =\left[\begin{array}{cc}1& 0.5\\ 0.5& 0.25\end{array}\right]$. We further truncate any a_1,i < −0.1 at -0.1 to create increasing PSA trends. At a given time t_k, we assume the measurement error ε_k,i ∼ N(0, σ²) with σ² = 0.1. Note that we observe ${\text{PSA}}_{k,i}={\text{PSA}}_{k,i}^0$ before the earliest of either SADT initiation or recurrence, and then ${\text{PSA}}_{k,i}^0$ will not be observed.

5.1.2 Different Treatment Regimes and Observed Treatment Time

For each patient, we consider 10 regimes with regime-specific thresholds of {b₁, b₂, ⋯, b₁₀} = {−1.0, −0.5, ⋯, 3.5}. Based on patient i's SADT free PSA trajectory { ${\text{PSA}}_{k,i}^0:k=0,\cdots ,15$}, we can calculate the regime specific SADT initiation time as $U_i^{b_1}$, $U_i^{b_2}$, ⋯, $U_i^{b_{10}}$ for all 10 regimes, where $U_i^{b_j}$ is determined from Equation (1) with b = b_j (let $U_i^{b_j}=\infty$ if ${\overline{\mathit{g}}}^{b_j}=\overline{\mathbf{0}}$). We generate the index of the observed regime B_i at random from {b₁, b₂, ⋯,b₁₀} for patient i. Thus, the observed treatment time for patient i who is following g^B_i $U_i^{B_i}$, which we denote as U_i for simplicity of notation. Based on this data generation process, both the counterfactual treatment initiation time for each regime of interest and the observed treatment initiation time are determined by the SADT free PSA measurements. We show in Web Appendix D that this procedure helps us to prevent extreme weights among the regimes of interest.

5.1.3 Model for Recurrence and Fully Compliant Data

We simulate the recurrence time for patient i according to a Cox model with hazard function, for t ∈ (0, t_K]:

$${\lambda }_i(t)={\lambda }_{0}exp[{\mathit{\theta }}_0^T{\mathit{V}}_{0,i}+{\theta }_1{X}_i(t)+{\gamma }_i(t)I(t>U_i)],$$ (6)

where λ₀ = 0.2, θ₀ = (0.2, 0.3)^T, and θ₁ = 0.3. Patient i's baseline T-stage is sampled from {1, 2, 3, 4} with probability p = (0.33, 0.59, 0.07,0.01)^T, which is used to generate V_0,i. The treatment effect, γ_i(t), is defined as

$${\gamma }_i(t)=\{\begin{array}{cc}min\{{\gamma }_{0,i}+{\beta }_2(t-U_i),0\}& \text{if}{\gamma }_{0,i}<0\\ max\{{\gamma }_{0,i}-{\beta }_2(t-U_i),0\}& \text{if}{\gamma }_{0,i}>0,\end{array}$$ (7)

where γ_0,i = β₀ + β₁X_i(U_i), with (β₀, β₁, β₂) = (−1.0, −0.4, 0.2). Thus, the initial treatment effect γ_i(U_i) = γ_0,i linearly depends on X_i(U_i), the true SADT free PSA value at the time point U_i. After that, the magnitude of the treatment effect γ_i(t) decays over time until it shrinks to zero. The time to recurrence is generated for patient i as $T_i^{\ast }=S_i^{-1}(W_i)$, where

$$S_i(t)=exp\{-{\int }_0^t{\lambda }_i(s)\mathit{\text{ds}}\},$$ (8)

and W_i ∼ Uniform(0,1), then $T_i^{\ast }$ is rounded up to the closest visit time as T_i, or censored at t_K. Similarly, for each regime g^b_j, j = 1, ⋯, 10, we calculate the time to recurrence $T_i^{b_j}$ for patient i according to the counterfactual treatment initiation time $U_i^{b_j}$.

5.2 Simulation set-up of Scenario 2: Nonlinear PSA trends and more candidate regimes

To better understand the performance of the proposed method in practice, we consider the following scenario with more realistic PSA trajectories. In addition, we generate the observational data from a larger number of candidate regimes to increase randomness.

5.2.1 PSA Models

In the absence of SADT, a typical trajectory of PSA has three phases (0: starting-value, 1: short-term evolution, 2: long-term evolution). Here we consider a shorter study length with t_K = 12 years. Following Proust-Lima et al. (2008) and Taylor et al. (2013), for patient i at t ∈ (0, t_K], we simulate SADT free PSA values from the following mixed model to recreate these phases as:

$${\text{PSA}}_{k,i}^0=X_i(t_k)+{\varepsilon }_{k,i}=({\alpha }_0+a_{0,i})+({\alpha }_{11}+{\mathit{\alpha }}_{12}^T{\mathit{V}}_{0,i}+a_{1,i})f(t_k)+({\alpha }_{21}+{\mathit{\alpha }}_{22}^T{\mathit{V}}_{0,i}+a_{2,i})t_k+{\varepsilon }_{k,i},$$ (9)

where again X_i(t) is the underlying true SADT free PSA for t ∈ (0, t_K], and f(t) = (1 + t)^−1.5 − 1 is used to model the short-term decreasing trend, the linear in t term is used to model the long-term increasing trend. (a_0,i, a_1,i, a_2,i) ∼ MVN(0, Σ) are subject-specific random effects with $\sum =\left[\begin{array}{ccc}1.0& 1.0& 0.15\\ 1.0& 2.6& 0.45\\ 0.15& 0.45& 0.5\end{array}\right]$. (α₀, α₁₁, α₁₂, α₂₁, α₂₂) are fixed effect parameters with α₀ = 1.0, α₁₁ = 1.5, α₁₂ = (0.2, 0.2)^T, α₂₁ = 0.1, and α₂₂ = (0.2, 0.5)^T, and V_0,i is generated the same as in Scenario 1. At a given time t_k = k = 0,1, ⋯, 12, we assume ε_k,i ∼ N(0, σ²) with σ² = 0.2.

5.2.2 Different Treatment Regimes and Observed Treatment Time

To give more heterogeneity to the treatment assignment mechanism, we generate the observed treatment time and survival outcome for patient i with threshold B_i, which is drawn from a discrete uniform distribution with 100 evenly spaced values {−2.00, −1.95, ⋯, 2.95}. The observed treatment time for patient i is then $U_i=U_i^{B_i}$. Note that in the analysis we still restrict our interest to evaluating the counterfactual outcomes from 10 regimes {b₁, b₂, ⋯, b₁₀} = {−2.0, −1.5, ⋯, 2.5}.

5.2.3 Model for Recurrence and Fully Compliant Data

Following Proust-Lima et al. (2008), we let the hazard function depend on both true PSA and its slope, for t ∈ (0, t_K],

$${\lambda }_i(t)={\lambda }_{0}exp[{\mathit{\theta }}_0^T{\mathit{V}}_{0,i}+{\theta }_1{X}_i(t)+{\theta }_2{X}_i^{\prime }(t)+{\gamma }_i(t)I(t>U_i)].$$ (10)

where the true slope of SADT free $\text{PSA}{X}_i^{\prime }(t)=({\alpha }_{11}+{\mathit{\alpha }}_{12}^T{\mathit{V}}_{0,i}+a_{1,i}){(1+t)}^{-2.5}+({\alpha }_{21}+{\mathit{\alpha }}_{22}^T{\mathit{V}}_{0,i}+a_{2,i})$ is the derivative of X_i(t) from Model (9). The time to recurrence T_i is then generated from (7), (8) and (10) with λ₀ = 0.15, θ₀ = (0.8, 0.9)^T, θ₁ = 0.1, θ₂ = 0.1, β₀ = 10.0, β₁ = −10.0 and β₂ = 0.2. The same models are used to define the counterfactual to recurrence $T_i^{b_j}$ for each regime g^b_j, j = 1, ⋯, 10.

5.3 Simulation Results

Figure 1 shows the average Nelson-Aalen survival curves for given regimes estimated using different methods. Figures 1a and 1b show the estimation for regime b = 2.0 in Scenario 1, while Figures 1c and 1d show the estimation for b = −1.0 in Scenario 2. As can be seen, the survival curves estimated naively from the observational data without using weights are all biased away from the fully adherent curves. In contrast, both the pooled logistic regression based estimation and the proposed method can help reduce such bias in Scenario 1, where the data generation is relatively simple and thus more consistent with pooled logistic regression. In Scenario 2, the PSA trajectory has a complicated shape, and therefore the treatment adherence mechanism is hard to fit well using the pooled logistic regression method. As shown in Figure 1c and 1d, the survival curve estimated by the proposed method is very close to the counterfactual fully adherent curve, while the curve estimated by the pooled logistic method shows bias compared to the fully adherent curve. Similar results are also observed for other regimes.

Figure 1.

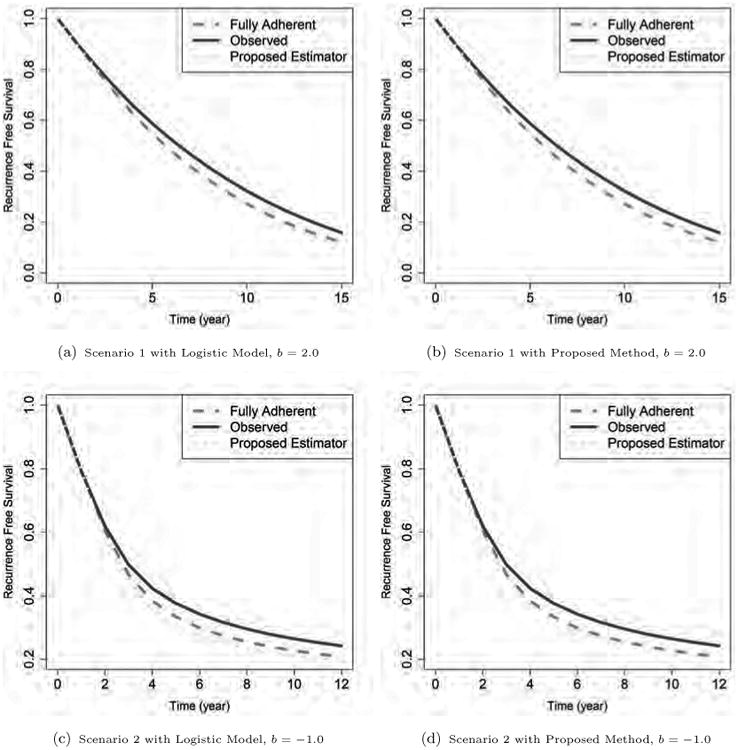
The estimated survival curves for different simulation schemes. The regime specific true curves (obtained from the counterfactual fully adherent cohorts) are shown in dashed lines. The solid lines are unweighted estimates from the observed data (obtained by censoring subjects when they are no longer adherent with given regimes), and the dotted lines are for the proposed weighted estimates. The upper panels are from regime b = 2.0 in Scenario 1, and the lower panels are from regime b = -1.0 in Scenario 2. The two panels on the left show estimation from the pooled logistic method, while the panels on the right show results from the proposed Random Forest based method. All curves are obtained by averaging over 500 simulations.

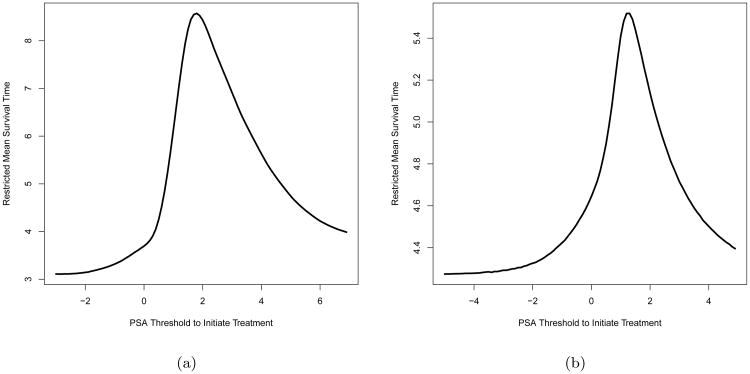
In both scenarios, we approximate the true RMST, ${\mu }_0^b$, for any given b by the Monte Carlo simulation of a very large regime specific cohort (n = 10⁷). Figure 2 plots ${\mu }_0^b$ over different b for both scenarios. Among the regimes under consideration, ${\mu }_0^b$ is maximized at around b = 2.0 with ${\mu }_0^b=8.432$ years for Scenario 1 (Figure 2a). While for Scenario 2, the optimal DTR is when b = 1.0, which yields the maximum ${\mu }_0^b$ at 5.518 years (Figure 2b). Table 1 summarizes the estimated RMST μ̂ for the regimes of interest. In both scenarios, we can see that 1) μ̂ from the fully adherent cohort is close to ${\mu }_0^b$ in Figure 2, which suggests that these estimates can well approximate the true population quantities in our simulations, and 2) the proposed estimator yields the maximal average μ̂^b at true optimal regime and also correctly identifies the true optimal regime with highest frequency.

Figure 2.

True ${\mu }_0^b$ under Scenario 1 (Figure 2a) and Scenario 2 (Figure 2b) in the simulation study. In each figure, The x-axis stands for the regime specific PSA threshold for SADT initiation b, while the y-axis stands for the true regime specific RMST ${\mu }_0^b$ calculated from Monte Carlo method. Each point in the plots above are calculated from 10⁷ Monte Carlo samples.

Table 1. Restricted Mean Survival Time for Regimes of Interest in Simulation Studies.

	Regime	Full Adherent		Unweighted		Pooled Logistic		Proposed Method
		μ̂	opt%	μ̂	opt%	μ̂	opt%	μ̂	opt%
Scenario 1	b1 = −1.0	4.016 (0.067)	0%	4.953 (0.121)	0%	4.039 (0.079)	0%	4.047 (0.073)	0%
	b2 = −0.5	4.876 (0.075)	0%	5.721 (0.115)	0%	4.671 (0.083)	0%	4.884 (0.080)	0%
	b3 = 0.0	5.920 (0.091)	0%	6.578 (0.117)	0%	5.563 (0.100)	0%	5.918 (0.094)	0%
	b4 = 0.5	6.787 (0.103)	0%	7.225 (0.124)	0%	6.425 (0.121)	0%	6.797 (0.107)	0%
	b5 = 1.0	7.589 (0.113)	0%	7.785 (0.129)	0%	7.286 (0.135)	0%	7.600 (0.120)	0%
	b6 = 1.5	8.340 (0.110)	0%	8.407 (0.128)	0%	8.159 (0.135)	0%	8.335 (0.131)	0%
	b7 = 2.0	8.729 (0.114)	99.6%	8.919 (0.134)	3.8%	8.656 (0.147)	92.0%	8.710 (0.146)	93.6%
	b8 = 2.5	8.503 (0.116)	0.4%	8.949 (0.143)	96.2%	8.421 (0.163)	8.0%	8.488 (0.158)	6.4%
	b9 = 3.0	8.068 (0.114)	0%	8.668 (0.148)	0%	7.984 (0.175)	0%	8.045 (0.171)	0%
	b10 = 3.5	7.632 (0.111)	0%	8.324 (0.156)	0%	7.519 (0.215)	0%	7.472 (0.310)	0%
Scenario 2	b1 = −2.0	4.872 (0.078)	0%	5.417 (0.096)	0%	4.153 (0.121)	0%	4.639 (0.103)	0%
	b2 = −1.5	4.921 (0.079)	0%	5.402 (0.093)	0%	4.293 (0.109)	0%	4.687 (0.099)	0%
	b3 = −1.0	4.991 (0.079)	0%	5.410 (0.092)	0%	4.544 (0.110)	0%	4.829 (0.098)	0%
	b4 = −0.5	5.091 (0.078)	0%	5.456 (0.091)	0%	4.867 (0.106)	0%	5.047 (0.093)	0%
	b5 = 0.0	5.294 (0.079)	0%	5.572 (0.091)	0%	5.298 (0.117)	0.2%	5.380 (0.095)	0%
	b6 = 0.5	5.757 (0.082)	0.6%	5.766 (0.093)	80.4%	5.891 (0.153)	30.0%	5.862 (0.101)	29.0%
	b7 = 1.0	5.848 (0.088)	99.4%	5.736 (0.096)	19.6%	5.927 (0.219)	50.4%	5.890 (0.108)	71.0%
	b8 = 1.5	5.562 (0.084)	0%	5.488 (0.095)	0%	5.658 (0.336)	6.2%	5.563 (0.112)	0%
	b9 = 2.0	5.315 (0.081)	0%	5.280 (0.092)	0%	5.499 (0.431)	4.8%	5.307 (0.120)	0%
	b10 = 2.5	5.138 (0.080)	0%	5.135 (0.092)	0%	5.372 (0.575)	8.4%	5.102 (0.134)	0%

Note: The values in parentheses are the empirical standard deviations calculated from 500 MC replications, %opt is the percentage for the given regime to be identified as the optimal regime among the 500 replicates

For Scenario 1, μ̂^b from the unweighted dataset shows a notable bias compared to the RMST of the fully adherent data, and it is maximized at regime 8 for most of the replications, which is incorrect. As shown by the frequency of being identified as the optimal regime, over the 500 simulations, 99.6% of the fully adherent datasets yield regime 7 as the true optimal, while only 3.8% pick regime 7 as the optimal using the unweighted method. Both the pooled logistic method and the proposed method can correct the bias and identify regime 7 with b₇ = 2.0 as the optimal one with the highest frequency (92.0% and 93.6% respectively). This is not surprising because the data generating process in Scenario 1 can be well approximated by the model specification of the pooled logistic regression. In Scenario 2, the fully adherent data show that regime 7 has the largest μ̂^b, and is the optimal regime in 99.4% of the 500 simulations. Again, the unweighted estimator prefers a different regime (regime 6) in 80.4% of the simulations, which is biased. Since in Scenario 2, the data generating process is more complicated and thus the models employed in the pooled logistic regression are misspecified, the pooled logistic method can only identify regime 7 as the optimal in 50.4% of the simulations. In contrast, the proposed method has a much higher rate of correctly identifying the optimal regime (71.0%). Comparing to the estimation from pooled logistic method, the average RMSTs given by the proposed method are also closer to the ones from fully adherent data. Thus we can see that the proposed flexible model works more robustly in correctly picking up the true optimal regime in different scenarios and reduces the bias more effectively when estimating the population survival outcome.

6. Analysis of the Prostate Cancer Data

It is of great interest to learn from the observational data about how different regimes are expected to perform in the future and whether some common guidelines could be suggested. To this end, we apply the proposed method on our prostate cancer recurrence dataset.

There are 2781 patients in the dataset of which 222 patients (< 8.0%) have follow-up time longer than 10 years. Thus, we compare μ̂^b with t_K = 10 years in the analysis. We consider regular visits at every 0.2 years, which was followed by most patients. For patients who missed visits and thus had interval longer than 2 years, we restrict to the time period when they were actively followed, and arbitrarily censor them at 0.2 years after the last visit before such long interval. Other than that, the last observation is carried forward to impute missing PSA measures. In total, 245 patients (8.8%) received SADT. We consider DTRs g^b as defined earlier, where b is the cut-off for the logarithm of (PSA+0.1). In clinical practice, PSA may be considered as in the “alert zone” from 3 ng/ml to 30 ng/ml, and a SADT is commonly seen to be initiated in that zone. Thus, we focus on regimes in that zone with b ∈ {1.1, 1.2, ⋯, 3.5}.

In the dataset, there is a wide range of treatment initiation times and PSA values at the time of initiation. This suggests the need for the treatment initiation model to have flexibility in order to accommodate the unknown relationships. Thus, we estimate the weights through Random Forests with input covariates PSA, empirical slope of PSA (the increment of PSA since the previous visit), baseline T-stage, time t and all two-way interactions. In addition to the regime specific adherence weight $w_{A,k}^b$, we also account for possible bias from non-administrative censoring by IPCW. If we denote the censoring indicator in the original observational dataset at time t_k by C_org,k, then the IPCW weights for k = 1,…, K are

$$w_{C,k}=\prod _{j=0}^k\frac{P(C_{\mathit{\text{org}},j}=1|{\overline{\mathit{C}}}_{\mathit{\text{org}},j-1}=\overline{\mathbf{1}},{\mathit{L}}_0={\mathit{l}}_0)}{P(C_{\mathit{\text{org}},j}=1|{\overline{\mathit{C}}}_{\mathit{\text{org}},j-1}=\overline{\mathbf{1}},{\overline{\mathit{O}}}_j={\overline{\mathit{o}}}_j,{\overline{\mathit{A}}}_{j-1}={\overline{\mathit{a}}}_{j-1})}$$ (11)

where the censoring probability models in both the numerator and denominator are fitted with the same covariates as we used in the adherence models using Random Forest regression. Thus, the overall weight used in estimation for each person-time piece is $w_b^k=w_{A,k}^b\times w_{C,k}$.

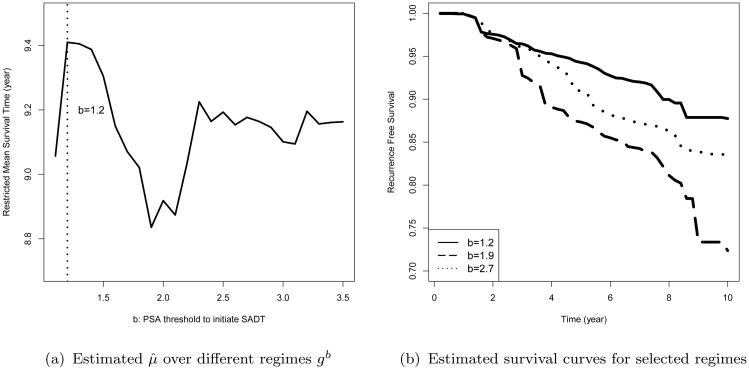
Figure 3a shows that the regime with b = 1.2 (3.22 ng/ml PSA) is identified as g^opt by the proposed method, and the corresponding estimated restricted mean time to recurrence under this regime is μ̂^b = 9.46 years. Figure 3b presents the weighted Nelson-Aalen estimators for the estimated optimal regime along with two other regimes. Our results suggest to initiate the SADT at an earlier stage when PSA raises to the “alert zone”, which is consistent with the common understanding of clinical practice.

Figure 3.

The survival estimation for regime specific time to recurrence in the prostate cancer dataset. Panel (a) shows the relationship between the restricted mean time to recurrence estimated by the proposed method μ̂^b and the regime specific PSA threshold for SADT initiation b. Panel (b) shows the weighted Nelson-Aalen curves estimated for three regimes, which includes the estimated optimal regime b = 1.2 (solid line), along with two other regimes b = 1.9 (dashed line) and b = 2.7 (dotted line).

7. Discussion

Motivated by the clinical need in prostate cancer treatment, we describe a method to estimate the optimal DTR from observational data that can accommodate complex unknown dependency of the treatment assignment as well as regime adherence mechanism on time-dependent and time-independent covariates. The proposed method provides an extension of the traditional inverse probability weighting method to allow for flexibilities simultaneously in two ways: (1) for the adherence mechanism, the Random Forest regression allows us to capture a large range of different treatment models, and (2) for the survival outcome, the non-parametric estimation allows us to put minimal structure assumptions on the estimator. The proposed estimating procedure can be implemented with most commonly used statistical software. Compared to logistic models for treatment initiation, the bootstrap procedure within the Random Forest regression can effectively avoid unstable and very extreme probability estimates. For example, in the real data application, for the regime b = 1.2 (the estimated optimal) compliant dataset, the estimated weights have a median of 0.91, with 2.5% and 97.5% quantiles as 0.50 and 3.14. Notice that these weights are cumulative products of up to 50 conditional probabilities, which means that most of the estimated probabilities are close to 1. Furthermore, compared to methods involving dynamic programming, the proposed method is computationally feasible even for problems with a relatively large number of decision time points. Thus, it is a powerful tool in clinical studies and public health practice, where there are more than a handful of possible decision points to initiate the treatment or intervention.

One common concern with machine learning based methods is overfitting. Tree size control and pruning procedures are used in tree based models to deal with this issue. In Random Forests, the bootstrap procedure and random selection of covariates for each tree will also help to reduce overfitting. In our simulation studies, we choose the tuning parameters according to the “out-of-bag” errors, which come from data not used for fitting each tree. We find the results very close to the prediction errors given by 5-fold cross-validation in both scenarios. Although larger number of trees are likely to increase accuracy, it will also lead to increased computational burden. In our case, there is no obvious improvement when ntree goes above 1000, so we set ntree = 1000. In general, we recommend cross-validation to select tuning parameters (Van der Laan and Robins, 2002), if there is a large discrepancy between the “out-of-bag” prediction error and the cross-validation prediction error.

One needs to be cautious when instrumental variables (IVs) exist, because including IVs in the weight models may create practical positivity violations and thereby lead to unstable weights, increased variance, and poor confidence interval coverage. From our experience with additional simulations, including IVs in the weight model for the proposed method does not severely affect the results. However, in general, if there is prior knowledge that allows us to identify a variable as an IV rather than a confounder, then it is better to exclude that variable from the weight model.

In this prostate cancer study, the patient's data are only collected at each visit, but the cancer recurrence events are more likely to actually happen at some point in the interval between adjacent visits. Since we are considering time intervals as small as 0.2 years, the bias introduced by treating the events as happening at the visits is likely to be ignorable. However, a more precise model would be desired to handle the event time as interval censored. This would be of more importance when the interval between visits are longer. Additional methodology will also be required to adjust for possible bias in censoring under such settings.