LUTE (Local Unpruned Tuple Expansion): Accurate Continuously Flexible Protein Design with General Energy Functions and Rigid Rotamer-Like Efficiency

Abstract

Most protein design algorithms search over discrete conformations and an energy function that is residue-pairwise, that is, a sum of terms that depend on the sequence and conformation of at most two residues. Although modeling of continuous flexibility and of non-residue-pairwise energies significantly increases the accuracy of protein design, previous methods to model these phenomena add a significant asymptotic cost to design calculations. We now remove this cost by modeling continuous flexibility and non-residue-pairwise energies in a form suitable for direct input to highly efficient, discrete combinatorial optimization algorithms such as DEE/A* or branch-width minimization. Our novel algorithm performs a local unpruned tuple expansion (LUTE), which can efficiently represent both continuous flexibility and general, possibly nonpairwise energy functions to an arbitrary level of accuracy using a discrete energy matrix. We show using 47 design calculation test cases that LUTE provides a dramatic speedup in both single-state and multistate continuously flexible designs.

1. Introduction

Protein design algorithms compute protein sequences that will perform a desired function (Donald, 2011). They generally do this by minimizing the energy of a desired binding or structural state [or some combination thereof (Leaver-Fay et al., 2011; Hallen and Donald, 2015)] with respect to sequence (Desmet et al., 1992; Floudas et al., 1999; Kuhlman and Baker, 2000; Georgiev et al., 2008, 2014; Karanicolas and Kuhlman, 2009; Donald, 2011; Gainza et al., 2012). Given a model of the conformational space of a protein and its energy function, which maps conformations to their energies, this is a well-defined computational problem (Donald, 2011).

Previously, this minimization problem has been most efficient to solve if two restrictions are imposed on the model. First, the conformational space of the protein is modeled as discrete. Specifically, each residue takes on conformations from a discrete set [typically, experimentally observed side chain conformations known as rotamers (Janin et al., 1978)]. Hence, we optimize with respect to the amino acid type and rotamer of each residue. Second, the energy function is assumed to be residue pairwise, that is, it is assumed to be a sum of terms that each depend on the amino acid types and conformations of at most two residues.

A large body of efficient algorithms has been developed for this restricted case of the protein design problem, many of which offer provable accuracy. In particular, the dead-end elimination (DEE) algorithm (Desmet et al., 1992) removes rotamers that provably cannot be part of the global minimum energy conformation (GMEC). The A* algorithm from artificial intelligence (Hart et al., 1968) finds the optimal conformation using these unpruned rotamers (Leach and Lemon, 1998). This DEE/A* framework has been generalized to model free energies for each sequence instead of simply GMECs (Lilien et al., 2005; Georgiev et al., 2008) (the 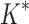algorithm). It has also been generalized to optimize combinations of stability and specificity by minimizing, with respect to sequence, a linear combination of the conformationally optimized energies of several bound and unbound states of a protein, instead of just the energy of a single state (Hallen and Donald, 2015) (the COMETS algorithm). Several methods in addition to DEE/A* have also been used to address the protein design problem. Some of these, such as Metropolis Monte Carlo and simulated annealing (Lee and Levitt, 1991; Kuhlman and Baker, 2000), lack provable guarantees of accuracy, and thus may miss the optimal conformation significantly (Simoncini et al., 2015). Other algorithms with provable accuracy are also available, largely building on techniques from integer linear programming (Kingsford et al., 2005; Roberts et al., 2015) and weighted constraint satisfaction (Traoré et al., 2013; Roberts et al., 2015; Traoré et al., 2016). Notably, treewidth- and branch width-based algorithms, such as TreePack (Xu and Berger, 2006) and BWM (Jou et al., 2015), solve this problem with provable accuracy in polynomial time for systems whose residue interaction graph has treewidth or branch width bounded by a constant (Jou et al., 2015).

However, proteins are actually continuously flexible, and continuous flexibility both in the side chains (Gainza et al., 2012) and backbone (Hallen et al., 2013) has been shown to result in significantly lower energies and biologically better sequences (Gainza et al., 2012; Hallen et al., 2013). Although a residue side chain will usually be found in the vicinity of the modal conformation for a rotamer, its dihedral angles will often differ from this mode by 10° or more (Janin et al., 1978). These continuous adjustments are often critical for determining what conformations are sterically feasible (Gainza et al., 2012). Thus, incorporation of continuous flexibility modeling substantially increases the accuracy of designs. The minDEE and iMinDEE methods (Georgiev et al., 2008; Gainza et al., 2012) do this for continuous side chain flexibility, and DEEPer (Hallen et al., 2013) for simultaneous continuous side chain and backbone flexibility. These methods replace the traditional discrete rotamers used in DEE/A* with voxels in the conformation space of each residue, called residue conformations (RCs). An RC is defined as an amino acid type together with bounds on each of the conformational degrees of freedom of the residue (e.g., side chain dihedrals) (Hallen et al., 2013). The modal conformation for a rotamer is usually found at the center of this voxel. In this model, the conformation space of an entire protein is a union of voxels, each of which is constructed as the cross-product of single-residue voxels. Thus, each voxel in the conformation space of the entire protein is represented by a list of RCs, one for each residue being modeled as flexible. RCs are constructed to be small enough that we can use local minimization to find the optimal energy within the voxel. This applies to both the single-residue and entire-protein voxels.

However, the global minimum energy in this model could not previously be computed directly by DEE/A*. Instead, DEE/A* was used to enumerate RC lists (protein conformational voxels) in order of a lower bound on minimized energy (Georgiev et al., 2008; Gainza et al., 2012; Hallen et al., 2013). Subsequently, the optimal energy for each RC list with a sufficiently low-energy lower bound was computed by minimization. The lower bound was computed from minimized pairwise interaction energies (Georgiev et al., 2008). This minimization was accelerated significantly by precomputing polynomials to approximate the energy landscape, using the EPIC algorithm (Hallen et al., 2015). However, minimization was still the bottleneck in continuously flexible designs and prevented them from approaching the efficiency of designs with discrete flexibility. In essence, these previous methods modeled continuous flexibility by modifying DEE/A* and making it do much more work. In contrast, LUTE achieves much greater efficiency by representing continuous flexibility in a form suitable for direct input into DEE/A*.

We must also address the question of the energy function. The energy landscape of a real protein is not residue pairwise, or otherwise exactly described solely as the sum of local terms. There is, however, ample evidence that protein interactions are local in a more general sense (Zhang and Zhang, 2003; Flocke and Bartlett, 2004; Vizcarra et al., 2008; Hallen et al., 2015)—that is, that the cross-derivative of the energy with respect to conformational degrees of freedom of two residues will tend to zero fairly quickly as the distance between the residues increases. These properties are also observed for more realistic energy functions that return an energy for the entire protein, rather than breaking the energy into terms as molecular mechanics does. For example, the Poisson–Boltzmann model for implicit solvation (Sitkoff et al., 1994) and quantum-chemical models return an energy for the entire system on which they are run. Thus, a viable approach to modeling protein energies more realistically is to infer local terms from full-protein energies. Vizcarra et al. (2008) apply this approach to the Poisson–Boltzmann model, calculating pairwise energies from differences in full-protein conformational states and achieving a pairwise energy matrix that quite accurately matches the Poisson–Boltzmann energies of full conformations.

However, their method can only accommodate rotamer pairs, does not support continuous flexibility, and can only be used when substituting a single rotamer into a conformation is possible while maintaining the conformation of the other residues. This is impossible when residues share conformational degrees of freedom, which is typically needed for backbone flexibility (Georgiev and Donald, 2007; Hallen et al., 2013), and may also cause problems in the case of steric clashes. Also, DEE/A* has been generalized to accommodate higher-than-pairwise energy terms if these terms are computed explicitly for particular tuples, for example, triples of residues (LuCore et al., 2015). However, most energy functions modeling higher-than-pairwise effects, including Poisson–Boltzmann, return a single energy for the entire system, rather than a sum of explicit local terms as required by algorithms such as those in LuCore et al. (2015).

Hence, today's protein and drug designers are faced with a choice. They can neglect continuous flexibility and energy terms that are not explicitly local (e.g., explicitly pairwise), thus incurring significant error. Or they can pay a massive overhead to incorporate them—by enumerating many conformations (for continuous flexibility) or searching exhaustively (for nonpairwise energy functions). We now offer a way around this dilemma. We construct an energy function that is an explicit, discrete sum of local energy terms, which are associated with tuples of RCs. This function maps RC lists, which represent voxels in the conformation space of a protein, to energies. But it will approximate, to arbitrary accuracy, the minimized voxel energy, which can be computed with any energy function: no need for residue pairwiseness or any other local representation. Computing this approximation is a machine-learning problem, and we solve it with a least-squares method.

Our approach has some resemblance to cluster expansion methods, which have previously been used in quantum mechanics (Čížek, 2009) and to represent optimized energies for protein sequences (Grigoryan et al., 2006, 2009). However, as discussed in Hallen et al. (2015), approximations of energy surfaces can be much more compact if unrealistically high-energy regions of conformational space are excluded from the approximation (and from the subsequent conformational search). Thus, unlike cluster expansion methods, we exclude pruned tuples of RCs, making our derived energy function a local unpruned tuple expansion (LUTE). Because conformational and sequence search using the LUTE energy function is a discrete optimization problem of the type solved by DEE/A*, BWM*, and other very efficient algorithms, it allows designs to run quickly using these algorithms, while still approximating continuous flexibility and highly realistic energy functions to a high level of accuracy.

We have implemented LUTE in the OSPREY (Georgiev et al., 2008, 2009; Gainza et al., 2013) open-source protein design package, which has yielded many designs that performed well experimentally—in vitro (Stevens et al., 2006; Gorczynski et al., 2007; Chen et al., 2009; Frey et al., 2010; Georgiev et al., 2012; Roberts et al., 2012; Rudicell et al., 2014) and in vivo (Gorczynski et al., 2007; Frey et al., 2010; Roberts et al., 2012; Rudicell et al., 2014) as well as in nonhuman primates (Rudicell et al., 2014). OSPREY contains a wide array of flexible modeling options and provably accurate design algorithms (Georgiev et al., 2009; Gainza et al., 2013), allowing LUTE to be used for many types of designs.

By presenting LUTE, this article makes the following contributions:

• 1. A method to represent continuous flexibility and general energy functions to arbitrary accuracy in an LUTE that can be used directly as input to discrete combinatorial search algorithms such as DEE/A*.

• 2. A free implementation of LUTE in our laboratory's open-source OSPREY protein-design software package (Georgiev et al., 2008, 2009; Chen et al., 2009; Frey et al., 2010), available for download (Georgiev et al., 2009) as free software (Georgiev et al., 2009), supporting representation of both continuous side chain and backbone flexibility and of molecular mechanics and Poisson–Boltzmann energy functions.

• 3. Integration of LUTE with the DEE/A* (Leach and Lemon, 1998), iMinDEE (Gainza et al., 2012), BWM* (Jou et al., 2015), and COMETS (Hallen and Donald, 2015) algorithms for sequence and conformational search.

• 4. Bounds on the time and space complexity of protein design calculations that model continuous flexibility and/or use energy functions with nonlocal terms. The time and space complexity are exponential merely in the branch width w of the residue interaction graph, and thus the designs can be done in polynomial time for systems whose branch width is bounded by a constant.

• 5. Experimental results for 47 computational design calculations on 36 protein structures using LUTE, which demonstrate its accuracy and efficiency in single-state designs, multistate designs, and for both n-body Poisson–Boltzmann and pairwise energy functions.

2. Methods

The basic strategy of LUTE is to create a discrete, quick-to-evaluate energy matrix that tells us everything we need to know for design purposes about the continuous energy landscape of a protein. We now describe this energy matrix and how it works.

Our goals in protein design [both GMEC (Leach and Lemon, 1998; Gainza et al., 2012) and binding/partition function (Lilien et al., 2005; Georgiev et al., 2008) calculations] can be posed in terms of a discrete function 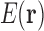that maps an ordered list 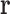of RCs to an energy. The list 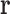contains exactly one RC per residue and thus represents a voxel 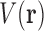in conformation space, where a vector 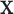of sequence and conformational degrees of freedom satisfies 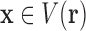if the degree-of-freedom bounds defined by each RC in 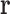are respected by every degree of freedom in 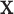. The conformational degrees of freedom in 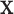will generally be continuous internal coordinates, for example, side chain dihedrals. We let 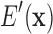denote the energy of the protein system, as a function of all its degrees of freedom.

For calculation of the GMEC E_g, we wish to minimize 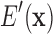with respect to 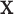. Letting R be the set of all possible voxels, the domain over which we minimize is a finite union of voxels :

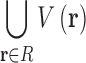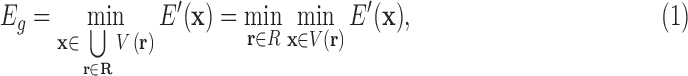which can be expressed in the form 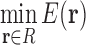, where

Similarly, partition function calculations seek to calculate the partition function

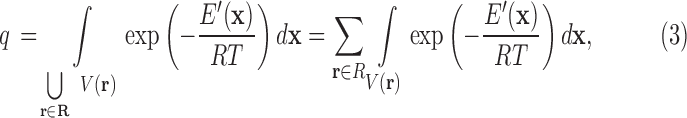where R is the gas constant and T is the temperature. Letting

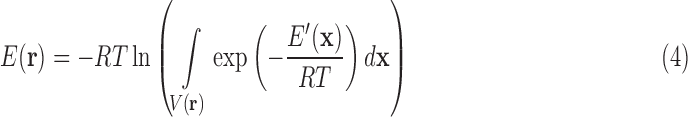we have a formulation of q in terms of the discrete free energy function :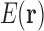

Alternatively, if we use the definition of Equation 2 to define 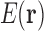, then Equation 5 gives us the approximation used in Lilien et al. (2005) and Georgiev et al. (2008) for the partition function.

Because 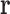is a discrete variable, the energy 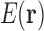can be decomposed as a sum of energies associated with tuples of RCs (Fig. 1). If all the RCs in a tuple are in the list 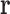, then that tuple's energy will contribute to 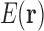. Most higher order tuples of RCs consist of residues too far apart to have higher order interactions, and thus do not contribute significantly to the energy [see Section 1 and Hallen et al. (2015)]. We can reduce the number of tuples needed substantially further if we only try to represent favorable, nonclashing conformations. By eliminating high-energy conformations, this restriction of conformational space greatly reduces the range of energy values over which 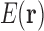must be accurate. To achieve this, we prune tuples that cannot be part of favorable conformations, and consider only conformations whose tuples are all unpruned. Our expansion is much more efficient to compute after provably unfavorable tuples are pruned. Hence, we are able to represent the energy 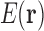as a local unpruned tuple expansion (LUTE).

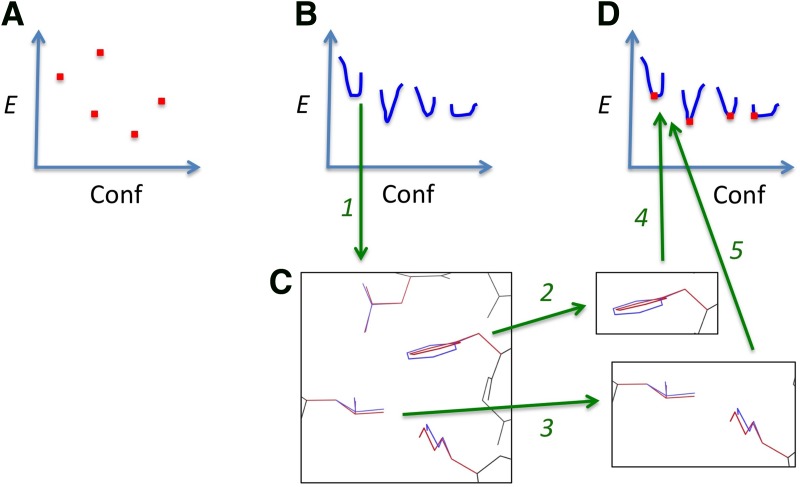
FIG. 1.

LUTE makes continuously flexible design efficient by representing continuous flexibility using local, discrete energy terms. (A) Protein design with discrete flexibility searches over a discrete (although large) conformational space (Conf), looking for low-energy (E) conformations. Highly efficient algorithms such as DEE/A* are available for this problem. (B) Protein design with continuous flexibility must search over a large space of voxels (blue) in a continuous conformational space, but we are usually interested only in the minimum energy point of each voxel. We thus want a way to search combinatorially over these minimum energy points. (C) The minimized energy of a voxel in protein conformational space depends on all rotamers in the voxel (arrow 1). But we can expand this minimized energy as a sum of local contributions from low-order tuples (e.g., pairs) of residues (arrows 2 and 3). (Minimized conformations shown in red, ideal rotamers in blue). (D) This expansion, known as LUTE, gives us a discrete combinatorial search problem of the same form as protein design with discrete flexibility (arrows 4 and 5). But this new discrete problem searches over the minimum energy points (red) of voxels in continuous conformational space (blue). We can solve this problem very efficiently. Figure shows Leu 29, Leu 51, Phe 55, and Lys 59 of the Atx1 metallochaperone [PDB id 1CC8 (Rosenzweig et al., 1999)]. LUTE, local unpruned tuple expansion.

Let us consider a conformational space with continuous and discrete degrees of freedom, consisting of RCs, and a mapping 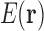that we can readily calculate. For example, in a typical continuously flexible design, 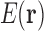is defined by Equation (2), which we assume can be calculated by local minimization. Suppose we have a set T of tuples of RCs at different residue positions. T can contain pairs but also may contain triples, etc. We then define our LUTE as a mapping 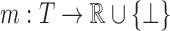. m defines a real coefficient for each tuple 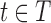, except for pruned tuples, for which 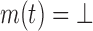. 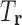Let denote the set of tuples in T that consist only of RCs in 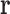. For example, if T is the set of all possible RC pairs, then 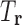will consist of all pairs of RCs in the list of RCs 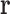. Then LUTE predicts 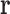to be a pruned conformation if 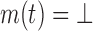for any 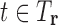, and otherwise it predicts 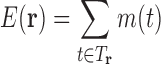. We refer to the data structure representing mapping m as the LUTE energy matrix. We call it an energy matrix because it takes a form similar to that of traditional pairwise energy matrices (Desmet et al., 1992; Leach and Lemon, 1998; Gainza et al., 2012; Hallen et al., 2013), although it contains significantly different numerical values when computed for the same design system. In practice, expansions in pairs and sometimes triples have worked well (see Section 3, Section B in the Supplementary Material).

Most algorithms for protein design with discrete rotamers take a matrix of pairwise energies as input. By simply substituting a LUTE energy matrix for this pairwise energy matrix, we can convert any of these algorithms into an equally efficient design algorithm that searches a continuous search space instead of a discrete search space, and/or that optimizes a nonpairwise energy function instead of a pairwise energy function. The LUTE energy matrix is computed once, before the search, which takes only polynomial time in the number of residues. For example, we need quadratic time to compute a LUTE matrix for which T is all pairs of RCs. Details of the computation by least squares of the LUTE matrix, and of the use of this matrix in search algorithms, are provided in the Supplementary Material.

3. Results

We present here complexity results and computational experiments regarding the performance of LUTE. In Section 3.1, we show that the combination of LUTE with the BWM* (Jou et al., 2015) search algorithm is guaranteed to solve continuously flexible protein designs in polynomial time given a residue interaction graph with branch width bounded by a constant. In Sections 3.2 and 3.3, we present 30 single-state and 17 multistate protein design calculations using LUTE. We measure the gains in efficiency provided by LUTE and its ability to accurately and efficiently perform calculations that, due to their large amount of continuous flexibility (Section 3.2) or nonpairwise energy function (Section 3.3), are inaccessible to previous algorithms. These results include designs with both continuous side chain and backbone flexibility. Side chain dihedrals were allowed 9° of continuous motion in either direction relative to the modal value for each side chain rotamer (Janin et al., 1978), whereas backbone flexibility (when present) was modeled as in Hallen et al. (2013).

3.1. Polynomial time protein design with continuous flexibility

Protein design in the general case is NP-hard (Pierce and Winfree, 2002; Chazelle et al., 2004). In practice, however, many designs exhibit special properties that make them more tractable. For example, the residue interaction graph—the graph whose edges encode non-negligible interactions between pairs of residues—of practical designs often has low branch width. It has been previously shown that protein design with discrete rotamers can be performed in asymptotic time exponential only in the branch width (Jou et al., 2015) w. Furthermore, these branch widths can be small irrespective of the number of mutable residues (Jou et al., 2015). Thus, for many protein designs with discrete rotamers, the corresponding GMEC can be found in polynomial time. If one substitutes the LUTE matrix for the discrete pairwise energy matrix in this complexity result, then design with continuous flexibility and a constant-bounded branch width can be solved in polynomial time as well. We can make this rigorous using the following theorem, whose proof is provided in Section E of the Supplementary Material. In this theorem, a LUTE energy function is a function 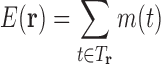, where 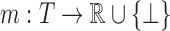maps RC tuples to real coefficients (for this purpose, the coefficient 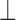of a pruned tuple is effectively 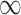). Let n be the number of mutable residues, q be the maximum number of allowed RCs at any mutable residue position, and and 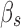be the time and space costs, respectively, to compute the branch decomposition. This theorem establishes the complexity both of GMEC calculations and of enumeration of subsequent conformations in gap-free ascending order of energy. The latter is essential for calculation of partition functions, which can be used to account for entropy in predictions of binding (Lilien et al., 2005; Georgiev et al., 2008; Jou et al., 2015).

Theorem 3.1. For a LUTE energy function whose residue interaction graph has branch width w, the GMEC can be computed in 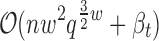time and 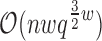space, and each additional conformation can be enumerated in order of LUTE energy in 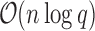time and 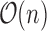space.

3.2. Continuous flexibility

LUTE single-state designs were run on 23 protein design systems from Hallen et al. (2015) with 4–16 mutable residues, as well as five larger systems (17–40 mutable residues), to measure the efficiency of LUTE and to observe the behavior of LUTE on the larger systems. Many of these larger systems are intractable by previous methods (except post-hoc minimization methods that do not account for continuous flexibility during search). The results show that the discrete DEE/A* search with LUTE is dramatically more efficient than EPIC, which offers previously state-of-the-art efficiency for continuously flexible design (Hallen et al., 2015) (Fig. 2). They also demonstrate that LUTE can handle very large continuously flexible designs—including a 40-residue side chain placement, which covers a large fraction of the residues in the Atx1 metallochaperone (Fig. 4, left), and a 20-residue design on the same structure with 5 amino acid types allowed at every position. Furthermore, the LUTE energy matrix consistently represented the true energy landscape very closely (Fig. 3). Optimal sequences and conformations with LUTE differed significantly from the same designs run without continuous flexibility: the same top conformation was returned in only 2 of the 28 single-state designs. On average, 31% of the RCs in the optimal conformations differed from each other. This is consistent with previous work showing that protein design calculations with and without continuous flexibility differ significantly in their results (Gainza et al., 2012; Hallen et al., 2013).

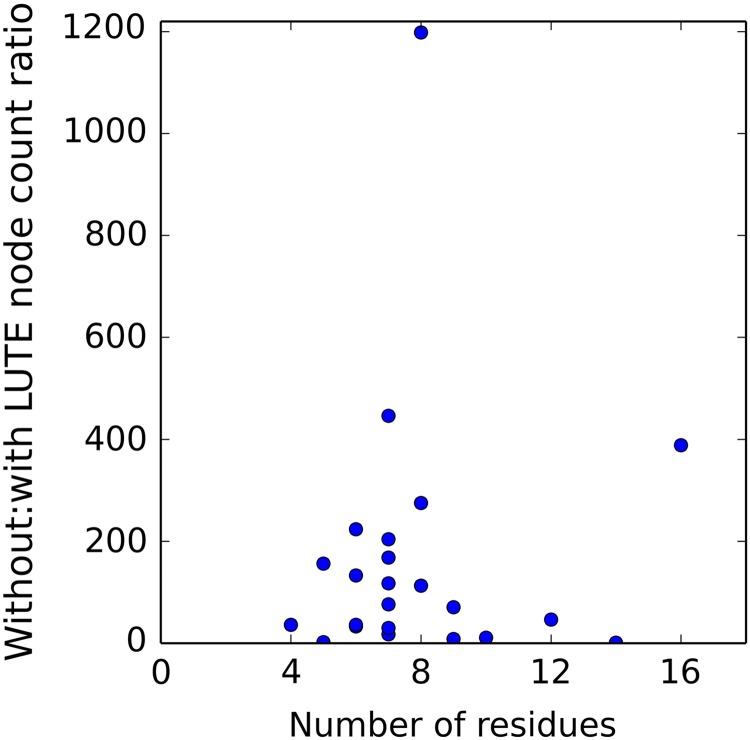
FIG. 2.

LUTE markedly reduces the cost of continuously flexible conformational search. Ratios (without LUTE:with LUTE) of the number of nodes in the A* tree before enumeration of the GMEC (or of the last conformation if several conformations closely spaced in energy were calculated; see Hallen et al. (2015)), versus number of flexible residues. A 20-residue side chain placement with node ratio 2 × 10⁵ is not shown because it would break the scale. GMEC, global minimum energy conformation.

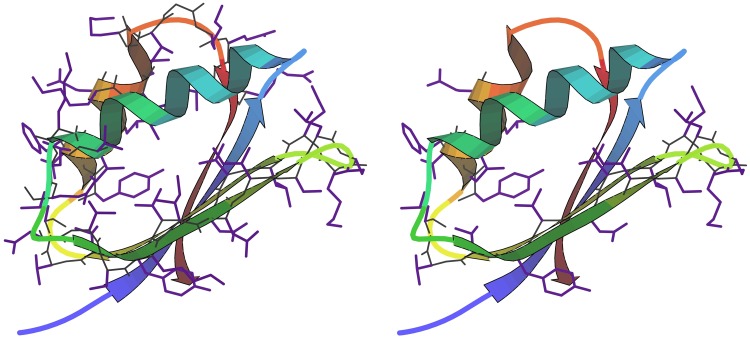
FIG. 4.

LUTE enables very large provably accurate protein designs with continuous flexibility (left) and with Poisson–Boltzmann energy functions (right). Left: previous protein designs with continuous flexibility only finished when performed with significantly fewer flexible residues than designs with discrete rotamers. Even 20-residue designs were often intractable. But LUTE solved a side chain placement problem with continuous flexibility, in which 40 residues (purple) were made flexible in the Atx1 metallochaperone [PDB id 1CC8 (Rosenzweig et al., 1999)]. Right: previous designs using the Poisson–Boltzmann energy function could not optimize this function directly, but only used Poisson–Boltzmann energies to rerank top hits from optimization of a simpler, pairwise energy function. But LUTE can optimize the Poisson–Boltzmann energy function directly—for example, in a side chain placement of 20 residues (purple) of Atx1.

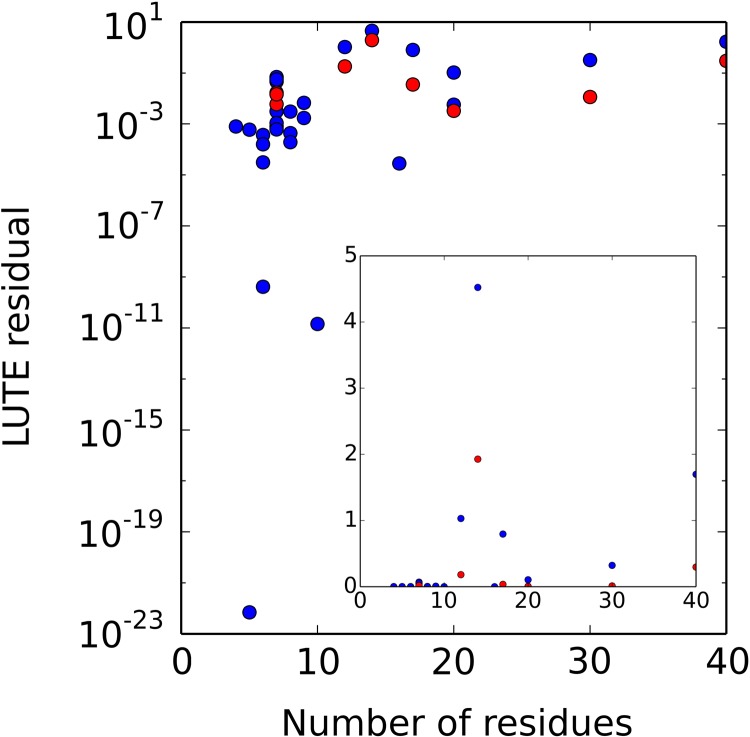
FIG. 3.

LUTE accurately represents continuously minimized energies. Residuals for LUTE ((kcal/mol)²) on the cross-validation data set, measuring the difference between the EPIC energy and a pairwise expansion (blue) or one with sparse triples (red; computed only if pairwise residual exceeded 0.01). x axis: number of flexible residues. Inset: All the same data plotted on a linear scale.

For many systems, LUTE achieved a fit with residual under 0.01 (kcal/mol)² with only a pairwise expansion. In cases when the pairwise expansion's residual was higher, an expansion in sparse triples was performed instead. In all but one case, the triples expansion's residual was less than thermal energy at room temperature [0.59 kcal/mol, i.e., 0.35 (kcal/mol)²], and thus deemed insignificant.

The one outlier case was a 14-residue design on ponsin (PDB id: 2O9S). It exhibited significant local minimization errors, which caused even the matrix of pairwise lower bound energies (computed before LUTE precomputation begins) to have errors of at least 10 kcal/mol. These errors indicate the failure of either our local minimizer or our assumption that local minimization suffices within RCs. As a result of these errors, the LUTE residual even with triples was 1.9 kcal/mol for this system, seven times worse than the next worst residual (the 40-residue Atx1 design). Our software now detects this problem and warns the user before the LUTE computation begins.

Seventeen multistate protein designs were also performed, using a combination of LUTE with our COMETS (Hallen and Donald, 2015) multistate protein design algorithm (see Section C in the Supplementary Material). The systems from these designs were taken from Hallen and Donald (2015); details are provided in Section G of the Supplementary Material. The same designs were run with and without continuous flexibility, with LUTE used in the continuous case. As discussed in Hallen and Donald (2015), COMETS provably returns the same results as exhaustive search over sequences, but it provides a speedup compared with that exhaustive search by (a) considering only a portion of the sequences in the search space explicitly and (b) only performing a full conformational optimization for a small portion of the sequences in (a). However, previously (Hallen and Donald, 2015), (a) was only significant in designs without continuous flexibility and (b) was much more pronounced without continuous flexibility. LUTE brings continuously flexible COMETS designs up to speed with discrete designs on the same system (Supplementary Fig. S3).

3.3. Designs that provably optimize Poisson–Boltzmann energies

We also ran LUTE conformational optimization calculations on two proteins using the Poisson–Boltzmann energy function, which is nonpairwise. This energy was evaluated using Delphi (Nicholls and Honig, 1991; Rochia et al., 2002) in place of the pairwise EEF1 (Lazaridis and Karplus, 1999) solvation energy that is used by default in OSPREY. Interestingly, triple energies did not provide significant benefit here, but LUTE was found to describe the Poisson–Boltzmann energy landscape with a high degree of accuracy. Previous work has shown that an accurate pairwise representation can be obtained for Poisson–Boltzmann energies of discrete, rigid rotamers (Vizcarra et al., 2008), but our LUTE results show that a very accurate representation of continuously minimized Poisson–Boltzmann energies is possible as well. With continuous flexibility, a six-residue side chain placement on the unliganded TIR1/IAA7 complex [PDB code 2P1Q (Tan et al., 2007)] with continuous flexibility achieved a total residual of 6 × 10⁻⁴ and took about 4 days. Furthermore, a 20-residue side chain placement without continuous flexibility on the bacterial metallochaperone protein Atx1 [PDB code 1CC8 (Rosenzweig et al., 1999); Fig. 4, right] was solved in 2.5 hours, with total residual 0.04 (kcal/mol)². Unlike previous protein design calculations that use Poisson–Boltzmann energies, our new calculations provably return the minimum of the (LUTE-approximated) Poisson–Boltzmann energy over the entire conformational space, rather than simply over a set of top hits from an initial search that used a cheaper energy function.

4. Conclusions

The protein design problem enjoys a wide array of powerful algorithms for conformational and sequence search. These algorithms take a discrete energy matrix and perform sequence optimizations, both in the single-state and multistate cases. At the same time, previous work in bioinformatics and quantum chemistry has made great progress toward quantitatively accurate modeling of the flexibility and energy landscapes of biomolecular systems. Uniting these fields to perform designs with highly realistic modeling would result in great biomedical impact, both in protein and in drug design. However, because state-of-the-art flexibility and energy modeling methods do not produce a discrete matrix, there is a gap between these fields. LUTE offers a strategy to bridge this gap. By representing continuous flexibility and general energy functions in a discrete matrix, it greatly increases the realism of the modeling that discrete combinatorial optimization algorithms such as DEE/A* can directly accommodate. We thus believe that LUTE can serve as a foundation for greatly improved biomolecular design protocols.

Acknowledgments

We would like to thank Drs. Kyle Roberts and Pablo Gainza for providing PDB files and scripts for testing, all members of the Donald Lab for helpful comments, and the PhRMA and Dolores Zohrab Liebmann foundations (M.A.H.) and NIH (grant R01-GM-78031 to B.R.D.) for funding.

Author Disclosure Statement

The authors declare that no competing financial interests exist.