Abstract.
We describe a postacquisition, attribute-based quality assessment method for brain magnetic resonance imaging (MRI) images. It is based on the application of Bayes theory to the relationship between entropy and image quality attributes. The entropy feature image of a slice is segmented into low- and high-entropy regions. For each entropy region, there are three separate observations of contrast, standard deviation, and sharpness quality attributes. A quality index for a quality attribute is the posterior probability of an entropy region given any corresponding region in a feature image where quality attribute is observed. Prior belief in each entropy region is determined from normalized total clique potential (TCP) energy of the slice. For TCP below the predefined threshold, the prior probability for a region is determined by deviation of its percentage composition in the slice from a standard normal distribution built from 250 MRI volume data provided by Alzheimer’s Disease Neuroimaging Initiative. For TCP above the threshold, the prior is computed using a mathematical model that describes the TCP–noise level relationship in brain MRI images. Our proposed method assesses the image quality of each entropy region and the global image. Experimental results demonstrate good correlation with subjective opinions of radiologists for different types and levels of quality distortions.
Keywords: magnetic resonance imaging, image quality, entropy, contrast, standard deviation, total clique potential, Bayes formula
1. Introduction
Virtually, all spheres of medicine need information contained in medical images. Structural information based on the chemical and physical properties that distinguish different anatomical structures is highly desired in medical images. This requirement makes a magnetic resonance imaging (MRI) system a popular imaging modality for the study of human anatomy, diagnosis of neurological diseases, clinical trials of drugs for the monitoring, and treatment of neurological diseases.1–3 An MRI system can display images in three different perpendicular planes and has the potential to discriminate the constituent soft anatomical structures with high spatial and contrast resolution.
The quality of a medical image is strongly dependent on the acquisition procedures.4 During acquisition, there are several factors relating to the imaging system; the actions of the operator and the subject under investigation that limit the attainment of an ideal quality image. Image quality in radiation-based imaging systems is dependent on radiation dose.5 There is a trade-off between image quality and patient safety.6 The antiscatter grids determine the level of contrast in digital mammography images.7 The quality of reconstructed SPECT images is influenced by the number of projection angles.8 In breast ultrasound images, artifacts are caused by improper positioning of the nipple relative to the breast mass and loose contact between the breast mass and the transducer.4 In MRI images, noise is the result of trade-off between signal-to-noise ratio (SNR), image resolution, and length of scan time.9 Bias fields are the combined effects of nonuniform sensitivity of radio-frequency coils and nonuniformity of static fields.10 Motion of the patient, respiration, blood flow, and patient position relative to the isocenter of the magnetic bore introduce blur and extraneous features into the image.11,12 Chemical shift and partial volume artifacts are the result of improper parameter settings.13 These numerous factors that influence the acquisition procedures make quality evaluation a nontrivial and complex task.14,15
Popular objective quality evaluation methods, such as root-mean-square error (RMSE), SNR, and structural similarity index,16 were designed to solve research problems that were not related to image interpretation but on efficient compression, storage, and transmission of images. Their formulation assumes that all classes of medical images and all other natural images have the same descriptive features. Medical images exhibit characteristics, such as texture, grayscale color, noise, and homogeneity, that distinguish them from each other and other classes of natural images. There are many definitions of peak signal-to-noise ratio, SNR, and mean square error, which make it difficult to compare quality measures from different imaging system, modalities, and researchers.8 Quality indices derived from these popular methods do not always correlate with the performance of observers using the imaging system on the task for which they are intended.8
Some of the problems associated with the popular quality assessment methods were addressed when task-based quality assessment methods were introduced to the medical imaging and computer vision community.17–19 The philosophy behind a task-based quality assessment is the belief that a rigorous quantification of image quality should be defined by specifying a clearly defined task and the observer who will be performing the task. In medical imaging, the task can be a classification or estimation task. An example of a classification task is the detection of lesions in brain MRI images of patients diagnosed with multiple sclerosis disease. A quantification of brain atrophy in patients diagnosed with Alzheimer’s disease is an example of an estimation task. The observer can be human, human model, or Bayesian ideal observer.20,21 The efficacy of task-based quality assessment reported in Refs. 20, 22, and 23 is the motivation behind pioneering research in the field of task-based adaptive imaging. Task-based adaptive imaging has been applied for the optimization of imaging systems parameters,5,8,24 optimization of image quality in imaging systems,21,25,26 evaluation of cardiac ejection fraction estimation algorithms,27 and the evaluation of diffusion-weighted MRI segmentation algorithms.28
The mainstream approach to brain MRI image quality evaluation methods such as29–35 focus on the acquisition stage. The several parameters associated with MRI system acquisition process are exploited to evaluate and optimize image quality. There are few contributions on postacquisition quality assessment of brain MRI images. Postacquisition quality evaluation is an important step in the quality control procedures of clinical research organizations (CROs) because brain measurements derived from MRI images are susceptible to differences in MRI system sequence parameters.36 Quality evaluation ensures that the variations in the quality of MRI images from different MRI system manufacturers, different clinical trial sites, and different acquisition protocols are assessed and standardized before they are fed to automated image analysis systems.
We identified and reviewed five contributions in the literature on postacquisition quality evaluation of brain MRI images. The report in Ref. 37 applies analysis of variance (ANOVA) algorithm to assess the variation of several quality measures with different levels of distortions. Mortamet et al.38 combine the detection of artifacts and estimation of noise level to measure the image quality. In Ref. 39, a null space analysis and just noticeable difference scanning method were proposed as a better quality metric compared to RMSE. The popular SNR is the quality metric adopted in Ref. 40. Subjective quality assessment was reported in Ref. 41.
The design of current postacquisition evaluation methods regards the brain as a single region. They will be inefficient for application in region-based brain MRI analysis. The contribution by Gedamu et al.,40 which adopts SNR, is diagnostically misleading34 because it cannot discriminate the quality of two images that are perceptually dissimilar.39,42 A significant contribution by Mortamet et al.38 is the adoption of artifacts as quality attributes. Since several types of distortions combine with ideal features to manifest as image quality attribute,43 the adoption of artifacts and noise in Ref. 38 are too few attributes to evaluate the quality of an image.44 There is a risk of ambiguity in quality measures that are based on the use of ANOVA models.45 ANOVA limits the performance of the technique proposed in Ref. 37 to the detection of distortion. It cannot transform the different levels of distortion into a quality index. Trained MRI readers, such as radiologists, vary in their subjective evaluations.46 Intrareader as well as interreader variability can be high. The need to reduce interreader variability through consensus with other readers coupled with negotiation around several types and levels of distortions34 makes the subjective method proposed in Ref. 41 inefficient to manage the large volume of MRI data in CRO.47
Motivated by the successful application of Bayesian model observer in task-based quality evaluation, we propose a postacquisition, attribute-based quality evaluation method for brain MRI images. Section 2 describes the theory behind our proposed method. Materials and methods are described in Sec. 3. Results from quality measure experiments are shown in Sec. 4 and discussed in Sec. 5. Section 6 concludes this report.
2. Theory
2.1. Relationship between Entropy and Classical Quality Attributes
The Shannon entropy of an image expresses the diversity of gray-level pixels.48 It is defined as
| (1) |
where is defined as
| (2) |
is the probability of each gray level and gives the number of pixels in the image.
The classical quality attributes of a brain MRI slice include contrast, sharpness, noise, and brightness. Several contributions in the literature establish the relationship between entropy and the classical quality attributes. The reports in Refs. 49 and 50 show that image contrast can be expressed using entropy. Entropy is widely used to quantify image details by the measurement of sharpness.51–53 The contributions in Refs. 54–56 establish the relationship between entropy and minimum mean square error (MMSE). The MMSE can be regarded as a function of SNR, a measure of noise level. The contributions in Refs. 57 and 58 demonstrate entropy as the combination of different image quality attributes. The relationship between brightness and entropy has been exploited to develop brightness-preserving histogram equalization algorithms.59,60 Furthermore, entropy maximization has been adopted in Refs. 61 and 62 to improve the quality of tomographic images.
Our proposed method aims to predict the image quality of a specific region-of-interest in an MRI slice. Global entropy computed according to Eq. (1) is of no use for our proposed method because it regards the image as a single region. Our proposed method will require a segmentation task. It is necessary to incorporate spatial information into the image before the segmentation task.63 We incorporate the spatial information according to Ref. 64 by defining a small neighborhood by window size within the image so that the entropy of can be written as
| (3) |
where is defined as
| (4) |
is the probability of grayscale in the neighborhood, is the number of pixels with grayscale in the neighborhood, and is the local entropy of neighborhood .
2.2. Bayesian Framework
2.2.1. Bayes theorem
Given that the MRI slice is a grayscale image, convolution with a fixed-size entropy filter extracts the local entropy feature image . Let the entropy image be segmented into separate regions . The regions are the low-entropy region and the high-entropy region . For each entropy region, we make separate observations of image quality attributes by the use of appropriate filters to extract the local contrast feature image , the local standard deviation feature image , and the local sharpness feature image . According to Bayes theory,65 the posterior probability of each local entropy region given each observation is
| (5) |
where is the prior belief of the event before the actual observation , is the likelihood, and the denominator is a normalizing constant referred to as the total probability.
2.2.2. Prior belief
The prior belief in each entropy region is based on four principles. First, we incorporate the initial steps for implementing task-based quality assessment.66–68 Multiple estimates of each entropy region for each patient in a given population can be computed from slices in an MRI volume data.66 Second, brain MRI images are geometrically similar69 across age, gender, and race. Third, they are statistically simple70 as evident from the few constituent homogeneous regions that can be used to describe an ideal slice. Fourth, Rician distribution of pixels at low SNR can be modeled as Gaussian at high SNR.71,72 Based on these principles, we regard entropy as a random variable generated from each slice in an MRI volume database. According to Ref. 73, the invocation of the central limit theorem on number of data gives a normally distributed data with mean and variance
| (6) |
Accurate measurement of entropy is limited by the presence of noise.74 Analytically, entropy increases with sharpness but there is no fair correlation between entropy and noise.57 The report in Ref. 57 suggests that entropy can be considered as a quality index only if noise can be considered as a unique type of information, which can be distinguished from Shannon entropy. We follow the suggestion in Ref. 57 by applying the results of the experiment in Ref. 75 to distinguish noise from entropy and hence determine the best estimate of . The MRI slice is modeled as a Markov random field63,70,76,77 but without reference to a prior model image. Clique potential computed from each neighborhood, according to Ref. 63, is summed to obtain which we refer to as the total clique potential (TCP) for the image. A threshold classifies the TCP energy of the image into either the noise energy band or the entropy energy band so that the prior belief is defined as
| (7) |
where is the cumulative probability when the -score of the entropy value for is used to standardize the normal distribution in Eq. (6), 0.5 is the maximum possible value of , and is the TCP energy of the slice.
2.2.3. Likelihood
The likelihood is the matching of the structural information in an entropy region to the corresponding region in a feature image where image quality attribute is observed
| (8) |
where is the number of pixels common to both and and is the number of foreground pixels.
2.2.4. Posterior probability
The posterior probability is computed in a three-step hierarchical process.
-
1.
First step
The initial step is the posterior probability of a local entropy region given any of local contrast, local standard deviation, and local sharpness. This gives the quality score for each quality attribute observed from a feature image. They are the contrast quality attribute , the standard deviation quality attribute , and the sharpness quality attribute . These attributes can be generally expressed as(9) -
2.
Second step
The second step is the quality index for each entropy region. It is the average of the three quality attributes for each local entropy region(10) -
3.
Third step
The last step is the quality index for the MRI slice. It is the average quality score for the low- and the high-entropy regions(11)
3. Materials and Methods
3.1. Materials
Data used for the performance evaluation of our proposed method were obtained from three sources. They are from the NeuroRx Research Inc., the BrainCare Oy, and the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database.
Thirty one MRI volume data from two sources were used as test data. Twenty-one volume data were from NeuroRx and 10 volume data from BrainCare. Each slice from NeuroRx has 2.4-mm thickness with a dimension of in a 60-slice volume data. BrainCare data have a thickness of 7.4 mm with a dimension of in a 24-slice volume data. NeuroRx data consist of 10 conventional T1 images that were originally acquired with bias fields. The remaining data from NeuroRx were without any perceived distortion. They are three T2, three T1, three PD, and two fluid attenuation inversion recovery (FLAIR) images. All the 11 MRI volume data from BrainCare had no perceived distortion. They are three T2, three T1, two PD, and two FLAIR images. The description of the test data is displayed in Table 1.
Table 1.
Description of test data utilized for the performance evaluation of our proposed method for the quality evaluation of an MRI slice.
| Categories of experiment | Type of MRI volume data | Number of MRI volume data | Number of slices |
|---|---|---|---|
| MRI volume data without perceived distortion | T2 | 2 | 40 |
| T1 | 2 | 30 | |
| PD | 5 | 30 | |
| FLAIR | 4 | 30 | |
| MRI volume data degraded by bias fields | T1 | 10 | 100 |
| MRI volume data degraded by motion blur | T2 | 2 | 30 |
| T1 | 2 | 30 | |
| MRI volume data degraded by noise | T2 | 2 | 30 |
| T1 | 2 | 30 | |
| Total | 31 | 350 |
Two hundred and fifty MRI volume data from ADNI database were used to build a standard normal distribution of random variables. The random variable is the percentage composition of an entropy region in a subject MRI volume data. Each volume data from ADNI were acquired using high-resolution T1 magnetization-prepared rapid gradient echo (MPRAGE) pulse sequence. Images acquired using MPRAGE pulse sequence were our choice to build a quality model because they exhibit superior gray-white matter contrast compared to the conventional T1 and other structural brain MRI images.78–80 Each slice in a volume data has thickness of 1.2 mm and dimension of . The details of ADNI acquisition protocol and the initial processing steps are available in Ref. 81. We seek the opinion of radiologists in the selection of MRI volume data on the ADNI website. This is to ensure that only MPRAGE MRI volume data that meet the expected high-quality attributes are selected for the quality model. Furthermore, we seek MRI data of subjects without lesions or with very mild lesions. For each MRI data, slices toward the most inferior and most superior sections are discarded because they highlight more of scalp and bone structures than brain structures. The number of useful slices for each subject varies between 50 and 85. A total of 12,005 slices were derived from the 250 MRI volume data.
3.2. Generation of Distortions
The test data were evaluated in their original state of acquisition and for different levels of artificially induced distortions. Different levels of motion blur and Rician noise were artificially induced on images that are without perceived distortion. Motion blur was induced on a slice by convolving it with a special filter that approximates the linear motion of a camera. The linear motion is described by two parameters of the motion blur point spread function 82
| (12) |
where is the linear distance in pixels and is the angular distance in degrees. The range of the linear and angular distances is and , respectively. Both linear and angular distances were linearly spaced into 20 data points so that the filter generated 20 increasing levels of motion blur. Rician noise was generated in a three-step process. Gaussian noise is generated in the first step. The noise level is quantified as a percentage of the maximum pixel intensity level in the test image. For a percent Rician noise level, the standard deviation of the equivalent normal distribution is given as
| (13) |
where is the maximum pixel intensity.83 In the second step, we simulate the real and imaginary components in the complex plane of the MRI acquisition process by adding two separate and identical Gaussian noise levels to the test image. The third step computes the magnitude of the complex data. The Rician noise level was scaled from 1% to 20% in steps of 1%.
3.3. Methods
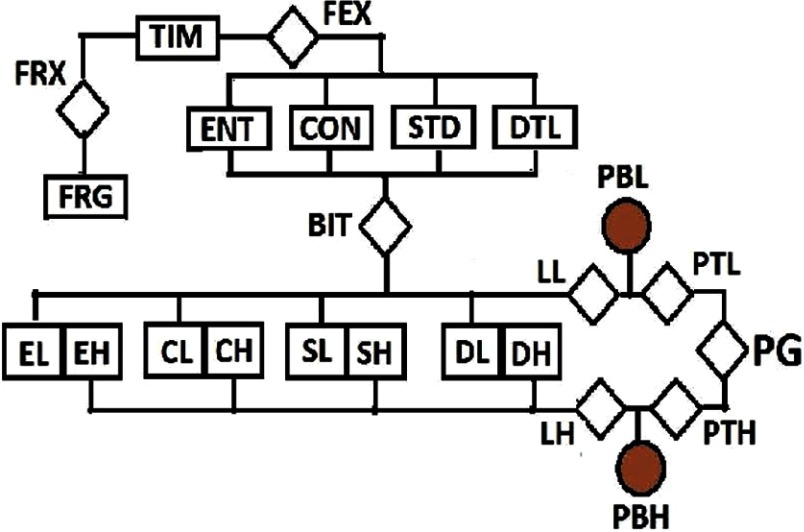
The algorithm was implemented in the MATLAB® computing environment. The flow chart in Fig. 1 and the images in Fig. 2 explain how our proposed method works. The six stages in the computation of quality index for an MRI slice are explained below.
Fig. 1.
The flow chart of postacquisition quality evaluation for a brain MRI image. The event of interest, local entropy (ENT), is extracted (FEX) from the test image. Three separate observations: local contrast (CON), local standard deviation (STD), and local sharpness (DTL) feature images are also extracted (FEX) from the same test image. These images, except foreground (FRG), are transformed (BIT) to the binary domain for classification into low- and high-energy regions. Each region (EL and EH) in the local entropy feature image (ENT) is combined with corresponding region in the contrast (CL and CH), standard deviation (SL and SH), and sharpness (DL and DH) feature images to obtain the likelihood (LL and LH) for each observation. For each region, Bayes rule combines the prior belief (PBL and PBH) with the likelihood (LL and LH) corresponding to each feature image to compute quality score for each quality attribute. The total quality score for each region (PTL and PTH) is the weighted sum of the quality score of each quality attribute. The global quality score (PG) of the slice is the weighted sum of the total quality score (PTL and PTH) for each region.
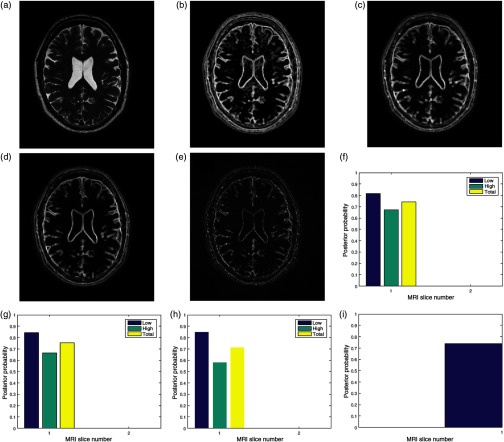
Fig. 2.
Bayesian framework inspired postacquisition quality assessment of (a) a brain MRI slice (TIM) in an MRI volume data. The event of interest, (b) the local entropy (ENT) is extracted from the test image. Three separate observations of image quality are (c) local contrast (CON), (d) local standard deviation (STD), (e) and local sharpness (DTL) feature images. The four feature images are transformed to the binary domain and classified into the low- and the high-energy regions. For each region, the posterior probability of each region given any of the observations gives quality score for (f) contrast quality attribute, (g) standard deviation quality attribute, and (h) sharpness quality attribute. The total quality score for each region is the average quality scores from each quality attribute. The average total quality score from each region is the (i) global quality score.
3.3.1. Foreground extraction
Foreground extractor FRX segments the test image TIM shown in Fig. 2(a) into two regions: the foreground FRG region and the background region. The foreground region contains only the pixels that describe the anatomical structures in the slice. The foreground extractor is based on the Otsu method for a global image threshold.84
3.3.2. Feature extraction
Feature extractor FEX consists of four different local filters. Three filters, entropy, contrast, and standard deviation, are based on conventional filtering. The local sharpness filter was derived from Haar wavelet.65 These local filters extract four image features from the original slice. They are local entropy ENT in Fig. 2(b), local contrast CON shown in Fig. 2(c), local standard deviation STD shown in Fig. 2(d), and local sharpness feature image shown in Fig. 2(e). The choice of filter size is determined by trade-off between spatial accuracy and computational efficiency. Generally, efficient performance of a filter is determined by the number of neighboring pixels enclosed by its window. Larger filter size tends to dilate the original edge thickness that demarcates boundaries. This will cause loss of fine details in the image during the filtering process.85 Filter size that is too small relative to the image dimension will result in loss of spatial coherence in the filtered image. Loss of spatial coherence manifests as discontinuous edges in the filtered image. For these reasons and based on our experience during the performance evaluation, we recommend filter sizes of and for images with dimensions comparable to and , respectively.
3.3.3. Binarization
A binary image transformer BIT computes the mean of each feature image. The mean is adopted as the global threshold to transform each feature image into a binary image. The binary image clusters each feature image into low entropy (EL), low contrast (CL), low standard deviation (SL), low details (DL) regions and corresponding high energy regions; high entropy (EH), high contrast (CH), high standard deviation (SH), and high details (DH). The variable assigned to an energy region is quantified by its percentage composition in the slice. The percentage composition is the ratio of the number of pixels in the region to the number of pixels in the foreground.
3.3.4. Prior belief
Prior belief (PBL) in the low-entropy region (EL) and the prior belief (PBH) in the high-entropy region (EH) are computed according to Eq. (7). The TCP of the image is compared to a threshold set at to determine if the image can be classified as belonging to the noise energy band or the entropy energy band.
For , the prior belief (PBL and PBH) is the deviation of the percentage composition (EL and EH) in a slice from a standard normal distribution of corresponding percentage composition. The normal distribution of random variables was built from MRI data of 250 subjects obtained from ADNI.
For , there are two methods to compute the prior belief. When a noise estimation algorithm is available, TCP is computed according to the mathematical model that expresses TCP–noise level relationship in Ref. 75. In the absence of a noise estimation algorithm, the TCP is computed directly from the test image before insertion into the mathematical model.
3.3.5. Likelihood
The pixels in the low-energy region (CL, SL, and DL) and the high-energy region (CH, SH, and DH) of the observation images are separately matched, without registration, with pixels in the corresponding region (EL and EH) of the entropy image. The ratio of the number of their common elements to the number of foreground pixels is expressed by . The ratio of the number of pixels in each region to the number of foreground pixel gives . Both and are inserted into Eq. (8) to derive three separate likelihood for each entropy region.
3.3.6. Quality index
The quality index for the contrast [Fig. 2(f)], standard deviation [Fig. 2(g)], and sharpness [Fig. 2(h)] quality attributes in each of the low- (EL) and high- (EH) entropy regions is computed according to Eq. (9). Quality score (PTL and PTH) for each entropy region is computed according to Eq. (10). The quality attributes were assigned equal weight because each attribute complements each other. The global quality score (PG) for the slice [Fig. 2(i)] is computed according to Eq. (11) and each region is assigned equal weight.
3.4. Validation of Results
Our proposed method was validated with subjective experiments conducted with a group of human observers. The group consists of four radiologists and one MRI reader. MRI reader is a trained professional with experience working on MRI images that are affected by pathology.40 The experiment was conducted with the aid of QuickEval,86 a web-based tool for psychometric image evaluation provided by the Norwegian Colour and Visual Computing Laboratory at the Norwegian University of Science and Technology, Gjøvik, Norway. We choose the mean opinion score (MOS) subjective experiment method because of its popularity and simplicity. MOS is the average of the quality scores assigned to an image by multiple viewers.87 There are four categories of the experiment. They are MRI volume data without perceived distortion, MRI volume data originally acquired with bias fields, MRI volume data artificially degraded with motion blur, and MRI volume data artificially degraded by Rician noise. Table 1 shows the categories of the experiment and the description of the MRI volume data utilized for the experiment. The observer assigns a score from 101 possible quality scores to each low- and high-energy regions of a slice. The possible scores are between 0 and 100, in steps of 1. Each region has equal weights, thus the global quality score is the average of the low- and high-entropy regions. In the category of MRI volume data with artificially induced distortion, each observer was first presented with an undistorted version of an MRI slice. This was followed by four different increasing levels of distortion of the original slice. The distorted levels are 5, 10, 15, and 20. The relationship between our objective results and the score assigned by human observers was determined using the Spearman’s rank correlation coefficient 88
| (14) |
where , the number of observations is the total number of slices contained in all the volume data in each category of the experiment and is the difference between the two ranks of each observation.
4. Results
In this section, we provide results of the experiments on five MRI volume data. One T2 and a conventional T1 volume data are from NeuroRx Inc. The T1 data were originally degraded by bias fields during acquisition. The data from BrainCare Oy are two T2 and a conventional T1 volume data.
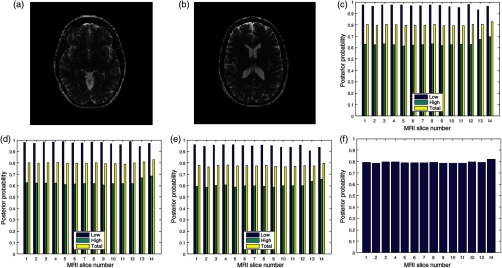
4.1. MRI Volume Data without Perceived Distortion
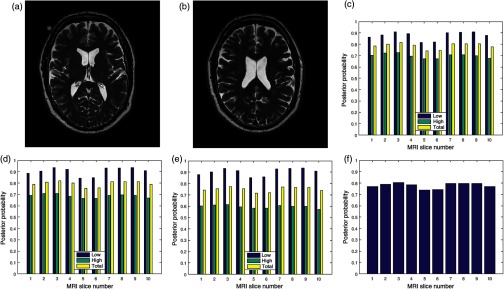
Two slices in a T2 volume data from BrainCare are shown in Figs. 3(a) and 3(b). The slices are without perceived distortion. The plots of the posterior probability for the low-, high-energy region, and total probability of the contrast, standard deviation, and sharpness quality attributes are shown in Figs. 3(c)–3(e), respectively. Each quality attribute had average low-energy quality score of 0.85. The high-energy region of the contrast and standard deviation quality attributes had average of 0.7 compared to corresponding sharpness quality score of 0.6. The global quality score for 10 successive slices in the volume data is in Fig. 3(f).
Fig. 3.
Two slices (a) slice number 1 and (b) slice number 5 in a T2 MRI volume data from BrainCare Oy, (c) contrast attribute quality scores, (d) standard deviation attribute quality scores, (e) sharpness attribute quality scores, and (f) global quality scores for 10 successive slices in the MRI volume data.
Another two slices are shown in Figs. 4(a) and 4(b). They are in a T1 volume data from BrainCare and are without perceived distortion. The plots of the posterior probability shown in Figs. 4(c)–4(e) have an average of 0.7 and 0.5 for the low- and the high-energy regions of the contrast, standard deviation, and sharpness quality attributes, respectively. The average total score for each quality attribute is 0.55. Global quality scores for 10 successive slices in the volume data are shown in Fig. 4(f).
Fig. 4.
Two slices (a) slice number 2 and (b) slice number 5 in a T1 MRI volume data from BrainCare Oy, (c) contrast attribute quality scores (d) standard deviation attribute quality scores, (e) sharpness attribute quality scores, and (f) global quality scores for 10 successive slices in the MRI volume data.
Figures 5(a) and 5(b) are two slices in a NeuroRx T2 volume data considered to be without perceived distortion. The average of the quality scores shown in Figs. 5(c)–5(e) for the low- and high-entropy regions is 0.9 and 0.6, respectively. The average quality score for 14 successive slices in the volume data [see Fig. 5(f)] is 0.8.
Fig. 5.
Two slices (a) slice number 1 and (b) slice number 7 in a T2 MRI volume data from NeuroRx Research Inc., (c) contrast attribute quality scores, (d) standard deviation attribute quality scores, (e) sharpness attribute quality scores, and (f) global quality score for 10 successive slices in the MRI volume data.
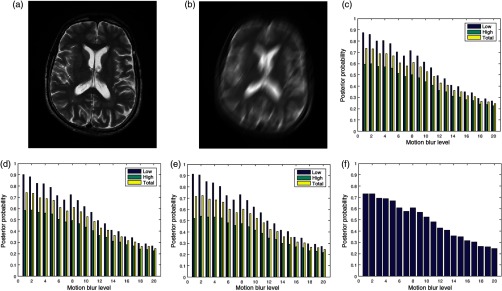
4.2. MRI Volume Data Degraded by Motion Blur
The image in Fig. 6(a) was degraded by 20 different levels of motion blur. Figure 6(b) is the degraded version of the image in Fig. 6(a) with motion blur level of 20. The plots of the posterior probability corresponding to the low- and the high-entropy regions for each quality attribute are shown in Figs. 6(c)–6(e). These plots and the plot in Fig. 6(f) show a decrease in quality scores for different levels of degradation by motion blur. At a insignificant level of blur, the quality score for the low-entropy region is close to 0.9 for the three quality attributes. The quality scores decrease in proportion to the successive increase in blur level to quality score of 0.4 for motion blur level of 20. In the high-entropy region, the three quality attributes exhibit different profiles. Contrast and standard deviation decrease from 0.6 to 0.4 and 0.6 to 0.35, respectively. There is slight increase from 0.5 to 0.55 in the level of details for motion blur increase from 1 to 5. This can be attributed to an increase in sharpness at the onset of motion blur. Subsequently, there is a progressive decrease in quality score from 0.55 to 0.3 for motion blur level decrease from 6 to 20. The plot in Fig. 6(f) shows a general decrease in image quality with increasing levels of motion blur.
Fig. 6.
(a) A slice in a T2 MRI volume data from BrainCare Oy is artificially degraded by motion blur. The degradation was scaled from 0 to 20. (b) Degraded version of the image corresponding to motion blur level of 20. (c) The contrast attribute quality scores, (d) standard deviation attribute quality scores, (e) sharpness attribute quality scores, and (f) global quality scores for the different levels of motion blur.
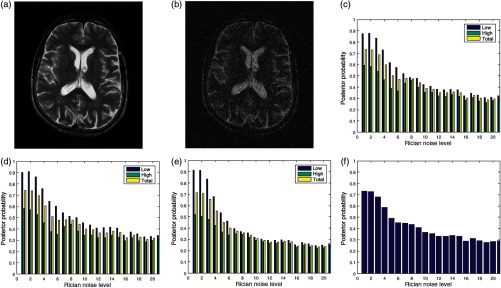
4.3. MRI Volume Data Degraded by Noise
Figures 7(a) and 7(b) are the original image and its degraded version, respectively. The Rician noise level varies from 1% to 20%. The image in Fig. 7(b) is degraded by 20% Rician noise. The plots of the posterior probabilities of the three quality attributes for the low- and the high-entropy regions are shown in Figs. 7(c)–7(e). The global quality score is shown in Fig. 7(f). The plots of the contrast and standard deviation quality attributes shown in Figs. 7(c) and 7(d) have very close corresponding quality scores. In the absence of noise, the quality score for the high-entropy region of the sharpness quality attribute is 0.5 compared to 0.6 for the other quality attributes. At 20% Rician noise level, quality score is about 0.3 across regions and the three quality attributes. Loss of details is clearly evident when the visual quality of the original image in Fig. 7(a) is compared to its degraded version in Fig. 7(b). Figure 7(f) shows a general decrease of image quality with increasing noise level.
Fig. 7.
(a) A slice in a T2 MRI volume data from BrainCare Oy is artificially degraded by different levels of Rician noise. The Rician noise level was scaled from 0 to 20. (b) Degraded version of the image corresponding to Rician noise level of 20. (c) The contrast attribute quality scores, (d) standard deviation attribute quality scores, (e) sharpness attribute quality scores, and (f) global quality scores for the different levels of Rician noise.
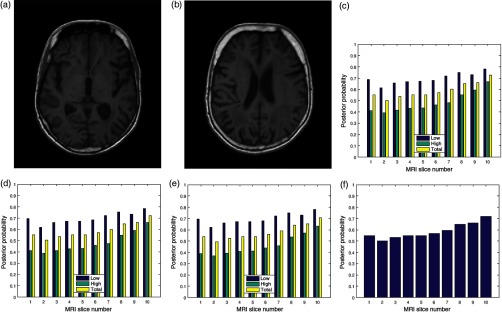
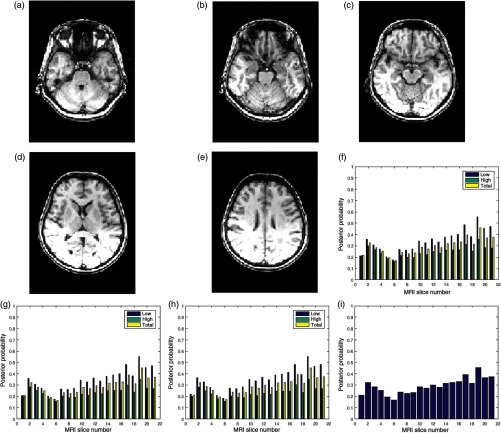
4.4. MRI Volume Data Degraded by Bias Fields
Figures 8(a)–8(e) are five slices in a 60-slice T1 MRI volume data. The volume data were degraded by bias fields during its acquisition, and the slices exhibit different configurations of bias fields. The three quality attributes of 21 successive slices in the volume data are displayed in Figs. 8(f)–8(h). There are variations in the quality scores for the different slices. The global quality scores of slice numbers 4, 6, 8, 14, and 19 shown in Fig. 8 are 0.2, 0.2, 0.25, 0.3, and 0.5, respectively.
Fig. 8.
Five slices (a) slice number 4, (b) slice number 6, (c) slice number 8, (d) slice number 14, and (e) slice number 19 in a T1 MRI volume data from NeuroRx Research Inc. The data were originally acquired with bias fields. (f) Contrast attribute quality scores, (g) standard deviation attribute quality scores, (h) sharpness attribute quality scores, and (i) global quality scores for 21 successive slices in the MRI volume data.
4.5. Validation of Results
The objective scores recorded by our proposed method and the scores recorded by human observers for T2, T1, FLAIR, and PD images without perceived distortion are shown in Table 2. In this category, there is an average of 30%, 20%, 30%, and 30% disparity between our proposed method and the scores recorded by human observers for T2, T1, FLAIR, and PD weighted images, respectively.
Table 2.
Result of validation studies for T2, T1, FLAIR, and PD MRI volume data without perceived distortion.
| MRI sequence | Average objective quality score | Average subjective quality score | Correlation coefficient | ||||
|---|---|---|---|---|---|---|---|
| Low | High | Global | Low | High | Global | ||
| T2 | 0.85 | 0.7 | 0.75 | 0.7 | 0.6 | 0.65 | 0.75 |
| T1 | 0.7 | 0.65 | 0.6 | 0.6 | 0.55 | 0.6 | 0.7 |
| FLAIR | 0.85 | 0.7 | 0.8 | 0.75 | 0.55 | 0.6 | 0.65 |
| PD | 0.9 | 0.6 | 0.8 | 0.7 | 0.5 | 0.6 | 0.7 |
Tables 3 and 4 show that the category of images degraded by motion blur and noise exhibit common trend. For the low, high, and global regions, our proposed method and human observers recorded gradual decrease in quality scores for increasing level of motion blur. The correlation coefficient exhibits the same trend in both categories. Thus, it can be inferred that humans tend to agree with each other when they view high-quality images than when viewing low-quality images.
Table 3.
Result of validation studies for T2 MRI volume data degraded by motion blur.
| Distortion level | Average objective quality score | Average subjective quality score | Correlation coefficient | ||||
|---|---|---|---|---|---|---|---|
| Low | High | Global | Low | High | Global | ||
| 0 | 0.9 | 0.65 | 0.8 | 0.8 | 0.7 | 0.75 | 0.7 |
| 5 | 0.75 | 0.6 | 0.65 | 0.7 | 0.6 | 0.65 | 0.8 |
| 10 | 0.6 | 0.5 | 0.55 | 0.5 | 0.4 | 0.45 | 0.7 |
| 15 | 0.5 | 0.3 | 0.4 | 0.4 | 0.3 | 0.35 | 0.65 |
| 20 | 0.3 | 0.2 | 0.25 | 0.2 | 0.1 | 0.15 | 0.6 |
Table 4.
Result of validation studies for T2 MRI volume data degraded by Rician noise
| Distortion level | Average objective quality score | Average subjective quality score | Correlation coefficient | ||||
|---|---|---|---|---|---|---|---|
| Low | High | Global | Low | High | Global | ||
| 0 | 0.9 | 0.6 | 0.75 | 0.75 | 0.6 | 0.65 | 0.8 |
| 5 | 0.6 | 0.5 | 0.55 | 0.7 | 0.6 | 0.65 | 0.7 |
| 10 | 0.45 | 0.55 | 0.5 | 0.5 | 0.5 | 0.5 | 0.65 |
| 15 | 0.4 | 0.3 | 0.35 | 0.3 | 0.3 | 0.3 | 0.6 |
| 20 | 0.35 | 0.3 | 0.3 | 0.3 | 0.2 | 0.25 | 0.6 |
Validation by human observers on conventional T1 images degraded by bias fields is shown in Table 5. Objective quality scores predicted by our proposed method and the scores recorded by human observers for the low, high, and global regions differ by 10%, 30%, and 15%, respectively.
Table 5.
Result of validation studies for conventional T1 MRI volume data degraded by bias fields.
| Region | Average objective quality score | Average subjective quality score | Correlation coefficient |
|---|---|---|---|
| Low | 0.45 | 0.4 | 0.8 |
| High | 0.4 | 0.3 | 0.7 |
| Global | 0.4 | 0.35 | 0.65 |
5. Discussion
MRI image-derived region-based features can serve as strong biomarkers for monitoring the dissemination in space and time of neurological diseases, such as multiple sclerosis, Alzheimer’s disease, and Parkinson’s disease. MRI-derived region-based features include regional atrophy measurements in multiple sclerosis patients,89–91 hippocampal volume change in Alzheimer’s disease patients,92 substantia nigra, and the locus ceruleus volume change within the basal ganglia for Parkinson’s disease patients.93,94
The importance of optimized objective quality evaluation methods for the different tasks in medical images was highlighted in Ref. 67. The high-quality region-based quality measurement for brain MRI images was reiterated in the recommendation by the European Collaborative Research Network that studies MRI in multiple sclerosis.95 One aspect of the recommendation is the use of high-quality brain MRI images for clinical research to prevent inaccurate diagnosis. The second aspect outlined region-based criteria for establishing multiple sclerosis dissemination in space and time. They are the presence of at least one lesion in at least two of four different regions of T2 brain MRI images. The regions are juxtacortical, periventricular, infrantentorial, and the spinal cord.
Like natural images, distortion processes have different effects on the different homogeneous regions of the brain.96 Noise introduces isolated edges,97 resulting in unwanted details in the smoothly varying white matter and ventricle regions. Fine details that define the high density of edges in the cortical gray matter region are eroded by noise. Noise reduces the sharpness between the boundaries of different homogeneous regions. These effects make the task of edge detection and preservation difficult.98 The smoothen effect of blur99 makes it difficult to characterize the texture features that distinguish the white matter and the thalamus regions. Bias fields corrupt the natural homogeneity of the major anatomical structures by introducing new smoothly varying intensity levels.100
This report addresses the need to provide high-quality region-based quality assessment for brain MRI images. The proposed method computes image quality index for the low-, high-energy region, and the whole-brain. The low-energy region is dominated by the white matter structure. The high-energy region includes the high density of edges that characterize the cerebral cortex and the boundaries that demarcate the different anatomical structures. The whole-brain is the brain regarded as a single region. Based on the performance evaluation results, the following subsections discuss the different characteristics of our proposed method.
5.1. Good Correlation with Human Observers
In all the categories of the experiment, the results show very good correlation () between our proposed method and the subjective evaluation by human observers. This indicates that our proposed method correlates with the human visual system. The high correlation can be attributed to four factors. They are the efficient performance of our proposed algorithm, expertise of the human observers, the wide interval between distortion levels, and the number of observations. The expertise of the observers is more likely a combination of specific visual and cognitive skills derived from medical training and experience in detecting and determining the diagnostic importance of radiographic findings.101 The observers, by their expertise, have knowledge of successive slices extracted from the same MRI volume data. Their visual perception of the small variations in the image quality between the different but successive slices will be reflected in the subjective evaluation. The interval between the different levels of distortion is reasonably large for the human eye to efficiently discriminate between the different levels of perceived distortions in the images. The number of data points used for computation of the correlation coefficient is reasonably high. The minimum number of data points in each category of the experiment is 30.
5.2. Good Classification of Image Quality
The results show that our proposed method demonstrates good classification of image quality across the slices in an MRI volume data, across MRI data acquired with different acquisition protocols, as well as different types and levels of perceived distortion.
5.3. Efficient Management of MRI Analysis
In CRO, quality attributes of an image are an important consideration during the subjective evaluation of automated image analysis systems. Subjective quality evaluation can be a cumbersome task for a trained reader. The good correlation between the outputs of our proposed method and expert human observers indicates that our proposed method can contribute to the efficient management of the large volume of data in CRO and meet the deadline to deliver image analysis reports to the sponsoring pharmaceutical organizations.
5.4. Reduction in Gaze Duration
In the evaluation of MRI-derived atrophy metrics, the reader’s visual attention changes with the different metrics. Visual attention is on the white matter region during white matter atrophy measurement. The focus changes toward the cortical gray matter region during gray matter atrophy measurement and to the whole-brain for whole-brain atrophy measurement. We believe that, as in mammography, gaze duration is a useful predictor of missed lesions in brain volumetric analysis.102 Objective method, such as our proposed method, can reduce gaze duration, improve the discernment, and accuracy of lesion detection by a trained MRI reader.
5.5. Reduction in Consensus Time
Some image analysis tasks, such as semiautomated identification of lesions, require the consensus of at least two experts. These tasks can be time-consuming because of variability in the visual judgment of the experts. Our proposed method can help find a common ground between two trained MRI readers and speed-up consensus between experts in quality assessment. The interexpert variability is much higher when it comes to image qualities that are considered borderline cases because the human visual system has no clearly defined threshold of quality index. Our proposed method can be used as a tool to define a quality index threshold that classifies an image into acceptable quality image and poor quality image.
5.6. Standardization of Image Quality
Daily very large volumes of MRI data are transferred from clinical trial sites around the globe to CRO that manage clinical trials for pharmaceutical organizations. This new quality evaluation method will find useful application in CRO environments to enforce the standardization of variations in the quality attributes of MRI images from different manufacturers, different clinical trial sites, and different acquisition protocols.
5.7. Computational Efficiency
The proposed quality evaluation system is computationally efficient. Processing the feature images required for the computation of quality index does not require additional resources, such as computationally intensive image registration algorithm. Operation of the algorithm is carried out in the binary domain.
5.8. Comparison with Task-Based Quality Evaluation without Ground Truth
Imaging methods can be referred to as any combination of image acquisition protocol, system, or parameters and image reconstruction, processing, or analysis methods used to obtain some quantitative value.67 It is often difficult and even impossible to have access to an ideal reference also referred to as a gold standard.103,104 In specific applications, few images or imaging methods selected to act as reference image are far from ideal because in the real-world, an ideal image or imaging method does not exist.66,105 The use of phantom is not an effective approach for evaluation because it lacks the ability to model the complex anatomy and physiology of the human system as well as image acquisition artifacts that are usually encountered in real images.67,104
Six characteristics are common to our proposed method and task-based methods such as in Ref. 66. First, both methods have three requirements. The requirements for our proposed method are quality attributes, Bayes model of an observer expressed by the prior belief, and figure of merit expressed by the posterior probability. The requirements for task-based methods are a task of interest, an observer performing the task and figure of merit. Second, they adopt statistical techniques. Our proposed method is based on Bayes framework while the task-based approach adopts linear regression. Third, the statistical techniques incorporate features for optimizing objective quality. Optimization in the task-based method requires an initial guess as the midpoint of the search space followed by maximum likelihood optimization. Our proposed method also requires an initial guess expressed by a prior belief in the entropy of specific image region. The prior belief is updated using Bayes rule. Fourth, both methods require a large number of patient data from a given population to attain the no-gold standard, although this can be regarded as a setback for both techniques. Fifth, both techniques assume that the statistical distribution for the ideal values of the parameter under investigation belong to a given family of parameterized distribution. Sixth, the lack of ground truth has been addressed by our proposed method and existing task-based quality evaluation methods, such as Refs. 66–68, 103, and 106.
There are three differences between our proposed method and task-based quality evaluation methods. First, there is difference in one of their three requirements. Our proposed method requires specification of image quality attributes while a task of interest is needed to be specified in task-based quality evaluation. Second, the specification of image quality attributes limits the application of our proposed method to images. Assessment methods change with the task at hand.107 For this reason, task-based method is considered as a rigorous approach to quality evaluation. Third, both methods have different roles in some specific image processing and image analysis task. An example is an estimation task such as brain atrophy measurement. Brain MRI images are the inputs to the algorithms. Our proposed method is related to the task-based method in same manner as the input images are related to the algorithms for processing and analysis task. Our proposed method can be said to play a primary role by assessing the input images. Task-based method can be considered playing a tertiary role by assessing the algorithms with its input images.
5.9. Recommended Quality Score for Images of Acceptable Quality
The quality index is based on a probability scale. An ideal MRI slice will have quality score of 1. A perfectly bad slice will have quality index of 0. The quality score for a real MRI slice will lie between 0 and 1. We recommend a quality score threshold of 0.4 to determine if a slice is of acceptable quality or without acceptable quality. This recommendation is with reference to the horizontal asymptote of 0.5 for the mathematical model that expresses the relationship between TCP and noise level.75 The reasoning here is that the asymptote is a natural threshold that separates the energy band into two separate regions dominated by noise and entropy, respectively. Furthermore, a slice monotonically losses its sharpness quality with increasing distance on either of the thresholds. The recommended threshold is 20% less than the horizontal asymptote.
6. Conclusions
We hereby propose a postacquisition quality assessment method for structural brain MRI images. Our proposed method is significant because of the increasing interest in the use of the MRI system for monitoring disease progression in multiple sclerosis, Alzheimer’s disease, and other neurological diseases. We exploit the relationship between entropy and the classical image quality attributes to develop quality measures for brain MRI images. Entropy is regarded as the aggregate of image quality attributes. Local contrast, local standard deviation, and local sharpness are the tests of quality attribute. Quality measure is formulated as a probability problem with focus on the different homogeneous regions of the brain. Bayes theorem is applied to compute the quality scores. Experimental results demonstrate that our proposed method gave good quality measures across images with different acquisition protocols, different types, and levels of distortion and correlates with subjective evaluation by human observers. It will be suitable for automated environments and in applications where specific regions of the brain are required for image analysis. This method will encourage the use of MRI images of acceptable quality in MRI-based clinical trials, ensure accurate diagnosis, and improve the performance of a trained reader in the performance evaluation of image analysis systems. The algorithm does not require image registration. It operates on binary images and thus has the potential of real-time operation. Current work regards the brain as consisting of the low- and the high-entropy regions. In the future, the low-entropy region will be segmented into five separate regions: white matter, thalamus, ventricle, cortical gray matter, and basal ganglia. This will increase the utility of our proposed method for the monitoring and diagnosis of multiple sclerosis disease, Alzheimer’s disease, and Parkinson’s disease.
Acknowledgments
Data collection and sharing for this project were funded by ADNI (National Institutes of Health Grant No. U01 AG024904) and Department of Defense ADNI (Award No. W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research and Development, LLC; Johnson and Johnson Pharmaceutical Research & Development LLC; Lumosity; Lundbeck; Merck and Co., Inc.; Meso Scale Diagnostics, LLC; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health. The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California. Marius Pedersen has been supported by the Research Council of Norway, Project No. 247689 IQ-MED: image quality enhancement in MEDical diagnosis, monitoring and treatment.
Biographies
Michael Osadebey obtained his master’s degree with distinction in biomedical engineering from Tampere University of Technology, Finland, in 2009 and his PhD in engineering and computer science from Concordia University, Montreal, Canada, in 2015. His PhD study was focused on the processing of MRI images of the brain. He is a MRI Reader at NeuroRx Research Inc. a Montreal-based clinical research organization (CRO). His duties at NeuroRx include application of advanced image analysis software in the reading of MRI data of neurological diseases patients undergoing clinical trial drug treatment.
Marius Pedersen received his BSc degree in computer engineering and MiT degree in media technology both from Gjøvik University College, Norway, in 2006 and 2007, respectively. He completed his PhD program in color imaging from the University of Oslo, Norway, sponsored by Oce in 2011. He is currently employed as an associate professor at NTNU Gjøvik, Norway. He is also the director of the Norwegian Colour and Visual Computing Laboratory (Colourlab). His work is centered on subjective and objective image quality.
Douglas Arnold is the director of Magnetic Resonance Spectroscopy Lab, McGill University, Montreal, Canada, and the president/CEO NeuroRx Research Inc., a Montreal-based CRO. He is a neurologist with special expertise in MRI. His personal research interests are centered on the use of advanced neuroimaging techniques to assess the pathological evolution of multiple sclerosis and Alzheimer’s disease and to quantify the effects of therapy on these diseases.
Katrina Wendel-Mitoraj obtained her PhD in biomedical engineering from Tampere University of Technology in 2010. Her PhD study was focused on electroencephalography electrode sensitivity distributions. She is the CEO and founder of BrainCare Oy. BrainCare Oy is a Tampere University of Technology spin-off company founded in 2013 to deliver personalized solutions to improve the quality of life of epilepsy patients. The organization recently concluded clinical trials for an innovative mobile application and supporting solutions for long-term monitoring for epileptic patients.
Disclosures
Dr. Michael Osadebey reports no potential conflicts of interest. Dr. Marius Pedersen reports no potential conflicts of interest. Dr. Douglas Arnold reports no potential conflicts of interest. Dr. Katrina Wendel-Mitoraj reports no potential conflicts of interest.
References
- 1.Arnold D., et al. , “Long-term efficacy in MRI and no evidence of disease activity outcomes in patients with relapsing-remitting multiple sclerosis treated with peginterferon beta-1a,” Neurology 84(14 Suppl.), 7.266 (2015). [Google Scholar]
- 2.Frisoni G. B., et al. , “The clinical use of structural MRI in Alzheimer disease,” Nat. Rev. Neurol. 6(2), 67–77 (2010). 10.1038/nrneurol.2009.215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hashemi R. H., Bradley W. G., Lisanti C. J., MRI: The Basics, Lippincott Williams & Wilkins, Philadelphia: (2012). [Google Scholar]
- 4.Schwaab J., et al. , “Automated quality assessment in three-dimensional breast ultrasound images,” J. Med. Imaging 3(2), 027002 (2016). 10.1117/1.JMI.3.2.027002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Barrett H. H., et al. , “Task-based measures of image quality and their relation to radiation dose and patient risk,” Phys. Med. Biol. 60(2), R1 (2015). 10.1088/0031-9155/60/2/R1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Abouei E., Lee S., Ford N. L., “Quantitative performance characterization of image quality and radiation dose for a CS 9300 dental cone beam computed tomography machine,” J. Med. Imaging 2(4), 044002 (2015). 10.1117/1.JMI.2.4.044002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chen H., et al. , “On image quality metrics and the usefulness of grids in digital mammography,” J. Med. Imaging 2(1), 013501 (2015). 10.1117/1.JMI.2.1.013501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kupinski M. A., Barrett H. H., Small-Animal SPECT Imaging, p. 233, Springer, New York: (2005). [Google Scholar]
- 9.Pižurica A., et al. , “A versatile wavelet domain noise filtration technique for medical imaging,” IEEE Trans. Med. Imaging 22(3), 323–331 (2003). 10.1109/TMI.2003.809588 [DOI] [PubMed] [Google Scholar]
- 10.Sled J. G., Zijdenbos A. P., Evans A. C., “A nonparametric method for automatic correction of intensity nonuniformity in MRI data,” IEEE Trans. Med. Imaging 17(1), 87–97 (1998). 10.1109/42.668698 [DOI] [PubMed] [Google Scholar]
- 11.Qin L., et al. , “Prospective motion correction using tracking coils,” Magn. Reson. Med. 69(3), 749–759 (2013). 10.1002/mrm.v69.3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Caramanos Z., et al. , “Gradient distortions in MRI: characterizing and correcting for their effects on SIENA-generated measures of brain volume change,” NeuroImage 49(2), 1601–1611 (2010). 10.1016/j.neuroimage.2009.08.008 [DOI] [PubMed] [Google Scholar]
- 13.Kaur P., et al. , “Protocol error artifacts in MRI: sources and remedies revisited,” Radiography 13(4), 291–306 (2007). 10.1016/j.radi.2006.03.011 [DOI] [Google Scholar]
- 14.Wang Z., Bovik A. C., Lu L., “Why is image quality assessment so difficult?” in IEEE Int. Conf. on Acoustics, Speech, and Signal Processing (ICASSP’02), Vol. 4, p. IV–3313, IEEE; (2002). 10.1109/ICASSP.2002.5745362 [DOI] [Google Scholar]
- 15.Pedersen M., et al. , “Attributes of image quality for color prints,” J. Electron. Imaging 19(1), 011016 (2010). 10.1117/1.3277145 [DOI] [Google Scholar]
- 16.Wang Z., et al. , “Image quality assessment: from error visibility to structural similarity,” IEEE Trans. Image Process. 13(4), 600–612 (2004). 10.1109/TIP.2003.819861 [DOI] [PubMed] [Google Scholar]
- 17.Barrett H. H., et al. , “Model observers for assessment of image quality,” Proc. Natl. Acad. Sci. U. S. A. 90(21), 9758–9765 (1993). 10.1073/pnas.90.21.9758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Barrett H. H., et al. , “Objective assessment of image quality. II. Fisher information, Fourier crosstalk, and figures of merit for task performance,” J. Opt. Soc. Am. A 12(5), 834–852 (1995). 10.1364/JOSAA.12.000834 [DOI] [PubMed] [Google Scholar]
- 19.Barrett H. H., “Objective assessment of image quality: effects of quantum noise and object variability,” J. Opt. Soc. Am. A 7(7), 1266–1278 (1990). 10.1364/JOSAA.7.001266 [DOI] [PubMed] [Google Scholar]
- 20.Abbey C. K., Barrett H. H., “Human-and model-observer performance in ramp-spectrum noise: effects of regularization and object variability,” J. Opt. Soc. Am. A 18(3), 473–488 (2001). 10.1364/JOSAA.18.000473 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kupinski M. A., et al. , “Ideal-observer computation in medical imaging with use of Markov-chain Monte Carlo techniques,” J. Opt. Soc. Am. A 20(3), 430–438 (2003). 10.1364/JOSAA.20.000430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Myers K. J., Barrett H. H., “Addition of a channel mechanism to the ideal-observer model,” J. Opt. Soc. Am. A 4(12), 2447–2457 (1987). 10.1364/JOSAA.4.002447 [DOI] [PubMed] [Google Scholar]
- 23.Park S., et al. , “Incorporating human contrast sensitivity in model observers for detection tasks,” IEEE Trans. Med. Imaging 28(3), 339–347 (2009). 10.1109/TMI.2008.929096 [DOI] [PubMed] [Google Scholar]
- 24.Barrett H. H., et al. , “Adaptive SPECT,” IEEE Trans. Med. Imaging 27(6), 775–788 (2008). 10.1109/TMI.2007.913241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Freed M., et al. , “A prototype instrument for single pinhole small animal adaptive SPECT imaging,” Med. Phys. 35(5), 1912–1925 (2008). 10.1118/1.2896072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Favazza C. P., et al. , “Implementation of a channelized Hotelling observer model to assess image quality of x-ray angiography systems,” J. Med. Imaging 2(1), 015503 (2015). 10.1117/1.JMI.2.1.015503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jha A. K., et al. , “Task-based evaluation of segmentation algorithms for diffusion-weighted MRI without using a gold standard,” Phys. Med. Biol. 57(13), 4425–4446 (2012). 10.1088/0031-9155/57/13/4425 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kupinski M. A., et al. , “Comparing cardiac ejection fraction estimation algorithms without a gold standard,” Acad. Radiol. 13(3), 329–337 (2006). 10.1016/j.acra.2005.12.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pruessmann K. P., et al. , “Sense: sensitivity encoding for fast MRI,” Magn. Reson. Med. 42(5), 952–962 (1999). 10.1002/(ISSN)1522-2594 [DOI] [PubMed] [Google Scholar]
- 30.Griswold M. A., et al. , “Generalized autocalibrating partially parallel acquisitions (GRAPPA),” Magn. Reson. Med. 47(6), 1202–1210 (2002). 10.1002/(ISSN)1522-2594 [DOI] [PubMed] [Google Scholar]
- 31.Mistretta C., et al. , “Highly constrained backprojection for time-resolved MRI,” Magn. Reson. Med. 55(1), 30–40 (2006). 10.1002/(ISSN)1522-2594 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tsao J., Boesiger P., Pruessmann K. P., “k-t BLAST and k-t SENSE: dynamic MRI with high frame rate exploiting spatiotemporal correlations,” Magn. Reson. Med. 50(5), 1031–1042 (2003). 10.1002/(ISSN)1522-2594 [DOI] [PubMed] [Google Scholar]
- 33.Breuer F. A., et al. , “Dynamic autocalibrated parallel imaging using temporal grappa (TGRAPPA),” Magn. Reson. Med. 53(4), 981–985 (2005). 10.1002/(ISSN)1522-2594 [DOI] [PubMed] [Google Scholar]
- 34.Miao J., et al. , “A new perceptual difference model for diagnostically relevant quantitative image quality evaluation: a preliminary study,” Magn. Reson. Imaging 31(4), 596–603 (2013). 10.1016/j.mri.2012.09.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Miao J., Huo D., Wilson D. L., “Quantitative image quality evaluation of MR images using perceptual difference models,” Med. Phys. 35(6), 2541–2553 (2008). 10.1118/1.2903207 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chalavi S., et al. , “Quantitative and qualitative assessment of structural magnetic resonance imaging data in a two-center study,” BMC Med. Imaging 12(1), 1 (2012). 10.1186/1471-2342-12-27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Woodard J., Carley-Spencer M., “No-reference image quality metrics for structural MRI,” Neuroinformatics 4(3), 243–262 (2006). 10.1385/NI:4:3 [DOI] [PubMed] [Google Scholar]
- 38.Mortamet B., et al. , “Automatic quality assessment in structural brain magnetic resonance imaging,” Magn. Reson. Med. 62(2), 365–372 (2009). 10.1002/mrm.v62:2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Prieto F., et al. , “Metrics for quantifying the quality of MR images,” in Proc. of the 17th Annual Meeting of ISMRM, p. 4696 (2009). [Google Scholar]
- 40.Gedamu E. L., Collins D., Arnold D. L., “Automated quality control of brain MR images,” J. Magn. Reson. Imaging 28(2), 308–319 (2008). 10.1002/jmri.v28:2 [DOI] [PubMed] [Google Scholar]
- 41.Heckel F., et al. , “Evaluation of image quality of MRI data for brain tumor surgery,” Proc. SPIE 9787, 97871L (2016). 10.1117/12.2214944 [DOI] [Google Scholar]
- 42.Liu B., “Parallel magnetic resonance imaging: theory, algorithm and applications,” PhD Dissertation, Milwaukee, Wisconsin, aAI3318277 (2008). [Google Scholar]
- 43.Mittal A., Moorthy A., Bovik A., “No-reference image quality assessment in the spatial domain,” IEEE Trans. Image Process. 21(12), 4695–4708 (2012). 10.1109/TIP.2012.2214050 [DOI] [PubMed] [Google Scholar]
- 44.Larson E. C., Chandler D. M., “Most apparent distortion: full-reference image quality assessment and the role of strategy,” J. Electron. Imaging 19(1), 011006 (2010). 10.1117/1.3267105 [DOI] [Google Scholar]
- 45.McCarthy G., Wood C. C., “Scalp distributions of event-related potentials: an ambiguity associated with analysis of variance models,” Electroencephalogr. Clin. Neurophysiol./Evoked Potentials Sect. 62(3), 203–208 (1985). 10.1016/0168-5597(85)90015-2 [DOI] [PubMed] [Google Scholar]
- 46.Krupinski E. A., “The importance of perception research in medical imaging,” Radiat. Med.-Med. Imaging Radiat. Oncol. 18(6), 329–334 (2000). [PubMed] [Google Scholar]
- 47.De Stefano N., et al. , “Assessing brain atrophy rates in a large population of untreated multiple sclerosis subtypes,” Neurology 74(23), 1868–1876 (2010). 10.1212/WNL.0b013e3181e24136 [DOI] [PubMed] [Google Scholar]
- 48.Monica B., Fundamentals in Information Theory and Coding, Springer, Berlin, Heidelberg: (2011). [Google Scholar]
- 49.Deng G., “An entropy interpretation of the logarithmic image processing model with application to contrast enhancement,” IEEE Trans. Image Process. 18(5), 1135–1140 (2009). 10.1109/TIP.2009.2016796 [DOI] [PubMed] [Google Scholar]
- 50.Agaian S. S., Silver B., Panetta K. A., “Transform coefficient histogram-based image enhancement algorithms using contrast entropy,” IEEE Trans. Image Process. 16(3), 741–758 (2007). 10.1109/TIP.2006.888338 [DOI] [PubMed] [Google Scholar]
- 51.Hassen R., Wang Z., Salama M. M., “Image sharpness assessment based on local phase coherence,” IEEE Trans. Image Process. 22(7), 2798–2810 (2013). 10.1109/TIP.2013.2251643 [DOI] [PubMed] [Google Scholar]
- 52.Erasmus S., Smith K., “An automatic focusing and astigmatism correction system for the SEM and CTEM,” J. Microsc. 127(2), 185–199 (1982). 10.1111/jmi.1982.127.issue-2 [DOI] [Google Scholar]
- 53.Wang J., Liu X., “Measurement of sharpness and its application in ISAR imaging,” IEEE Trans. Geosci. Remote Sens. 51(9), 4885–4892 (2013). 10.1109/TGRS.2013.2273554 [DOI] [Google Scholar]
- 54.Guo D., et al. , “Estimation in Gaussian noise: properties of the minimum mean-square error,” IEEE Trans. Inf. Theory 57(4), 2371–2385 (2011). 10.1109/TIT.2011.2111010 [DOI] [Google Scholar]
- 55.Verdú S., Guo D., “A simple proof of the entropy-power inequality,” IEEE Trans. Inf. Theory 52(5), 2165–2166 (2006). 10.1109/TIT.2006.872978 [DOI] [Google Scholar]
- 56.Freiman A., Pinchas M., “A maximum entropy inspired model for the convolutional noise PDF,” Digital Signal Process. 39, 35–49 (2015). 10.1016/j.dsp.2014.12.011 [DOI] [Google Scholar]
- 57.Gabarda S., Cristóbal G., “Blind image quality assessment through anisotropy,” J. Opt. Soc. Am. A 24(12), B42–B51 (2007). 10.1364/JOSAA.24.000B42 [DOI] [PubMed] [Google Scholar]
- 58.Hadjidemetriou E., Grossberg M. D., Nayar S. K., “Multiresolution histograms and their use for recognition,” IEEE Trans. Pattern Anal. Mach. Intell. 26(7), 831–847 (2004). 10.1109/TPAMI.2004.32 [DOI] [PubMed] [Google Scholar]
- 59.Dhal K. G., et al. , “Entropy based range optimized brightness preserved histogram-equalization for image contrast enhancement,” Int. J. Comput. Vision Image Process. 6(1), 59–72 (2016). 10.4018/IJCVIP [DOI] [Google Scholar]
- 60.Wang C., Ye Z., “Brightness preserving histogram equalization with maximum entropy: a variational perspective,” IEEE Trans. Consum. Electron. 51(4), 1326–1334 (2005). 10.1109/TCE.2005.1561863 [DOI] [Google Scholar]
- 61.Zhu H., et al. , “Conditional entropy maximization for pet image reconstruction using adaptive mesh model,” Comput. Med. Imaging Graphics 31(3), 166–177 (2007). 10.1016/j.compmedimag.2007.01.001 [DOI] [PubMed] [Google Scholar]
- 62.Byrne C. L., “Iterative image reconstruction algorithms based on cross-entropy minimization,” IEEE Trans. Image Process. 2(1), 96–103 (1993). 10.1109/83.210869 [DOI] [PubMed] [Google Scholar]
- 63.Jha A. K., et al. , “A clustering algorithm for liver lesion segmentation of diffusion-weighted MR images,” in IEEE Southwest Symp. on Image Analysis & Interpretation (SSIAI’10), pp. 93–96, IEEE; (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Yan C., Sang N., Zhang T., “Local entropy-based transition region extraction and thresholding,” Pattern Recognit. Lett. 24(16), 2935–2941 (2003). 10.1016/S0167-8655(03)00154-5 [DOI] [Google Scholar]
- 65.Barrett H. H., Myers K. J., Foundations of Image Science, John Wiley & Sons, Hoboken, New Jersey: (2013). [Google Scholar]
- 66.Kupinski M. A., et al. , “Estimation in medical imaging without a gold standard,” Acad. Radiol. 9(3), 290–297 (2002). 10.1016/S1076-6332(03)80372-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Jha A. K., Caffo B., Frey E. C., “A no-gold-standard technique for objective assessment of quantitative nuclear-medicine imaging methods,” Phys. Med. Biol. 61(7), 2780–2800 (2016). 10.1088/0031-9155/61/7/2780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Jha A. K., et al. , “Practical no-gold-standard evaluation framework for quantitative imaging methods: application to lesion segmentation in positron emission tomography,” J. Med. Imaging 4(1), 011011 (2017). 10.1117/1.JMI.4.1.011011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Wendel K. E., “The influence of tissue conductivity and head geometry on EEG measurement sensitivity distributions,” PhD Dissertation, Tampere University of Technology (2010). [Google Scholar]
- 70.Zhang Y., Brady M., Smith S., “Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm,” IEEE Trans. Med. Imaging 20(1), 45–57 (2001). 10.1109/42.906424 [DOI] [PubMed] [Google Scholar]
- 71.Jha A. K., Rodríguez J. J., Stopeck A. T., “A maximum-likelihood method to estimate a single ADC value of lesions using diffusion MRI,” Magn. Reson. Med. 76(6), 1919–1931 (2016). 10.1002/mrm.26072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Walker-Samuel S., et al. , “Robust estimation of the apparent diffusion coefficient (ADC) in heterogeneous solid tumors,” Magn. Reson. Med. 62(2), 420–429 (2009). 10.1002/mrm.v62:2 [DOI] [PubMed] [Google Scholar]
- 73.Barrett H., Myers K., “Statistical characterization of radiological images: basic principles and recent progress,” Proc. SPIE 6510, 651002 (2007). 10.1117/12.716908 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Jayawardena A. W., Xu P., Li W. K., “Modified correlation entropy estimation for a noisy chaotic time series,” Chaos 20(2), 023104 (2010). 10.1063/1.3382013 [DOI] [PubMed] [Google Scholar]
- 75.Osadebey M., Bouguila N., Arnold D., “The clique potential of Markov random field in a random experiment for estimation of noise levels in 2D brain MRI,” Int. J. Imaging Syst. Technol. 23(4), 304–313 (2013). 10.1002/ima.v23.4 [DOI] [Google Scholar]
- 76.Geman S., Geman D., “Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images,” IEEE Trans. Pattern Anal. Mach. Intell. PAMI-6(6), 721–741 (1984). 10.1109/TPAMI.1984.4767596 [DOI] [PubMed] [Google Scholar]
- 77.Li S., Markov Random Field Modeling in Image Analysis, 3rd ed., Chapter 2, Springer Publishing Company, Inc., London: (2009). [Google Scholar]
- 78.Shiee N., et al. , “Reconstruction of the human cerebral cortex robust to white matter lesions: method and validation,” Hum. Brain Mapp. 35(7), 3385–3401 (2014). 10.1002/hbm.22409 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Mugler J. P., Brookeman J. R., “Three-dimensional magnetization-prepared rapid gradient-echo imaging (3D MP RAGE),” Magn. Reson. Med. 15(1), 152–157 (1990). 10.1002/(ISSN)1522-2594 [DOI] [PubMed] [Google Scholar]
- 80.Reimer P., et al. , Clinical MR Imaging, Springer, Berlin, Heidelberg: (2010). [Google Scholar]
- 81.Jack C. R., et al. , “The Alzheimer’s disease neuroimaging initiative (ADNI): MRI methods,” J. Magn. Reson. Imaging 27(4), 685–691 (2008). 10.1002/(ISSN)1522-2586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Deshpande A. M., Patnaik S., “A novel modified cepstral based technique for blind estimation of motion blur,” Optik–Int. J. Light Electron Opt. 125(2), 606–615 (2014). 10.1016/j.ijleo.2013.05.189 [DOI] [Google Scholar]
- 83.Coupé P., et al. , “Robust Rician noise estimation for MR images,” Med. Image Anal. 14(4), 483–493 (2010). 10.1016/j.media.2010.03.001 [DOI] [PubMed] [Google Scholar]
- 84.Otsu N., “A threshold selection method from gray-level histograms,” IEEE Trans. Syst. Man Cybern. 9(1), 62–66 (1979). 10.1109/TSMC.1979.4310076 [DOI] [Google Scholar]
- 85.Lee J. S., “Digital image enhancement and noise filtering by use of local statistics,” IEEE Trans. Pattern Anal. Mach. Intell. PAMI-2(2), 165–168 (1980). 10.1109/TPAMI.1980.4766994 [DOI] [PubMed] [Google Scholar]
- 86.Van Ngo K., et al. , “Quickeval: a web application for psychometric scaling experiments,” Proc. SPIE 9396, 93960O (2015). 10.1117/12.2077548 [DOI] [Google Scholar]
- 87.Streijl R. C., Winkler S., Hands D. S., “Mean opinion score (MOS) revisited: methods and applications, limitations and alternatives,” Multimedia Syst. 22(2), 213–227 (2016). 10.1007/s00530-014-0446-1 [DOI] [Google Scholar]
- 88.Corder G. W., Foreman D. I., Nonparametric Statistics: A Step-by-Step Approach, John Wiley & Sons, Hoboken, New Jersey: (2014). [Google Scholar]
- 89.Smith S. M., et al. , “Accurate, robust, and automated longitudinal and cross-sectional brain change analysis,” NeuroImage 17(1), 479–489 (2002). 10.1006/nimg.2002.1040 [DOI] [PubMed] [Google Scholar]
- 90.Nakamura K., et al. , “Pairwise Jacobian integration method to measure grey matter atrophy in multiple sclerosis,” in Int. Society for Magnetic Resonance in Medicine Workshop on Multiple Sclerosis as a Whole-Brain Disease (2013). [Google Scholar]
- 91.Nakamura K., et al. , “Jacobian integration method increases the statistical power to measure gray matter atrophy in multiple sclerosis,” NeuroImage: Clin. 4, 10–17 (2014). 10.1016/j.nicl.2013.10.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Liedes H., et al. , “Predicting change in hippocampal volume using MRI features from baseline,” Alzheimer’s Dementia 12(7), P550–P551 (2016). 10.1016/j.jalz.2016.06.1075 [DOI] [Google Scholar]
- 93.Castellanos G., et al. , “Automated neuromelanin imaging as a diagnostic biomarker for Parkinson’s disease,” Mov. Disord. 30(7), 945–952 (2015). 10.1002/mds.v30.7 [DOI] [PubMed] [Google Scholar]
- 94.Sasaki M., et al. , “Neuromelanin magnetic resonance imaging of locus ceruleus and substantia nigra in Parkinson’s disease,” NeuroReport 17(11), 1215–1218 (2006). 10.1097/01.wnr.0000227984.84927.a7 [DOI] [PubMed] [Google Scholar]
- 95.Filippi M., et al. , “MRI criteria for the diagnosis of multiple sclerosis: MAGNIMS consensus guidelines,” Lancet Neurol. 15(3), 292–303 (2016). 10.1016/S1474-4422(15)00393-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Xue W., et al. , “Gradient magnitude similarity deviation: a highly efficient perceptual image quality index,” IEEE Trans. Image Process. 23(2), 684–695 (2014). 10.1109/TIP.2013.2293423 [DOI] [PubMed] [Google Scholar]
- 97.Liu C., et al. , “Automatic estimation and removal of noise from a single image,” IEEE Trans. Pattern Anal. Mach. Intell. 30(2), 299–314 (2008). 10.1109/TPAMI.2007.1176 [DOI] [PubMed] [Google Scholar]
- 98.Pizurica A., et al. , “A versatile wavelet domain noise filtration technique for medical imaging,” IEEE Trans. Med. Imaging 22(3), 323–331 (2003). 10.1109/TMI.2003.809588 [DOI] [PubMed] [Google Scholar]
- 99.Kurimo E., et al. , “The effect of motion blur and signal noise on image quality in low light imaging,” in Scandinavian Conf. on Image Analysis, pp. 81–90, Springer; (2009). [Google Scholar]
- 100.Osadebey M., Bouguila N., Arnold D., “Brain MRI intensity inhomogeneity correction using region of interest, anatomic structural map and outlier detection,” in Applied Computing in Medicine and Health, Al-Jumeily D., et al., Eds., Vol. 1, pp. 79–98, Morgan Kaufmann, London: (2015). [Google Scholar]
- 101.Krupinski E. A., Borah J., “Eye tracking helps improve accuracy in radiology,” Biophotonics Int. 13(6), 44–49 (2006). [Google Scholar]
- 102.Krupinski E. A., “Visual scanning patterns of radiologists searching mammograms,” Acad. Radiol. 3(2), 137–144 (1996). 10.1016/S1076-6332(05)80381-2 [DOI] [PubMed] [Google Scholar]
- 103.Hoppin J. W., et al. , “Objective comparison of quantitative imaging modalities without the use of a gold standard,” IEEE Trans. Med. Imaging 21(5), 441–449 (2002). 10.1109/TMI.2002.1009380 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Vovk U., Pernus F., Likar B., “A review of methods for correction of intensity inhomogeneity in MRI,” IEEE Trans. Med. Imaging 26(3), 405–421 (2007). 10.1109/TMI.2006.891486 [DOI] [PubMed] [Google Scholar]
- 105.Chow L. S., Paramesran R., “Review of medical image quality assessment,” Biomed. Signal Process. Control 27, 145–154 (2016). 10.1016/j.bspc.2016.02.006 [DOI] [Google Scholar]
- 106.Henkelman R. M., Kay I., Bronskill M. J., “Receiver operator characteristic (ROC) analysis without truth,” Med. Decis. Making 10(1), 24–29 (1990). 10.1177/0272989X9001000105 [DOI] [PubMed] [Google Scholar]
- 107.Glick S., Tomosynthesis Imaging, Taylor & Francis, New York: (2014). [Google Scholar]