Topological and thermodynamic factors that influence the evolution of small networks of catalytic RNA species

Abstract

An RNA-directed recombination reaction can result in a network of interacting RNA species. It is now becoming increasingly apparent that such networks could have been an important feature of the RNA world during the nascent evolution of life on the Earth. However, the means by which such small RNA networks assimilate other available genotypes in the environment to grow and evolve into the more complex networks that are thought to have existed in the prebiotic milieu are not known. Here, we used the ability of fragments of the Azoarcus group I intron ribozyme to covalently self-assemble via genotype-selfish and genotype-cooperative interactions into full-length ribozymes to investigate the dynamics of small (three- and four-membered) networks. We focused on the influence of a three-membered core network on the incorporation of additional nodes, and on the degree and direction of connectivity as single new nodes are added to this core. We confirmed experimentally the predictions that additional links to a core should enhance overall network growth rates, but that the directionality of the link (a “giver” or a “receiver”) impacts the growth of the core itself. Additionally, we used a simple mathematical model based on the first-order effects of lower-level interactions to predict the growth of more complex networks, and find that such a model can, to a first approximation, predict the ordinal rankings of nodes once a steady-state distribution has been reached.

INTRODUCTION

The properties of RNA that allow it to fold, form transient nucleotide pairs, and to catalyze chemical reactions make this molecule a good model system to study abiogenesis (Joyce 2002; Higgs and Lehman 2015). In fact, it is the plasticity in these functions that allow RNA to form complex reaction networks, where a variety of catalysts and substrates interact in a dynamic fashion that mimics the lack of organized individuality that would have characterized the primordial soup. Mechanisms by which discordant collections of molecules could have coalesced into a system of reduced entropy such as a collective autocatalytic set (CAS) would have been critical to the formation of nascent living systems (Jain and Krishna 1998; Hordijk et al. 2012; Steel et al. 2013). Yet, from an experimental standpoint, these mechanisms have been inadequately studied and are generally uncharacterized.

Previously, we used the ability of fragments of the Azoarcus group I intron ribozyme to spontaneously self-assemble into covalently contiguous ribozymes to show that both simple and complex RNA-based reaction networks can arise (Vaidya et al. 2012). These networks can be created in large part because of our ability to manipulate the sequence of the 3-nucleotide (nt) internal guide sequence (IGS), whose propensity to bind to a complementary 3-nt triplet (termed a “tag”) in another RNA molecule determines the rate at which self-assembly from fragments into ribozymes takes place (Hayden and Lehman 2006; Draper et al. 2008; Yeates et al. 2016). Figure 1 is a schematic of these events, and indicates how small interdependent networks can form among RNA fragments with variable IGS and tag sequences.

FIGURE 1.

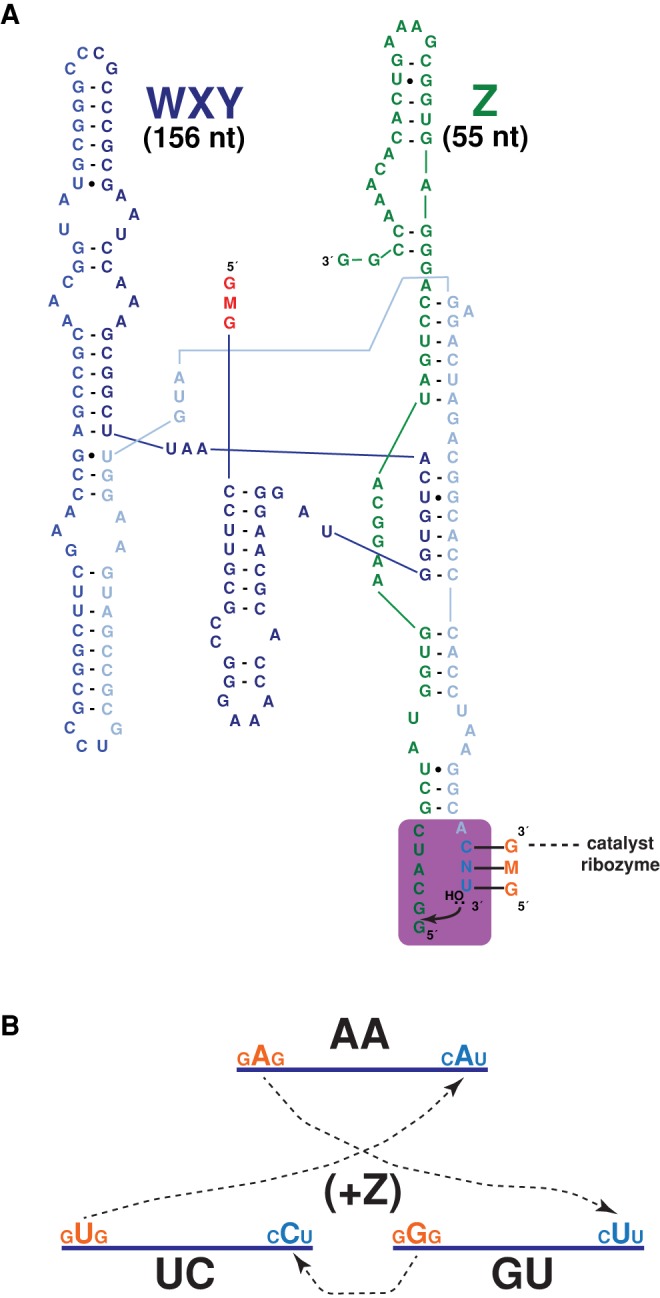
The Azoarcus ribozyme covalent self-assembly network. (A) The secondary structure of the ribozyme fragments and the catalytic event of the WXY+ Z → WXYZ reaction. The internal guide sequence (IGS) of the ribozyme lies at the 5′ end and is GMG, where M is free to vary among the four possible nucleotides. The IGS of one catalyst (symbolized by the “catalyst ribozyme”; it can be a covalently contiguous WXYZ or a noncovalent binding of a WXY to a Z) binds to the terminal 3 nt (CNU) of the WXY fragment in another molecule and catalyzes the recombination reaction shown, liberating a free G nucleotide and joining the substrate WXY with the Z. This reaction works at maximal rate if M and N form a Watson–Crick pair. (B) An example of the three-membered network possible if the M and N nucleotides are not complementary within a particular WXY molecule. Here the WXY species are symbolized by blue lines, and each can be denoted by just specifying these M and N nucleotides, such that this network is AA + UC + GU, which form the RPS core described below. The self-assembly of the network requires the presence of the Z substrate, indicated by the “+Z” in the center of the diagram.

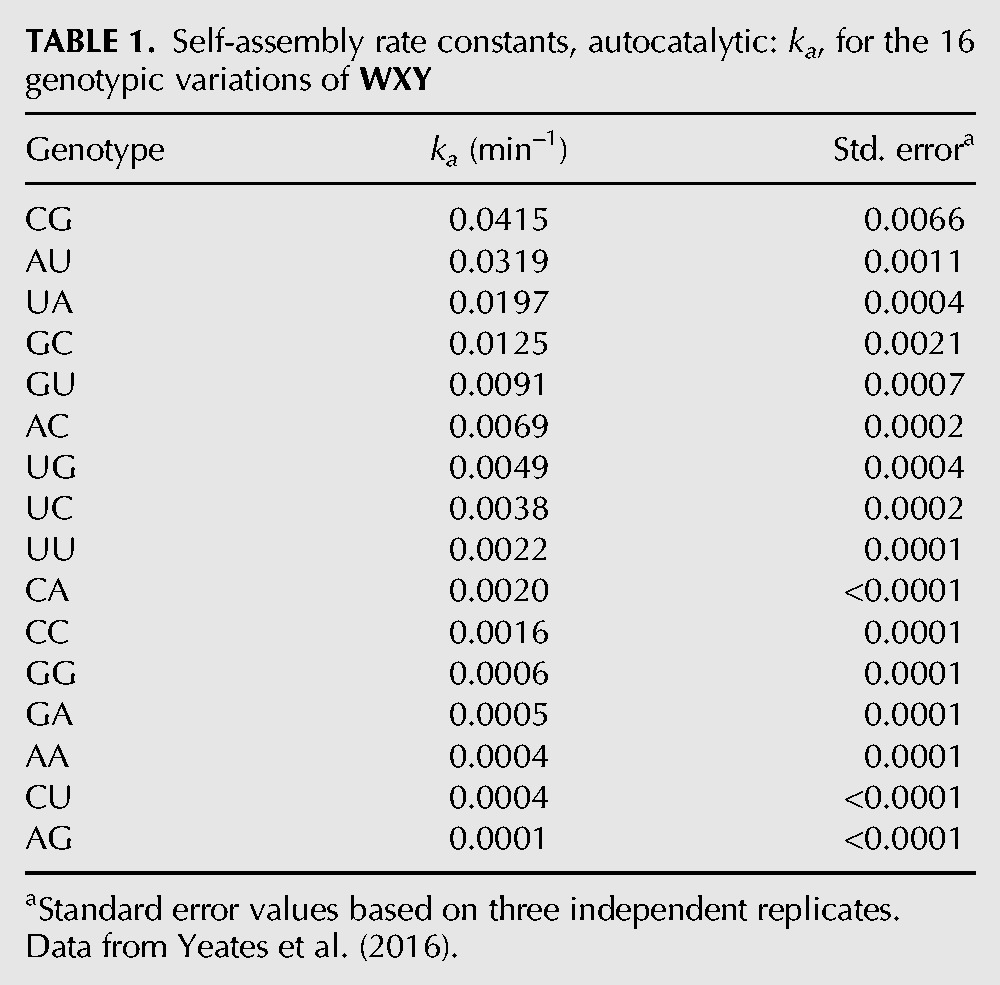
We have characterized kinetics of the self-assembly of 16 possible IGS-tag variants in a model 2-fragment reaction scheme: WXY+ Z → WXYZ. In this scheme, the IGS exists on the 5′ of the larger (∼150 nucleotides [nt]) RNA fragment WXY, while the tag exists on its 3′ end. The smaller (∼50 nt) Z fragment is invariant in this reaction and serves as a substrate (or “food” in the language of autocatalytic set theory) for self-assembly. We varied the middle nucleotide of the IGS (M) and tag (N) sequences to measure the self-assembly rates of all 16 possible _GMGWXY_CNU genotypes (Yeates et al. 2016); see Table 1. We have found that the predicted thermodynamic binding strength of the IGS-tag trinucleotides roughly correlates with rates of self-assembly (Satterwhite et al. 2016), demonstrating that it is possible to rationally engineer small networks of WXY RNA variants and anticipate how they might behave. Specifically, two-membered networks, and in one case a three-membered network, can be well characterized using the framework of game theory, such that the dynamics of WXYZ production can be predicted if the middle nucleotides of the IGS and tag sequences in the reaction mixture are known (Yeates et al. 2016).

TABLE 1.

Self-assembly rate constants, autocatalytic: k_a, for the 16 genotypic variations of WXY

However, the means by which such small RNA networks assimilate other available genotypes in the environment to grow and evolve into the more complex networks that are thought to have existed in the prebiotic milieu (King 1982) and that we have observed (Vaidya et al. 2012) remain unclear. From a theoretical standpoint, we have discussed six key parameters that should affect such evolution: (i) viable cores; (ii) connectivity kinetics; (iii) information control; (iv) scalability; (v) resource availability; and (vi) compartmentalization (Nghe et al. 2015). In the current study, we will focus on the first two of these to test their influence on the growth of three- and four-membered RNA networks. “Viable cores” are subsets of the total reaction network that are strongly connected to the rest of the network and thought to play a disproportionate role in driving prebiotic network evolution (Vasas et al. 2012). “Connectivity kinetics” refers to the topology of “who is connected to whom and in what way,” and network theory predicts this to be another key determinant of network evolution, e.g., growth by preferential attachment (Barabasi and Albert 1999). To date, these ideas remain purely theoretical, but here we have an opportunity to examine their manifestation in an experimental system of catalytic RNAs.

RESULTS AND DISCUSSION

Experimental setup

We designed several small three- and four-membered RNA networks that had the power to test the effects of cores and connection topology on overall network efficiency. Our first measure of efficiency, which can roughly be equated to a chemical kinetic fitness (Pross 2005) was the composite rate of production of full-length WXYZ ribozymes. Because each network is initiated with only WXY and Z fragments, neither of which in isolation has any catalytic activity, and because the full-length WXYZ ribozymes average at least a twofold catalytic rate enhancement over their noncovalent versions (i.e., WXY|Z, where the “|” represents association only with hydrogen bonds) (Vaidya et al. 2012), this measure is justified. In some instances we could also measure the growth rate of individual nodes (WXYZ genotypes) by individually radiolabeling the WXY species with 5′-³²P via polynucleotide kinase. A combination of network-wide and node-specific growth measurements gives a robust picture of evolutionary dynamics in a non-Darwinian setting.

To begin, we focused on constructing a three-membered core whose dynamics were known from previous work (Yeates et al. 2016). This is the rock-paper-scissors (RPS) trio that results when the WXY genotypes AA, UC, and GU are incubated in a 1:1:1 molar ratio with equimolar Z (i.e., 3 equivalents). We use a two-letter abbreviation to represent WXY genotypes: The first letter denotes the middle nucleotide of the IGS, while the second letter represents the middle nucleotide of the tag; genotype UC is _GUGWXY_CCU, for example. The AA + UC + GU trio is considered a core because the balanced set of interactions within ensures robust growth (Fig. 1B). Specifically in this case, the genotype AA (either the noncovalent complex WXY|Z or the covalently contiguous WXYZ) strongly catalyzes the assembly of genotype GU, which in turn strongly catalyzes the genotype UC, which in turn strongly catalyzes the assembly of AA. This closed loop is robust because the IGS of one member forms a Watson–Crick (WC) pair with the tag of the next member in the cycle. While non-WC pairings can result in productive complexes, the WC pairs produce the highest rate enhancements by far (Table 1; Yeates et al. 2016). Using total WXYZ production as a metric, we then measured the growth rate of this core. Initiating the reaction with 0.5 µM of each WXY genotype RNA and 1.5 µM Z, we found the total growth rate in 100 mM MgCl₂ at 48°C in the initial burst phase (0–5 min) to be 0.0070 ± 0.0003 µM/min. This value serves as a baseline for later comparisons when additional nodes are added or subtracted.

Increasing Watson–Crick linkages increases the rates of the core and network

With a baseline RPS core growth rate in hand, we could add or subtract nodes in various topologies to test their effects on core growth rate and total network growth rate. First we added one new node that created zero, one, two, or three new W–C linkages in the network (Fig. 2). The addition of a CU node, which should be primarily a “receiver” from the RPS core, lowered the core growth rate from 0.0070 to 0.0062 µM/min. (Note that we measured each rate in triplicate, and found standard errors typically in the 0.0001–0.0003 range; see Fig. 2. Thus we deemed changes in growth rates of 0.0003 µM/min or more to be significant.) This result matches with intuitive expectations that “selfish” entities in isolation can draw resources from an existing network (Takeuchi and Hogeweg 2008). Conversely, the addition of an AG node, which should primarily be a “giver” to the RPS core, raised the core growth rate to 0.0073 µM/min. Again this matches with intuitive expectations, although such results have not previously been confirmed experimentally in an RNA system.

FIGURE 2.

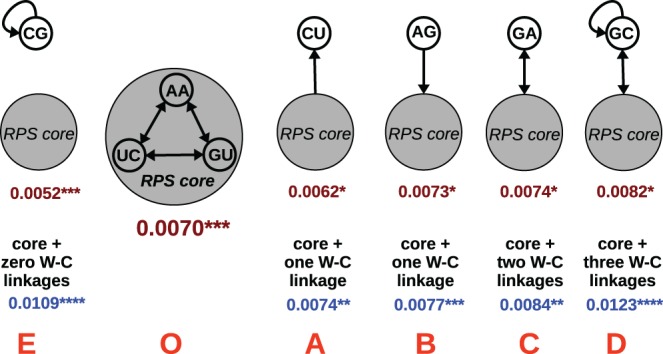
Effects of adding a single node to a three-membered core. Network names in red. The core-specific growth rates, in µM/min, are in crimson, while the overall total network growth rates are in blue. The number of asterisks denotes the standard error: one = ±0.0001 µM/min; two = ±0.0002 µM/min; three = ±0.0003 µM/min; four = ±0.0004–0.0006 µM/min. All networks depend on the presence of Z for growth.

Of interest however is that the addition of either the CU or the AG node had a similar effect on the overall network growth rate, raising it to 0.0074 or 0.0077 µM/min, respectively. This suggests that the overall degree of connectivity within an RNA network (the parameter K in graph theory) influences total network growth rate in a positive fashion. As further evidence in support of this conclusion, the addition of a GA node, which should both give and receive from the RPS core and increases the number of W–C linkages by two, has the effect of both increasing the total growth rate to 0.0084 µM/min and increasing the RPS core growth rate to 0.0074 µM/min. Furthermore, the addition of a GC node, which not only both gives and receives from the RPS core but itself is autocatalytic, thereby increasing the total number of W–C linkages by three, results in an even greater positive increase on core and total network growth rates, the former rising to 0.0082 and the latter to 0.0123 µM/min. On the other hand, the addition of the CG node, which is autocatalytic but does not connect to the core through a W–C linkage, has a large detrimental impact on the core growth rate (to 0.0052 µM/min) while increasing the overall growth rate. Presumably this is because its autocatalytic assembly competes with the core for the resource molecule, Z.

In aggregate, these results demonstrate that the addition of linkages generally enhances overall network growth rate but has a variable influence on core growth rates. In a prebiotic evolutionary setting, the implication is that polymer networks would be expected to grow via assimilation of new nodes that enter the environment. One nontrivial mechanism for the appearance of a “new” node is if the salt concentration of the milieu were to rise, for example, by water evaporation in a “warm little pond” scenario (Damer and Deamer 2015), reducing the stringency of base-pair formation such that fewer nucleotide pairs, or weaker pairs, could now form among RNA species. Thus far, the results are an empirical confirmation of the predictions of Jain and Krishna, who modeled the evolution of prebiotic networks and detected a strong driving force for cooperativity and interdependence (Jain and Krishna 2001).

Chemically balanced networks grow at equal rates

Next we sought to examine the role of node composition in RNA network growth. Previously, we determined that a fully cooperative three-membered network could out-compete three fully selfish networks when they were not tied together by the use of a common substrate (Vaidya et al. 2012). Now the question is whether two chemically balanced networks, but with different connection topologies, would behave similarly or not, when the substrate, Z in this case, is common. By “chemically balanced” we mean the same number of G–C and A–U nucleotide pairs exist in the IGS-tag pairings when the network as a whole is considered. But the effects of nearest-neighbor interactions may confound a simple enumeration of the numbers of such Watson–Crick pairs, such that different topologies could lead to different network growth rates. To this end, we compared two four-membered networks (Fig. 3). We constructed these two networks such that each had one U, C, A, and G in the first position (middle nucleotide of the IGS) and one U, C, A, and G in the second position (middle nucleotide of the tag). However, one network (CA + AG + GU + UC) was fully connected in a cycle via W–C pairs, while the other (AU + CG + UA + GC) contained four self-assembling nodes. These networks contain exactly the same chemical compositions but have disparate topologies, properties that are uncommon in networks of RNA having exactly 4-nt choices.

FIGURE 3.

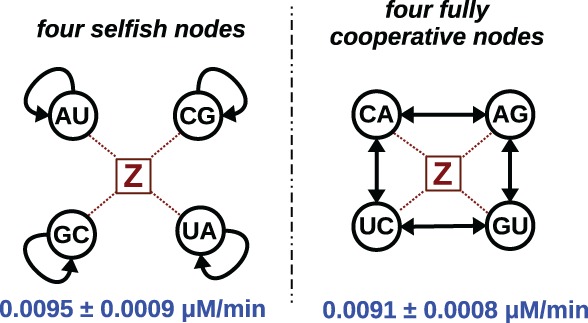
Comparison of two “chemically balanced” topologies of four nodes. The overall growth rates (blue) of two networks are indistinguishable. Both are dependent on the same RNA substrate molecule, Z. This is denoted by the red dotted lines; the Z molecule feeds each node.

When we supplied equimolar (e.g., 4×) of the substrate Z to each network, we found that the net self-assembly was not significantly different between them (Fig. 3). The fully connected network produced WXYZ molecules at a rate of 0.0091 ± 0.0008 µM/min, while the “selfish” network assembled at a rate of 0.0095 ± 0.0009 µM/min. As these two values are equivalent, we can conclude that some degree of asymmetry is needed to impart a selective difference between two possible genotypic networks. This was the case in our previous work with three-membered networks in which W + XYZ, WX + YZ, and WXY + Z were competed and in which cooperation was seen to win out (Vaidya et al. 2012). Such asymmetry would certainly have been a feature of any truly prebiotic scenarios where such a precise balance of chemical compositions would not have been likely. In fact there is only one possible fully selfish four-membered network, and dozens of possible four-membered networks that include cooperativity.

Serial dilution experiments

To help translate the above results to evolutionary dynamics that might be operational in a prebiotic setting, we next performed them in a serial dilution format. Here, as demonstrated previously (Yeates et al. 2016), a reaction can be initiated with equimolar ratios of each WXY species plus a total molar equivalent of the Z RNA. The reaction is allowed to run for a very short time (e.g., 5 min), and then a small fraction, typically 10%, of the reaction mixture is transferred to a fresh tube containing new WXY and Z. Typically eight such transfers (“bursts”) are done, and the total amounts of each WXYZ species are tracked as a function of burst number.

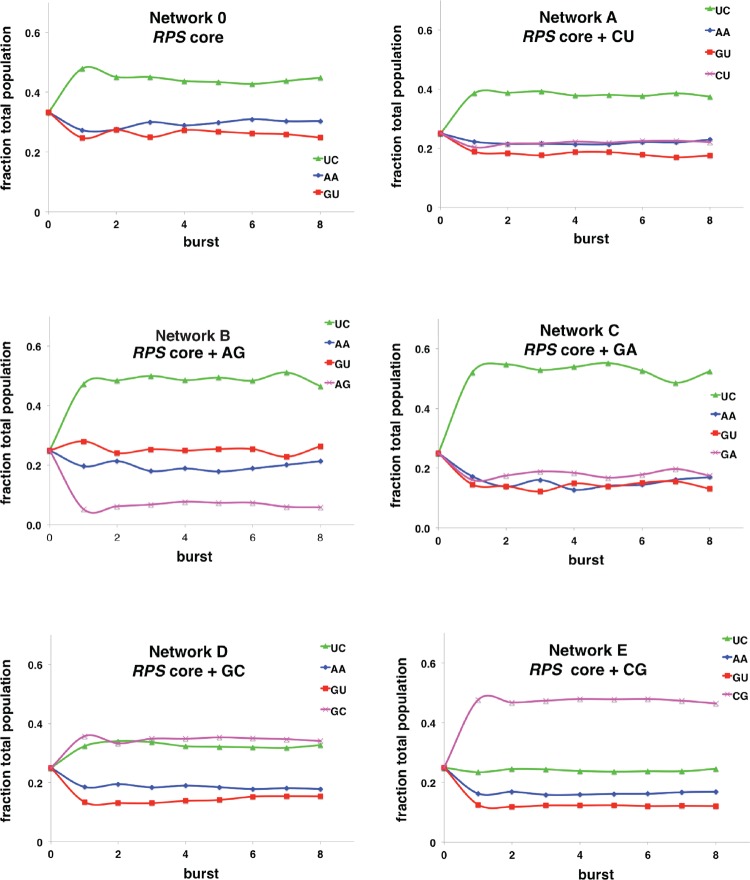
For each of the reaction networks shown in Figure 2, we performed these serial dilution experiments over eight bursts and tracked the molar proportion of each RNA WXYZ species as a fraction of total RNA (Fig. 4). In these experiments, one can follow the relative abundances of each node, while visualizing the overall dynamics of the population. Specifically, in the case of the three species in the RPS core (Fig. 4; Network 0), each node starts off solely as WXY in equimolar ratios (fraction of 0.33 each) but after a few bursts reaches a steady state in which the UC species (now as full-length WXYZ) dominates somewhat at about half the total moles, while the AA and GU species comprise the balance. In this three-membered network (Network 0), UC is kinetically favored over the other two because the steady-state ratio in which UC dominates represents the optimal eigenvector solution to a 3 × 3 payoff matrix into which the individual pairwise rates (Table 1) are input (Yeates et al. 2016).

FIGURE 4.

Empirical results from serial dilution experiments. In each burst, the WXY genotypes were allowed to react with equimolar Z RNA for 10 min, after which time 10% of the reaction volume was transferred to a new tube with fresh buffer and RNA. The fraction of each species was tracked in parallel test tubes using specific ³²P-labeled WXY species as tags and then plotted as the molar fraction of the total population.

Adding nodes increases the complexity of the system beyond what a theoretical analysis might be able to handle. Our previous experimental results in the RPS situation matched theoretical predictions reasonably well, at least with respect to the ordering of the nodes at steady state (UC >> AA > GU), but the extrapolation of self-assembly data to networks containing 2, 3, and more nodes becomes increasingly challenging (Yeates et al. 2016). To increase the evolutionary relevance of the current analysis, we performed the serial dilution experiments on the same networks shown in Figure 2 where single nodes were added to the RPS core (Fig. 4; Networks A–E). In each case a steady-state populational composition was reached after two or three bursts, and a clear ordinal ranking of genotypes became established. In these plots, the fate of the added fourth genotype (Fig. 4; purple traces) can easily be seen within the context of the RPS core. The dynamics of the added species vary dramatically, from the low steady-state proportions of added AG genotype in Network B, to the dominant proportion of the CG genotype in Network E. These data provide a complementary means of following network dynamics as the single-burst data given in Figure 2. Overall, the experimental results, both the single-burst data and the serial dilution data, can be understood by the application of graph theory to this biochemical system. Adding or subtracting nodes perturbs the network growth dynamics in a predicable fashion provided the node connectivity topologies are considered.

Simulation of network dynamics

We wondered whether the measured fractions of species could be predicted as a function of the connectivity of the network. Thus we constructed a simulation model using a first-order description as an approximation of the self-assembly dynamics, using the procedure described in the Materials and Methods.

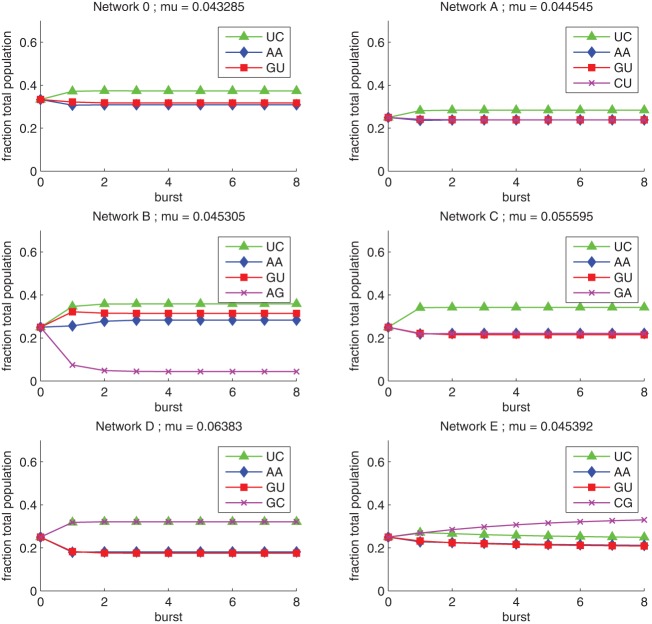
For each of the six networks analyzed in Figure 4, we plotted the predicted dynamics of each network (Fig. 5). The long-term ranking of species fractions was predicted very well within measurement error (Fig. 6). For the three-membered core network (Network 0), UC dominated AA and GU, the latter two being represented at nearly equal fractions. Each of the five other networks (A–E) consisted of adding one species that connects to the core in different ways. This resulted in different ranking of the newly introduced species relative to the core species (Fig. 5). This ranking could be correctly predicted as a function of its connection to the core: In Networks A and C, new species CU and GA were expressed at similar levels as GU and AA, all being dominated by UC; in Network B, species AG clearly ranked below all those of the core; in Network D, GC fraction was similar to the UC fraction, dominating other species; in Network E, CG fraction was clearly above the core.

FIGURE 5.

Predicted dynamics of the six RNA self-assembly networks shown in Figure 2. See text for the mathematical approach used. These predictions match experimental results shown in Figure 4 well, especially in terms of ordinal ranking of genotypes; see Figure 6. Mu represents the predicted total network growth rate constants.

FIGURE 6.

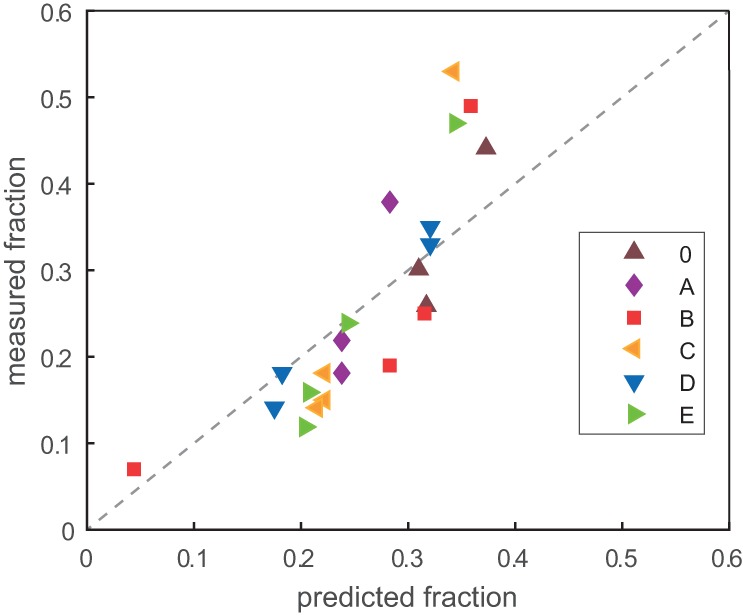
Correlation between measured (y-axis; from Fig. 4) and predicted (x-axis; from Fig. 5) fraction of the total population for genotypes in the evolving networks. Each dot represents a node in a network studied herein, and they are colored by network according to the key. The dotted line represents the perfect correlation of y = x, but as the individual data points are themselves interdependent, calculation of a standard correlation coefficient is not relevant.

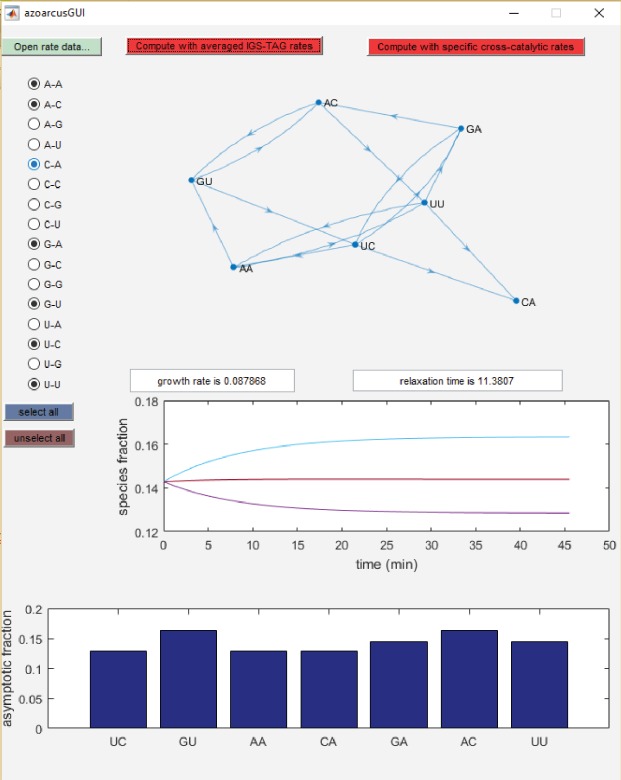
To help experimental design and interpretation, we developed an application with Matlab to predict network behavior based on the model above. This application is made available as a free standing Windows executable (available on request from the authors), in which three columns of input data are required. We designed this application to work with the Azoarcus ribozyme self-assembly networks, but in principle it can be used for any type of molecular network. The user first loads a text file of measured rates (third column) as a function of the catalyst (first column) and substrate (second column). The user can then choose either (i) to use a specific cross-catalytic value for each pair of species, using a self-catalysis rate of the IGS-tag combination by default in cases when a cross-catalytic rate has not been yet measured; or (ii) to proceed similarly as described above, by computing an average of all available measurements for a given IGS-tag combination. We found that approach (ii), which we used for Figure 5, led to much better predictions than approach (i) in this experiment. However, we anticipate that as more exhaustive and precise single-rate measurements are performed, approach (i) should become more precise than approach (ii). Once one has selected a set of species participating in the network, and upon clicking on one of the “compute” buttons, the application displays the network structure, the predicted long-term fractions, the predicted growth rate, the typical relaxation time before reaching asymptotic fractions (as given by the inverse of the difference between the two largest eigenvalues of A), and a time course of species fractions from equimolar initial conditions. See Figure 7 for a typical screenshot of the application as applied to our Azoarcus ribozyme network data.

FIGURE 7.

Screenshot of the Matlab application to predict RNA network growth rates and topological connections.

Conclusions

Group I ribozymes can catalyze the recombination of RNA oligonucleotide substrates in vitro to produce new combinations of sequences (Zaug and Cech 1986; Riley and Lehman 2003). Consequently, RNA-directed recombination of other ribozymes has great potential to illuminate the means by which RNAs can form networks of reactions. Here, we have tracked the dynamics of network growth in three- and four-membered self-assembling RNA networks in four complementary manners: empirical total growth rates, empirical core growth rates, empirical single-node growth rates, and predicted single-node growth rates. From these data we conclude that RNA networks will grow faster with more internal node connections, that chemically balanced networks should grow at equal rates, and that the averaging of lower-order empirical rate data can allow a reasonable prediction of the dynamics of higher-order network growth. We propose that primordial RNA networks could have grown and been under the strong influence of kinetic selection to expand by the assimilation of additional nodes.

MATERIALS AND METHODS

Preparation of RNAs and ribozymes

The variants of the Azoarcus ribozyme were transcribed from double-stranded DNA templates prepared by recursive PCR gene synthesis (Engels and Uhlmann 1988). To make the WXYZ variants, six partially overlapping single-stranded DNA oligonucleotides were incubated in equal molar ratios in eight-cycle PCR-like reactions using Vent DNA polymerase (New England Biolabs). Transcriptions of full-length ribozymes and longer RNA fragments such as WXY were carried out in reaction mixtures containing 1× transcription buffer (15 mM MgCl₂, 25 mM Tris [pH 7.5], 5 mM dithiothreitol, 2 mM spermidine), 2 mM rNTPs, 10 µL eightfold concentrated PCR DNA, and 1200 U of T7 RNA polymerase (Fermentas) in a 200 µL volume for 4–12 h at 37°C. The resulting RNA was purified on 8% polyacrylamide/8 M urea gels. DNA oligonucleotides were purchased from IDT. Shorter RNA oligonucleotides, including the Z fragment, were purchased from TriLink Biotechnologies.

Single-pot network kinetics

Reaction mixtures containing WXY (0.5 µM) of each genotype, equimolar Z (1.5 µM in three-membered networks and 2.0 µM in four-membered networks), and ³²P-labeled WXY (≤0.003 µM) of each genotype, were heated to 80°C for 2 min then cooled to 48°C. Reactions were initiated with the addition of reaction buffer (100 mM MgCl₂ and 30 mM EPPS, pH 7.5). For time points samples were drawn and rapidly quenched (125 mM EDTA and 2× loading dye containing formamide and bromophenol blue) over 0–5 min and used for rate comparison experiments. WXY and WXYZ RNA bands were separated on 8% polyacrylamide/8M urea gels. Visualization and quantification was done with a Typhoon Trio+ variable mode phosphorimager and its accompanying ImageQuant software (GE Healthcare). A product ratio was calculated by comparing the RNA in the product WXYZ band to the unreacted WXY band (fraction reacted = [reacted/(reacted + unreacted)]). To determine individual genotype WXYZ production, reaction mixtures were made as a master mix without ³²P-labeled WXY. The master mix was then divided into three or four reaction tubes, depending on the number of genotypes being tracked, and each tube was doped with the specific ³²P-labeled-WXY genotype being followed.

Serial dilution experiments

To perform the serial dilution kinetic experiments as shown in Figure 4, a master mix reaction mixture was formed containing equimolar of each WXY genotype (0.5 µM) and Z (1.5 or 2.0 µM). The mixture was then divided into three or four equal volumes, depending on the number of genotypes being compared. Each part was doped with ³²P-labeled aliquot (<0.01 µM) of one of the WXY genotypes. The reaction mixtures were then aliquoted into eight tubes each (one for each burst). All tubes were heated up to 80°C for 2 min and then cooled to 48°C. The reaction in the first tube was initiated with the addition of reaction buffer (providing each reaction with a final concentration of 100 mM MgCl₂ and 30 mM EPPS, pH 7.5). At 5 min, 10% of the solution volume from tube #1 was transferred to tube #2, and tube #1 was placed on ice. Reaction buffer was immediately added to tube #2 while tube #1 was subsequently quenched with an equal volume of quench solution. The transfer protocol was repeated through eight bursts. The master mix containing ³²P-labeled WXY was used as a negative control for the assay. Gel separation, visualization, and quantitation were performed the same as for the kinetic assays above.

Simulations

We considered the following first-order dependence of the production rates, denoting x_i as the concentration of species i:

$${\dot{x}}_i=a_{i1}\cdot x_1+a_{i2}\cdot x_2+\cdots +a_{in}\cdot x_n.$$

The set of corresponding equations for every production rate ${\dot{x}}_i$ can be written as

$$\dot{X}=A\bullet X,$$

where X = (x₁, …, x_n) is the vector of species concentrations and A is the matrix whose coefficients correspond to the catalytic strengths a_ij. Such a first-order description is the simplest approximation of the dynamics taking into account the diversity of cross-catalytic interactions between species. However, such an approximation is justified only for a certain range of conditions. In particular, it cannot account for nonlinear effects that can occur over arbitrary time windows, such as saturations due to substrate limitations, or higher-order interactions between catalytic molecules.

By performing serial dilutions after reaction times that are short (10 min) compared to saturation regimes, the conditions of our experiment are optimal for this first-order approximation to be valid. In these conditions, catalysts can be considered as largely limiting compared to substrates. Each a_ij thus represents the initial production rate of species x_i per unit of catalyst x_j, given all other components fixed, including fragment and food concentration. Note that the existence of a unique long-term exponential growth state is not given in general; but in our case, it has been shown to be guaranteed by the positivity of all a_ij, even in the presence of slight saturations (Gaubert and Gunawardena 2004). This stable growth state is found by resolving the equation $A\bullet X_M=\mu \cdot X_M$ for the largest eigenvalue μ of A. An explicit calculation was previously provided for the two-species case (Yeates et al. 2016). The current results extend to a higher number of species, where long-term fractions are given by the components (x₁, …, x_n) of the eigenvector X_M, normalized such that $\sum _{i=1,\dots ,N}{x}_i=1$. Notably, this long-term state being unique (Gaubert and Gunawardena 2004), it is necessarily independent of the initial conditions, the influence of the latter being apparent only during an early transient of the reaction, a phenomenon that we experimentally observed to occur within the first round of the serial transfer (Fig. 4).

To determine the different values a_ij, one would ideally measure independently the accumulation rate of every species by doping in every other species. Although this approach was possible and successful for a limited number of two-member networks, it is not currently realistically accessible for larger networks, as the number of cross-catalytic rates becomes very large quickly as additional members of the networks are added. To overcome this limitation, we rather used a simplified estimate of these rates based on known molecular substrate-recognition mechanisms, where interactions are specified only by the IGS of the catalyst and the tag of the substrate. This approach reduces to 16 different rates for each IGS-tag combination. Each rate was then computed by taking the average of the rates that had been previously measured in the two member-doping experiments for the same IGS-tag combination.