GillesPy: A Python Package for Stochastic Model Building and Simulation

Abstract

GillesPy is an open-source Python package for model construction and simulation of stochastic biochemical systems. GillesPy consists of a Python framework for model building and an interface to the StochKit2 suite of efficient simulation algorithms based on the Gillespie stochastic simulation algorithms (SSA). To enable intuitive model construction and seamless integration into the scientific Python stack, we present an easy to understand, action-oriented programming interface. Here, we describe the components of this package and provide a detailed example relevant to the computational biology community.

I. Introduction

Stochasticity has recently been recognized as an essential feature of cellular processes. Extrinsic noise may be caused by fluctuations in the physical environment or properties of the individual cell (e.g. cell age or size), and may be captured in dynamic models through time-varying noise in model parameters. Intrinsic noise is caused by the low copy numbers of genes, transcripts, and proteins, and spatial inhomogeneity within the cell. Intrinsic noise in particular has gained attention, due to its essential role in cellular processes such as genetic toggle switches, noise-driven oscillation, cell polarization, and cell population dynamics [1–5].

Deterministic ordinary differential equation (ODE) models of biochemical processes are useful and accurate in the high-concentration limit, but fail to accurately capture stochastic cellular dynamics, as they assume spatial homogeneity and continuous biomolecule concentration. To address the issue of quantized concentrations we can replace deterministic ODEs with a continuous-time discrete-space Markov process, with the probability density of the system governed by the chemical master equation (CME). The CME is expensive to solve directly due to the curse of dimensionality, and more often Gillespie’s SSA method is used to generate a trajectory that is a statistically correct sample of the probability density. An ensemble of trajectories can be generated via a Monte Carlo method to form a basis for statistical analysis, a process which can be computationally-intensive for large systems or large ensembles.

The original SSA has been extended to include methods for more efficient exact and approximate simulations, including the optimized-direct method, composition-rejection method, and τ-leaping [6–9]. For a recent review, see [10]. Many of these improved methods have been distributed in the popular StochKit2 software package [11]. StochKit2 provides an efficient C-implementation of algorithms for discrete stochastic simulation with a command-line interface. StochKit2 models must be created in StochML format, and simulation trajectories are returned as CSV files.

With its wide variety of numerical libraries and statistical packages, Python has become one of the most commonly used and effective languages in computational biology. In order to optimize computational biology workflow and simplicity in working with stochastic model building and simulation, we have created the GillesPy package. GillesPy combines a Python-based model construction toolkit with the computational efficiency of the StochKit2 C-based SSAs. GillesPy builds on StochKit2, and provides many enhancements to the model construction and simulation workflows. The model construction toolkit allows simple setup and parameterization of the CME. For stochastic simulation, StochKit2 automatically inspects the model to be simulated and selects the most efficient SSA formulation based on the model size (direct method for small, composition-rejection method for large, see [11] for a complete description). For deterministic simulation, GillesPy uses the StochKitODE solver from the StochSS software suite, which uses the CVODES solvers from the Sundials software package [12]. The GillesPy package encapsulates the entire process in Python, for seamless integration with other computational packages or statistical analysis. GillesPy also supports the import of SBML models.

In this work, we describe the features and use of GillesPy, and provide a relevant example for efficient simulation and numerical stability analysis of a genetic toggle switch.

II. Mechanistic Modeling of Biological Systems

GillesPy is designed to simulate dynamic mechanistic models of biochemical networks. In mechanistic models the dynamic behavior of the system is built up from individual interactions between biochemical species. Typically, this is a finite number of species and reactions interacting probabilistically in a well-stirred domain. This is in contrast to empirical models, which focus on mathematical functions based on external characteristics such as dose-response curves. In these models the external dynamic behavior of the system is captured by a set of mathematical equations, in a “top down” approach, and as a result has reduced predictive power [13]. Mechanistic models, unlike empirical models, can be used to predict the system’s future behavior, or its behavior under perturbation. Mechanistic models differ in that they may be used to probe hypotheses about the underlying reaction pathways rather than simply the in-out behavior of a system. Often, complicated reaction pathways may be simplified through the use of Michaelis-Menten or Hill type kinetic equations. GillesPy does allow for Michaelis-Menten and Hill propensity functions, as these types of functions are quite common. However, we caution that the developer of a model must always be careful to check the validity of the assumptions of these model reduction functions [14–16].

III. GillesPy Design

GillesPy is designed to follow the “pythonic” object-oriented principles, thus biochemical models in GillesPy are constructed in an object-oriented fashion. To construct a new model you define a new class that extends a base model gillespy.Model. The model constructor defines the parameters, species, and reactions of the biochemical system by associating the like named objects (Parameter, Species, Reaction) from the gillespy Python package. Once defined, users interact with their model by instantiating instances objects of the model. These objects may be use to generate simulation trajectories of the biochemical systems through their .run() method. This command calls the StochKit2 C-solvers to simulate the provided model. StochKit2 selects the computationally-optimal algorithm for simulating each model.

After a simulation is completed, the resulting trajectories are returned as Numpy arrays into the Python interface, where the data is available for processing by the large library of scientific Python tools. Model fitting, statistical analysis, or visualization is not directly handled within GillesPy, as there are numerous mature software packages for these purposes commonly used in the scientific Python community (e.g. DEAP [17] for model fitting through evolutionary algorithms, pandas [18] for statistical analysis, or Matplotlib [19] for visualization). The following section demonstrates the building and simulation of a simple and biologically relevant example.

IV. Example: A Bistable Genetic Switch

Bistable stochastic genetic switches have been shown to play important roles in cellular differentiation [20]. As the system has two equilibria, deterministic simulations fail to accurately capture the random switching between states. Figure 1 is a diagram of the genetic toggle switch, showing how each of the two promoters expresses a gene that is the inhibitor for the opposite promoter. Here, we demonstrate using GillesPy to simulate a bistable switch from [2]. The deterministic equations comprising this switch are:

$$\frac{dU}{dt}=\frac{a_1}{1+V^{\beta }}-U$$ (1)

$$\frac{dV}{dt}=\frac{a_2}{1+U^{\gamma }}-V$$ (2)

where U and V are co-repressor concentrations. Here, the parameters a₁ and a₂ are synthesis rates of U and V respectively. Parameters β and γ represent the cooperativity of each repressor. We create a stochastic model from these equations by converting them to four stochastic reaction channels: synthesis and degradation of U and V respectively.

$$\begin{array}{cc}\mathrm{Ø}\stackrel{\frac{{\alpha }_1}{1+{\left[V\right]}^{\beta }}}{\to }U,& U\stackrel{\mu \left[U\right]}{\to }\mathrm{Ø}\end{array}$$ (3)

$$\begin{array}{cc}\mathrm{Ø}\stackrel{\frac{{\alpha }_2}{1+{\left[U\right]}^{\gamma }}}{\to }V,& V\stackrel{\mu \left[V\right]}{\to }\mathrm{Ø}\end{array}$$ (4)

We note that this simple model does not explicitly differentiate between transcription and translation of U and V.

Fig. 1.

A schematic showing the genetic switch model from Gardner et al. [2].

Constructing this model in Python begins with creating a model object by inheriting from GillesPy’s model class:

class BistableToggleSwitch (gillespy.Model):

We create and add parameters within this object by:

a1 = gillespy. Parameter (‘a1’, expression =4)
self.add parameter ([a1, …])

and equivalently add species and reactions. We then simulate this model by invoking:

model = BistableToggleSwitch ()
results = model.run ()

A single simulation showing U and V populations using both stochastic and deterministic solvers over the course of 100s is shown as Figure 2.

Fig. 2.

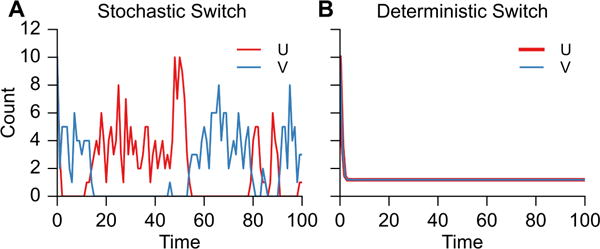
Stochastic and deterministic simulation of the genetic toggle switch with GillesPy. Bistability is evident in the stochastic model of this switch (with β = γ = 2.0).

Here, the difference between stochastic and deterministic results is visually evident. For identical initial populations of U and V, the deterministic system evolves to a metastable state with equal U and V. For non-identical initial conditions, the system evolves to a stable state where only the species with a higher initial population is produced (not shown). Meanwhile, the stochastic simulation of this system shows dynamic switching between U-dominated and V-dominated states, as seen in Ref [2], regardless of the choice of initial condition. Spontaneous switching between stable states is never observed under deterministic conditions. The full code for this model and simulation is available at: http://github.com/GillesPy/gillespy/asGeneticToggleSwitch.ipynb.

Exploring model dynamics via a parameter sweep is a common task in computational biology. To perform a simple parameter sweep, we allowed our model to accept parameter arrays and assign these values to parameters upon initialization of the model object. Thus, GillesPy was used to algorithmically generate, simulate, and analyze model dynamics without forcing the user to manually create or parameterize different models. Instead, the user can simply use a loop (or a parallel loop) to parameterize a dynamically-generated model, perform simulations, analyze simulation trajectories, and return summary statistics.

As noted in Ref. [2], the mono- or bistability of the switch system is dependent on the values of cooperativity parameters (β, γ), and promoter strengths (αs). Eqns. 1 and 2 yield stable solutions where $\frac{dU}{dt}=\frac{dV}{dt}=0$. For low cooperativity, this results in a single monostable steady state. Increased cooperativity results in an increased nonlinearity, and sigmoidal switch-like behavior of the promoter [21]. The sigmoidal shape of promoter kinetics results in two stable states, and one metastable state for the system. For this example, we investigated how the cooperativity parameter affects bistability by repeatedly generating and simulating the stochastic model with parameters β = γ ∈ [0, 4.0]. Figure 3 demonstrates the results of this process for varying β and γ in increments of 0.1. For our example, α₁ = α₂ = 10.0, and a bimodal distribution of states first appeared at approximately β = γ > 1.3, indicating that this is where the transition to bistability occurs. This critical bistability threshold would increase with a lower α, as lower (or unbalanced) promoter activity results in less switch-like behavior.

Fig. 3.

Investigating bistability through β and γ. (A) Histograms of state (U − V) for three selections of cooperativity parameters β and γ. (B) Heatmap of state probability for a range of β and γ in increments of 0.1. A bimodal state distribution first appears when β = γ > 1.3. Simulations were performed for 25,000s and sampled in increments of 1s for each parameterization. Parallelization through IPython enables this computationally-intensive simulation to be performed on an 8-CPU desktop machine in approximately 5 minutes.

V. Parallel Processing With MOLNs

GillesPy has been integrated with, and is distributed with MOLNs, a cloud computing platform for computational systems biology that focuses on reproducibility and scalability [22]. MOLNs allows computational scientists to easily create compute clusters using cloud computing resources. It further provides methods for automatically parallelizing workflows for computing large ensembles of trajectories or for conducting global parameter sweeps. This is combined with a facility for efficient post-processing of the resulting stochastic trajectories, designed to maximize data locality by distributing the code to worker nodes where the data is generated. This facility is built to utilize the simple to use programming paradigm of MapReduce [23]. The user interface for this system is an interactive web-based environment, the IPython Notebook [24]. These computable documents combine code, equations, narrative text, visualizations, images as well as other media. Integration with MOLNs provides GillesPy users with a simple and powerful interface to scale their computational workflows using public or private cloud computing infrastructures.

VI. Conclusion

GillesPy is an open source package for stochastic model building and simulation, and a Python interface to the StochKit2 solvers. GillesPy runs on Linux/Unix or Mac OS X. It is freely available under GPL version 3. Installation instructions and downloads are available at: http://github.com/GillesPy/gillespy. We welcome both bug reports and requests for assistance on our Github page.