Planning Beyond the Next Trial in Adaptive Experiments: A Dynamic Programming Approach

Abstract

Experimentation is at the heart of scientific inquiry. In the behavioral and neural sciences, where only a limited number of observations can often be made, it is ideal to design an experiment that leads to the rapid accumulation of information about the phenomenon under study. Adaptive experimentation has the potential to accelerate scientific progress by maximizing inferential gain in such research settings. To date, most adaptive experiments have relied on myopic, one-step-ahead strategies in which the stimulus on each trial is selected to maximize inference on the next trial only. A lingering question in the field has been how much additional benefit would be gained by optimizing beyond the next trial. A range of technical challenges has prevented this important question from being addressed adequately. The present study applies dynamic programming (DP), a technique applicable for such full-horizon, “global” optimization, to model-based perceptual threshold estimation, a domain that has been a major beneficiary of adaptive methods. The results provide insight into conditions that will benefit from optimizing beyond the next trial. Implications for the use of adaptive methods in cognitive science are discussed.

Experimentation in the behavioral and neural sciences involves the process of presenting stimuli to observers and measuring their responses (e.g., categorization, response time, brain activity), with the goal of inferring the structural and functional properties of the underlying process. The quality of the inferences that can be drawn depends on the quality of the data collected. High-quality data, and thus better inference, can be obtained by improving the informativeness of measurement (Myung & Pitt, 2009). This is a constant issue in the discipline, where the signal-to-noise ratio in the data can be poor.

One means of improving measurement is by using adaptive data collection methods, in which the course of the experiment is tailored to each participant as a function of how that participant has responded in preceding trials. Developed under the general rubric of optimal experimental design, methods of adaptive design optimization (ADO; also known as adaptive measurement, adaptive estimation, and active learning) maximize the efficiency of statistical inference across successive observations. ADO, which is commonly formulated within the Bayesian inference framework, finds an optimal stimulus for the next trial based on observations from past trials. Optimization can be applied to any type of inference, whether it be testing a hypothesis or estimating certain quantities (e.g., model parameters), and the use of ADO in experimentation is growing in behavioral research (Cavagnaro, Gonzalez, Myung, & Pitt, 2013; DiMattina & Zhang, 2011; Klein, 2001; Kontsevich & Tyler, 1999; Lesmes, Jeon, Lu, & Dosher, 2006; Rafferty, Zaharia, & Griffiths, 2014; Remus & Collins, 2008; Watson & Pell, 1983).

One simple form of ADO, popularized in psychophysics, is the staircase procedure, which adjusts stimuli incrementally (e.g., increasing or decreasing stimulus intensity by predetermined units) based on the observer’s response (e.g., detecting or failing to detect a stimulus). Staircase procedures with various down-up rules have been proposed and their properties have been systematically studied (Dixon & Mood, 1948; Kaernbach, 1991; Levitt, 1971). Other approaches to ADO have used rigorous, statistical criteria for determining when to alter the next stimulus (Hall, 1981; Taylor & Creelman, 1967), and precisely how much to alter it (Kontsevich & Tyler, 1999; Watson & Pelli, 1983). Perhaps the most advanced form of ADO is one that integrates Bayesian sequential inference with information theory to achieve the maximum accrual of information about the unknown quantity being inferred. On each trial, every stimulus in the experimental design is evaluated on its potential informativeness given the data already collected and the objective of the experiment (e.g., parameter estimation). The stimulus that is predicted to provide the largest gain in information is used on the next trial (Cavagnaro, Pitt, Myung, & Kujala, 2010; Kontsevich & Tyler, 1999; Kujala & Lukka, 2006).

By design, adaptive methods involve sequential decision-making. Common among the above approaches is that they consider only the dependency between adjacent trials, operating under the assumption that accumulated information over the course of the entire experiment is optimized by choosing the stimulus that is expected to elicit the most information on the next trial. Intuitively, because this one-step-ahead optimization ignores the consequence of each choice for trials beyond the next step, it is reasonable to believe that taking such consequences into account might further improve the accuracy of inference. Despite intermittent explorations of two-step-ahead optimization (Kelareva, Mewing, Turpin, & Wirth, 2010; King-Smith, Grigsby, Vingrys, Benes, & Supowit, 1994; Pelli, 1987), this conjecture has not been systematically examined, making it a long-standing and unresolved issue in the field.

Researchers, in fact, have studied theoretical properties of adaptive estimation and shown that one-step-ahead optimization is asymptotically optimal, meaning that it can be as efficient as methods of any look-ahead abilities under a schedule of sufficiently many trials (Chaudhuri & Mykland, 1995; Kujala, 2016; Wynn, 1970). However, in situations where only a limited number of trials can be administered in practice (e.g., time or cost constraints), these theoretical results do not answer the question of how many trials are necessary for one-step-ahead optimization to achieve a desired level of precision for a certain inference problem. Likewise, the question of how much additional benefit would be gained, if any, by optimizing beyond the next trial is difficult to address until the method is actually implemented for a particular problem.

The purpose of the present paper is to explore the application of dynamic programming (DP), a technique that can be used for planning far ahead into the future, to adaptive behavioral experiments for model-based inference. With the help of DP, the present study implemented multiple-steps-ahead optimization and examined its performance in a commonly encountered, particular context. The estimation of perceptual thresholds was chosen as a testbed for the investigation, along with a fully Bayesian implementation of the threshold model. Threshold estimation has been a building block in many assessments of the health and functioning of sensory systems in clinical and research settings, making the performance and utility of adaptive estimation procedures of considerable interest (Klein, 2001; Leek, 2001).

We perform a simulation study to explore how multiple look-ahead depths (1–100 trials) affect parameter inference. The effect of look-ahead depths is examined under two different constraints concerning stimulus choice: One represents a common practice of threshold estimation as well as the problem analyzed by the current theories of asymptotic optimality, and the other induces a condition that would benefit from increased look-ahead depths. Implications of results for the use of adaptive methods in general cases, and further connections between these results and existing theories, will be discussed.

Dynamic Programming

Since the seminal work by Richard Bellman in the 1950’s (Bellman, 1957), dynamic programming has referred to a variety of methods that take advantage of recursive local structure in a sequential decision problem to find a globally optimal solution. DP has been applied to a wide range of problems that involve making decisions across varying time horizons, including operations research, automatic control, artificial intelligence, and economics (Bertsekas, 2012; Judd, 1998; Powell, 2011; Sutton & Barto, 1998).

Most DP applications can be conceptualized as shortest-path problems. Consider the network of nodes shown in Figure 1. Nodes represent certain states that one should go through in the process of solving a problem, such as navigating between cities. Edges connecting the nodes represent possible transitions from one state to another, made by the problem solver. At any state during the task (e.g., C₁–C₃), the solver needs to make a decision that determines a transition to the next state (D₁–D₂). The decision should be made carefully because each resulting transition is associated with a cost (e.g., travel time), represented by the numbers on the edges of the network.

Figure 1.

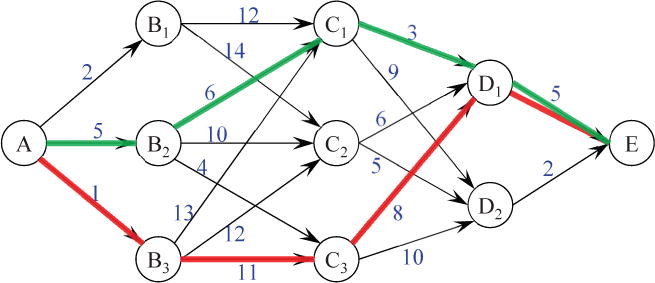
Network depicting the shortest-path problem. Nodes represent locations (e.g, cities), and the numbers adjacent to the arrows, or directional edges, connecting the nodes represent the cost (distance) of moving from one node to another. The red line from A to E is the path (global cost of 25) taken when using one-step-ahead optimization, a strategy in which the next node that is chosen is always the least costly. The green line denotes the shortest path from A to E (global cost of 19), and can be identified through backward induction by looking beyond the next node to consider the costs of future transitions between nodes.

Suppose that one tries to find the path from the initial state A to the goal state E that incurs the smallest global cost (e.g., elapsed time) caused by all required transitions. One approach to finding the shortest path is to loop over all possible paths and map all associated global costs to identify the smallest one. Such a brute-force method is rarely viable because the number of required operations (i.e., determining all costs) grows exponentially as the number of decision stages increases, making brute-force computation impractical. With DP, in contrast, the number of required operations increases only linearly.

DP achieves a solution by exploiting the problem’s recursive structure in the following fashion. It begins in the last stage, either state D₁ or D₂, where no decision needs to be made because there is only one transition for each. The costs associated with states in this stage (i.e., 5 for D₁ and 2 for D₂) are stored in a table. At the second-to-last stage (i.e., C₁–C₃), the optimal decision that leads to the smallest global cost can be made with the stored knowledge of possible consequences in the next stage (D). For example, at state C₁, one can evaluate two alternative transitions, C₁→D₁ versus C₁→D₂, by computing their eventual costs: 3+5=8 for C₁→D₁→E and 9+2=11 for C₁→D₂→E. Obviously, the optimal choice is C₁→D₁ because its global cost is smaller (8 as opposed to 11). In the same way, one can determine optimal decisions at each of the remaining possible states in the stage, C₂ and C₃, by comparing the eventual costs of alternative transitions from each. The optimal costs and transitions corresponding to each state are stored. Going one step backward (B₁–B₃), the optimal decision can be made, again, by utilizing globally optimal decisions at the subsequent stage (C) stored from the previous computation. The results are recorded in the same fashion. By carrying accumulated knowledge backward through the transition sequence in this manner, a system of sequential decisions is established (i.e., a table of optimal decisions and associated global costs at each state). To solve a shortest-path problem from any starting state, one simply follows optimal decisions referenced in the system as moving forward across stages, the process of which is called forward evaluation (global cost of 19 if starting from A; green line in Figure 1).

One may wonder what would be the solution to the shortest-path problem if the one-step-ahead strategy in conventional adaptive experimentation were applied across all transitions. The path generated by seeking the smallest local cost at every transition is shown in red in Figure 1, and it does not result in the smallest possible global cost (25 vs. 19).

The procedure of working backward to find the shortest path is known as backward induction (Bellman, 1957). Backward induction requires two fundamental assumptions. One is that as long as a certain state is reached, the globally optimal decision at that state will not be affected by the previous path of transitions. The other is that the global cost of a decision at any state must be defined as a function of the local cost due to a transition to an immediate, subsequent state and the global cost associated with that (subsequent) state. Put another way, the problem must be decomposable into a form in which a local cost of a transition and a global cost after it constitute a new global cost at a greater depth. Under these conditions, global optimization can be broken down into recurring local optimization problems, as illustrated in the example.

In the above example, note that the solver goes through all possible states to compute and store their respective optimal decisions and global costs. This algorithm is known as exact DP or exact backward induction. For many problems in practice, however, exact DP becomes computationally infeasible when the space of all possible states is large (i.e., high-dimensional). To overcome this hurdle, either probabilistic methods (estimating globally optimal costs by sampling paths of states and decisions) or deterministic methods (approximating the state space with simpler representations) are employed. The collection of various such techniques has been developed under the rubric of approximate DP (Bertsekas, 2012; Powell, 2011).

Statistical inference in adaptive experimentation can be implemented as a dynamic program in which the goal is to maximize the total inferential gain over all trials, or a set of trials of any length. We performed simulations to observe whether and how much savings are achieved in perceptual threshold estimation when DP is used and the length of the look-ahead horizon is varied.

Using DP for Threshold Estimation

In cognitive science, DP has been proposed as a model of ideal, sequential decision-making behavior (Busemeyer & Pleskac, 2009; Lee, Zhang, Munro, & Steyvers, 2011), but its use for fully Bayesian inference of a probabilistic process model (i.e., sequentially updating the entire posterior distribution on each observation) has yet to be explored. Such use of DP presents unique computational challenges to overcome, and its implementation for the inference of even a very simple model (e.g., with a single parameter) can be highly nontrivial. The reason for this is that the posterior distributions of a model parameter represent the states of knowledge that a DP algorithm should go through across multiple stages (i.e., experimental trials), and the possible posterior distributions grow exponentially to a computationally intractable level as data accumulate. Specifically, a major challenge that must be overcome in DP implementation is how to characterize all possible posterior distributions, which would emerge from each new potential observation, on an approximate state space of a manageable size. To describe the problem and our solution to it in context, we begin with a brief introduction to model-based perceptual threshold estimation. Readers wishing to skip the details of implementation should turn to the section “Simulation Experiments.”

Perceptual thresholds are often measured by having participants make one of two response alternatives (e.g., did you see a flash of light?) after presentation of a stimulus at a given level (e.g., intensity). For the underlying threshold to be measured, it can be treated as the location parameter of an S-shaped psychometric function that is to be estimated under Bayesian inference. The commonly used log-Weibull psychometric function (Watson & Pelli, 1983) has the form

$${\mathrm{\Psi }}_{\theta }(d)=.5+.48\left[1-\exp \left({10}^{(1.5/20)(d-\theta )}\right)\right]$$ (1)

which returns the probability of correct detection Ψ_θ(d) with the input of stimulus intensity d given that the underlying threshold is θ. In this particular function, the upper limit (due to attention lapse), lower limit (due to guessing), and slope of the function are given some assumed values (.98, .5, and 1.5, respectively). Given a stimulus in each trial, a participant’s binary response is assumed to be generated from a Bernoulli distribution with its parameter (probability of success) governed by the psychometric function. To estimate θ, a diffusely dispersed distribution (conventionally, uniform or Gaussian with a large variance) is set as a prior belief about θ, and receives Bayesian updating to provide a posterior distribution given the observation of responses.

Let us observe the correspondence between this problem of threshold estimation and the shortest-path problem described earlier. In threshold estimation, the knowledge states that the estimation process should go through across successive trials (stages) are the posterior distributions of the threshold θ after observing responses in each trial. The decision to make before each trial is the choice of a stimulus to present from a predefined stimulus space (usually a discretized continuum of intensities). After observing a response to the chosen stimulus, the posterior of θ is updated, or a transition to the next state is made. The reward of each transition, rather than the cost in the shortest-path problem, is the improved quality of the resulting posterior (e.g., the degree to which the distribution is concentrated on a value) relative to that of the previous state. What one wants to optimize globally at the end of a measurement session is the quality of the final posterior distribution relative to the prior initially set at the start of the measurement session.

A notable difference unique to threshold estimation is that the transition is not determined solely by the choice of a decision alternative but also depends on the participant’s response which can only be predicted probabilistically. Key to the application of DP, however, is a consistent metric for the reward (or cost) of a transition that is assigned to the current, given state, not whether the transition is made deterministically to a single state, or probabilistically to one of multiple states in the next stage. What is computed and stored in each step of backward induction is the global reward and optimal decision based on such a metric. Information theory (Cover & Thomas, 2006) provides a theoretically sound metric for the quality of Bayesian updating given probabilistic observations.

Within information theory, the amount of knowledge one can expect to gain upon the next trial by using a certain stimulus is quantified by the expected information gain associated with that stimulus choice. Formally, the expected information gain after the next trial is

$$H_t(\mathrm{\Theta })-H_{t+1}(\mathrm{\Theta }|Y_{t+1},d_{t+1})$$ (2)

where H_t(Θ), defined by ${\mathbb{E}}_{\mathrm{\Theta }|y_1,\dots ,y_t}\left[-\log \mathrm{\Theta }\right]=-{\displaystyle \int p(\theta |y_1,\dots ,y_t)\log p(\theta |y_1,\dots ,y_t)d\theta }$, denotes the entropy of the knowledge state Θ (posterior distribution of thresholds) upon trial t, and the second term $H_{t+1}(\mathrm{\Theta }|Y_{t+1},d_{t+1})={\mathbb{E}}_{Y_{t+1}|d_{t+1}}[H_{t+1}(\mathrm{\Theta })]$ is the conditional entropy of the next state given potential observation Y_t+1 made with stimulus d_t+1 in trial t+1. Here, the prediction of Y_t+1 is made by the posterior predictive distribution given all previous observations up to the current trial t, or $p(y_{t+1}|y_1,\dots ,y_t)={\displaystyle \int p(y_{t+1}|\theta )p(}\theta |y_1,\dots ,y_t)d\theta$. As such, the quantity measures an expected decrease in entropy (or uncertainty) about the estimated parameter after the next trial.

One-trial-ahead optimization finds the stimulus that maximizes the above metric that represents the improved quality of a posterior distribution that would be achieved immediately after the next trial (e.g., the Psi method by Kontsevich & Tyler, 1999).¹ To go beyond one-trial-ahead optimization, one must consider expected information gain after presenting a sequence of multiple stimuli ahead of the current trial. The expected information gain after k additional trials is expressed as

$$H_t(\mathrm{\Theta })-H_{t+k}(\mathrm{\Theta }|Y_{t+1},\dots ,Y_{t+k},d_{t+1},\dots ,d_{t+k})$$ (3)

where the second term, defined as ${\mathbb{E}}_{Y_{t+1},\dots ,Y_{t+k}|d_{t+1},\dots ,d_{t+k}}[H_{t+k}(\mathrm{\Theta })]$, is the conditional entropy of Θ given a sequence of potential observations $Y_{t+1},\dots ,Y_{t+k}$ ahead made with stimulus choices $d_{t+1},\dots ,d_{t+k}$. Expecting that the measurement session will be finished after k trials, k-trial-ahead optimization prescribes that one should select the stimulus $d_{t+1}^{\ast }$ for the next trial which comes first in the sequence $d_{t+1}^{\ast },\dots ,d_{t+k}^{\ast }$ that maximizes the expected information gain defined above.

As with the shortest-path problem, one can work backward to maximize the expected information gain over multiple trials. Backward induction applies because, at any given state, there is a predetermined rule for computing transition rewards (i.e., expected information gain) and the additivity of local rewards (Equation 2) towards a global reward (Equation 3) holds.² For each of all possible states in the second-to-last trial, or trial t+k−1, the optimal stimulus $d_{t+k}^{\ast }$ for the last trial can be found using one-trial-ahead optimization. Repeat this for all possible states in trial t+k−1 and store the corresponding optimal stimuli and expected information gains in a table. Then, going one trial backward, for each of possible states in trial t+k−2, find the optimal stimulus $d_{t+k-1}^{\ast }$ using the fact that, whatever transition to the next state is made, the maximized expected information gain from that state on can be looked up from the table previously filled. This means that the required computation is no more expensive than one-trial-ahead optimization because the algorithm needs to loop over stimulus choices only for the next trial and choices in the future are already reflected in the results in the look-up table. By repeating this procedure until the current trial t is reached, the optimal stimulus $d_{t+1}^{\ast }$ in trial t+1 can be found.

In fact, the idea of applying DP by means of backward induction to parameter estimation of statistical models was introduced early in statistics (DeGroot, 1962), but actual implementations of the procedure have been limited to shallow look-ahead depths (maximum 4) for simple models. A distinctive computational challenge has been that, unlike the shortest-path or other sequential decision-making problems, the space of possible states (i.e., all possible posterior distributions) is not preset to a manageable size but increases exponentially as observations accumulate over trials. If a low-dimensional sufficient statistic exists to summarize posterior distributions, the state space may be discretized and represented on a grid (Brockwell & Kadane, 2003). However, sufficient statistics do not always exist, and this is the case for threshold estimation.

In overcoming the challenge, the current implementation adopted constrained backward induction (Müller, Berry, Grieve, Smith, & Krams, 2007), in which the state space is approximated by a low-dimensional statistic that can adequately describe posterior distributions. While the basic concept of this approach is solid, it is not in the form of a straightforward recipe, and therefore requires a problem-specific treatment. A key characteristic of the posterior distributions arising from model-based threshold estimation is their highly asymmetric tail thicknesses, especially in early trials. In an effort to find succinct yet adequate representations of these distributions, which are clearly not among standard parametric families (e.g., Gaussian), we created a model formulated by the weighted sum of a Gaussian probability density and a sigmoid function of the form

$$p(\theta |\mu ,\sigma ,\delta ,\eta )=\frac{1}{c}\left[\exp \left(-\frac{{(\theta -\mu )}^2}{2{\sigma }^2}\right)+\delta \frac{1}{1+\exp \left(\eta \frac{\theta -\mu }{\sqrt{3}\sigma /\pi }\right)}\right]$$ (4)

where c is a normalizing constant, and the four parameters μ, σ, δ and η determine the location, dispersion, degree of asymmetry, and direction of asymmetry of the distribution, respectively. To elaborate further, the second term is a cumulative distribution function of a logistic distribution whose mean and variance are matched to those of the Gaussian distribution in the first term (μ and σ²), and its contribution to the distribution’s asymmetric shape is controlled by the parameter δ, a positive value introducing some asymmetry (0 for no asymmetry). The parameter η takes either 1 or −1, making the distribution heavy on the right or left tail, respectively. The space of these parameters was represented on a grid and treated as the state space for backward induction.

As there is no formulaic way to guarantee the adequacy of the approximation, we assessed its performance in three different ways. First, we checked the modeled distributions’ visual fit to actual posterior distributions generated from simulated experiments, in which responses were sampled both randomly and from psychometric functions, and found a close fit in all cases. Second, because backward induction with no approximation (i.e., exact DP) is possible up to three-trial-ahead optimization, it can serve as a benchmark. We therefore compared the accuracy of threshold estimation between two implementations of backward induction with and without approximation. We found identical results beyond a meaningful level of precision. Last, to confirm the adequacy of the grid resolution of the discretized state space, we examined the performance of a series of threshold estimation sessions in which the grid resolution of approximate DP was increased gradually, and found estimation results converge before reaching the resolution set for the study. Refer to the Supplementary Material for further detail about the backward induction and forward evaluation algorithms for threshold estimation.³

Simulation Experiments

Different look-ahead depths for perceptual threshold estimation were evaluated in two conditions. The first, unconstrained, condition assumed a simple, conventional procedure in which any of the preset spectrum of stimuli on the studied physical dimension (e.g., visual contrast, luminance intensity) could be selected in each measurement trial with no restriction on their order of presentation. In the second, order-constrained, condition, dependencies on stimulus choice were imposed across the experiment. Once a stimulus was presented from one of ten equally spaced bins, future stimuli could be chosen only from the same bin or bins lower on the continuum (i.e., weaker stimuli) in subsequent trials.

Creation of the order-constrained condition was motivated by a consideration of the dependencies involved in planning multiple trials ahead in some disciplines, such as clinical trials in drug development or intervention research in medicine─a decision in one stage, for instance, renders continuation of dosage trials, transition to the next test phase, or termination of the whole process. By necessity, these domains have drawn on longer-horizon optimization methods (Berry, 2006; Carlin, Kadane, & Gelfand, 1998; Collins, Murphy, & Strecher, 2007). The requirement on stimulus choice in the order-constrained condition should also create a strong sequential dependency across decision-making trials, possibly accentuating the effect of further-ahead optimization. Our hope was that comparison of this with the unconstrained condition could help determine the principle behind the performance of optimizing beyond the next trial. Although such an order constraint is rarely used when measuring auditory and visual thresholds, its use is commonplace in taste and odor studies (ASTM E679-04, 2011; Tucker & Mattes, 2013).

In the unconstrained and order-constrained conditions, simulated threshold estimation sessions were conducted in which the look-ahead depth of stimulus optimization was manipulated. First, conventional, one-trial-ahead optimization served as a baseline against which algorithms with longer look-ahead distances were compared.⁴ Second, assuming that a measurement session is scheduled to finish in a fixed number of trials, full-horizon optimization was implemented. Using the procedure of k-trial-ahead optimization described earlier, the algorithm starts with the look-ahead depth k made equal to the total number of trials in the experiment (100), and then, over the course of the session, decreases the depth incrementally to match the remaining number of trials. Last, algorithms for intermediate-horizon optimization were included to assess the relationship between horizon depth and any improvement in inference. Given a look-ahead depth k less than the total number of trials, this algorithm starts with k-trial-ahead optimization and maintains it until the number of remaining trials is reduced to k. After that point, the look-ahead depth is decreased incrementally to match the number of remaining trials. Intermediate values of k were 5, 20, and 50.

In all simulations, the data-generating structure was the log-Weibull psychometric function shown in Equation 1. In each measurement session, the true, underlying threshold was sampled from a uniform prior distribution of log intensities ranging from −60 to −0.9 dB. In each trial of a session, an optimal stimulus was determined by the algorithm of the given look-ahead depth from the range of log intensities −66 to −0.2 dB discretized in approximately 0.5 dB steps. Then, a response to it was generated by Bernoulli sampling from the assumed psychometric function value at the optimal stimulus. In each simulation condition, 100,000 independent replications of measurement sessions, each consisting of 100 trials, were made with underlying thresholds drawn from the uniform distribution. We also performed a sensitivity analysis of sampling densities on parameter (threshold of the psychometric function in Equation 1, not of the approximation model in Equation 4) and stimulus spaces, and found that convergence of estimation performance occurs before reaching the densities employed to generate the results presented in this paper.

Results

To examine how efficiently the threshold is estimated over measurement trials, estimation error was quantified by the root mean squared error (RMSE) defined by

$$\text{RMSE}({\widehat{\theta }}_t)=\sqrt{\mathbb{E}\left[{({\widehat{\theta }}_t-{\theta }_{\text{TRUE}})}^2\right]}$$ (5)

where ${\widehat{\theta }}_t$ is the estimate of the threshold for a simulated session, which was obtained as the posterior mean after observing trial t’s outcome, θ_TRUE is the true, underlying threshold for that session. The expectation is assumed to be over all underlying thresholds and replicated sessions, and hence was replaced by the sample mean over 100,000 simulated sessions. Smaller values indicate greater accuracy of threshold estimation.

Figure 2 shows the error in threshold estimation observed under the two constraint conditions (left and right panels) with different optimization depths (curves in each panel). When stimulus selection was unconstrained, no benefit was provided by looking further ahead than one trial. The gray curve in Figure 2a shows the RMSEs (y-axis) over 100 trials (x-axis) incurred by one-trial-ahead optimization. The estimation error drops quickly with observations in the first 20 to 30 trials, but after that, the rate of error reduction slows greatly as more data are collected. If the longer look-ahead horizons in the other conditions improved inference, those curves should be below this one. That just the opposite is found over the majority of trials for all but the 5-trial-ahead condition (i.e., they are above the gray curve) gives the wrong impression that inference was generally worse, except in the last few trials where the curves converged to values close to each other. For proper interpretation of these results, however, it is necessary to understand the goals of these algorithms.

Figure 2.

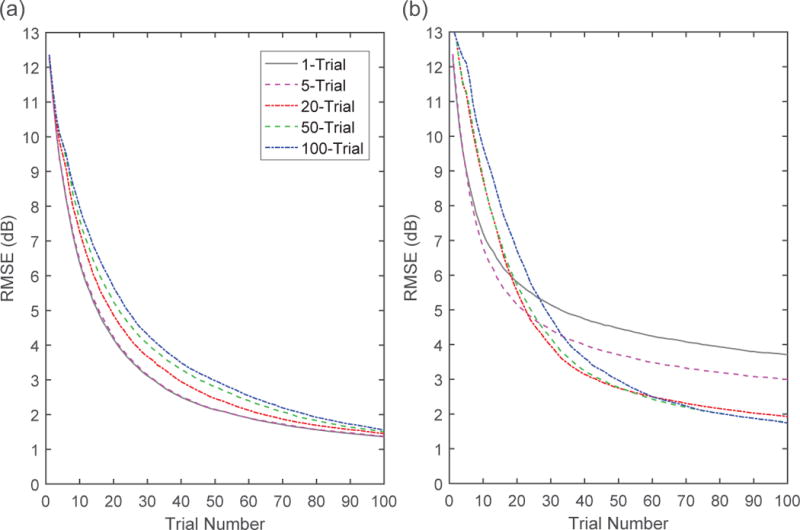
Performance of the five different look-ahead horizons when stimulus choice was unconstrained (a) and order-constrained (b) across trials. Each graph shows threshold estimation error (RMSE) as a function of trial number in the experiment. The depth of the horizon had no effect on final error levels in the unconstrained condition, whereas estimates were reduced by up to 2 dB in the constrained condition when the look-ahead horizon was the length of the experiment (100 trials). Precision bands are not included in the graphs because standard errors of the values are infinitesimal due to the large sample size (100,000). RMSE = root mean squared error.

The reason for the banana-shaped pattern, where the curves diverge in the center but converge at the endpoints, is due to the different goals of the one-trial versus multi-trial-ahead optimization. In DP applications with long look-ahead horizons, a drop in performance during the early stages is not a surprise but a common phenomenon. This is because the algorithm is designed to seek longer-term gains rather than the highest immediate gains. Hence, the performance of farther-ahead optimization must be duly evaluated after many decision stages have passed. In particular, in the case of a finite-horizon problem like the current one (i.e., with a fixed number of decision stages), it must be assessed when the session is close to its end and the longer-term gains are harvested by decreasing the look-ahead depth. This means that even if looking further ahead than one trial were not necessary in the unconstrained condition, or one-trial-ahead optimization were sufficient to achieve the highest possible reduction of error, longer-horizon optimization should exhibit the same level of performance at the end of a session, but not necessarily in the middle of it. Indeed, the gap between their RMSEs and those of the one-trial-ahead algorithm is negligible when the session ends, meaning that looking ahead beyond the next trial offers no benefit.⁵

The reason why this gap is not completely reduced to zero after 100 scheduled trials is due to approximation error in the DP algorithms. Recursive computing over many stages with approximate terms (e.g., approximate states in the current implementation), which is often the nature of DP applications, causes approximation error to propagate continually over the stages, resulting in performance degradation below the theoretically highest level (Gaggero, Gnecco & Sanguineti, 2013). For this reason, using DP with the deepest possible horizon may not automatically improve inference, and this is evident in our application of DP in the unconstrained condition. As can be seen at the last trial in the results graph, error propagation increases as the look-ahead horizon (20, 50, 100 trials) increases. On the other hand, shorter horizons make the algorithms converge to the one-trial-ahead optimization, as shown by the one- and five-trial-ahead algorithms being nearly indistinguishable.

One may wonder whether the efficiency of threshold estimation might be improved if the approximation errors in multi-trial-ahead optimization were eliminated. If there were truly some benefit, it might be exhibited even in two- or three-trial-ahead optimization though the effect could be small. To address this suspicion, we performed the unconstrained, exact form of backward induction (cf., constrained backward induction in Müller et al., 2007) in which no approximation to the state space was made up to depths of three trials. The results were indistinguishable from the one-trial-ahead optimization. In addition, comparisons were also made with the two- and three-trial-ahead algorithms based on approximated states (i.e., current DP implementation). All RMSE curves were on top of one another. The fact that the performance of the currently implemented DP algorithm was identical to that of the exact DP algorithm also served as an independent check of the adequacy of implementation.

The above results demonstrate that, contrary to intuition, looking further ahead in stimulus optimization provides no benefit for threshold estimation in the unconstrained condition, meaning that the commonly used one-trial-ahead optimization is not only sufficient, but optimal. The same conclusion, however, was not drawn when a strong sequential dependency was introduced to stimulus selection. Figure 2b shows the RMSEs of the five different, look-ahead algorithms under the measurement procedure that constrained the order of stimulus presentation, and as can be seen, differences in final error levels are evident. The one-trial-ahead curve drops rapidly for the first 20 trials, but then struggles to decrease thereafter. By contrast, the algorithms that look further ahead start with greater error during the initial 15 trials, trailing behind those algorithms with shorter horizons. Soon after this point (no later than trial 30), the benefits of looking further ahead start to accrue, with the curves of the longer-horizon conditions dipping below the 1-trial condition. These benefits continue to increase across trials for the longer-horizon conditions (20, 50, 100), so that by the end of the experiment, RMSE has been reduced to about 50% (2 dB) of that in the 1-trial condition. There seems to be a limit to the benefit of looking further ahead, as indicated by negligible difference between the 20- and 50-trial-ahead and full-horizon algorithms at the last trial.

Overall, as the look-ahead depth increases, the RMSE reduction is slower initially, but persists longer, resulting in considerably lower error by trial 100. This pay-off in seeking long-term gains by holding back from immediate gains is a clear distinction from what was observed in the unconstrained condition, and comes about by a shift in the stimulus selection strategy. Under the order constraint, selecting stimuli that provide immediate gains without considering the consequences of that decision for stimulus choices in future trials quickly leaves the algorithm with a severely limited range of stimuli to choose from. In contrast, algorithms with greater look-ahead vision avoid falling into this trap by being more conservative in selecting stimuli, with look-ahead depth modulating how conservative the algorithm behaves; the longer the horizon, the more conservative the choice of stimuli. Note that none of these strategies, including the 100-trial, yields a final RMSE as low as that in the unconstrained condition in the left graph (1.74 vs. 1.36 dB). This is because the constraint itself imposes a cost in estimation by restricting stimulus choice.

Discussion

Adaptive methods are used in behavioral experiments to maximize scientific inference with the goal of improving measurement precision and accelerating knowledge acquisition. To date, they have achieved this goal by optimizing inference on the next trial. A lingering question has been whether additional benefit would be gained by optimizing beyond the next trial. Dynamic programming (DP), a tool that can be used for planning into the future, is well suited to this problem because it provides a means of solving the otherwise intractable computation involved in multi-trial-ahead optimization. In short, it is a “smart” means of assessing the quality of each next trial by considering the quality of possible subsequent trials.

A technique that enables one to look into the future when conducting an experiment is truly appealing. However, given the nontriviality of its implementation, one would rightly wonder whether it is really necessary. It is entirely possible that one-trial-ahead, myopic optimization is sufficient for the given problem, or looking further ahead, even far into the future, might offer no appreciable benefit to justify using DP. Because it is generally not possible to know the answer to this question in advance in a laboratory setting, researchers are faced with the dilemma of not knowing which to use unless the two are compared. The present demonstration of the performance of multi-trial-ahead optimization in the unconstrained condition resolves this issue in the domain of perceptual threshold estimation: Looking further ahead than one trial in selecting stimuli has no additional benefit.

Until now, practitioners measuring thresholds in the clinic or laboratory had to acknowledge the unresolved issue surrounding the optimality of their adaptive method (e.g., King-Smith et al., 1994; Kontsevich & Tyler, 1999; Lesmes, Lu, Baek, & Albright, 2010). The present results enable practitioners to be confident that the conventional, one-trial-ahead method is not just sufficient, but optimal as long as there are no sequential dependencies.

Because our main interest in this study was in the effect of look-ahead depth on the performance of adaptive experiments, we made the simplifying assumption that the data-generating process is identical to the theoretical model. The behavior of multi-trial-ahead optimization under a misspecified model will need to be investigated to understand the full consequences when used in empirical settings (e.g., a model of non-stationary adaptation simulates the generating process). Ultimately, considering that all models are approximations, what needs to be decided is whether the benefits obtained by the use of sequentially global optimization overshadow any losses incurred by the use of an approximate model or the approximation error in the method. This will be a domain-specific problem.

Application to Other Contexts

It is reasonable to wonder how well the results would generalize to other model-based experimental settings. As we note above, the methodology does not permit theoretical proofs to answer this question, but insight into when use of DP could be productive can be gained by considering why the current results are produced. Generally, the problem of adaptive estimation of a statistical model is defined as selecting, in each trial of an experiment, a design for the next trial (d_t+1; e.g., the next stimulus to present) that maximizes the employed reward function (e.g., expected information gain after the next trial) given the current knowledge of the model parameter θ (e.g., posterior distribution) as an input. This problem statement, in fact, contains two hidden premises: (a) Given the current knowledge state, the next design is fully determined by maximizing the same reward function on the same domain of possible designs throughout all trials, and is not affected by any other conditions specific to a particular trajectory of data in the previous trials; and (b) once the design d_t+1 is chosen, the model’s prediction of y_t+1 depends only on θ, being independent of design choices and resulting data in the previous trials, or symbolically,

$$p\left(y_{t+1}|\theta ,d_{t+1}\right)=p\left(y_{t+1}|\theta ,d_{t+1},(y_t,d_t),\dots ,(y_1,d_1)\right).$$ (6)

The unconstrained threshold estimation in the current study satisfies both of these conditions but the constrained estimation violates the first one due to the additional decision criterion concerning previous stimulus choices. Current theories of asymptotic optimality (Chaudhuri & Mykland, 1995; Kujala, 2016; Wynn, 1970) are restricted to adaptive estimation problems in which the above conditions are met.⁶

Suspecting that, in the case of unconstrained threshold estimation, what asymptotic theories take as “sufficiently many” trials after which the optimality of one-trial-ahead optimization is in effect may be a very small number, we performed yet another simulation in which full-horizon optimization was applied with the total scheduled trials ranging from 2 to 15. To detect small differences, 500,000 independent sessions with full-horizon or one-trial-ahead optimization were run for each session length (2 to 15). The results confirmed our suspicion. We found that the full-horizon method has an infinitesimal edge over the one-trial-ahead optimization, but only up to a session length of 9. The RMSE differences in dB units (one-trial-ahead minus full-horizon; estimated standard error of the difference in parentheses) for session lengths 5 to 9 were 0.0926 (0.0176), 0.0671 (0.0172), 0.0624 (0.0166), 0.0816 (0.0160), and 0.0186 (0.0153), respectively. Despite small effects, it is unlikely that we obtained this sequence of outcomes by chance since they are, by design, independent of each other. Beyond the length of 9, however, whether due to the convergence of the two methods or the approximation error in DP, full-horizon optimization did not outperform one-trial-ahead optimization.

These results with very short yet full look-ahead horizons contribute to our understanding of the optimality of one-trial-ahead optimization in two ways. First, the advantage of multiple-trial-ahead optimization with finite horizons does exist and can be demonstrated with the help of DP, the specifics of which cannot be predicted by asymptotic theories. Second, although the benefit exists, in the case of unconstrained threshold estimation, it is a negligible amount and quickly overshadowed by one-trial-ahead optimization after a small number of trials. These additional data combined with our main findings prompt us to conjecture that if the experimental environment is similar to unconstrained threshold estimation, looking further than one trial in adaptive estimation would provide no appreciable benefit. This will be the case for many modeling problems in cognitive science, as they are mechanically similar to the situation studied here. For example, models of attention, categorization, and decision making usually have a simple parametric form and involve a small number of parameters. The dimensionality of the experimental design in which the models are evaluated is relatively low, and the sampling error in data can be high, requiring a large number of trials to achieve adequate precision of inference. Interestingly, this includes the item response theory (IRT) models assumed in computerized adaptive testing (CAT). While backward induction has been applied to the problem of pass-fail CAT or adaptive mastery testing with states approximated by number-correct scores (Lewis & Sheenan, 1990; Vos & Glas, 2010), multistage-ahead optimization of item-level CAT for ability parameter inference has not been investigated due to computational intractability.

In contrast to the unconstrained condition, the order-constrained condition involves making stimulus selections that are governed by choices of preceding stimuli, preventing the selection from being based solely on the expected information gain criterion. Any candidate stimulus outside the constraint will force expected information gain to be zero, overriding the actual value that would be used if there were no such constraint. With the constraint in place, there exists a bad choice of a stimulus, the quality of which cannot be seen under one-trial-ahead optimization, but can cause an adverse effect on estimation in the long run because it severely restricts the range of stimulus choices later on.⁷

The application of DP under sequential dependency is not limited to an order constraint on stimuli, but can apply to settings in which the dependency of participant responses across trials itself is the subject of study and built into the models. Examples of models that should benefit from DP include models of learning and dynamic decision making. Processing models in these areas are usually first-order Markovian models in which a participant’s latent state keeps being updated with each new observation and the model’s prediction depends on the most recent state (Busemeyer & Pleskac, 2009; Busemeyer & Stout, 2002; Chechile & Sloboda, 2014; Falmagne, 1993; Fries, 1997). These models, by construction, require not only the knowledge of model parameters but also the design choices and participant responses in preceding trials in order to give the predicted probability of data in the next trial (i.e., they violate the condition in Equation 6). To estimate the parameters of these models, it would be advantageous to look far ahead in optimizing the designs sequentially.

In summary, the current study demonstrates a multi-step-ahead adaptive method in action, the results of which are not predicted by an asymptotic theory alone, in a problem domain of considerable significance (psychometric function estimation). The results suggest that when there are dependencies of a certain form between trials, efficiency and precision in experimentation can be improved by looking beyond the next trial to identify the next optimal stimulus to present.