Abstract
Large-conductance Ca2+-dependent K+ (BKCa) channels are important regulators of electrical activity. These channels colocalize and form ion channel complexes with voltage-dependent Ca2+ (CaV) channels. Recent stochastic simulations of the BKCa-CaV complex with 1:1 stoichiometry have given important insight into the local control of BKCa channels by fluctuating nanodomains of Ca2+. However, such Monte Carlo simulations are computationally expensive, and are therefore not suitable for large-scale simulations of cellular electrical activity. In this work we extend the stochastic model to more realistic BKCa-CaV complexes with 1:n stoichiometry, and analyze the single-complex model with Markov chain theory. From the description of a single BKCa-CaV complex, using arguments based on timescale analysis, we derive a concise model of whole-cell BKCa currents, which can readily be analyzed and inserted into models of cellular electrical activity. We illustrate the usefulness of our results by inserting our BKCa description into previously published whole-cell models, and perform simulations of electrical activity in various cell types, which show that BKCa-CaV stoichiometry can affect whole-cell behavior substantially. Our work provides a simple formulation for the whole-cell BKCa current that respects local interactions in BKCa-CaV complexes, and indicates how local-global coupling of ion channels may affect cell behavior.
Introduction
Mathematical modeling has played an important role in investigations of cellular electrophysiology at least since the works on neuronal action-potential generation by Hodgkin and Huxley (1). In the Hodgkin-Huxley model and most of its descendants, the system of ion channels is coupled globally via the membrane potential or the bulk cytosolic Ca2+ concentration. However, some ion channels are colocalized, implying that the activity of one channel may affect the other via local control. Electrical activity is thus a result of the complex interactions of local and global coupling of ion channels. Of note, the standard Hodgkin-Huxley formulation does not take into account local coupling of channels.
Large-conductance Ca2+- and voltage-dependent K+ (BKCa, KCa1.1) channels, ubiquitously found in excitable cells where they shape electrical activity (2), provide an example of such ion channels, whose activity is influenced locally by associated voltage-gated Ca2+ channels (CaVs). BKCa channels have a single-channel conductance of ∼100 pS in physiological conditions (3), and are activated by Ca2+ and transmembrane voltage, which is seen as a Ca2+-dependent left-shift of the BKCa activation curve (4, 5, 6). In neurons (7, 8, 9, 10) and vascular myocytes (11), BKCa channels colocalize with CaVs, which exposes the BKCa channels to the Ca2+ nanodomains below the mouth of the CaV channels (12, 13, 14, 15), where the local Ca2+ concentration reaches the tens of micromolar that are required for activating the BKCa channels at physiological voltages (2, 16). There is increasing evidence for a direct coupling between BKCa and CaV channels, forming BKCa-CaV ion channel complexes with a stoichiometry of 1–4 CaV channels per BKCa channel (2, 11), and differences in stoichiometry likely affect channel activity. Intuitively, we expect that more CaVs per complex would augment the BKCa open probability, both because of higher local Ca2+ concentration when the CaVs open simultaneously, and because of greater probability that at least one of the CaVs is open at any given time.
Recently, Cox (17) presented a Markov chain model for a BKCa-CaV complex with 1:1 stoichiometry, and performed Monte Carlo simulations that provided important insight into the open probability of BKCa channels during depolarizations and action potentials, and how e.g., inactivation of CaVs directly influence BKCa channel activity. Such Monte Carlo simulations are computationally intensive and explicit mathematical relations between assumptions and consequences are not available. Monte Carlo simulations have also been performed for whole-cell simulations of electrical activity to investigate the effects of stochastic ion channel kinetics, for example for Ca2+-sensitive SK and BKCa channels controlled by local Ca2+ dynamics (18, 19). When stochasticity is not of interest, to speed up simulations, many models of whole-cell electrical activity that include BKCa channels express this current in a simplified way that neglects local effects due to the BKCa-CaV complexes (20, 21) or use heuristic expressions involving the whole-cell Ca2+ currents (22, 23), which may not respect the dynamics within BKCa-CaV complexes. Alternatively, diffusion of Ca2+ around a CaV (or a cluster of synchronized CaVs) has been simulated to investigate, e.g., how BK channels inherit properties of the CaVs, and how distance between channels influence BKCa activity (10). Another frequent approach (which, however, neglects local interactions) is to model Ca2+ dynamics in one or more shells beneath the cell membrane, which then drives BKCa channels (24, 25, 26). The computational intensity is increased in such a model because local Ca2+ concentrations resulting from buffering and diffusion must be simulated in addition to ion channel gating.
It would therefore be advantageous to have a simple but mechanistically correct model of the BKCa current, which respects the local effects of BKCa-CaV coupling, and that can be inserted in Hodgkin-Huxley-type models of whole-cell electrical activity. Such a model would also make explicit how local effects and stochastic ion channel kinetics are reflected in average, whole-cell behavior of BKCa channels with the advantage compared to simulations that the dependence on parameters can be read directly from the formulas of the reduced model. Here we achieve both these aims. Our approach is similar to analyses of Ca2+-dependent inactivation of Ca2+ channels (27), and local control of ryanodine receptors in dyadic subspaces (28, 29). Importantly, in the nanodomains controlling BKCa activity, Ca2+ is fast enough to avoid the need for, e.g., a probability-density approach for handling local Ca2+ dynamics correctly at the whole-cell level (30). We use the mechanistically correct description of single BKCa-CaV complexes with 1:1 stoichiometry developed by Cox (17) as the natural starting point for constructing a reduced model for BKCa-CaV complexes with 1:n stoichiometry to be inserted into a whole-cell model of electrical activity. Our results give insight into the simulations of single BKCa-CaV complexes, and clarify that it is the local effects of ion channel kinetics rather than stochasticity per se that determine whole-cell activity.
Materials and Methods
BKCa channel model
We describe the BKCa channel with a model of single-channel gating with two states (closed and open). Fig. S1 A shows a schematic representation of the model, where X corresponds to the closed state and Y to the open state. The mathematical description of BKCa voltage- and calcium-dependent activation is given by the following:
| (1) |
where pY represents the open probability for the BKCa channel, and k− and k+ are the voltage- and calcium-dependent rate constants. As shown in the Supporting Material, from relatively mild assumptions and experimental evidence, we can express these rates as the following:
| (2) |
| (3) |
where Ca denotes the Ca2+ concentration at the BKCa channels. At fixed Ca2+ levels, BKCa activation is well described by Boltzmann functions (6, 8, 16). Hence, we assume that the voltage-dependent rate constants, w−, for the transition from the open to closed state, and w+, for the transition from the closed to open state, have the following standard forms:
| (4) |
| (5) |
where the parameters w−0 and w+0 are voltage-independent.
There is evidence that at fixed V, Ca2+ stabilizes the open state (4), i.e., f− should decrease with Ca, and that >1 Ca2+ ion is needed for BKCa activation, which is a sigmoidal function of the Ca2+ concentration (4, 16). The calcium-dependent relations are therefore modeled by the following:
| (6) |
| (7) |
where Kyx and Kxy are the calcium affinities when the channel closes and opens, respectively, and nyx and nxy are the corresponding Hill coefficients. By using the relationships in (4), (5), (6), (7), we get the following formulas for the equilibrium open fraction of BKCa channel activation, , and the corresponding time constant :
| (8) |
| (9) |
where
| (10) |
| (11) |
We use global optimization to estimate the model parameters providing the best fit to the experimental data (17), consisting of BKCa open probabilities and time constants as functions of voltage, at different Ca2+ concentrations. In particular, we formulate an optimization problem to minimize the sum of the squared errors between the simulated responses produced by the model and the corresponding experimental data as follows:
| (12) |
where θ is the set of model parameters, and and are the experimental BKCa steady-state open fraction and corresponding time constants, respectively, at the given voltage Vi for the jth experiment (corresponding to a given Ca2+ concentration). and are the simulated equilibrium open fraction of the BKCa channel and the corresponding time constants of the model, respectively, at the given Vi for the jth experiment. For the optimization, we use a hybrid genetic algorithm (GA) (31) that combines the most well-known type of evolutionary algorithm with a local gradient-based algorithm (32). We use the function “ga” from the software MATLAB (The MathWorks, Natick, MA) Global Optimization Toolbox and fmincon from the MATLAB Optimization Toolbox as the local algorithm. We repeat the hybrid GA algorithm several times and select the parameter set that gives the best fitting. Table S1 reports the optimal model parameters, and Fig. S1, B–G shows the fits to the data.
CaV channel model
We describe the calcium channel dynamics with the following model (27):
| (13) |
| (14) |
| (15) |
where c corresponds to the closed state, o to the open state, and b to the inactivated (blocked) state of the calcium channel; h represents the fraction of Ca2+channels not inactivated, δ is the rate for channel inactivation, and γ is the reverse reactivation rate; and α and β represent the voltage-dependent Ca2+ channel opening rate and closing rate, respectively, and have the following forms:
| (16) |
| (17) |
As shown in Sherman et al. (27), the processes of activation and inactivation can be approximately separated in time, because activation is much faster than inactivation. In particular, we achieve the following model for the activation variable, mCaV,
| (18) |
where
| (19) |
and the following equation for inactivation:
| (20) |
As for the BKCa channel, we use a global optimization method to optimize the parameters of (16), (17) to fit the experimental data presented by Cox (17), i.e., peak open probabilities and time constants as functions of voltage. For the values of γ = 0.0020 ms−1 and δ = 0.0025 μM−1 ms−1 ×[CaCaV], we use those reported by Cox (17). CaCaV is the Ca2+ concentration at the internal mouth of the channel and defined by Eq. S1 with r = 7 nm, representing the distance of the sensor for Ca2+-dependent inactivation from the channel pore. Note that the relation given by Eq. 17 allows scaling of the amount of channel activation at high voltage values according to the experiments (i.e., not all the calcium channels are open even for high voltages). Table S1 reports the optimal parameters for the CaV activation model.
BKCa-CaV complex with 1:1 and 1:n stoichiometries
Combining the models for BKCa and CaV channels, we obtain the models of the 1:1 (see Results and Supporting Material, Model of the 1:1 BKCa-CaV Complex and Timescale Analysis and Model Simplifications) and 1:n BKCa-CaV complexes (see Results and Supporting Material, Model for BKCa Activation in Complexes with k Noninactivated CaVs and its Approximation). Ca2+ levels sensed by the BKCa channel were assumed to reach steady state immediately after CaV opening or closure (17), and the steady-state Ca2+ concentration Cao resulting from influx through a single CaV was calculated by an explicit formula (see Eq. S1), assuming that CaV and BKCa channels are r = 13 nm apart (2, 9). At V = 0 mV, Cao ≈ 19 μM (see Supporting Material, Model of the 1:1 BKCa-CaV Complex and Table S2 for further details). In the case of more than one CaV per complex, the linear buffer approximation (33) was used to summarize Ca2+ levels when more than one CaV is open. We note that k+c ≈ 0 (see Supporting Material, Model of the 1:1 BKCa-CaV Complex and Table S1) because the background Ca2+ concentration Cac is much below the levels needed for BKCa activation at physiological voltages (2). Thus, a BKCa channel opens only when a CaV in the complex is open. This approximation is used widely in our derivations, and is supported by the fact that Ca2+ influx via CaVs is needed to open BKCa channels (34), and that the submembrane Ca2+ concentration of some hundreds of nanomolar that a BKCa in a complex without open CaVs would sense, is too low to activate BKCa channels at physiological voltages (2, 17).
We refer to the Supporting Material for details on mathematical analysis of the time to first BKCa channel opening using phase-type distributions (35) (see Supporting Material, Model of the 1:1 BKCa-CaV Complex), and timescale analysis used for model reduction borrowing ideas from enzyme kinetics (36) (see Supporting Material, Timescale Analysis and Model Simplifications and Model for BKCa Activation in Complexes with k Noninactivated CaVs and its Approximation), as well as for details on the whole-cell models investigated (see Supporting Material, Whole-Cell Models).
Availability of models and computer code
MATLAB code containing the files for generating the results presented in the main text and Supporting Material is provided as an additional Supporting File S1.
Results
A simple Markov chain model of the BKCa-CaV complex
Cox (17) presented a stochastic model of a single CaV2.1 (P/Q-type) controlling a BKCa channel (α-subunits only) via local Ca2+. The channels were located 13 nm apart, corresponding to physical coupling (2, 9). The CaV was described by a seven-state Markov chain, and when the Ca2+ channel opened or closed, the local Ca2+ level was assumed to reach equilibrium instantaneously, in accordance with simulations of Ca2+ diffusion (12, 13, 17). The calculated local Ca2+ concentration was then assumed to drive a 10-state Markov chain model of the BKCa channel, and Monte Carlo simulations were performed.
We set out to simplify the description of the 7 × 10-state Markov chain model of the BKCa-CaV complex. This was achieved by assuming a three-state model for CaV (27) with states closed (C), open (O), or inactivated (B, for blocked) (see Materials and Methods). Parameters were adjusted to reproduce traces from Cox (17). The BKCa channel was represented by a model with only two states, closed (X) or open (Y) (see Materials and Methods). The transitions between states were supposed to depend on voltage and local Ca2+, which was assumed to reach equilibrium instantaneously, and depend on voltage via the single-channel Ca2+current (17). Parameters describing BKCa kinetics were fitted to data from Cox (17). Combining these two models, we obtain a six-state model of the BKCa-CaV complex (Fig. 1 A) that shows behavior similar to the 70-state model used by Cox (17) (Fig. 1, B and C). Our simplified BKCa model does not describe details of single-channel kinetics, which is not our scope here, but reproduces satisfactorily activation curves and times (Fig. S1), as well as whole-cell currents (Figs. S4 and S5), thus making it appropriate for analysis of whole-cell BKCa activity.
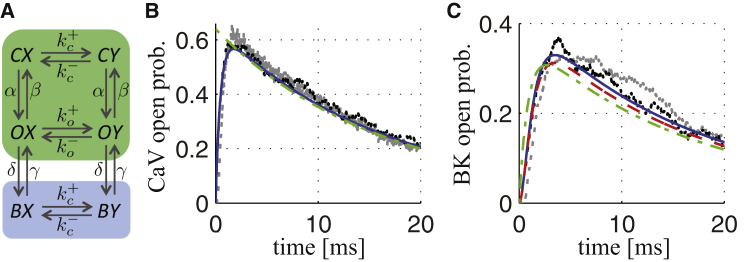
Figure 1.
Six-state model of the BKCa-CaV complex with 1:1 stoichiometry and its simplification. (A) Shown here is a scheme indicating the six states and voltage-dependent transitions. C, O, and B refer respectively to closed, open, and inactivated states of the CaV, whereas X and Y indicate the closed and open states of the BKCa channel. The subscripts o and c on the horizontal transition rates indicate dependence on the Ca2+ concentration below an open (respectively, closed) Ca2+ channel. At physiological voltages, the transition to a state with an open BKCa channel occurs virtually only when the CaV is open (k+c ≈ 0). The green box indicates states with noninactivated CaVs, whereas the blue box highlights states with inactivated CaVs. The transitions between the colored boxes are slow compared to transitions within boxes. (B) Shown here are simulated CaV open probabilities in response to a voltage step from −80 to 0 mV, obtained from the seven-state Markov chain model (gray; (17)), the three-state Markov chain model C, O, B (black; (27)), the ODE model corresponding to the three-state model ((13), (14), (15); blue), and the corresponding model assuming instantaneous activation mCaV = mCaV,∞ (Eq. 20; dash-dotted green). (C) Shown here are simulated open probabilities, in response to a voltage step from −80 to 0 mV, for BKCa channels controlled by CaVs in complexes with 1:1 stoichiometry, obtained from the original 70-state Markov chain model (gray; (17)), the six-state Markov chain model (A; black), the ODE model corresponding to the six-state model (Eqs. S6–S11; blue), the simplified Hodgkin-Huxley-type model (Eq. 25; dashed red), and the corresponding model assuming instantaneous activation mCaV = mCaV,∞ (dash-dotted green; see main text). In (B) and (C), one-thousand realizations were simulated for the Markov chain models, and the average of these Monte Carlo simulations is shown. To see this figure in color, go online.
Time to first opening
Interestingly, Cox (17) found that not all simulated BKCa channels open during 20 ms depolarizations or imposed action potentials. We now study the time to the first opening of the BKCa channel during a depolarization, which mathematically corresponds to the first time the Markov chain Z corresponding to Fig. 1 A visits one of the states CY, OY, or BY starting from state CX. We denote the time to first opening TCX,Y, which is a random variable. Simulations show that eventually all BKCa channels open, and that the probability of channel opening before a given time t, P(TCX,Y < t), shows biphasic behavior (Fig. S2). Taking advantage of the fact that transitions from CX to CY, and from BX to BY have virtually zero probability (BKCa channels open only if the CaV is open), we obtain explicit formulas for the average time to first opening E(TCX,Y) and, more generally, for the distribution function P(TCX,Y < t) using phase-type distribution results for Markov chains (35) (see Supporting Material, Time to First Opening and Phase-Type Distributions), as follows:
| (21) |
| (22) |
where is the subtransition rate matrix of Z corresponding to states {CX, OX, BX}. Thus, the average time to first opening is inversely related to the opening rates of the CaV and BKCa, and to the rate of reactivation after inactivation of the CaV. The involvement of these two processes explains the biphasic behavior, because escape from inactivation is much slower than channel opening. Eq. 22 states that P(TCX,Y < t) is 1 minus the probability of not having left {CX, OX, BX} before t, and makes it explicit that ∼15% of BKCa channels do not open during a 20 ms depolarization (17), because P(TCX,Y < 20 ms) ≈ 85% with our parameters (Fig. S2).
A concise deterministic model of cellular BKCa activity derived from multiscale principles
1:1 stoichiometry
For Hodgkin-Huxley-type whole-cell simulations, we do not need to know the state of each single BKCa channel, but it suffices to follow the BKCa open probability pY over time, because in the presence of many channels the whole-cell BKCa current is IBK = gBK pY(V − VK), where gBK is the maximal whole-cell BKCa conductance and VK is the K+ reversal potential.
The time evolution of the probability distribution of the Markov chain Z corresponding to the six-state model in Fig. 1 A can be described by a system of five ordinary differential equations (ODEs) because the probabilities sum to 1. Denote, for ψ ∈ {C, O, B} and ξ ∈ {X, Y}, the state probabilities pψξ(t) = P(Z(t) = ψξ). Then pY(t) = pCY(t) + pOY(t) + pBY(t). As shown in Fig. 1 C, the average fraction of open channels calculated from Monte Carlo simulations of the Markov chain is well approximated by pY obtained from the ODE system.
Although the reduction to five ODEs for the description of the BKCa-CaV complexes is already a substantial reduction compared to Monte Carlo simulations, we wish to obtain an expression for the BKCa current of Hodgkin-Huxley form. Such a simplification provides further insight into the regulation of BKCa activity by CaVs, and provides the base for concise handling of BKCa-CaV complexes with 1:n stoichiometry.
We performed detailed timescale analysis (see Supporting Material, Timescale Analysis and Model Simplifications) based on the fact that re- and inactivation of CaVs are slower than (de-)activation. Thus, on a fast timescale, the average fraction of noninactivated CaVs, h = 1 –(pBX + pBY), is assumed to be constant, and the model splits into two submodels with, respectively, four and two states (Fig. 1 A, green and blue).
In the system of ODEs describing the state probabilities of the corresponding reduced four-state Markov chain (Fig. 1 A, green), it turns out that the dynamics of state CY is the fastest because CaV kinetics and BKCa-channel closure, when the CaV is closed, are faster reactions than BKCa gating in the presence of an open CaV (see Fig. S3). Assuming quasi-steady state for CY, we derive a single ODE describing the gating variable mBK, which models the fraction of open BKCa channels in complexes with noninactivated CaV (see Supporting Material, Model Simplifications), as follows:
| (23) |
with steady state and time constant given by the following:
| (24) |
Here, mCaV is defined by Eq. 18 and denotes the activation variable for the CaV in the complex, which is routinely characterized in patch-clamp experiments and included in models of electrical activity via the time-constant, τCaV, and the steady-state activation function, mCaV,∞ (see Eq. 19). From these quantities, α = mCaV,∞/τCaV and β = 1/τCaV − α can be calculated. Note that Eq. 24 makes it explicit how mBK,∞ inherits properties of the associated Ca2+ channel type, as has been found experimentally (10, 37).
Now, because BKCa channels close rapidly in complexes with inactivated CaVs (blue in Fig. 1 A), we have pY ≈ mBKh. Thus, the BKCa current is approximated by the standard Hodgkin-Huxley expression
| (25) |
where mBK is given by Eq. 23, and h is the inactivation function of the CaVs (see (15), (20)). As shown in Fig. 1 C, the open-probability expression mBKh approximates the Monte Carlo simulations very well. From Eq. 25 it is evident that the BKCa channels in BKCa-CaV complexes exhibit inactivation because of inactivation of the associated CaVs, and with approximately identical dynamics, as found in experiments (8) and Monte Carlo simulations (Fig. 1; (17)).
In many whole-cell models (e.g., (20, 21, 22, 23)), the Ca2+ currents are assumed to activate instantaneously, which precludes calculation of α and β. Implicitly, such models assume that CaV gating is infinitely faster than the kinetics of other channels in the model. In our setting, this assumption corresponds to investigating the BKCa-CaV model defined by (23), (24), (25) in the limit α, β → ∞. This leads to and , which are completely defined from BKCa kinetics and mCaV,∞. In combination with (23), (25), this model approximates the full system decently, except for the initial phase before CaV activation reaches equilibrium (Fig. 1 C, green). For whole-cell models neglecting CaV activation kinetics, this initial-phase error should be of no more concern that the error in the Ca2+ current resulting from the steady-state assumption for CaV activation (Fig. 1 B, green).
Complexes with multiple Ca2+ channels
As mentioned, a BKCa channel can bind up to four CaVs (2, 11). We extend our model to incorporate such cases, assuming that the n CaVs are all located 13 nm from the BKCa channel (2, 9, 17). Near the CaVs, the linear buffer approximation (33) holds, and the Ca2+ profile from n channels can be calculated by superimposing n nanodomains found for single, isolated CaVs.
One could in principle extend the Markov chain model in Fig. 1 A to a model with 3 × n × 2 states. We take another approach to keep the model tractable. As discussed in the previous section, CaV inactivation is slow compared to other processes. We therefore assume that on a fast timescale, the fraction h of noninactivated CaVs is constant, and note that the BKCa channel closes rapidly when all CaVs in the complex are inactivated.
Consider a BKCa-CaV complex with k ∈ {1,..., n} noninactivated CaVs. Neglecting inactivated CaVs, because they do not contribute to BKCa activation, such a complex can be described on the fast timescale by a Markov chain model with 2 × (k + 1) states (Fig. 2 A). As for the case of 1:1 stoichiometry, we can approximate the dynamics of the BKCa open probability by a single ODE (see Supporting Material, Model for BKCa Activation in Complexes with k Noninactivated CaVs and its Approximation). Denote this open probability by , and note that in Eq. 23. Then, we have the following:
| (26) |
where and are explicit functions of V, directly or via the local Ca2+ concentration (see Eq. S36). The probability that k noninactivated CaVs are present in a complex with n CaVs is , and the whole-cell BKCa current, is approximated by the following:
| (27) |
which involves n ODEs (Eq. 26) for the activations variables , and one ODE for h (h = 1 – b, where b is given by Eq. 20). As shown in Fig. 2 C, this expression provides a good approximation to the results from Monte Carlo simulations of the full Markov Chain. Note that if the CaVs do not inactivate, Eq. 27 reduces to the following:
| (28) |
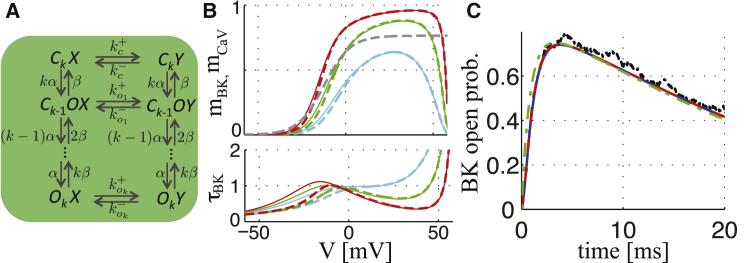
Figure 2.
Multiple CaVs per BKCa-CaV complex. (A) Shown here is the Markov chain model for complexes with k noninactivated CaVs. (B) Shown here are steady-state BKCa activation functions (upper) and time constants (lower) for BKCa channels in complexes with 1 (cyan), 2 (green), or 4 (red) CaVs given from Eq. 26 (see Eq. S36 for the details; solid) or from the approximation defined by Eq. 29 (dashed). The gray dashed curve shows the CaV activation function mCaV,∞, for comparison. (C) Shown here are simulated BKCa open probabilities in response to a voltage step from −80 to 0 mV, obtained from Monte Carlo simulations of the Markov model of n inactivating independent CaVs controlling a BKCa channel (black), from the ODE model of all states in (A) coupled to CaV inactivation (Eq. 27; Eqs. S19–S25; solid blue), from the reduced ODE model considering CaV activation kinetics ((26), (27); dashed red), and from the simplification assuming mCaV = mCaV,∞ ((29), (27); dash-dotted green). To see this figure in color, go online.
We can now easily investigate how different stoichiometries of the BKCa-CaV complexes influence, e.g., activation of the BKCa channels. As expected, we find that the activation curve is shifted upwards as the number of CaVs per complex increase (Fig. 2 B, upper). Interestingly, a left shift of the activation curve is seen when n increases. For example, with n = 4 CaVs per BKCa channel, BKCa activation is half-maximal at V ≈ −14 mV, compared to V ≈ −5 mV when n = 1, and half-maximal CaV activation at V ≈ −12 mV. This result is due to the fact that the probability of at least one CaV being open is greater with more channels in the complex. For higher voltages, the single channel current decreases and the CaV open probability increases, with the result that, at strongly positive voltages, BKCa activation decays more gradually at n = 1 than for higher n. This difference is because the local Ca2+ level obtained with a single open CaV is insufficient for complete BKCa activation, and therefore the presence of more CaVs per complex becomes advantageous, because the CaVs may open simultaneously, leading to higher local Ca2+ levels. This interpretation also underlies the finding that BKCa activation is faster with higher n at positive voltages (Fig. 2 B, lower).
As mentioned above, many whole-cell models assume instantaneous activation of CaVs. This assumption implies that vertical transitions in Fig. 2 A are in quasi-equilibrium, and hence that, e.g., , with notation as for the case of 1:1 stoichiometry. Then, follows Eq. 26 with
| (29) |
This simplified expression provides decent fits to activation functions (Fig. 2 B, upper) and simulated currents (Fig. 2 C), and—in our experience—yields reliable results in whole-cell simulations for cells with relatively slow action potential dynamics, as shown below, despite a slight underestimation of at negative voltages (Fig. 2 B, lower).
Whole-cell simulations of electrical activity shaped by BKCa-CaV complexes
We now illustrate the type of whole-cell modeling that can be performed readily with our Hodgkin-Huxley-type model of the BKCa current controlled locally by CaVs in BKCa-CaV complexes.
BKCa-CaV stoichiometry controls fAHP in a neuronal model
It is well established that in many neurons, BKCa channels play an important role in action potential (AP) repolarization and fast after-hyperpolarization (fAHP), i.e., the undershoot seen after an AP (2, 38), which is important, e.g., for controlling firing frequency and transmitter release. We here adapt a model of AP generation and fAHP in hypothalamic neurosecretory cells (20) to investigate how BKCa-CaV complexes influence fAHP. In the original model, CaVs are assumed not to inactivate, and to activate instantaneously. We modified the model to include CaV activation dynamics with time constant τCaV = 1.25 ms (37, 39), and inserted our whole-cell BKCa model (Eq. 28) in place of the original representation of BKCa currents.
Our results suggest that more than one CaV channel is needed in the BKCa-CaV complex to develop fAHP that is reduced by BKCa-channel blockers (Fig. 3 A). The difference between 1:1 and 1:n BKCa-CaV stoichiometry is not a simple result of more BKCa conductance. Increasing the BKCa conductance fourfold in the case of 1:1 stoichiometry, much more than the difference between the activation functions and (Fig. 2 B), leads to less fAHP than for 1:4 stoichiometry (Fig. 3 A, inset). Thus, differences in BKCa activation kinetics and the shapes of activation functions (Fig. 2 B) play a nontrivial role in shaping APs.
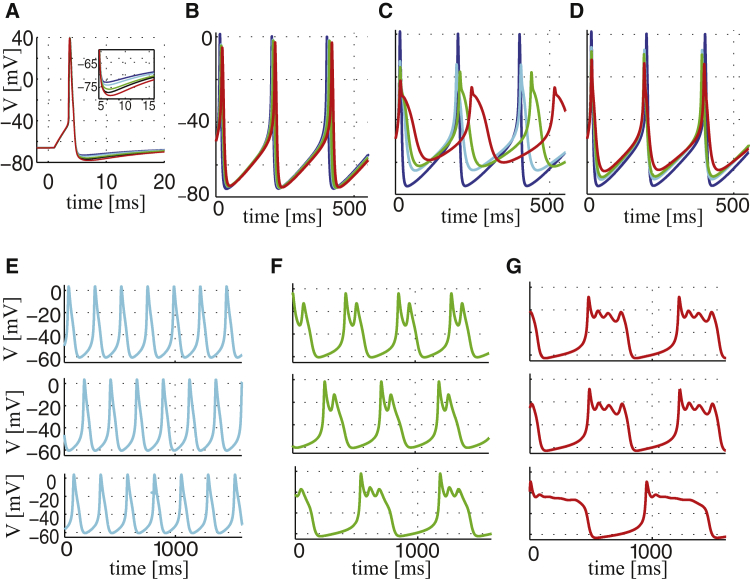
Figure 3.
Whole-cell simulations. (A) Shown here is a simulated AP in a neuronal model (20) with 1:n stoichiometry BKCa-CaV complexes with n = 1 (cyan), n = 2 (green), or n = 4 (red). The whole-cell BKCa current is described by Eq. 28 (i.e., BKCa coupled with noninactivating CaVs), where the BKCa activation, , is modeled by Eq. 26 (see Eq. S36 for the details) and gBK = 1 mS cm−2. The blue curve shows the case of BKCa block (gBK = 0 mS cm−2), and the trace in black displays the result with n = 1, gBK = 4 mS cm−2. The inset shows a zoom-in on the fAHP. (B–D) Shown here are simulated APs in a model of human β-cells (22) with BKCa channels located in complexes with n T-type (B), L-type (C), or P/Q-type (D) CaVs, with n = 1, 2, or 4. The whole-cell BKCa current is described by Eq. 27 (with inactivating T- and L-type CaVs) or Eq. 28 (with noninactivating P/Q-type CaVs), where is modeled by Eq. 29. Color coding as in (A). (E–G) Shown here is simulated activity in a model of lactotrophs (21) with 1:n BKCa-CaV complexes with n = 1 (E), n = 2 (F), or n = 4 (G). The whole-cell BKCa current is described by Eq. 28, where is modeled by the complete BKCa model with 2 × (n + 1) states (Fig. 2A) described using Eqs. S19–S25 (upper traces), by Eq. 26 (middle traces), and by Eq. 29 (lower traces). To see this figure in color, go online.
Different CaV types affect electrical activity differently in a model of human β-cell electrophysiology
In our recent model of electrical activity in human β-cells (22, 23), we modeled the BKCa-current heuristically. The BKCa open probability was proportional to the whole-cell Ca2+ current, and this expression was found to reasonably reproduce published data (40) regarding the BKCa activation function and the effects of BKCa block on AP firing (22).
We now assume that the BKCa channels form complexes with either T-, L-, or P/Q-type CaVs (22, 40), and vary the BKCa-CaV stoichiometry. As explained in greater detail in the Supporting Material, the different types of CaV differ with respect to activation and inactivation properties, and whole-cell conductance (22, 23). The resulting BKCa model is then fit to experimental I-V data (40) (Fig. S7), and inserted in the whole-cell model. T-type CaVs inactivate rapidly (22, 40), and do not activate much BKCa current during the relatively broad action potentials. For this reason, simulated BKCa block results in almost no increase in AP height (Fig. 3 B), in contrast to experiments (40).
In human β-cells, L-type Ca2+ channels show inactivation on a timescale comparable to the duration of an AP (22, 40). When coupled to BKCa channels in the model, good fits to the BKCa I-V activation curve are obtained, but for different values of the maximal whole-cell BKCa conductance gBK (Fig. S7). In simulations of electrical activity, BKCa currents controlled by L-type CaVs reduce AP height, independently of the number of CaVs per complex (Fig. 3 C).
BKCa-CaV complexes with P/Q-type Ca2+ channels, which activate at very depolarized potentials and show very slow inactivation in human β-cells (22, 40), lead to BKCa currents that activate at slightly more depolarized potentials than in experiments, except for the case of 1:4 BKCa-CaV stoichiometry (Fig. S7). Simulated application of a BKCa channel antagonist increases AP height ∼15 mV, in good correspondence with experiments. Assuming fewer CaVs per complex, leads to poorer fit of the I-V curve and to less difference between APs obtained with operating and blocked BKCa channels (Fig. 3 D).
We conclude that AP firing is affected differently by BKCa currents depending on the CaV type controlling BKCa activity, due to differences in activation and inactivation properties. Because BKCa block stimulates insulin secretion in human (40) and mouse (41) β-cells, a better understanding of the interaction between different types of CaVs and BKCa channels may provide novel insight into insulin release in health and disease.
Bursting behavior depends on BKCa-CaV stoichiometry in a model of pituitary cells
In pituitary cells, BKCa channels have been found to be intimately involved in the genesis of so-called plateau bursting, which consists of a few small oscillations riding on a depolarized plateau, and is important for secretion (42, 43). We now investigate how BKCa-CaV properties affect such bursting activity in a model of electrical activity in pituitary lactotrophs (21). In this model a single Ca2+-channel type is present, which is assumed to activate instantaneously and not to inactivate. The BKCa current was modeled as a purely voltage-dependent current, neglecting Ca2+ dependency (21). In place of this simplified representation, we substitute our concise BKCa model controlled by CaVs in complexes.
With 1:1 stoichiometry, spiking electrical activity is observed, because insufficient BKCa current is generated (Fig. 3 E). In contrast, with more than one CaV per complex, plateau bursting appears with the number of small oscillations per burst depending on the number of CaVs per BKCa-CaV complex (Fig. 3, F and G). Although the quantitative behavior is independent of the approximation for , minor qualitative differences are present. The approximation given by Eq. 26 reproduces very well the behavior obtained from the complete model for the BKCa-CaV complex (Fig. 3, F and G, upper and middle panels), whereas the further simplification given by Eq. 29 produces smaller and more spikes per burst. Nonetheless, considering parameter uncertainties and experimental variations, even Eq. 29 produces reliable results.
Discussion
Models of cellular electrical activity typically do not consider local control in ion channel complexes. This fact is probably to a large extent because of the large computational costs of detailed simulations of Markov chain models (17) or reaction-diffusion models (10) that consider single complexes. In contrast, in the field of Ca2+ modeling, global procedures that respect local mechanisms have been presented (28, 29, 30).
We here applied similar methods to the BKCa-CaV complex to obtain Hodgkin-Huxley representations of the BKCa current that correctly take local control into account. Importantly, in our approach the effects of ion channel colocalization are handled via a deterministic model representation by averaging the stochastic dynamics in single ion channel complexes appropriately. Our timescale analysis allowed us to handle scenarios with more than one CaV per BKCa-CaV complex, thus providing important insight into the role of channel stoichiometry. Treating such cases via direct stochastic simulations of the BKCa and CaV simulations would be computationally cumbersome, and would not provide the same kind of analytical understanding. For example, we found explicit expressions for the time to first opening of a BKCa channel, thus providing theoretical insight into simulation results (17). Our findings also highlighted that CaV per complex left shifts the BKCa activation curve, because the presence of more CaVs increase the probability that at least one CaV is open and activates the associated BKCa channel.
We illustrated the usefulness of our theoretical results by applying the concise representations of BKCa currents to previously published whole-cell models of electrical activity. We chose a model of neuronal APs that has previously been used to investigate how BKCa channels contribute to fAHP (20). The simulations based on our BKCa-CaV model suggest that the kinetics of BKCa activation, which depends on the number of associated CaVs (Fig. 2), influence fAHP generation. It would be interesting to investigate experimentally whether defective BKCa-CaV coupling underlies disturbances in fAHP generation, as predicted by the model. In Xenopus motor nerve terminals, BKCa-CaV coupling differs between the release face and the nonsynaptic surface of varicosities (44), which, in the light of our simulations, may indicate spatial heterogeneity with respect to, e.g., fAHP.
We went on to investigate how the activation and inactivation properties of specific types of Ca2+ channels assumed to be present in BKCa-CaV complexes influence whole-cell electrical activity in a model of human β-cells (22). Because both the coupling of BKCa channels to L- and P/Q-type CaVs and the different stoichiometries of the complexes allow for simulations comparable to experiments, our findings do not allow us to conclude on the structure of BKCa-CaV complexes in human β-cells. Further insight into the control by CaVs of BKCa channels, which are involved in regulation of insulin release (40, 41), may lead to a better understanding of β-cell function and how it becomes disturbed in diabetes.
Finally, a model of pituitary cells (21) was used to study the role of BKCa channels in the generation of plateau bursting, which is important for secretion of pituitary hormones (42). We found that a reduced number of CaVs per complex, for example because of disturbed BKCa-CaV coupling, may abolish bursting activity. Our simulations showed that even the simplification given by Eq. 29 provided reliable results (Fig. 3, E–G). Similar conclusions hold for the β-cell model (see Fig. S7). Interestingly, this was not the case in the neuronal model (20) (Fig. S6), likely because of the shorter neuronal AP being more sensitive to the kinetics of BKCa activation.
A general strategy to distinguish between different configurations of the BKCa-CaV complex could be to first estimate the maximal whole-cell BKCa conductance, for example by depolarizations to highly positive voltages to activate BKCa channels independently of CaV activity (16), and then to fit I-V curves obtained from voltage-clamp depolarizations (37, 40) using the expressions presented here.
In summary, we have presented a concise Hodgkin-Huxley-type model of BKCa currents that take into account local control in BKCa-CaV complexes with different stoichiometries. Our model should be useful for whole-cell simulations of electrical activity in neurons and other excitable cells. The approach should be relatively straightforward to apply to other ion channel complexes, e.g., the Cav3-Kv4 complex (45).
Author Contributions
All authors performed research, prepared Supporting Material, revised the article, and approved the final version. F.M., A.T., and M.G.P. prepared figures. F.M. developed methods. M.G.P. conceived research and wrote the article.
Acknowledgments
We thank Carles Rovira, University of Barcelona, for useful discussions during early phases of the work.
Editor: Arthur Sherman.
Footnotes
Supporting Materials and Methods, seven figures, three tables, and one data file are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30451-4.
Supporting Material
References
- 1.Hodgkin A.L., Huxley A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Berkefeld H., Fakler B., Schulte U. Ca2+-activated K+ channels: from protein complexes to function. Physiol. Rev. 2010;90:1437–1459. doi: 10.1152/physrev.00049.2009. [DOI] [PubMed] [Google Scholar]
- 3.Pallotta B.S., Magleby K.L., Barrett J.N. Single channel recordings of Ca2+-activated K+ currents in rat muscle cell culture. Nature. 1981;293:471–474. doi: 10.1038/293471a0. [DOI] [PubMed] [Google Scholar]
- 4.Barrett J.N., Magleby K.L., Pallotta B.S. Properties of single calcium-activated potassium channels in cultured rat muscle. J. Physiol. 1982;331:211–230. doi: 10.1113/jphysiol.1982.sp014370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cox D.H., Cui J., Aldrich R.W. Allosteric gating of a large conductance Ca-activated K+ channel. J. Gen. Physiol. 1997;110:257–281. doi: 10.1085/jgp.110.3.257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Latorre R., Brauchi S. Large conductance Ca2+-activated K+ (BK) channel: activation by Ca2+ and voltage. Biol. Res. 2006;39:385–401. doi: 10.4067/s0716-97602006000300003. [DOI] [PubMed] [Google Scholar]
- 7.Grunnet M., Kaufmann W.A. Coassembly of big conductance Ca2+-activated K+ channels and L-type voltage-gated Ca2+ channels in rat brain. J. Biol. Chem. 2004;279:36445–36453. doi: 10.1074/jbc.M402254200. [DOI] [PubMed] [Google Scholar]
- 8.Berkefeld H., Sailer C.A., Fakler B. BKCa-Cav channel complexes mediate rapid and localized Ca2+-activated K+ signaling. Science. 2006;314:615–620. doi: 10.1126/science.1132915. [DOI] [PubMed] [Google Scholar]
- 9.Müller A., Kukley M., Dietrich D. Nanodomains of single Ca2+ channels contribute to action potential repolarization in cortical neurons. J. Neurosci. 2007;27:483–495. doi: 10.1523/JNEUROSCI.3816-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rehak R., Bartoletti T.M., Zamponi G.W. Low voltage activation of KCa1.1 current by Cav3-KCa1.1 complexes. PLoS One. 2013;8:e61844. doi: 10.1371/journal.pone.0061844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Suzuki Y., Yamamura H., Imaizumi Y. Caveolin-1 facilitates the direct coupling between large conductance Ca2+-activated K+ (BKCa) and Cav1.2 Ca2+ channels and their clustering to regulate membrane excitability in vascular myocytes. J. Biol. Chem. 2013;288:36750–36761. doi: 10.1074/jbc.M113.511485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chad J.E., Eckert R. Calcium domains associated with individual channels can account for anomalous voltage relations of CA-dependent responses. Biophys. J. 1984;45:993–999. doi: 10.1016/S0006-3495(84)84244-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Simon S.M., Llinás R.R. Compartmentalization of the submembrane calcium activity during calcium influx and its significance in transmitter release. Biophys. J. 1985;48:485–498. doi: 10.1016/S0006-3495(85)83804-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Neher E. Vesicle pools and Ca2+ microdomains: new tools for understanding their roles in neurotransmitter release. Neuron. 1998;20:389–399. doi: 10.1016/s0896-6273(00)80983-6. [DOI] [PubMed] [Google Scholar]
- 15.Fakler B., Adelman J.P. Control of KCa channels by calcium nano/microdomains. Neuron. 2008;59:873–881. doi: 10.1016/j.neuron.2008.09.001. [DOI] [PubMed] [Google Scholar]
- 16.Berkefeld H., Fakler B. Ligand-gating by Ca2+ is rate limiting for physiological operation of BKCa channels. J. Neurosci. 2013;33:7358–7367. doi: 10.1523/JNEUROSCI.5443-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cox D.H. Modeling a Ca2+ channel/BKCa channel complex at the single-complex level. Biophys. J. 2014;107:2797–2814. doi: 10.1016/j.bpj.2014.10.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stanley D.A., Bardakjian B.L., Ditto W.L. Stochastic amplification of calcium-activated potassium currents in Ca2+ microdomains. J. Comput. Neurosci. 2011;31:647–666. doi: 10.1007/s10827-011-0328-x. [DOI] [PubMed] [Google Scholar]
- 19.Anwar H., Hepburn I., De Schutter E. Stochastic calcium mechanisms cause dendritic calcium spike variability. J. Neurosci. 2013;33:15848–15867. doi: 10.1523/JNEUROSCI.1722-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Roper P., Callaway J., Armstrong W. AHP’s, HAP’s and DAP’s: how potassium currents regulate the excitability of rat supraoptic neurones. J. Comput. Neurosci. 2003;15:367–389. doi: 10.1023/a:1027424128972. [DOI] [PubMed] [Google Scholar]
- 21.Tabak J., Toporikova N., Bertram R. Low dose of dopamine may stimulate prolactin secretion by increasing fast potassium currents. J. Comput. Neurosci. 2007;22:211–222. doi: 10.1007/s10827-006-0008-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pedersen M.G. A biophysical model of electrical activity in human β-cells. Biophys. J. 2010;99:3200–3207. doi: 10.1016/j.bpj.2010.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Riz M., Braun M., Pedersen M.G. Mathematical modeling of heterogeneous electrophysiological responses in human β-cells. PLOS Comput. Biol. 2014;10:e1003389. doi: 10.1371/journal.pcbi.1003389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Khaliq Z.M., Gouwens N.W., Raman I.M. The contribution of resurgent sodium current to high-frequency firing in Purkinje neurons: an experimental and modeling study. J. Neurosci. 2003;23:4899–4912. doi: 10.1523/JNEUROSCI.23-12-04899.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jaffe D.B., Wang B., Brenner R. Shaping of action potentials by type I and type II large-conductance Ca2+-activated K+ channels. Neuroscience. 2011;192:205–218. doi: 10.1016/j.neuroscience.2011.06.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Anwar H., Hong S., De Schutter E. Controlling Ca2+-activated K+ channels with models of Ca2+ buffering in Purkinje cells. Cerebellum. 2012;11:681–693. doi: 10.1007/s12311-010-0224-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sherman A., Keizer J., Rinzel J. Domain model for Ca2+-inactivation of Ca2+ channels at low channel density. Biophys. J. 1990;58:985–995. doi: 10.1016/S0006-3495(90)82443-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hinch R., Greenstein J.L., Winslow R.L. A simplified local control model of calcium-induced calcium release in cardiac ventricular myocytes. Biophys. J. 2004;87:3723–3736. doi: 10.1529/biophysj.104.049973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Greenstein J.L., Hinch R., Winslow R.L. Mechanisms of excitation-contraction coupling in an integrative model of the cardiac ventricular myocyte. Biophys. J. 2006;90:77–91. doi: 10.1529/biophysj.105.065169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Williams G.S.B., Huertas M.A., Smith G.D. A probability density approach to modeling local control of calcium-induced calcium release in cardiac myocytes. Biophys. J. 2007;92:2311–2328. doi: 10.1529/biophysj.106.099861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lobo F.G., Goldberg D.E. IEEE International Conference on Evolutionary Computation. Institute of Electrical and Electronics Engineers; Indianapolis, IN: 1997. Decision making in a hybrid genetic algorithm; pp. 121–125. [Google Scholar]
- 32.Fleming P.J., Purshouse R.C. Evolutionary algorithms in control systems engineering: a survey. Control Eng. Pract. 2002;10:1223–1241. [Google Scholar]
- 33.Neher E. Usefulness and limitations of linear approximations to the understanding of Ca++ signals. Cell Calcium. 1998;24:345–357. doi: 10.1016/s0143-4160(98)90058-6. [DOI] [PubMed] [Google Scholar]
- 34.Marcantoni A., Vandael D.H.F., Carbone E. Loss of Cav1.3 channels reveals the critical role of L-type and BK channel coupling in pacemaking mouse adrenal chromaffin cells. J. Neurosci. 2010;30:491–504. doi: 10.1523/JNEUROSCI.4961-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Buchholz P., Kriege J., Felko I. Springer Briefs in Mathematics. Springer; Berlin, Germany: 2014. Input modeling with phase-type distributions and Markov models. [Google Scholar]
- 36.Segel L.A., Slemrod M. The quasi steady-state assumption: a case study in perturbation. SIAM Rev. 1989;31:446–477. [Google Scholar]
- 37.Berkefeld H., Fakler B. Repolarizing responses of BKCa-Cav complexes are distinctly shaped by their Cav subunits. J. Neurosci. 2008;28:8238–8245. doi: 10.1523/JNEUROSCI.2274-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Storm J.F. Action potential repolarization and a fast after-hyperpolarization in rat hippocampal pyramidal cells. J. Physiol. 1987;385:733–759. doi: 10.1113/jphysiol.1987.sp016517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Joux N., Chevaleyre V., Hussy N. High voltage-activated Ca2+ currents in rat supraoptic neurones: biophysical properties and expression of the various channel α1 subunits. J. Neuroendocrinol. 2001;13:638–649. doi: 10.1046/j.1365-2826.2001.00679.x. [DOI] [PubMed] [Google Scholar]
- 40.Braun M., Ramracheya R., Rorsman P. Voltage-gated ion channels in human pancreatic β-cells: electrophysiological characterization and role in insulin secretion. Diabetes. 2008;57:1618–1628. doi: 10.2337/db07-0991. [DOI] [PubMed] [Google Scholar]
- 41.Houamed K.M., Sweet I.R., Satin L.S. BK channels mediate a novel ionic mechanism that regulates glucose-dependent electrical activity and insulin secretion in mouse pancreatic β-cells. J. Physiol. 2010;588:3511–3523. doi: 10.1113/jphysiol.2009.184341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Stojilkovic S.S., Zemkova H., Van Goor F. Biophysical basis of pituitary cell type-specific Ca2+ signaling-secretion coupling. Trends Endocrinol. Metab. 2005;16:152–159. doi: 10.1016/j.tem.2005.03.003. [DOI] [PubMed] [Google Scholar]
- 43.Tagliavini A., Tabak J., Pedersen M.G. Is bursting more effective than spiking in evoking pituitary hormone secretion? A spatiotemporal simulation study of calcium and granule dynamics. Am. J. Physiol. Endocrinol. Metab. 2016;310:E515–E525. doi: 10.1152/ajpendo.00500.2015. [DOI] [PubMed] [Google Scholar]
- 44.Sun X.-P., Yazejian B., Grinnell A.D. Electrophysiological properties of BK channels in Xenopus motor nerve terminals. J. Physiol. 2004;557:207–228. doi: 10.1113/jphysiol.2003.060509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Anderson D., Mehaffey W.H., Turner R.W. Regulation of neuronal activity by Cav3-Kv4 channel signaling complexes. Nat. Neurosci. 2010;13:333–337. doi: 10.1038/nn.2493. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.