Estimating the parameters of background selection and selective sweeps in Drosophila in the presence of gene conversion

Significance

The level of DNA sequence variation at a site in the genome is affected by selection acting on genetically linked sites. We have developed models of selection at linked sites to explain the observed negative relation between the level of nearly neutral variability in Drosophila genes and their protein sequence divergence from a related species. We use fits of these models to polymorphism and divergence data to show that selective sweeps are the main determinants of this pattern. We obtain estimates of the strengths of selection on advantageous mutations and the proportions of new mutations that are selectively advantageous. Gene conversion, a major source of genetic recombination within genes, has a large effect on these parameter estimates.

Abstract

We used whole-genome resequencing data from a population of Drosophila melanogaster to investigate the causes of the negative correlation between the within-population synonymous nucleotide site diversity (π_S) of a gene and its degree of divergence from related species at nonsynonymous nucleotide sites (K_A). By using the estimated distributions of mutational effects on fitness at nonsynonymous and UTR sites, we predicted the effects of background selection at sites within a gene on π_S and found that these could account for only part of the observed correlation between π_S and K_A. We developed a model of the effects of selective sweeps that included gene conversion as well as crossing over. We used this model to estimate the average strength of selection on positively selected mutations in coding sequences and in UTRs, as well as the proportions of new mutations that are selectively advantageous. Genes with high levels of selective constraint on nonsynonymous sites were found to have lower strengths of positive selection and lower proportions of advantageous mutations than genes with low levels of constraint. Overall, background selection and selective sweeps within a typical gene reduce its synonymous diversity to ∼75% of its value in the absence of selection, with larger reductions for genes with high K_A. Gene conversion has a major effect on the estimates of the parameters of positive selection, such that the estimated strength of selection on favorable mutations is greatly reduced if it is ignored.

Advances in population genomics are shedding light on the question of the extent to which patterns of DNA sequence variation and evolution are affected by selection at sites that are genetically linked to those under investigation (1–3). Two main processes have been invoked as causes of such “hitchhiking” effects. The first involves selective sweeps (SSWs), in which a selectively favorable mutation spreads all or part of the way through the population, causing a reduction in the level of variability at nearby sites (4). The second is background selection (BGS) (5), whereby the elimination of deleterious mutations results in the removal of linked variants. Both processes can be viewed heuristically as causing a local reduction in effective population size (N_e), resulting in reductions in within-population variability and the effectiveness of selection. Variability increases with the product of N_e and the mutation rate, and the fixation probability of a mutation is determined by the magnitude of the product of N_e and the strength of selection (6). These effects have important implications for the evolutionary significance of recombination and sexual reproduction (1, 7, 8).

Because genetic recombination reduces associations between linked variants, the effects of hitchhiking on a genome region are expected to be negatively correlated with the local rate of recombination (9). There is now a large body of evidence for positive correlations between the recombination rate of a gene and its level of variability and molecular adaptation (1–3, 9). The contributions of SSWs and BGS to reductions in variability have long been a matter for debate, because they can have similar effects on both levels of variability and the shapes of gene genealogies. This question has been especially intensively studied using population genomic data on Drosophila. Three broad categories of approach can be distinguished. The first attempts to interpret patterns of variability by using estimates of the extent of adaptive evolution in coding or functional noncoding sites, ignoring BGS (10, 11). The second uses estimates of the distribution of fitness effects (DFE) of new deleterious mutations to ask whether BGS alone can account for most of the observed patterns (12, 13). The third uses whole-genome data on levels of polymorphism and divergence in different classes of nucleotide sites to fit the parameters of both BGS and SSWs, without using prior knowledge of the DFE or the extent of adaptive evolution (3, 14). Although all three approaches agree in suggesting a substantial effect of hitchhiking on the typical level of variability in a gene, they disagree about the quantification of the contributions of the two causes of hitchhiking.

Here, we describe an approach that involves fitting models of both BGS and SSWs to an important aspect of the population genomic data—the negative relation between the level of synonymous nucleotide site diversity (π_S) in a Drosophila melanogaster gene and K_A, its nonsynonymous site (NS) divergence from a related species, first noted by Andolfatto (15) and confirmed in later studies (16, 17). We used whole-genome polymorphism data on a Rwandan population of D. melanogaster, previously analyzed for different purposes (18–20). By binning genes into sets with similar K_A values with respect to divergence from Drosophila yakuba, or along the D. melanogaster lineage since its divergence from its closest relative Drosophila simulans, we estimated the parameters of the DFE and the extent of positive selection on NS sites for bins with different K_A values. We also estimated these parameters for untranslated regions (UTRs) of coding sequences, which show levels of selective constraint that are intermediate between those for synonymous and nonsynonymous sites (21).

Using recent estimates of rates of crossing over and gene conversion for D. melanogaster (22, 23), we found that the effects of BGS can account for only part of the observed relation between π_S and K_A, so that SSW effects need to be invoked. We estimated the average strength of selection on positively selected mutations, and the proportion of new mutations that are advantageous, for both NS and UTR sites. A unique aspect of our approach is that it includes gene conversion in the SSW as well as the BGS models, which has a major effect on the parameter estimates. Because we found that the results using the D. melanogaster–D. yakuba comparison had better statistical properties than those for the D. melanogaster lineage, probably because they provided more accurate estimates of the rates of adaptive evolution, we focus attention on the former. From now on, we will refer to the two datasets as mel-yak and mel, respectively.

Empirical Results

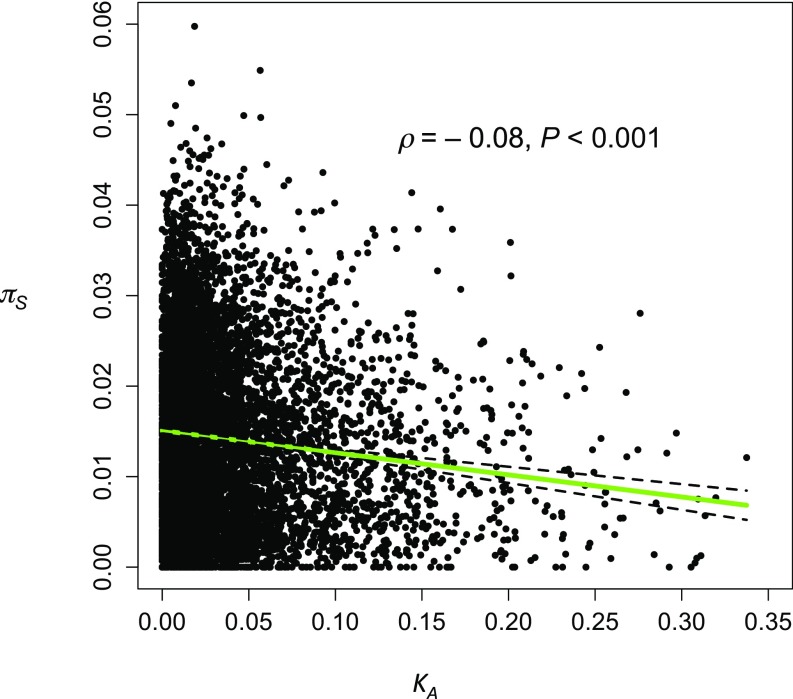
We first asked whether there was a relation between π_S and K_A for autosomal genes located in regions with normal rates of crossing over, using data on all available genes (Materials and Methods, Primary Data Analyses); this is displayed in Fig. 1 and SI Appendix, Fig. S1, for mel-yak and mel, respectively. The Spearman rank correlations for the two datasets were small but significantly negative: mel-yak ρ = −0.082, P < 0.001; mel ρ = −0.077, P < 0.001). After correcting for the covariates described in Materials and Methods (SI Appendix, Table S1), the relations were still significant and negative (ρ = −0.129, P < 10⁻¹⁶ for mel-yak; ρ = –0.130, P < 10⁻¹⁶ for mel), with a multiple regression coefficient of –0.052 for mel-yak, and −0.195 for mel. In contrast, the rank partial correlations between π_A and K_A were positive, with ρ = 0.412, P < 10⁻¹⁶ in mel-yak and ρ = 0.428 in mel, as has previously been found (e.g., ref. 16). This result implies that the level of selective constraint on a coding sequence is negatively correlated with its K_A value, consistent with the result from the DFE-α analyses described next.

Fig. 1.

The plot of synonymous diversity (π_S) for genes in a Rwandan population of D. melanogaster against their nonsynonymous divergence from D. yakuba (K_A); ρ is the Spearman rank correlation coefficient. The green line is the least-squares linear regression (the dashed lines are its 95% CIs).

To examine the potential contributions of BGS and SSWs to the pattern for π_S, we applied DFE-α (24) to each of 50 bins of K_A values, assuming gamma distributions of the selection coefficients for deleterious mutations within bins, as described in Materials and Methods, Primary Data Analyses (Table 1 and SI Appendix, Tables S2 and S3). The Spearman rank correlations for the mel-yak comparison across bins for π_S versus ω_a and π_S versus ω_na were –0.681 (P = 5 × 10⁻⁸) and –0.727 (P = 2.26 × 10⁻⁹). Here, ω_a is the ratio of the rate of substitution of positively selected NS mutations to the rate of substitution of synonymous mutations as measured by the synonymous site divergence K_S (25); ω_na is the corresponding ratio for substitutions of neutral or slightly deleterious NS mutations (26) and is an inverse measure of the level of selective constraint on the protein sequence. For mel, the rank correlations were −0.829 (P < 10⁻¹³) and −0.845 (P < 10⁻¹³), respectively. However, because both ω_a and ω_na for NS sites increase across bins of K_A (SI Appendix, Table S2), these results do not distinguish between their respective contributions to the patterns for π_S. To pursue this question, it is necessary to generate predictions for both the BGS and SSW models. The relevant theory is described in Materials and Methods and SI Appendix, sections 1–6. In the next section, we investigate the effects of BGS alone on the relation between π_S and ω_na, to examine the extent to which BGS could explain the observed relation between π_S and K_A.

Table 1.

Effects of gene conversion (GC), BGS, and SSWs on parameter estimates from the mel-yak data

UTR	BGS	GC	Mean γα	Mean pa (×104)	γu	pu (×104)	πr max	πr mean	r
+	+	+	249	2.21	213	9.04	0.882	0.756	0.924
−	+	+	197	2.76	—	—	0.975	0.836	0.918
+	−	+	319	1.82	197	9.74	0.925	0.793	0.922
−	−	+	297	1.95	—	—	0.992	0.850	0.918
+	+	−	122	4.41	135	10.4	0.867	0.742	0.927
−	+	−	95.6	5.59	—	—	0.971	0.830	0.920
+	−	−	188	3.07	119	16.1	0.923	0.792	0.922
−	−	−	176	3.29	—	—	0.992	0.850	0.919

The data used in Fig. 3 for the standard gene model and standard rates of mutation and crossing over were applied to estimates of the parameters of positive selection and synonymous site diversity from models with (+) or without (−) selective effects on UTRs, BGS, and GC. When GC was present, the low rate of Fig. 3 was assumed. π_{r max} is the maximum value of the mean synonymous site diversity of a gene, relative to its value in the absence of selection; π_{r mean} is the corresponding mean value over bins. Other variables are defined in the text.

Potential Effects of BGS Alone

The following argument shows how a negative relation between ω_na and synonymous diversity could arise. First, because ω_na is the component of K_A/K_S caused by the fixation of neutral or weakly deleterious mutations, stronger selection against deleterious mutations should reduce ω_na and hence K_A (SI Appendix, Fig. S3, shows that genes with lower K_A have lower ω_na). Second, stronger selection can also reduce the strength of BGS for a single gene, leading to higher synonymous diversity (SI Appendix, Eq. S5). This pattern results from the fact that weakly deleterious mutations achieve higher equilibrium frequencies than more strongly selected mutations, so that a closely linked neutral mutation has a higher chance of association with a mutation that is destined to be eliminated from the population (5).

To make this analysis quantitative, we used both an exact summation formula and a more tractable, but approximate, integral method; each of these included BGS effects of both NS and UTR sites, and are described by Eq. 1 of Materials and Methods, and SI Appendix, Eqs. S10b and S12, respectively. The equations take both gene conversion and crossing over into account and determine the mean value of E over all synonymous sites in a gene, where E is the negative of the natural logarithm of the ratio of the predicted value π_S at a site to its value in the absence of BGS, π₀. The larger E, the greater the reduction in diversity due to BGS. A subsidiary question is the extent to which the two methods for determining E agree.

We calculated the mean E value for a gene, using a broad range of assumed ω_na values of NS mutations. For the summation results, we assumed the “standard” D. melanogaster gene model (27), described in Materials and Methods before Eq. 1. This model has five exons of 100 codons each, interrupted by four introns of 100 bp. For the integral method, we assumed 500 codons without introns. We also assumed gamma distributions of the selective effects of deleterious mutations, with a shape parameter, β, of 0.3 for both UTRs and NS sites, because this is a typical value from estimates of the DFE (SI Appendix, Tables S2 and S3). We assumed ω_na = 0.15 for 3′- and 5′-UTRs, regardless of the value of ω_na for NS sites; this value is also consistent with the DFE-α results. We assumed u = 4.5 × 10⁻⁹ for the mean mutation rate per base pair, which is in the midrange of values from direct estimates for single nucleotide mutations in D. melanogaster (28, 29). We then used SI Appendix, Eq. S13, to calculate the mean selection coefficients for NS and UTR mutations from the assigned values of ω_na for NS and UTR sites, assuming an effective population size of 10⁶, by applying equation 23 of ref. 30.

The crossing-over rate per base pair, r_c, was set to the standard value of 1 × 10⁻⁸ for D. melanogaster in regions with nonzero rates of crossing over, averaging over the two sexes (19). A recent whole-genome sequencing analysis of a single cross (23) gave estimates of the rate of initiation per base pair of noncrossover gene conversion events (g_c) and mean tract length (d_g) of 1 × 10⁻⁸ per base pair and 440 bp, respectively, whereas a recombinant inbred line experiment (22) gave g_c = 5 × 10⁻⁸ and d_g = 500 bp. Because these estimates differ considerably, we generated results for both sets of values.

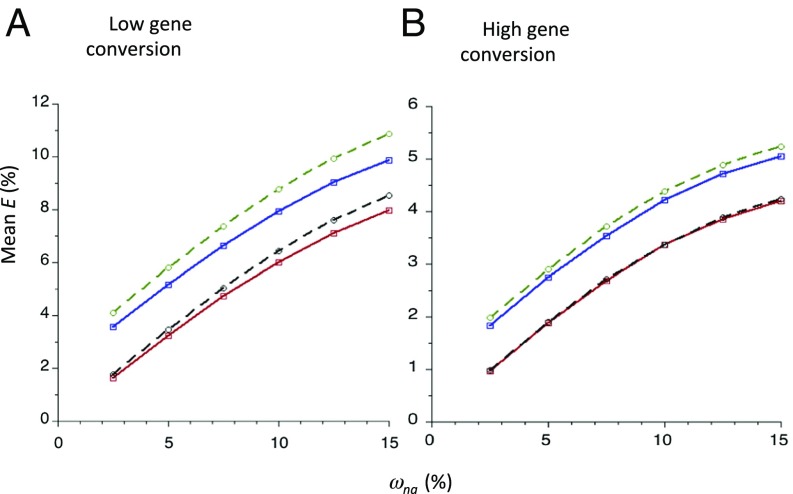
Fig. 2 shows the BGS effects caused by NS mutations alone, as well as the joint BGS effects of NS and UTR mutations. These increase with ω_na for NS sites, implying that π_S declines with ω_na, consistent with the properties of SI Appendix, Eq. S5. The relationship between mean E and ω_na is close to linear, tailing off somewhat at high values of ω_na. The integral model gives slightly larger estimates of mean E for a gene than the summation model. Both models are sensitive to the gene conversion parameters, with the smaller g_c and d_g values giving substantially stronger effects than the larger values, as would be expected as a result of the lower net recombination rates. These results show that BGS can indeed have larger effects on genes with larger values of ω_na and hence K_A, and is therefore a possible contributory factor to the negative relation between synonymous site diversity and K_A. An intuitive explanation for this pattern was given at the beginning of this section.

Fig. 2.

This plots the theoretical values of mean E (percent) against values of mean ω_na (percent) for the standard model of a single gene with five exons of 100 codons each; a gamma distribution of selection coefficients with β = 0.3 was assumed, with γ_c = 5. For the results obtained by the summation method (red and blue solid lines), the exons were separated by four introns of 100 bp. For the results obtained from the integral model (black and green dashed lines), a continuous stretch of coding sequence was assumed. The green and blue lines show the net BGS effects arising from both NS and UTR sites; the black and red lines show the effects for NS sites alone. Two-thirds of coding sites were assumed to result in NS mutations. The rate of crossing over per base pair was 1 × 10⁻⁸, and the mutation rate was 4.5 × 10⁻⁹ per base pair. The gene conversion parameters for the low gene conversion case (A) were g_c = 1 × 10⁻⁸ and d_g = 440; for the high gene conversion case (B), g_c = 5 × 10⁻⁸ and d_g = 500. No large effect mutations were allowed.

We also examined the effects of varying the sizes of exons and introns on the results (SI Appendix, Tables S4–S6). Varying the length of exons from 50 to 200 codons increases E for the largest ω_na value (0.15) by 0.05 when UTR effects were included, with the “standard value” being intermediate (SI Appendix, Table S4). This implies that exon size needs to be taken into account in relating the BGS predictions to the population genomic results. As shown in SI Appendix, Table S5, the mean (“observed”) values over exon lengths for the summation model were only slightly higher than the values for the integral model for the standard length (“predicted”), suggesting that using the predictions from the latter should give a good approximation to the BGS effect for a given bin of K_A values. Intron size or their presence/absence had a much smaller effect on the results, with a maximum difference of less than 0.04 between BGS effects with no introns and long introns (SI Appendix, Table S6). Accordingly, only the standard values of intron length and number were used in the analyses described below.

Results of Data Analyses

Comparisons of BGS Predictions with the Observed Relation Between π_S and K_A.

If the observed relation between π_S and K_A is due to hitchhiking, the parameters of selection against deleterious mutations and/or favorable mutations for a given gene must be related to its K_A value. To investigate this question, and to apply the theoretical results to the data, we used the DFE-α (24) results from NS sites for each of 50 bins of K_A values (SI Appendix, Table S2). In addition, we used DFE-α estimates for UTR sites from the whole unbinned dataset, as described in Materials and Methods, because there was no evidence for systematic differences among bins in the proportion of substitutions that were adaptive (α) or the shape parameter of the DFE (β). We used realistic values of the mutation rate per base pair and the gene conversion parameters g_c and d_g, as well as the proportion (p_l) of large effect mutations with selection coefficient t_l that lies outside the range of the gamma distributions used to infer the DFE, as proposed in ref. 31. We applied the procedures described in Materials and Methods and SI Appendix, sections 1–3, to estimate mean E values for each bin.

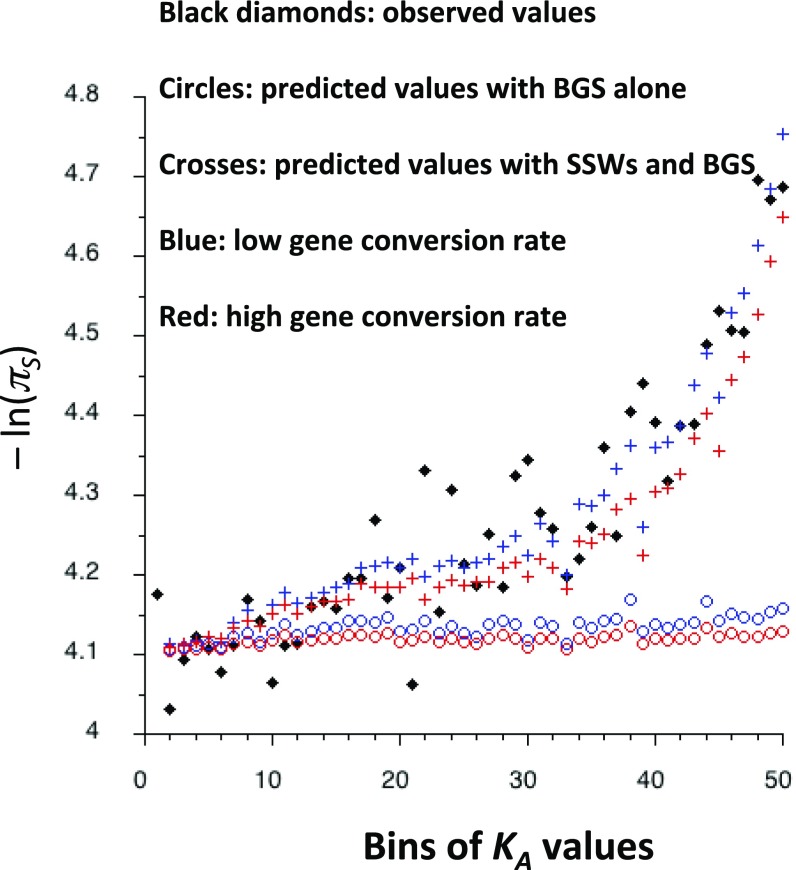
Fig. 3 shows plots of the negatives of the natural logarithms of the mean π_S values for each bin for the mel-yak data, together with the corresponding values predicted from the linear regression of −ln(π_S) on K_A, as well as the predictions of mean E for each bin using the integral model of gene conversion (the predictions including SSWs are also shown, obtained as described in the next section). The comparable plots for mel are shown in SI Appendix, Fig. S2. In addition, SI Appendix, Figs. S3 and S4 show that, as might be expected, the means of the scaled selection coefficients (given by γ = 4N_et, where t is the selection coefficient against mutant heterozygotes) for both NS and UTR deleterious mutations decline with increasing K_A, although the relation for NS sites is quite noisy, especially for the mel-yak data (despite the noise, the Spearman rank correlation was – 0.616 for mel-yak, P < 0.001). It is evident that the BGS predictions are inadequate to represent the increase in −ln(π_S) with K_A, even for the favorable case of a low rate of gene conversion. Although the BGS effects provide good predictions for the first 10 bins, they increase much more slowly with K_A than does −ln(π_S). This reflects the fact that β for NS sites is negatively related to K_A (SI Appendix, Fig. S5), so that the higher K_A bins have wider distributions of selection coefficients, implying that more mutations tend to fall into the regions where BGS is ineffective.

Fig. 3.

The black diamonds are the observed values of −ln(π_S) for each bin of K_A values for autosomes, corrected for the correlation between π_S and K_S as described in Materials and Methods, Primary Data Analyses. The circles are the theoretical values of mean E for each bin, obtained by the integral model of BGS, assuming a single gene with 500 NS sites. The crosses are the predicted values of −ln(π_S) for each bin, given by the combined BGS and SSW models at NS and UTR sites. Red and blue correspond to the low and high gene conversion rates used in Fig. 2. The mutation rate and crossing-over parameters are as in Fig. 2, except that large effect mutations constitute 15% of all mutations, with a selection coefficient against heterozygotes of 0.044.

The quantitative agreement between the predicted and observed values was assessed by comparing the linear regression coefficients on K_A for −ln(π_S) and mean E for a bin. For the data used in Fig. 3, the regression coefficient for −ln(π_S) was 3.81 ± 0.21 (the SE was obtained from normal distribution regression theory). The regression coefficients (b) for mean E for the low and high rates of gene conversion were 0.236 ± 0.039 and 0.0935 ± 0.0208, respectively, indicating a significant difference between the two regression coefficients in each case. Similar results were obtained with the mel data. There was only a small difference between the examples in Fig. 3, which assumed that 15% of the total number of mutations had strongly deleterious effects (t_l = 0.044), and cases without any major effect mutations. In the absence of major effect mutations, there was a weakening of the BGS effects for a given bin of K_A; b for mean E was barely affected with the low gene conversion rate and decreased to 0.0574 ± 0.0122 with the high gene conversion rate.

The sensitivity of the results to variation in the mutation and crossing-over parameters was explored by using rates of mutation and crossing over with the mel-yak data that were either one-half or twice the “standard” values used above (SI Appendix, Table S7). As expected, higher mutation rates and lower crossing-over rates were associated with larger b values for E. The results were much more sensitive to the mutation rate than the crossing-over rate, especially with the high gene conversion rate. In no case, however, did the b values approach that for –ln(π_S).

To provide a more rigorous test of the ability of BGS to explain the relation between π_S and K_A, we generated 500 bootstrap values of all of the variables for each bin separately (Materials and Methods), reran the regression analyses for each bootstrap replicate, and determined the proportion of cases in which the regression coefficient for –ln(π_S) was less than that for E, as well as upper and lower percentiles of the distributions of both regression coefficients, and of the difference between them. For the low gene conversion rate and other parameters used in Fig. 3 for the mel-yak data, 100% of the bootstraps had a larger regression coefficient for –ln(π_S) than for mean E, with upper and lower 2.5 percentiles of the difference of (3.18, 4.04). The upper and lower 2.5 percentiles for the regression coefficients were (3.42, 4.25) for –ln(π_S) and (0.14, 0.32) for mean E. As would be expected, with the high gene conversion rate, the difference between the two regression coefficients was more pronounced, with upper and lower 2.5 percentiles of (0.05, 0.14) for the mean E regression, and (3.34, 4.18) for the difference. There is thus good evidence that the BGS model cannot fully account for the relation between π_S and K_A. Similar results were obtained for the mel data.

The only obvious alternative explanation is that a higher incidence of SSWs is occurring in genes with higher K_A values, resulting in greater reductions in π_S than in genes with low K_A. This hypothesis is qualitatively consistent with the fact that bins with higher K_A have larger ω_a values (SI Appendix, Table S2). We explore this possibility quantitatively in the next section.

Estimates of the Selection Parameters for Selectively Favorable Mutations.

We now describe the estimates of the parameters for beneficial mutations, obtained using the procedures described in Materials and Methods, Expected Effects of SSWs on a Single Gene and Estimating Positive-Selection Parameters. These are based on the standard equations for the effects of a SSW (32), which can be used to predict the effects of sweeps of favorable NS and UTR mutations on the mean π_S of genes in a given bin (SI Appendix, section 4). In addition, the contribution of BGS to the reduction in π_S for the bin was estimated as described above; the net predicted value of π_S/π₀ with both BGS and SSWs was then found using SI Appendix, Eq. S16c.

We assumed constancy, across bins of the scaled selection coefficient for positively selected UTR mutations, γ_u, given the weak observed relations between K_A and α for UTRs (Materials and Methods, Primary Data Analyses). For NS sites, we used a model in which the scaled selection coefficient for positively selected mutations, γ_a, was linearly related to the ratio of K_A to its maximum value, yielding different γ_a estimates for each bin. The intercept and slope of this model, together with γ_u, provide three parameters to be estimated by fitting the predictions to the data. As described in Materials and Methods, the parameter estimates were obtained by minimizing the sum of squares (SSD) of deviations between the predicted and observed values of −ln(π_S) for each bin for all but the first bin; this bin was used to estimate the value of –ln(π₀). Given the estimates of γ_a and γ_u, together with the empirical estimates of the rates of adaptive substitutions of favorable NS and UTR mutations (ν_a and ν_u), the proportions of new NS and UTR mutations (p_a and p_u) that are beneficial can be obtained from SI Appendix, Eq. S19, as in ref. 33.

Fig. 3 shows the fits to the observed values for mel-yak of the predicted values of −ln(π_S). As for the previous calculations with BGS alone, both low and high gene conversion rates were used. The fits are clearly far better than with BGS alone. The goodness of fit was assessed from the Pearson correlation coefficient (r) between the observed and expected values across the 49 bins used for the fit. The r values were 0.924 and 0.918 for the low and high gene conversion rates, respectively; the corresponding minimum SSDs were 0.193 and 0.296. These two measures show that the low gene conversion rate gives a better fit than the high gene conversion rate. The corresponding estimates for UTR sites of γ_u were 213 and 260, respectively; the values of p_u were very similar for each bin, with means of 9.03 × 10⁻⁴ and 8.41 × 10⁻⁴.

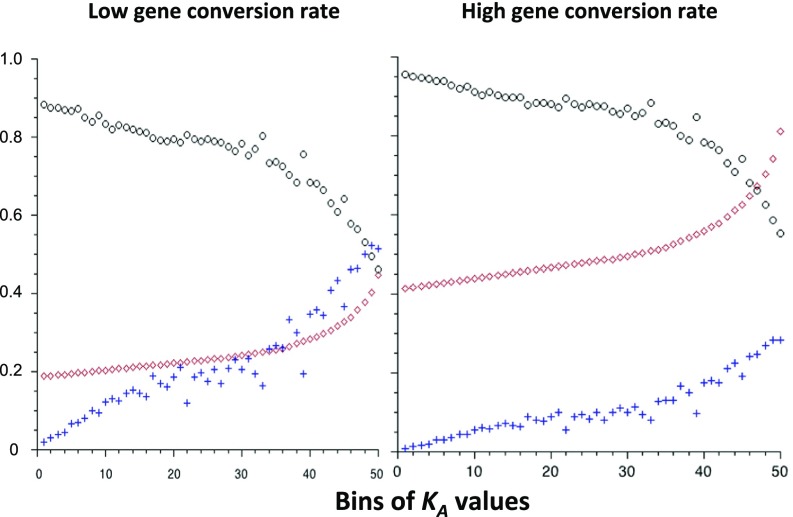
Fig. 4 shows estimates of γ_a, p_a, and the ratio of synonymous diversity relative to neutral expectation (π_rel = π_S/π₀) for each bin of K_A values, assuming either low or high gene conversion rates. γ_a and p_a increase with increasing K_A, and π_rel declines. The mean values of γ_a and p_a over bins were 249 and 2.21 × 10⁻⁴, respectively, for the low gene conversion rates, and 508 and 8.41 × 10⁻⁴ for the high gene conversion rates. The estimated values of π₀ were 0.019 and 0.017 for the low and high gene conversion rates, with corresponding π_rel values of 0.758 and 0.843, respectively.

Fig. 4.

The black circles are the predicted values of π_S relative to its expected value in the absence of hitchhiking; the red diamonds are the estimates of γ_a (multiplied by 10⁻³); the blue crosses are the estimates of p_a (multiplied by 10³). The other parameters are as in Fig. 3, assuming effects of BGS and SSWs at both NS and UTR sites.

Corresponding results were obtained for the mel data (SI Appendix, Fig. S2), which yielded somewhat lower estimates of mean γ_a of 119 and 434 for the low and high gene conversion rates, respectively; the corresponding γ_u values were 97.5 and 260. Accordingly, the corresponding mean proportions of adaptive mutations were higher than for mel-yak: 4.31 × 10⁻⁴ and 1.23 × 10⁻⁴ for NS sites, and 3.80 × 10⁻³ and 7.17 × 10⁻⁴ for UTR sites. The r values were substantially lower than for mel-yak: 0.812 and 0.820 for the low and high gene conversion rates, respectively, implying poorer fits to the data. This difference probably arises from the fact that the underlying rate of adaptive protein sequence evolution (obtained from αK_A: SI Appendix, Eq. S17) for individual bins of K_A, which was used in the sweep analyses, was less accurately estimated from the mel than the mel-yak data; the mean over all bins of the coefficient of variation of αK_A from the bootstrap analyses described below was 18.5% for mel compared with 14.4% for mel-yak, a 22% lower value for mel-yak relative to mel. Given the higher relative errors in the estimates of αK_A when there are fewer substitutions, and the dependence on the adaptive γ estimates to variation across bins in αK_A, this result is not surprising. We have accordingly focused attention on the mel-yak results.

We explored the question of the effects of BGS and gene conversion on the parameter estimates for adaptive mutations, by obtaining estimates from the original mel-yak data with/without BGS, gene conversion, and UTRs; these are shown in Table 1. Ignoring BGS causes an overestimation of γ_a, although the relative size of the effect is smaller than that of gene conversion. It seems that fairly accurate estimates of γ_a can thus be obtained if BGS is ignored, but not if gene conversion is ignored. The effects on p_a are in the opposite direction, as would be expected. Ignoring UTRs has only a slight effect on the estimates of γ_a and p_a for NS sites, but causes a considerable overestimation of π_rel.

The effects of varying the mutation rate and rate of crossing over were also examined (SI Appendix, Table S8). With the low rate of gene conversion and the standard mutation rate, a low rate of crossing over greatly reduced the estimate of γ_a, as did a high mutation rate for all rates of crossing over. The estimate of γ_u was also reduced by a low mutation rate, except with a high rate of crossing over. With the high rate of gene conversion, these effects are largely absent. In all cases, however, the mean γ values for both NS and UTR sites were well over 100, and the proportions of advantageous mutations were of the order of 10⁻⁴.

We also examined the question of possible bias introduced by binning (14), by dividing the mel-yak data into 100 instead of 50 bins of K_A values; the only substantial effect on the parameter estimates was to reduce the point estimate of γ_u to 151, from 213 with 50 bins, and the correlation between predicted and observed −ln(π_S) to 0.86 from 0.92, suggesting that binning has only minor effects on the estimates.

The statistical reliability of the parameter estimates was examined by generating 250 bootstrapped estimates of the parameters, using the procedure described in Materials and Methods, and fitting the model with BGS and SSWs at NS and UTR sites to all 50 bins. Table 2 and SI Appendix, Table S9, show the results for the mel-yak data and mel data, respectively, assuming standard values of the mutation rate, rate of crossing over and gene structure, for cases with zero, low, and high rates of gene conversion. An important conclusion is that there is good support from the mel-yak data for a significantly positive slope for the relation between γ_a and K_A, despite the fact that the magnitude of the slope has a wide distribution (an upper bound of 1,000 was set by the program). We can thus have some confidence in the conclusion that γ_a increases with K_A. It is less clear whether the intercept is nonzero, except when the high rate of gene conversion is assumed. The other parameters appear to be estimated with fairly good accuracy, supporting the conclusion that γ_u and the mean of γ_a across bins are of the order of 100 or more, that the mean proportions of positively selected NS and UTR mutations are ∼10⁻⁴ and 10⁻³, respectively, and that synonymous nucleotide site diversity is substantially reduced below neutral expectation by selection at linked sites. With the low rate of gene conversion, which is probably the most realistic case (Discussion), there is no overlap between the 2.5% percentiles for the correlation coefficients for the observed and predicted values of −ln(π_S) between the mel-yak and mel data, supporting the conclusion that the mel-yak data provide the more reliable estimates.

Table 2.

Bootstrapped mel-yak estimates of parameters of positive selection and synonymous site diversity

Variable	Zero GC	Low GC	High GC
r	0.85 (0.79, 0.90)	0.85 (0.78, 0.90)	0.84 (0.77, 0.89)
Intercept for γa	46 (10, 142)	130 (10, 277)	546 (410, 610)
Slope for γa	267 (56, 500)	383 (111, 722)	764 (278, 1000)
Mean γa	107 (73, 163)	218 (141, 315)	721 (583, 840)
pa (×104)	5.2 (3.2, 7.6)	2.5 (1.7, 3.6)	0.74 (0.60, 0.9)
γu	106 (10, 177)	157 (66, 232)	379 (177, 510)
pu (×104)	28 (11, 190)	13 (8.2, 29)	5.4 (3.8, 11)
πr max	0.88 (0.84, 0.92)	0.90 (0.87, 0.94)	0.93 (0.91, 0.96)
πr mean	0.76 (0.72, 0.80)	0.78 (0.75, 0.81)	0.81 (0.79, 0.83)

The data used for Fig. 3 were analyzed, with 250 independent bootstraps for each bin of K_A values, performed as described in Materials and Methods. The entries show the means and (in brackets) the upper and lower 2.5 percentiles of the bootstrap distributions of the relevant parameter estimates. GC, gene conversion.

Discussion

There are several points of general interest among the results described above. First, it seems likely that the relatively small values of the gene conversion parameters in ref. 23 are correct, rather than those of ref. 22, given their agreement with the classical results for the rosy locus (34, 35) and their better fit to the data. If this is the case, the point estimate of the mean scaled selection coefficient (γ_a) for positively selected NS mutations for the mel-yak data is ∼250 (Table 1); with N_e = 10⁶, this corresponds to a heterozygous selection coefficient for a beneficial mutation of 6.25 × 10⁻⁵. The estimate of the scaled selection coefficient (γ_u) for a positively selected UTR mutation is only slightly lower than the mean of γ_a, ∼210. The estimated mean proportion of new NS mutations that are adaptive, p_a, is ∼2 × 10⁻⁴, compared with 10⁻³ for the corresponding proportion for UTR mutations, p_u. This difference is consistent with the higher sequence divergence rate of UTRs. However, the bootstrap results shown in Table 2 and SI Appendix, Table S9 (middle columns) show that these parameter estimates have wide CIs, so that the point estimates should be treated with caution. Nonetheless, it seems clear that the scaled selection coefficients are of the order of 100.

Second, the level of selective constraint on a coding sequence, as measured by ω_na or the scaled selection coefficient for a deleterious NS mutation, is strongly negatively correlated with K_A (SI Appendix, Table S2 and Fig. S3). Together with the results shown in Fig. 4, which show that both γ_a and p_a increase with K_A, this suggests that more constrained coding sequences are less likely to experience positively selected NS mutations than weakly constrained sequences, and positively selected mutations have smaller selective advantages when constraint is high. However, α itself does not correlate significantly with K_A (Spearman rank correlation ρ = 0.063, P > 0.6, for mel-yak), in contrast to what has been found for comparisons of different regions of the same protein (36).

It is also interesting to note that the selective constraints on UTR sequences seem to be stronger for genes with stronger constraints on NS sites (SI Appendix, Fig. S4), reflecting the positive correlation between K_U and K_A, although there does not seem to be a strong correlation between the parameters of positive selection for UTR sites and K_A (Materials and Methods, Primary Data Analyses). This parallels the negative, but nonlinear relationships between UTR length and K_A seen in the binned data (SI Appendix, Figs. S6 and S7), which show that both 3′- and 5′-UTR lengths fall off rapidly with K_A at small values of K_A but level off at very high values. There has been a debate concerning the extent to which UTR sequences and the lengths of UTR are under the control of selection (37–41). The patterns we have just described, and the fact that our results and previous Drosophila studies (14, 21, 42) have revealed both positive and negative selection on UTR sequences, argue against nonadaptive hypotheses for their evolution, such as that of refs. 37 and 38.

Another important finding is that the inclusion of gene conversion in SSW models considerably increases γ_a estimates (with a corresponding decrease in p_a) (Tables 1 and 2). This suggests that future investigations, in which it may be possible to obtain more precise parameter estimates, should include gene conversion in sweep models. Consistent with the effect of the presence or absence of gene conversion, use of the higher estimate of the gene conversion rate from ref. 22 gave smaller estimates of the effect of BGS and larger γ estimates than when the lower value of ref. 23 was used (Figs. 3 and 4). These findings reflect the fact that, as has long been known, noncrossover gene conversion is a major source of intragenic recombination events in Drosophila (34), and affects the extent of associations between polymorphic variants within genes (43). Inclusion of gene conversion increases the effective rate of recombination in a gene, so that larger selective effects of mutations are needed to explain a given reduction in diversity at linked sites. Ignoring BGS increases the estimates of both γ_a and γ_u when gene conversion is included in the model, although the order of magnitude of the γ estimates is not changed if gene conversion and/or BGS are ignored. Curiously, omission of UTR effects had only a small effect on the estimates of the NS sweep parameters (Table 1).

Our results also suggest that selection at linked sites causes a large reduction in synonymous site variability relative to the expectation in the absence of such selection (Table 1 and Figs. 3 and 4), but that this effect is greatly mitigated by a high rate of gene conversion. For the standard model (with BGS, UTR effects, and a low rate of gene conversion), the mean reduction in π_S below the null expectation was ∼24%; without BGS, the reduction was 21%, and omitting UTRs reduced it to 16%. These estimates are much lower than the estimated reduction of ∼80% in ref. 14, the most comprehensive previous analysis of this question. The discrepancy does not primarily reflect the inclusion of gene conversion in our model, because omission of gene conversion increased our estimated net reduction only to 26% (Table 1, row 5).

Our model considers only the effects of selective events in genes themselves, which are likely to be the main contributors to correlations between π_S and K_A; it must therefore underestimate the overall effect of hitchhiking on diversity. A chromosome-wide diversity reduction of ∼45% for an autosome due to BGS alone was estimated in ref. 12; use of this in SI Appendix, Eq. S16c, together with the estimated rate of coalescence due to sweeps of 0.26 (obtained by equating the predicted value of π_S/π₀ = 0.793 for sweeps in the absence of BGS to the right-hand side of SI Appendix, Eq. S16c), gives a net mean reduction in diversity of ∼60%. Further reductions would be caused by sweeps of strongly selected mutations in other genomic regions; the combined effects of these and BGS across genes (13) may well be important in determining the overall pattern of variability across the genome.

We have assessed the extent to which our model of intragenic hitchhiking effects can explain the well-established relation between π_S and recombination (9) by applying the estimates of BGS and SSWs for the low gene conversion rate to predictions of the mean π_S for different values of the rate of crossing over. For values around one-eighth of that of the standard value of 1 cM per Mb, the slope of π_S against this measure of the rate of crossing over was ∼4 × 10⁻³, and approached 1.1 × 10⁻³ for a rate of 2 cM per Mb (this covers most of the range for the plot of autosomal π_S against rate of crossing over in figure 2 of ref. 18). The estimated multiple regression coefficient for π_S on crossing-over rate for mel-yak was ∼8.4 × 10⁻³ ± 0.2. It seems clear, therefore, that intragenic effects can account for only part of the relation between diversity and rate of crossing over.

Another interesting finding is the strong parallelism between the overall patterns of substitutions observed for the relatively distant D. melanogaster–D. yakuba comparison and for the D. melanogaster lineage. The linear regression coefficient for mel K_A on mel-yak K_A was 0.147 ± 0.001, with an r² of 0.63. The intercept (0.001 ± 0.0001) did not differ significantly from zero, and the slope is close to the ratio of the mean mel K_A to the mean mel-yak K_A (0.157), as would be expected if the underlying substitution rates are the same for both comparisons. This suggests that the mean rate of protein sequence evolution has been remarkably constant along the lineage connecting D. melanogaster and D. yakuba. Furthermore, the estimated mean rates of adaptive substitutions for both NS and UTR sites are very similar for mel-yak and mel (see the discussion after SI Appendix, Eq. S22).

A final notable feature is the sizeable positive multiple regression coefficient of π_S on Fop, the frequency of optimal codons in a gene (SI Appendix, Table S1). This is unexpected, because selection on codon use reduces synonymous site diversity (44), so that a negative relation between Fop and π_S would be expected. However, there is little evidence for ongoing selection on codon use at polymorphic synonymous sites in D. melanogaster, in contrast to D. simulans, except for genes with very high codon use bias (45), so that the expected direct effect of selection on codon use on π_S in our data is probably negligible. A plausible explanation is that both SSWs and BGS affect π_S and Fop in a similar way by reducing the N_e for a gene (27, 46). There is a strong negative correlation between K_A and Fop in the binned data (SI Appendix, Table S2), so that introducing a correction for Fop would bias the estimates of the effects of hitchhiking by incorrectly reducing the difference between values of π_S for low and high values of K_A.

We can also ask how our estimates of the parameters of positive selection compare with those from previous studies of Drosophila. Some previous estimates of γ_a obtained with relatively limited data were summarized in ref. 11; these estimates varied from 10 to 10⁴ depending on methodology. More recently, whole-genome data have been used for this purpose. Values of about 24 for γ_a and 0.005 for p_a were obtained in ref. 33, using estimates of the excess of high-frequency derived NS variants within a sample from a population in combination with DFE-α. These very low γ_a and high p_a values (compared with ours) probably reflect the fact that only relatively weakly selected NS mutations are likely to be captured among segregating NS mutations, and would have rather small effects on diversity at linked sites, whereas strongly selected mutations can contribute to NS divergence. The method of ref. 33 may thus underestimate mean γ_a by capturing only a fraction of the spectrum of effects, whereas the approach used here misses the effects of very weakly selected NS mutations. Weak positive selection of this magnitude causes only a minor reduction in diversity, because intragenic gene recombination dilutes its effect; with a rate of adaptive evolution corresponding to the middle of the range of the bins of K_A, −ln(π_S) is reduced below the neutral value by only 4.6% by NS SSWs with γ_a = 24 (assuming our standard gene model with the low rate of gene conversion) but is reduced by 25% when γ_a = 250. Sweeps with γ_a of the order of 100 are needed to account for the relation between π_S and K_A, even in the absence of gene conversion.

A composite likelihood approach to fitting both BGS and SSW models to patterns of polymorphism and divergence across the D. melanogaster genome, without using information on α or the DFE for deleterious mutations, was applied by Elyashiv et al. (14). They inferred a substantial fraction of NS substitutions with γ_a around 40 or less (36%), and a much smaller fraction (3.5%) with γ_a = 1,300; a mean γ_a of 309 can be obtained from their table S1 (using the entries for data corrected for missing substitutions). As noted above, the weak selection coefficient category cannot account for the π_S versus K_A relation, and the larger ones are probably inferred from intergene sweep and BGS effects. UTR substitutions were all in the low range of γ values, in contrast to our results. The reason for this is unclear, although their UTR estimate was very noisy.

The advantage of the approach of Elyashiv et al. (14) is that it uses all available information on synonymous site diversity, together with divergence at synonymous and NS and putatively selected noncoding sequences, without the need to bin data or fit a specific continuous distribution of selection coefficients. On the other hand, the inference procedure fits an arbitrary prior discrete distribution of selection coefficients for both deleterious and favorable mutations, and does not take into account potential functional determinants of these selection coefficients or information on the site frequency spectra at putatively selected sites, in contrast to our use of DFE-α and the effects on π_S of differences in K_A among genes. Further theoretical and simulation work is needed to provide methods that exploit the full range of information from population genomic data.

In common with other approaches to estimating the parameters of positive selection, we have made several more or less unrealistic assumptions. First, our treatment of BGS and SSWs assumes panmixia and a constant effective population size. Given that BGS seems to have relatively little effect on the γ and p estimates (Table 1), the main question is the effect of demographic factors on the SSW estimates. Inclusion of these complications in methods for estimating selection parameters is a challenging problem. However, we note that the spread to a high frequency of a favorable mutation in a population spread over a two-dimensional environment is much slower than in a panmictic population, which implies that there is more opportunity for recombination to dilute the effects of SSWs than with panmixia (47). This process would thus cause our γ estimates to be smaller than the true values, and the p estimates to be larger.

Second, we have assumed “hard” sweeps, based on unique mutations, rather than “soft sweeps” based on recurrent mutations or mutations arising from standing variation (48). If soft sweeps are prevalent in Drosophila, as has recently been argued (49), then the same pattern of bias as from a subdivided population would arise (50, 51). (Note, however, that gene conversion of a favored mutation onto an ancestral haplotype could generate the appearance of a soft sweep.) The opposite would apply to incomplete sweeps (52), if their incidence in a gene is correlated with its K_A value. These were omitted from our models because they do not affect K_A. However, the lack of evidence for intermediate-frequency NS and synonymous variants in pooled site frequency spectra for the Rwandan population of D. melanogaster, as seen in figure 5 of ref. 33, suggests that incomplete sweeps are relatively infrequent in this population. If favorable mutations do not arise as single events, the estimates of the proportions of favorable mutations are likely to be overestimated as well.

These considerations mean that the estimates of the parameters of positive selection obtained in this and previous studies need to be treated with caution, and will no doubt be revised with future improvements in inference procedures. It seems clear, however, that hitchhiking effects greatly reduce neutral or nearly neutral sequence diversity in genes in normally recombining regions of the Drosophila genome. There is increasing evidence that this is also true for many other organisms (1, 3). Such processes have important implications for attempts to estimate demographic parameters, which usually ignore these complications, as has been pointed out before (53–56). This is especially important when selection at linked sites distorts gene genealogies and hence site frequency spectra, because these are the main basis for inferring demographic parameters. There is evidence from our unbinned data for mel-yak that K_A is weakly positively correlated with the proportion of singletons at synonymous sites (Spearman partial rank correlation, ρ = 0.044, P = 0.002), consistent with increased distortions of the frequency spectra caused by hitchhiking in genes with large K_A, as was previously found by Andolfatto (15). The problem of relating the magnitude of these effects to the BGS and SSW models remains to be explored.

Materials and Methods

Primary Data Analyses.

We used polymorphism data for coding sequences of 7,099 autosomal genes, using 17 haploid genomes from the Gikongoro (Rwanda) population of Drosophila melanogaster provided by the Drosophila Population Genomics Project 2 (57), with Drosophila yakuba as an outgroup. The coding sequence data were filtered and analyzed as described in materials and methods in ref. 19. We excluded 225 genes located in the autosomal heterochromatic regions and on chromosome 4, where crossing over is absent (19, 58). We obtained diversity and divergence statistics for synonymous and NS sites, as well as for 5′- and 3′-UTRs for D. melanogaster genes with UTR annotations. For the analyses of UTRs, we followed the annotations of Flybase, version 5.33, masking any UTRs included in coding sequences and excluding UTRs with no available sequence in the outgroup, leaving a dataset of 5,992 genes with 3′- and/or 5′-UTRs. After applying a Kimura two-parameter correction (59), the mean level of divergence of UTR sequences between species, K_U, was 0.10, which is intermediate between the mean values for NS sites (K_A = 0.038) and synonymous sites (K_S = 0.262).

We also analyzed a second dataset where we used parsimony to infer derived substitutions that occurred along the branch separating D. melanogaster from its common ancestor with D. simulans, with two outgroups, D. simulans and D. yakuba. For this analysis, we used the D. melanogaster–D. simulans–D. yakuba gene alignments of ref. 60, from which we selected the coding and UTR regions corresponding to our chosen transcripts. We applied a custom Perl script to infer ancestral versus derived substitutions along the D. melanogaster lineage, counting nonsynonymous and substitutions as in ref. 19. For NS sites, the genes included in this dataset were a subset of the previous set (6,372 genes); there were 5,891 genes with 3′- and/or 5′-UTR sequences. The means of K_U , K_A, and K_S were 0.021, 0.006, and 0.053, respectively.

We calculated Spearman nonparametric partial correlations between π_S and K_A using the R function “pcor.test,” available at www.yilab.gatech.edu/pcor.R, with 95% CIs obtained by bootstrapping across genes. We used the following statistics for each gene as covariates: codon use bias, measured as the proportion of optimal codons (Fop); synonymous divergence (K_S), a proxy for the mutation rate of each gene; gene expression, measured using RNAseq (average log₂ reads per kilobase of transcript per million mapped reads across all developmental stages of D. melanogaster); smoothed effective rates of crossing over (centimorgan per megabase) from Loess regression fits to the rates of crossing over from the D. melanogaster data of ref. 22, multiplied by one-half to correct for the absence of recombination in males; GC content of short introns (<80 bp); the coding sequence (CDS) length of each gene. For further details concerning these measures, see refs. 18, 20, and 58.

For the analyses of NS sites, we applied DFE-α (24) to each of 52 (mel-yak) or 53 (mel) sets of genes binned by K_A, to estimate the following parameters: β, the shape parameter of a gamma distribution of the heterozygous fitness effects of deleterious NS mutations (the DFE); α, the proportion of adaptive substitutions; ω_a = α K_A/K_S, the rate of adaptive substitutions for NS mutations relative to the neutral rate; ω_na = (1 – α) K_A/K_S, the rate of nonadaptive substitutions (due to fixations of neutral or slightly deleterious mutations) relative to the neutral rate (26). Binning was necessary, because DFE-α parameter estimates for single genes are very imprecise.

We ensured that each bin included at least 50 genes (SI Appendix, Table S2) and removed bins with negative estimates of α (the bin with the lowest K_A in each case). We also excluded the last bin of mel-yak and the last two bins of mel, which contained genes with a broad range of very high K_A values that yielded anomalous estimates of α and/or β; this excluded only 74 and 81 genes for the mel-yak and mel datasets, respectively. This left a total of 50 bins for each NS dataset: 6,748 genes for mel-yak, and 5,397 genes for mel (SI Appendix, Table S2). The binned data gave similar linear regression coefficients for the relation between π_S and mean K_A for a bin (–0.026, mel-yak; –0.179, mel) to those for the unbinned K_A ∼ π_S relation (slope = –0.028, mel-yak; –0.177, mel).

To run DFE-α, we used a demographic model where the population at initial size N₁ (set to 100) experienced a step change to N₂ at n generations in the past. We also generated replicate bootstrap estimates of all of the variables for each bin separately by resampling genes 1,000 times within a given bin and running DFE-α for each bootstrap.

We also applied DFE-α to UTRs for genes binned by K_A, for both the mel-yak and mel data (SI Appendix, Table S3). (Note that these bins do not contain exactly the same genes as in the NS site analyses.) Least-squares quadratic regressions gave little evidence for significant relations between K_A and the primary DFE-α parameters, α and β, for the two types of UTR. The linear regression coefficient on K_A for α for 5′-UTRs for mel-yak had P = 0.041; no other coefficient approached significance. Given the number of tests, and the fact that normal distribution tests are likely to exaggerate significance, it seems safe to treat α and β for UTRs as independent of K_A, which reduces the complexity of the models used in the data analyses.

K_U values were, however, strongly related to K_A for the binned data. For mel-yak, the quadratic regressions of K_U on K_A were y = 0.068 + 1.54x – 6.08x² for 3′-UTRs and y = 0.0087 + 0.641x – 1.901x² for 5′-UTRs. For mel, the regressions were y = 0.016 + 1.12x – 27.4x² for 3′-UTRs, and y = 0.019 + 0.330x for 5′-UTRs (there was no evidence for a significant quadratic term in this case). For all coefficients shown, P < 0.005. These were used to obtain values of K_U for the K_A bins used in the BGS and SSW models in the final data analyses described below.

Similarly, the lengths of the UTRs were strongly negatively related to K_A, with the relation being strongest for low K_A values (SI Appendix, Figs. S6 and S7). For the mel-yak binned data, a quartic regression on K_A gave the best fit for 3′-UTRs, with y = 469–1.18 × 10⁴ x + 1.73 × 10⁵ x² – 1.05 × 10⁴ x³ + 2.22 × 10⁴ x⁴ (P < 0.002 for all but the quartic coefficient, for which P < 0.02); for 5′-UTRs, a quadratic gave a good fit, with y = 258–2.88 × 10³ x + 1.21 × 10⁴ x² (P < 0.0001 for all coefficients). For mel, quadratic regressions on K_A gave good fits for both types of UTR, with y = 430–3.02 × 10⁴ x + 7.96 × 10⁵ x² for 3′-UTRs, and y = 279–1.95 × 10⁴ x + 5.06 × 10⁵ x² for 5′-UTRs (P < 0.0001 for all coefficients). These equations were used to predict UTR lengths in the models used in the final data analyses.

Because of the lack of evidence for correlations between K_A and the parameters of positive selection, for the final data analyses we used estimates of the DFE-α parameters for UTRs obtained from the data as whole (see above). For the mel-yak data, the shape parameters of the gamma distribution assumed for the DFE were β = 0.330 and β = 0.328 for 3′- and 5′-UTRs, respectively; the corresponding α values were 0.471 and 0.580. Similar values were found for the mel data (β = 0.336 and β = 0.359, for 3′- and 5′-UTRs, respectively; α = 0.553 and 0.548). Because the values for the two types of UTR were similar, we treated them as identical, and used the mean values of the relevant variables as parameters in the models of BGS and SSWs. Because K_U was found to increase across the bins of K_A, we estimated ω_a and ω_na for the UTRs in a given bin by multiplying the ratio of the predicted value of K_U for the bin to K_S for the bin by α and 1 – α, respectively, after adjusting K_S for the effect of codon use on substitution rate by applying SI Appendix, section 5, Eq. S22.

Modeling BGS.

To model the effect of BGS on a single gene, we first used a modification of the approach of ref. 27, in which the effects of selected sites within a gene on neutral diversity at a focal site were estimated by summing the contributions from all of the selected sites. We assumed a gene model with n_ex exons, each of length l_ex base pairs and interrupted by n_ex – 1 introns each of length l_in. NS deleterious mutations occurred only in the first two sites of a codon.

The expected nucleotide site diversity at a focal neutral site j, relative to its value in the absence of selection, is denoted by B_j. It is convenient to work with E_j = – ln(B_j) for the purpose of relating theory to data. Using the natural logarithm of equation 4 in ref. 61, we have the following:

$$E_j\approx {\displaystyle \sum _i}\frac{u_i{t}_i}{{\left[t_i\mathrm{+}{r}_{ij}\left(1-t_i\right)\right]}^2},$$ [1]

where u_i is the mutation per base pair at site i, t_i is the selection coefficient against heterozygotes for a mutation at the ith site, r_ij is the frequency of recombination between nucleotide sites i and j, and the summation is taken over all base pairs in the gene.

To calculate r_ij, we used equation 3 of ref. 27:

$$r_{ij}=d_{ij}{r}_c\mathrm{+}{g}_c{d}_g\left[1-\exp \left(-d_{ij}/d_g\right)\right],$$ [2]

where d_ij is the separation between sites i and j in base pairs, r_c is the rate of crossing over per base pair, g_c is the rate of initiation of noncrossover-associated gene conversion events per base pair in female meiosis, and d_g is the mean length of a gene conversion tract in base pairs. The tract length of a conversion event was assumed to follow an exponential distribution (35).

We also developed an integral approximation, which ignores the presence of introns (SI Appendix, section 1, Eq. S10b). This was found to give a good approximation to Eq. 1 (Fig. 2) and was used in all of the analyses of fits of the models to the data, because it was computationally more efficient. To obtain predictions for a given distribution of selection coefficients, the procedures described in SI Appendix, sections 2 and 3, were applied.

As mentioned in Materials and Methods, Primary Data Analyses, UTRs show levels of divergence between species (K_U) that are intermediate between those for NS and synonymous sites, and proportions of substitutions attributable to positive selection that are similar to those for NS sites. The BGS effects of UTR mutations were modeled in a similar way to NS sites, either by summation as in Eq. 1 or by integration (SI Appendix, Eq. S12) over the BGS effects of the UTR sites at either end of the gene, and then integrating over t values drawn from a truncated gamma distribution assigned to UTR mutations.

To compare the predictions of the models to the observed values of −ln(π_S) for each bin, we corrected for the possible effect on π_S of differences among bins in K_S (15). The regression coefficient for −ln(π_S) on K_S was estimated by dividing the multiple regression coefficient for π_S on K_S for the unbinned data by the mean of K_S. We then multiplied this regression coefficient by the difference between mean K_S for a bin and the mean of K_S over all bins, and adding the product to −ln(π_S) for the bin. We also applied this procedure to the crossing-over rate, because this also had a substantial effect on π_S (SI Appendix, Table S1); although other variables had significant multiple regression coefficients, the effect sizes were small, with the exception of Fop, and they were thus ignored. In Discussion, we provide reasons for disregarding the effect of Fop.

Expected Effects of SSWs on a Single Gene.

The combined effects of BGS and SSWs were modeled by a modification of the summation model described above, using the commonly made assumption that sweeps are sufficiently rare that the effects of different sweeps on synonymous site diversity can be treated as independent of each other (14, 62), and that BGS effects are independent of sweep effects (3, 14, 63) (SI Appendix, section 4, Eq. S16).

Estimating Positive-Selection Parameters.

To estimate the parameters of positive selection, the effects of SSWs were included in the predictions of diversity relative to its value in the absence of selection (π₀), using SI Appendix, Eq. S16c. This can be used to determine the deviation, dev_j, between the observed and predicted values of –ln(π/π₀) for the jth bin. For a given pair of values of the scaled selection coefficients γ_a and γ_u for NS and UTR sites for a bin, all of the variables that appear in the second term on the right-hand side of SI Appendix, Eq. S18, can be computed by using the empirical estimates for the bin from DFE-α of the rates of adaptive substitutions for NS and UTR sites (ν_a and ν_u) used in SI Appendix, Eq. S17. For NS sites, we used a model in which γ_a was a linear function of the ratio of K_A to its maximum value, which yields different γ_a estimates for each bin, whereas γ_u was assumed to be constant across bins, because the DFE-α analyses described in Primary Data Analyses, suggested that α for UTRs were constant across bins. We then used SI Appendix, Eq. S18, to search for a set of parameters of positive selection that minimized the sum of squares of dev_j, SSD, as described after SI Appendix, section 4, Eq. S19.

To obtain CIs for the parameter estimates, bootstrapping over genes within each bin was carried out. Here, we used grids of seven values of each variable, with only two iterations of the search, because the computation times were long (several days on a desktop computer).