The mechanics of state dependent neural correlations

Abstract

Simultaneous recordings from large neural populations are becoming increasingly common. An important feature of the population activity are the trial-to-trial correlated fluctuations of the spike train outputs of recorded neuron pairs. Like the firing rate of single neurons, correlated activity can be modulated by a number of factors, from changes in arousal and attentional state to learning and task engagement. However, the network mechanisms that underlie these changes are not fully understood. We review recent theoretical results that identify three separate biophysical mechanisms that modulate spike train correlations: changes in input correlations, internal fluctuations, and the transfer function of single neurons. We first examine these mechanisms in feedforward pathways, and then show how the same approach can explain the modulation of correlations in recurrent networks. Such mechanistic constraints on the modulation of population activity will be important in statistical analyses of high dimensional neural data.

Introduction

A main challenge in systems neuroscience is to understand the patterns of neural activity that support sensory processing¹, memory², decision making³, and cognition⁴. This activity emerges from interactions between neurons⁵, as well as bottom-up sensory and top-down modulatory inputs⁶. Determining how neural circuits give rise to these activity patterns will provide constraints on theories of neural computation, as well as bridges between physiology and cognition.

Different statistical approaches have been used to successfully uncover the important features of network activity, such as the functional coupling within a network⁷, the dimensionality of population responses⁸, and their variability^9,10,11. While these approaches allow us to identify the essential statistical features of large scale network activity, they give little insight into the physiological causes of the observed activity patterns. Moreover, the high dimensionality and the limited amount of available data obtained from neural recordings require the development of new statistical approaches^12,13. As recordings from larger and larger groups of neurons become more common¹⁴, identifying constraints on the recorded activity will become essential. Computational models that capture the essential biophysical properties of actual neurons can be better constrained and interpreted than models that make no assumption about the dynamics of individual units and their interactions.

Mechanistic models have long been used to understand the receptive field organization and trial-averaged dynamics of single neuron responses. Most famously, Hubel and Wiesel postulated the structure of thalamic projections to cortex from single neuron firing responses to bars of light at various orientations¹⁵. Others have used mechanistic models to examine the impact of feedforward¹⁶ and recurrent^17,18 neural architectures on stimulus selectivity, providing targeted predictions for subsequent experimental studies of vision^19,20 and other modalities^21,22. This approach is not restricted to sensory areas where neural responses are easily affected by changes in stimuli. For example, there has been extensive work in building circuit models of persistent activity in pre-frontal cortex during working memory tasks²³, and the formation of grid cell responses in hippocampus²⁴, all replicating trial-averaged single neuron responses. We propose to extend this modeling approach by outlining how specific biophysical aspects of cellular and circuit structure can explain the joint variability of pairs of spike trains.

Of particular interest is the trial-to-trial covariability between the spiking activity from simultaneously recorded neuron pairs. These noise correlations provide a simple and robust measure of the internal coherence of neural activity²⁵. There is a vibrant debate about how noise correlations impact neural coding^26,27,28,29. However, in this review we focus on the relation between noise correlations and underlying circuit and cellular mechanics.

Noise correlations are frequently attributed to the presence of common afferent projections to a neuron pair³⁰. A variety of mechanisms, however, can lead to correlated neural responses. On the one hand, direct common projections are not required if the presynaptic ensembles are themselves correlated³¹. On the other hand, correlations due to shared excitatory and inhibitory projections can cancel one another yielding low net correlations despite shared afferent input³². Correlations can also reflect local recurrent connectivity^33,34,35, or feedforward inputs such as those induced by fluctuations in bottom-up or top-down projections³⁶. Finally, the cellular nonlinearities involved in the transfer of input currents to spike outputs are also important in shaping neural correlations^37,38,39. It is this diversity in the circuit and cellular causes of noise correlations that make them challenging to study from a mechanistic perspective.

An often-used strategy in systems neuroscience is to record neural activity under different neural states. State comparisons have been made between spontaneous and stimulus evoked neural activity⁴⁰, when attention is directed within or outside the receptive field of a population⁴¹, different levels of arousal⁴², and active versus passive sensory acquisition⁴³. State modulation is essential to understanding neural activity that is specific to a certain neural computation. It also serves another purpose: It offers important clues about the circuit and cellular mechanisms underlying collective neural activity. Different mechanisms could explain the correlations observed under a single state. However, only some of these mechanisms will be consistent with observations from multiple states.

We begin our review with a partial listing of the increasing number of experiments showing state dependent modulation of neural correlations. We next synthesize several theoretical results into one general framework that includes three mechanisms of correlation modulation: pre-synaptic correlations, internal fluctuations, and neural transfer. We explore these distinct mechanisms separately using a feedforward circuit model, highlighting their differences. We finish by discussing how these insights can inform the analysis of correlation modulation in recurrent networks of spiking neurons, where several mechanisms can be simultaneously engaged. Our review highlights how modulations in neural correlations could provide a window into the physiology that underlies state dependent changes in the nervous system.

Modulation of neuronal correlations

Simultaneous recordings from large populations of neurons are becoming commonplace in systems neuroscience¹⁴. Consider two spike trains from the k^th trial of such an experiment, $y_1^k(t)={\sum }_m\delta (t-t_{1m}^k)$ and $y_2^k(t)={\sum }_m\delta (t-t_{2m}^k)$, where the Dirac delta function, $\delta (t-t_{im}^k)$, represent the m^th spike from neuron i. The spike count correlation coefficient^44,25 between the two spike trains is:

$$\rho (n_1^k,n_2^k)=\frac{\text{Cov}(n_1^k,n_2^k)}{\sqrt{\text{Var}(n_1^k)\text{Var}(n_2^k)}}.$$

Here $n_i^k={\int }_0^T{y}_i^k(t)dt$ is the random spike count computed over a duration T on trial k, and $\text{Cov}(n_1^k,n_2^k)$ and $\text{Var}(n_i^k)$ denote the covariance and variance over trials, respectively. When ρ appears without a subscript, it always refers to output spike correlations. Over small durations (T ~ 1 – 10 ms) ρ measures spike train synchrony, while over long durations (T ~ 10² – 10³ ms) it captures the shared fluctuations in the firing rates of the two neurons over trials.

A growing list of studies show large heterogeneity in correlations measured across the nervous system, as well as from neuron pairs within the same brain region^25,45,46,47. Nevertheless, the average correlation coefficient across paired spike trains in a cortical population is typically small, ranging from 0.01 to 0.3 depending on the brain region, brain state, and joint stimulus preference of the neuron pair^48,25,45. Here we primarily consider long-timescale correlations, although our general framework is applicable to arbitrary time windows.

Neuronal correlations are modulated by a variety of factors including attention and arousal, learning, as well as stimulus onset and type. In this study we will consider correlation changes induced by a broadly defined state change of the nervous system (see Box 1). We present a partial list of examples in Table 1 with each entry describing two states, labeled A and B. For each case we list the relative change of correlation from state A to B, as well as the trial duration T over which ρ is measured. Table 1 shows that ρ can be modulated considerably in different animals, brain regions, cognitive contexts, and when measured over various durations, T. The three final entries in Table 1 highlight correlation modulation determined by intracellular recordings, results that are especially important when establishing physiological mechanisms.

Box 1: Neural State.

The operating state of the brain, or simply state, refers to the context under which neural activity is recorded. This includes several possibilities, such as: The cognitive state is determined by an animal’s level of arousal, attentional focus, or degree of engagement in a task. In the absence of a stimulus or task the neural network is in the spontaneous state, as opposed to an evoked state. Stimuli that do not directly drive a neuron, yet recruit a non-classical surround can change the processing state of a neuron. A change in stimulus features within a neuron’s receptive field may change its firing rate. However, it does not change the context under which the neural activity is observed, and hence such stimulus features do not determine a state.

Table 1. Examples of state dependent modulation of neural correlation ρ between two states.

We denote the two states with A and B, and the correlations measured in each state by ρ^A and ρ^B with ρ^A > ρ^B unless otherwise noted.

System	Modulation	Window length T	ρB/ρA	Reference
Extracellularly recorded spike trains
Electrosensory (fish)	Spatially broad (A) vs. compact (B) stimuli	50ms	~ 0.68	132
V4 (macaque)	Unattended (A) vs. attended (B) (spatial)	200ms, 100ms	~ 0.70, 0.66	96,133
V4 (macaque)	Unattended (A) vs. attended (B) (spatial+contrast discrimination)	333ms	~ (0.85,1.05)1	134
V4 (macaque)	Attended with PFC lesion (A) vs. attended (B)	150ms	~ 0.75	135
V1 (macaque)	Spontaneous (A) vs. evoked (B) activity	100ms	~ 0.63	48
V1 (macaque)	Non-adapted (A) vs. adapted (A) responses	1.86s	~ 0.78 2	136
V1 (macaque)	Spontaneous (A) vs. stimulation of the non-classical surround (B)	600ms	~ 0.85	137
V1 (macaque)	Anesthetized (A) vs. awake (B)	500ms	~ 0.14	10
V1 (macaque)	Attended with drug application3 (A) vs. attended without drug (B)	300ms	~ 0.60, 0.4, 1.8	138
V1 (mouse)	Low (A) vs. high (B) arousal	10s, 150ms	~ −0.22, 0.8	139,140
V1 (mouse)	Stationary (A) vs. locomotion (B)	100ms	~ 0.45	141
A1 (macaque)	Passive (A) vs. detection task (B)	Not given	~ 0.5 4	142
PFC (rhesus)	Untrained (A) vs. trained (B)	100ms	~ 0.5	143
MSTd (macaque)	Untrained (A) vs. trained (B)	100ms	~ 0.2 5	129
MT (rhesus)	Task cooperation (A) vs. competi- tion (B)	~ 650ms	~ (0.65,1.55) 6	144
Piriform cortex (mouse)	Pre-task (A) vs. odor sniff (B)	120ms	~ 0.12	145
CLM (European starling)	untrained (A) vs. task-relevant (B)	565ms	~ (0.35, 1.65) 7	146
Area 17 (cat)	Perpendicular (A) vs. aligned (B) surround grating	1ms	~ 0.8 8	147
V1 (cat)	Flashed stimuli (A) vs. drifting grating (B)	100ms	~ 0.5	45
Intracellularly recorded membrane potentials
V1 (cat)	Spontaneous (A) vs. evoked (B) activity	0–10 Hz 9	~ 0.75	148
Barrel cortex (mouse)	Quiet wakefullness (A) vs. active whisking (B)	2 ms	~ 0.5	149
V1 (macaque)	Spontaneous (A) vs. evoked (B) activity	0.5–4 Hz 10	~ 0.5	150

¹Neuron pairs were grouped according to their task tuning similarity (TTS). Neuron pairs with TTS > 1 show an attention mediated decrease in ρ, while pairs with TTS < −1 show an increase.

²Restricted to neuron pairs with ρ^A > 0.

³Three different drugs were applied to recorded neurons during a cued spatial attention task: DL-2-amino-5-phosphonopentanoic acid (APV), 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX), and an NMDA receptor agonist; relative correlations are listed in that order.

⁴Restricted to neurons with similar tuning.

⁵Trained and untrained correlations are obtained from separate animals.

⁶Task specifics placed neuron pairs to have either a cooperative relation to one another, or a competitive one. Neuron pairs were grouped according to the difference in their preferred direction of motion (PD), and competition decreased ρ for neuron pairs with PD < 135°, while it increased ρ for pairs with PD > 135°.

⁷Neuron pairs with signal correlation > 0.4 show a relative modulation of 0.65, while pairs with a signal correlation < 0.4 show a modulation of −0.65.

⁸Since firing rate changes were negligible the measures were computed only from Cov(y₁, y₂).

⁹Computed from the integrated spectral coherence between simultaneously recorded membrane potentials.

¹⁰Computed from the integrated spectral coherence between simultaneously recorded membrane potential and nearby local field potential.

In sum, the diversity in the conditions and states in which modulations in correlation have been observed suggests that distinct cellular and circuit mechanisms may be responsible. We next present a unified framework to discuss and compare a number of mechanisms that can impact the correlation coefficient, ρ, as well as how it is modulated across brain states.

Central framework for correlation modulation

Biological neural circuits consist of neurons belonging to a variety of cell classes wired in complex ways. It is tempting to try to infer the structure of these circuits and the physiological properties of neurons within them from multicellular recordings from subsets of neurons. Such an approach is fraught with difficulties⁴⁹, many of which are due to the fact that only part of the population is observed. Here we describe an alternative strategy that is more modest in scope, but provides a general framework for discussing how modulations in spiking correlations depend on biophysical changes in the underlying circuit to which the neurons belong.

To start, we consider a pair of simultaneously recorded neurons (Fig. 1, black triangles) that are members of a larger, yet unknown, neural circuit (Fig. 1, colored symbols). To simplify our analysis we assume that neurons in the pair are not directly coupled (although this is not required for our treatment). In this case any correlations between spike trains of the neuron pair are inherited from correlations between their inputs. Under this assumption, we will explore how the cellular properties of the postsynaptic neurons, and those of the presynaptic circuit that drives them, influence correlation transfer.

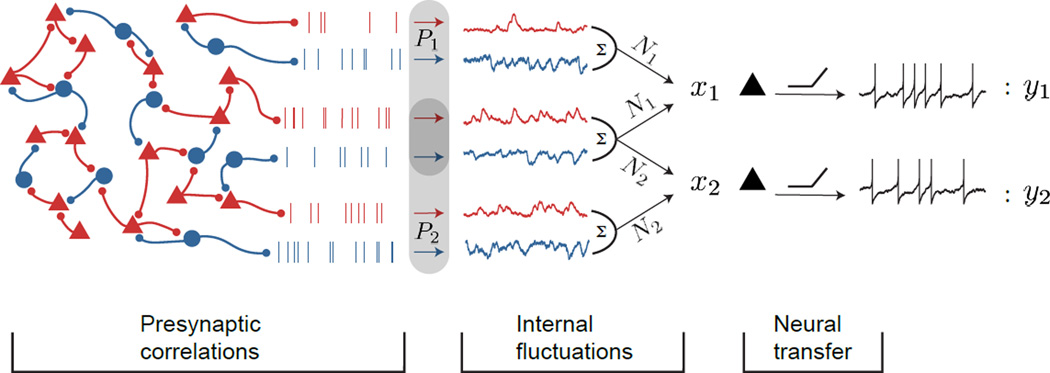
Figure 1. Schematic illustration of correlation transfer in networks of spiking neurons.

We consider a pair of unconnected neurons (black triangles) that receive input from a presynaptic population of excitatory neurons (red triangles) and inhibitory neurons (blue circles). Covariability, Cov(P₁, P₂), in the presynaptic inputs, P₁ and P₂, to the postsynaptic pair is due to a combination of shared anatomical projections leading to a shared input (overlap between P₁ and P₂) and correlations between the activity of the presynaptic populations. This presynaptic activity along with internal synaptic and cellular fluctuations, N_i, determine the postsynaptic currents, x_i (i = 1, 2) in each of the two postsynaptic cells. Finally, the nonlinear spike generation mechanism translates these postsynaptic currents into the output spike trains, y₁ and y₂.

On trial k of the experiment neuron i of our pair (i = 1 or 2) responds to its afferent inputs, $x_i^k(t)$, with $n_i^k$ spikes over the window T. We consider values of T that are much larger than the synaptic and membrane timescale of the neurons, thereby not explicitly measuring the fine temporal structure of the spike trains. For simplicity, we assume that Var(n₁) = Var(n₂) = Var(n), so that the correlation coefficient between the responses from the neuron pair is $\rho =\frac{\text{Cov}(n_1,n_2)}{\text{Var}(n)}$.

The two neurons do not interact directly, so ρ ≠ 0 implies that the presynaptic inputs to the neurons, x₁(t) and x₂(t), are themselves correlated. We quantify this correlation using the input covariance Cov(x̂₁, x̂₂), between the integrated synaptic inputs, ${\widehat{x}}_i^k={\int }_0^T{x}_i^k(t)dt$. When the input covariance, is small we can use the linear approximation:

$$\text{Cov}(n_1,n_2)\approx L^2\text{Cov}({\widehat{x}}_1,{\widehat{x}}_2).$$ (1)

to relate input and output covariance³⁷. Here L = L₁ = L₂ is the linear response of the target neuron^50,51. Briefly, for weak common fluctuations, s(t), we have 〈n_i〉 ≈ 〈n_io〉 + L_iŝ, where 〈·〉 denotes the expectation over trials, 〈n_io〉 is the mean spike count of the of neuron i at its operating point (defined by s = 0), and $\widehat{s}={\int }_0^{T}s(t)dt$. The common fluctuations then simply perturb the neuron pair’s joint activity about an operational point (where Cov(n_1o, n_2o) = 0). If the operating point changes (say through a modulation), the linear approximation may change L but Eq. (1) remains valid. However if perturbations are too large, this linear approximation can break down, although it could still provide qualitative insights. For large time windows, T, the response function L/T is approximately the derivative (slope) of the firing rate – input curve of a neuron at the operational point^37,38.

We assume that the response of each neuron is the result of a leaky, potentially nonlinear integration of its inputs. The total integrated input, x̂_i(t), includes presynaptic and postsynaptic components. The covariance between presynaptic inputs, Cov(P₁, P₂), is determined by both common projections to the neuron pair, as well as correlations in the activity of the presynaptic pool of neurons^32,31. From the vantage point of a postsynaptic neuron pair these sources are indistinguishable. If we neglect synaptic and dendritic nonlinearities then we have that Cov(x̂₁, x̂₂) ∞ Cov(P₁, P₂), where the covariance on the right is between the activities, $P_i^k$, of the population presynaptic to neuron i on trial k (Fig. 1).

Postsynaptic effects, such as stochastic vesicle release from synaptic contacts or channel fluctuations, are another well studied source of variability^52,53. Since these fluctuations are private to each neuron, we assume that they are uncorrelated between the neuron pair. Further, they are also likely uncorrelated with the activity of the presynaptic population, so that Var(x̂_i) ∞ Var(P_i) + Var(N_i), where N_i is the postsynaptic noise (integrated over T) within neuron i (Fig. 1).

The total correlation coefficient of the inputs is then

$${\rho }_x=\frac{\text{Cov}({\widehat{x}}_1,{\widehat{x}}_2)}{\text{Var}(\widehat{x})}=\frac{\text{Cov}(P_1,P_2)}{\text{Var}(P)+\text{Var}(N)}=\frac{\rho P}{1+R_x}.$$

where R_x = Var(N)/Var(P) and ρ_P = Cov(P₁, P₂)/Var(P). We again assume that the two neurons are statistically identical, so that Var(x̂) = Var(x̂₁) = Var(x̂₂), and similarly for the other variances. The coefficient R_x then measures the excess fluctuations in the input current due to internal processes in each neuron. Ultimately, we are interested in the variability of the spiking output of a neuron, n_i. Unfortunately there is no simple linear relationship between Var(n_i) and Var(x̂_i)⁵⁴, as there is for Cov (see Eq. (1)). This makes it difficult to determine the excess variability in the spike response due to internal fluctuations, R_y, from only the knowledge of R_x. However, we make the reasonable assumption that there is a monotonic relationship between them (i.e when R_x increases so too does R_y). In our review we use this observation to simplify our exposition, and hereafter make no distinction between R_x and R_y.

Finally, we consider the network to be in one of two states (labelled A and B) that differ in their spike count pairwise correlation coefficient ρ. This analysis then yields the following expression for the ratio of spike count correlations, ρ^A and ρ^B in the two states, A and B:

$$\frac{{\rho }^B}{{\rho }^A}=\left(\frac{{\rho }_P^B}{{\rho }_P^A}\right)·{\left(\frac{1+R^B}{1+R^A}\right)}^{-1}·{\left(\frac{L^B}{L^A}\right)}^2.$$ (2)

The modulation in the output correlation between the two states results from three separate terms:

1. ${\rho }_P^B/{\rho }_P^A$ captures state dependent changes in the correlations of the presynaptic input;

2. [(1 + R^B)/(1 + R^A)]⁻¹ captures state dependent changes in the internal fluctuations within each neuron in the pair;

3. [L^B/L^A]² captures state dependent changes in the response gain of the transfer from synaptic input to the neurons’ output. Generally L^A ≠ L^B, since the linearization about the operational point at state A will typically differ from that at state B.

We next explore each of these modulatory terms in our feedforward network.

Three mechanisms of correlation modulation

There are several distinct ways to model a state change within the network. For example, neuromodulation through the activation of cholinergic and monoaminergic pathways can have diverse effects on the cellular and synaptic properties in a network⁵⁵. Alternatively, the temporal dynamics of large scale neural activity as measured by electroencephalogram (EEG) and local field potential (LFP) recordings, show qualitative differences when comparing two distinct neural states⁴¹. This can be modeled by changing the statistics of the global input to the network^9,10,11,56. In our framework a presynaptic pool of excitatory and inhibitory neurons (red and blue respectively in Fig. 2) project to a representative neuron pair (Fig. 2, black). We model the shift from state A to state B as an increase in a static external drive to the presynaptic neuron population (Fig. 2, a1,b1, and c1 vs. a2, b2, and c2). This modeling choice is sufficient to cause changes in both the firing rate and correlations of the postsynaptic pair and can be loosely interpreted as capturing a wide array of neuromodulation schemes. We examine this general model of modulation (see Methods: general feedforward model) in three examples, each highlighting a different mechanism of correlation modulation.

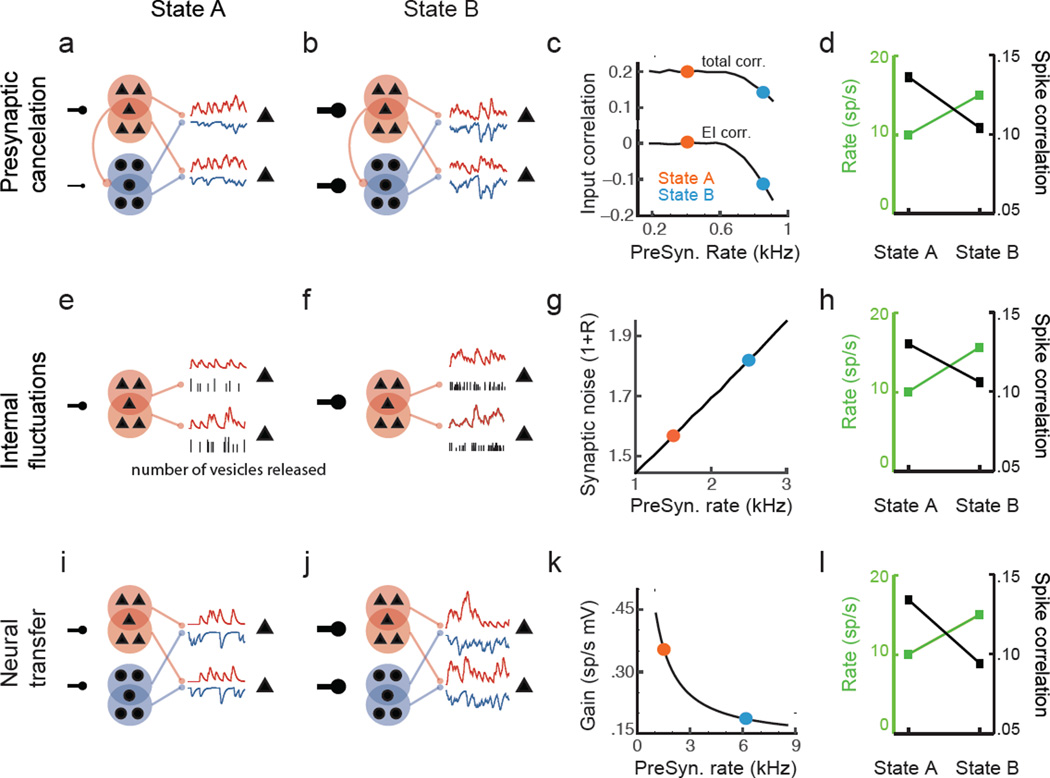
Figure 2. Three mechanisms for correlation modulation.

(a) The presynaptic excitatory (E) population (red) and the inhibitory population (blue) both project to the postsynaptic neuron pair. In state A the presynaptic populations are weakly driven, with a slight asymmetry favoring the E population (a1). In contrast, both presynaptic E and I populations are driven strongly in state B (a2). The increase in presynaptic rate uncovers an anticorrelation between the E and I currents, ultimately decorrelating the overall synaptic inputs to the postsynaptic pair (a3). The result of the modulation from state A to B is to both increase the postsynaptic firing rate (a4, green) and decrease spike count correlation (a4, black). (b) The synapses linking presynaptic activity to postsynaptic current are probabilistic, with activity dependent reliability of vesicle release (we show only the E population for schematic brevity). In state A the presynaptic populations are weakly driven and the number of vesicles released per presynaptic spike, and their reliability, is high (b1). In contrast, in state B the presynaptic population fires at a higher rate, resulting in less reliable synaptic transmission (b2). The decrease in synaptic reliability from state A to B increases the synaptic noise to signal ratio, 1 + R (b3). As in a4, the transition from state A to B has the effect of both increasing the postsynaptic firing rate (b4, green) and decreasing the spike count correlation (b4, black). (c) The presynaptic E and I populations project balanced, conductance based inputs to the postsynaptic pair. In state A the firing rates of the presynaptic populations are low, and the overall synaptic fluctuations are small (c1). In contrast, in state B the presynaptic rates are higher, resulting in larger fluctuations in the input to the postsynaptic pair (c2). The increase in conductance based fluctuations between state A and B reduces the spike response gain (L) (c3). As in a4, the transition from state A to B increases the postsynaptic firing rate (c4, green) and decreases the spike count correlation (c4, black).

Modulating presynaptic correlations

We start by analyzing the effect of changes in the correlations in the pool of presynaptic neurons (see Methods: Modulating presynaptic correlations). Here, as in other examples, the target pair of neurons receive correlated excitatory (E) and correlated inhibitory (I) inputs via an overlapping set of projections from the presynaptic pool. In the present case we also include direct connections from excitatory to inhibitory neurons within the presynaptic pool itself. These connections can correlate the inhibitory activity received by one neuron in the pair with the excitatory activity received by the other neuron. The covariance of the total presynaptic activity, ${\widehat{P}}_i^k={\widehat{E}}_i^k+{\widehat{I}}_i^k$ over trials is computed as:

$$\text{Cov}({\widehat{P}}_1,{\widehat{P}}_2)=\text{Cov}({\widehat{E}}_1,{\widehat{E}}_2)+\text{Cov}({\widehat{I}}_1,{\widehat{I}}_2)+\text{Cov}({\widehat{E}}_1,{\widehat{I}}_2)+\text{Cov}({\widehat{I}}_1,{\widehat{E}}_2).$$ (3)

In state A both excitatory and inhibitory presynaptic pools are weakly driven, resulting in low firing rates in the presynaptic populations and subsequently low firing rates of the postsynaptic neuron pair. The low rates in the presynaptic populations allow the spike threshold nonlinearity of the presynaptic cells to suppress neural transfer (the response gain L of the presynaptic populations is small). This compromises the presynaptic inhibitory pool’s response to projections from the excitatory presynaptic population. In particular, the low firing rates in the inhibitory pool imply that the excitatory input fluctuations given to the inhibitory pool are poorly transferred by the inhibitory pool to the postsynaptic neuron pair. This results in approximately uncorrelated outputs of the excitatory and inhibitory pool, Cov(Ê_i, Î_j) ≈ 0 (Fig. 2, a3 orange dot). In this case ${\rho }_P^A$ is due primarily to overlapping projections with Cov(Ê₁, Ê₂) > 0 and Cov(Î₁, Î₂) > 0 (Fig. 2, a3 orange dot).

In state B the presynaptic pool of neurons fires at a higher rate, increasing the net input to the postsynaptic pair, yielding a higher postsynaptic firing rate compared to state A (Fig 2, a4 green). Further, since the drive to the inhibitory pool in state B is larger than in state A then the spiking nonlinearity of the inhibitory neurons does not compromise their response to the projections from the excitatory pool. Thus the activity of the presynaptic inhibition is correlated with that of the presynaptic excitation. However, since inhibition is hyperpolarizing while excitation is depolarizing, the projections from the excitatory pool to one postsynaptic neuron are anticorrelated with the inhibitory projections to the other postsynaptic neuron. In the end, Cov(E_i, I_j) < 0 (Fig. 2, a3 blue dot), and this negative covariability cancels the positive covariability due to overlapping projections. This has the effect of reducing overall input correlations, so that ${\rho }_P^B/{\rho }_P^A<1$ (Fig. 2, a3 blue dot). This leads to a reduction in output correlations (Fig 2, a4 black) with ρ^B/ρ^A < 1 (via Eq. 2). In this example the linear transfer function remained approximately constant between the two states (L^A ≈ L^B) and we did not model private fluctuations (R^A = R^B = 0).

Excitatory and inhibitory currents are widely reported to be strongly correlated with one another^57,58,59. In our model such correlations are due to feedforward excitatory and the associated disynaptic inhibitory pathways from the presynaptic population – a canonical circuit in the brain⁶⁰. The functional consequences of this type of connectivity were first investigated using trial-averaged single neuron activity, with delayed inhibition creating a ‘window of opportunity’ for neural responses ^61,62,21,63. More recent studies have investigated the influence of this circuit structure on correlations between excitation and inhibition and the covariability of population responses. In the whisker barrel cortex of rodents this circuit structure supports an active decorrelation of the spiking activity between putative excitatory and inhibitory units when measured in the stimulus evoked state, when compared to the spontaneous state^64,65. A functionally similar feedforward circuit in the electrosensory system of weakly electric fish drives a decorrelated state when stimuli are spatially broad as opposed to spatially compact^66,67. The example presented above was based on the models developed in those studies.

The cancelation of overall input current covariability by anti-correlated excitatory and inhibitory inputs to neuron pairs was initially studied by Renart, de la Rocha et al.³². However, they considered the case of recurrently coupled cortical networks, as opposed to the feedforward structure analyzed above. They showed that in balanced networks of neurons⁶⁸ the large sources of correlation due to shared projections within and outside the circuit were robustly and fully cancelled, stabilizing an asynchronous network state. Conditions under which such cancellation occurs have been clarified in further studies of recurrently coupled networks of model spiking neurons^69,70. Modulation of correlations is difficult to study in these cases, mainly because correlations are very small (on the order of the inverse of the network size). We will revisit correlation modulation in recurrent networks in a later section.

In sum, the circuit mechanisms that determine pre-synaptic covariability are diverse, and a complete treatment is beyond the scope of this review. Nevertheless, in many cases a cancellation between various sources of opposing pre-synaptic correlations is a key component.

Modulating postsynaptic noise

To demonstrate the influence of private noise on correlation transfer, we consider a model in which synaptic release is random (see Methods: Modulating internal fluctuations). Every presynaptic spike releases a random number of synaptic vesicles to the postsynaptic neuron⁵³. This is due to both the nature of vesicle release and the fact that vesicles are replenished at random times. Vesicle recovery dynamics result in activity-dependent changes in the synaptic current’s mean and variability. This type of synaptic dynamics is standard in models of short term synaptic depression and has been widely used in past studies^{71,72,73,74,75}.

We again consider the response of our model neuron pair in two states. In state A the modulatory drive is weak and presynaptic populations fire at a low rate. In this case, the variability in the postsynaptic current, Var(N), is due primarily to probabilistic vesicle release, since vesicle uptake almost always happens before the next spike arrival. Thus the relative synaptic noise, R^A = Var(N^A)/Var(P^A), is small (Fig. 2, b3 blue dot). As a result the output correlation, ρ^A, is only weakly diluted by synaptic noise.

In contrast, the larger modulatory drive in state B results in higher presynaptic and postsynaptic firing rates (Fig. 2, b4 green). Higher postsynaptic activity results in increased depression of synaptic transfer due to vesicle depletion. The probabilistic nature of vesicle recovery increases fluctuations in the synaptic current, so that relative synaptic noise, R^B, is larger than in state A (Fig. 2, b3 orange dot). Since vesicle recovery is independent across synapses such increased variability dilutes input correlations, ${\rho }_x^B$. This results in a modulation of output spiking correlations with ρ^B < ρ^A (Fig. 2, b4 black).

Variability due to internal release and recovery dynamics within individual synapses is a well documented component of synaptic dynamics^76,53. Previous studies focused on the impact of such synaptic variability on the information transmission across a synapse^77,75. Here we follow our past study⁷⁸ and show how input correlations are diluted by synaptic variability in a firing rate dependent manner (see also⁷⁹).

Synaptic variability is not the only cause of correlation dilution. Alternative mechanisms only need two features: First, the variability must be independent across neurons, so that Cov(x̂₁, x̂₂) is unaffected by changes in state, and second, the variability must be activity dependent so that Var(N)/Var(P) changes with the state^80,81. A multitude of biophysical mechanisms satisfy these requirements, including fast membrane potential fluctuations due to stochastic openings and closings of ion channels^52,81, action potential threshold fluctuations due to finite-sized populations of axonal sodium channels⁸², and slow fluctuations in the cellular excitability of neurons⁸³.

Modulating neural transfer

In the previous example the intensity of background synaptic fluctuations changed the input statistics. We next show how it can also influence output correlations by changing the response gain (L) of a neuron (see Methods: Modulating neural transfer). In our example the drive from the presynaptic populations is balanced, meaning that both excitation and inhibition increase with the modulatory input (Fig. 2, c1 and c2). We chose parameters so that the total mean presynaptic input to the target pair is approximately state-independent (through a cancelation of excitation and inhibition currents), but the overall variability of the synaptic input increases with the modulatory drive so that Var(P^B) > Var(P^A). Further, the modulation was such that despite the increase in variance the presynaptic correlations remained fixed, i.e. ${\rho }_P^B={\rho }_P^A$. Finally, we neglect synaptic variability, so that R^A = R^B = 0. Thus, any change in output correlation, ρ, cannot be due to a change in input correlation, ρ_x.

Modeling work^84,85,86,87, dynamic-clamp slice experiments^88,89, and in vivo whole cell recording⁹⁰ have all demonstrated that increases in conductance-based input fluctuations lower L. Indeed, in our model since in state B synaptic fluctuations are larger than in state A, it follows that L^B < L^A (Fig. 2 c3). Thus, despite the increase in firing rate between state A and B (Fig. 2, c4 green), and the absence of changes in the input correlations, ${\rho }_x^A={\rho }_x^B$, we nevertheless observe ρ^B < ρ^A (Fig. 2, c4 black). The reduction of L by increased synaptic activity is well studied⁸⁸, and the subsequent decrease in output correlations under this modulation scheme has been previously noted⁸⁹.

Calculating the response gain, L, and determining its impact on the collective behavior of neuronal populations has a long history^91,50,51. In particular, the example of a pair of uncoupled neurons driven by partially correlated inputs has been extensively studied. Formally, the nonlinear transfer between continuous input and spike response ensures that ρ < ρ_x ^{92,37,39,93,94}, yet the influence of the nonlinearity can be controlled by several factors. In many neuron models L increases with the firing rate of a neuron resulting in a relationship between firing rates and ρ^37,38,95. This prediction has been verified in a variety of experimental studies^25,96,10,95, and firing rate is often a core determinant of output correlation⁴⁵. However, in general, output spiking correlations and firing rate do not have a prescribed relation, as our examples illustrate (Fig. 2 a4,b4,c4).

Neural excitability can shape how input correlations are transferred to output correlations, with neural integrators favoring spike count correlations measured over long timescales⁹³, while resonator and phasic membrane dynamics show enhanced short timescale synchrony^97,98,99,100. Subthreshold cellular dynamics, such as spike frequency adaptation¹⁰¹ or fast membrane tracking of slow synaptic inputs⁹² also shape L and hence the transfer of correlation. Increased cellular heterogeneity between the postsynaptic neuron pair typically reduces ρ^38,102, particularly when measured over short timescales^38,103,104. These studies all explicitly considered the case of correlation transfer for a neuron pair; however the cellular and synaptic mechanisms that determine the response gain of a neuron have been a long standing topic of interest¹⁰⁵. Our theory suggests that all of these gain control mechanisms will also influence correlation transfer.

Distinguishing between the mechanisms

These three examples demonstrate how distinct cellular and circuit mechanisms impact both firing rates and pairwise correlations. We have chosen model parameters so that the changes in firing rate and correlations are nearly identical in all three cases (Fig. 2, a4,b4, and c4). This illustrates an inherent difficulty in using changes in output statistics to infer the biophysical mechanisms that have caused them.

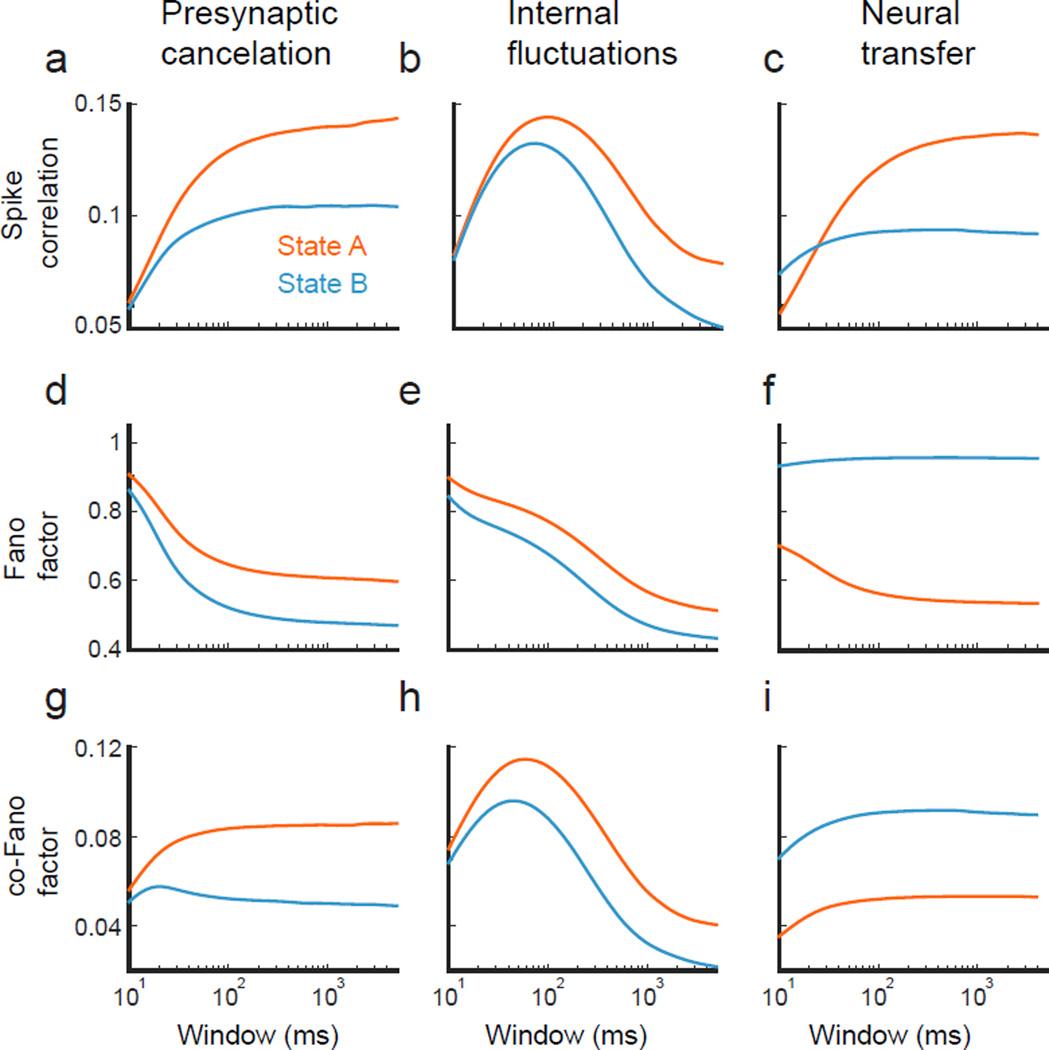
One way to distinguish the mechanisms underlying correlation modulation is to consider spiking correlations ρ as a function of the time window (T) over which they are computed, because different mechanism modulate correlations on different timescales ^89,78,101. In general, ρ increases with the time window¹⁰⁶, as in the case of the feedforward model with non-plastic synapses (Fig. 4a1 and a3). However, plastic synapses with short-term depression have long timescale vesicle uptake dynamics (~ 400 ms), attenuating low frequency pre- to post-synaptic transfer. Consequently, broadband presynaptic activity is not correlated with post-synaptic responses over long timescales, and hence ρ is reduced for T > 400ms (Fig. 4a2). While measuring ρ as a function of T can help distinguish some mechanisms from others (Fig. 4a1 and a3 vs. a2), it does not provide a perfect diagnostic. Indeed, some qualitatively distinct mechanisms may only show quantitative differences in the timescale dependence of ρ (Fig. 4a1 vs. a3).

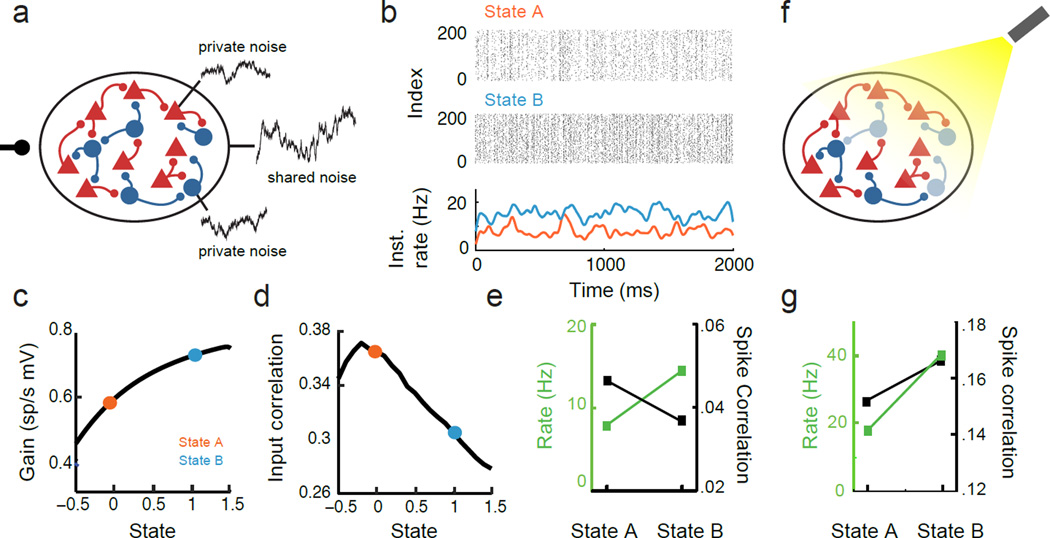
Figure 4. Correlation modulation in recurrent networks.

a. Schematic of recurrent excitatory (E) and inhibitory (I) network. The neurons in the network receive a global source of shared fluctuations, alongside individual sources of private variability. b. Spike train rasters (top) and instantaneous firing rates (bottom) of the E-neuron population in state A and B. c. Change in spike response gain (L) as modulatory drive (state) is varied. d. Change in presynaptic correlation to a representative pair of neurons within the population as modulatory drive (state) is varied. e. The result of the modulation from state A to B is to both increase the postsynaptic firing rate (green) and decrease spike count correlation (black). f. Schematic showing a silencing of a portion of the inhibitory population through activation of halorhodopsin. g. Same as e) but with half of the inhibitory neurons hyperpolarized.

Another way to distinguish the mechanisms is to recall that ρ is defined as a ratio:

$$\rho =\frac{\text{Cov}(n_1,n_2)}{\text{Var}(n)}=\frac{\text{CoF}(n_1,n_2)}{F(n)}.$$

In the second equality we used the co-Fano factor⁹³, CoF(n₁, n₂) = Cov(n₁, n₂)/〈n〉 and the Fano factor, F(n) = Var(n)/〈n〉 (〈n〉 is the mean spike count). A decrease in ρ between state A and B may be due to either 1) a larger decrease in CoF(n₁, n₂) than F(n), or 2) a larger increase in F(n) than CoF(n₁, n₂). The cancelation of presynaptic covariability through feedforward inhibition or the increase in variability through probabilistic vesicle release both lead to a reduction in ρ as in the first case (Fig. 4b1 vs. c1 and b2 vs. c2). In contrast, larger overall variability with increased background fluctuations coupled with a reduced gain leads to a reduction in ρ as in the second case (4b3 vs. c3). However, as with timescales, separating modulations of ρ into modulations of spike count Fano and co-Fano factors can only give partial information about underlying biophysical mechanisms.

It is possible to indirectly measure the stimulus-response gain L of a neuron by ranging over a stimulus parameter. If the stimulus dependence and the sources of input variability are known (or can be approximated) then one can account for changes in ρ by changes in L⁶⁶. Manipulations of a neural circuit by pharmacological or optogenetic means can give further insights into how the organization of pre-synaptic correlations, ρ_P, or post-synaptic variability, R, contributes to state-dependent changes in ρ (see next section).

The most direct method to characterize the mechanisms responsible for state dependent changes in correlation remains to use whole-cell recordings of membrane potential voltage fluctuations. Whole cell recordings give information about both the synaptic inputs and spike outputs, allowing us to measure input correlations, Cov(x₁, x₂), internal fluctuations, R, and response gain, L, directly. In vivo whole cell recording is challenging. However, there are several studies where pairwise correlations have been modulated and simultaneously membrane potentials, or a membrane potential and local field potential have been recorded (see Table 1). Studies of this type continue to be well suited to uncover the physiological basis of state-dependent correlation modulation.

Correlation modulation in recurrent networks

Thus far we explored correlation modulation in a simple feedforward circuit (Figs. 1 and 2). However, a primary characteristic of cortical networks is large recurrent projections between neurons. Theoretical neuroscientists have developed and analyzed various models of recurrent networks of excitatory and inhibitory neurons^107,108,109. These models have provided key insights into the mechanisms that shape spike train correlations. For instance, networks with rapid but delayed recurrent inhibition produce fast timescale correlated activity in the γ frequency range (30–70 Hz)^110,50,111, but often show negligible correlations on slow timescales. Networks with weak or balanced coupling produce slow-timescale correlated activity whose magnitude scales inversely with system size, becoming exceedingly small in networks with thousands of neurons^{34,69,35,32,112}. However, we are far from a complete understanding of self-generated correlated activity in recurrently networks of spiking neurons.

Clustered feedforward¹¹³, clustered recurrent^114,115,116, and spatially distributed network architectures^47,117,118 can all produce correlated activity between spiking neurons. In such networks, only neurons that belong to the same cluster or are close to one another are strongly correlated. Indeed, experiments show that noise correlations are large for neuron pairs that are reciprocally connected¹¹⁹ (same putative cluster), similarly tuned or are nearby in space to one another⁴⁸. However, the mean correlation between neuron pairs that fall outside these categories are also positive on average⁴⁸.

Large parallel recordings from neural populations show that spiking correlations have some simple features: network-wide correlations can be largely explained by a one dimensional source of shared fluctuations, often treated as a latent variable in statistical approaches^{120,11,10,9,56}. The origin of this source is not known. A straightforward (albeit phenomenological) way to model these dynamics is to drive a network of spiking neurons with a spatially coherent input that represents an external source of fluctuations^{121,122,123,56,28,94}. We employ this strategy to study correlation modulation in recurrent networks.

We consider a network of model excitatory (E) and inhibitory (I) spiking neurons with dense, recurrent connections between them (see Methods: Correlation modulation in recurrent networks). Weak feedforward input fluctuations, F(t), are shared by all neurons (providing feedforward covariability Cov_F), alongside private fluctuations specific to each neuron in the network (Fig. 4a). The shared fluctuations are the largest source of network covariability in the model. In addition, we assume that there is a modulatory input similar to that of our previous models (Fig. 2) and simply depolarizes all neurons (different magnitude for E and I neurons). This modulatory input does not affect the external fluctuations F(t).

In response to the modulation, E neurons have a higher time-averaged firing rate in state B than state A (Fig. 4b,e). In both states the shared fluctuations produce significant variability in the population-averaged instantaneous firing rates (Fig. 4b, lower panel). If the strength of shared input fluctuations is small compared to private fluctuations then the linear response framework assumed in Eq. (2) is valid^{121,122,124,112,66,28}. In this case the intuition developed from our feedforward analysis will apply to a representative pair of neurons selected from the recurrent network. However, to understand the modulation of neural correlations, ρ, we must understand the combined modulations of the correlations in their presynaptic inputs P, the transfer of presynaptic activity to synaptic current x, and the gain of the postsynaptic response to those currents, L.

The nonlinearity of the transfer between synaptic input and spike response allows the gain L to be state-dependent. In our model we have that L^A < L^B (Fig. 4c). This differs from our previous analysis (Fig. 2 c3) since the network model has current-based synapses, while the feedforward case has conductance-based synapses, mimicking a high conductance state⁸⁹. With current-based synapses and moderate firing rates, an increase in firing rate results in an increase in L, which is supported both by in vitro^37,105 and in vivo²⁰ recordings. Thus, in our model it is expected that the modulation will produce L^B/L^A > 1.

Any pair of neurons in our network are correlated through the shared fluctuations F(t) via two pathways: the direct feedforward component that provides input with covariance Cov_F between neurons, and the indirect pathway via recurrent excitatory and inhibitory projections between neurons in the network that also receive F(t). To simplify the exposition we consider the joint common recurrent input R(t) = E(t) + I(t). The full covariance of the presynaptic input to a neuron pair then decomposes as:

$$\text{Cov}(P_1,P_2){\text{=Cov}}_F+{\text{Cov}}_R+2{\text{Cov}}_{FR}.$$

Here Cov_R is the covariability due to common recurrent input to the neuron pair, while Cov_FR is the interaction between the feedforward and recurrent pathways. This decomposition is similar to feedforward case shown in Eq. (3). While the feedforward input F(t) is state invariant, the recurrent activity R(t) changes with state. In our model the inhibitory pathway is dominant, making Cov_FR < 0 because dynamic recurrent inhibition acts to partially cancel the feedforward drive^121,69. The modulatory input enhances this cancellation so that ${\text{Cov}}_R^A+2{\text{Cov}}_{FR}^A>{\text{Cov}}_R^B+2{\text{Cov}}_{FR}^B$, ultimately yielding Cov^A(P₁, P₂) > Cov^B (P₁, P₂) (Fig. 4d).

The combined effect of the modulation is then to produce two opposing manipulations of correlation transfer. An increase in response gain (L^B/L^A > 1) occurs in tandem with a decorrelation of the presynaptic input (Cov(P₁, P₂)^B/Cov(P₁, P₂)^A < 1). Our theory in Eq. (2) suggest that the response gain modulation will produce an increase in correlation in state B, that is ρ^B/ρ^A > 1, while the presynaptic correlation modulation lead to decrease, ρ^B/ρ^A < 1. We chose parameters and a modulation so that the latter effect dominates, and the spike correlation is reduced in state B (Fig. 4e). In general, modulatory inputs result in state changes in multiple stages of correlation transfer. Nonetheless, the ideas presented in this review can help disentangle the various effects of a network modulation on the spike train correlations of pairs of neurons within the network.

As in the feedforward networks, it is difficult to use spike train data alone to dissect the individual contributions of gain and pre-synaptic correlation modulations in a recurrent network. Further probing of the network can, however, give insight into the mechanisms of correlation modulation. To illustrate, we model an experiment where light is used to activate interneurons expressing halorhodopsin in a cortical network (Fig. 4e). We assume that light hyperpolarizes a fraction (50%) of the I cells in our model. Removing a large fraction of recurrent inhibition changes state dependent modulations in two important ways. First, the increase in firing rates in going from state A to B is much larger (Fig. 4f, green). Second, spike correlations now increase with the state modulation (Fig. 4f, black).

With weaker inhibition the cancellation of feedforward correlations Cov_F through Cov_FR is attenuated. Thus, when halorhodopsin is activated the decorrelation in neural activity through recurrent inhibition is compromised. Further, the increase in firing rate with decreased inhibition allows L to increase to a larger extent as the network transitions from state A to B. The combination of these effects lead to an increase in ρ with the state change when inhibition is reduced. Had recurrent inhibition not been a primary component of the mechanism underlying the state dependent dependent modulation in the control case, then we would not expect to observe these qualitative changes.

This example shows how contemporary circuit manipulation techniques can be used to test concrete predictions about state-dependent correlation changes in recurrent networks. We have confined our analysis to recurrent networks with weak coupling and where neurons receive external sources of fluctuations^{121,122,66,34,69,35}. In this case linear response techniques are valid. The network simply transforms global input fluctuations into network-wide spiking correlations. However, when coupling is stronger the network can generate globally coherent activity^110,50,111 and strong ¹²⁵ or slow^115,126. The complete analysis of such dynamics involves the nonlinear network properties, and hence the factorization in Eq. (2) is not applicable. Such behavior is beyond the scope of this review.

Conclusion

We presented a general framework for analyzing the physiological mechanisms underlying the modulations of neuronal correlations. We demonstrated our theory using several examples; however, the list of mechanisms we considered was not exhaustive. The large number of factors that modulate intrinsic cellular properties, as well as synaptic excitation and inhibition, suggest that many distinct mechanisms control neuronal correlation. Our theoretical approach allows for an easier navigation of this large space, and the development of a circuit-based understanding of state-dependent modulation of neuronal activity.

Unravelling the mechanics of correlation modulation in vivo will require a concerted experimental effort. We noted that whole-cell recordings will give invaluable data to validate the aspects of certain mechanisms over alternative ones. In addition, the combination of genetic specification¹²⁷ and targeted optogentic manipulation of neural circuits¹²⁸ promises to provide fundamental insights into neural correlations. Finally, analysis of population-wide recordings describes how pairwise correlations are distributed across large groups of neurons^{120,11,10,9,56}. Extending our theory to networks of neurons is straightforward^121,122,34. However, understanding how the dimensionality of population-wide input correlation is represented by the spike responses of interconnected neurons is an open challenge.

The changes in correlated activity we describe may have a number of consequences for neural coding. Theoretical^26,123 and experimental^96,129,130 studies show that changes in correlations can increase the accuracy with which stimulus can be decoded from the population response. Further, increased synchrony has also been shown to precede behaviorally relevant events¹³¹. However, recent work has exposed that it is the degree of overlap between the structure of population noise correlations and population stimulus tuning that ultimately identifies the correlations that limit information transfer²⁸. This implies that conclusions about the effect of noise correlations on neural coding should be made with care.

We have come a long way in characterizing the mechanics underlying the responses of single neurons. Understanding circuit and cellular modulations of the collective activity of neural populations will be an essential step toward understanding the brain.

Figure 3. Dissecting correlation modulation.

(a) Output correlation coefficient ρ as a function of the window T over which spike trains are counted. The pre-synaptic correlations (column 1), internal fluctuation (column 2), and neural transfer (column 3) examples are identical to those of Figure 2. (b) The Fano factor F(n) = Var(n)/〈n〉 for the same data as panel a. (c) The co-Fano factor CoF(n₁, n₂) = Cov(n₁, n₂)/〈n〉 for the same data as panel a.