Cautionary Note on Using Cross-Validation for Molecular Classification

Abstract

Purpose

Reproducibility of scientific experimentation has become a major concern because of the perception that many published biomedical studies cannot be replicated. In this article, we draw attention to the connection between inflated overoptimistic findings and the use of cross-validation for error estimation in molecular classification studies. We show that, in the absence of careful design to prevent artifacts caused by systematic differences in the processing of specimens, established tools such as cross-validation can lead to a spurious estimate of the error rate in the overoptimistic direction, regardless of the use of data normalization as an effort to remove these artifacts.

Methods

We demonstrated this important yet overlooked complication of cross-validation using a unique pair of data sets on the same set of tumor samples. One data set was collected with uniform handling to prevent handling effects; the other was collected without uniform handling and exhibited handling effects. The paired data sets were used to estimate the biologic effects of the samples and the handling effects of the arrays in the latter data set, which were then used to simulate data using virtual rehybridization following various array-to-sample assignment schemes.

Results

Our study showed that (1) cross-validation tended to underestimate the error rate when the data possessed confounding handling effects; (2) depending on the relative amount of handling effects, normalization may further worsen the underestimation of the error rate; and (3) balanced assignment of arrays to comparison groups allowed cross-validation to provide an unbiased error estimate.

Conclusion

Our study demonstrates the benefits of balanced array assignment for reproducible molecular classification and calls for caution on the routine use of data normalization and cross-validation in such analysis.

INTRODUCTION

Reproducibility of scientific experimentation has become a major concern because of the perception that many published biomedical studies cannot be replicated.^1-3 A recent commentary by Collins and Tabak⁴ outlined the problem, drawing attention to the importance of valid experimental design, especially in the preclinical setting. This has been backed up by recent changes to the format of grant submissions to the National Institutes of Health to draw reviewers’ attention to the scientific rigor of the experimental design.⁵ In this article, we draw attention to a crucial feature of the design of molecular classification studies. We show that, in the absence of careful design to prevent artifacts caused by systematic differences in the processing of specimens, established tools, such as data normalization and cross-validation, will be ineffective in eliminating inflated overoptimistic findings.

Developing molecular classifiers that aid in treatment selection is an important ongoing problem for precision medicine.^6,7 An essential characteristic of a classifier is the misclassification error rate, which is defined as the measurement of how the classifier will perform when applied in practice (to an independent data set). Traditionally, a routine method for assessing a classifier’s error rate is cross-validation of the same data used for training the classifier (ie, the training data set), through rotational estimation of random data splits^8,9; under the implicit assumption that the training data set is reproducible, cross-validation can provide a nearly unbiased estimate of the error rate.¹⁰ Cross-validation has been frequently used for assessing molecular classifiers: a review of the literature shows that from 2000 to 2015, leading oncology journals published 74 molecular classification studies, among which 19 (26%) used cross-validation as the sole approach for assessing the error rate and 11 (15%) used split-sample validation, in which the data were randomly split into training and test data sets (Data Supplement).

Molecular data, however, often consist of irreproducible nonbiologic variations that arise from the experimental handling process, which we call handling effects throughout this article.^11-14 For example, assays are usually processed in batches, and each batch will typically have systematic differences in the output metrics, leading to potential bias if suitable adjustments are not used to offset these systematic effects. Handling effects have been extensively studied for the problem of molecular biomarker discovery and are often addressed by normalization in the data preprocessing step.^11,15,16 The same normalization strategy has been used routinely to smooth out the data for molecular classification: among the aforementioned 74 studies, 61 (82%) explicitly stated that normalization was used (Data Supplement). However, it has not been appreciated that normalization can undersmooth handling effects (that correlate with the outcome of interest) or oversmooth the inherent biologic variations in the data, both leading to a spurious error rate estimated by cross-validation. This overlooked connection between data preprocessing and data analysis may explain some of the optimistic yet irreproducible molecular classifiers reported in the literature.

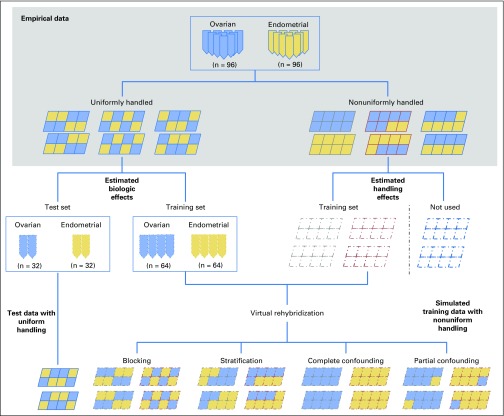
We are able to demonstrate this overlooked complication of cross-validation using a unique pair of microRNA (miRNA) array data sets that we previously collected.¹⁷ These two data sets were generated for the same set of tumor samples as follows. Arrays in one data set were collected with uniform handling to minimize handling effects, whereas arrays in the other data set were collected with nonuniform handling and exhibited handling effects. In this study, we used the former data set to approximate the ideal case and to estimate biologic effects for each sample; we used the latter data set to estimate handling effects for each of its arrays (by subtracting the corresponding biologic effects). Data were simulated by randomly reassigning arrays to samples (without replacement), followed by adjusting the observed biologic effect of each sample using the estimated handling effect of its assigned array, a technique that we call virtual rehybridization (Fig 1).

Fig 1.

Illustration of the overall design of the simulation study on the basis of resampling from the paired microarray data sets on the same set of tumor samples.

For the reassignment of arrays to samples, we examined two schemes that resulted in different types of handling effects. First, we used a typical batch allocation scheme, in which arrays were assigned to sample groups in the order of array collection (ie, earlier arrays assigned to one group and later arrays to the other), leading to handling effects confounded with the groups being compared. In the second allocation scheme, we used a strategy designed to ensure that comparison between groups was unbiased, in which arrays were assigned evenly in terms of collection order (using statistical principles, such as blocking and stratification), leading to handling effects balanced between sample groups.^18-20 More specifically, for microarrays that come in multiplex units (ie, multiple arrays placed on the same array slide), each multiplex unit served as an experimental block; blocking means assigning arrays in each block to the comparison groups in proportion to their numbers of samples. When arrays are handled in multiple experimental batches, each batch serves as a stratum; stratification means assigning arrays in each batch to each group proportionally. Comparisons of data from the two designs allowed us to estimate the biases induced by unbalanced handling effects directly. Blocking and stratification have been shown to alleviate the negative impact of handling effects on molecular biomarker discovery.¹⁷ In this article, we examine their role on classification in connection with cross-validation and data normalization.

Our simulation study illustrates the intricate interplay between data generation, data preprocessing, and cross-validation for molecular classification. It offers insights into the desired practice of study design and data analysis for such studies, so that research sources can be optimally used to generate quality molecular data and allow the development of reproducible classifiers.

METHODS

Microarray Data Collection

A set of 192 untreated primary gynecologic tumor samples (96 endometrioid endometrial tumors and 96 serous ovarian tumors) were collected at Memorial Sloan Kettering Cancer Center from 2000 to 2012. Their use in our study was approved by the Memorial Sloan Kettering Cancer Center Institutional Review Board. The samples were profiled using the Agilent Human miRNA Microarray (Release 16.0, Agilent Technologies, Santa Clara, CA), following the manufacturer’s protocol. This array platform contains 3,523 markers (representing 1,205 human and 142 human viral miRNAs) and multiple replicates for each marker (ranging from 10 to 40). In addition, it has eight arrays on each glass slide (ie, the experimental block) arranged as two rows and four columns.

Two data sets were obtained from the same set of samples using different methods of experimental handling. The first data set (referred to hereafter as the uniformly handled data set) was handled by one technician in one run, and its arrays were randomly assigned to tumor samples using blocking (by both array slide and row-column location on each slide). The second data set (the nonuniformly handled data set) was handled by two technicians in five runs (each happened on a different day): the first 80 arrays by one technician (who was the technician for the uniformly handled data) in two runs and the last 112 by a second technician in three runs; its arrays were assigned in the order of sample collection with no blocking, mimicking typical practice. More details on data collection can be found in the article by Qin et al.¹⁷

As a proof of concept, we used tumor type (endometrial cancer v ovarian cancer) as the outcome variable for classification. Among a total of 3,523 markers on the array, 351 (10%) were significantly differentially expressed (P < .01) between the two tumor types on the basis of the uniformly handled data set. To be consistent with the typical signal strength in a molecular classification study, we halved the between-group differences for the 351 significant markers (by reducing their levels of expression in ovarian samples by half of the ovarian-v-endometrial between-group differences), reducing the number of significant markers to 63 (2%); a similar reduction of sample group differences was also applied to the nonuniformly handled data. Having previously observed that the variation among replicates for the same marker was small, we used only the first 10 replicates for each of the 3,523 markers in this study so that computational time could be saved; this reduction made no difference in the number of significant markers.

Analysis of the Uniformly Handled Data

The analysis for the uniformly handled data set consisted of the following main steps: (1) randomly split the data into a training set (n = 128) and a test set (n = 64), balanced by tumor type; (2) preprocess the training data and the test data; (3) build a classifier using the preprocessed training data; and (4) assess the error rate of the classifier using the preprocessed test data. This analysis was repeated for 1,000 random splits of the training set and test set. More details for each analysis step are provided in the following sections.

Data preprocessing.

Data preprocessing included three steps: (1) log2 transformation, (2) quantile normalization for training data and frozen quantile normalization for test data (ie, mapping the empirical distribution of each individual test-set sample to the frozen empirical distribution of the normalized training data),²¹ and (3) marker-replicate summarization using median.¹⁷

Classifier building.

Two classification methods were used, including one nonparametric method, prediction analysis for microarrays (PAM),²² and one parametric method, the least absolute shrinkage and selection operator (LASSO).²³ R packages pamr²⁴ (for PAM) and glmnet²⁵ (for LASSO) were used. The tuning parameter for each method was chosen using five-fold cross-validation.

Classifier error estimation.

Classification accuracy was measured using the misclassification error rate (ie, the proportion of samples that were misclassified). The error rate was evaluated by both external validation (where the final model of each classifier was built on the entire training data and applied to predict the group label for each sample in the test data) and cross-validation of training data.

Generation and Analysis of the Simulated Data

First, we used the uniformly handled data set to approximate the biologic effect for each sample and the difference between the two arrays (one from the uniformly handled data set and the other from the nonuniformly handled data set, subtracting the former from the latter) for the same sample to approximate the handling effect for each array in the nonuniformly handled data set. The 192 samples were randomly split in a 2:1 ratio into a training set (n = 128) and a test set (n = 64), balanced by tumor type; a nonrandom subset of the 192 arrays (n = 128; the first 64 and last 64 arrays in the order of array processing) were used for the training set (Appendix Fig A1, online only).

Second, for the training set, data were simulated through virtual rehybridization by first assigning arrays to sample groups using a confounding design or a balanced design and then summing the biologic effect for a sample and the handling effect for its assigned array. Simulation allowed us to examine the use of various array-assignment schemes and also the level of variability among different pairings of arrays and samples within each scheme.

• We examined two completely confounding designs for array assignment in the training set: (1) the first 64 arrays in the training set were assigned to endometrial samples and the last 64 arrays to ovarian samples; and (2) the first 64 arrays in the training set were assigned to ovarian samples and the last 64 to endometrial samples. The former design was called Complete Confounding 1 and the latter Complete Confounding 2 (Appendix Fig A1). We also examined two partially confounding designs: they had the same array assignment as the two Complete Confounding designs, except that for 10% of the arrays, the sample-group labels were randomly selected and swapped. These two designs were called Partial Confounding 1 and Partial Confounding 2, respectively. The level of confounding was measured by the moderated R² statistic between the sample group and the most correlated principal component of nonsignificant markers distinguishing the two groups, as described in Leek et al.¹³

• We examined the use of blocking (by array slide) and stratification (by array batch) to balance array assignment between the two sample groups under comparison. For the Agilent miRNA array, each eight-plex array slide served as an experimental block; blocking means assigning arrays in each eight-array block to the two groups in proportion to their numbers of cases (ie, four arrays to each group in our study). The arrays from the nonuniformly handled data were handled in five batches. Each batch serves as a stratum; stratification means assigning arrays in each batch to each group proportionally.

Third, the analysis for each simulated data set followed the same steps as previously described for the analysis of the uniformly handled data: (1) data preprocessing, (2) classifier training, and (3) classifier error estimation using both cross-validation and external validation. The only difference was that here, external validation was based on the test data from the uniformly handled data set and served as the gold standard for the misclassification error estimation.

For a given split of samples to training set versus test set, 1,000 data sets were simulated and analyzed for each array-assignment scheme. We examined multiple sample splits and observed similar trends regarding the role of the array-assignment scheme and training-data normalization on cross-validation. Results are reported here for one split and in the Data Supplement for another split.

RESULTS

Cross-Validation in the Absence of Handling Effects

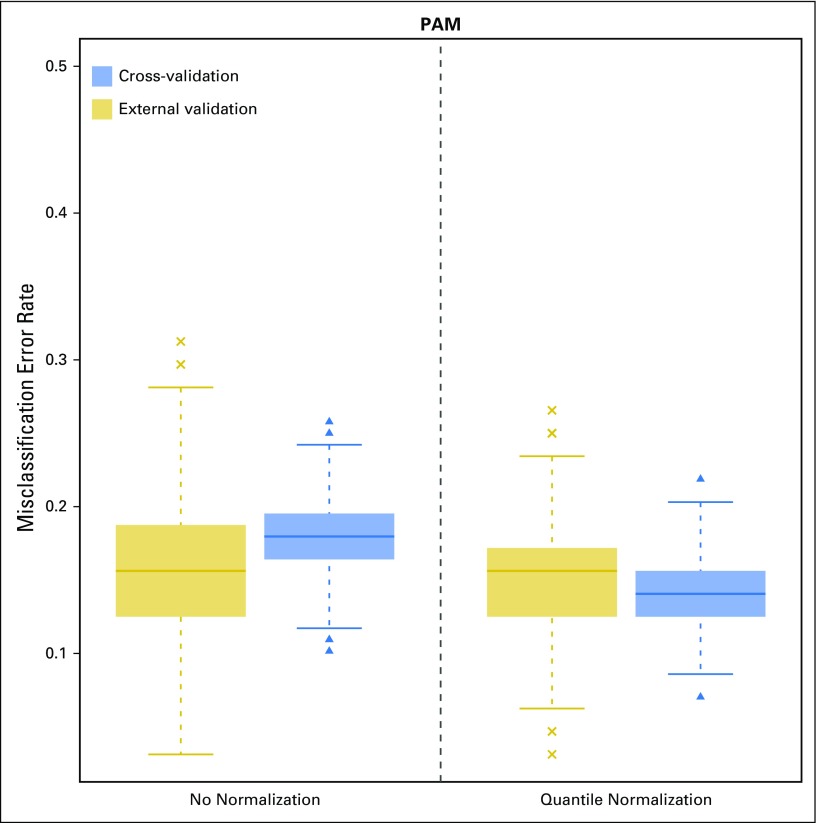
We first evaluated the use of cross-validation for classification error estimation (Fig 2, gold graphs) compared with the use of external validation (Fig 2, blue graphs), derived from the results generated from the study with no handling effects. This analysis was based on 1,000 random training-versus-test splits of the uniformly handled data set, and the level of variability in the error rate reflected the level of sampling variability between various splits of the training set and test set. Before applying normalization to training data, error rates on the basis of cross-validation (median, 18.0%; interquartile range [IQR], 16.4% to 19.5%) were comparable with those on the basis of external validation (median, 15.6%; IQR, 12.5% to 18.8%), confirming that cross-validation provided a nearly unbiased estimate when the data were reproducible. After normalization, error rates on the basis of cross-validation dropped noticeably (median, 14.1%; IQR, 12.5% to 15.6%), whereas error rates on the basis of external validation barely changed (median, 15.6%; IQR, 12.5% to 17.2%), indicating that normalization may have oversmoothed the data and hence led to underestimation of the error rate by cross-validation. In other words, normalization may be problematic when the data were collected with uniform handling.

Fig 2.

Box plots of classification error on the basis of 1,000 training-versus-test-set splits of the uniformly handled data set using the prediction analysis for microarrays (PAM) method. The error rate was estimated using (1) cross-validation and (2) external validation in test data. The x-axis indicates the normalization status of the training data (Appendix Table A1, online only).

Cross-Validation in the Presence of Confounding Handling Effects

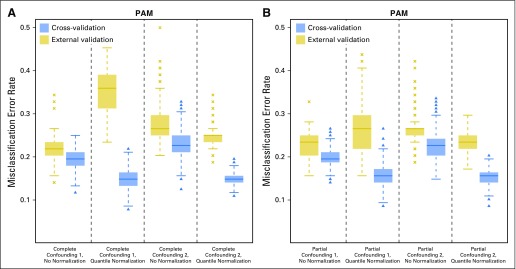
We next examined the performance of cross-validation before and after data normalization, when the training data were generated from the confounded assignment schemes. The level of confounding in the simulated data was moderate, with the R² statistic being 19% for Complete Confounding 1 and 17% for Complete Confounding 2, comparable to a number of published studies.^13,26-31 As shown in Figure 3A, compared with external validation (where the classification error was assessed by applying the classifier to samples in an independent test data set), cross-validation underestimated the error rate, with the level of underestimation considerably worsened after applying normalization to the data. Before normalization, error rates on the basis of cross-validation (Complete Confounding 1: median, 19.5%; IQR, 18.0% to 21.1%; Complete Confounding 2: median, 22.7%; IQR, 21.1% to 25%) were consistently lower than those on the basis of external validation (Complete Confounding 1: median, 21.9%; IQR, 20.3% to 23.4%; Complete Confounding 2: median, 26.6%; IQR, 25.0% to 29.7%). After normalization, error rates on the basis of cross-validation (Complete Confounding 1: median, 14.8%; IQR, 13.3% to 16.4%; Complete Confounding 2: median, 14.8%; IQR, 14.1% to 15.6%) were lower to a much greater extent than were those on the basis of external validation (Complete Confounding 1: median, 35.9%; IQR, 31.2% to 39.1%; Complete Confounding 2: median, 25.0%; IQR, 23.4% to 25.0%). Similar patterns of error underestimation by cross-validation and data normalization were also observed for the two partially confounding array-assignment schemes (Partial Confounding 1 and Partial Confounding 2; Fig 3B). In short, cross-validation, which by definition is based on random splits of the training data, fails to distinguish the biologic signal from confounding handling effects and, as a result, does not provide an unbiased estimate of classification error, and the level of underestimation can be exacerbated when applying normalization to the data.

Fig 3.

Box plots of classification error on the basis of 1,000 simulated data sets under a confounding design using the prediction analysis for microarrays (PAM) method: (A) Complete Confounding designs (Appendix Table A2, online only), and (B) Partial Confounding designs. The error rate was estimated with (1) cross-validation and (2) external validation using the corresponding test set (with the same training-versus-test-sample split) from the uniformly handled data (Appendix Table A3, online only). The x-axis indicates the confounding design and the normalization status of the training data.

Cross-Validation in the Presence of Balanced Handling Effects

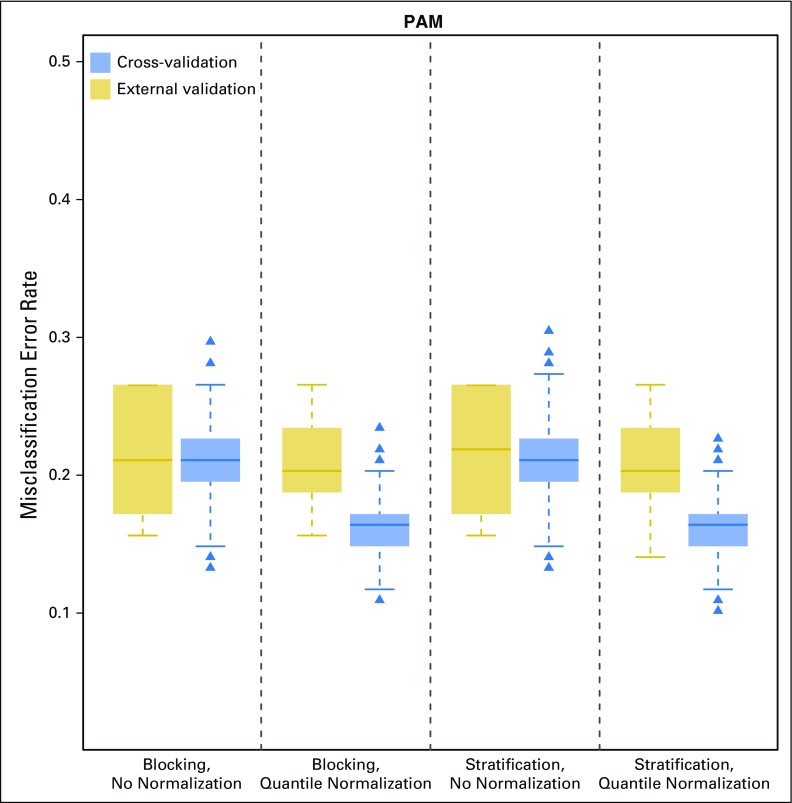
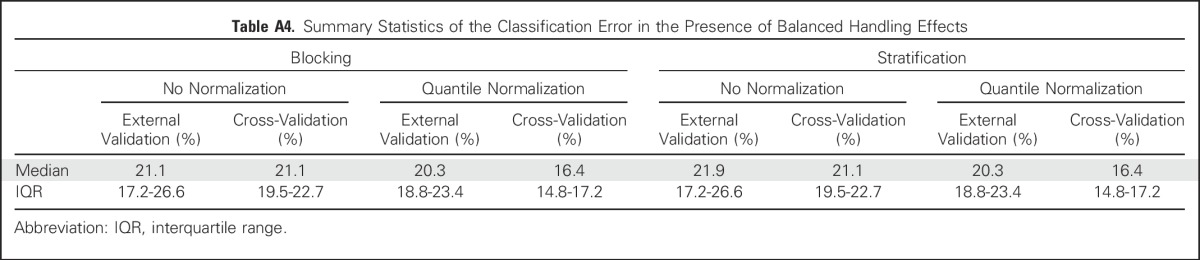
Figure 4 shows the results when the data possessed handling effects that were balanced between the two sample groups via the use of blocking or stratification. In the presence of balanced handling effects, error rates on the basis of cross-validation (blocking: median, 21.1%; IQR, 19.5% to 22.7%; stratification: median, 21.1% IQR, 19.5% to 22.7%) were comparable to those on the basis of external validation (blocking: median, 21.1%; IQR, 17.2% to 26.6%; stratification: median, 21.9%; IQR, 17.2% to 26.6%). However, normalization still led to underestimation of the classification error using cross-validation (blocking: median, 16.4%; IQR, 14.8% to 17.2%; stratification: median, 16.4%; IQR, 14.8% to 17.2%) compared with external validation (blocking: median, 20.3%; IQR, 18.8% to 23.4%; stratification: median, 20.3%; IQR, 18.8% to 23.4%). Our results suggest that careful study design that balances handling effects between sample groups can effectively circumvent their negative impact on the validity of cross-validation for error estimation.

Fig 4.

Boxplots of classification error on the basis of 1,000 simulated data sets under a balanced design using the prediction analysis for microarrays (PAM) method. The error rate was estimated with (1) cross-validation and (2) external validation using the corresponding test set (with the same training-versus-test sample-split) from the uniformly handled data. The x-axis indicates the balanced design and the normalization status of the training data (Appendix Table A4, online only).

Cross-Validation Under Additional Simulation Scenarios

In our study, training data were normalized once before cross-validation. Even when normalization was made a part of (k-fold) cross-validation (ie, the k-1 folds data were renormalized and the kth fold was frozen normalized to the k-1 folds), error underestimation was still observed (Data Supplement).

In recent years, statistical methods for batch effect correction have been developed to account for handling effects resulting from known or unknown array processing batches, without making the assumption that there are few or symmetric differential expression in the data as many normalization methods do.¹⁶ Examples of such methods include ComBat,³² remove unwanted variation (RUV),³³ and surrogate variable analysis (SVA).³⁴ We also applied these methods (either alone or followed by quantile normalization) to the test data in the simulation study, using their implementation in R packages sva (for ComBat and SVA)³⁵ and ruv (for RUV).³⁶ As shown in the Data Supplement, ComBat alleviated the level of underestimation by cross-validation in some cases but exacerbated the level of classification error at times; SVA resulted in little change in the results; RUV led to poor classification results across the board, likely because the negative control markers included on the Agilent miRNA array are not suitable to serve as the negative control markers required by RUV.

In addition to the PAM method, we also used another popular classification method called LASSO and observed similar results regarding the impact of confounding handling effects, the role of normalization, and the benefits of balanced array assignment (Data Supplement). We also examined the use of other existing normalization methods and observed similar results (results not shown).

In addition to the aforementioned simulation scenarios, we also performed simulation at the original level of biologic signal where the number of significant markers was 351 and with an amplified level of handling effects (by adding a constant to arrays assigned to endometrial samples) where the moderate R² statistic increased to 50%. When the biologic signal was strong, the classification error rate was consistently low, regardless of the study design and the normalization method (Data Supplement). When the amount of handling effects increased, data normalization started to show a beneficial effect (Data Supplement).

We note that molecular classification is a complicated problem that depends on the nature of the collected data (such as the level of biologic signal and the relative amount of confounding handling effects) and involves many analysis decisions (such as the method of classification and the source of the validation data). We are making the data and code used in our study publicly available and encourage interested readers to use them to explore the topic.

DISCUSSION

Despite the ever-increasing accumulation of molecular data, it has been challenging to translate the data into accurate and reproducible molecular classifiers for clinical use.^2,37 This challenge can be attributed to a number of biologic and technical factors, such as a typically weak level of molecular signal, an overwhelming proportion of irrelevant markers measured, and the influence of handling effects encountered in the data collection process. Handling effects come from technical variations that arise in the experimental process, which can potentially be controlled to improve classification. We have demonstrated that confounding handling effects can lead to biased estimates of the misclassification error rates when using cross-validation and that post hoc data normalization may worsen the bias. We also showed that careful study design through balanced array assignment can preserve the validity of cross-validation for estimating the misclassification error. As a result, our data strongly support the use of careful study design on the basis of statistical principles such as blocking and stratification to ensure the reproducibility of molecular classifiers. For data that exhibit confounding handling effects, caution should be used when applying post hoc data normalization, because it may lead to underestimation of the misclassification error on the basis of cross-validation.

We would like to stress again that the development and assessment of a molecular classifier is an involved multistep process for which the analysis steps and decisions should be carefully planned and documented. Analysts have many degrees of freedom, which may help customize the analysis to the data set under analysis and at the same time lead to difficulty in reproducing the model with other data sets. It is extremely important to carefully evaluate analysis options and document the methods used for each analysis step.³⁸

A major strength of our study is that the unique pair of array data sets on the same set of samples allowed us to conduct resampling-based simulations, rather than parametric-model–based simulations. This allowed us to evaluate the impact of handling effects, the role of data normalization, and the benefit of careful study design in the context of a real experiment. Theoretically, a proper parametric simulation study with known error quantities would be helpful as well. However, the error structure for high-throughput molecular data is complex (because of, eg, the deviation from normality for some of the markers and the existence of weak or strong correlations between some markers) and difficult to model. In our best attempt at a parametric simulation study, where the group-specific mean and group-specific standard deviation, estimated from the empirical data, were used to simulate normally distributed data as the biologic effects, we confirmed the main message of our article, the overoptimistic tendency of cross-validation and the benefits of careful design via the use of blocking or stratification. We also found that, in the presence of careful study design, external validation resulted in an extremely small classification error rate, which is likely due to the idealized normal distribution and the lack of intermarker correlation in the parametrically simulated data. The paired data design and the virtual-rehybridization simulation design can also be applied to other types of molecular profiling platforms. In summary, our study provides strong evidence for the use of careful study design for developing and validating accurate and reproducible molecular classifiers.

Additional material

Supplementary data supplied by authors.

Appendix

Fig A1.

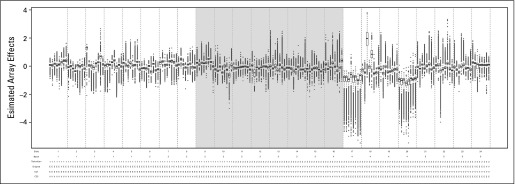
Box plots of the estimated handling effects for 192 arrays in the nonuniformly handled data set. Array allocation to the training set is indicated by the shading: white for the training set and gray for not used. Below the x-axis are labels for the array slide (indexed as 1-24), handling batch (indexed as 1-5), handling technician (indexed as 1 and 2), sample group assignment in the empirical data (E for endometrial; V for ovarian), and sample group assignment for the simulated designs: Complete Confounding 1 (CC1) and Complete Counfounding 2 (CC2).

Table A1.

Summary Statistics of the Classification Error in the Absence of Handling Effects

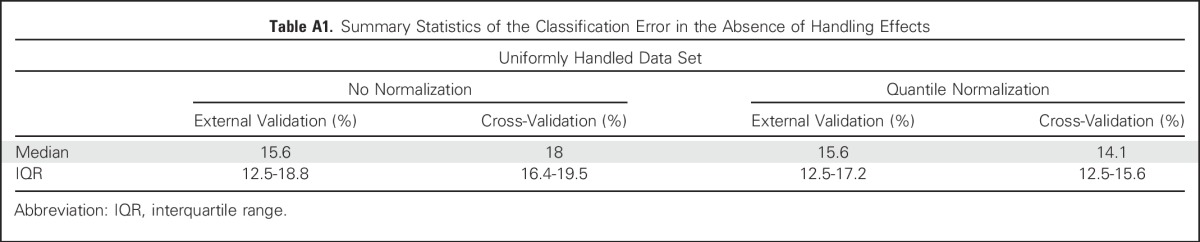
Table A2.

Summary Statistics of the Classification Error in the Presence of Complete Confounding Handling Effects

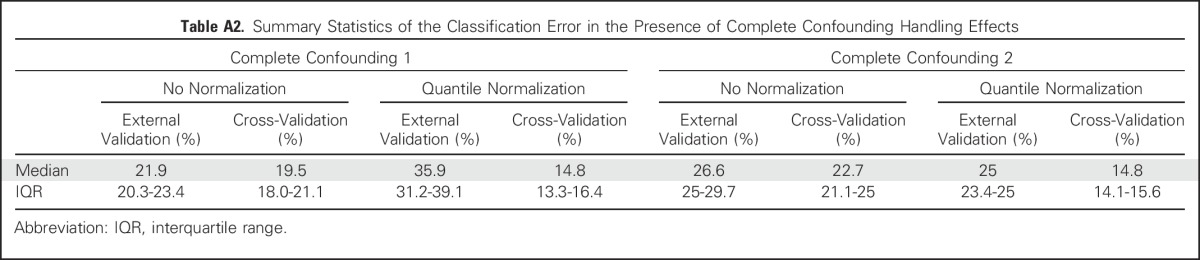
Table A3.

Summary Statistics of the Classification Error in the Presence of Partial Confounding Handling Effects

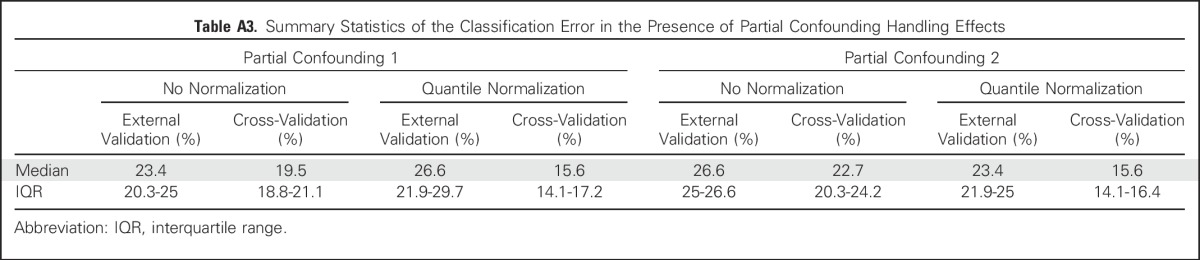
Table A4.

Summary Statistics of the Classification Error in the Presence of Balanced Handling Effects

AUTHOR CONTRIBUTIONS

Financial support: Li-Xuan Qin

Administrative support: Li-Xuan Qin

Provision of study materials or patients: Li-Xuan Qin

Manuscript writing: All authors

Final approval of manuscript: All authors

AUTHORS' DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

Cautionary Note on Using Cross-Validation for Molecular Classification

The following represents disclosure information provided by authors of this manuscript. All relationships are considered compensated. Relationships are self-held unless noted. I = Immediate Family Member, Inst = My Institution. Relationships may not relate to the subject matter of this manuscript. For more information about ASCO's conflict of interest policy, please refer to www.asco.org/rwc or jco.ascopubs.org/site/ifc.

Li-Xuan Qin

Employment: MedImmune (I)

Huei-Chung Huang

No relationship to disclose

Colin B. Begg

No relationship to disclose