The landscape of genetic complexity across 5,700 gene expression traits in yeast

Abstract

Many studies have identified quantitative trait loci (QTLs) that contribute to continuous variation in heritable traits of interest. However, general principles regarding the distribution of QTL numbers, effect sizes, and combined effects of multiple QTLs remain to be elucidated. Here, we characterize complex genetics underlying inheritance of thousands of transcript levels in a cross between two strains of Saccharomyces cerevisiae. Most detected QTLs have weak effects, with a median variance explained of 27% for highly heritable transcripts. Despite the high statistical power of the study, no QTLs were detected for 40% of highly heritable transcripts, indicating extensive genetic complexity. Modeling of QTL detection showed that only 3% of highly heritable transcripts are consistent with single-locus inheritance, 17–18% are consistent with control by one or two loci, and half require more than five loci under additive models. Strikingly, analysis of parent and progeny trait distributions showed that a majority of transcripts exhibit transgressive segregation. Sixteen percent of highly heritable transcripts exhibit evidence of interacting loci. Our results will aid design of future QTL mapping studies and may shed light on the evolution of quantitative traits.

Most heritable traits show continuous variation in a population. Such quantitative traits have been a subject of intensive study (see refs. 1–4 for reviews). Identification of genetic polymorphisms underlying quantitative traits, known as quantitative trait loci or QTLs, is of interest in medical genetics, where they can provide insights into disease mechanisms and lead to new diagnostics and therapeutics, and in agricultural genetics, where they can aid breeding programs. Genetic factors underlying quantitative traits also play a crucial role in evolutionary theory. Most quantitative traits appear to be genetically complex, i.e., controlled by multiple QTLs (2).

Linkage mapping of QTLs has been reported for thousands of quantitative traits. In a handful of cases, the DNA sequence polymorphisms underlying a quantitative trait have been identified (4–8). However, it has proven difficult to comprehensively identify the multiple QTLs that combine to determine the complex genetic architecture of a trait, largely because of limitations in the statistical power of mapping experiments (9). As a result, the principles that govern genetic complexity remain an area of active research. Are traits more likely to be controlled by a few loci of large effect or many loci of small effect (10, 11)? Are most QTL effects additive, or do QTLs often act in a nonadditive (epistatic) manner (12)? Does inheritance of alleles from a given parent at multiple QTLs usually affect a trait in the same direction, as predicted by certain evolutionary models (13)? In addition to elegant theoretical advances (1, 10, 11, 13), several studies have surveyed large numbers of traits empirically to identify genetic trends (14–16). But many questions remain.

Recently, we and others have shown that gene expression levels, as measured with DNA microarrays, can be treated as quantitative traits, allowing thousands of such traits to be studied simultaneously (6, 17–19). These studies have demonstrated that levels of many transcripts vary among genetically diverse individuals in a species, and that linkage mapping can be used to identify hundreds of QTLs that underlie this variation. Here, we use a cross between two strains of the budding yeast Saccharomyces cerevisiae to extract general principles about the complex genetics of quantitative traits from this large data set. Examination of QTL detection for thousands of expression traits allows us to make inferences about the distribution of QTL numbers and effect sizes across traits. We also use trait distributions in parent strains and their progeny to study the prevalence of different classes of inheritance patterns that underlie genetic variation in gene expression.

Materials and Methods

Expression Measurements. As parent strains we used BY4716 (BY for short), isogenic to the lab strain S288C, and the wild isolate RM11-1a (RM for short) (6, 17). We grew 6 independent cultures of BY, 12 of RM, and 1 of each of 112 segregants, isolated RNA, and hybridized cDNA to microarrays as described in ref. 6. Each array (20) assayed 6,216 yeast ORFs, 13 of which were spotted twice, but we did not consider data from the 496 ORFs rejected by Kellis et al. (21). We did not incorporate special corrections for potential cross-hybridization (22). The remaining ORF set comprised 5,740 spots and 5,727 genes. Each hybridization was done in the presence of the same BY reference material, and all reported expression values are log₂(sample/BY reference), averaged over two dye-swapped arrays. Results in the text were obtained from data normalized by subtracting the mean log₂(sample/BY reference) over all spots for every array. For comparison (see below), we also normalized data using the maanova package, downloaded from www.jax.org/staff/churchill/labsite/software/anova/rmaanova. Normalizing the complete data set of all segregant and parent arrays at once, we performed spatial lowess smoothing, followed by a mixed-model ANOVA with dye, array, and sample as random factors (23), then eliminated data from flagged spots before further analysis.

Genetic Linkage. We genotyped segregants at 2,957 markers, performed linkage calculations using the Wilcoxon test, and assessed significance via permutations, as described in ref. 17. The false discovery rate (FDR) (24) was computed as the ratio between the expected false positive count and the number of transcripts with detected linkage, as in ref. 25, with π₀ = 1. Results in the text are the average of 10 independent permutations; the FDR = 0.05 cutoff corresponded to a nominal P < 5.7 × 10^-5. Linkage results did not vary appreciably when array data were normalized with ANOVA methods, when 100 permutations were used, or when a t test was used to detect linkage (data not shown). Because of numerical overflow during computations, for any linkage with -ln(P) > 36.8, we assigned it to have exactly -ln(P) = 37.

Proportion of Variance Explained by QTLs. We repeated the linkage and permutation tests as above on a randomly selected “detection set” of 56 segregants. For each transcript that linked to at least one QTL at the FDR = 0.05 significance level in this calculation, we used the remaining 56 segregants as the “estimate set” to estimate the proportion of genetic variance in transcript levels explained by the QTL, as described in ref. 26. Data in the text and Table 1 represent the distribution over all transcripts that linked in any of 10 independent detection/estimate sets. If the estimated proportion of genetic variance explained by a QTL was <0 (26), we assigned it to be identically 0 (10% of QTLs); if the estimate was >1, we excluded it (3% of QTLs). Transcripts with estimated heritabilities <0 (see below), or <2 parental or segregant measurements without missing data, were excluded (5% of transcripts).

Table 1. Unbiased estimates of percent genetic variance explained by detected QTLs, in real and simulated data.

Variance explained	Data	Four-locus model	Best model
0–10	0.26	0.11	0.2
10–20	0.15	0.27	0.18
20–30	0.14	0.33	0.16
30–40	0.13	0.2	0.12
40–50	0.09	0.07	0.09
50–60	0.07	0.02	0.06
>60	0.16	0.004	0.2
Median	0.27	0.24	0.27

Numbers in each cell represent the fraction of QTLs in a given data set that explain a percent of genetic variance in a given range. Data: QTLs detected across all real transcripts. QTLs detected in the subset of highly heritable transcripts were not significantly different (data not shown). Four-locus model: QTLs simulated under a model of four additive loci of equal effect. Best model: QTLs simulated under the best-fit additive model for highly heritable transcripts. QTLs with negative estimates were not included. When transcripts linked to multiple loci, results are for the QTL with the most significant P value in the linkage test.

Simulations. For each genetic model of interest and each transcript, we proceeded as follows (27). We simulated environmental and measurement error with the normal distribution, and adjusted the effect size of QTLs in the model such that the heritability (see below) calculated from simulated segregants and parents agreed with the heritability from a single real transcript. We did not attempt to model explicitly the specific sources of variation associated with microarray data. Details are described in Supporting Text, which is published as supporting information on the PNAS web site. For each simulated transcript we assessed the significance of linkage to simulated loci and estimated the proportion of variance they explained as above, using FDR = 0.05 cutoffs for significant linkage from the real data. Data in the text and Table 1 represent the average over 10 independent simulations. Transcripts from the real data with h² < 0 or a lot of missing data were excluded (see above).

Statistically Significant Heritability. We calculated the heritability of each real transcript as 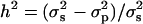, where 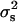and 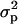are the variance among phenotype values in the segregants and the pooled variance (28) among parental measurements, respectively. Heritabilities calculated this way can be inflated by outliers, but we found this to be a problem for only a small fraction of transcripts (data not shown). We determined the significance of heritabilities via permutation: For each transcript, we combined all BY, RM, and segregant trait values, then reassigned values to null parents and null segregants at random from this pool. FDRs were computed as above, and the FDR = 0.05 cutoff was h² > 0.687.

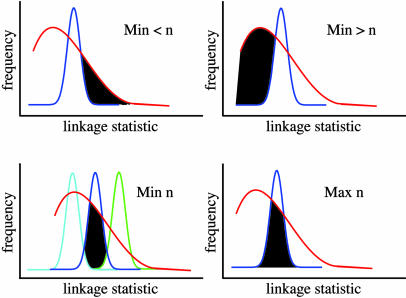
Minimum and Maximum Estimates of Complexity. We performed linkage calculations on real data and on simulated transcripts controlled by n loci of equal effect for n = 1–10, as above, using only the subset of real transcripts with significant heritabilities. In addition, for each simulated transcript, we modeled linkage to a false positive locus by choosing a linkage P value at random from the permutation test on real data. For every transcript, we identified the most significant linkage P value across all loci tested, including false positives in the case of simulated data. Given this set of peak linkage statistics across all transcripts for the real and simulated data, we constructed histograms as follows. We split the range of linkage statistics into bins of one natural log unit; then we computed f_ir, the fraction of transcripts with a linkage statistic falling into each bin i in the real data, and f_in, the fraction of transcripts with a linkage statistic falling into each bin i in the simulation of each n-locus model. We then interpreted the real data with reference to the simulations. For example, transcripts linking more significantly than one would expect under an n-locus model are consistent only with simpler models (n - 1, n - 2,...). Thus, to estimate the minimum proportion of real transcripts controlled by fewer than n loci, we computed m_n, the mean linkage statistic among all transcripts in the n-locus simulation; then, for linkage statistics more significant than this value, we calculated the excess density in the distribution of real transcripts relative to the simulation, by computing f_ir - f_in for each bin i to the right of m_n and summing these differences across all bins (Fig. 1 Upper Left). Likewise, to estimate the minimum proportion of transcripts controlled by more than n loci, for each bin i to the left of m_n, we computed f_ir - f_in and summed these differences across all bins (Fig. 1 Upper Right). To estimate the minimum proportion of transcripts that could be controlled by n loci, we calculated the density in the distribution of real transcripts that was consistent with the n-locus model and no other: For each bin i, we computed z = max(f_in+1, f_in-1), then min(f_ir - z, f_in), and then summed the latter minima, if positive, across all bins (Fig. 1 Lower Left). To estimate the maximum proportion of transcripts that could be controlled by n loci, for each bin i, we computed min(f_ir, f_in) and summed these minima across all bins (Fig. 1 Lower Right). Results in Table 1 are an average over 10 independent simulations.

Fig. 1.

Cartoon illustrating the calculation of bounds on complexity. Each curve represents the results of linkage mapping on many highly heritable transcripts. The x axis represents, for a given transcript, the most significant linkage statistic across all loci tested; statistics are ordered by increasing significance. The y axis shows the proportion of transcripts with a given linkage statistic. In each panel, the red curve represents observed data and the blue curve indicates a simulation of transcripts controlled by n additive QTLs of equal effect. (Upper Left) Black shading represents the minimum proportion of real transcripts less complex than the n-locus model. (Upper Right) Black shading represents the minimum proportion of real transcripts more complex than the n-locus model. (Lower Left) Cyan and green curves represent results from simulations of transcripts controlled by n + 1 and n - 1 additive QTLs of equal effect, respectively; black shading represents the proportion of real transcripts consistent with the n-locus model and no other. (Lower Right) Black shading represents the maximum proportion of real transcripts consistent with the n-locus model.

Model Fit. We considered models in which the proportion of transcripts controlled by n loci of equal effect was given by (1 - α)λ^(n-1)/c. Here, c is a normalization constant, λ is the geometric parameter, 1 ≤ n ≤ 10, and α is the proportion of traits more complex than n = 10, which we call higher-order traits. We considered two different models for higher-order traits. In the null model, all higher-order traits had no QTLs with individual effects above the level of noise. In the 30-locus model, all higher-order traits were controlled by 30 loci of equal effect. In either case, we expressed the distribution of peak linkage statistics across all transcripts as a combination of the distributions from the n-locus and higher order models. Binning this distribution as above, and given the parameters α and λ, we write f_iλα, the fraction of all transcripts with linkage statistics falling into the ith bin, as

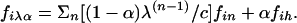To parameterize, we first ran 10 linkage simulations of highly heritable transcripts under a model of n loci of equal effect, for n = 1–10. We also ran 10 simulations of the 30-locus model and 10 permutations of real transcripts for the null model. Next, we computed the fraction of transcripts with a peak linkage statistic falling into each bin i in the real data, f_ir, in each n-locus model, f_in, and under each higher-order model, f_ih. Plugging these into the composite formula above, we fit the α and λ parameters to maximize the likelihood of the real data, f_ir, given the prediction from simulations, f_iλα, across all bins, using maximum-likelihood software available on request. Maximum-likelihood estimates for the 30-locus model were α = 0.45 and λ = 1.15, giving a log-likelihood of -9,001; for the null model, α = 0.22 and λ = 1.32, giving a log-likelihood of -9,577. Because the null model gave a weaker likelihood, we concluded that most higher-order transcripts could be modeled with a number of loci >10 but still finite. We used the 30-locus model for further analysis.

Directional Test. In a Mendelian trait, on average 50% of segregant trait values will fall between those of the parents. To identify transcripts that significantly exceeded this expectation, we identified 2,790 transcripts differentially expressed between the parents at FDR = 0.05, using methods described in ref. 17. For each such transcript, we counted the number of segregants with trait values between parental means and then assessed significance, P, by means of a cumulative binomial test with an underlying probability of 0.5. We used the Bonferroni correction to estimate false positives; the FDR = 0.05 cutoff, computed as above, corresponded to P = 0.0084. For simulated data, we applied the binomial test to transcripts simulated under additive genetic models as above, using the FDR = 0.05 significance cutoff from the real data. Power for n = 2 was 98% and for all higher n was 100%.

Transgressive Test. We defined transgressive segregation in terms of the pooled standard deviation, σ (28), of both parents. Given a cutoff, d, we tabulated for each transcript the number, j, of segregants whose expression level lay at least dσ higher than the mean expression level of the higher parent or dσ lower than the mean expression level of the lower parent. To determine significance, for each transcript we combined all BY, RM, and segregant phenotype values, then reassigned values to null parents and null segregants at random from this pool and tabulated j in each such null transcript. The total number of such null traits with j greater than a given threshold j₀ represented the genome-wide false positive count at j₀. The FDR was computed as the ratio between the estimated false positive count at j₀ and the number of real transcripts with j > j₀. Results were averaged over 10 permutations. The FDR = 0.05 cutoff corresponded to j = 58 segregants for d = 1.0, j = 35 segregants for d = 1.5, j = 21 segregants for d = 2.0, j = 13 segregants for d = 2.5, and j = 8 segregants for d = 3.0. Simulations, described in Supporting Text, indicated that the test with d = 2.0 gave approximately maximal power under a range of transgressive models, as shown in Fig. 5, which is published as supporting information on the PNAS web site; results from real data in the text were obtained with this test. For power results given in the text, we ran 10 simulations of additive models for each of n = 2, 4, 6, and 8 using the heritability-based approach as above, except that at half the loci, the “high” allele conferred a decrease in expression instead of an increase.

Epistasis Test. We adapted the Δ statistic from Lynch and Walsh (1), which assigns significance P based on a t test for the difference between midparent and segregant mean phenotype values, as detailed in Supporting Text. To estimate false positive counts, for each transcript we combined all segregant and parent values, then assigned them at random to one of two null parent groups or a null segregant group and reran the test. Results were averaged over 10 permutations; the FDR = 0.05 cutoff corresponded to -ln(P) = 6.55. To estimate power, we simulated the model in which segregants with either parental allele combination all had one expression level and those with nonparental combinations all had another. Across highly heritable transcripts controlled by this model with two or three loci, 99% and 100%, respectively, passed the epistasis test at the significance level corresponding to FDR = 0.05 in the real data. We also simulated the model in which segregants with one parental allele combination had one expression level and all other segregants had another. Across highly heritable transcripts controlled by this model comprising two loci, 68% passed the epistasis test, and with three loci, 100% passed the test. Simulations are described in detail in Supporting Text.

Results

Strength of Detected QTLs. We searched for linkage between transcript levels and genetic markers in 112 segregants as described in refs. 6 and 17. We detected at least one QTL for each of 2,984 transcripts at a FDR (see Materials and Methods) of 0.05. Linkage results were robust to different normalization procedures and linkage tests (see Materials and Methods). To assess the strengths of detected QTLs, we computed the fraction of variance among segregant trait values that was explained by each locus (26). We eliminated bias in the calculation (29) by detecting QTLs in half the segregants and using the remaining segregants to study locus effects. Because this procedure reduced power in the linkage calculation, we could only estimate fractions of variance for a subset of linking transcripts. In 10 realizations of the method, on average, we made estimates for 1,038 transcripts. Across this data set, we measured the proportion of transcripts with QTLs explaining a fraction of variance in a given range (Table 1). The median fraction of variance explained was 27%, with a range of QTL strengths from <10% to near 100%. This range could reflect true differences in QTL strengths across transcripts, but some differences are also expected as a consequence of estimating fractions of variance explained in a finite sample.

We next wished to interpret the data with reference to a simple model. We carried out computer simulations in which each transcript level was controlled by four additive loci with equal effects; the number of loci was chosen to match the median fraction of variance explained in the real data. A comparison of simulated and real data suggests (Table 1) that we should expect considerable spread in estimated proportions of variance explained due to sampling variance but not to the extent seen in the real data. Thus, underlying genetic architectures must differ across transcripts.

Relatively few transcripts showed evidence of loci with large effects. The strongest QTL explained >50% of genetic variance for only 23% of mapped transcripts (Table 1) and <30% of genetic variance for more than half of mapped transcripts (Table 1), suggesting that weak undetected QTLs account for the rest of the genetic variance in each such transcript. Examination of transcripts with multiple detected unlinked QTLs did not alter this conclusion (data not shown).

Predicting the Distribution of Inheritance Patterns Across Transcripts. Variation of a given transcript level among the segregants can arise from genetic factors (inheritance of different combinations of parental alleles) and nongenetic factors (for example, measurement noise or small differences in experimental conditions). The fraction of variance in segregant phenotypes attributable to genetic factors is known as the heritability. Because a major goal of this study was to analyze the distribution of underlying inheritance patterns across transcripts, and such analyses may not be meaningful for transcripts influenced primarily by nongenetic factors, we chose to focus on a subset of transcripts for which genetic factors predominated (that is, for which heritability was high). We tested for statistically significant heritability as described in Materials and Methods; 3,546 transcripts met this criterion, all with heritabilities >69%. Of these, only 2,091 transcripts (59%) showed linkage to at least one QTL. Because the remaining transcripts are highly heritable, and the statistical power of our study to detect QTLs with large effects is high (see below), these transcripts must be controlled by QTLs with effects too small to be detected by our approach. Failure to detect any QTLs for a highly heritable trait can be explained by one of two scenarios, both involving multiple loci. In the first scenario, the trait is controlled by many loci with small additive effects, with no single locus strong enough to be detected. In the second scenario, the trait is controlled by loci that interact nonadditively such that any one locus has little marginal effect. Each scenario is likely to apply to some transcripts (see below).

The fraction of highly heritable transcripts with no detected loci can be used to further examine genetic complexity and the effect sizes of QTLs that underlie transcript levels. To do so, we carried out simulations of the power of our study to detect QTLs of a given effect size under two genetic models. In the first, the genetic variation in each transcript was controlled by n loci with equal additive effects, whereas in the second, the variation was due to one main locus of a given effect, with the rest of the variance accounted for by loci with infinitesimal effects. Although these simulations used a simplified error model (see Materials and Methods), they are of use in allowing us to interpret the rate of mapping QTLs across real transcripts. We found that our study had >90% power to detect at least one locus for transcripts with n ≤ 7 under the first model or to detect a main locus explaining >25% of genetic variance under the second model. Power was near the observed detection rate of 59% for n = 13 under the first model and for the main locus explaining 19% of genetic variance under the second model.

To gain additional insight into additive genetic models consistent with our data, we considered the peak linkage statistic of each transcript, regardless of whether each exceeded a threshold for detection. A very significant statistic indicates the presence of a locus with strong effect, whereas a weak statistic suggests that all loci underlying that transcript have weak effects. From these data, we sought to estimate the relative prevalence of different levels of genetic complexity across transcripts. As illustrated in Fig. 1, we attempted to place bounds on the fraction of transcripts that could be explained by each value of n, by comparing the distributions of linkage statistics for simulated data sets with different values of n to the distribution in the real data. Results (Table 2) indicate that few transcripts have simple genetics. Only 3% of all highly heritable transcripts have linkage statistics consistent with single-locus inheritance; at most, 17–18% can be explained by models with one or two loci, consistent with the observation above that a detected QTL explained >50% of genetic variance for ≈20% of the transcripts. Approximately half of the transcripts require models with n > 5, and almost a third require models with n > 8.

Table 2. Estimated bounds on the proportion of highly heritable transcripts with a given inheritance pattern.

n	Min ≤ n loci	Min > n loci	Min n loci	Max n loci
1	0.03	0.97	0.03	0.03
2	0.05	0.83	0.02	0.15
3	0.07	0.71	0.01	0.25
4	0.09	0.60	0.01	0.33
5	0.11	0.49	0.03	0.42
6	0.13	0.42	0.05	0.47
7	0.15	0.35	0.04	0.52
8	0.17	0.30	0.08	0.56
9	0.18	0.26	0.06	0.58
10	0.20	0.22	0.07	0.61

The second through fifth columns represent, respectively, the minimum proportion of highly heritable transcripts that could be controlled by n or fewer additive loci of equal effect; the minimum proportion that could be controlled by more than n loci; the minimum proportion that could be controlled by exactly n loci; and the maximum proportion that could be controlled by exactly n loci. See Fig. 1 for an illustration of methods.

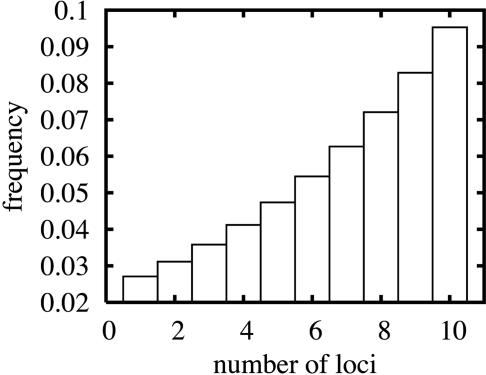
The bounds in Table 2 constrain the range of additive models consistent with our data. We next sought to fit a single model that best described the frequency of transcripts consistent with inheritance patterns of n = 1, 2,..., n_max additive loci with equal effect. For simplicity, we used a geometric distribution to describe the frequency of highly heritable transcripts with a given value of n and arbitrarily set n_max to 10. The geometric distribution has a single adjustable parameter, λ, that ranges from 0 to infinity. In our case, λ > 1 implies higher frequencies for larger values of n, whereas λ < 1 implies higher frequencies for smaller values of n. Because we obtained evidence that some transcripts require values of n > 10 (see above), we added an additional parameter α, such that a fraction 1 - α of transcripts was described by the geometric distribution over n = 1–10 while the remaining fraction α was described by a single model with more complex genetics (30 loci of equal effect). We estimated the parameters λ and α by maximum likelihood (see Materials and Methods). The best fit to the distribution of linkage statistics was obtained for λ = 1.15 and α = 0.45. In a model with this choice of parameters, 55% of transcripts are divided among those consistent with values of n between 1 and 10, with frequencies ranging from ≈3% for n = 1 to ≈10% for n = 10 (Fig. 2); the remaining 45% of transcripts are consistent with 30 additive loci of equal effect. This model captured the distribution of real linkage statistics with reasonable accuracy (Fig. 6, which is published as supporting information on the PNAS web site) and also gave a distribution of fraction of variance explained by detected QTLs similar to that observed in the data (Table 1). We note that this model merely provides a single scenario of additive effects consistent with our data, and we do not expect it to accurately represent the full distribution of locus effects within and across transcripts; the model also explicitly ignores interactions.

Fig. 2.

Distribution of inheritance patterns in best-fit additive model. Each bar represents an inheritance pattern involving additive loci of equal effect. Bar heights give the proportion of highly heritable transcripts predicted to have each type of inheritance under the fitted geometric model.

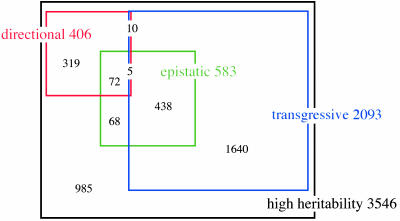
Directional Genetics. We have presented several lines of evidence for multilocus genetics among most heritable transcripts in the yeast genome. We next sought to classify different types of multilocus inheritance and determine the prevalence of each. We first considered the case of additive QTLs with inheritance from a given parent at a majority of loci affecting the phenotype in the same direction. We call this a directional model, after its hypothesized role in directional selection (13). Under the most extreme directional model, segregants inheriting all loci from each parent have the phenotype level of that parent, whereas all other segregants have phenotypes between those of the two parents. We developed a statistical test for this class of genetics by counting, for each transcript, the segregants with phenotype values between those of the parents. Of 3,546 highly heritable transcripts, 406 (11%) passed the directional test (Fig. 3); the top-ranking example is shown in Fig. 4 Left. Power simulations indicated that >98% of transcripts controlled solely by additive loci of equal effect would pass the directional test. This finding suggests that most transcripts with simple directional genetics have been identified.

Fig. 3.

Prevalence of different inheritance patterns among highly heritable transcripts. The black rectangle represents all transcripts with high heritability. Colored squares and numbers represent the transcripts with high heritability that pass the indicated tests for inheritance patterns. Black numbers in overlapping squares represent transcripts that pass multiple tests; the black number at the lower left represents highly heritable transcripts that do not pass any of the tests.

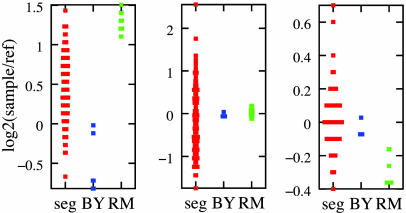
Fig. 4.

Expression of genes with strongest evidence for directional, transgressive, and epistatic genetics. In each panel, the first column shows data from 112 segregants and the second and third columns show replicate measurements in the BY and RM parents, respectively. (Left) The cytochrome c reductase subunit YPR191W/QCR2, the annotated gene giving the most significant statistic in the test for directional genetics. (Center) The histidine and purine biosynthetic enzyme YMR120C/ADE17, which gave the most significant statistic in the test for transgressive segregation. (Right) The transcriptional regulator YML051W/GAL80, the annotated gene that gave the most significant statistic in the test for epistasis.

Transgressive Segregation. Next we considered additive QTLs with opposing effects, i.e., the allele from a given parent at some loci elevates transcript levels and at other loci lowers transcript levels. Given this type of inheritance, segregants with nonparental allele combinations may have higher or lower expression levels than those of either parent, a phenomenon called transgressive segregation. Because previous qualitative approaches to detect transgression (e.g., refs. 30–32) may not be suitable for genome-wide application, we developed a statistical test for transgressive segregation (described in Materials and Methods), based on the number of segregants whose expression levels fall far outside the parent means. Of 3,546 highly heritable transcripts, 2,093 (59%) passed our test at FDR = 0.05 (Fig. 3); Fig. 4 Center shows the transcript that scored most significantly. To assess the power of the test, we ran simulations of highly heritable transcripts controlled by two to eight opposing loci of equal effect; >80% passed the test in all cases, showing that the test has high power to detect transcripts controlled predominantly by additive, opposing QTLs. We conclude that transgression is widespread, affecting the majority of highly heritable transcripts. Even more transcripts may be controlled by more complex transgressive inheritance, involving loci with weaker effects that are not detected by the test.

Epistasis. We next considered epistatic interactions, in which the effect of one QTL on a trait depends on another QTL. We used a modified version of the epistasis test of Lynch and Walsh (1), which tests for a difference between the mean expression levels of segregants and parents, because the means are equal for any additive inheritance pattern. Of 3,546 highly heritable transcripts, 583 (16%) passed the epistasis test (Fig. 3); Fig. 4 Right shows the top-scoring transcript from an annotated gene in this analysis. Power simulations involving highly heritable transcripts controlled by two or three loci, under several epistatic models, indicated that our test had 70–100% power to detect such transcripts (see Materials and Methods). Thus, our estimate of the number of highly heritable transcripts with strong interactions between a few loci may be reasonably accurate. Many additional transcripts may have more complex epistatic inheritance patterns that are undetectable by the test.

Discussion

Complexity and Mapping. We surveyed the genetics of a large collection of similar phenotypes (the transcript levels of all yeast genes) in an attempt to extract general principles about quantitative traits and QTLs. Our results indicate considerable genetic complexity in the data. Unbiased estimates of QTL strength revealed a wide range in the proportions of variance explained by mapped loci, with the majority of transcripts mapping to weak QTLs. Model-based analyses of mapping rates indicated that only a small proportion of transcripts appear to have simple inheritance, whereas most have a reasonably high effective number of loci. We also fit an analytic form for the distribution of genetic architectures across transcripts. Although the quantitative details of the fit are model-dependent, the general conclusions may be useful as a starting point for power simulations in future studies of quantitative traits. Additionally, we identified hundreds of transcripts consistent with each of three classes of inheritance pattern, predictions that can help refine QTL mapping procedures (12, 15, 33).

Among highly heritable transcripts, the median genetic variance explained by the strongest detected QTL was 27%, and QTLs for other transcripts explained even less variance. This finding is consistent with the idea that most variation with very large effects should have been fixed in or eliminated from stable populations (10), although we also observed that 3% of highly heritable transcripts followed essentially monogenic inheritance. Our ability to detect such weak loci via linkage reflects in part the involvement of multiple loci in the genetics of most transcripts, increasing the chances that at least one locus is detectable because of a favorable statistical fluctuation in the same direction as the effect of the locus (27). Our estimates of QTL strength are consistent with those seen previously in other systems. QTLs explaining <10% of variance are routinely reported in the QTL mapping literature (e.g., refs. 1, 34, 35), and even these low estimates are probably biased upward (27). The high effective number of QTLs for most highly heritable transcripts and the small effect sizes of detected QTLs suggest that QTL mapping and identification of the underlying polymorphisms will continue to be challenging endeavors in model and agricultural organisms and especially in humans.

Transgressive Segregation. Transcripts with an excess of segregant values outside those of the parents (transgressive segregation) were much more prevalent than transcripts with an excess of segregant values inside those of the parents (directional genetics). A majority of highly heritable transcripts showed transgressive segregation, consistent with the results of metaanalyses of different traits in plants and animals (16, 36). Widespread transgression in the yeast transcriptome could be the result of genetic drift, i.e., the fixation over time, in one strain, of mutations that increase and decrease a transcript level with little effect on fitness. It has also been suggested that such opposing QTLs may be a mechanism for generating diversity in subsequent generations (16). Interestingly, among highly heritable transcripts, 21% of those passing the test for transgressive segregation also passed the test for epistasis, whereas only 11% of those which did not show transgression passed the epistasis test (Fig. 3). This finding suggests that additive QTLs of opposite effect may not be exclusively responsible for transgression (16, 32, 36).

Epistasis. The prevalence of epistatic interactions among loci is important in evolutionary theory, because a trait under epistatic control may require a relatively rare combination of several mutations to arise before a phenotypic change is observed (37, 38). Epistasis also complicates QTL mapping, because most mapping methods rely on detecting the additive effects of individual loci and have little power to detect epistatic QTLs with small marginal effects (12). We obtained evidence for epistatic interactions underlying 16% of highly heritable transcripts. We also failed to detect any additive QTLs for ≈40% of highly heritable transcripts, raising the possibility that some or all of these are controlled by interacting QTLs.

Physiological Phenotypes. Transcriptional phenotypes may differ from physiological phenotypes because of different biological and technical sources of variation. Nevertheless, given the extensive genetic complexity observed here, we conclude that transcript levels may serve as a good model for the genetics of complex cellular and physiological traits. Indeed, many macroscopic phenotypes may have a basis in gene expression. Noncoding polymorphisms known to affect transcription have been implicated in HIV-1 resistance (39) and diabetes risk (40) in humans, plant morphology in maize (41), muscle growth in pigs (8), and fruit weight in tomato (42). Schadt et al. (18) mapped a QTL controlling obesity in mouse to a locus that also affected transcript levels of related genes. We have shown that clumpy growth of yeast cells maps to the same locus as the expression of daughter-specific genes involved in mitosis and budding (6). In keeping with these observations, several groups have used expression profiling to choose among gene candidates when physiological traits map to large genetic regions (43–45).

Genetic studies of quantitative traits have identified many loci for specific traits in humans, plants, and experimental organisms. Understanding the complexity of multilocus genetics is an important challenge in the field. Analysis of thousands of quantitative traits in parallel offers the ability to extract general principles about quantitative genetics; such insights can provide a step toward the prediction of inheritance patterns for traits of particular interest, which can lead to the improvement of QTL mapping procedures (12, 15, 33).