Mechanosensitive Adhesion Explains Stepping Motility in Amoeboid Cells

Abstract

Cells employing amoeboid motility exhibit repetitive cycles of rapid expansion and contraction and apply coordinated traction forces to their environment. Although aspects of this process are well studied, it is unclear how the cell controls the coordination of cell length changes with adhesion to the surface. Here, we develop a simple model to mechanistically explain the emergence of periodic changes in length and spatiotemporal dynamics of traction forces measured in chemotaxing unicellular amoeba, Dictyostelium discoideum. In contrast to the biochemical mechanisms that have been implicated in the coordination of some cellular processes, we show that many features of amoeboid locomotion emerge from a simple mechanochemical model. The mechanism for interaction with the environment in Dictyostelium is unknown and thus, we explore different cell-environment interaction models to reveal that mechanosensitive adhesions are necessary to reproduce the spatiotemporal adhesion patterns. In this modeling framework, we find that the other motility modes, such as smooth gliding, arise naturally with variations in the physical properties of the surface. Thus, our work highlights the prominent role of biomechanics in determining the emergent features of amoeboid locomotion.

Introduction

Cell movement is required in many physiological and pathological processes such as the immune system response and cancer metastasis (1, 2). One of a broad spectrum of migratory mechanisms is amoeboid migration, characterized by repetitive cycles of fast shape changes. The prototypical example is a chemotaxing single-cell amoeba Dictyostelium discoideum (3), but similar mechanisms are employed by neutrophils, lymphocytes, and some tumor cells (4, 5, 6, 7). These rapid shape changes occur periodically and in coordination with traction forces that drive cell locomotion, allowing these cells to quickly adapt to different environments and develop rapid velocities (8, 9, 10). Although key molecular processes involved in amoeboid locomotion are known, it remains unclear how these processes are coordinated to give rise to this form of migration (3, 11).

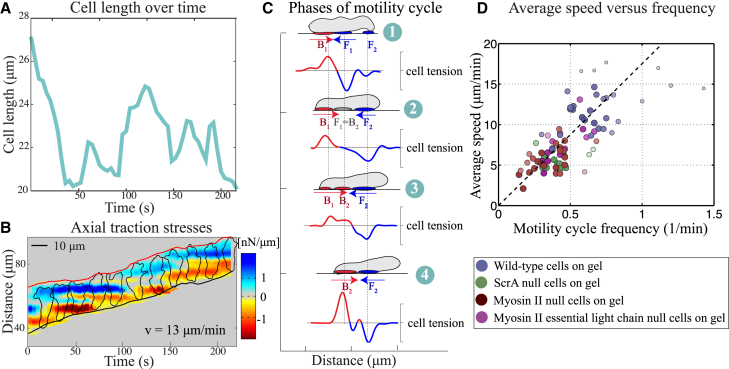
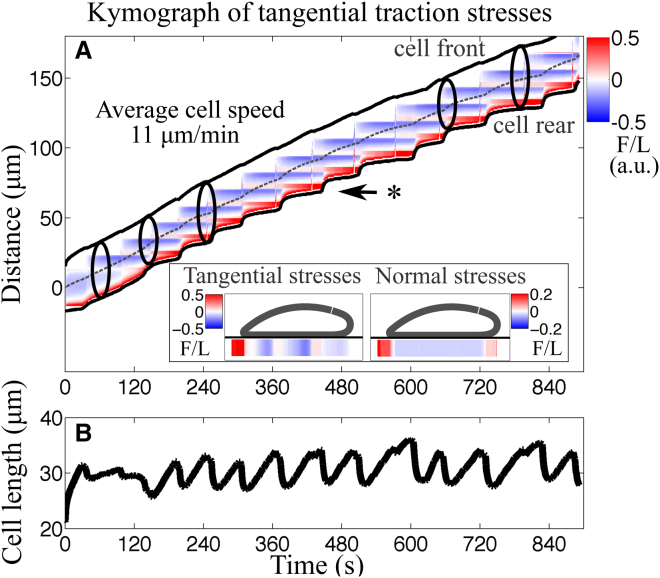
Amoeboid movement is exhibited by the amoeba, Dictyostelium, chemotaxing on flat surfaces. Here, we present typical measurements of the traction stresses and cell length of the crawling amoeba as those measured in Meili et al. (10) and Bastounis et al. (12). In the presence of a chemoattractant gradient, a motility cycle is initiated through polymerization of actin filaments at the leading edge (13, 14). The four phases of this motility cycle are (3, 6): 1) a pseudopod forms as the cell body elongates (increase in cell length), 2) the pseudopod adheres to the substrate through mechanisms that remain to be identified (cell length reaches a maximum), 3) the cell body contracts after pseudopod attachment (decrease in cell length), and 4) the cell rear retracts and detaches as the adhesive links at the rear of the cell release and allow advancement of the cell body (cell length reaches a minimum). Notably, the phases of the motility cycle correlate with the cyclic lengthening-shortening events observed in measurements of Dictyostelium body length over time (Fig. 1 A) (10).

Figure 1.

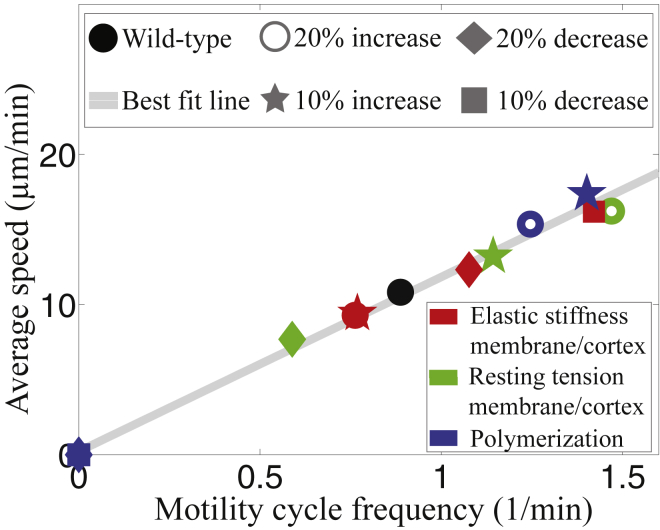
Features of amoeboid motility are exemplified by the chemotaxing unicellular Dictyostelium amoeba. (A) The plot of the body length over time shows periodic lengthening-shortening events. (B) Given here is a spatiotemporal representation of the instantaneous magnitude of the tangential tensions (force per length) as a function of the position along the cell trajectory (vertical axis) and time (horizontal axis) for a representative wild-type Dictyostelium cell. The tension measurements yield from integrating axial stresses across the cell width and we use these tensions to understand the traction stresses involved in motion. (C) Schematic representation given, showing the four phases of motility cycle with snapshots of the instantaneous cell shape, location, and magnitude of traction adhesions and axial tensions. Front and back adhesions are shown as blue and red ovals underneath the cell, whereas the gray oval represents weak adhesions. The numbers correspond to the phases of the motility cycle. (D) Shown here is a scatter plot of the average migration speed as a function of the frequency of the motility cycle for different mutants. The dashed line is the least squares fit to the data, v = 18f showing that the cells perform a motility cycle with an average step length of 18 μm. The circles represent individual cells but to better visualize the correlation, the f-v plane was divided into rectangular tiles of equal area, and the size and the color of each data point were scaled according to the total number of data points that fall on each specific tile (i.e., its rate of occurrence). As a result, darker, larger circles represent those data points that were observed more often in our experiments, and vice versa. Statistical information for the stride length per cell type is presented in Fig. S5. Details for experimental data acquisition are in the Supporting Material. To see this figure in color, go online.

The traction forces applied on the surface by the crawling cell are also correlated with the phases of the motility cycle (Fig. 1 B) (12). Regions of elevated traction forces are thought to be indicators of where the cell adheres to the substrate (15, 16), so that Dictyostelium adheres to the substrate in either two or three distinct physical locations (Fig. 1 B). Generally, axial stresses are negative at the cell front (directed inward toward the cell rear) and positive at the cell rear (directed inward toward the front). Shortly after a new pseudopod forms, the cell establishes a new adhesion site under the nascent pseudopod. The “old” front adhesion site becomes the “new” back adhesion site, whereas the “old” back adhesion site is lost once the cell passes its position. Thus, the front adhesion site is “recycled” to a back adhesion site, as indicated by the horizontal bands of elevated forces with a lifetime similar to the period of the motility cycle (Fig. 1 B). Although the evidence is clear that adhesion sites do not form randomly but have well-defined dynamics that are synchronized with the phases of the motility cycle (8, 9, 12) (Fig. 1 C), the mechanism responsible for these spatiotemporal adhesion patterns is unknown. Further, the molecules involved in generating adhesive forces are also unknown (17, 18).

The synchronization of adhesion dynamics with periodic length changes causes Dictyostelium to engage in step-like locomotion; as the cell crawls, it forms sequential adhesion sites that remain fixed on the surface and stable during the motility cycle. Interestingly, this stepping motion is robust as illustrated by the analysis of five mutant strains of Dictyostelium, which shows that these cells also exhibit step-like movement and, furthermore, regulate their locomotion so that the stride length is unaffected in several, but not all, conditions (Fig. 1 D) (10, 19). Together, these observations imply that the migration speed is determined by a highly coordinated yet well-conserved mechanism involving actin polymerization for pseudopod extension and contraction of the cell body, together with a synchronized mechanism for attachment and detachment of adhesions to the surrounding environment. In particular, we are motivated by questions of how these key cellular processes achieve front-to-back coordination and the emergent periodic cycles of cell length changes that are needed for locomotion. We are also interested in understanding how these intracellular processes are synchronized with the formation and rupture of adhesions to the surface to give rise to the reported spatiotemporal dynamics of traction forces.

Although biochemical mechanisms have long been thought to underlie aspects of cell motility, recent work has also implicated biomechanical mechanisms (20, 21, 22, 23). Here, we hypothesize that the periodic morphological changes emerge from the force-dependent action of actin polymerization at the leading edge and the mechanical response of the outer cell membrane and its underlying actomyosin cortex, together with a force-sensitive interaction with the surface. In support of this hypothesis, we present a simple mechanochemical model that captures all observed features of amoeboid locomotion: spatiotemporal distribution of traction stresses, recycling of cell-substrate adhesions, and the emergence of periodic lengthening-shortening events. An exploration of different cell-environment interaction models reveals that mechanosensitive adhesions are necessary to explain the localization and recycling of adhesion sites during a motility cycle. Further, when adhesion and surface parameters are varied, other experimentally observed motility modes emerge in our model.

Materials and Methods

Model

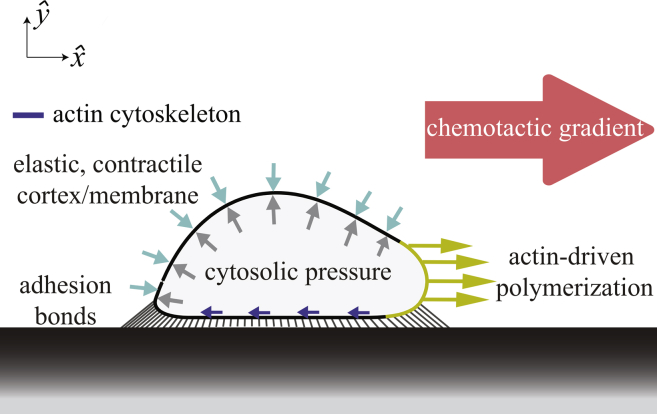
We developed a continuous two-dimensional (2D) mechanical model of an amoeboid cell polarized in a fixed direction (Fig. 2). The cell crawls in the horizontal direction with surface attachments between the cell and the surface below it. The outer cell membrane and its underlying actomyosin cortex are represented as a single structure with position X(s,t) = (x(s,t), y(s,t)), where t is time and s is the local parametric coordinate on the structure. Here, $\hat{x}$ is a unit vector in the horizontal direction of crawling whereas $\hat{y}$ is in the vertical direction. The cell cytoplasm is represented as a viscous fluid with instantaneously equilibrated internal pressure. Our model consists of a balance of forces involving the response of the combined membrane-cortex structure, the interaction force between the cell and the surface, the intracellular pressure that enforces volume incompressibility of the cell, the polymerization machinery driving the forward motion, the cytoskeleton that transmits polymerization forces to the underlying surface, and a viscous drag force with the surrounding environment, as follows:

$$\xi \frac{\partial \mathit{X}}{\partial t}={\mathit{F}}_{\text{membrane}/\text{cortex}}+{\mathit{F}}_{\text{pressure}}+{\mathit{F}}_{\text{polymerization}}+{\mathit{F}}_{\text{cytoskeleton}}+{\mathit{F}}_{\text{surface}}.$$ (1)

Here, we assume a velocity-dependent drag with the environment, where ξ denotes the viscous drag coefficient. We now focus on the constitutive laws of these cellular forces.

Figure 2.

Given here is a schematic of model, with a side view of a Dictyostelium cell polarized in a fixed direction of a chemotactic gradient. Our mechanical model of an amoeboid cell has four cellular components: combined membrane-cortex structure, viscous cytosol, actin-driven polymerization at the leading edge, and interaction with the substrate. The arrows along the ventral surface of the cell represent the action of the actin cytoskeleton. To see this figure in color, go online.

Outer cell membrane and actomyosin cortex

The cell membrane and the actomyosin cortex structure are treated as a single elastic, contractile structure (24, 25). The elastic force density is computed by ${\mathit{F}}_{\text{membrane}/\text{cortex}}=\left(\partial /\partial s\right)\left(T\hat{\tau }\right)$, where T is tension and $\hat{\tau }$ is the tangent vector to the curve X(s,t). The tension is given by T = γ + k(|∂X/∂s| −1), which describes a linearly elastic spring with stiffness k and resting tension γ.

Intracellular fluid

The cytosol is modeled as a viscous medium and is assumed to have a resting internal pressure p₀ and resting volume V₀. The pressure force is given by ${\mathit{F}}_{\text{pressure}}=\left(p_0+{\kappa }_{\text{cell}}\text{ln}\left(V/V_0\right)\right)\hat{n}$, where $\hat{n}$ denotes the outward normal unit vector and κ_cell is a bulk modulus. Given the other forces acting on the membrane-cortex, the resting pressure is selected to ensure cell volume conservation, $\int \mathit{F}·\hat{n}ds=\xi \int \partial \mathit{X}/\partial t·\hat{n}ds=0$, whereas the volumetric correction term further ensures volume conservation is maintained throughout the simulation.

Actin-driven polymerization

The mechanical origin of these protrusive forces caused by directional polymerization of F-actin filaments is a well-studied problem (21). It has been shown that branching actin networks have a force-velocity relation at the leading edge, v = v(F_L), where F_L is the force against the protrusion (26, 27, 28). In the region of polymerization, we assume the following one-dimensional (1D) model for the leading edge velocity due to directional polymerization of F-actin filaments against the cell membrane,

$$v={\rho }_1{e}^{-{\rho }_2{F}_L}-{\rho }_3.$$ (2)

Force-velocity relations of this form were observed theoretically (21) and experimentally in a certain region of the load forces (26, 27, 28). Here, ρ_1,2,3 are parameters from measurements of the force-velocity relation at the leading edge. An equivalent way to formulate this relation is to assume the polymerization force is a function of the protrusion rate: F_{polymerization} = F_{polymerization}(v). Then, the force-balance equation in the direction of motion (Eq. 1) at the cell front has the following form:

$$F_{\text{polymerization}}\left(v\right)+F_L=\xi v.$$ (3)

Together, Eqs. 2 and 3 describe our 1D model for driving the cell front forward. We compute F_L as the average magnitude of the forces on the membrane-cortex structure in the region of polymerization, and solving Eq. 3 determines the leading edge velocity at each time step. Details of implementation in the 2D case are discussed in Fig. S2.

Unlike cell types that form thin, actin-rich lamellipodia to crawl, in Dictyostelium, actin polymerization occurs in a large frontal region corresponding to roughly 20–30% of the cell length (29). Accordingly, we define the region of polymerization, $\mathcal{P}$, as a region of fixed arclength of 21% of the undeformed membrane-cortex boundary centered about the horizontal extremum of the boundary (Fig. 2, yellow line).

Cytoskeleton

The cytoskeleton transmits the polymerization forces to the surface; the protrusive forces at the leading edge are integrated over the region of polymerization and distributed uniformly to the region of cell-surface contact to ensure zero sum of polymerization and cytoskeletal forces, as follows:

$${\mathit{F}}_{\text{cytoskeleton}}=-\frac{{\int }_{\mathcal{P}}\left|{\mathit{F}}_{\text{polymerization}}\right|ds}{{\int }_{\mathcal{C}}ds}\hat{x}.$$

The membrane-cortex structure is defined to be in the region of contact, $\mathcal{C}$, if it is within 5 μm of the substrate in the vertical direction. Without this model of the cytoskeleton, the driving forces would be unbalanced.

Cell-surface interaction

We assume the cell crawls on top of a flat rigid surface along the horizontal axis. The cell interacts with an underlying flat surface through both physical adhesive connections and a repulsive force due to contact with the surface: F_surface = F_steric + F_adhesion. Below a certain distance, δ_w, the cell feels a nonspecific steric force of the form: ${\mathit{F}}_{\text{steric}}=-k_{\text{steric}}\left(\left|y\left(s,t\right)\right|-{\delta }_w\right)\hat{y}$, where k_steric represents a stiffness of the steric interaction.

Little is known about the adhesion kinetics in Dictyostelium, and thus the form of the adhesion force is the main object of our investigation. In this article, we explore models for the adhesive force resulting from the distribution of bonds that behave as elastic linear springs: ${\mathit{F}}_{\text{adhesion}}=\zeta N\left(t,s\right)\left(\left|\mathit{X}-{\mathit{X}}_{\text{surface}}\right|/{\ell }_0-1\right)\left(\mathit{X}-{\mathit{X}}_{\text{surface}}\right)/\left|\mathit{X}-{\mathit{X}}_{\text{surface}}\right|$, where ℓ₀ is the length of the spring in its undeformed state, and X_surface stands for locations along the flat substrate. The position of X_surface is determined per bond during bond formation; when an adhesive bond forms it binds to the surface directly below the membrane-cortex structure. For the lifetime of the bond, the binding position remains fixed along the surface. At each site, the adhesive force is the result of the local bond density per adhesion site, N(t,s), and a constant adhesive stiffness, ζ. In the article, we will consider models with dynamic bond formation and rupture; thus, the local bond density can vary between zero to full occupancy of a site, 0 ≤ N(t,s) ≤ 1.

The full model and the discretization method are in the Supporting Material. Model parameters are provided in Table S1.

Motility assumptions

Our modeling hypothesis is that mechanics drive both the cycles of extension-contraction of the cytoskeleton and coordinated adhesion kinetics to give rise to the complex and highly synchronized features of stepping amoeboid motility. To reveal the mechanism responsible for these two processes and their coordination through biomechanics, we make minimal modeling assumptions and introduce complexity in the constitutive laws of mechanical forces as motivated by the results of the simulations.

During pseudopod extension, experimental data of traction forces in Dictyostelium show that the pseudopod does not initially attach to the surface (12, 30). Motivated by these observations, the simulated pseudopod must achieve a minimal length of 10 μm before attachment. Once the length condition is met, proximity to surface determines if discrete points are available for binding. Whereas symmetry of the problem is broken by polymerization at the leading edge, to move, the cell needs to communicate leading-edge forces to the cell rear and rupture the back adhesions. The rupture of adhesions is assumed to be force sensitive and modeled as a piecewise constant function, as follows:

$${\mathit{F}}_{\text{adhesion}}=\{\begin{array}{cc}\zeta N\left(t,s\right)\left(\left|\mathit{X}-{\mathit{X}}_{\text{surface}}\right|/{\ell }_0-1\right)\frac{\mathit{X}-{\mathit{X}}_{\text{surface}}}{\left|\mathit{X}-{\mathit{X}}_{\text{surface}}\right|}& \text{if}\frac{\left|{\mathit{F}}_{\text{adhesion}}\right|}{N}<F_{\text{critical}}\\ 0& \text{otherwise},\end{array}$$ (4)

for a threshold adhesive load, F_critical. Adhesions can break at any spatial or temporal location and no biochemical coordination between the front and the rear of the cell is prescribed. The formation of adhesions is determined by the proximity of the membrane-cortex structure to the surface. In the following sections, we explore three models for cell-substrate adhesion interaction: 1) spatially uniform adhesions with fixed bond density, 2) spatially nonuniform adhesions with fixed bond density, and 3) uniform adhesions with dynamic bond density. Details of adhesion models and the resulting motion are discussed later.

Results

Traction patterns for a simulated cell with uniformly distributed adhesions

Initially, adhesions are modeled by linearly elastic springs with constant bond density of full occupancy, N = 1, in Eq. 4. A similar adhesion model for cell-surface interaction has been previously used to explain the dynamics of adherent cells (23, 31, 32). We find that the mechanical model detailed above is sufficient to result in coordinated locomotion at a constant speed as indicated by the time evolution of the cell centroid (Fig. 3 A, dashed line; Movie S1).

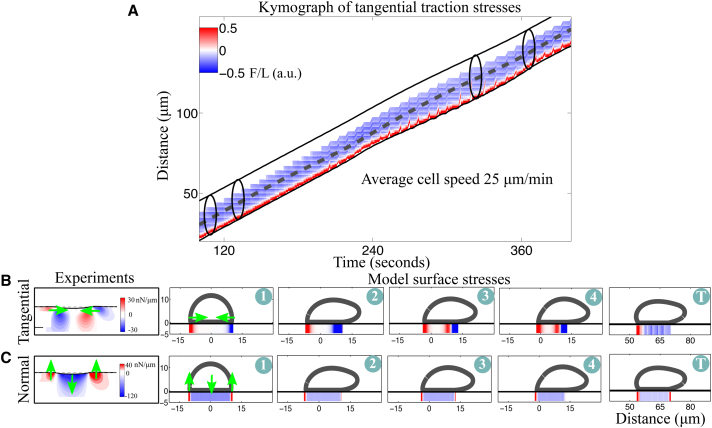
Figure 3.

A simulated cell with spatially uniform cell-surface adhesions crawls, but without the features of stepping locomotion. (A) Given here is a kymograph of axial traction stresses (force per length) as a function of the position along the cell trajectory at a given time. The constant slope of the instantaneous position of the front and back cell edges (inclined black lines) indicates small length changes. The black contours are hypothetical cell outlines at different time instances. (B and C) Given here are snapshots of the cell outline and the corresponding tangential stresses (B) and normal stresses (C). The first panel shows experimental data during the first phase of the motility cycle. The following panels are model results at four time instances during the motility cycle and one panel later in time (t = 179 s). The green arrows indicate the direction of the forces during the first phase of the cycle. To see this figure in color, go online.

The resulting movement indicates that the model does capture the emergence of coordination between extension of the front and rupture of back adhesions and notably, in the absence of biochemical signaling. Here, the coordination is achieved through the mechanical response of the membrane-cortex structure. As the cell lengthens due to pseudopod extension, the elastic forces in the membrane-cortex structure become elevated. Together with the cell curvature, these elevated forces induce a strain on rear adhesions that eventually break due to their force-dependent response. Whereas elastic forces point inward at the cell front and rear, at the front, polymerization forces push outward, providing partial counterbalance and thus, a bias to preferentially rupture rear adhesions. However, the emergent movement has none of the features of stepping locomotion observed in wild-type crawling cells (see Fig. 1, A and B). The cell length remains relatively constant (∼10% change compared to the fluctuations in Fig. 1 A) and the lack of horizontal patches in the kymograph of axial stresses is evidence that adhesion sites are not fixed on the surface or recycled as the cell crawls (comparing Figs. 3 A to 1 B).

In the spatial distribution of traction stresses, we observe localization of forces along the cell periphery that is similar to what is observed in experimental data of traction stresses during the extension phase (Fig. 3, B and C). Following the time evolution of the axial stresses, we see that as the cell elongates, back adhesions rupture one-by-one (Fig. 3 B, 2–T). Because adhesions are everywhere on the ventral part of the cell, when the rearmost adhesion ruptures, the one immediately adjacent to it will rupture as the cell lengthens. This results in a gradual gliding of the back with adhesions that form and disappear as the cell moves across the surface. In fact, gliding locomotion is exhibited by Dictyostelium cells when placed on poly-L-lysine coated surfaces (Fig. S6). We presume this is because the increased nonspecific cell-surface interaction on this substrate results in spatially uniform interaction. More generally, stepping motility must arise from more complex dynamics than uniformly distributed, linearly elastic springs with force-dependent rupture.

A nonuniform spatial distribution of adhesions is required for stepping motility

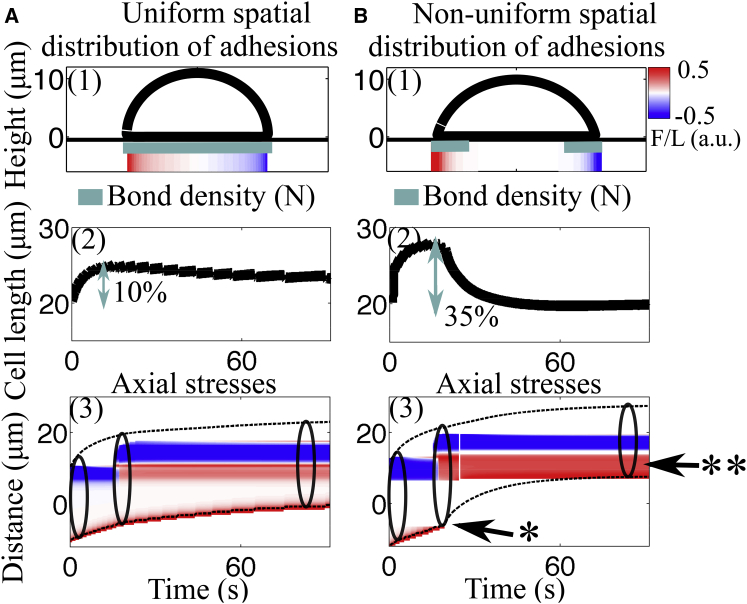
In the previous adhesion model, the small morphological changes can be attributed to the lack of a contraction in the cell body due to a continual gliding of the cell rear. One way to prevent gliding and achieve length contraction is to assume that there are no adhesions near the center, thus prescribing a nonuniform spatial distribution of adhesions. With no consideration to how this nonuniformity is achieved, we test this hypothesis by comparing the cell length and spatiotemporal dynamics of axial stresses in the two models: uniform and nonuniform distribution of adhesions (Fig. 4). The nonuniform spatial distribution of adhesions is prescribed by fixing the bond density to be nonzero only in a region 6 μm from the cell front and rear (as illustrated in Fig. 4 B1).

Figure 4.

Given here is a comparison of emerging motility when varying the spatial distribution of adhesions. For these simulations, the cell is polymerizing for only 60 s. (A1) and (B1) Shown here is the cell outline along with spatial profile of tangential surface stresses. The spatial distribution of adhesion sites along the ventral part of the cell is shown by the blue line. For nonuniform distribution of adhesions, bond density is prescribed to be nonzero only in a region near the cell front and rear. (A2 and B2) Shown here is a time evolution of cell length; a lengthening-shortening event is captured with prescribed spatial localization of adhesions. (A3 and B3) Given here are kymographs of axial traction stresses as a function of the position along the cell trajectory at a given time. When nonuniform distribution of adhesions is assumed, the rear adhesion site is lost (^∗) and the front adhesion site remains fixed on the surface but is reused as a rear adhesion site at the end of the motility cycle (^∗∗). To see this figure in color, go online.

With nonuniformly spaced adhesions, we obtain an extension-contraction event in the time evolution of cell length (Fig. 4 B2). When all of the rear adhesions rupture, the cell cannot adhere to the surface in any location other than the front, and thus the rear membrane rolls up. As the membrane-cortex structure rolls up and contracts, what was initially the front adhesion site is now located at the rear of the cell and the cell pulls upward and inward on these bonds (Movie S4). The complete loss of rear adhesions immediately after pseudopod attachment can also be seen in the kymograph of axial stresses (Fig. 4 B3, single asterisk). Although contraction of cell length was expected through localization of adhesions, nontrivially we also observe recycling of the front adhesion site to a back adhesion site at the same location on the surface (Fig. 4 B3, double asterisks).

The lengthening-shortening event, the complete loss of rear adhesions, and the recycling of adhesion sites suggest that this model is closer to reproducing the stepping locomotion observed in amoeboid cells. For the model to capture features of amoeboid migration, we had to assume adhesions exist only at the cell periphery, corresponding to regions of elevated axial stresses. The presence of adhesions only in regions of large stresses is also supported by traction force microscopy imaging data (8, 12, 33).

Periodic length changes emerge from a mechanosensitive cell-surface interaction

One way to achieve adhesion formation only in regions of elevated forces is by allowing bonds to form in response to an applied external load. In fact, some biological adhesive bonds are force-sensitive and can weaken (slip bonds) or strengthen (catch bonds) with applied force (34). In particular, catch bonds are characterized by the physical property that at intermediate forces their lifetime increases with increasing force. Such bonds are found in α₅β₁-integrins involved in adhesion of human-derived lymphoma cells (35) but also in cadherins that mediate cell-cell adhesion (36). This description can be modeled in different ways and here we follow the form given by Novikova and Storm (37). To incorporate force-sensitive bond kinetics, we add an equation for the time-evolution of the bond density in our existing mechanical model of a crawling cell, as follows:

$$\frac{\partial }{\partial t}N\left(t,s\right)=k^{+}{\eta }_0\left(1-N\right)-k^{-}N\text{exp}\left(-\frac{\alpha \left|\mathit{F}\right|/N}{k_{\text{B}}T}\right).$$ (5)

The first term represents the formation of new bonds at a rate proportional to a constant binding rate, k⁺ (M⁻¹ time⁻¹) and an unsaturated substrate ligand concentration, η₀ (M). The second term represents force-dependent unbinding with a zero-force unbinding rate, k⁻ (time⁻¹), and a microscopic length scale characterizing the unbinding transition, α. The explicit Euler time integration scheme is used to evolve Eq. 5 at every discrete point on the ventral part of the cell, and the updated bond density is then used to compute the adhesion force in Eq. 4 locally and at every time instance.

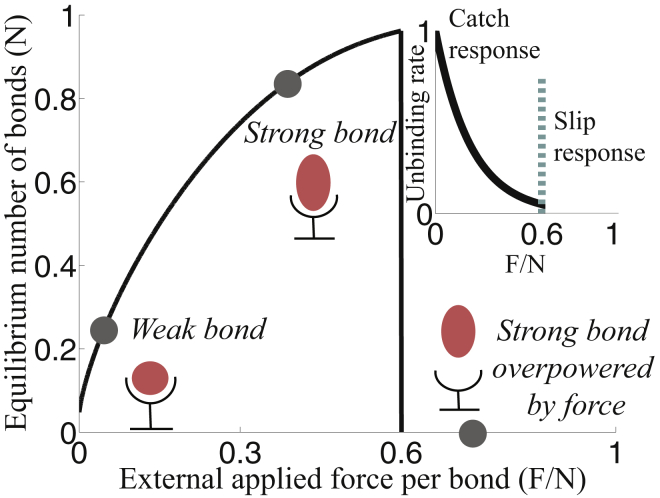
Additionally, our model for cell-surface interaction includes the slip response of bonds through F_critical in Eq. 4; if the external force exceeds a threshold load, bonds immediately rupture. Under these assumptions, we find that at a low applied force, the steady-state bond density is nearly zero, but as force increases, the bond density should increase as well, mimicking the physical property that the bond lifetime increases with increasing force (Fig. 5). The addition of a time evolution equation for the bond density in response to an applied load reproduces the observation that Dictyostelium adheres to the surface in regions of large forces.

Figure 5.

Shown here are the dynamics of force-sensitive bonds in a single adhesion site. Equilibrium number of bonds per adhesion site is given as a function of the external applied force per bond. The inset shows the unbinding rate of a bond as a function of the applied force density. Distinct points are identified in both plots for different values of applied force density: |F|/N = 0.1 (low), 0.3 (intermediate), and 0.75 (exceeds threshold load). To see this figure in color, go online.

Upon including mechanosensitive bond kinetics for uniformly spaced adhesions in our model, the emerging motility is reported by the spatiotemporal patterns of the axial traction stresses and the time evolution of the cell length (Fig. 6; Movie S2). We chose values for adhesion parameters, k⁺, k⁻, and F_critical (Table S1), to match the experimentally measured migration speed and we found that the values for these adhesion parameters are comparable to those in other cell types (Table S2). A parameter exploration is discussed later. We find high density bonds localized at the cell periphery, with distinct and recycled adhesion sites seen by the horizontal patches in the kymograph, and periodic oscillations in cell length; these are all characteristics of stepping amoeboid motility presented in the experimental measurements in Fig. 1, A and B. The simulated cell moves at a roughly constant speed of 11 μm/min (the reported values for Dictyostelium are 9–12 μm/min (3)). The cell undergoes repetitive lengthening-shortening cycles with a period of ∼1 min (the reported period for Dictyostelium is 0.93 min (12)) and an average amplitude of 6 μm. With a periodicity similar to the period of the motility cycle (∼80 s), a fixed location on the surface identified as a front adhesion site is recycled to a rear adhesion site (Fig. 6, asterisk). These distinct, recycled adhesion sites and periodic oscillations in cell length emerge as a result of the cell geometry, mechanical response of the cell, and force-sensitive interaction with the surface. The transmission of leading edge forces to rupture back adhesions in a coordinated manner is still established through the mechanical response of the membrane-cortex structure. The instantaneous patterns of three-dimensional (3D) traction stresses continue to resemble the spatial arrangement of the experimental 3D traction stresses in Dictyostelium (Fig. 6 A, inset).

Figure 6.

Stepping locomotion is observed in a simulated cell with mechanosensitive cell-surface interaction. (A) Given here is a kymograph of the tangential traction stresses as a function of the position along the cell trajectory at a given time. The inclined lines indicate the instantaneous position of the front and rear cell edges whereas the dashed line represents the cell centroid position. The black outlines are hypothetical cell outlines. The asterisk shows evidence for recycling adhesions; adhesion sites are fixed on the substrate during a motility cycle. The inset shows the instantaneous spatiotemporal patterns of the tangential (left) and normal (right) traction stresses at t = 585 s. (B) The time evolution of the cell length shows periodic extension-contraction events with a period of ∼1 min and an average amplitude of 6 μm. To see this figure in color, go online.

Stride length does not depend on cell mechanical parameters

We performed a series of simulations with perturbations to cellular mechanical parameters. By varying the resting tension, the elastic spring constant, and the strength of polymerization (i.e., ρ₁) individually, we obtain the averaged cell length, period of motility cycle, and migration speed (Table S2). Based on these observations together with visual inspection of kymographs of traction stresses, we report that cells exhibit either stepping locomotion or get stuck to the surface.

The mean speed of migration is plotted as a function of the frequency of the motility cycle to reveal a linear scaling, v = λ f (Fig. 7). The constant of proportionality, λ, represents the average step length advanced by the cell per cycle and it suggests that cells perturbed from baseline parameters not only use stepping motility, but do so by preserving their stride length, λ = 12 μm. The model observation that stride length is preserved across parameter perturbations is also reported in biological mutants (Fig. 1 D) (10, 19).

Figure 7.

Cell speed dependence on frequency of motility cycle is given. Shown is a scatter plot of the average migration speed versus the frequency of the motility cycle for simulated cells with various perturbations to mechanical parameters. The solid line is the least squares fit to the data, v = 12f. To see this figure in color, go online.

Three of the perturbations to mechanical parameters show that cells get stuck to the surface. A decrease of the resting tension in the model weakens the transmission of leading edge forces to rupture back adhesions, resulting in immobility. Similarly, lowering the leading edge forces inhibits migration because the driving forces need to be large enough to overcome adhesion to the surface. In the Supporting Material, we show that decreasing either the threshold rupture load (F_critical) or the pseudopod attachment length (L_pseudopod) parameter from its baseline value results in a smaller stride length.

Phase diagram of emergent migration modes

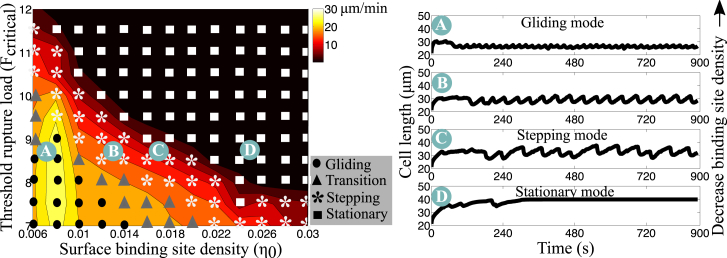
Next, we performed a series of simulations to establish how the adhesion parameters affect migration in our model. The cell mechanical parameters are held constant and two adhesion parameters are varied: the surface binding site density, η₀, and the threshold rupture force, F_critical. By simultaneously varying these two adhesion parameters, we obtain contour plots of the mean cell speed (Fig. 8). In the 2D parameter-space exploration, we visually identified three emergent motility modes based on the time-evolution of cell length: 1) a gliding mode characterized by oscillations with average amplitude <2 μm; 2) a stepping mode characterized by oscillations with average amplitude between 5 and 8 μm; and 3) a stationary mode characterized by an average migration speed <2 μm/min. Based on this classification, we constructed a phase diagram of migration modes on top of the contour plots of average cell speed (Fig. 8).

Figure 8.

Simulated average cell speed is shown as a function of two adhesion parameters. Cell migration speed is reported as a function of two adhesion parameters: the threshold rupture load (F_critical), and the surface binding site density (η₀). The symbols indicate the emergent migratory modes: circle, gliding mode; star, stepping mode; and square, stationary mode (speed below 2 μm/min). Triangles indicate transition between gliding and stepping modes. For a fixed threshold rupture load, F_critical = 8.5 a.u., we vary the surface binding site density and report the cell length over time in (A)–(D). The surface binding site density is (A) η₀ = 0.006 (gliding mode), (B) η₀ = 0.012 (transition), (C) η₀ = 0.016 (stepping mode), and (D) η₀ = 0.024 (stationary). To see this figure in color, go online.

To mimic biological experiments with different substrate coatings, we consider the resulting motion due to variations only in the surface binding site density (Fig. 8, A–D; Movie S3). At low binding site density, the cell cannot initiate a motility cycle because the low bond formation prevents pseudopod attachment to the surface. When the binding site density is increased, the cell shows gliding-like motility with small length changes and traction stresses similar to Fig. 3 A, in particular no evidence of recycling of adhesion sites. As the surface binding site density is further increased, we observe a switch in the motility mode from gliding to stepping. The mean cell speed decreases, the amplitude of the oscillations in length increases, and patterns of stationary and recycled adhesion sites emerge in the kymograph of axial stresses. When binding site density is further elevated, the cell cannot overcome adhesion forces to rupture back adhesions and the cell is stuck to the surface. The transition in motility modes from gliding to stepping to stationary reflects the competition between the elastic response of the cell and the cell-substrate adhesion. In the fast motility mode (i.e., gliding), the cell crawls using short-lived adhesions that do not exhibit force-sensitivity, but when adhesion forces are considerably stronger, the cell cannot rupture adhesions and remains stuck to the surface. Step-like locomotion emerges when the adhesion parameters are in a range similar to the strength of the elastic response. Similar transitions can be obtained by varying the other adhesion parameters.

Our model predicts that gliding motility occurs when adhesions are weakened (Fig. 8, bottom-left corner). Because we cannot perform experiments with different ligand concentration, we analyzed experiments with talin A-null Dictyostelium cells. Talin A is an actin-binding cytoskeletal protein capable of anchoring the actin cytoskeleton to adhesion proteins (38). Whereas in animal cells talin constructs and regulates focal adhesions, in Dictyostelium it may be involved in the control of motility as defects in cell-surface interaction are observed in moving cells (39, 40). Preliminary data shows that talin A-null cells move faster and with smaller length changes than wild-type cells (Fig. S7), which suggests these cells glide. This experimental result is similar to our model prediction that Dictyostelium cells establishing weaker cell-surface interaction employ a gliding-like motility mode.

Discussion

The existing paradigm for the locomotion of Dictyostelium, a model organism of amoeboid motility, has been proposed to be the result of complex biochemical and biophysical processes coupled to biomechanics (3). Here, we show that a simple mechanochemical model could explain the observed phenomena of amoeboid motility: periodic morphological changes, the spatiotemporal dynamics of 3D traction stresses, adhesive sites that are fixed on the surface and recycled through a motility cycle, and the emergent step-like locomotion with preserved stride length across mechanical perturbations. To capture all of these complex, highly synchronized features, we needed to incorporate the mechanical response of the membrane and cortex, force-sensitive actin-driven polymerization, and force-sensitive interaction with the surface. Despite the coarseness of our simple model, perturbations to the mechanical model parameters impact the frequency of the motility cycle and the migration speed consistent with experiments. In particular, simulated cells perturbed from baseline parameters continue to crawl in a stepwise manner by conserving the stride length. We further find that the mode of the movement could evolve in response to surface properties: for small availability of surface binding site, cells use a gliding mode with small-amplitude oscillations in length; a stepping mode is found at intermediate binding site density; and a stationary mode is observed when the availability of binding sites is too large. The three behaviors have been observed in experiments of motile Dictyostelium cells but here we show that cells mediate the transition from one mode to another in response to properties of the environment. Further, we find that the migration of talin A-null cells, which display weak anchoring between adhesions and cytoskeleton, is consistent with our model prediction for low surface binding site density. We also find that a gliding motion is exhibited by simulated cells with cell-substrate adhesion modeled by only slip bonds with a sharp rupture threshold (shown in Fig. 3 A). This model result is also observed in Dictyostelium cells with enhanced nonspecific adhesion, such as on poly-L-lysine-coated surfaces (Fig. S6).

Three mechanisms have been proposed to contribute to amoeboid cell migration: actin polymerization, myosin-mediated contraction, and force from osmotic pressure (3). Our model includes force-dependent polymerization at the leading edge, and pressure, which ensures volume conservation but does not drive motility. Contraction enters our model through resting tension in the membrane-cortex but is not coordinated explicitly. Although it has been suggested that myosin II motor proteins mediate the contraction phase, myosin II-deficient Dictyostelium cells continue to employ cyclic oscillations between extension and retraction phases (15, 41, 42). This suggests that perhaps a different machinery might be responsible for the coordinated rupture of rear adhesions. Here, we explore this hypothesis by including neither a contraction at the cell rear due to myosin II motors nor a biochemical synchronization between the cell front and rear. We find that the front-to-back communication could be achieved through the mechanics of the membrane-cortex structure only. The polymerization forces at the leading edge cause the cell to deform and thus, exert pulling forces on the cell-substrate adhesions at the rear. Further, we observe that simulated cells with weakened tension continue to crawl but with a slower speed and a longer period of migration (Fig. 7). Although this does resemble the behavior reported in myosin II null cells (Fig. 1 D), myosin II motors serve multiple functions including contraction and actin cross linking, and thus direct comparison between our mechanical perturbation to tension and myosin II null cells is difficult. Slower locomotion is also experimentally reported with decreases in polymerization activity. Dictyostelium cells lacking the SCAR protein, an upregulator of the branched F-actin nucleation complex Arp2/3 (43), exhibit decreased dendritic polymerization of F-actin at the cell front (42). These mutant cells undergo motility cycles of decreased frequency and have slower migration speeds (Fig. 1 D). This observation is consistent with variations in the rate of polymerization parameter, ρ₁, in the model (Fig. 7).

Our model highlights the necessary components for amoeboid locomotion and their spatiotemporal coordination through mechanics. The effects of biochemical signaling and myosin-mediated contraction at the cell rear may be important for other biological functions, but we find that those are not required to produce amoeboid motility in our model. Recently, other models have highlighted the relevance of mechanics alongside biochemistry in understanding cellular processes. The model in Wolgemuth (44) demonstrates that a simple model incorporating stick-slip adhesions and contractile forces is sufficient to capture the emergence of periodic lamellipodial contractions. Another model coupled actin retrograde flow with interaction with the substrate to reveal the mechanism of how a cell is able to sense and respond to the physical properties of the local environment (22). Here, we contribute to this line of work by illustrating how the mechanical cellular components achieve coordination at the cellular level to give rise to periodic oscillations in cell length and stepping locomotion observed in crawling amoeboid cells.

One emergent characteristic of our model is the localization of tangential traction stresses and adhesions and their apparent spatial recycling seen by the horizontal patches in kymographs. However, we do differ from experiments in that during any particular phase of the motility cycle we have three or four distinct adhesion sites rather than the two or three as reported experimentally. We attribute this difference to the simplified model of the actin cytoskeleton: in our formulation, the cytoskeleton transmits the leading edge forces to the surface on the entire region of contact. A more detailed spatial model of the transmission of forces in the cytoskeleton would not change the main results of this work, specifically the emergent cycles of morphological extension and retraction, distribution of 3D traction forces, or spatiotemporal adhesion patterns from a mechanosensitive cell-surface interaction. Similar results are also observed with a gradual slip response rather than the sharp threshold response we presented originally in Eq. 4 (S6).

Any form of cell locomotion must rely on the interaction of the cell with the surface to enable pseudopod extension and retraction of the cell rear, and in Dictyostelium the molecular basis for this interaction is unknown. Specifically, the Dictyostelium genome does not carry genes for integrins or any of the other extracellular matrix proteins (45). There has been evidence to suggest that actin foci act as the active “feet” of Dictyostelium (8). Actin foci are dynamic structures localized at the ventral surface of cells and are coordinated with the repetitive cycles of morphological extension and retraction that occur during migration. Interestingly, the foci are fixed on the surface during migration and are found in regions where significant traction forces are exerted on the substratum (8). Our force-sensitive description of cell-substrate interaction is consistent with the existing hypothesis about actin-foci “feet”. Although our prediction does not imply a specific adhesion complex, we propose that this interaction must have a force-sensitive response to produce the reported spatiotemporal dynamics of traction stresses and the periodic cycles of morphological changes. Although the role of specific adhesion versus nonspecific adhesion in Dictyostelium is still unclear (45), altering mechanosensing in these cells has been shown to be important in adhesion to the substrate and migration speed (46). Our work suggests that amoeboid motility shares many key features with the motility of higher eukaryotic cells, including, for example, the formation of catch bond adhesions seen in integrins. It remains to be seen whether this mechanosensitive interaction with the surrounding is also the underlying mechanism for the experimental observations of a bimodal relationship between motility speed and the stiffness of the extracellular matrix for 3D amoeboid migration.

Author Contributions

C.A.C., J.C.d.Á., and R.D.G. designed the project. C.A.C., S.W., and R.D.G. developed the model with input from A.M. C.A.C. performed and analyzed the computer simulations. J.C.d.Á. and E.B. performed and analyzed the biological experiments.

Editor: David Odde.

Supporting Material

Movie S1. Simulated Cell Exhibits Gliding-like Motility when Cell-Surface Interaction Is Modeled by Linear Springs

Top panel shows the instantaneous cell outline along with the axial traction stresses. The inset is a zoom-in view of the ventral part of the cell to show the spatiotemporal dynamics of adhesions. Cell length is plotted as a function of time in the bottom panel.

Movie S2. Stepping Locomotion Is Exhibited by a Cell with Mechanosensitive Adhesions to the Surface

Top panel shows the instantaneous cell outline along with the axial traction stresses. The inset is a zoom-in view of the ventral part of the cell to show the spatiotemporal dynamics of adhesions. The color and width of the adhesion links is linearly scaled to the bond density; a black link corresponds to full occupancy, i.e., N = 1, and lighter, thinner links indicate low-density bonds. Cell length is plotted as a function of time in the bottom panel.

Movie S3. Transitions in Emergent Motility Modes Are Reported as a Function of the Surface Binding Site Density

For different surface binding site densities, the left-hand side plots show the time evolution of cell length whereas the right-hand side plots show the instantaneous cell outline along with the axial traction stresses. Four different values of surface binding site density are considered in order of increasing value: η₀ = 0.006, 0.012, 0.016, 0.024. At low binding site density (top panel), the average cell speed is 20 μm/min and the motion shows small amplitude oscillations in length changes. The identification of the motility mode as gliding is based on the small amplitude of morphological changes (<2 μm). As binding site density is increased, we observe a switch in migration mode from gliding to transition (second panel) to stepping (third panel). The identification of the motility mode as stepping is based on the amplitude of morphological changes (average amplitude between 5 and 8 μm). The mean cell speed decreases whereas the amplitude of length oscillations increases. If binding site density is further increased, the cell does not migrate across the surface and its length reaches a plateau value. The motility mode is classified as stationary because the average speed is <2 μm/min.

Movie S4. Simulated Cell Exhibits Recycling of Adhesion Sites when Cell-Surface Interaction Is Modeled by Nonuniform Linear Springs

The movie shows the instantaneous cell outline along with the axial traction stresses for a cell adhering to the surface only near the cell front and rear. At the end of the motility cycle, what was initially the front adhesion site is now located at the rear of the cell and the cell pulls upward and inward on these adhesion bonds.